Probing the Role of Dynamics in Hydride Transfer Catalyzed by Lactate Dehydrogenase

Abstract

The dynamic nature of the interconversion of pyruvate to lactate as catalyzed by lactate dehydrogenase (LDH) is characterized by laser-induced temperature jump relaxation spectroscopy with a resolution of 20 ns. An equilibrium system of LDH·NADH plus pyruvate and LDH·NAD⁺ plus lactate is perturbed by a sudden T-jump, and the relaxation of the system is monitored by NADH emission and absorption changes. The substrate binding pathway is observed to be similar, although not identical, to previous work on substrate mimics: an encounter complex is formed between LDH·NADH and pyruvate, which collapses to the active Michaelis complex. The previously unresolved hydride transfer event is characterized and separated from other unimolecular isomerizations of the protein important for the catalytic mechanism, such as loop closure, a slower step, and faster events on the nanosecond-microsecond timescales whose structural basis is not understood. The results of this study show that this approach can be applied quite generally to enzyme systems and report on the dynamic nature of proteins over a very wide time range.

INTRODUCTION

Modern paradigms for enzymatic catalysis all include atomic motion of the catalyst and reactants, either implicitly or explicitly. Binding of a substrate to form the Michaelis complex involves certain kinds of motions of various molecular groups within the protein: formation of encounter complex(es), movement of the substrate toward the enzyme active site, desolvation of substrate, and often loop or flap closure or domain motion. Once the Michaelis complex is formed, movements of atoms and groups at the binding site occur to bring about the proper catalyzed chemistry and achieve these catalytic states with the incredible rate enhancements approaching 10¹⁸ relative to uncatalyzed reactions. Atomic motion on all timescales, from femtoseconds to seconds, can be important for an enzyme to carry out catalysis (1,2).

There are several reasons why so little is understood about the dynamic nature of proteins and how this is coupled to function. One is simply that much of the protein's atomic motion may not be obviously relevant to function. Much atomic motion of any finite assembly held together by noncovalent forces will be stochastic in nature, although it is clear that enzymes “use” such motion mechanistically, all the while restricting the system's degrees of freedom to bring about catalysis. Another, perhaps more important reason, is that there are a paucity of experimental and theoretical approaches that can adequately cover kinetics over the wide range of timescales of enzymatic catalysis. For experimentalists, the faster timescales below a millisecond are particularly problematic, although there has been substantial technical development over the past decade in characterizing submillisecond events in proteins (see, e.g., Callender and Dyer (3) and Palmer (4)).

We are interested in the mechanism of the enzyme l-lactate dehydrogenase (EC 1.1.1.27, LDH), which catalyzes reduction of pyruvate by NADH to produce lactate and NAD⁺. The reaction proceeds sequentially: the NADH cofactor binds first to the enzyme, followed by substrate binding, structural and chemical rearrangements, lactate release, and finally NAD⁺ dissociation. Neglecting the cofactor binding steps, the minimal kinetic model is given in Eq. 2 below. The chemical step of the on-enzyme reaction includes direct stereospecific transfer of a hydride ion from the C2 carbon of lactate to C4 of NAD (Fig. 1), and a proton is assumed to be transferred from the lactate hydroxyl to N3 nitrogen of His-195 (5–7). The catalytic act requires significant conformational changes to properly position the substrate and coenzyme, to bring interacting molecular groups to the right places at the right times, and to produce the electric field configuration most favoring catalysis (8). One event that has been kinetically characterized is “loop closure”, occurring on the millisecond timescale, whereby a surface polypeptide loop (residues 98–110 in pig heart LDH) closes over the active site after substrate binding and opens to release the product (9,10). This structural rearrangement is generally taken as the rate-limiting step (10). Hydride transfer appears to proceed faster because no H/D primary isotope effect is observed in stopped-flow studies of the enzyme chemical kinetics. The rate of the chemical step has not yet been measured reliably.

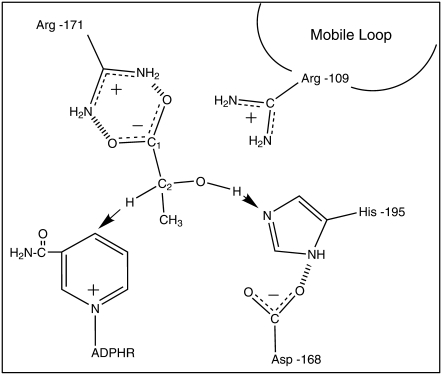
FIGURE 1.

Cartoon of the important active site molecular groups for the LDH-catalyzed reaction from the lactate side. A hydride ion is transferred from lactate to NAD⁺, forming NADH, and a proton moves to His-195.

To study the dynamics of LDH (and nearly all enzyme-catalyzed reactions), specialized techniques are needed because, apart from loop closure, the dynamic nature of this enzyme reaction involves fast, submillisecond atomic motions, including the key hydride transfer step. Observation of kinetics at submillisecond timescales is achieved here by employing laser-induced temperature-jump relaxation spectroscopy, an approach that in perspective may provide resolution on the picosecond timescale (11–13). The relaxation spectrometers employed in this study have a resolution of ∼10 ns. T-jump relaxation experiments monitor the return to equilibrium of a chemical system after a sudden increase in temperature, produced in our studies by absorption of pulsed laser light tuned to a weak near-infrared water band.

Therefore, if it is possible to set up the lactate dehydrogenase system as a reaction system of interconverting species, where at least some of the species are well populated (as will be shown below), then relaxation methods can probe the kinetics of interconversion. One advantage to relaxation studies, besides vastly superior time resolution and general applicability, is that, in a kinetic system like that above where there are fast (such as hydride transfer) and slow events (such as loop closure), fast events relax before slow steps. Hence, they can be observed in relaxation studies because they are not being “masked” by rate-limiting slow features as can often be the case in studies employing slower mixing approaches. The approach taken here is quite novel and should provide a general methodology in studies of protein dynamics.

Relaxation studies rely on suitable spectroscopic probes to follow evolving structure. In this study, both transient NADH visible fluorescence emission and UV absorption measurements are performed. Pyridine nucleotide-dependent dehydrogenases are convenient objects for spectroscopic studies because NADH produced in the catalyzed reactions has characteristic absorption and fluorescence properties that allow it to be reliably monitored. Thus, the chemical hydride transfer event shows up well in absorbance measurements. The absorption band of NADH with a maximum near 340 nm is practically unaffected by binding to enzymes and is therefore a probe for total NADH concentration. On the other hand, fluorescence emission of NADH is very sensitive to enzyme and substrate binding because the NADH emission quantum yield strongly varies when LDH binds NADH.

We have performed a number of studies recently on the dynamic nature of substrate binding to LDH, using T-jump relaxation spectroscopy so that fast timescales were probed. The substrate pyruvate was replaced by an excellent substrate mimic, oxamate (NH₂(C=O)COO⁻), so that atomic motion associated with the binding pathway can be separated from that associated with chemical steps occurring during catalysis. The results suggest that LDH·NADH occupies a range of conformations, some competent to bind substrate (“open” structure; a minority population) and others noncompetent (“closed”), in fast equilibrium with each other in accord with a “select fit” model of binding (14,15). It appears that the two species differ in the rearrangement of low-energy hydrogen bonds as would arise from changes in internal hydrogen bonding and/or increases in the solvation of the protein structure. The binding competent species binds ligand to form an “encounter complex” at or very near diffusion-limited speeds, suggesting that the binding pocket is substantially exposed to solvent in these species. This would be in contrast to the putative “closed” structure in which the binding pocket resides deep within the protein interior.

These studies also suggest that binding may take place along several distinct pathways so that the “encounter complex” may represent a range of conformations. Once the encounter complex is formed between the open structure and the substrate, the protein-ligand complex appears to fold to form a compact productive complex in an all-or-nothing-like fashion with all the important molecular interactions that make up the catalytic binding pocket coming together at the same time (16–18). Because the current study probes the entire dynamic pathway, both binding and the chemistry, in one set of measurements, the previous work will serve to help disentangle binding steps from kinetic events associated with the chemical transformation of on-enzyme substrate to product.

METHODS AND MATERIALS

Laser-induced T-jump

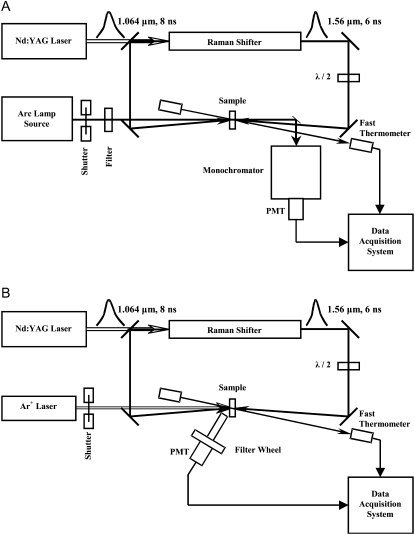
To study the LDH-catalyzed reaction, we first allow the system to come to equilibrium at some initial temperature. The sample temperature is rapidly changed (T-jump), and the relaxation kinetics of the system is probed by optical absorption or fluorescence emission as the system reestablishes at its new higher temperature. For such studies, we have built a laser-induced T-jump experimental setup (Fig. 2) that can raise the temperature within a small volume of sample in ∼10 ns. This temperature jump is produced by irradiating the sample with pulsed infrared (IR) emission at 1561 nm wavelength, in a weak absorption band of water. The absorption coefficient at this wavelength, α₁₅₆₁ = 0.95 cm⁻¹ (19,20), is high enough to produce a noticeable temperature jump, yet low enough to produce a jump sufficiently uniform in a sample of 0.5 mm thickness. The sample is heated in the irradiated spot of 1–1.5 mm diameter by 5–20 K. The necessary IR emission is generated by Raman shifting the fundamental (1064 nm) of a Powerlite 7010 Q-switched Nd:YAG laser (Continuum, Santa Clara, CA). The Raman shifter cell, model 101 PAL-RC (Light Age, Somerset, NJ), has a 1-m path length and is filled with deuterium gas at 650 psi. Both forward- and back-scattered beams from the Raman shifter are directed toward the sample from two sides to obtain a more uniform longitudinal heating pattern. Polarization of the forward beam is rotated by 90 degrees to avoid Bragg grating formation inside the sample. The sample temperature after the jump is monitored over time by probing changes in water IR absorption at 1460 nm.

FIGURE 2.

Optical layouts of the laser-induced temperature-jump relaxation spectrometers. The top diagram shows the absorption spectrometer, and the bottom one illustrates the fluorescence spectrometer. Both forward- and back-scattered beams from the Raman shifter are directed toward the sample from two sides to obtain a more uniform longitudinal heating pattern. Polarization of the forward beam is rotated by 90° to avoid Bragg grating formation inside the sample.

To monitor UV-Vis absorption changes in the sample, a collimated and sharply (∼0.5 mm) focused beam of light from a Photomax arc lamp source (Oriel Instruments, Stratford, CT) with a 75-W Xe lamp is passed through the heated spot of the sample and then directed to a monochromator (model 270M, Instruments SA, Edison, NJ) with an H6780-03 photomultiplier tube module (Hamamatsu, Bridgewater, NJ). The light incident on the sample is prefiltered with a wide-band optical filter. When fluorescence detection is used, the fluorescence is excited by an Innova 200 Ar-ion laser (Coherent, Palo Alto, CA) emitting a group of lines near 360 nm (351.1 and 363.8 nm), or near 300 nm (300.3 and 302.4 nm). The excitation beam is focused on the sample in a spot of ∼0.3 mm diameter, in the center of the IR-heated spot. The fluorescence emission is collected at ∼50°. This light, after passing through a three-lens spatial filter with a narrow-band interference filter in the parallel part of the beam, is detected by a R4220P photomultiplier tube (Hamamatsu). To select NADH fluorescence, we used a 450 nm narrow-band filter with the bandwidth of 40 nm FWHM. The signal from the photomultiplier tube, after a laboratory-made transimpedance preamplifier with 3-ns response time, is sent to a CS82G digitizing PCI board (Gage Applied, Lachine, QC, Canada) for data acquisition at 1 GS/s sampling rate. The absorption signal from a photomultiplier tube module with a similar preamplifier is further amplified five times with SR445 fast amplifier (Stanford Research Systems, Sunnyvale, CA) and sent to another input of the same digitizing board. The incident intensities of the excitation or absorption beam, and of the fast IR thermometer transmitted beam, are measured with photodiodes (Thorlabs, Newton, NJ), and the signals are acquired with CS1450 digitizing PCI board (Gage Applied). To avoid sample bleaching under strong illumination with excitation or absorption beam, a Uniblitz shutter (Vincent Associates, Rochester, NY) opens the beam a few milliseconds before the heating pulse and closes it 1 ms after the end of data acquisition. Timing of all events is determined by a DG535 delay generator (Stanford Research Systems) controlled from a computer via a GPIB interface. The water bath controlling sample temperature, the thermocouple thermometer measuring it, and the 270M monochromator all communicate with the computer via an RS232 serial interface. For the computer control of the setup, a laboratory-made program is used written in LabVIEW (National Instruments, Austin, TX). The T-jump kinetic response from pure buffer, measured in a special series of experiments, was subtracted from all absorption kinetics.

Steady-state absorption spectra were measured on a Beckman DU7400 spectrophotometer (Beckman Instruments, Fullerton, CA). Measurements of steady-state fluorescence spectra were performed with a Fluoromax-2 spectrometer (Instruments SA).

Materials

Pig heart LDH (Roche Diagnostics, Indianapolis, IN) was dialyzed at 4 C in 8000 MWCO SpectraPor 7 tube (Fisher Scientific, Pittsburgh, PA) against pH 7.55 0.1 M Tris-HCl buffer (enzyme grade, UltraPure, GIBCO BRL Life Technologies, Gaithersburg, MD) three times for 20–25 h for each run, then concentrated using Centricon YM-10, 10,000 MWCO regenerated cellulose filters (Millipore, Bedford, MA). NAD⁺ free acid and NADH sodium salt, both Grade 1, 100% purity (Roche Diagnostics), l-lactate sodium salt, 98% purity (Sigma Chemical, St. Louis, MO), C2-deuterated sodium-l-lactate, 98.7% atom D, 98.5% chemical purity (C/D/N Isotopes, Pointe-Claire, QC, Canada), and pyruvate monosodium salt (Boehringer, Mannheim, Germany) were used as received. Fresh solutions of all reagents were prepared for each experiment.

The equilibrium in the LDH-catalyzed reaction is strongly shifted to the lactate/NAD⁺ side, and the solution equilibrium constant is

(1)

Therefore, to observe any significant changes in the concentration of NADH, the reaction requires excess lactate and NAD⁺. In the kinetic measurements, lactate concentrations were mainly in the range 2–10 mM, which is well below the self-inhibition level of 26 mM (21), and NAD⁺ concentration was 0.5 mM. To maximize absolute concentrations of bound reagents, we used the highest concentrations of enzyme that did not show signs of aggregation. Usually LDH concentration was ∼0.46 mN (in moles of active sites, given that LDH is a tetramer). The resulting total concentrations of NADH and pyruvate were typically in the range of 100–250 μM. Within the time period of our studies, we did not see any traces of the NAD-pyruvate adduct, which can be produced slowly at high concentrations of pyruvate (22).

RESULTS

In T-jump relaxation spectroscopy, a rapid temperature change of a chemical system in equilibrium results in an out-of-equilibrium condition; the kinetics of the system's relaxation are then monitored as the system responds. For the problem at hand, we are interested in the dynamics of the on-enzyme chemistry of the pyruvate-lactate interconversion catalyzed by LDH as given in the simplified scheme

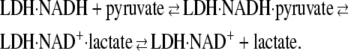(2)

Equation 2 is a minimal description; there may be more steps, as will be demonstrated below. In addition to the existence of on-pathway chemical species not represented in Eq. 2, other side reactions also occur. For example, NADH and NAD⁺ both dissociate from LDH, lactate is known to inhibit LDH·NADH at high concentrations, and pyruvate reacts slowly with LDH·NAD⁺ to form the NAD-pyruvate adduct bound to the protein. The conditions here were chosen to minimize these side reactions while maximizing observation of the chemical step. T-jump relaxation spectroscopy is quite a useful approach to study the kinetics of fast chemical reactions like the hydride transfer step of the LDH on-enzyme interconversion of pyruvate to lactate or fast structural rearrangements of the enzyme·ligand system. In relaxation spectroscopy, fast steps can occur independently of slow steps under favorable conditions and so are not necessarily rate-limited. Moreover, the resolution available to our studies, ∼20 ns, is quite sufficient to resolve even the fastest events.

Steady-state equilibrium

The first goal of the study is to determine the concentrations of various species as a function of various conditions with a view of optimizing signal. The binding constants or Michaelis constants of the reaction in Eq. 2 are known: 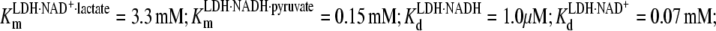and the equilibrium between LDH·NADH·pyruvate and LDH·NAD⁺·lactate is close to 1 so that initial guesses of optimal concentrations are possible. We shall essentially monitor directly the dynamics of the NADH side of the reaction because our probes of structure are the absorbance and emission of NADH; both spectra are isolated from any other absorption and emission features of the protein or NAD⁺. The fluorescence emission of NADH is very sensitive to enzyme and substrate binding: the quantum yield of NADH in solution increases ∼2.5 times on binding to LDH (23,24) and drops ∼10 times on the binding of substrate to the LDH·NADH binary complex (25,26). The absorption of NADH is little affected by whether or not it is in solution or complexed with LDH. Hence, emission studies yield the concentration of the binary LDH·NADH complex, whereas absorption studies yield the total amount of NADH in the reaction mixture, both to good approximation. As mentioned in Methods, the lactate side of this chemical system is substantially more stable than the pyruvate side. Species on the pyruvate side of this system can be populated by saturating the system with lactate. LDH at high concentrations is mixed with high concentrations of NAD⁺, typically in stoichiometric amounts, forming the binary complex LDH·NAD⁺. This minimizes the concentrations of unbound NAD⁺ and NADH in the reaction mixture and also maximizes signal size. The binary complex is then mixed with high concentrations of lactate, and the system is allowed to equilibrate. We found that we could achieve concentrations of ∼500 μM active sites of protein rather routinely (we use throughout the units of “Normality”, N, as active site concentration; pig heart LDH is a homotetramer), which were quite stable for our purposes. Hence, most of our measurements were carried out at close to this concentration of LDH with about the same concentration of total added NAD⁺.

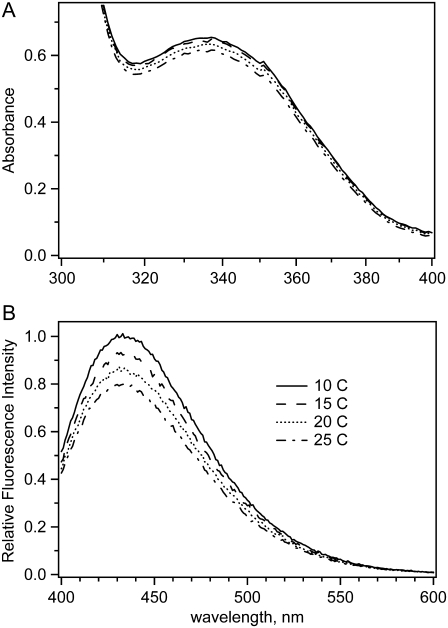
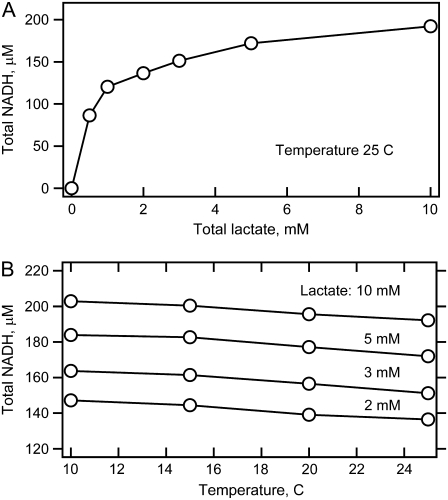
Fig. 3 shows the absorption and fluorescence spectra of the reaction system at equilibrium at initial concentrations of 0.46 mN LDH, 0.5 mM NAD⁺, and 5 mM lactate mixed as described above. From these data and the known values of the absorbance coefficients, the total amount of NADH produced by the reaction is determined. Fig. 4 shows NADH concentration as a function of temperature and the amount of added lactate. As predicted, addition of lactate populates the NADH side of Eq. 2. Most of our studies were carried out at lactate concentrations of 2–10 mM. At 5 mM lactate, for example, ∼0.2 mM total NADH is produced. This leaves 0.3 mM total NAD⁺. Using the literature values for the various binding and Michaelis constants, we estimate the following concentrations: [LDH·NADH] = 50 μM; [pyruvate] = 50 μM; [LDH·NADH·pyruvate]_total = 170 μM, [LDH·NAD⁺·lactate] = 160 μM; [LDH·NAD⁺] = 40 μM. At these conditions, there is little inhibition of the LDH·NADH complex by lactate because the K_I for lactate with LDH·NADH is 26 mM (21). In addition, at these low pyruvate concentrations, the formation of the adduct reaction between pyruvate and NAD⁺ is very slow; the adduct does not form in significant amounts within our measurement time (27). The adduct complex also shows absolutely no dynamic features on the timescales investigated here (22) and cannot yield spurious kinetic signals.

FIGURE 3.

Temperature dependence of (A) absorption and (B) fluorescence spectra of the reaction system: total initial concentrations of LDH 0.46 mN, NAD⁺ 0.5 mM, and lactate 5 mM at pH 7.55. The path length in absorption measurements was 1 cm.

FIGURE 4.

Total concentration of NADH produced in the reaction system with 0.44 mM LDH and 0.5 mM added NAD⁺ as a function of total amount of added lactate and temperature.

For the highest stable LDH concentration, and nearly stoichiometric concentration of NAD⁺, the absorption spectra (as in Fig. 3 A) show a surprisingly small decrease in the total amount of produced NADH on temperature elevation, with the rate: Δ[NADH]/ΔT = −0.77 μM/K, roughly independent of lactate concentration between 2 mM and 10 mM (Fig. 4 B). This rate corresponds to an apparent ∼0.8 kcal/mol enthalpy difference between total LDH·NADH and total LDH·NAD⁺, with LDH·NADH being lower. The corresponding NADH fluorescence spectra (Fig. 3 B) show a stronger intensity decrease than the absorption spectra because of an additional effect of collision quenching. The shapes of both absorption and fluorescence spectra do not change with temperature.

T-jump relaxation kinetics

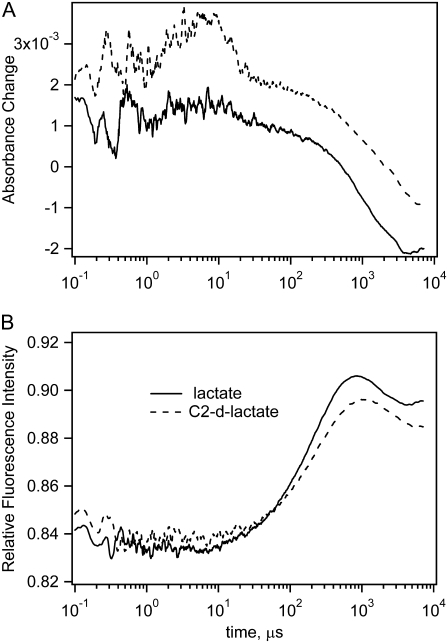
Typical T-jump-induced changes of NADH absorption and fluorescence, spanning five time decades, are shown in Fig. 5 at initial concentrations of 0.46 mN LDH, 0.5 mM NAD⁺, and 5 mM lactate. For total lactate concentrations ranging from 2 to 10 mM, all kinetics exhibit similar features that differ only somewhat in their values of specific rates and amplitudes. The absorption kinetics measured at 340 nm (upper graph) exhibit a nearly single-exponential drop of total NADH concentration, of roughly the same magnitude as that observed in the steady-state spectra. The time constant of this drop varies between 1 and 3 ms, with increasing final equilibrium temperature yielding a faster relaxation time. A minor positive-going amplitude relaxation signal with 100–200 μs time constant is also observed in the absorption results. Fluorescence kinetics, measured at 450 nm with excitation near 360 nm, display a significant rise of intensity in the few hundred microsecond time range, followed by a small drop in the 1–2-ms time range. The intensity rise is similar to that observed earlier for the LDH·NADH·oxamate complex (17). Both pyruvate and oxamate strongly quench NADH fluorescence when bound to LDH. Therefore, fluorescence intensity increases on pyruvate or oxamate unbinding from LDH·NADH. Absorption and fluorescence changes after 5 ms may be affected by cooling of the heated spot because diffusional cooling of the sample occurs with an ∼30-ms time constant. In some of the emission studies, there sometimes appears a fast signal (20 ns − 1 μs) with very low amplitude.

FIGURE 5.

Absorption (upper graph) and fluorescence (lower graph) T-jump kinetics of the reaction system: LDH 0.46 mM, NAD⁺ 0.5 mM, and lactate 5 mM (total initial concentrations). A bump between 1 and 20 μs contains some artifact.

Primary kinetic H-D isotope effect

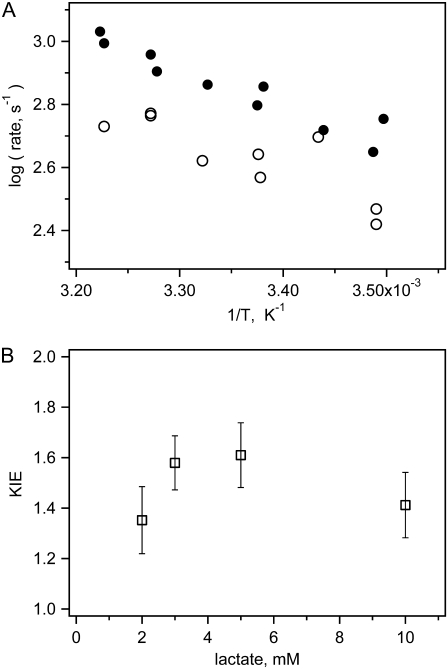
The chemical step is most easily identified because this is the only step that affects absorption changes of the NAD⁺ cofactor (see below). It also shows the effects of deuteration at the C2 position of lactate because this hydrogen/deuteron is the one stereospecifically transferred. Hence, to determine which kinetic features, if any, represent hydride transfer, we performed kinetic experiments using C2 deuterated lactate as a substrate. These reaction systems show similar NADH absorption and fluorescence kinetics, but the kinetic rates of some steps are slower (Fig. 6). For deuterated lactate, the rise of fluorescence intensity in the few hundred microseconds time range is ∼10% slower, and the absorption drop in the same time range is much slower than that for lactate. An Arrhenius plot of the NADH absorption relaxation rates for the 5 mM lactate reaction system with deuterated and nondeuterated lactate is presented in Fig. 7. The kinetic amplitudes do not depend on lactate deuteration, but the relaxation rates are 1.2–1.8 times lower for deuterated lactate. The corresponding values of kinetic isotope effect are shown in the lower graph. To calculate them, we used average values of the relaxation rates from different experiments for each final equilibrium temperature. Our numbers for the deuterium kinetic isotope effect (KIE) are close to the values obtained from maximum steady-state velocity of deuterated NADH oxidation: KIE_D = 1.35 for beef heart LDH, KIE_D = 1.41 for beef muscle LDH (28), and KIE_D = 1.75 for rabbit muscle LDH (29).

FIGURE 6.

Absorption (upper graph) and fluorescence (lower graph) kinetics for reaction systems with LDH 0.46 mM, NAD⁺ 0.5 mM, lactate 5 mM (total initial concentrations) (solid line) or C2-deuterated lactate (dotted line). Temperature jump from 24.0°C to 32.5°C. A bump between 1 and 20 μs in the top graph of the absorption kinetics is an artifact.

FIGURE 7.

Apparent kinetic isotope effect. Upper graph shows kinetic rates for reaction system with lactate (solid circles) or C2-deuterated lactate (open circles) in Arrhenius coordinates for reaction system with LDH 0.46 mM, NAD⁺ 0.5 mM, lactate 5 mM (total initial concentrations). The lower graph shows ratio of average rates for all temperatures as a function of lactate concentration.

Computer simulations

The LDH-catalyzed reaction includes at least seven successive steps, and the kinetic behavior of this reaction system is determined by at least 14 rate constants of which only few are known reliably:

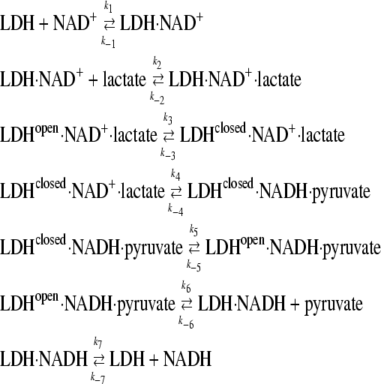(3)

The nomenclature “open” and “closed” refers to conformations of the protein where the surface mobile loop (residues 98–110) is either open or closed; it is likely that there are other protein structural changes that accompany this loop motion. Therefore, it is not possible to resolve, as was done for oxamate binding (17), kinetic equations to obtain the rate constants for particular reaction steps. To obtain an approximate estimate of the individual rate constants for hydride transfer and loop dynamics, we used computer simulations. Gepasi, biochemical reaction simulation program, ver. 3.30 (30–32) allows reconstruction, from known individual rate constants, the kinetic response of a reaction system as it comes to equilibrium from a given initial state.

To simulate experimental T-jump kinetics, we used a two-step procedure. In the first step, we found the equilibrium concentrations of all species at the initial temperature. These concentrations were used as initial conditions for the kinetic simulation. The approach to the new equilibrium is simulated using variable kinetic rate constants at the final temperature. For these simulations, we chose the reaction system with 0.46 mM LDH, 0.5 mM NAD⁺, and 5 mM lactate. Two pairs of absorption and fluorescence kinetics from experiments measured in nearly matching temperature ranges were used for simulating T-jumps from 14.5°C to 23.5°C and from 24.0°C to 32.5°C. We used the following overall simulation strategy. First, an initial guess of the rate constants at 24.0°C was made based on literature data; and, from a simulation run, we found the equilibrium concentrations of all components. Then we adjusted a few of the least reliable rate constants to obtain the correct total NADH concentration. Using the resulting concentrations, we ran an iterative series of simulations to obtain reconstructed kinetics as close as possible to the experimental data. The resulting rate constants for 32.5°C and the initial rates for 24.0°C were extrapolated to 14.5°C, and from simulation, the equilibrium concentrations were found. The rate constants were again slightly adjusted to obtain the correct total NADH concentration at 14.5°C, and the results were used for simulation of the experimental kinetics for T-jump from 14.5°C to 23.5°C. The resulting rate constants for 23.5°C were extrapolated to 24.0°C, equilibrium concentrations were found from simulation, and these results were used for second-approximation simulation of the experimental kinetics for the 24.0–32.5°C T-jump.

To calculate the amplitudes of the fluorescence kinetics, we used the following relative values of the emission coefficients (17): 1, 0.12, 0.09, 0.4 for LDH·NADH, LDH^open·NADH·pyruvate, LDH^closed·NADH·pyruvate, and NADH, respectively. The resulting fluorescence intensity profile was properly normalized for comparison with experimental fluorescence kinetics. With the same purpose, a proper offset was added to simulated absorption kinetics. The simulation results for both nonisotope-edited and C2-deuterated lactate are shown in Table 1. The simulation results are sensitive to the initial approximations for the rate constants, and for many of them only an order of magnitude is known. The kinetic rate constants in Table 1 represent the best fit. Errors of these rate constants, shown in the footnote to the table, were evaluated as standard deviations of their values in the number of nearly successful simulations.

TABLE 1.

Rate constants, barrier heights, and enthalpies obtained from computer simulations of experimental T-jump kinetics

	Lactate				C2-d-Lactate
Rate constants	23.1°C	32.5°C	ΔG‡, kcal/mol	ΔH, kcal/mol	23.0°C	32.5°C	ΔG‡, kcal/mol	ΔH, kcal/mol
k1, M−1s−1	5.8 × 106	6.19 × 106	1.2	0.9	5.8 × 106	6.19 × 106	1.2	0.9
k−1, s−1	500	559	2.1		500	559	2.1
k2, M−1s−1	3.00 × 107	3.043 × 107	0.27	1.7	3.00 × 107	3.043 × 107	0.27	1.7
k−2, s−1	1.05 × 105	1.17 × 105	2.0		1.05 × 105	1.17 × 105	2.0
k3, s−1	430	940	14.8	−0.18	410	860	13.9	0.24
k−3, s−1	217	470	14.7		200	425	14.1
k4, s−1	700	1350	12.5	1.60	372	880	16.2	1.44
k−4, s−1	637	1337	14.1		343	876	17.6
k5, s−1	240	210	−2.5	5.1	355	350	−0.3	3.3
k−5, s−1	520	595	2.6		755	888	3.0
k6, s−1	750	1750	16.1	10.4	545	1430	18.1	8.4
k−6, M−1s−1	1.48 × 107	2.01 × 107	5.7		1.16 × 107	1.95 × 107	9.7
k7, s−1	32	90	19.4	9.5	32	90	19.4	9.5
k−7, M−1s−1	3.3 × 107	5.6 × 107	9.9		3.3 × 107	5.6 × 107	9.9

The reaction system: 0.46 mN LDH, 0.5 mM NAD⁺, and 5 mM lactate or C2-deuterated lactate. Fitting results are shown in bold; all other values are initial approximations. The number of significant digits does not represent precision of the absolute values. The errors evaluated from the spread of values through the number of nearly successful simulations are: k₃, ±40%; k₋₃ and k₋₆, ±30%; k₄ and k₋₄, ±20%; k₅ and k₋₅, ±50%; and k₆, ±15%.

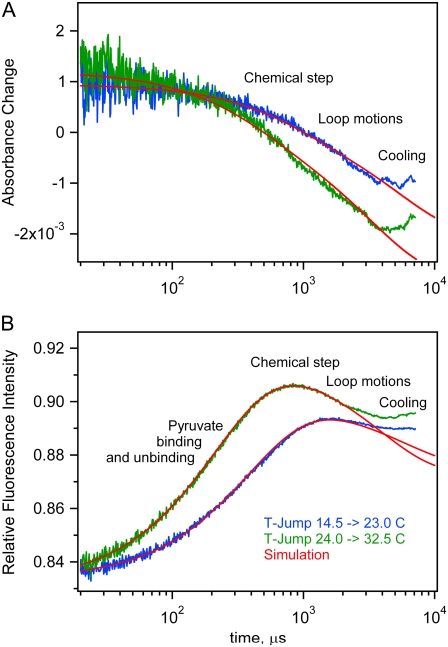
The simulated kinetics are shown as overlays to the data in Fig. 8. In the process of adjustments of the rate constants to obtain best possible fits to the experimental kinetics, we varied the rates of loop dynamics (k₃, k₋₃, k₅, and k₋₅), chemical step (k₄ and k₋₄), and pyruvate unbinding (k₆ and k₋₆). Other processes affect the kinetics much less, and we kept their initial guess values slightly adjusted to get correct equilibrium amounts of total NADH.

FIGURE 8.

Computer simulations of T-jump kinetics for the reaction system LDH 0.46 mM, NAD⁺ 0.5 mM, and lactate 5 mM (total initial concentrations) superimposed on the experimental data. The approximate timing assignments of specific events are loosely placed on the diagrams.

The simulation process offers some tentative assignment of the observed kinetic features to specific reaction steps. To visualize contributions from individual reaction steps into T-jump kinetics, we modulated the kinetic rate constants, one at a time, and determined how this affects the simulated fluorescence and absorption kinetics (see Supplementary Material, Data S1). The absorption drop between 10 and 500 μs depends mainly on the chemical step (k₄ and k₋₄). This might be expected because the chemical step is the only step directly affecting absorption changes and is affected by deuteration of the C2 position of lactate. The tail of the absorption kinetics from 0.5 to 5 ms also depends significantly on the loop dynamics (k₃, k₋₃, k₅, and k₋₅). Pyruvate “off” and “on” rate constants practically do not affect the absorption kinetics, but in fluorescence kinetics, the rise of intensity between 10 and 200 μs almost exclusively depends on pyruvate “off” and “on” rate constants (k₆ and k₋₆). The fluorescence drop near 1 ms is mainly determined by loop dynamics and less by the chemical step.

DISCUSSION

The purpose of this work is twofold. One is to see if temperature jump relaxation spectroscopy can be used to monitor the dynamics of an enzyme system. Our previous work has shown that the kinetics of binding of a substrate mimic can be determined with atomic resolution with the best time resolution that this type of spectroscopy can provide. The current results extend the approach to probe dynamic issues associated with a reacting enzyme system. It appears that this approach can be of rather broad and general use. The only requirement is that the chemical system must contain interconverting species with enthalpy differences, so that a change in temperature will result in the relaxation of the system to a new equilibrium. This condition will likely be met in the large majority of chemical systems.

The second purpose of this work is to learn specifically about the dynamics of the (pig heart) lactate dehydrogenase-catalyzed system. Neglecting binding steps between the protein and cofactor, the following is the kinetic scheme of substrate/product binding/release and chemical steps at 23.1°C (Table 1; bimolecular steps are given in M⁻¹s⁻¹ and unimolecular steps in s⁻¹):

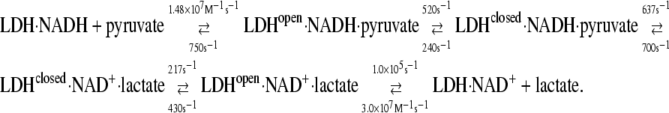(4)

The hydride transfer step has never been resolved for the native enzyme because it occurs too fast for conventional approaches. Hydride transfer has been resolved in either mutated proteins or poor substrates, where the chemical step proceeds relatively slowly (9,33,34). Here, however, the step has been resolved for the native substrate. The chemical step rates from the lactate and pyruvate sides are given by the rate constants k₄ and k₋₄ in Eq. 3, 700 and 637 s⁻¹ at 23.1°C, respectively, with a kinetic isotope effect (k^protonated/k^deuterated) of 1.9 (Table 1). The chemical step is resolved from the slower and previously observed protein isomerization, occurring within a few milliseconds, generally taken to involve the closure of the catalytically important surface loop (residues 98–110) over the active site (10) (other motions are also likely (14)). Previous studies on impaired LDHs or poor substrates have typically yielded a KIE of ∼3 for hydride transfer so that a KIE of 1.9 for the chemical step suggests that the transfer of the hydride is accompanied and partly masked by other motions. We find that the “internal equilibrium constant” consisting of the rate constants involved in the chemical step, k₄/k₋₄, is very close to 1. This is predicted for enzymes like LDH, where catalyzed chemical equilibria are close to 1 within cells (35,36). In fact, it is a necessary requirement to maintain efficient flux through the catalytic pathway.

The results suggest that some very fast molecular motions of the enzyme·substrate complex, important for catalysis, are happening as well. In the datasets, small-amplitude transients were often observed at 20 ns − 1 μs in the NADH emission studies and 100–200 μs time constant in the measurements of NADH absorption, which are associated with unimolecular events of the LDH·NADH·pyruvate complex. These steps, although observed, have not been incorporated into the kinetic scheme of Eq. 4 or in the modeling; it is difficult to characterize quantitatively these transients by the present probes of structure because of their small amplitudes. However, given that these signals are a result of environmental effects on the structure of the reduced nicotinamide ring and the importance of the ring's structure for proper catalysis, these results show that faster timescale motions could play an important role in LDH's mechanism. These could, for example, be a modulation of the ring's structure imposed by the surrounding protein.

For example, it is generally believed that the “active” conformation of the ternary complex has the reduced nicotinamide ring in a conformation in which the angle of the C₄ ring carbon with respect to the other carbon atoms is around 10–15° with the pro-R hydrogen (A side) in a pseudoaxial geometry and the pro-S hydrogen (B side) pseudoequatorial. The pro-R hydrogen is thereby activated for hydride transfer and is brought into very close alignment with the proper side of the substrate's C₂ carbon for hydride transfer. Structural studies of substrate mimics bound to LDH·NADH show that this conformation is that adopted by the bound NADH by a majority of the ternary complex (18,37). However, these same studies also show a minor form of the ternary complex, one where the out-of-the-plane distortion of the C₄ carbon is somewhat less and the pro-S hydrogen adopts a pseudoaxial geometry whereas the pro-R hydrogen is pseudoequatorial. The observed fast transients could be interconversions between such conformations of the ring, such as those between a pseudoaxial pro-R hydrogen, and representative of the protein active site “directing” the complex toward conformations poised for catalysis. The signals that we have observed on the fastest timescales are too small for us to assign structural attributes. However, T-jump relaxation studies employing IR difference spectroscopy are well suited for this purpose (16,18). Such studies are ongoing.

We have performed a number of T-jump relaxation studies on the binding of an excellent substrate mimic, oxamate ((NH₂(C=O)COO⁻), to LDH·NADH (14–18). Enzymatic catalysis can be viewed as involving two separate, but equally mechanistically important, events. One is the shuttling of substrate and product by the enzyme and the formation of the proper structure of the active site; the other is to carry out catalyzed chemistry. The purpose of these studies was to examine in some considerable detail how binding takes place. Studies with substrate mimics can be carried out without chemical events so that binding is studied without that complication. A protein is an inherently dynamic system with an enormous number of possible structures and degrees of freedom. Enzymes must reduce the possible number of structures to a sufficiently small set so that, in a search through the conformation space of the system, on-enzyme chemical catalysis can take place in a timely fashion. At the same time, a substantial amount of dynamic freedom must also remain to permit substrate binding/product release on the same timescale.

We found that binding proceeds via a binding-competent subpopulation of the protein to form a protein-ligand encounter complex. Once the encounter complex is formed between LDH·NADH and oxamate, the corresponding pyruvate species labeled as LDH^open·NADH·pyruvate in Eqs. 3 and 4, this complex appears to “fold” to form a compact productive complex, presumed to be the LDH^closed·NADH·pyruvate complex above, in an all-or-nothing-like fashion with all the important molecular interactions coming together at the same time (18). The production of the catalytically competent protein-substrate-like complex has strong similarities to kinetic pathways found in two-state protein-folding processes. In addition to the productive-like complex, the substrate mimic encounter complex also collapses to a dead-end complex via a branched reaction to form the major populated (productive-like) and minor (dead-end-like) bound species.

In the current studies, which show both binding and chemical steps because actual substrates are employed, the minimal kinetic model required to fit the data included the formation of encounter complex between LDH·NADH and pyruvate and LDH·NAD⁺ and lactate, collapse to form a chemically active species (LDH^closed·NADH·pyruvate and LDH^closed·NAD⁺·lactate in Eqs. 3 and 4), and loop closure/opening steps, all in accord with the substrate mimic studies. What is not observed is the formation of any significant dead-end complex. This, of course, makes sense from the point of view of designing an efficient enzyme (and LDH is quite an efficient enzyme). It is of interest that, whereas oxamate is in almost all ways a very good substrate mimic (it is isoelectric and isosteric to pyruvate; its dissociation constant with LDH·NADH is close to that of pyruvate's K_m; it seems to be placed just right in the binding pocket), the actual dynamics of binding it to LDH·NADH is not quite the same as found for the actual substrate, pyruvate.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.