Quantitative Analysis of G-Actin Transport in Motile Cells

Abstract

Cell migration is based on an actin treadmill, which in turn depends on recycling of G-actin across the cell, from the rear where F-actin disassembles, to the front, where F-actin polymerizes. To analyze the rates of the actin transport, we used the Virtual Cell software to solve the diffusion-drift-reaction equations for the G-actin concentration in a realistic three-dimensional geometry of the motile cell. Numerical solutions demonstrate that F-actin disassembly at the cell rear and assembly at the front, along with diffusion, establish a G-actin gradient that transports G-actin forward “globally” across the lamellipod. Alternatively, if the F-actin assembly and disassembly are distributed throughout the lamellipod, F-/G-actin turnover is local, and diffusion plays little role. Chemical reactions and/or convective flow of cytoplasm of plausible magnitude affect the transport very little. Spatial distribution of G-actin is smooth and not sensitive to F-actin density fluctuations. Finally, we conclude that the cell body volume slows characteristic diffusion-related relaxation time in motile cell from ∼10 to ∼100 s. We discuss biological implications of the local and global regimes of the G-actin transport.

INTRODUCTION

Cell migration is a ubiquitous process underlying morphogenesis, wound healing, and cancer, among other biological phenomena (1). It is based on actin dynamics in cells' protrusive appendages enveloped by the cell membrane (2). In these appendages, actin turns over between networks of filaments (F-actin) and monomers (G-actin) in the cytoplasm. ATP hydrolysis associated with actin cycle produces an asymmetry at the two actin filaments ends, so the filaments are polarized with their barbed, growing ends oriented toward the front and their pointed, shortening ends toward the rear. As a result, actin monomers disassemble from the filament's pointed ends, and assemble onto the barbed ends resulting in the nonequilibrium process of treadmilling. At the front of the cell, the growing barbed ends of the filaments adhering to a substratum abut the leading edge and push it forward until capping proteins block the growth, while nascent filaments replace the capped ones. Meanwhile, the pointed ends disassemble, producing G-actin, which spreads by diffusion and assembles onto the uncapped barbed ends at the front. At the rear of the cell, the cell body is pulled forward by myosin contraction and possibly other, poorly understood processes, completing the cell migration cycle (reviewed in Mogilner and Oster (3)).

Here, we do not discuss adhesion and contraction aspects of the motility process (for reviews, see Vicente-Manzanares et al. (4) and Carlsson and Sept (5)), and concentrate on the treadmilling of the actin arrays. The central quantitative questions about these arrays are: how fast can the steady treadmilling be, what are factors limiting the treadmilling rates, and how rapidly can these arrays reorganize in response to cell signals? The rate of actin monomers' disassembly from the pointed end is 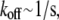whereas the rate of assembly at the barbed end is 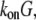where 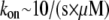and G is the G-actin concentration measured in 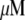units. 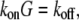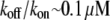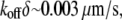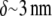Thus, for individual treadmilling filaments, the balance of the assembly and disassembly in the steady state, predicts the so-called critical G-actin concentration in the order of (6) and the treadmilling rate in the order of where is the filament elongation after one monomer's assembly (3). In fact, the rapid cells crawl two orders of magnitude faster (7). This paradox was resolved by the funneling mechanism (8): synergistic action of ADF/cofilin with other actin accessory protein increases the effective disassembly rate about two orders of magnitude. Then, the G-actin concentration 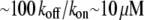can be maintained, and the treadmilling rate 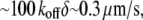in the range of the observed cell migration speeds, would be achieved.

This estimate assumes an optimal treadmilling regime, at which the growing barbed ends are concentrated at the cell's leading edge, their growth is mechanically unhindered, and the G-actin concentration is uniform across the cell. There is still only limited understanding of how synergistic actions of nucleation/branching Arp2/3 complexes, disassembly-regulating ADF/cofilin proteins, and capping proteins focus the growing filament tips at the front and maintain the great ratio of shortening pointed to growing barbed ends (2), and we do not address this problem here. Also, we do not discuss in quantitative detail the effect of the cell membrane resistance on the protrusion: theoretical estimates (9) demonstrate that a few hundred growing filament tips maintained per micron of the leading edge (10) are slowed just a little by the membrane tension. Here we analyze how the actin assembly/disassembly and transport maintain high 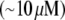G-actin concentration at the cell front.

The importance of respective estimates is emphasized by two experimental studies (11,12): the first one showed that inhibiting actin disassembly led within seconds to slowing down the protrusion (11); the second one observed that the ratio of G-/F-actin is lower at the front of migrating compared to nonmigrating cells (12). The authors of these studies suggested the following interpretation of the results: the protrusion requires tight coupling-to-filament disassembly, in part because ongoing actin-filament assembly uses free actin monomers derived from filament disassembly, in preference to monomer stored in the cytoplasm, and in part because G-actin is relatively limited at the cell's leading edge.

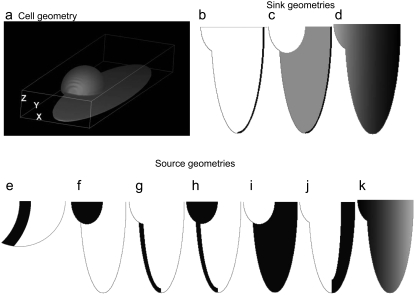
For the analysis, we will use the fish keratocyte cell as a representative system (7). This cell moves rapidly and persistently with characteristic speeds of ∼0.3 μm/s, with hardly any change in cell shape, speed, or direction over many minutes (13). The distribution and function of most of the major molecular players involved with cell motility in keratocytes are comparable to other well-characterized cells (14), whereas their simple shape makes them particularly amenable to physical modeling (15). Keratocytes display the characteristic “canoe shape” first described by Goodrich (16), characterized by an elliptical cell body with a smooth-edged, thin lamellipod running along one side of the cell body and smoothly curving around each end (Fig. 1 a). The lamellipod is a broad, flat sheet-like protrusive appendage that is 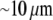long (front-to-rear), ∼20–40 μm wide (side-to-side), and only ∼0.1–0.2 μm thick (ventral-to-dorsal; see Fig.1 a) (10,17). Behind the lamellipod is the cell body, containing the cell nucleus and other organelles, which looks like a half-ellipsoid a few microns in dimensions (Fig.1 a) (18). Other rapidly motile cells are less steady, have a more “ragged” and/or elongated (in the direction of protrusion) shape and sometime thicker lamellipodia, but the orders of magnitudes of the speed and dimensions are similar to those characteristic for the keratocyte.

FIGURE 1.

Cell shape and G-actin source and sink. (a) Geometry of the motile fish keratocyte cell. (b) Sink of G-actin along the leading edge. (c) Sink across the lamellipod is added to that at the leading edge. (d) Sink decreases linearly from the front to the rear. (e) Geometry of the lamellipodial fragment and the G-actin source at the rear. (f–k) G-actin sources at the cell body (f), rear of the lamellipod (g), combination of both (h), uniformly distributed along the lamellipod (i), along the leading edge (j), and linearly decreasing from the rear to the front (k).

Recently accumulated biological and physical data make mathematical analysis of the G-actin transport timely and quantitative, not just conceptual. The diffusion rate of actin monomers in the cytoplasm, which varies depending on cytoskeleton density (19), and is slower than that in an aqueous medium, is measured to be 5–6 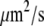(20). The spatial localization of the actin assembly and disassembly is less certain, perhaps because it varies among cells. A number of studies ascertained that the net assembly of F-actin is concentrated in the narrow ( 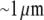wide) zone at the lamellipodial leading edge (21–23); however, data also suggest that in addition, there could be significant sites of actin assembly away from the leading edge (23), or that assembly is distributed more or less uniformly throughout the lamellipod (22). One study concludes that the F-actin disassembly occurs in the rear half of the lamellipod and in the cell body (23); other experiments indicate that the disassembly takes place throughout the lamellipod (21,22). Another recent unpublished study suggests that the disassembly could be focused to the narrow strip along the lamellipodial rear (C. Wilson and J. Theriot, Stanford University, personal communication, 2008).

Besides diffusion, convective flow of the cytoplasm can either assist or hinder diffusion in delivering the G-actin to the leading edge, depending on the flow direction. Such flow can be generated by the myosin-powered contraction at the cell rear that creates pressure gradients driving the cytoplasm through the actin meshwork (24); its existence, direction, and magnitude are also sensitive to membrane permeability regulated by aquaporin channels (25,26,15). Numerous indirect data point at such flow existence (25–27), for example, experiments reported a few years ago showed forward traffic of G-actin in fibroblasts that was faster than can be accounted for by the diffusion (27). Very recent experimental estimates of the cytosol fluid streaming in keratocytes showed that the flow is steady, directed from the cell body toward the leading edge in the cell frame of reference, and its magnitude is tens of percent of the cell speed (K. Keren and J. Theriot, Stanford University, personal communication, 2008). The same experiments demonstrated that when myosin contraction was inhibited, the flow remained significant, but its direction changed backward. Another factor that could affect the G-actin transport is the involvement of the monomers in reactions with actin-binding proteins, such as profilin and thymosin (6). Experiments also suggest that in slower crawling cells, the G-actin pool can be abundant, and the motility is limited by a small number of growing actin filaments (28). In such cells, external signals can upregulate rapidly the number of the uncapped barbed ends at the front, thereby accelerating protrusion (29). A related open question is what determines the characteristic timescale of this acceleration—actin filament dynamics or the diffusion of the monomers to the protrusion site?

In Mogilner and Edelstein-Keshet (9), we analyzed a detailed one-dimensional model of the G-actin reactions and diffusion. Then, in Rubinstein et al. (15), we simulated these reactions and diffusion in the two-dimensional (2-D) lamellipodial fragment. However, in the 2-D, model we did not consider the fact that the ventral-to-dorsal lamellipodial thickness increases a fewfold toward the rear (K. Keren, personal communication). This thickness variability affects the diffusive and convective G-actin fluxes. Besides, in the presence of the cell body, the G-actin transport is essentially a three-dimensional (3-D) problem. In addition, influence of the spatial localization of the assembly and disassembly sites was never considered systematically. Finally, the actin assembly was treated as a boundary condition before (9,15), rather than a more realistic spatially explicit process. Here, for the first time, we solve numerically the 3-D diffusion-drift-reaction equations of the G-actin transport in the realistic geometry of the steadily motile cell. The solutions provide spatial G-actin profiles and characteristic transient times, indicate existence of two (global and local) regimes of the G-actin transport, and generate suggestions for future quantitative experiments.

MATHEMATICAL MODEL OF THE G-ACTIN TRANSPORT

We model the 3-D cell shape as shown in Fig. 1 a: the lamellipod is represented by the flat ellipsoid that is 30 μm wide, 10 μm long, and ∼0.2 μm high at the front (the height increases to ∼1 μm closer to the rear). The cell body is represented by the half-ellipsoid that is 10 μm wide, 7 μm long, and 4 μm high. We also model the nucleus in the cell body as a sphere truncated at the bottom and impenetrable to both G-, and F-actin (Fig. 2 a). Simulations showed that the nuclear dimensions do not affect the results significantly. For comparison, we also simulate the G-actin transport in the 2-D crescent-shaped lamellipodial fragment (Fig. 1 e) that mimics the observed cytoplast shapes and dimensions (length and width ∼10 μm) (30).The boundary condition at all boundaries (both in the 2-D and 3-D models) is no flux of G-actin through the cell membrane.

FIGURE 2.

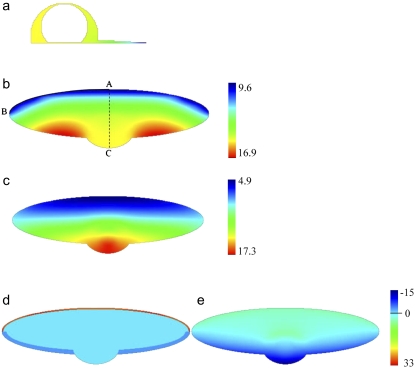
Steady-state G-actin distributions (a–c, in μM units) and spatial distributions of the net assembly (d–e, term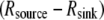 in μM/s units) with the G-actin source along the lamellipodial rear and sink along the leading edge (a: view from the side; b and d: view from above) and with the source and sink distributed throughout the lamellipod (c and e: view from above). The lines AB and AC show the line profiles of the G-actin concentrations in Fig. 3.

Mathematically, the G-actin concentration is described by the functio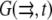n (in 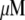(micromolar) units), where is either 2-D or 3-D spatial coordinate in microns, and t is time in seconds. The G-actin concentration's dynamics is governed by the following reaction-diffusion equation:

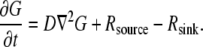(1)

Here 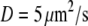is the diffusion coefficient, and 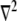is the Laplace operator describing either 2-D or 3-D diffusion,

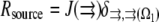(2)

is the reaction term describing the G-actin source (site and amplitude of the F-actin depolymerization), and

(3)

is the reaction term responsible for the G-actin sink (site and amplitude of the F-actin polymerization). 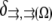is the Kroneker symbol, which is equal to zero if a point in space described by coordinate 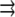does not belong to a region 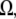and is equal to one if it does. 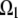is the notation for the region where the F-actin disassembly takes place, and 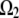is the notation for the region where the actin filaments grow (we also retain the same notations to denote the respective region volumes).

Equation 1 stems from the conservation of the total number of the actin subunits in the cell. Equation 2 is based on the implicit assumptions, well supported by many experiments, that the effective disassembly rate of the pointed ends (barbed end disassembly can be neglected) is insensitive to the G-actin concentration. Equation 3 assumes, after multiple experiments, that the effective assembly rate of the barbed ends (pointed end assembly can be neglected) is proportional to the local G-actin concentration.

The proportionality parameter k in the sink term can be estimated as follows: there are ∼200 filaments per 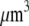(10) near the leading edge. Assuming that most of these filaments are uncapped and growing with the rat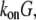e where 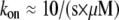(6) and taking into account that 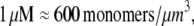we have 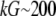filaments per 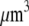× 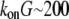filaments per 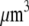× 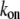G ∼ (200 filaments per 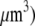× (10/(s × (600 monomers/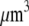))) × G ∼ (3/s) × G. Thus, the value 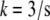gives the order of magnitude of the sink at the leading edge. There could be also assembly and corresponding sink away from the leading edge, likely of lower magnitude.

In the particular case when the F-actin disassembly takes place at the very rear of the lamellipod, the source magnitude, J, can be estimated as follows: length of ∼200 filaments per 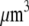grown at the leading edge is ∼0.5 μm (10), so there are about ∼0.5 μm/3 nm ∼150 monomers per filament, and about (200 filaments per 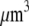) × (150 monomers per filament) ∼ 3 × 10⁴ monomers per 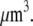Using Avogadro's number allows conversion of this amount into 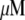units: 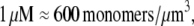and so 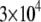monomers per 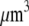is equal to 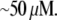In the steady motility regime, if the width of the depolymerization zone is in the micron range and locomotion rate is in the tenth of micron per second range, then the rate of disassembly is ∼(0.3 μm/)/(1 μm) ∼ 0.3/s, and so 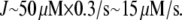According to these estimates, a new filament appears closer to the leading edge within a couple of seconds, and then exists for a few tens of seconds before completely disassembling closer to the rear. Actin turnover rates were not measured directly in the keratocyte cells, but these estimates agree with recent measurements in other cells using speckle techniques that suggest that the order of magnitude of the actin turnover rates in motile cells is the inverse of a few tens of seconds (22,31). These estimates also compare well with the recent in vitro measurements (32).

In a more general case, the source amplitude can be estimated using balance considerations: if the G-actin concentration in the vicinity of all growing filaments is equal to the same constant 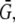then 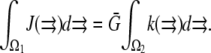To move at the observed rates, this G-actin concentration has to be 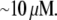Therefore, in simulations, we first define the sink and then normalize the source so that 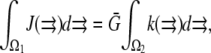where 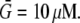For example, if the source and sink are constant within volumes 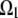and 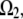respectively, then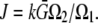

Following the discussion in the introduction, we consider the assembly region, 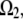to be 0.3 μm wide and localized to the region of the leading edge (up to the sides of the lamellipod where the tangent to the lamellipodial boundary is parallel to the direction of cell movement; Fig. 1 b). Note, that though the average filament length is comparable with the width of the assembly region, ∼0.3 μm, the mesh size (characteristic distance between the barbed ends) is only a few tens of nanometers, so a continuous model is a reasonable approximation for the assembly process. Besides this main case, we also consider three other cases: in one of them, an additional sink characterized by the coefficient 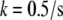and spread uniformly across the lamellipod is added to 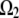(Fig. 1 c). In another case, the sink is also spread across the lamellipod and decreases linearly from the front to the rear, so that the ratio of the coefficient k at the rear to that at the front is 1:3 (Fig. 1 d). Finally, we consider the sink localized to the leading edge but with spatially graded amplitude, so that the rate of the G-actin “consumption” along the leading edge has an inverted parabolic profile with a maximum at the edge center, and minimum (zero) at the sides. Mathematically, in this case,

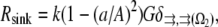(4)

where a is the arc coordinate along the leading edge (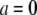 at the center), andAis the length of the leading edge arc from the center to the side. The reason for considering this last case is the recent discovery that the F-actin density along the leading edge is graded, so that this density has the inverted parabolic profile being maximal at the center and minimal at the sides (17,33). The sink is proportional to the local density of the growing barbed ends, which in turn is proportional to the F-actin density.

There are significant stochastic variations in the numbers of the growing filaments (17). Stochastic fluctuations of assembly and disassembly of F-actin were also observed by fluorescent speckle microscopy (34). To explore influence of the stochastic fluctuations in the G-actin sink on the G-actin distribution, we performed the following simulation. We introduced five sudden “spark”-like changes in the amplitude of the sink along the leading edge:

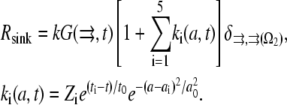(5)

Each “spark” was modeled as a spatial Gaussian shape, exponentially decaying in time after sudden appearance, where 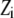is the spark amplitude (random number uniformly distributed in the range from −0.5 to 0.5), 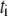is the random time of the spark appearance (uniformly distributed random number in the region of the simulated time interval; 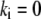at 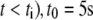is the characteristic decay time, a is the arc coordinate along the leading edge, 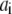is the spark coordinate (random number uniformly distributed along the leading edge), and 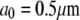is the characteristic size of the sink fluctuations. At 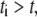the respective term in Eq. 5 is equal to zero. Characteristic time and length can be gleaned from the leading edge F-actin density data reported in Lacayo et al. (17).

To explore the consequences of all possible reported locations of the F-actin disassembly, we simulated the cases shown in Fig. 1, e–k (for the lamellipodial fragment in e and whole cell in f–k): disassembly along the rear edge of the lamellipod, e.g., in the cell body (f), in both of them (h), distributed across the lamellipod (i), and concentrated along the leading edge (j). In the last case, the width of the disassembly zone was 3 μm. We also considered the case when the disassembly takes place in the whole cell (k), yet biased to the rear: the disassembly rate changes linearly in the anterior-posterior direction so that the ratio of the disassembly rate at the very rear to that at the very front is 3:1. In the dorsal-ventral directions, the lamellipodial parts of the disassembly domains span the whole thickness of the lamellipod. When the disassembly took place in the cell body, we localized it to a layer 0.5 μm thick at the ventral surface, due to some data suggesting denser F-actin at the ventral surface (35). The data are not strong, however, so we also simulated disassembly in the whole cell body, and observed no significant difference in this case. In all cases, we normalized the total source so that 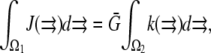where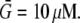

We also considered convective flow in addition to the diffusion. This case is described by the diffusion-drift-reaction equation

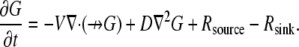(6)

Here, 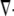is the divergence operator in 2-D or 3-D, 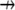is the unit vector showing the direction of the flow, and V is the flow speed. In Rubinstein et al. (15), we simulated the effect of a 2-D slow vortex-like flow that had almost no effect on the G-actin transport. Here, we simulate either forward- or backward-directed uniform flow that is expected to play a more significant role. Such flows were recently measured (K. Keren and J. Theriot, Stanford University, personal communication, 2008). Therefore, we use in the simulations 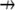either in the direction of movement, or opposite to it, and the estimated value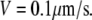

Finally, we considered reactions of the actin monomers with actin-binding proteins. Following Rubinstein et al. (15), we omitted here the fast ADP-ATP and ADF/cofilin-profilin exchanges on G-actin (6) that were considered in Mogilner and Edelstein-Keshet (9) and were shown to have little effect on the G-actin transport. Here we consider the case when concentrations of two actin-binding proteins—thymosin and profilin—are great resulting in almost all the monomers being bound to either thymosin or profilin (6,9). The corresponding two densities– 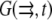and 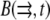(actin-profilin and actin-thymosin, respectively)—are governed by the following system of equations:

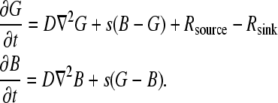(7)

Here, s = 2/s is the rate of the effective reaction of the thymosin/profilin exchange (9,15). Note that G-actin-thymosin does not assemble into F-actin, and when F-actin disassembles, the monomers are converted first into the form bound to profilin.

Note also that the model (7) is a very simplified version of the motile cell biochemistry. There are considerable and poorly understood nonlinear effects in the reactions of actin with thymosin and profilin (36–38), in addition to incompletely known in vivo concentrations of these proteins. It was shown in Mogilner and Edelstein-Keshet (9) and Bindschadler and McGrath (38) that at high, yet realistic, concentrations of thymosin and profilin, i), the concentration of G-actin not associated with either of these actin binding protein is very small, ii), the concentrations of the G-actin-thymosin and G-actin-profilin are of the same order of magnitude, and iii), that the effective rate of the thymosin/profilin exchange on the actin monomers takes place at the second scale. In this article, we consider the influence of the reactions of the actin monomers with the actin-binding proteins on a conceptual, rather than detailed, level. Therefore, we assume for simplicity the equal rates of the thymosin-to-profilin and of the profilin-to-thymosin exchange, and neglected the concentration of G-actin not associated with either of these actin binding proteins. Finally, let us note that the monomers' diffusion coefficient may vary across the lamellipod, depending on the cytoskeleton volume fraction. However, assuming that such variations are less than an order of magnitude, which is supported by recent bead-tracking experiments (K. Keren, Stanford University, personal communication, 2008), this does not change results significantly.

Numerical analysis

The diffusion-drift-reaction equations have been solved in the Virtual Cell computational framework (39), a general-purpose tool designed to test quantitatively cell biological hypotheses and models. The algorithm utilizes a finite-volume discretization scheme that guarantees full mass conservation. The advection fluxes are computed using a hybrid method that switches between central difference and upwind discretization schemes depending on the local Peclet number. (The Peclet number, Pe, is a dimensionless number relating the rate of flow advection, V, to its rate of diffusion, D: Pe = VL/D, where L is the characteristic length.) The 3-D and 2-D computational domains were sampled uniformly, which resulted in a structured orthogonal grid with the mesh sizes of 0.1 μm and 0.02 μm for the 3-D and 2-D simulations, respectively. To discretize the diffusion-drift-reaction equations in time, the Virtual Cell uses a first-order backward Euler scheme with an explicit treatment of the reaction term. In all simulations, integration was performed with a 0.1 s time step, which is faster than characteristic transport, branching and capping processes' times. Computation of 500 time steps performed on the grid of 1,206,000 volume mesh nodes yielding acceptable accuracy takes several minutes. All computations were performed on a Windows computer node with an Intel Xeon 2.8 GHz CPU.

RESULTS

Scaling analysis of the reaction-diffusion problem

To understand the G-actin transport qualitatively, let us consider the steady state G-actin distribution in the simplest one-dimensional case, when actin densities, source, and sink only vary along the anterior-posterior direction. In this case, the reaction-diffusion problem has the form 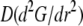+ 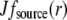− 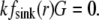Choosing the ratio 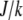as the characteristic scale of the G-actin concentration, and 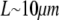— characteristic lamellipodial size—as the length scale, we can introduce the nondimensional variables g = 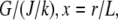and rescale the reaction-diffusion equation

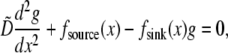(8)

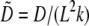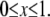where and Taking into account that 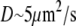and 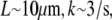we estimate 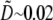as a small parameter.

Let us consider three cases. First, let source and sink be localized at the very rear and front, respectively: 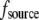= 1, x < l, 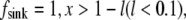and zero otherwise. Then, using the no flux boundary conditions, the approximate analytical solution of Eq. 8 can be easily found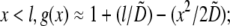: for for 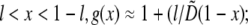and for 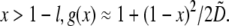In dimensional units, this solution has the following simple meaning. At the leading edge, 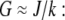growing filaments are all concentrated at the leading edge, therefore they all share the same G-actin concentration, which is not affected by the rate of diffusion, but rather is determined by the balance of assembly and disassembly, 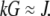However, diffusion is important: it established the constant gradient 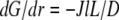across the lamellipod responsible for the diffusive flux of the G-actin from the rear to the front. The steepness of this gradient is inversely proportional to the diffusion coefficient, so the slower the diffusion is, the greater is the increase of the G-actin concentration toward the rear. The G-actin flux 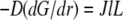does not depend on the diffusion coefficient. This is the case of the “global” transport: assembly and disassembly regions are widely separated; diffusion moves actin monomers throughout the lamellipod, where neither assembly nor disassembly takes place.

In this case, it is easy to calculate the ratio of the G-actin concentration at the leading edge to its average over the lamellipod as 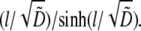This ratio becomes exponentially small when 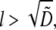so if the growing filaments are distributed at the front of the cell in the zone wider than 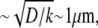the filaments at the rear of that zone would consume most of the monomers, and dampen the G-actin concentration at the leading edge to the extent of significantly slowing the cell.

Second, let both source and sink be spread throughout the lamellipod, but the source dominates in the middle and at the rear, whereas the sink at the front, namely = 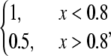and 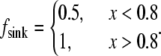In this case, approximate analytical solution of Eq. 8 has the form: 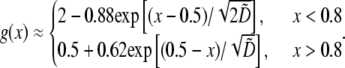The meaning of this solution is also simple: there is a “local” balance of assembly and disassembly across most of the lamellipod: in the middle and at the rear, the G-actin concentration is such that 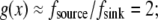at the front, 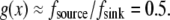In the middle and at the rear and front, 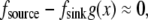and the diffusion term disappears—there is no diffusive transport of monomers. Closer to the front, there is a boundary layer, dimensional width of which is of the order 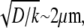where the G-actin concentration decreases rapidly in the forward direction providing the forward diffusive flux of the monomers. Importantly, this flux effectively transports the monomers only locally, from the narrow (∼1 μm) zone at the rear of the boundary layer to similarly narrow zone at the front of this layer. In this case, some of the G-actin ‘consumed’ at the front would be ‘produced’ right there, and some – moved by diffusion from right behind the leading edge.

Finally, if both source and sink are distributed smoothly across the lamellipod, for example, 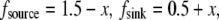then the local balance of assembly and disassembly determines the G-actin concentration everywhere: 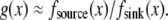The diffusive term then is very small, of the order 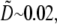and there are no regions with significant net assembly or disassembly. (Even singular perturbation corrections at the edges are small.)

To summarize, this qualitative analysis suggests that two regimes—local and global—of the actin turnover in migrating cells are possible. If in the middle of the lamellipod there are ∼4 growing filaments or less per cubic micron, so that 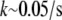or less, then actin monomers can be transported by diffusion across distances μm without being assembled. In this case, the regions of assembly at the front and disassembly at the rear are separated. On the other hand, if there are 20 or more growing filaments per cubic micron everywhere in the lamellipod (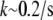 or greater), then actin monomers can be transported by diffusion only as far as a few microns before being assembled, and the actin turnover is local: roughly speaking, G-actin is “consumed” at the same location where it is “produced”. In the local regime, if the source and sink are graded smoothly across the cell, no conspicuous regions of the net assembly and disassembly would appear. If there are abrupt jumps in the distributions of the source and sink, micron-wide adjacent layers where the net assembly and disassembly takes place can be expected around such jumps. In what follows, we support the intuition built by this qualitative analysis by solving the reaction-diffusion equations numerically in a realistic geometry.

Diffusion establishes the G-actin gradient across the lamellipod

We solved reaction-diffusion Eqs. 1–3 describing the 3-D G-actin distribution in the steadily motile cell and in the lamellipodial fragment. Fig. 2 shows the asymptotically stable stationary distributions in the side view (concentration in the vertical plane through the middle of the cell) and in the top view (in the horizontal ventral plane, 0.1 μm above the ventral surface of the cell). The G-actin concentration varies just a little in the vertical direction in the cell body, and is almost constant in the ventral-dorsal direction in the lamellipod, as expected because of the lamellipodial thinness. The G-actin concentration reveals the characteristic anterior-posterior gradient that is due to the fact that the F-actin depolymerization is biased toward the rear, whereas the assembly is biased to the front. The resulting gradient (decrease of the G-actin concentration from the rear to the front) generates the diffusive flux of monomers from the rear to the front, which is significant if the regions of assembly and disassembly are separated in space, and insignificant if they overlap. The results are qualitatively unchanged when either the cell size varies up to twofold (as is the case in the cell population (17,40)), or the diffusion coefficient changes up to twofold.

Fig. 2, d and e, shows the computed spatial distribution of the net actin assembly 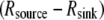in two cases. Fig. 2, d and e, illustrates characteristic differences in the observable net actin assembly distribution in the “global” and “local” cases: in the former situation, the well-defined regions of assembly (at the front) and disassembly (at the rear) are separated by the zero net assembly in the middle of the cell. In the latter situation, the net assembly (that changes less from the front to the rear than in the former case) varies smoothly across the cell.

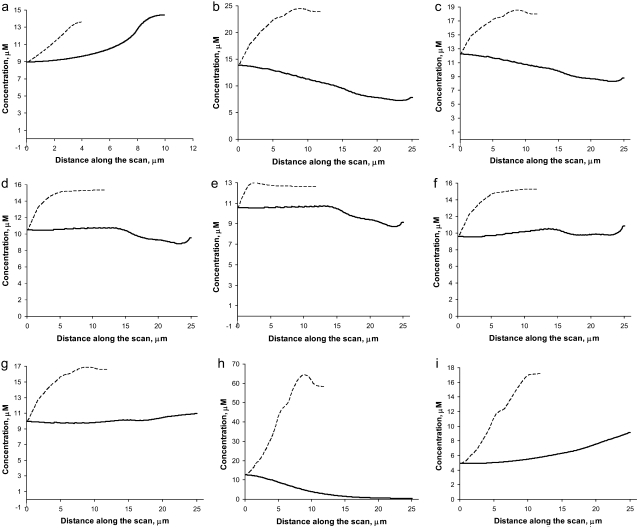
In Fig. 3, we show the line profiles of the F-actin density in the anterior-posterior direction, and along the leading edge. The important result is that under almost all plausible conditions, the G-actin concentration drops less than twice from the rear to the front of the cell. Providing the funneling balance between the depolymerization and polymerization of actin maintaining ∼10 μM average G-actin concentration in the cell, the G-actin concentration at the leading edge would be still ∼10 μM, sufficient to maintain the protrusion rate of tenths of a micron per second. Note that in the cases depicted in Fig. 3, a–c and f and g, the assembly region at the leading edge is separated from the disassembly region at the rear, and in these cases actin turnover in the cell is global: the diffusion recycles actin monomers across the lamellipod. On the other hand, in the cases shown in Fig. 3, d, e, and i, the disassembly is partially colocalized with the assembly, and actin turns over locally at the cell leading edge. Note that in the “local” cases there is still some short-range diffusion of the G-actin from the middle to the very front of the lamellipod. Also, comparing Fig. 3 d with 3 f, it is clear that the order of magnitude of the G-actin concentration at the leading edge is not sensitive to the exact location of the disassembly region.

FIGURE 3.

Line profiles of the steady-state G-actin concentrations in the posterior-anterior direction (dashed) and along the leading edge (solid) for (a) the keratocyte fragment and (b–i) the whole cell with (b) source in the cell body; (c) source is in the cell body and chemical kinetics added; (d) source distributed evenly throughout the lamellipod; (e) source along the leading edge; (f) source along the rear edge; (g) source in the cell body and graded sink; (h) source in the cell body and additional uniformly distributed sink; and (i) source linearly decreasing from the rear to the front and sink linearly decreasing from the front to the rear.

The only exception is the interesting case shown in Fig. 3 h, in which the disassembly is at the rear, whereas there is significant assembly both at the leading edge, and that distributed across the lamellipod: density of the growing filaments is six times higher at the front than in the middle of the lamellipod, but the volume with the high density of the growing filaments is much smaller than the total lamellipodial volume, so that only ∼30% of the growing filaments are at the leading edge. In this case, the G-actin is largely “consumed” by low-density filament tips at the rear of the lamellipod, before the G-actin reaches the front. The G-actin concentration decreases exponentially toward the front and sides of the lamellipod because of that consumption. Despite this decrease, at the center of the leading edge, the G-actin concentration does not drop below ∼10 μM, but the G-actin concentration decreases rapidly to ∼1 μM toward the sides of the leading edge. Thus, in this regime, the protrusion of most of the leading edge would be too slow, and the cell of the considered shape would not move effectively.

G-actin concentration at the leading edge can be graded

The G-actin distribution from the center to the sides of the leading edge depends on the lamellipodial shape and can either be almost constant (if the disassembly is along the lamellipodial rear (Fig. 3 f)), or can decrease from the center to the sides (if the disassembly takes place in the cell body (Fig. 3, b, c, and h)), or can increase from the center to the sides (Fig. 3 a and k). This is biologically relevant because according to the geometric theory of the cell shape (13), the local protrusion rate proportional to the local G-actin concentration has to decrease from the center to the sides. Thus, if the disassembly occurs in the cell body, the G-actin-diffusion can be the cell shape regulator. In other cases, the membrane resistance and/or other mechanical processes has to be responsible for slowing down the actin filament growth at the cell sides. Note, that in the case of the graded F-actin density and sink along the leading edge (Eq. 4) and the disassembly in the cell body, the distribution of the G-actin along the leading edge becomes almost constant (compare panels b and g of Fig. 3).

G-actin transport is not sensitive to the convective flow and chemical reactions

To test the influence of the cytoplasmic drift on the G-actin transport, we solved numerically Eq. 6 and compared the stationary G-actin distributions with those in the cases of the absent drift, with all other conditions being equal. The drift almost does not change the lateral G-actin distribution. It increases (decreases) the ratio of the rear-to-front G-actin concentration when the drift is rearward (forward) by ∼15% in all cases (and even less if the disassembly is near the front). As expected, the forward drift “blows” the monomers forward, “assisting” the diffusion flux in increasing the front G-actin concentration, whereas the rearward drift diminishes the effect of the diffusion, but the respective effects are relatively small. Intuitively, the smallness of the effect is easily understood from the dimensionless combination VL/D ∼ 0.2, which is the ratio of the characteristic drift speed to the effective speed of the diffusion flux (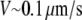 is the drift speed, 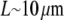is the lamellipodial size, and 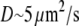is the diffusion coefficient).

Similarly, the numerical solution of Eqs. 7 illustrates that exchange of profilin and thymosin on the monomers has little stationary spatial effect (compare panels b and c of Fig. 3). Chemical reactions, however, can have significant effect on the transient cell movements. For example, a lot of thymosin can “store” great amount of monomers, and then “unload” them if concentration of profilin abruptly increases causing a burst of rapid protrusion.

Diffusion-related relaxation time in motile cells

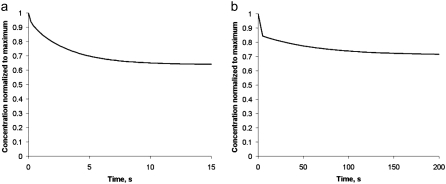
To consider diffusion influence on transient motile effects, we simulated the abrupt 50% increase in the sink amplitude (similar to the observed phenomenon (28,29) explained by the abrupt increase in the number of the uncapped barbed ends), and recorded the temporal change in the G-actin concentration at a number of points along the leading edge. As expected, the G-actin concentration relaxes from a higher to a lower value. Characteristic relaxation time for the 2-D lamellipodial fragment is ∼10 s (Fig. 4 a), which is expected, because this time is of the order of the diffusion time across the lamellipod, 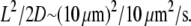Interestingly, the relaxation process in the whole cell is much longer: after the initial fast (∼10 s) decline, the G-actin concentration decreases more over ∼100 s (Fig. 4 b).

FIGURE 4.

Time series for transient changes in the G-actin density near the leading edge after sudden increase of the sink in (a) lamellipodial fragment and (b) whole cell.

Qualitatively, this result can be understood as follows. Initially, ∼10 s after additional polymer tips appear, G-actin redistributes in the lamellipod, establishing steeper gradient. Then, due to a relatively narrow “corridor” between the cell body and the lamellipod, and the large volume of the cell body, it takes much more time for the G-actin stored at the cell rear to diffuse and be assembled at the leading edge. 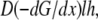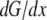The total G-actin forward flux in the lamellipod can be estimated as where is the spatial gradient of the G-actin in the anterior-posterior direction, h is the lamellipodial height, and l is its width. 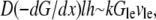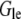This flux is “consumed” at the leading edge, so where is the G-actin concentration at the leading edge, and 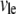is the volume over which the growing filaments at the leading edge are distributed. 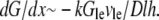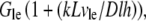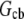Hence, Neglecting small G-actin gradients and respective short time transients within the cell body, we can estimate G_cb ∼ G_le − (dG/dx)L∼ where is the G-actin concentration at the rear of the cell, in the cell body. We can estimate now how much lower the G-actin concentration at the front of the cell than that at the rear would be during a few tens of seconds of the relaxation process: 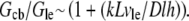Using the characteristic values k ∼ 3/s, L ∼ 7 μm, v_le ∼ 0.2 μm · 0.3 μm · 30 μm ∼ 2 μm³, D ∼ 5 μm²/s, l ∼ 15 μm, h ∼ 0.2 μm, we obtain the ratio 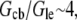so if tens of micromolar of G-actin are stored in the cell body, and the number of growing filaments is suddenly increased at the leading edge, then G-actin in the 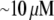range can be maintained at the leading edge. To estimate how long this concentration can be maintained, we can consider the situation, in which continuous F-actin disassembly is stopped, and the polymerization at the leading edge is sustained by the G-actin stored in the cell body only. In this case, the balance of the total G-actin in the cell can be written in the form 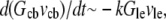where 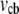is the cell body volume. Using the relation between 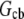and 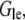we can re-write this equation in the form 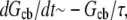where the relaxation time is 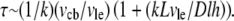Using the parameters above, plus the approximate cell body volume 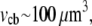we estimate 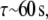similar to the computed value.

G-actin concentration at the leading edge is not sensitive to fluctuations of the F-actin density

Finally, we simulated stochastic spatial-temporal fluctuations in the sink as described above. Despite significant stochastic fluctuations of the assembly (tens of percent in amplitude), the maximal point-by-point changes in the G-actin concentration never exceeded 4% due to the smoothing effect of the diffusion. We also simulated stochastic spatial-temporal oscillations in the amplitude of the source similar to those in the sink and obtained similar results.

DISCUSSION

In this article, we numerically simulated the spatial distribution of the G-actin in the motile cell cytoplasm in realistic 3-D geometry. Our calculations demonstrate that in most of the cases, the G-actin concentration decreases ∼1.5 times from the rear to the front. When F-actin disassembly takes place at the rear while the G-actin is “consumed” by growing filaments at the leading edge, then passive diffusion in the cytosol is efficient in delivering the monomers down the gradient across the cell. Alternatively, when F-actin disassembly and assembly are distributed throughout the cell and partially colocalize, the role of diffusion is just to smoothen the G-actin concentration, and the actin turnover becomes local: monomers assemble into filaments just a few microns away from their disassembly sites. The characteristic density of growing filaments in the middle of the lamellipod, below which the G-actin transport is global and above which is it local, is but a few filaments per cubic micron. Both global and local transport mechanisms could be effective: to maintain high G-actin concentration at the front, it is sufficient either to concentrate significant F-actin disassembly close to the leading edge or to disassemble F-actin at the rear. In the last case, though, it is important not to have any significant actin growth in the middle of the lamellipod, because otherwise, the monomers would be “consumed” before reaching the front. A simple estimate shows that most of the growing filaments in this case have to be concentrated not farther than 1 μm from the leading edge. The G-actin transport mechanism is robust: neither reactions with actin-binding proteins, nor cytoplasmic flows, nor stochastic fluctuations of the monomer sources/sinks change the G-actin distributions significantly.

Qualitatively, in the global case, most of the actin subunits assemble into filaments, stay immobile in the lab coordinate system for tens of seconds, then disassemble closer to the rear and undergo a biased forward diffusion for another ∼10 s, whereas in the local transport, the actin subunits “hop” between the F- and G-actin forms every ∼1 s. Understanding which of the two regimes of actin transport is operational in migrating cells would be important because the interplay among local, second- and micron-scales, motility mechanisms with the global, and cell-size-scale processes is crucial for the way the cell motility and polarity are regulated and organized. (Interestingly, both vigorous assembly and disassembly are observed near the leading edge of the dynamic cells (34).) At the present, accurate quantitative data are lacking to determine definitively whether local or global G-actin transport takes place. However, our theory predicts that in the case of the local transport, there are no separated regions of significant net actin assembly or disassembly in the cell, whereas in the case of the global transport, there has to be significant net actin assembly along the leading edge and disassembly at the rear. The data ((23); C. Wilson and J. Theriot, Stanford University, personal communication, 2008) favor a significant net actin assembly at the very front and net disassembly at the rear, so in steadily motile keratocyte cells the global G-actin transport is more likely. An open question is how the cell manages to cap the barbed filaments ends with such spatial precision that the concentrations of such growing ends at the front and elsewhere differ by orders of magnitude.

In the future, if and when a fluorescent probe allowing the measurement of G-actin concentration in live cells becomes available, the following measurements and calculations will have to be made to quantitatively understand the spatial-temporal mode of the actin transport. First, the spatial map of the net assembly 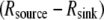has to be computed from the measured F-actin density and F-actin flow field by using the divergence theorem, as was done by Schaub et al. (23). Second, because 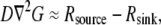one would have to check that 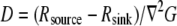is approximately a constant, and, knowing the orders of magnitude of both diffusion coefficient and F-actin density (the latter from electron microscopy), one can calibrate the measured G-actin density. Third, the density of the growing filament tips can be measured, for example, by using kabiramide C staining of the live cells for marking the uncapped barbed ends (41). This would provide the function 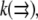and then finally 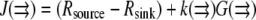can be computed.

The calculations predict no drastic changes of the G-actin concentration along the leading edge and sides of the lamellipod. Especially, in the cases corresponding to Fig. 3, d–g, the G-actin concentration is almost constant along the leading edge and sides of the lamellipod. This result is interesting in light of theories explaining the characteristic curvature of the leading edge (gradual lagging behind of the cell sides relative to the front center) by a spatially graded local protrusion rate along the cell front (13,17): the protrusion rate is maximal at the center of the leading edge and is gradually decreasing to the sides. The local protrusion rate is proportional to the local G-actin concentration and to a factor slowing the rate down by an increase in membrane resistance per filament (9). In the cases when the G-actin concentration is almost constant along the leading edge and sides of the lamellipod, the observed decrease in the density of the actin filaments from the front center to the sides could lead to the increase in membrane resistance per filament and spatial grading of the protrusion rate. In these cases, the membrane tension, rather than the G-actin availability, would regulate the cell shape (42). However, it is also possible that in the case of sufficiently low membrane tension, the graded G-actin concentration that is lower at the sides than at the center in some cases (Fig. 3, b and c) can be the regulator of the cell shape. Curiously, in the 2-D lamellipodial fragment, the predicted G-actin concentration is higher at the sides than at the center (Fig. 3 a).

Calculation of the relaxation times in the 3-D cell in response to abrupt changes in the number of filaments growing at the leading edge reveals that the G-actin concentration in the cell takes ∼100 s to stabilize after initial rapid (∼10 s) change. Note that slowing down of the protrusion within seconds after inhibiting actin assembly was observed (11). This long relaxation time after the rapid initial change is explained by slowness of the monomer flux through the narrow entry between the voluminous cell body and flat lamellipod: it takes a long time for this slow flux, proportional to the area of the lamellipod/cell body interface, to equilibrate the total number of monomers in the cell body with changed G-actin distribution in the lamellipod. This effect can be important for transient bursts of motility that can be sustained for tens of seconds by utilizing the G-actin pool stored in the cell body. In relatively slow transient cell movements, actin filament dynamics can change within seconds, whereas significant cell shape changes take minutes (28,29). Therefore, our calculations predict that the G-actin concentration transients occur on the intermediate timescale—slower than the actin assembly pattern, but faster than the changes in the cell geometry.

The calculations presented here can be useful in the future analysis of the transport of other parts of the actin machinery across the motile cell. Proteins larger than actin would have smaller effective diffusion coefficients, so the convective flows may play a greater role in their transport. In fact, such proteins can get stuck in the actin mesh (the mesh size is ∼30 nm (10)), so active, i.e., motor-based or membrane-mediated transport may be needed in those cases. Interesting future extension of our model could be coupling it to a mechanistic model of the F-actin disassembly that can be enhanced by the myosin contraction at the rear (30). Similarly, it will be worthy to explore a possible influence of cell body rotations (18,23) on the actin transport.

Recently, very detailed models describing the mutual interactions of the small G-proteins, and their effects on dynamics of actin filaments and mechanical aspects of the actin-myosin network, were suggested (43,44). These models, by building on earlier efforts, were able to predict realistic polarization, shapes, and movements of the keratocytes. We considered here a much simpler subproblem—G-actin transport—not included explicitly in Maree et al. (43) and Dawes et al. (44). Because the G-actin transport is but a part of the motile machinery, we did not examine the cell shape and polarity; nevertheless, our analysis indicates that the G-actin distribution could have an important effect on cell shape and speed. One of the future challenging problems will likely be a coupling of the G-actin transport model to a full model of the dynamic cell shape as a free boundary domain. Such a combined simulation would answer quantitative questions about cell polarity, shape, speed, and transient movements.