Factors Influencing Local Membrane Curvature Induction by N-BAR Domains as Revealed by Molecular Dynamics Simulations

Abstract

N-BAR domains are protein modules that bind to and induce curvature in membranes via a charged concave surface and N-terminal amphipathic helices. Recently, molecular dynamics simulations have demonstrated that the N-BAR domain can induce a strong local curvature that matches the curvature of the BAR domain surface facing the bilayer. Here we present further molecular dynamics simulations that examine in greater detail the roles of the concave surface and amphipathic helices in driving local membrane curvature. We find that the strong curvature induction observed in our previous simulations requires the stable presentation of the charged concave surface to the membrane and is not driven by the membrane-embedded amphipathic helices. Nevertheless, without these amphipathic helices embedded in the membrane, the N-BAR domain does not maintain a close association with the bilayer, and fails to drive membrane curvature. Increasing the membrane negative charge through the addition of PIP₂ facilitates closer association with the membrane in the absence of embedded helices. At sufficiently high concentrations, amphipathic helices embedded in the membrane drive membrane curvature independently of the BAR domain.

INTRODUCTION

Cells rely on protein machinery to remodel membranes during vesicle budding events required for endocytosis, exocytosis, and intracellular transport. Proteins are also required to create the complex membrane shapes that define organelles, such as the Golgi apparatus, endoplasmic reticulum, and T-tubule networks. This cellular machinery often utilizes a common set of conserved structural modules to change membrane curvature and thereby create the necessary membrane shapes (1,2). One common motif is a scaffolding framework that presents a target curvature to the membrane. For example, clathrin coats polymerize on the membrane surface with an intrinsic curvature, as do the COPII proteins (3). The COPII protein Sec23/24p has a concave surface lined with positively charged residues. Thus, this protein combines a curvature scaffold with residues that can attract the negatively charged lipid species in the membrane and induce the membrane to adopt the curvature of the surface (4). Since clathrin and Sec23/24p apparently lack the rigidity to force the membrane to adopt their intrinsic shape (2,5), they work together with the proteins epsin and Sar1p, respectively, to create the required membrane curvature (6,7).

Epsin and Sar1p contain another common curvature-inducing motif: an amphipathic helix that inserts parallel to the surface of the bilayer at the junction between the hydrophilic lipid headgroups and hydrophobic tails. These amphipathic helices can generate membrane curvature by creating asymmetry between the two leaflets of the bilayer (2,6–9). At sufficiently high concentrations, helix insertion may cause membranes to tubulate by creating a global disparity between the surface areas of the two leaflets. This mechanism, known as the bilayer couple mechanism, is not generally relevant to cellular systems since the surface area of the cellular membrane is much greater than the area of the inserting proteins (2); however, it may be relevant to liposome tubulation experiments with a sufficiently high protein/lipid ratio. Nevertheless, the insertion of helices also creates local asymmetry, which may generate local membrane curvature via a local spontaneous curvature mechanism. The degree of local curvature created depends on the dimensions of the inserting helices, their depth of penetration into the bilayer, and their local concentration (2).

The BAR (Bin, Amphiphysin, Rvs) domain is a crescent-shaped dimer with positively charged residues lining its concave surface and positively charged, flexible loops at either end of the dimer. The N-BAR domain, which contains an N-terminal amphipathic helix in addition to the positively charged concave surface of the BAR domain, is found in various proteins, including amphiphysin and endophilin, and uses all of these structural motifs to generate membrane curvature (10–17). Experiments have provided evidence that the rigid concave shape of the BAR domain, the positively charged residues on the concave surface, and the presence or absence of N-terminal amphipathic helices are important factors in the ability of these domains to generate membrane curvature (1,11,12,18). How all of these structural features work together to drive membrane curvature in vivo is a topic of much current interest (1,2,18,19).

By permitting the direct observation of atomistic-level interactions, molecular dynamics (MD) simulations provide an opportunity to resolve specific steps in the process of membrane curvature induction by N-BAR domains and obtain insight into the mechanisms involved at the atomistic level. In particular, although experiments allow observations of the global effects of these proteins on lipid bilayers, MD simulations are very useful for understanding how individual proteins and specific structural features interact with lipids to create local membrane perturbations that lead to the observed global membrane behavior.

Our recent MD simulations (20) have demonstrated that Drosophila amphiphysin (dAmph) N-BAR domains (13) can mold the membrane surface to the concave surface presented by the BAR domain. In those MD simulations it was not clear how much of the observed curvature induction was due to the electrostatic attraction between the negatively charged membrane and the positively charged residues on the N-BAR domain concave surface, and how much was due to the asymmetry created by the amphipathic helices embedded in the membrane. In this work we present additional simulations that provide insight into the role of these important N-BAR structural features in driving the observed membrane curvature. We observe that N-BAR domains that lack key positively charged residues on the concave surface, or fail to maintain a stable orientation on the membrane surface do not drive strong local curvature even with their N-terminal helices embedded in the bilayer. On the other hand, we find that N-BAR domains that do not have their amphipathic helices embedded in the bilayer fail to maintain close association with the bilayer and therefore do not induce curvature, although increasing the charge in the bilayer through the addition of PIP₂ near key positively charged residues enables the N-BAR domain to bind stably without its helices embedded in the membrane. We also observe that, at sufficiently high concentrations, amphipathic helices generate membrane curvature independently of the BAR domain. These findings indicate that the charged concave surface is capable of driving local membrane curvature with little, if any, contribution from the amphipathic helices beyond maintaining the BAR domain anchored to the bilayer. Nevertheless, if amphipathic helices are able to accumulate at a higher concentration than probed by these N-BAR simulations they may also contribute substantially to local membrane curvature. Thus, these simulations provide insight into the probable roles of these structural modules for a given configuration and concentration on the membrane surface.

METHODS

General simulation details

The original coordinates for the dAmph BAR domain were obtained from Peter et al. (13) (Protein Data Bank (PDB) ID code 1URU). Each MD system reported here consists of an N-BAR domain and lipid bilayer solvated in water and NaCl at a concentration of 0.15 M. The CHARMM22 (21) and CHARMM27 (22) force field parameters were used to describe the lipid and protein interactions. Except as noted below, the lipid bilayer consists of 70% dioleoylphospatidylcholine (DOPC) and 30% dioleoylphosphatidylserine (DOPS). Each solvated N-BAR/lipid system has dimensions of ∼47 × 10 × 16 nm and consists of ∼740,000 atoms. All dynamics runs were performed in the same manner as previous simulations. The simulations were run in the constant NPT ensemble with fully anisotropic pressure coupling (zero surface tension) and periodic boundary conditions (23). A Langevin thermostat with a damping coefficient of 0.5 ps⁻¹ was used to maintain the system temperature at 310 K. The system pressure was maintained at 1 atm by using a Langevin piston barostat (24) with a piston period of 2 ps and a damping time of 2 ps. Short-range nonbonded interactions were cut off smoothly between 10 and 12 Å. The particle mesh Ewald algorithm (25) was used to compute long-range electrostatic interactions at every time step. All covalent hydrogen bonds were constrained by the SHAKE algorithm (or SETTLE for water) (23,26), permitting an integration time step of 2 fs. System construction was done using the CHARMM (27) and VMD (28) software packages. Images of the MD system were generated using VMD. System minimization, equilibration, and dynamics were carried out using the NAMD (29) software package.

PIP₂ parameterization

To generate the PIP₂ parameters (D. Lupyan, unpublished data), ab initio quantum chemistry calculations were done using the Gaussian03 package (30) for geometry optimization and for determination of the distribution of partial charges on inositol 1,4,5-trisphosphate (IP₃) (D. Lupyan, Mount Sinai School of Medicine, personal communication, 2007). These calculations were run using the Hartree-Fock level of theory with a 6-31G* basis set. Electronic properties were calculated in vacuum as well as with the polarized continuum model representing water as an implicit solvent using Pauling's atomic radii and 1.2 as the scaling factor for the definition of the solvent-accessible surfaces. The electrostatic potential partial atomic charge distribution of IP₃ was derived using the restrained electrostatic potential method (31). The charges were designed to ensure that the addition or removal of a phosphate group on any of the inositol ring phosphorylation sites (C3, C4, C5) will result in a difference of −2 net charge. Using this methodology, one can conduct simulations with different isomeric forms of phosphoinositides without reoptimizing their geometries and recalculating their partial charges. The complete PIP₂ lipid was formed by joining the PIP₂ headgroup to the glycerol backbone via a CHARMM patch in the same manner as for DOPS or DOPC. The joining carbon (and its associated hydrogens) on the glycerol backbone retained the partial charges of the original PIP₂ headgroup carbon at that position to conserve the exact charge (−5) of PIP₂.

N-BAR simulations

The simulations NBR1 and NBR2, and the original plain lipid bilayer (without the N-BAR domain) were extended from the 27-ns simulations reported previously (20), and some data from those simulations are presented for comparison and completeness. System construction, minimization, and equilibration for the N-BAR simulations reported here were performed essentially as described previously for NBR1 and NBR2 (20). Briefly, conjugate gradient minimization was performed on the BAR/lipid system for 36 ps, after which the system was heated to 310 K over 10 ps with restraints on the α-carbons of the N-BAR domain. The system was then subjected to velocity rescaling for 40 ps while the restraints on the α-carbons of the N-BAR domain were gradually reduced from a force constant of k = 100 kcal/mol/Ų to k = 0 before starting runs with Langevin dynamics and Langevin piston pressure control. The new simulations reported here, except for NBRH1, were also run for an additional 6 ns with velocity rescaling to 310 K every 100 steps before starting the dynamics runs. This consisted of 3 ns under constant volume with the protein and lipid atoms restrained with a force constant of k = 2 kcal/mol/Ų, and 3 ns with no restraints and Langevin piston pressure control.

The minimized configuration for simulation NBR3 was used as the starting point for the simulation of the mutated N-BAR domain in simulation NBR−. Structure and coordinate files for the mutated system were generated using the Mutate and Autoionize plug-ins in VMD. After the mutation of these 10 positively charged residues to neutral residues, 10 sodium ions were placed within the system to maintain electrostatic neutrality. These ions were placed at least 20 Å away from any protein or lipid atom. Conjugate gradient minimization was then performed for 1000 steps with all atoms except the solvent fixed, and then continued for an additional 1000 steps with everything except the solvent and mutated residues fixed. The subsequent equilibration was done as described above except that the final velocity rescaling with protein and lipid fixed was extended to just over 4 ns. After equilibration, the center of mass of the α-carbons of the mutated BAR domain was restrained along the y coordinate axis for the first 10 ns of dynamics with a force constant of k = 2 kcal/mol/Ų using SMD with the velocity set to 0.

The initial membrane and solvent configuration for the simulations with the unembedded helices (NBRH1–NBRH3) were taken from the original plain lipid bilayer simulations after 27 ns. The initial BAR domain configuration was taken from the simulation of the solvated BAR domain alone as reported previously (the same as for the original NBR1 and NBR2 simulations); however, the configuration for the N-terminal region in the random coil (as opposed to the α helix) configuration was taken after 9 ns from the simulation of the random coil N-BAR interacting with the smaller 25 nm bilayer, also as reported previously (20). These components were merged into a single system using CHARMM, and overlapping solvent atoms were removed. As done previously, several solvation shells were retained around the region of the protein close to the membrane when it was transferred to the lipid bilayer system. In NBRH3, SMD was performed on the center of mass of the α-carbons of the dissociated end of the BAR domain (residues 133–192). This loop was pulled back into contact with the membrane using a force constant of k = 1 kcal/mol/Ų and a velocity of 5 Å/ns.

The initial configuration for NBRHP1, the system containing phosphatidylinositol 4,5-bisphospate (PIP₂), was taken from the end of a system containing an N-BAR domain with unbound helices interacting with the standard 47-nm DOPS/DOPC bilayer. One phosphoserine and five phosphocholine headgroups were mutated to create six PIP₂ lipids. The mutated lipids were selected based on their projected proximity to either a BAR binding loop or one of four positively charged regions of the BAR arch created by Lys⁵⁸, Arg⁶⁵, Lys¹³², Lys¹³³, and Arg¹⁴⁰. After the mutations were completed, overlapping waters were removed. All atoms except those within 10 Å were restrained (k = 100 kcal/mol/Ų), and the system underwent 20 ps of conjugate gradient minimization and a brief heating (temperature reassignment every 50 steps for 10 ps). The restraints were gradually reduced over a period of 30 ps before conducting Langevin dynamics with identical parameters to those previously described.

It should be noted that in the BAR domain crystal structure (PDB ID: 1URU) there is a hydrogen bonding opportunity between the two monomers at His²¹⁹ when distinct nitrogens on this His residue are protonated on each monomer (i.e., in terms of the CHARMM topology, on one monomer His²¹⁹ is HSE and on the other monomer it is HSD). This procedure was followed for the simulations of the solvated BAR domain alone. However, when the BAR domain was propagated to the lipid systems, this asymmetry was accidentally not preserved, resulting in the loss of this hydrogen bond. The effect of this missing hydrogen bonding opportunity was minimal in these simulations because the BAR domain dimer remains robust and stable; however, this hydrogen bond should be included in future simulations for consistency.

Helix-only simulations

The initial structure for the membrane in the helix-only simulations was taken from the beginning of the original plain lipid bilayer simulation after the initial equilibration. Lipids, water, and ions were removed from the long edge of the box until 1000 lipids remained (350 DOPC and 150 DOPS per leaflet, ∼269,000 atoms). The horizontal area of the box was reduced from 47 × 10 nm to 47 × 6.7 nm incrementally with 1 ps conjugate gradient minimization per increment to eliminate overlapping atoms in the periodic images. Before the helices were added, system velocities were reassigned every 50 steps for 6 ps with a temperature increment of 6° until the system reached 310 K. The velocities were then rescaled every 50 steps for 20 ps, after which the ensemble was switched from constant NVT to constant NPT and an additional 8 ps of rescaling was performed. The system was then run for an additional 9.7 ns under constant NPT with Langevin dynamics to further equilibrate the membrane before adding the helices.

The initial coordinates for the helices were taken from the N-terminal helix that had remained closest to an α-helix at the end of simulation NBR1 (48 ns). A total of 10 helices were placed in the headgroup region of the bilayer in an antiparallel manner ∼22.5 Å apart and oriented perpendicular to the long axis of the bilayer. Counter ions were added to maintain system neutrality. The system was then subjected to multiple cycles of conjugate gradient minimization and manual translation of lipid headgroups to remove bad contacts. The lipids and protein were then fixed and the solvent was equilibrated for 5 ns.

Two initial configurations were created, designated H1 and H2. After the solvent equilibration was completed, the hydrogens were released, followed by the lipid headgroups and protein side chains, then the upper lipid tails, and finally the lower lipid tails and protein backbone of H1 (in this case “released” means changing the force constant from k = 100 kcal/mol/Ų to k = 0 kcal/mol/Ų on the given atoms) such that all atoms were unrestrained by the end of an additional 215 ps equilibration. In contrast, the helices of H2 were moved a few angstroms deeper into the headgroup region of the bilayer after the solvent equilibration (to bring them closer to the level of the phosphates). H2 was then reminimized with the backbone of the helices restrained. The system was again fully restrained and the atoms were then gradually released in the same order as described above (the force constant k was reduced from 100 to 10 to 1 to 0 kcal/mol/Ų) during 80 ps of equilibration. Dynamics were then run as previously described.

RESULTS

In our prior MD simulations (20), dAmph N-BAR domains with embedded N-terminal helices induced curvature in solvated 45 nm × 10 nm membranes composed of 30% DOPS and 70% DOPC within a simulation time span of 27 ns. To further understand how N-BAR domains drive local curvature, extensive additional simulations were performed in this work with modifications that provide insight into the role of each N-BAR domain structural element in generating membrane curvature. The key characteristics of these simulations and the main results are summarized in Table 1. The details of the simulations can be found in the Methods section.

TABLE 1.

Summary of simulation conditions and results

Simulation	Membrane composition	N-BAR	N-terminal helices	Binding of charged loops*	Membrane curvature
NBR1† NBR2	70% DOPC 30% DOPS	WT	Embedded (150 lipids/helix)‡	Strong	High
NBR3	70% DOPC 30% DOPS	WT	Embedded (150 lipids/helix)	Weak/dissociates	None
NBR–	70% DOPC 30% DOPS	Mutant§	Embedded (150 lipids/helix)	Moderate	Low¶
NBRH1 NBRH2 NBRH3	70% DOPC 30% DOPS	WT	Not embedded	Weak/dissociates	None
NBRHP1	70% DOPC 30% DOPS ∼1% PIP2‖	WT	Not embedded	Strong	Low¶
H1 H2	70% DOPC 30% DOPS	None	Embedded (30 lipids/helix)**	N/A	High

^*Comprising N-BAR residues 161–171, inclusive.

^†Simulations NBR1 and NBR2 reported in Blood and Voth (20).

^‡Approximate local concentration based on helix-occupied region within a single membrane leaflet. Concentration based on entire leaflet is 360 lipids/helix.

^§Five positively charged residues mutated to neutral residues on each BAR monomer as follows: K58Q, R65Q, K132Q, K133Q, and R140Q.

^¶Not distinguishable from curvature created from membrane undulations.

^‖Localized to membrane region beneath BAR domain. Local concentration ∼10%.

^**Concentration based on entire membrane leaflet is 50 lipids/helix.

Role of the positively charged concave surface

New simulations were performed to investigate the role of the positively charged concave surface of the BAR domain in driving membrane curvature. The first simulation, designated NBR3, is similar in its initial configuration to the “strong membrane bending” simulations NBR1 and NBR2 reported previously (20). Although these three simulations are similar in their initial configurations, it is expected that fluctuations in these atomistic-level interactions will result in each system exploring a different region of phase space (23). In previous work (20,32), this ability to explore fluctuations in molecular systems permitted the determination of two distinct binding orientations of BAR domains on the membrane, which resulted in differing degrees of induced membrane curvature. Similar membrane binding behavior to that predicted by these MD simulations was recently shown experimentally for the related F-BAR domain module (32). Thus, differences in the equilibrium behavior of these systems are a feature of these atomistic-scale investigations that provide insight into the mechanisms behind the average long timescale behavior of these molecules.

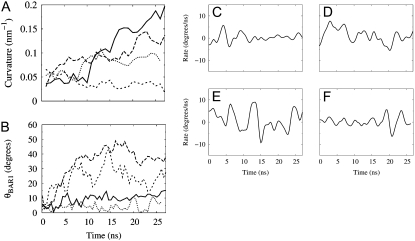
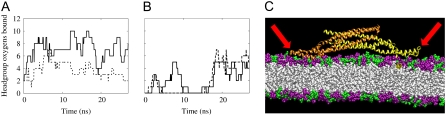
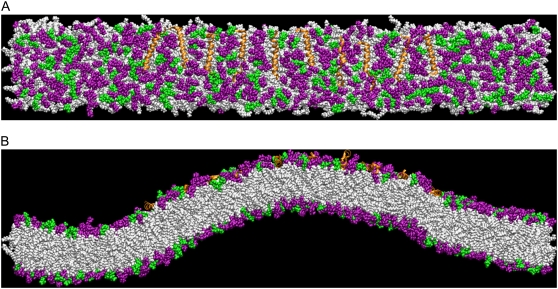
The induced curvature and corresponding orientation for the previous simulations NBR1 and NBR2 as well as for the current simulation NBR3 are shown in Fig. 1, A and B. In contrast to simulations NBR1 and NBR2, the N-BAR domain in simulation NBR3 does not induce membrane curvature (Fig. 1 A). Further analysis of specific molecular interactions in this system revealed differences in the behavior of the N-BAR domain, which influenced its ability to drive membrane curvature within the time span of these simulations. Fig. 1 B shows the orientation of the charged concave surface of the BAR domain with respect to the membrane surface. The orientation of the BAR domain in NBR3 fluctuates significantly throughout the simulation. In contrast, the prior simulations (20), NBR1 and NBR2, have long periods where the orientation of the BAR domain is stable. Interestingly, in NBR1 and NBR2, periods of stable orientation precede periods of N-BAR domain-induced curvature generation. This makes sense if the curvature is being driven by an electrostatic attraction, since a period of stable orientation will give the membrane time to respond and move in the direction of the attractive force, whereas, above a certain frequency, the membrane will not be able to keep up with the changing direction of the force and therefore will be unable to bind to the concave surface of the BAR domain. Fig. 1, C–E, depict the rate of change of the orientation of the BAR domain in simulations NBR1-3 as a function of simulation time. The BAR domain in NBR1 has a long period of remarkably stable orientation during which it drives a large local membrane curvature. In NBR2, the BAR fluctuates rapidly at the beginning of the simulation, but then settles into a more stable orientation. It then drives local membrane curvature, but it does so later in the simulation than NBR1. In both NBR1 and NBR2 there is a period of at least 10 ns of stable orientation before the BAR domain is able to generate strong local curvature. Throughout simulation NBR3, the concave BAR domain surface is moving almost constantly, and hence is unable to drive membrane curvature. Fig. 2 shows the binding of the positively charged loops (in this work, residues 161–171) at either end of the BAR domain to negatively charged residues in the bilayer. These loops are flexible and sometimes change conformation leading to more or less favorable orientations for binding the membrane (see Fig. S3, Data S1, in the Supplementary Material). Further inspection of the NBR3 simulation reveals that the unstable orientation of the BAR domain on the bilayer surface is due to the failure of these charged loops to bind strongly to the bilayer (Fig. 2, B and C). This is in contrast to NBR1, which binds strongly via these end loops throughout the simulation (Fig. 2 A).

FIGURE 1.

Membrane curvature and BAR domain orientation on the membrane surface. (A) Membrane curvature development for NBR1 (solid), NBR2 (long dash), NBR3 (short dash), and NBR− (dot). Simulations NBR1 and NBR2 were reported previously (20) and are presented here for comparison. Curvature is calculated as reported previously, except that only the thin bilayer section directly underneath the BAR domain is included, as opposed to the entire width along the short membrane axis (y axis). Each point is an average over 1 ns, with samples taken every 50 ps. (B) Altitudinal angle θ_BAR1 between the shortest principal axis of the BAR domain (initially directed along the y axis of the simulation cell) and the x, y plane (the plane of the membrane). Rate of change of the angle θ_BAR1 calculated from a smooth fit to the data in B for BAR domains in simulations NBR1 (C), NBR2 (D), NBR3 (E), and NBR− (F).

FIGURE 2.

Binding of flexible BAR domain loops to lipid headgroups. The binding of Arg and Lys residues to oxygen atoms on lipid headgroups is shown for simulations NBR1 (A) and NBR3 (B). The solid and dashed lines represent the left and right loops, respectively, as depicted in the simulation snapshots (e.g., C). For this study, these loops comprise residues 161–171, inclusive. Residues are considered bound if the nitrogen and oxygen atoms remain within 4.2 Å for at least 1 ns (50-ps sampling interval). The binding of these loops assists in stabilizing the interaction of the BAR domain with the lipid bilayer (compare with Fig. 1, C and E). (C) Close-up snapshot showing the charged binding loops (red arrows) on either end of the BAR domain dissociating from the bilayer surface after 13 ns in simulation NBR3. The DOPC headgroups are purple and the DOPS headgroups are green. The lipid tails are white. Water and NaCl are also present in the simulations, but are left out of the image for clarity. In this and other close-up snapshots, only about half of the 45-nm membrane is shown.

The failure of NBR3 to drive membrane curvature even with its N-terminal helices embedded in the bilayer indicates that the positively charged concave surface is critical for inducing the strong membrane curvature observed in NBR1 and NBR2. Therefore a second simulation, designated NBR−, was performed that was initially identical to NBR3 except that 10 of the positively charged Arg and Lys residues on the concave surface were mutated to the polar residue Gln. The mutations (five on each monomer) were as follows: K58Q, R65Q, K132Q, K133Q, and R140Q. These residues were selected because they interacted most strongly with the negatively charged lipid headgroups in simulations NBR1 and NBR2. Of these, Lys⁵⁸, Lys¹³², and Arg¹⁴⁰ are conserved among amphiphysins (13). Although the other residues are not highly conserved, all of these residues are found on the concave surface, directly exposed to the membrane. To eliminate any BAR domain orientation effects (like those observed in NBR3), the center of mass of the BAR domain in NBR– was gently restrained in the y coordinate direction for the first 10 ns. Throughout the simulation, the mutated BAR domain maintains a stable orientation with respect to the membrane surface, similarly to NBR1 (Fig. 1 F). Some curvature develops in the region of the BAR domain (Fig. 1 A), which appears to be a membrane undulation mode, since this degree of curvature can be observed in membranes in the absence of N-BAR domains (see Fig. S2, Data S1, in the Supplementary Material) and there is no binding of remaining charged residues to the lipid headgroups (see Fig. S4, Data S1). Further information on the potential role of membrane undulations in these simulations can be found in the Supplementary Material (Data S1). Despite this favorable membrane mode and the stable orientation of the concave surface, the N-BAR domain without key positively charged residues does not induce membrane curvature.

N-BAR domains with unbound N-terminal helices

Since the positively charged concave surface was critical to driving membrane curvature, it was tested whether the N-BAR domain could drive local membrane curvature without its N-terminal helices embedded in the membrane. To do this, simulations similar to NBR1 were performed, except that the N-terminal region of the N-BAR domain was not embedded in the bilayer. When not embedded in the bilayer, this N-terminal region exists as an unstructured random coil (13). Since the timescale for helix folding and membrane insertion is beyond the timescale that is accessible to these MD simulations, N-terminal regions that are not initially inserted into the bilayer as helices remain outside the bilayer as random coils throughout the simulations.

In the first simulation (denoted here as NBRH1) the N-BAR domain was placed in a region of negative curvature, next to a large positive undulation mode. As the simulation progressed, the membrane reorganized and the large undulation mode dissipated. Apparently as a result of this reorganization, the N-BAR domain lost tight contact with the membrane in that region, and eventually one end of the N-BAR domain dissociated from the bilayer. In a second simulation (NBRH2) with a longer initial equilibration time (but essentially the same starting configuration), the same end of the N-BAR domain eventually dissociated from the membrane. During the final simulation (NBRH3), the dissociated end of the N-BAR domain from NBRH2 was guided back into contact with the bilayer using steered MD (SMD) (33). In the absence of the large membrane reorganization that occurred in the first two simulations, the N-BAR domain remained associated with the bilayer; however, the charged end loops only managed to bind loosely to the bilayer after 24 ns (see Fig. S3, Data S1, in the Supplementary Material). In the absence of this tight binding by the charged end loops, the N-BAR domains with unbound N-terminal helices did not induce curvature in the lipid bilayer.

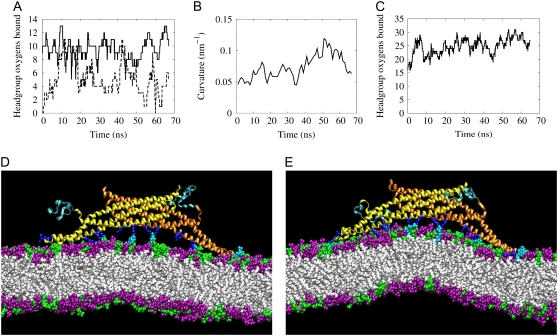
PIP₂ was added to the lipid bilayer near key charged residues of the N-BAR domain to test whether an increased membrane charge would facilitate tighter binding by the end loops and perhaps subsequent membrane bending in the absence of embedded N-terminal helices. It should be noted that, thus far, the fraction of negatively charged lipids in these simulations (30% phosphatidylserine) is lower than that contained in the Folch fraction I lipids (∼10% phosphatidylinositol, ∼50% phosphatidylserine, and other lipids) (34) that are often used in tubulation assays, so increasing the charge in the bilayer in this way is still quite conservative compared with experiments. To this end, several PS and PC headgroups were replaced with PIP₂ headgroups in the vicinity of the positively charged residues of the BAR domain end loops and concave surface. A simulation was then run with an N-BAR domain interacting with the DOPC/DOPS/PIP₂ bilayer, without its N-terminal helices embedded in the bilayer. In this simulation, designated NBRHP1, the end loops were able to maintain contact with the bilayer for a much longer period than other simulations with unbound helices—over 65 ns (Fig. 3 A). During the simulation the N-BAR appears to induce some curvature in the bilayer (Fig. 3 B), although the bending is not strong enough to be clearly distinguished from membrane undulation modes (see the Supplementary Material, Data S1). Nevertheless, this lack of strong bending is not due to a lack of binding of the concave surface as in simulations NBR3 and NBR–. As shown in Fig. 3, C–E, the residues of the concave surface are very strongly bound throughout the simulation. The reason for the lack of strong bending is that the PIP₂ headgroups, which extend further away from the bilayer surface than the PS headgroups, are tightly coordinated by the positively charged residues on the concave surface of the BAR domain even when the bilayer is relatively flat (Fig. 3 D). In contrast, in simulation NBR1 there is a significant gap between the PS headgroups and the residues of the concave surface when the bilayer is flat, causing the BAR domain to pull the bilayer closer to the concave surface to reach an electrostatic equilibrium. Thus, in the other N-BAR simulations, prolonged strong binding to the concave surface coincides with strong curvature induction (see Fig. S4, Data S1, in the Supplementary Material), whereas in simulation NBRHP1 strong binding results in much weaker curvature induction.

FIGURE 3.

Membrane interaction of the N-BAR with unbound N-terminal regions. (A) Binding of the charged end loops of the N-BAR domain to the DOPC/DOPS/PIP₂ membrane in simulation NBRHP1. (B) Local curvature of the bilayer in the region of the N-BAR domain. (C) The binding of Arg and Lys residues on the BAR concave surface to oxygen atoms on the lipid headgroups. (D) Simulation snapshot at the beginning of the simulation showing the N-BAR domain with unbound N-terminal coil regions (dark cyan) and the lipid bilayer containing PC (purple), PS (green), and PIP₂ (light cyan) headgroups. The basic residues on the protein (dark blue) interact strongly with the PIP₂ headgroups even when the bilayer is relatively flat. (E) Simulation snapshot at 55 ns during development of local membrane curvature. About half of the 45-nm membrane is shown.

Behavior of the embedded N-terminal helices

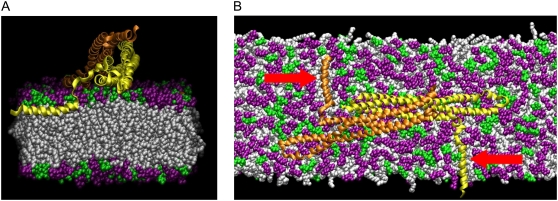
The behavior of the N-terminal helices during the N-BAR simulations (NBR1–3 and NBR–) was examined to see whether there were any differences in helix behavior that might account for differences in induced curvature in these simulations. The helices were initially modeled as α-helices, although it is predicted that they will not form perfect α-helices in the membrane (18). In fact, the α-helical structure of one of the helices of the original simulation NBR1 was disrupted during the minimization and equilibration process, and it formed a partial helix and partial coil. All of the other embedded helices in the N-BAR simulations remained close to the original α-helical structure. In all of these simulations the helices were embedded parallel to the surface of the bilayer near the level of the phosphates of the lipid headgroups (Fig. 4 A). This positioning of the helices was recently confirmed experimentally for endophilin (11). Embedding the two N-terminal helices of the N-BAR domain in the lipid bilayer results in a local concentration of ∼150 lipids/helix (considering only lipids in the leaflet of insertion). During these simulations the center of mass of the helices generally remained within 1–2 Å of the level of the lipid phosphates, although occasionally they fluctuated as far as 3–4 Å above or below this level (see Table S1, Data S1, in the Supplementary Material). The orientation of the helices with respect to the BAR domain has not been established, but it has been suggested that an orientation perpendicular to the long axis of the BAR domain may result in induction of membrane curvature along the same axis as the BAR domain (18). Thus, the helices were originally placed in this configuration, perpendicular to the long (x) axis of the membrane (Fig. 4 B). During the N-BAR simulations, the long axes of the embedded helices generally remained between 70° and 90° of the long axis of the membrane (see Fig. S5, Data S1, in the Supplementary Material). In these simulations, there do not appear to be any significant differences in behavior of the N-terminal helices that might account for differences in induced curvature. This indicates that the presence and stable orientation of the positively charged residues on the concave surface are the primary factors influencing curvature induction in these simulations.

FIGURE 4.

Orientation of the N-terminal helix. (A) Cross section along the long axis of the membrane showing the N-terminal helix embedded at the junction between the lipid headgroups (purple and green) and lipid tails (white). (B) Top view of the N-BAR domain showing both of the embedded N-terminal helices (red arrows). About half of the 45-nm membrane is shown.

Curvature induction by amphipathic helices

The protein epsin tubulates liposomes efficiently with just the amphipathic helix of its ENTH domain (6), and certain synthetically derived amphipathic helices are known to create tubules from liposomes at high protein concentrations (lipid/protein molar ratio of 10) (9). To test whether membrane bending by amphipathic helices can be observed in these MD simulations, systems were constructed containing 10 dAmph amphipathic helices embedded near the level of the lipid phosphates in a stretch of bilayer equal in length to those used in the N-BAR domain studies (see Fig. 5 A). This corresponds to a much higher local concentration of embedded helices (30 lipids/helix) than in the N-BAR simulations. As in simulation NBR1, some of these helices took on a partial helix, partial coil conformation during the simulations. In two separate simulations, designated H1 and H2, significant membrane bending occurred after 28 ns. The curvature continues to develop after 28 ns, and the result for H2 after 36 ns is shown in Fig. 5 B. Over the course of the 50 ns H2 simulation, the average position of the helices in the bilayer decreased from 1.8 to 0.32 Å above the level of the phosphates (excluding a single helix that formed a large coil that protruded from the surface of the bilayer). This position agrees quite well with the experimentally determined membrane position for the N-terminal helix of endophilin (11). No curvature developed in two identical control bilayers with no amphipathic helices embedded. Further studies will be required to determine whether a global bilayer couple mechanism or a local spontaneous curvature mechanism (2) is responsible for the observed curvature.

FIGURE 5.

Membrane curvature driven by amphipathic helices. (A) Top view of the membrane containing 10 embedded amphipathic helices (orange) after 36 ns. (B) Snapshot from the 10-helix simulation after 36 ns, showing the amphipathic helices inducing curvature in the membrane.

DISCUSSION

In our previously reported MD simulations (20), strong membrane curvature induction was observed by dAmph N-BAR domains having their N-terminal helices embedded in a membrane consisting of 30% DOPS and 70% DOPC. The simulations reported here provide insight into the roles of the positively charged concave surface and N-terminal helices of the N-BAR domain in driving the membrane curvature observed previously. It is found that the positively charged residues on the concave surface must be present and maintain a stable orientation with respect to the membrane to drive strong curvature. It is also found that the ability of the BAR domain to maintain a stable orientation on the bilayer surface depends on the binding of the charged end loops, which provide a stable platform for subsequent membrane deformation. These simulations suggest that the charged concave surface of the BAR domain is not acting only as a stabilizer of membrane curvature generated primarily by embedded helices, rather it is actually driving local membrane curvature in the absence of significant membrane curvature generation by embedded helices.

In the N-BAR simulations reported here, the local ratio of lipids to membrane-embedded helices is ∼150:1. These helices extend away from the BAR domain, in opposite directions, perpendicular to its long axis (see Fig. 4 B). In this arrangement and at this concentration in the membrane, the embedded N-terminal helices do not drive curvature strongly in the absence of the positively charged residues of the BAR domain concave surface; however, the embedded helices are essential for keeping the N-BAR domain closely associated with the bilayer. Without its N-terminal helices embedded in the membrane, the N-BAR domain is prone to dissociate from the bilayer surface. Increasing the negative charge of the membrane by adding PIP₂ near key positively charged residues enables the N-BAR domain to remain associated with the bilayer. The PIP₂ lipids bind quite strongly to the concave surface of the BAR domain. Nevertheless, the bilayer bending is not as strong as in previous simulations because the negatively charged phosphates on the PIP₂ headgroups, which were placed near the major positively charged residues of the BAR domain, extend far enough from the membrane surface that they are able to bind tightly to these residues without the need for strong bilayer bending. It is possible that this smaller degree of local bending would translate into tubules with a larger diameter, although this requires further investigation.

Placing high concentrations of amphipathic helices in the membrane (30 lipids/helix) enables them to cause membrane curvature in the absence of the BAR domain. Even though these embedded helices do not drive curvature strongly at the lower concentration that occurs in the N-BAR simulations, these helices are clearly capable of changing bilayer curvature at a sufficiently high concentration. Hence, it is still possible that, in addition to keeping the N-BAR closely associated with the bilayer, the two embedded helices in NBR1 make the bilayer easier to bend, and in this way work together with the charged concave surface to yield stronger curvature. This contribution of the embedded helices to membrane bending may be particularly effective if they are embedded directly below the BAR domain, as was proposed for endophilin (11). However, in these helix simulations we cannot yet distinguish whether the observed membrane curvature occurs due to a global area difference, or through a local change in spontaneous curvature of the bilayer. It is also possible that, at lower concentrations, the full effect of the embedded helices occurs over longer timescales than accessed in these simulations.

Experiments have shown that both amphipathic helices alone (6–9) and the BAR domain alone (13) lead to at least some membrane tubulation at sufficiently high concentrations. In general, the balance between these two structural motifs in driving curvature will depend on both the bilayer composition and charge (13) and the local concentration and depth of penetration of embedded helices in the bilayer (2). Further investigation will be required to determine how the variation of these parameters affects curvature induction by N-BAR domains. For instance, certain amphipathic helices may penetrate more deeply into the bilayer and thus drive curvature more vigorously, as likely occurs for helices that are modified by the addition of bulky hydrophobic residues (6,12). The simulations presented here indicate that, at a concentration of 150 lipids/helix, the embedded amphipathic helices of a dAmph N-BAR domain are not sufficient to drive significant membrane curvature. This suggests that for amphipathic helices to drive curvature on their own, as in the case of the epsin ENTH domain (6), they must either be more concentrated in the membrane or penetrate more deeply into the bilayer, or both. The N-BAR configuration tested here does not correspond to the tightest possible packing of these molecules on the membrane surface; therefore, the N-terminal helices may contribute more to curvature development in more tightly packed configurations. Experiments with endophilin have shown that it can still generate some tubules even when the BAR dimer is disrupted (10,11). Indeed, modifications that disrupt the BAR dimer may permit an even higher concentration of amphipathic helices to accumulate in the bilayer than would occur with the full dimer, thus enabling curvature generation by the N-terminal helices in the absence of the positively charged concave surface formed by the dimer. Therefore, under certain conditions the N-BAR amphipathic helices may directly and vigorously generate membrane curvature, whereas under other conditions they may contribute to robust curvature development primarily by anchoring the BAR domain to the bilayer. Thus, an important question is: how are N-BAR domains typically arranged on the membrane and what is the concentration and arrangement of their N-terminal helices in the bilayer?

The presence of striations on N-BAR induced tubules suggests that N-BAR domains oligomerize on the membrane surface during liposome tubulation (10,13–15). In addition, cross-linking of N-BAR proteins yields higher-order oligomers (10,14). F-BAR domains (35,36), a related family of curvature-inducing modules, also create striations on tubulated vesicles and recently were found to form oligomers (37). Very recently, high-resolution electron cryomicroscopy of F-BAR domains bound to lipid tubules revealed additional specific interactions between F-BAR domains that were undetected in the crystal structure and confirmed that oligomerization of these domains on membranes is essential for driving tubulation (32). The sensitivity of induced membrane curvature to the stability of the N-BAR domain on the membrane surface, reported in this work, further supports the idea that oligomerization is essential for robust curvature generation. It is therefore likely that oligomerization plays an important role in membrane tubulation by N-BAR domains.

It is interesting to consider that the N-terminal helices of N-BAR domains may be involved in N-BAR oligomerization. This possibility has been considered before as a potential alternative to helix insertion into the bilayer (18), but since it now seems clear that the N-terminal helices embed in the membrane (11), oligomerization by these helices, if it happens, must occur in the membrane. It is interesting that an N-terminal fragment of the endophilin N-BAR domain can be cross-linked into higher-order oligomers, but only in the presence of liposomes (10). In addition, experimental and theoretical studies suggest that amphipathic helices embedded in the lipid bilayer will cause membrane thinning, which will create a driving force to push the helices together in the membrane (38,39). These findings point to a mechanism by which N-BAR domains might oligomerize on the membrane surface via their N-terminal helices to drive membrane tubulation. Of interest, a study involving the interfacially adsorbed amphipathic helix melittin showed that the membrane perturbation by a melittin monomer was quite minimal, but dimerization of melittin greatly increased the membrane perturbation (40). Hence, in a configuration such as this, oligomerizing N-terminal helices might enhance bilayer curvature locally, through more significant disruptions of local membrane structure, even at concentrations at which monomeric helices would not generate curvature (19). In this study, although the embedded helices in the “helix only” simulation were free to diffuse in the membrane, the timescale simulated (∼50 ns) was not sufficiently long to determine whether they will dimerize.

While this work was under review, an experimental study (41) of the N-terminal amphipathic helix from the N-BAR domain of BRAP (breast cancer-associated protein)/Bin2 (42) was published that provides evidence for dimerization of this helix in an antiparallel arrangement, and also independently proposes this as a possible mechanism for N-BAR domain oligomerization on the membrane. The same study also finds no evidence for tubulation of liposomes by the N-terminal amphipathic helix of BRAP/Bin2. This issue awaits further clarification, since other studies have found tubulation by amphipathic helices alone (6–9). As mentioned above, differences between amphipathic helices may affect their ability to induce curvature in membranes, as shown in previous studies (8,9). Our simulations suggest that a high concentration of helices embedded near the level of the phosphates and aligned parallel to each other would be effective in inducing tubulation. It remains to be seen whether this sort of ordered alignment of embedded helices actually occurs in the bilayer, and at what concentration they accumulate.

Additional work is required to understand how these local membrane perturbations translate into global membrane remodeling events. The simulations reported here probe only local curvature development, and although they can provide insight into the mechanisms of larger deformations, they cannot directly address effects that require the interaction of multiple N-BAR domains. In addition, although our simulations are among the largest that can currently be performed and require great amounts of computing resources, they are still only just large enough to allow observation of membrane remodeling by a single N-BAR domain. Therefore, it is possible that the system size influences the behavior of the system to some degree. The restricted space along the short membrane axis may accelerate the observation of membrane curvature. In contrast, the restricted space along the long principal axis could have the opposite effect, making it more difficult to bend the membrane, since for high curvatures both a positive and negative curvature must develop to allow the membrane to meet up with its periodic image (as in simulations NBR1 and NBR2). Therefore, it will be critical to continue to explore the interaction between the membrane and multiple N-BAR domains for even larger membrane systems at full all-atom resolution.

Another computer modeling strategy is to employ coarse-grained (CG) molecular modeling, as was recently done by Arkhipov et al. (43) for multiple N-BARs on a patch of lipid bilayer. More specifically, these researchers placed on a segment of CG membrane six CG N-BAR domains in a staggered alignment. In turn, they observed bending of the membrane into a radius of curvature similar to certain of the N-BAR-induced tubulated liposome structures observed experimentally. That such a CG model of multiple N-BAR domains aligned in such a fashion can bend a membrane is not surprising given the molecular-scale results already presented in both prior work (20) and this study. A greater challenge for such coarse-grained modeling will be to not only accurately model the diversity and subtlety of the molecular-scale results reported here, but to also reproduce the full range of experimentally observed N-BAR-induced vesiculation and tubulation behavior of liposomes in vitro (13) as a function of N-BAR concentration and other experimental conditions.

With such larger goals in mind, the results of atomistic MD simulations can instead be bridged in a multiscale fashion to mesoscopic simulations (44,45) that can provide additional insight into the mechanisms of the global (as opposed to local) membrane remodeling events that are observed in experiments. For example, our multiscale simulations (45) using results from the previous atomistic-level N-BAR simulations (20) have provided insight into how the BAR-domain-induced curvature density and degree of anisotropy can lead to experimentally observed in vitro liposome vesiculation and tubulation behavior (13). Thus, in addition to providing atomistic-level insight into mechanisms of membrane deformation by N-BAR domains, this work also lays the foundation for future atomistic, CG, and multiscale studies to investigate in further detail how multiple interacting N-BAR domains work together on larger-length scales to induce global membrane remodeling.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.