Abstract
Diffusion through the extracellular space (ECS) in brain is important in drug delivery, intercellular communication, and extracellular ionic buffering. The ECS comprises ∼20% of brain parenchymal volume and contains cell-cell gaps ∼50 nm. We developed a random-walk model to simulate macromolecule diffusion in brain ECS in three dimensions using realistic ECS dimensions. Model inputs included ECS volume fraction (α), cell size, cell-cell gap geometry, intercellular lake (expanded regions of brain ECS) dimensions, and molecular size of the diffusing solute. Model output was relative solute diffusion in water versus brain ECS (Do/D). Experimental Do/D for comparison with model predictions was measured using a microfiberoptic fluorescence photobleaching method involving stereotaxic insertion of a micron-size optical fiber into mouse brain. Do/D for the small solute calcein in different regions of brain was in the range 3.0–4.1, and increased with brain cell swelling after water intoxication. Do/D also increased with increasing size of the diffusing solute, particularly in deep brain nuclei. Simulations of measured Do/D using realistic α, cell size and cell-cell gap required the presence of intercellular lakes at multicell contact points, and the contact length of cell-cell gaps to be least 50-fold smaller than cell size. The model accurately predicted Do/D for different solute sizes. Also, the modeling showed unanticipated effects on Do/D of changing ECS and cell dimensions that implicated solute trapping by lakes. Our model establishes the geometric constraints to account quantitatively for the relatively modest slowing of solute and macromolecule diffusion in brain ECS.
INTRODUCTION
The extracellular space (ECS) in brain consists of a jelly-like matrix in which blood vessels, neurons, glial and other cells are embedded. The ECS represents only ∼20% of brain parenchymal volume under normal conditions (1–3), but can contract and expand dynamically with changes in the brain cell volume in various pathologies, during neuronal stimulation, and on administration of osmotic agents (4,5). ECS dimensions were estimated initially using electron microscopy (EM) images from tissue treated with osmium tetroxide, glutaraldehyde, or freeze-substitution, giving very variable results depending on the method of fixation (6,7). Subsequent measurements of ECS dimensions with probes of increasing sizes suggested the presence of ∼40–60 nm connecting paths in brain ECS (8), two- to fourfold greater than those derived from EM images. Diffusion of solutes in the ECS is important in normal brain function, for nonsynaptic cell-cell communication, extracellular buffering of K+ and other ions/solutes, and access/elimination of metabolites/wastes (9–11). Diffusion in brain ECS is also important for delivery of drugs and other therapeutic agents such as antibiotics treating cerebral infection, chemotherapeutics for brain tumors and potentially viruses for gene delivery.
Despite its small volume and narrow cell-cell gaps of brain ECS, various experimental approaches have shown relatively modest reductions in solute and macromolecule diffusion in brain ECS. A considerable body of data has been generated using the tetramethylammonium (TMA+) method, which involves pulsed iontophoretic introduction of TMA+, and microelectrode detection of decreasing [TMA+] as it diffuses away from the injection site (2). TMA+ measurements in brain slices and intact brain give tortuosity (λ) values in the range 1.5–1.8 (3,12). By definition, tortuosity λ = (Do/D)0.5, where Do and D are diffusion coefficients in water and brain, respectively; thus, measured λ in brain is equivalent to Do/D = 2.2- to 3.2-fold slowing of diffusion in brain versus water. However, it is not possible to relate λ directly to geometric constraints for ECS diffusion because λ depends not only on ECS geometry but also on extracellular matrix viscosity and TMA+ interactions with ECS cell boundaries and matrix components.
Our lab developed a cortical surface photobleaching method to measure diffusion of noninteracting fluorescent molecules at the surface of brain cortex after staining of brain ECS by passive dye penetration through the intact dura (4,13). This method is suitable for measurements of diffusion of any interacting or noninteracting fluorescent molecules. Do/D for FITC-dextrans in mouse brain cortex was in the range 2.9–3.3, and found to be sensitive to brain cell swelling, aquaporin-4 gene deletion, and seizure activity. Measurements of anisotropic diffusion in spinal cord suggested that geometric constraints and viscous resistance offer comparable hindrances to solute diffusion in the ECS (14). Because total measured Do/D is the product of geometric and viscous factors, Do/D = (Do/D)g × (Do/D)v, each of the individual hindrance factors is ∼1.7 for relatively small, noninteracting solutes. Recently, we developed a microfiberoptic photobleaching method in which diffusion could be measured deep in tissues using a micron-size optical fiber (15). Application of this method to mouse brain cortex confirmed the findings from cortical surface photobleaching, and showed substantially greater slowing of diffusion for large macromolecules in deeper brain structures including thalamus and caudate nucleus (16).
Several mathematical models of solute diffusion in the ECS have been reported. In an early model of brain ECS, Kullmann and Rusakov (17) assumed a random assembly of space-filling obstacles for brain ECS and reported that the geometric tortuosity has a unique value λ = 1.4–1.5, irrespective of ECS shape and size. Chen and Nicholson (18) developed two-dimensional (2D) models in which the ECS is outlined by various geometric shapes. An obvious limitation of 2D models of three-dimensional (3D) diffusion in a complex, narrow ECS is reduction of the number of particle paths when diffusion is confined to a plane, as was confirmed by Harbe et al. (19). Regarding models of ECS diffusion in three dimensions, a first simple model assuming uniformly spaced convex cells concluded that the geometrical tortuosity cannot exceed 1.23 (20), much lower than experimental values. In an attempt to increase predicted λ, Tao et al. (21) included dead-space microdomains as evenly spaced square cavities in all brain cells. The model required ∼40% of the ECS to comprise such hypothetical cavities to predict experimental λ. Recently, Nandigam and Kroll (22) included expansions in the ECS to help explain the relatively large measured tortuousities. Their ECS model contained close-packed arrays of fluid membrane vesicles generated by minimizing configurational energy. ECS models to date have not included realistic brain cell and ECS dimensions, or nonzero size for diffusing solutes.
The purpose of our study was to model experimentally measured Do/D in mouse brain to understand the geometric constraints to diffusion in the ECS. We modeled the ECS diffusion of arbitrary-size solutes in three dimensions for a cell array in which cell size and cell-cell gap dimensions could be specified, and in which intercellular lakes at multicell contact points could be introduced. Predicted Do/D were compared with experimental Do/D in different regions of brain for diffusing solutes of different sizes, and after water intoxication to increase brain cell volume. Experimental constraints required that the model include lakes and short gap width, which could quantitatively account for experimentally measured Do/D with minimal adjustable geometric features.
MATHEMATICAL MODELING METHODS
Random-walk model of ECS diffusion in two dimensions
We created random-walk models of diffusion in brain ECS in both two and three dimensions. For modeling in two dimensions, ECS boundaries were outlined using Voronoi cells (16,19,23). Voronoi cells are defined as regions such that all points within each cell are closer to its seed point than to any other seed point in the domain (24). Harbe et al. (19) used two- and three-dimensional Voronoi diagrams previously to simulate diffusion in the brain ECS. Specification of the locations of seed points determines the size, shape, and density of Voronoi cells. A quasi-uniform arrangement was used in which seed points initially positioned on a square grid were displaced randomly in the x and y directions. Displacement distances were sampled from Gaussian distributions with standard deviation equal to 30% of grid spacing. The randomness and density of cell arrangement are specified from the standard deviation of the Gaussian distribution and the grid spacing, respectively. Lakes were created by trimming the corners of Voronoi cells, which involved shortening of all Voronoi cell edges. After lake generation, each modified Voronoi cell was shrunk to create connections between lakes, producing an ECS composed of lakes and connections between lakes (16,23).
Monte-Carlo simulations were used to generate trajectories for diffusion of point-like particles of zero diameter, permitting the particle center to approach arbitrarily near the walls of the Voronoi cells. Point particles were placed at random positions initially in the ECS area. At each time step, x and y displacements were sampled from normal distributions with zero mean and standard deviation (2DoΔt)1/2, where the Do is diffusion coefficient and Δt the time interval between successive frames. When a particle passed through a cell edge during the random walk, specular reflection was applied, returning the particle to the side of the cell edge originally approached. Do was 10 μm2/s and Δt was 1/1000 s. We confirmed Δt = 1/1000 was small enough for accurate computations, as Δt = 1/10,000 did not alter results. For each simulation, 350 particle trajectories were computed over 15 s, which is adequate for particles to diffuse over multiple cell distances.
Random-walk model of ECS diffusion in three dimensions
For modeling in three dimensions, we used cubic lattices and look-up tables to simplify the problem and reduce computation time. Particles moved between lattice points within the ECS, which were assigned in look-up tables that were generated for specified ECS geometries. Particles were initially positioned randomly on lattice points in the ECS. Each particle can move to one of the eight adjacent lattice points (referred to as “And move”: Δx = ±1 and Δy = ±1 and Δz = ±1) after each time step, Δt, with imposed periodic boundary conditions at the boundary of the simulation domain, and reflective boundary conditions at the tissue surface. Distances between lattice points in the x, y, and z directions are: 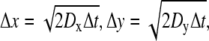 and
and 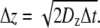 We consider only isotropic diffusion: Dx = Dy = Dz = Do. Because of intrinsic model symmetry, we can simulate without error a cell array with an infinite number of cells by considering a single cell with periodic boundary conditions. The largest cell size simulated was 10 μm and the domain contained 501 lattice points, giving a greatest lattice spacing of 0.02 μm and corresponding Δt of 2 × 10−5 sec. If a particle was directed to move outside of the ECS, it was instantaneous returned to the ECS using specular reflection conditions. We validated this lattice method and simulation program by: a), simulations of arrays of impermeable cylinders with different volume fractions whose analytic solution for diffusion coefficient is available (25) and; b), comparing with simulations using an “Or move” method (Δx = ±1 or Δy = ±1 or Δz = ±1) on a cubic lattice. The diffusion coefficients measured by our program were in good agreement with analytic solution (±4%) and with “Or move” simulations (see the Supplementary Material, Data S1).
We consider only isotropic diffusion: Dx = Dy = Dz = Do. Because of intrinsic model symmetry, we can simulate without error a cell array with an infinite number of cells by considering a single cell with periodic boundary conditions. The largest cell size simulated was 10 μm and the domain contained 501 lattice points, giving a greatest lattice spacing of 0.02 μm and corresponding Δt of 2 × 10−5 sec. If a particle was directed to move outside of the ECS, it was instantaneous returned to the ECS using specular reflection conditions. We validated this lattice method and simulation program by: a), simulations of arrays of impermeable cylinders with different volume fractions whose analytic solution for diffusion coefficient is available (25) and; b), comparing with simulations using an “Or move” method (Δx = ±1 or Δy = ±1 or Δz = ±1) on a cubic lattice. The diffusion coefficients measured by our program were in good agreement with analytic solution (±4%) and with “Or move” simulations (see the Supplementary Material, Data S1).
Modeling diffusion of nonzero size solutes
To simulate the diffusion of a particle with nonzero size, a limitation was introduced in the ECS region in which it could diffuse, which allowed particle diffusion only beyond a distance equal to its radius away from ECS boundaries. This parameter was implemented by virtual expansion of cells by the specified particle radius, allowing point-like particles to diffuse in the resultant reduced accessible volume. In this setting, a solute cannot diffuse past narrowings in the ECS where the intercellular distance is less than solute diameter.
Computation of diffusion coefficients from trajectories
The MSD for individual trajectories was computed as:
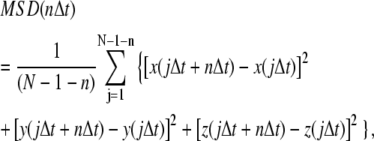 |
where x(t), y(t), and z(t) are the particle positions at time t, N is the total number of frames, n is the number of time intervals, and j is a positive integer. For analysis of trajectories in two dimensions the z-component in the above equation is deleted. Diffusion coefficients were determined from slopes of mean MSD versus time plots using >10 points on the straight portion of the mean MSD curve. The slope of MSD curve is 4DΔt for diffusion in two dimensions and 6DΔt for diffusion in three dimensions.
EXPERIMENTAL METHODS
Mice
Experiments were done on male, 25–30 g mice in a CD1 genetic background. Protocols were approved by the University of California San Francisco Committee on Animal Research.
Microfiberoptic epifluorescence photobleaching
Optical fibers (ThorLaboratories, Newton, NJ) were chemically etched to tip diameters of 2–5 μm and the tapered shaft was coated with a thin layer of aluminum, as described (16,23). Fluorescent dye was delivered into brain tissue using a dual-lumen device containing a micropipette through which dye-containing solution could be infused and a guide barrel for introduction of the optical microfiber.
Laser photobleaching was done by modulation of the first-order beam of an argon ion laser (∼1 W at 488 nm) using an acousto-optic modulator, as described (26). The beam was focused using a 20× objective lens onto an FC-type connector on the back of the optical fiber. Bleaching was accomplished by increasing laser illumination intensity 3000–6000-fold for 0.1–20 ms to reduce fluorescence by 30–40%. The low intensity probe beam used for acquisition produced <1% fluorophore bleaching for continuous recordings up to 5 s. Sample fluorescence collected by the optical fiber and objective lens was filtered (490 nm dichroic mirror, 510 nm long-pass filter) and detected by a photomultiplier.
Brain ECS diffusion measurements in mice
After anesthesia (intraperitoneal 2,2,2-tribromoethanol, 125 mg/kg) mice were immobilized in a stereotactic frame. Core temperature was maintained at 37–38°C. In some experiments water intoxication was produced by intraperitoneal injection of water (3% body weight) together with dDAVP (desmopressin acetate, 0.4 μg/kg), which is a well established model producing osmotic brain swelling and progressive rise of intracranial pressure. For microfiberoptic insertion the skull surface was exposed by a midline scalp incision and the skin was retracted. The site of the craniectomy was marked using stereotactic coordinates according to the Paxinos mouse brain map (27): frontal cortex (Bregma +1 mm), parietal cortex (Bregma −2.06 mm), occipital cortex (Bregma −2.46 mm), cerebellum (Bregma −3.00 mm), caudate nucleus (Bregma +1 mm), hippocampus (Bregma −2.06 mm), and thalamic nucleus (Bregma −2.06 mm), with all sites centered 1.2–1.4 mm lateral to midline. In most experiments two overlapping 1-mm diameter burr holes were created to give an approximately rectangular 1.5 × 1 mm space for insertion of the double-barrel microcapillary. The site of dye infusion was determined using the micropositioning system of the stereotactic frame. Intraparenchymal infusion of artificial cerebrospinal fluid (aCSF): (in mM) NaCl, 145; KCl, 4; MgCl2, 1; CaCl2, 2.5; KH2PO4, 1; glucose, 10; pH 7.4 containing FITC-dextran (10, 20, 70, 500, or 2000 kDa, 50 mg/mL) or calcein (40 mg/ml) was done at a rate of 0.15 μl/min for 15 min using an infusion pump. The fluorescent dye was allowed to penetrate the brain tissue surrounding the injection site for 20 min before measurements.
At each location, 5–8 photobleaching recovery measurements were made, with the fiber tip displaced 5–10 μm in depth to avoid repeat measurements at the exact same location. Averaged fluorescence recovery curves, F(t), were fitted to the semi-empirical equation (28): F(t) = (F0 + [ (F – F0) + F0](t/t1/2))[1+ (1/t1/2)]−1, where F is the prebleach fluorescence, F0 is the fluorescence immediately after bleaching, R is the mobile fraction (percentage recovery), and t1/2 is the half-time for recovery. This equation provided an excellent fit to the data, giving t1/2 as a single parameter describing the kinetics of fluorescence recovery. As validated previously (15), relative diffusion coefficient in aCSF versus brain (Do/D) was computed from t1/2 measured in brain versus aCSF: 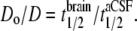
RESULTS
Diffusion of a small solute in brain ECS
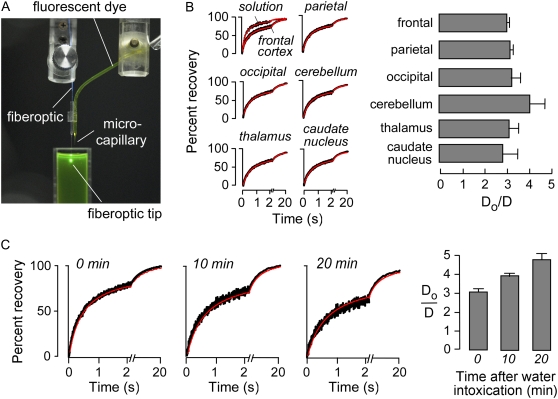
For comparison with model predictions microfiberoptic photobleaching measurements were done to establish a range of Do/D for diffusion of a small fluorescent solute, calcein, in various regions of brain. Fig. 1 A shows the dual-lumen device consisting of a microcapillary for dye delivery, and a glass capillary guide barrel for insertion of the optical microfiber. Fig. 1 B (left) shows representative fluorescence recovery curves for calcein in solution (aCSF) and in the ECS in different regions of brain. Do/D for calcein diffusion was remarkably similar throughout the brain in the range 3–4.1 (Fig. 1 B, right), corresponding to λ of 1.7–2.1.
FIGURE 1.
Experimental measurement of calcein diffusion in brain ECS in living mice. (A) Experimental setup, showing dual-lumen device housing a barrel to guide the microfiberoptic adjacent to a microcapillary for dye delivery. Conical illumination volume is produced at the fiberoptic tip. (B, left) Representative fluorescence recovery curves for microfiberoptic photobleaching measurements of calcein diffusion in ECS at indicated regions of mouse brain. (B, right) Averaged Do/D for calcein diffusion in aCSF versus brain ECS (SE, n = 4). (C, left) Recovery curves for calcein diffusion in cerebral cortex (400 μm beneath brain surface) before and at 10 and 20 min after intraperitoneal water administration. (C, right) Averaged data (SE, n = 4).
Mild water intoxication produced by intraperitoneal administration of water (3% body weight) was used as a simple maneuver to produce brain cell swelling (cytotoxic edema). Fig. 1 C (left) shows microfiberoptic photobleaching measurements of calcein diffusion in cerebral cortex at a depth of 400 μm from the brain surface. Under these mild water intoxication conditions there was progressive slowing of calcein diffusion, yet essentially complete fluorescence recovery. Do/D data are summarized in Fig. 1 C (right).
Random-walk model of ECS diffusion in two dimensions
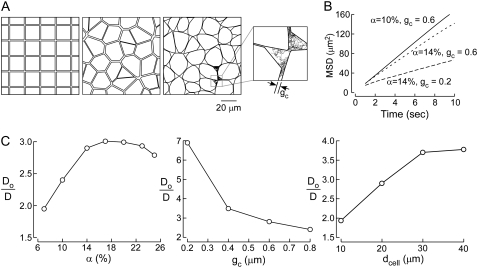
Fig. 2 A shows two-dimensional models of diffusion in brain ECS, each with the same area fraction, α, of 14% (equivalent to a measured 3D volume fraction of ∼20%). Fig. 2 A (left) shows a simple square lattice model with cells assembled as an array of square boxes, with point-like diffusing particles confined to the area outside of the boxes. Fig. 2 A (middle) shows a cell arrangement generated from a Voronoi diagram in which cell shape and size are irregular to more closely resemble brain. However, both models are fundamentally unrealistic in terms of measured ECS dimensions. Experimental determinations indicate typical α, cell size, and ECS gap width of ∼20%, 5–20 μm, and 50–100 nm, respectively. Neither the square nor Voronoi diagram models could satisfy these constraints, because these models require an ECS gap width of ∼1.5 μm to give 14% area fraction.
FIGURE 2.
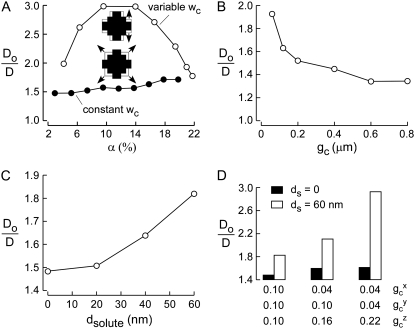
Two-dimensional models of diffusion in brain ECS. (A) Schematic of two-dimensional models: (left) square lattice model, α = 14%, gc = 1.45 μm; (middle) Voronoi cell model, α = 14%, gc ∼ 1.5 μm; and (right) Voronoi cell model with lakes at multicell contact points, α =14%, gc ∼ 0.6 μm. Inset at right shows random-walk path of a diffusing point-like particle. (B) Examples of MSD plots computed with the Voronoi cell-lake model. Parameters: dcell = 20 μm, with indicated gc and α. (C) Model behavior, showing Do/D for the Voronoi cell-lake model as a function of (left) α, (middle) gc, and (right) cell diameter, dcell. Parameters: (left) dcell = 20 μm, gc = 0.6 μm; (middle) α = 14%, dcell = 20 μm; (right) α = 14%, gc = 0.6 μm.
To overcome this fundamental constraint, lakes (local dilatations) were introduced at multicell contact point in the Voronoi cell model (Fig. 2 A, right). By changing lake size, it was possible to independently specify ECS width, area fraction, and cell size. To explore the behavior of this Voronoi cell-lake model we simulated two-dimensional Brownian random-walk diffusion; an example of the trajectory of a point-like particle is shown in the inset at the right in Fig. 2 A. Representative MSD plots for indicated α and gc are shown in Fig. 2 B, from computations of >350 trajectories, each with 15,000 time steps over 15 s. MSD curves were nearly linear, except at very early time points, similar to MSD curves for hop diffusion (29) and barrier diffusion (30). Diffusion coefficients were determined from the MSD curve slopes as described in the Mathematical Modeling section.
Do/D were computed for different α, cell-cell gap (gc), and cell diameter (dcell). In Fig. 2 C (left), dcell and gc were held fixed at 20 μm and 0.6 μm, respectively, and α was varied by changing lake size. For small α slowed diffusion (greater Do/D) was predicted for increasing α. This interesting behavior is a consequence of the reduced likelihood that a particle diffusing in a lake will find its exit (gap between lakes) with increased α and consequently lake size (at fixed cell/gap dimensions). At sufficiently high α, which depends on gap spacing, Do/D increases with increasing α. Fig. 2 C (middle) shows that greater gc increases Do/D, as anticipated. Fig. 2 C (right) shows reduced Do/D with increasing dcell at constant α and gc, which again is a consequence of the reduced likelihood of finding exit routes for large cells and lakes. These results introduce the concept of diffusive solute trapping by lakes, which is relevant as well to models of diffusion in three dimensions as described in the next section.
As alluded to in the Introduction, to compare the predictions of simulations with experimental data, we compare only the geometric hindrance, (Do/D)g, of ∼1.7 for small, point-like solutes. As seen in Fig. 2 C, Do/D simulated by the 2D model was much greater than this even though a substantially larger gap width was used for computations, 0.6 μm, than realistic values in the range 50–100 nm. Reducing gap width in two-dimensional models would further increase the difference between model predictions and experiment. We therefore developed models of ECS diffusion in three dimensions, reasoning that the multiplicity of diffusive pathways is predicted to reduce the hindrance to diffusion.
Random-walk models of ECS diffusion in three dimensions
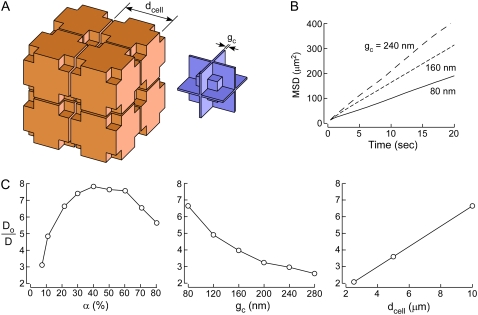
Fig. 3 A (left) shows the arrangement of cells for modeling diffusion in the ECS in three dimensions. Lakes were included at multicell contact points. Fig. 3 A (right) shows the geometry of the ECS in which particles diffuse. To minimize computational time cells were assembled on a cubic lattice with cell walls parallel to one of the three principal orthogonal planes. Cell size (dcell) and gap (gc) parameters could be specified, and by changing lake size α could be independently specified to model diffusion using realistic parameters, α ∼ 20% and gc ∼ 50 nm. Fig. 3 B shows representative MSD plots generated using this model. As found for the two-dimensional model, MSD curves were nearly linear for the 3D model. Fig. 3 C shows model behavior, with Do/D computed as a function of α, gc, and dcell. The model behavior was qualitatively similar to the 2D Voronoi cell-lake model in terms of increased Do/D with increasing α and dcell, and decreasing gc. However, although Do/D values were lower for the three-dimensional simulation for comparable parameters, as expected, they remained substantially greater than the experimental target Do/D of ∼1.7. Do/D was ∼7 for realistic dcell = 10 μm, α ∼ 21.5%, and gc = 80 nm.
FIGURE 3.
Three-dimensional model of diffusion in brain ECS. (A) Schematic of three-dimensional model of diffusion in brain ECS showing a cubic lattice arrangement of cells containing lakes at multicell contact points (left). ECS geometry with narrow gaps and lake regions (right). (B) Representative MSD plots. Parameters α ∼ 21.5%, dcell = 10 μm, and indicated gc. (C) Do/D as a function of (left) α, (middle) gc, and (right) dcell. Parameters: (left) dcell = 10 μm, gc = 80 nm; (middle) α ∼ 21.5%, dcell = 10 μm; (right) α ∼ 21.5%, gc = 80 nm.
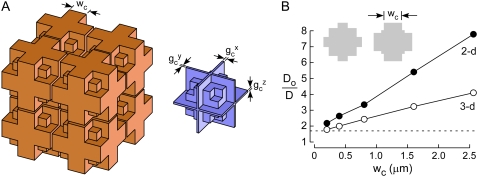
We could overcome this problem by modification of the three-dimensional model to allow independent specification of the width (wc) of the narrow gap between cells, as shown in Fig. 4 A. To specify wc at specified cell and ECS volumes, we introduced a volume-occupying mass in each lake. The rationale for this modification was the expectation that reduced wc would substantially reduce predicted Do/D, as well as morphometric data from electron micrographs regarding wc (see Discussion). Also, for subsequent computations requiring heterogeneity in gap dimensions, we allowed different gc in each of the orthogonal directions. Fig. 4 B shows Do/D as a function of wc in which the mass size was allowed to vary to maintain constant α. Do/D was reduced with smaller wc, such that the experimental target Do/D of ∼1.7 could be obtained in the three-dimensional model for wc ∼ 200 nm. For comparison, results are shown for a two-dimensional model with the same cross sections as the three-dimensional model. The two-dimensional model showed a similar behavior of reduced Do/D for smaller wc, although Do/D were greater than for the three-dimensional model.
FIGURE 4.
Modeling experimental Do/D by a 3D model with modified lakes. (A) Schematic of three-dimensional brain ECS model with modified lakes, showing (left) cell arrangement, and (right) ECS geometry. Lake dimensions were modified such that the gap width spacing (wc) could be independently specified. In addition, gap size in each direction could be independently specified to introduce gap heterogeneity. (B) Do/D as a function of wc for the three-dimensional model (open circles) and the 2D model (closed circles) with the same cross sections as the 3D model. Parameters: α ∼ 21.5%, gc = 80 nm, dcell = 10 μm. (For the 2D model α was 15.4–20.6%.) The experimental target line (dashed), Do/D = 1.7, is shown.
We further examined the behavior of this three-dimensional ECS model by varying α and gc, and investigated effects of introducing a finite diameter (dsolute) for the diffusing solute. The volume fraction α could be varied in two ways—by changing wc keeping lake mass size constant, and by changing lake mass size keeping wc constant (shown schematically in Fig. 5 A insets). Fig. 5 A shows Do/D as a function of α for varied (open circles) or fixed (solid circles) wc. Do/D with varied wc produced a similar α dependence as found in the two-dimensional lake model (Fig. 2), with decreasing Do/D as mass size increased. Decreased α is equivalent to cell swelling, which from experimental data (Fig. 1) results consistently in increased Do/D. Also, experimental measurements of osmotically altered volume fraction and tortuosity in rat cortical slices showed increased tortuosity with decreasing volume fraction from ∼20 to 12% (5). Cell swelling in vivo would likely change wc as well as mass size, so that increased Do/D is expected from the combination of the two modes of cell swelling. For the case of varied wc, Do/D increased abruptly from 1.8 to 3.0 as volume fraction decreased from that in normal brain of ∼20%, to that of ∼10% after water intoxication. However, for fixed wc Do/D decreased more subtly from 1.8 to 1.5 for decreasing α from 20 to 10%. Cell swelling could also reduce gc, which was kept constant in Fig. 5 A. Fig. 5 B shows that as expected, Do/D decreases with increasing gc, which was most pronounced for small gap spacing, gc < 100 nm. Therefore, relatively small reductions in gc caused by cell swelling could increase Do/D substantially.
FIGURE 5.
Characteristics of the modified lake model of 3D diffusion in brain ECS. (A) Do/D as a function of α. Two types of modifications were made to change α—altered wc (open circles) and fixed wc (altered lake mass, solid circles). Parameters: gc = 80 nm, dcell = 10 μm. (B) Do/D as a function of gc. Parameters: α = 21.8–22.6%, dcell = 10 μm. (C) Do/D as a function of dsolute. Parameters: gc = 100 nm, α = 21.9%, dcell = 5 μm. (D) Effect of heterogeneity in gc. Do/D shown for zero solute size (solid bars) and 60 nm solute size (open bars). Parameters: α = 21.9%, dcell = 5 μm.
Fig. 5 C shows the effect of diameter of the diffusing solute on Do/D. Gap size, gc, was 100 nm and solute diameter was increased from 20 to 60 nm. For nonzero solute size, the minimum distance between ECS walls and the center of the solute is the solute radius. As expected, the diffusion was progressively slowed with increasing solute size.
To investigate effects of nonhomogenous cell-cell gap, we chose three different configurations of cell gaps: a), (gcx, gcy, gcz) = (0.10, 0.10, 0.10) μm; b), (gcx, gcy, gcz) = (0.04, 0.10, 0.16) μm; and c), (gcx, gcy, gcz) = (0.04, 0.04, 0.22) μm. Other parameters, including α and dcell, were fixed, and the diffusion of point-like versus finite size solutes, dsolute = 0 and 60 nm, was simulated. Fig. 5 D shows that Do/D for a point-like solute was relatively insensitive to gap configuration, whereas Do/D for diffusion of the 60-nm diameter solute was increased by heterogeneity in gap spacing. As described further below, the concept shown by this computation, of ECS heterometricity, is relevant to account for size-dependent solute diffusion in deep brain structures.
Modeling of diffusion of macromolecule-size solutes in brain ECS
We previously reported strongly solute size-dependent Do/D in caudate nucleus that was proposed to arise from heterogeneity in cell/ECS geometry, which we called heterometricity (16,23). Although originally used to describe cell walls that are not parallel, we use the term heterometricity in this study to indicate any form of heterogeneity in ECS geometric parameters.
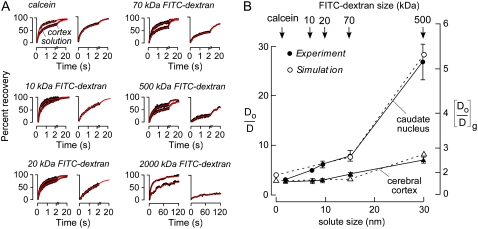
We carried out a more extensive set of Do/D measurements for a series of FITC-dextrans in the ECS of cerebral cortex and caudate nucleus, and simulated Do/D using the three-dimensional random walk model introduced in Fig. 4. FITC-dextran of 2,000 kDa has an approximate hydrodynamic radius of 44 nm (31), substantially greater than that of the 70 kDa FITC-dextran (∼14 nm) or calcein (∼2.8 nm) (8). Fig. 6 A shows fluorescence recovery curves for various FITC-dextrans in aCSF versus brain ECS. Fig. 6 B summarizes the solute size-dependent Do/D, showing substantially greater changes in Do/D in caudate nucleus versus cortex. Of note, fluorescence recovery was incomplete for the 2,000 kDa FITC-dextran, suggesting that cell-cell gap spacing is not much greater than 44 nm.
FIGURE 6.
Model comparisons with experimental data for solute size-dependent diffusion in mouse brain ECS. (A) Representative fluorescence recovery curves of indicated fluorescent dyes in cerebral cortex (left) and caudate nucleus (right). (B) Summary showing Do/D for ECS diffusion as a function of solute size (dsolute) in cerebral cortex (triangles) and caudate nucleus (circles) (SE, n = 5). Experimental data (solid) and simulated results (open) are overlaid. Simulation parameters: (gcx, gcy, gcz) = (40, 40, 40) nm for cerebral cortex, (gcx, gcy, gcz) = (10, 25, 45) nm for caudate nucleus, α ∼ 20%, dcell = 5 μm, wc = 90 nm.
The experimental data for calcein and the FITC-dextrans (up to 500 kDa), where fluorescence recoveries were nearly complete, was modeled, with parameters given in the legend to Fig. 6. For diffusion in cortex and caudate nucleus, a single set of geometric parameters was chosen that accurately predicted measured Do/D. As discussed further below, morphological studies show a stratified structure in cerebral cortex versus a nest-like organization for cells in caudate nucleus. This difference in cytoarchitecture may translate into greater solute-size dependence in caudate nucleus versus cortex.
DISCUSSION
The main purpose of this study was to model solute diffusion in three dimensions in brain ECS using realistic experimental data on solute diffusion, cell/ECS volume, and ECS dimensions. Significant constraints imposed by the experimental data required the inclusion of lakes at multicell contact points to predict geometric Do/D ∼ 1.7 for an ECS volume fraction α ∼ 0.2 and gap spacing 50–100 nm. The model also strictly required that the contact length of narrow cell-cell gaps be substantially smaller, by ∼50-fold, than cell size. The modeling yielded predictions for the sensitivity of solute diffusion to α, cell size, solute size, and ECS cell-cell contact geometry. The model has predictive value as shown by comparison of model results with experimental data on size-dependent solute diffusion and osmotically induced changes in ECS volume. The model also provided what we believe are new insights into the geometric determinants of ECS diffusion, predicting several unexpected results, such as the influence on Do/D of solute trapping by lakes and cell-cell contact geometry.
Our modeling approach involved simulation of Brownian diffusion on a cubic lattice with hard-wall reflective boundaries for specified cell/ECS geometry. The computation was simplified considerably by considering diffusion in a single ECS unit cell, with periodic boundary conditions, keeping track of x, y, and z indices specifying unit cell position. Computational accuracy was verified by independence of MSD curves on lattice spacing. An important finding of the simulations was that solute movement in the ECS, despite its complex and crowded geometry, was generally described by Brownian (nonanomalous) diffusion. Computed MSD curves were linear, following, as expected, a brief phase with greater slope representing diffusion in the extracellular matrix in the absence of geometric constraints. Brownian diffusion is free diffusion without obstacles. Diffusion in the brain ECS model is certainly far from free diffusion because of confinement of solute movement in the narrow space between closely packed cells. Nevertheless, MSD curves were linear (except the beginning of the curve), which is interesting and would have been difficult to predict a priori. However, there are several examples of complex diffusion that give near linear MSD plots, such as barrier diffusion (30) and hop diffusion (29).
A few prior studies have addressed effects of other forms of lakes. Chen and Nicholson (18) tested the effect of rounded corners on tortuosity, reporting increased tortuosity with increasing corner radius. If we consider the space generated by rounding cell corners as lakes, their result is consistent with the computations here. Similar effects were found in the model of Tao et al. (21), where cavities in cells were included. Also, the 3D model of Nandigam and Kroll (22) contained lake-like spaces between their spherical cells.
Our experimental approach to measure diffusion in brain ECS involved fluorescence recovery after photobleaching through an optical microfiber with micron-size tip that could be introduced stereotaxically into brain. The application of this approach for quantitative measurement of diffusion coefficients in solid, optically opaque tissues was validated previously (15) and applied to measurements of diffusion deep in tumor tissue (23) and brain (16). Unlike the TMA+ iontophoresis method, microfiberoptic photobleaching can be used to measure the diffusion of biologically relevant small and macromolecule-size solutes, and does not require correction for solute partitioning into cells.
We proposed previously that increased Do/D with increasing solute size is a consequence of heterogeneity in ECS dimensions, or heterometricity (16). Heterogeneity in cell-cell spacing in the ECS can produce strongly size-dependent diffusion because the diffusion of larger solutes is preferentially hindered by narrow cell-cell gaps. We previously modeled diffusion in two dimensions of an assembly of Voronoi cells where an ECS was created by reduction of Voronoi cell area in a manner that produced varying degrees of heterometricity. Here, for modeling of ECS diffusion in three dimensions, heterometricity was introduced by specification of different gap spacings on orthogonal surfaces of brain cells. Parameters could be selected that closely fitted experimental data on size-dependent solute diffusion in surface versus deep brain, supporting the concept that regional differences in heterogeneity in cell-cell gaps could account for differences in size-dependent diffusion.
Key requirements of the modeling done here, involving the presence of lakes and of narrow gaps at cell-cell contact points, are supported by morphological data. Notwithstanding fixation artifacts in electron microscopy, freeze-substitution electron micrographs show that the vast majority of brain ECS is contained in lake-like dilatations (6,32,33). Our model required lake volume to occupy ∼99% of ECS. Electron microscopy of brain also shows narrow cell-cell contacts as 30–50 nm wide gaps stretching between adjacent cell membranes, which expand into polygonal lakes of 200–500 nm size at multicell contact points (2,6,32,34). For measured, realistic α ∼ 20% and Do/D ∼ 3, our model required intercellular gap width ∼80 nm and lake size ∼800 nm, in general agreement with the morphometric data.
The model was applied to understand effects of acute brain cell swelling resulting in ECS volume contraction. Brain cell swelling is seen in cytotoxic brain edema, as occurs in water intoxication and consequent acute serum hyponatremia, ischemic stroke, head trauma, and meningitis (35,36). Acute brain cell swelling was produced using an established model of water intoxication involving intraperitoneal water administration. Mild water intoxication was used to model progressive brain cell swelling without creation of dead-space microdomains, which would manifest as incomplete fluorescence recovery (and require different modeling methods). The slowed ECS diffusion after brain cell swelling is attributable to reduced ECS volume fraction α. ECS volume contraction from cell swelling was modeled by independently varying the width and length of intercellular gaps. Brain slice data showed increased tortuosity from 1.6 to 1.9 (Do/D 2.6–3.6) with reduced α from 22 to 9% in response to changes in superfusate osmolality (5). These data correspond well to the model in Fig. 5 A in which ECS volume fraction is reduced to ∼11% by elongation of intercellular gap width keeping gc fixed. Our water intoxication data are also in agreement with these predictions, with a graded increase in Do/D from 3.1 to 3.8 to 4.8 after mild water intoxication in vivo, corresponding to reduced α from ∼22, 19, and 18%, respectively. Freeze-substitution electron micrographs show reduced lake size and near disappearance of the intercellular gaps with severe cell swelling in models of cortical spreading depression and asphyxia (6,34). From the modeling here, we propose that in addition to shrinkage of gap and lake size, increased length of the intercellular gaps is also an important determinant of ECS diffusion in cytotoxic brain edema.
Prior photobleaching measurements showed a 20–30% increase in Do/D for solute diffusion in brain ECS in mice lacking glial water channel AQP4 (4,16). The model here allowed us to estimate the difference in α that could account for the increased Do/D, assuming that AQP4 deficiency does not produce changes in the viscous properties of the extracellular matrix. According to the simulations in Fig. 5 A, Do/D of 4.2 in wild-type mice and 3.0 in AQP4 null mice for 70 kDa FITC-dextran (16) translates to a small increase in α from ∼20 to 22%. This quite modest predicted increase in α, if it is verified by direct experimental measurements, seems unlikely to explain the altered neuroexcitation and potassium buffering phenotypes found in these mice (37), suggesting the need to identify alternative mechanisms to account for the mouse phenotype data.
In summary, we have developed a mathematical model of diffusion in a three-dimensional ECS using realistic values for ECS volume fraction and cell-cell contact spacing. The model closely recapitulated experimentally determined diffusion coefficients in brain ECS, as well as effects of solute size and osmotic cell swelling. Our modeling approach is readily adaptable for computations of anisotropic and convective diffusion.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
This work was supported by grants EB00415, DK35124, EY13574, HL59198, DK72517, and HL73856 from the National Institutes of Health, and Research Development Program and Drug Discovery grants from the Cystic Fibrosis Foundation.
Editor: David W. Piston.
References
- 1.Mazel, T., Z. Simonova, and E. Sykova. 1998. Diffusion heterogeneity and anisotropy in rat hippocampus. Neuroreport. 9:1299–1304. [DOI] [PubMed] [Google Scholar]
- 2.Nicholson, C., and E. Sykova. 1998. Extracellular space structure revealed by diffusion analysis. Trends Neurosci. 21:207–215. [DOI] [PubMed] [Google Scholar]
- 3.Nicholson, C., K. C. Chen, S. Hrabetova, and L. Tao. 2000. Diffusion of molecules in brain extracellular space: theory and experiment. Prog. Brain Res. 125:129–154. [DOI] [PubMed] [Google Scholar]
- 4.Binder, D. K., M. C. Papadopoulos, P. M. Haggie, and A. S. Verkman. 2004. In vivo measurement of brain extracellular space diffusion by cortical surface photobleaching. J. Neurosci. 24:8049–8056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kume-Kick, J., T. Mazel, I. Vorisek, S. Hrabetova, L. Tao, and C. Nicholson. 2002. Independence of extracellular tortuosity and volume fraction during osmotic challenge in rat neocortex. J. Physiol. 542:515–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.van Harreveld, A., and S. K. Malhotra. 1967. Extracellular space in the cerebral cortex of the mouse. J. Anat. 101:197–207. [PMC free article] [PubMed] [Google Scholar]
- 7.van Harreveld, A., and F. I. Khattab. 1968. Perfusion fixation with glutaraldehyde and post-fixation with osmium tetroxide for electron microscopy. J. Cell Sci. 3:579–594. [DOI] [PubMed] [Google Scholar]
- 8.Thorne, R. G., and C. Nicholson. 2006. In vivo diffusion analysis with quantum dots and dextrans predicts the width of brain extracellular space. Proc. Natl. Acad. Sci. USA. 103:5567–5572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Agnati, L. F., M. Zoli, I. Stromberg, and K. Fuxe. 1995. Intercellular communication in the brain: wiring versus volume transmission. Neuroscience. 69:711–726. [DOI] [PubMed] [Google Scholar]
- 10.Somjen, G. G. 2002. Ion regulation in the brain: implications for pathophysiology. Neuroscientist. 8:254–267. [DOI] [PubMed] [Google Scholar]
- 11.Sykova, E. 1997. Extracellular space volume and geometry of the rat brain after ischemia and central injury. Adv. Neurol. 73:121–135. [PubMed] [Google Scholar]
- 12.McBain, C. J., S. F. Traynelis, and R. Dingledine. 1990. Regional variation of extracellular space in the hippocampus. Science. 249:674–677. [DOI] [PubMed] [Google Scholar]
- 13.Papadopoulos, M. C., D. K. Binder, and A. S. Verkman. 2005. Enhanced macromolecular diffusion in brain extracellular space in mouse models of vasogenic edema measured by cortical surface photobleaching. FASEB J. 19:425–427. [DOI] [PubMed] [Google Scholar]
- 14.Papadopoulos, M. C., J. K. Kim, and A. S. Verkman. 2005. Extracellular space diffusion in central nervous system: anisotropic diffusion measured by elliptical surface photobleaching. Biophys. J. 89:3660–3668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Thiagarajah, J. R., J. K. Kim, M. Magzoub, and A. S. Verkman. 2006. Slowed diffusion in tumors revealed by microfiberoptic epifluorescence photobleaching. Nat. Methods. 3:275–280. [DOI] [PubMed] [Google Scholar]
- 16.Zador, Z., M. Magzoub, S. Jin, G. T. Manley, M. C. Papadopoulos, and A. S. Verkman. 2008. Microfiberoptic fluorescence photobleaching reveals size-dependent macromilecule diffusion in extracullular space deep brain. FASEB J. 22:870–879. [DOI] [PubMed] [Google Scholar]
- 17.Rusakov, D. A., and D. M. Kullmann. 1998. Geometric and viscous components of the tortuosity of the extracellular space in the brain. Proc. Natl. Acad. Sci. USA. 95:8975–8980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen, K. C., and C. Nicholson. 2000. Changes in brain cell shape create residual extracellular space volume and explain tortuosity behavior during osmotic challenge. Proc. Natl. Acad. Sci. USA. 97:8306–8311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hrabe, J., S. Hrabetova, and K. Segeth. 2004. A model of effective diffusion and tortuosity in the extracellular space of the brain. Biophys. J. 87:1606–1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tao, L., and C. Nicholson. 2004. Maximum geometrical hindrance to diffusion in brain extracellular space surrounding uniformly spaced convex cells. J. Theor. Biol. 229:59–68. [DOI] [PubMed] [Google Scholar]
- 21.Tao, A., L. Tao, and C. Nicholson. 2005. Cell cavities increase tortuosity in brain extracellular space. J. Theor. Biol. 234:525–536. [DOI] [PubMed] [Google Scholar]
- 22.Nandigam, R. K., and D. M. Kroll. 2007. Three-dimensional modeling of the brain's ECS by minimum configurational energy packing of fluid vesicles. Biophys. J. 92:3368–3378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Magzoub, M., S. Jin, and A. S. Verkman. 2007. Enhanced macromolecule diffusion deep in tumors after enzymatic digestion of extracellular matrix collagen and its associated proteoglycan decorin. FASEB J. 22:276–284. [DOI] [PubMed] [Google Scholar]
- 24.Okabe, A., B. Boots, and K. Sugihara. 2000. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams. Wiley, New York, NY.
- 25.Sen, P. N., and P. J. Basser. 2005. A model for diffusion in white matter in the brain. Biophys. J. 89:2927–2938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Seksek, O., J. Biwersi, and A. S. Verkman. 1997. Translational diffusion of macromolecule-sized solutes in cytoplasm and nucleus. J. Cell Biol. 138:131–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Franklin, K. B. J., and G. Pazinos. 1997. The Mouse Brain in Stereotatic Coordinates. Academic Press, New York, NY.
- 28.Axelrod, D., D. E. Koppel, J. Schlessinger, E. Elson, and W. W. Webb. 1976. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 16:1055–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ritchie, K., X. Y. Shan, J. Kondo, K. Iwasawa, T. Fujiwara, and A. Kusumi. 2005. Detection of non-Brownian diffusion in the cell membrane in single molecule tracking. Biophys. J. 88:2266–2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jin, S., and A. S. Verkman. 2007. Single particle tracking of complex diffusion in membranes: simulation and detection of barrier, raft, and interaction phenomena. J. Phys. Chem. B. 111:3625–3632. [DOI] [PubMed] [Google Scholar]
- 31.Armstrong, J. K., R. B. Wenby, H. J. Meiselman, and T. C. Fisher. 2004. The hydrodynamic radii of macromolecules and their effect on red blood cell aggregation. Biophys. J. 87:4259–4270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bondareff, W., and R. Narotzky. 1972. Age changes in the neuronal microenvironment. Science. 176:1135–1136. [DOI] [PubMed] [Google Scholar]
- 33.van Harreveld, A., and F. I. Khattab. 1967. Changes in cortical extracellular space during spreading depression investigated with the electron microscope. J. Neurophysiol. 30:911–929. [DOI] [PubMed] [Google Scholar]
- 34.van Harreveld, A. 1966. Extracellular space in the central nervous system. Proc. K. Ned. Akad. Wet. C. 69:17–21. [PubMed] [Google Scholar]
- 35.Klatzo, I. 1994. Evolution of brain edema concepts. Acta Neurochir. Suppl. (Wien). 60:3–6. [DOI] [PubMed] [Google Scholar]
- 36.Liang, D., S. Bhatta, V. Gerzanich, and J. M. Simard. 2007. Cytotoxic edema: mechanisms of pathological cell swelling. Neurosurg. Focus. 22:E2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Verkman, A. S., D. K. Binder, O. Bloch, K. Auguste, and M. C. Papadopoulos. 2006. Three distinct roles of aquaporin-4 in brain function revealed by knockout mice. Biochim. Biophys. Acta. 1758:1085–1093. [DOI] [PubMed] [Google Scholar]