Cofactor Dependent Conformational Switching of GTPases

Abstract

This theoretical work covers structural and biochemical aspects of nucleotide binding and GDP/GTP exchange of GTP hydrolases belonging to the family of small GTPases. Current models of GDP/GTP exchange regulation are often based on two specific assumptions. The first is that the conformation of a GTPase is switched by the exchange of the bound nucleotide from GDP to GTP or vice versa. The second is that GDP/GTP exchange is regulated by a guanine nucleotide exchange factor, which stabilizes a GTPase conformation with low nucleotide affinity. Since, however, recent biochemical and structural data seem to contradict this view, we present a generalized scheme for GTPase action. This novel ansatz accounts for those important cases when conformational switching in addition to guanine nucleotide exchange requires the presence of cofactors, and gives a more nuanced picture of how the nucleotide exchange is regulated. The scheme is also used to discuss some problems of interpretation that may arise when guanine nucleotide exchange mechanisms are inferred from experiments with analogs of GTP, like GDPNP, GDPCP, and GDP 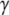S.

A BRIEF INTRODUCTION TO THE GTPASE FAMILY

Small GTPases form a superfamily of regulatory GTP hydrolases that are involved in core cellular processes such as messenger RNA (mRNA) translation, signal transduction, light perception, and intracellular trafficking (for reviews, see Sprang (1) and Bourne (2)). The GTPases oscillate between their GTP- and GDP-bound states via precisely regulated cycles of GTP hydrolysis and exchange of GDP for GTP. The factors that stimulate the hydrolytic activity and the GDP/GTP exchange of a GTPase are commonly referred to as the GTPase activating protein (GAP) (for a review, see Scheffzek and Ahmadian (3)) and the guanine exchange factor (GEF) (see Sprang (4)), respectively.

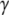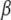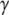During the last 30 years, nucleotide hydrolysis and exchange on GTPases have been extensively studied with biochemical and structural methods. Many x-ray crystal structures are now available for GTPases in the apo-state, in complex with GDP, GTP, the non hydrolysable GDPNP or GDPCP analogs or the slowly hydrolysable GTP S analog. In GDPNP and GDPCP, the oxygen atom bridging the - and -phosphates of GTP is substituted by an N or a C atom, respectively. In terms of bond angles and bond lengths, GDPNP is more similar to GTP than GDPCP. In GTP 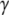S, one of the oxygen atoms at the 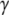-phosphate of GTP is substituted by a sulfur atom.

The GTP-binding domains in the GTPase family have similar sequences and overall structures, and five structural motifs involved in nucleotide binding have been identified (Fig. 1). The P-loop (Walker A), NKXD, and SAL motifs confer nonspecific GTPase binding to GTP and GDP. The switch I (effector) and switch II (Walker B) loops allow the GTPase to discriminate between GTP and GDP, and are thus essential for the conformational switches at the heart of GTPase function (1).

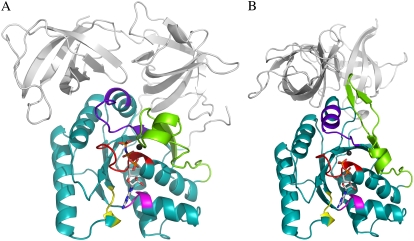
FIGURE 1.

D and T structures of the GTPase. A cartoon representation of conserved G-protein motifs in EF-T complexed with GDPNP (Protein Data Bank (PDB) entry 1TTT) (panel A), which is stabilized by tRNA binding in vivo, and GDP (PDB entry 1TUI) (panel B). Color code: P-loop (red), switch I and II (chartreuse and purple blue, respectively), the NKXD motif (yellow), and the SAL motif (magenta). The G domain is shown in teal. The largest conformational rearrangements observed between the GDPNP and GDP conformations in the nucleotide vicinity are located in the switch regions.

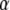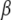The P-loop motif has the consensus sequence (G/A)XXXXGK(S/T), and binds strongly to the - and -phosphates of GDP and GTP. The NKXD motif, aided by the SAL motif, binds strongly to the guanine moiety and the ribose ring. Switch I normally contains a specific threonine, sometimes replaced by a serine, which coordinates an Mg²⁺ ion in a manner determined by the identity of the GTPase bound guanine nucleotide. The role of the threonine (or serine) is either to promote selective GTPase binding to GTP in relation to GDP or to prevent premature hydrolysis of the GTPase-bound GTP molecule (1).

Switch II accommodates the 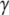-phosphate of GTP and is, together with a semiconserved residue that frequently is Gln and sometimes His, essential for the GTP hydrolysis reaction (1,5). Switch II often undergoes large rearrangements when GTP replaces GDP on the GTPase (Fig. 1) (1,6–8). These two conformations are often referred to as the GDP- and GTP-bound forms of the GTPase. Accordingly, switch II has been implicated as a major determinant of the overall changes in GTPase conformation in response to GTP hydrolysis or guanine nucleotide exchange (1), as verified by crystal structures of several GTPases in complex with either GDP or GDPNP, like p21 Ras (9,10), Gα (11,12), SelB (13), and EF-Tu (6–8).

According to the classical view, a GTPase should be in the active GTP conformation when bound to GTP and in a structurally distinct GDP conformation when bound to GDP. However, the GDP and GDPNP bound forms of several recently determined X-ray crystal structures of GTPases are virtually identical (14–16). This aberration from the classical view led to the suggestion that these GTPases must have a mode of action distinct from that of their classical counterparts (14). There is, as will be described in what follows, another explanation, which does not invoke a principally different mechanism for the seemingly deviating GTPases, but integrates them in a unified view of GTPase action. In brief, this is done quantifying the classical view of GTPase action starting from two simple questions: i), what is equilibrium constant between the GTP favored (T form) and the GDP favored (D form) conformations of a GTPase in the absence of guanine nucleotides, free or in complex with other ligands; and ii), how much better does GTP bind to the T form than to the D form and how much better does GDP bind to the D form than to the T form? These answers together with thermodynamic theory are then used to account for hitherto unexplained experimental observations within an extended framework of classical GTPase action and to predict the outcome of new experiments.

RAPID GUANINE NUCLEOTIDE EXCHANGE AND THEREAFTER

Nucleotide exchange on a GTPase, i.e., dissociation of GDP and association of GTP, is often catalyzed by GDP/GTP exchange factors (GEFs). The GEF concept originates in early reports on the p21 Ras GTPase (reviewed by Bourne (17)). For some GTPases that return GDP-bound to the free state after GTP hydrolysis, the rate constant for GDP dissociation is very small and potentially inhibitory for their rapid cycling back to their active state. A well-known example is the working cycle of elongation factor Tu (EF-Tu), which delivers aminoacyl-tRNA to the mRNA programmed ribosome in “ternary” complex with GTP (18). After delivery of aminoacyl-tRNA to the ribosome, EF-Tu returns to the free state in complex with GDP. The average time for spontaneous dissociation of GDP is ∼100 s and the cycling time for EF-Tu in the living cell is ∼1 s. However, rapid cycling of EF-Tu back to the GTP-bound state is made possible by the presence of the GEF elongation factor Ts (EF-Ts), present in the cell at a concentration much smaller than that of EF-Tu (19). When EF-Ts associate with EF-Tu·GDP, it brings EF-Tu to a conformation with low guanine nucleotide affinity and evokes rapid dissociation of GDP (20–22).

The structural corollary to these events is a rearrangement in the nucleotide-binding pocket of EF-Tu, affecting the DXXG motif and the following switch II loop (see Fig. 3 and Cherfils and Chardin (23) for a review). The aspartate in DXXG is, first, rearranged to destabilize its interaction with those water molecules that coordinate an Mg²⁺ ion, which is a major determinant of the affinity of the GTPase to guanine nucleotides. Second, the rearrangement destabilizes the interaction between the aspartate and the lysine in the P-loop, thereby removing an anchor point for nucleotide binding and thus reducing the affinity of the GTPase to guanine nucleotides (24–26). When the eukaryote homolog eEF1A of the bacterial EF-Tu binds to GEF eEF1B, an additional structural feature is that a lysine residue from eEF1Bα subunit interacts repulsively with the β-phosphate of the guanine nucleotide and thereby actively ejects it (27). A similar catalysis of GDP to GTP is performed by GRF1 on p21 Ras (17). The bacterial GTPase RF3, which recycles class-1 release factors after termination of protein synthesis, is a particularly interesting example. Here, the GEF is the ribosome itself, stalled at a stop codon and in complex with a class-1 release factor (28).

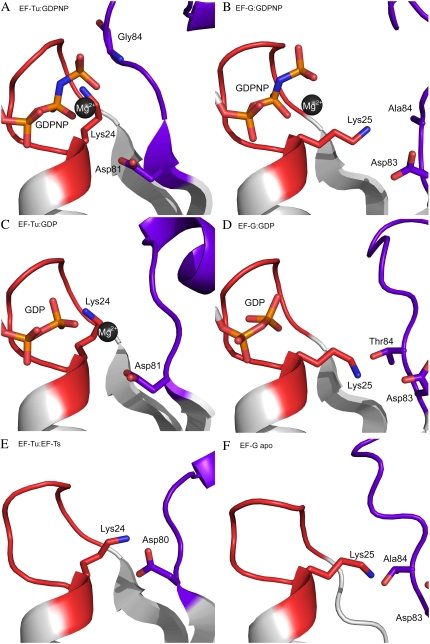
FIGURE 3.

Structural elements involved in GDP ejection and consequent GTP binding: response on GSF and GDS association with the GTPase. Cartoon representations of EF-Tu (PDB entry 1TTT) and EF-G (PDB entry 2BV3) in complex with GDPNP (panels A and B, respectively). GDP-bound structures of EF-Tu (PDB entry 1TUI) and EF-G (PDB entry 1DAR) are presented in panels C and D, respectively. Panels E and F show EF-Tu in complex with EF-Ts (PDB entry 1EFU) and the apo-form of EF-G (PDB entry 1ELO), respectively. Color codes are the same as in Fig. 1.

Sometimes, the GEFs discussed here are referred to as guanine nucleotide dissociation stimulators (GDS) (29–31), a name better adapted to their actual function (Fig. 2). However, even if rapid GDP dissociation and GTP binding occur spontaneously or are catalyzed by a GDS (GEF), this is just one part of guanine nucleotide exchange and conformational switching of a GTPase. For instance, EF-Tu binds GDP with orders-of-magnitude larger affinity than GTP (32,33), meaning that even residual amounts of GDP in the cytoplasm will prevent formation of GTP-bound EF-Tu. In fact, extensive exchange of GDP to GTP on EF-Tu requires the presence of yet another ligand, i.e., which binds tightly to the GTP-favoring state stabilizing it in preference to the GDP-favoring state. When eRF1 binds to the GTPase eRF3, the affinity to GTP of the latter is greatly increased (34–37). When, finally, the translocation GTPase EF-G binds to a naked or pretranslocation ribosome, its affinity to GDPNP increases greatly (38,39) and it undergoes a large conformational change (40), never observed for free EF-G. The ADP-ribosylation factor, regulating intracellular trafficking, only binds GTP when in complex with its effector (41), in analogy to the high GTP-affinity of EF-Tu, which requires the presence of aminoacyl-tRNA.

FIGURE 2.

Unified model for GTPase-bound nucleotide exchange regulation. After GTP hydrolysis in a GTPase, its reactivation requires dissociation of GDP and binding of a new GTP molecule. There are two types of GDP/GTP exchange factors (GEF). The guanine nucleotide dissociation stimulator (GDS) increases the rate of GDP dissociation by transiently stabilizing a conformation of the GTPase with small affinity to nucleotides. GTP binding may subsequently be stabilized by the GTP stabilizing factor (GSF), which shifts the equilibrium of the apo-form of the GTPase from the D toward the T conformation. In the case of EF-Tu, elongation factor EF-Ts acts as GDS, accelerating the rate of GDP/GTP exchange. However, free EF-Tu has about two orders of magnitude higher affinity to GDP than to GTP. Aminoacyl-tRNA greatly increases the affinity of EF-Tu to GTP, thereby acting as the GSF. Formation of the EF-Tu·GTP·aminoacyl-tRNA complex greatly favors GTP binding to the factor.

Three previously unaccounted features of GTPase action are hidden among these examples. The first concerns the equilibrium affinities of a GTPase to GDP and GTP and how these affinities depend on other ligands or cofactors. The second concerns the propensity of a GTPase to switch conformation upon guanine nucleotide exchange, and how this propensity is modulated by cofactors, other than the guanine nucleotides. The third concerns how chemical differences between GTP and its analogs affect nucleotide binding and the propensity of a GTPase to switch conformation. In the next section, we therefore discuss an equilibrium scheme for GTPase action, which accounts for their propensity to bind GTP in the presence of significant amounts of GDP in the cell, their propensity to switch conformation upon guanine nucleotide exchange, the effects on nucleotide binding and conformational switching by replacing GTP with its analogs, and the effects of ligands, other than GDP and GTP, on nucleotide binding and conformational switching.

EQUILIBRIUM SCHEME FOR GUANINE NUCLEOTIDE BINDING AND CONFORMATIONAL SWITCHING OF GTPASES

The basis of our analysis of guanine nucleotide binding to GTPases and their propensity to switch conformation upon guanine nucleotide exchange is this scheme with a GTP-favoring conformation, T, and a GDP-favoring conformation, D:

(1)

D and T are the nucleotide-free D and T conformations of the GTPase, respectively. Their equilibrium concentrations are related through [T]= K₀[D]. D·GDP is the D form in complex with GDP (dissociation constant 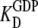), T·GDP is the T form in complex with GDP (dissociation constant 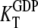), D·GTP is the D form in complex with GTP (dissociation constant 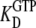), and T·GTP is the T form in complex with GTP (dissociation constant 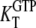). This scheme deviates from standard treatments, in that it focuses on the GTP favoring the T conformation and the GDP favoring the D conformation of the GTPase, rather than on its GTP- and GDP-bound states.

The parameters are related to the equilibrium constants in Scheme 1 by detailed balance (42):

(2)

Normally, GTP and GDP have strong preferences for the T and D forms of the GTPase, respectively, implying that both and are much larger than one. In standard experiments to determine equilibrium constants for the binding of GDP or GTP to a GTPase (18,39,43), one always estimates the effective or compounded (equilibrium) dissociation constants 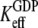or 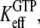respectively, reflecting the equilibrium mixture of the D and T forms of the GTPase. Accordingly, the two effective dissociation constants are operationally defined by the relations

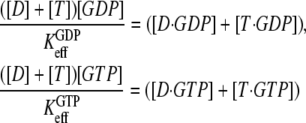(3)

and can therefore be expressed in terms of the parameters in Scheme 1 through

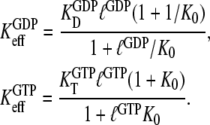(4)

The equilibrium probabilities P(GTP), P(GDP), or P(0) that the GTPase is bound to a GTP molecule, a GDP molecule, or is free, respectively, are related to the effective dissociation constants in Eqs. 3 and 4 through

(5)

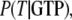
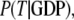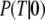Accordingly, the overall equilibrium probability, P(T), that the GTPase is in the T form is determined by the probabilities in Eq 5 and on the conditional probabilities and that the GTP-bound, GDP-bound, and free GTPase, respectively, are in the T form, i.e.,

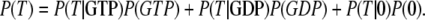(6)

The conditional probabilities in Eq. 6 are obtained by considering the special cases when the GTPase is populating only the lowest, only the highest, and only the middle row in Scheme 1, respectively:

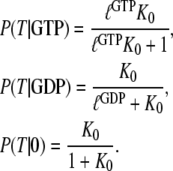(7)

From this follows that a GDP-bound GTPase is preferentially in the D form when 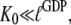a guanine nucleotide-free GTPase is preferentially in the D form when 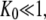and a GTP-bound GTPase is preferentially in the T form when 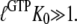However, when 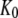is sufficiently small, it may happen that 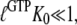although 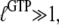implying that the GTP-bound GTPase preferentially remains in its inactive D form.

From Eqs. 5–7, we obtain an explicit expression for the probability 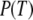that a small GTPase is in the T form:

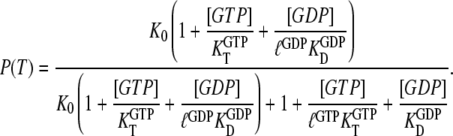(8)

To illustrate, consider the special but common case that 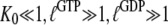and high concentrations of guanine nucleotides, so that the concentration of free GTPase is negligible, where Eq. 8 simplifies to

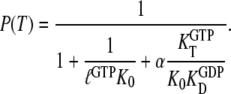(9)

The parameter 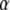is the ratio between the concentrations of GDP and GTP, which normally is quite small in the cytoplasm (44). A value much larger than 1 of the third term in the denominator illustrates the case that although 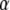may be small, the GTPase is preferentially GDP-bound and therefore inactive. When, in other words, the equilibrium ratio 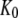between the concentrations 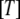and 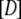of the apo-forms of the GTPase is very small, then the free GTPase may fail to adopt its active form either because the presence of GTP is not sufficient to induce the active conformation or because it remains GDP bound even when the concentration of GDP is much smaller than the concentration of GTP. As will be demonstrated below, both these hitherto unexplained scenarios do occur.

However, the situation may change radically in the presence of ligands, other than the guanine nucleotides, with different dissociation constants for the T (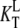) and D forms (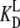) of the GTPase. The presence of such a ligand on the GTPase is accounted for by substituting the equilibrium constant 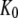in Scheme 1 with a compounded equilibrium constant 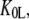defined as

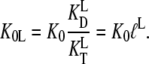(10)

When the ligand has much higher affinity to the T than to the D form of the GTPase, it means that 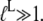Accordingly, addition of such a ligand would greatly reduce the second and third terms of the denominator in Eq. 9 and could thus induce a full switch from the D to the T form of the GTPase. Examples of this general principle of GTPase action will be given below.

In many recent experiments on GTPases, GTP has been replaced by one of its noncleavable or slowly cleavable analogs to avoid premature GTP hydrolysis. To account for such swaps, the dissociation constants 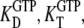and their ratio 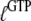must be replaced by their analog counterparts, e.g., 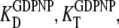and 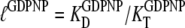for the GDPNP analog of GTP. As will be discussed below, it is likely that 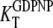is larger and 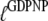is smaller than the corresponding GTP parameters, which may lead to ambiguous interpretation of experiments.

COFACTOR DEPENDENT GDP TO GTP EXCHANGE AND CONFORMATIONAL SWITCHING OF GTPASES

Unconditional conformational switching: classical GTPases

Here, we will use Scheme 1 to discuss a selected number of GTPases with respect to their affinities to guanine nucleotides and their ability to switch conformation upon guanine nucleotide exchange. We will start with a “classical” trio of GTPases, with focus on EF-Tu, which are able to switch conformation without any cofactor and then discuss a number of “aberrant” GTPases (14), for which conformational switching requires the presence of auxiliary factors.

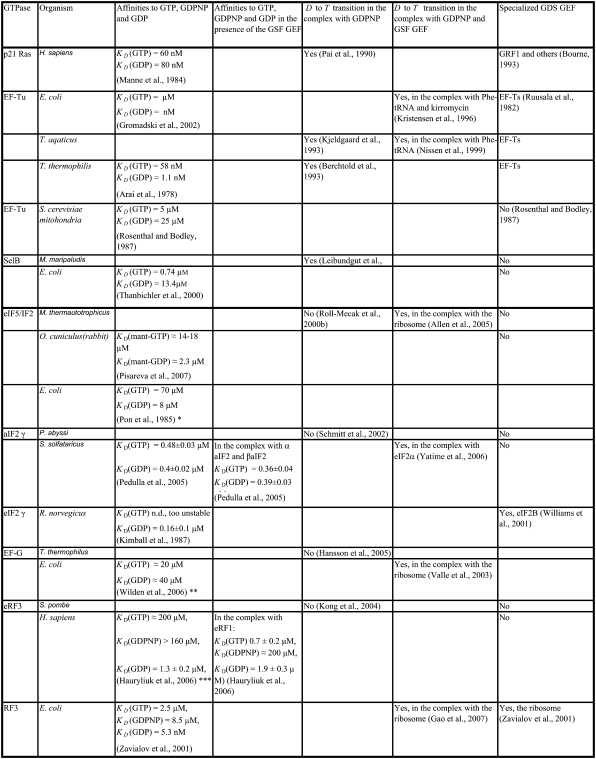
The three GTPases EF-Tu, p21 Ras, and SelB may be considered as classical in the sense that their GDPNP- and GDP-bound structures are distinct and correspond to their active and inactive forms, respectively (6,9,10,13). Ras and SelB have similar affinities to GDP and GTP, whereas EF-Tu has much smaller affinity to GTP than to GDP (Table 1) (33). This means that free EF-Tu will preferentially bind to GDP, even when the cytoplasmic concentration of GDP is much smaller than that of GTP (44), as explained by Eq. 9 above. However, the affinity of GTP to EF-Tu in binary complex with aminoacyl-tRNA is higher than the affinity of GDP to free EF-Tu (18,45). The fact that EF-Tu in the crystal switches conformation when GDP is replaced by GDPNP (or GTP) suggests that the conditional probability 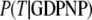(defined in Eq. 7), that EF-Tu in complex with GDPNP is in T conformation is close to 1, and hence that 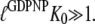The fact that EF-Tu binds GDPNP with much lower affinity than GDP means that 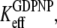as defined in Eq. 4, is much larger than 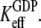Together with the inequalities 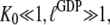this amounts to the following two equilibrium relations:

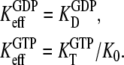(11)

TABLE 1.

Summary of available structural and biochemical data on the interactions of discussed GTPases with GTP, GDPNP and GDP nucleotides

K_D values given are effective K_D values as measured in the experiment.

^*similar results in (73)

^†similar results in (56)

^‡similar results in (36,37)

These relations mean that for free EF-Tu molecules, the measured dissociation constant, 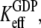for GDP binding is approximated by the dissociation constant, 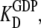for GDP binding to the D form of EF-Tu. In contrast, the measured dissociation constant, 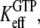is approximated by the dissociation constant 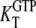for GTP binding to the T form of EF-Tu, divided by equilibrium constant 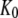that relates the equilibrium concentration of the apo T to the apo D form of the factor (Scheme 1). When, however, EF-Tu is in the binary complex with aminoacyl-tRNA, the effective dissociation constant for GTP binding to the factor is given by

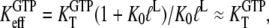(12)

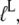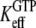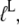where defined in Eq. 10, reflects the very large (32,33) affinity difference in the binding of aminoacyl-tRNA to the T and D forms of EF-Tu. Equation 12 clarifies how the affinity of GTP to EF-Tu increases from a small value (large ) for the free factor toward its maximal value (minimal ) by the preference, of aminoacyl-tRNA for the T compared to the D form of EF-Tu. In the case of EF-Tu, aminoacyl-tRNA also serves as an essential GTP stabilizing factor, allowing for extensive cellular exchange of GDP for GTP in the presence of a comparatively low, but significant, level of GDP in the cytoplasm. This can be seen by replacing 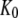by 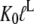in Eq. 9.

Conditional conformational switching: aberrant or neoclassical GTPases?

X-ray analysis of crystal forms of the GTPase EF-G, responsible for tRNA and mRNA translocation during protein elongation on the ribosome (46), shows that irrespective of the identity (GDP, GDPNP) or presence of guanine nucleotide, the structure of free EF-G is invariably the same. This conformation is stabilized by strong electrostatic interaction between the highly conserved P-loop lysine (Lys-25) and the DXXG aspartate (Asp-83) (Fig. 3) (16,47–49), similar to a corresponding electrostatic interaction observed for EF-Tu when in complex with EF-Ts (24–26). This electrostatic interaction may be responsible for the relatively weak guanine nucleotide binding that characterizes free EF-G (38,39,50), in analogy with the weak guanine nucleotide binding that characterizes EF-Tu in complex with EF-Ts (20,33). Instead of interacting with the γ-phosphate, the DXXG motif in EF-G is here locked internally onto Lys-25, and therefore does not stabilize GTP. A similar intramolecular lock has been observed in the structure of eEF2, which is the eukaryotic homolog of EF-G (51,52).

Similar results have been obtained for other GTPases involved in ribosome function, i.e., for the archeal initiation factor IF2/aIF5B (53), eukaryote initiation factor eIF2 (54), and the eukaryote termination factor eRF3 (14). In all these cases, the crystal conformation of the GTPase remains the same when GDP is swapped for GDPNP, a result so shocking that Kong and co-workers suggested that eRF3 cannot be a classical GTPase, but must be operating according to a radically different principle from the classical picture (14). One concern here is that GTP analogs such as GDPNP may be chemically too different from native GTP to induce a conformational switch that would occur when GDP is swapped for native GTP, and this will be further discussed below. However, in the case of the bacterial translocation factor EF-G, this is less likely, since small angle x-ray scattering experiments (55) suggest very similar solution structures for EF-G in apo form, bound to GDP and bound to GTP. Accordingly, it may well be that EF-G and the other “aberrant” GTPases enter the ribosome in complex with GTP, but in their inactive D form, rather than in their active T form (Scheme 1). If so, this is likely to have functional implications of considerable interest.

In terms of our equilibrium Scheme 1, the inability of the free GTPase to switch conformation is equivalent with fulfillment of the inequality

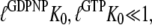(13)

although the GTP affinity to the free factor is similar to (50,56) or, in some buffer systems, even larger than the GDP affinity (Table 1) (50). For these factors, the effective dissociation constants for GDP and GTP binding in Eq. 4 can, we suggest, be approximated as

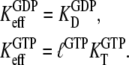(14)

Although the T forms of these GTPases free in solution have never been seen, the T forms do emerge in the presence of specific cofactors, i.e., eRF1 in the case of eRF3 (35), the naked or posttermination bacterial ribosome in the case of EF-G (40), the eukaryotic/bacterial ribosome in the case of eIF5B/IF2 (53). A particularly interesting case is provided by the archaean aIF2 and, by inference, the eukaryote eIF2. These initiation factors, which recruit initiator tRNA to the small ribosomal subunit (57), consist of three subunits, i.e., in the archaean case 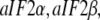and the GTPase 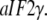When GDP is substituted with GDPNP, the structure of 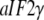alone remains unaltered (54), but it changes from D to T form when also 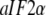is present (58). Accordingly, we suggest that although the inequalities in Eq. 13 are valid for these GTPases alone, the presence of a cofactor in each case with a binding preference by the factor 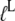to the T over the D form, the inequality

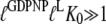(15)

is valid instead, which explains why the 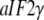changes structure upon the nucleotide switch conditional on the presence of its cofactor. From Scheme 1, we also predict large increases in the binding affinity for GDPNP (and GTP) for these GTPases when their cofactors are added, as verified by biochemical experiments (18,28,41,45). A logical name for cofactors that stabilize the GTP conformation (T form in Scheme 1) of GTPases would be GTP stabilizing factors (GSF) (Fig. 2).

An interesting case of ligand-induced stabilization also of the D form of a G-protein is revealed by the crystal structure of a 1:1:1 complex of Thermus thermophilus EF-Tu with GDP and the antibiotic aurodox. Although EF-Tu is GDP-bound, its structure is in the T form (59), as described in their Abstract: “GTP complex-like conformation of EF-Tu is observed, although GDP is bound to the nucleotide-binding site.” Our interpretation of this finding based on Scheme 1 and Eq. 10 is that aurodox greatly favors the T form of the factor, and that the affinity of GDP to the D form compared to the T form is insufficient to counteract the T form-favoring effect of aurodox.

From considerations presented above we propose that eRF3, eIF5B/IF2, EF-G, and 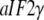are classical or, if preferred, neoclassical GTPases. That is, they do have functionally relevant T forms, albeit emerging in a cofactor-dependent manner. Further evidence for the classical nature of these factors is provided by sequence data, revealing identical DXXG sequences in eRF3, eIF5B/IF2, EF-G, and strong DXXG conservation among small GTPases in general (60). These conservation features, which reflect strong selection pressure in favor of these motifs (61), suggest a universal mechanism that is shared by all small GTPases, i.e., they are all fundamentally classical in a fundamental way. In this common mechanism, the interactions between the γ-phosphate of GTP and the Mg²⁺ ion with the switch II DXXG motif, as seen in the classical T form of small GTPases (1), would be preserved.

The bacterial class 2 release factor RF3, which rapidly recycles class 1 release factors after termination of protein synthesis, has a working cycle reminiscent of the cycles of both EF-Tu and EF-G. The crystal structure of GDP, but not GDPNP, bound RF3 has been determined (62). The spontaneous release of GDP from the free factor (28) is almost as slow as for EF-Tu (19), but its GEF or, preferably, GDS, is part of its target molecule, i.e., the bacterial ribosome in complex with a class 1 release factor and with a peptidyl-tRNA or a deacylated tRNA in the ribosomal P site (28,63). In contrast, stable binding of GTP requires removal of the peptide from the peptidyl-tRNA, allowing the ribosome to adopt its ratcheted conformation, in which the ribosomal subunits have undergone a relative rotation (40,64) bringing the deacylated tRNA, originally in the full P site (P/P site), to a hybrid P/E site (62). Accordingly, the latter ribosome complex is the GTP stabilizing factor for RF3, so that different states of the ribosome act as GDS and GSF for RF3.

This mode of operation of RF3 is principally similar to the GTPase “channeling”, previously identified in eukaryote systems (42), meaning that reaction intermediates are moved from complex to complex without entering the free state (for a review, see Marintchev and Wagner (65)). For instance, during GDP/GTP exchange on the eukaryotic elongation factor eEF1A, an analog EF-Tu, it forms a stable complex with eEF1B (the “GDS”), which leads to rapid dissociation of GDP. In the next step, aminoacyl-tRNA binds to eEF1A and displaces eEF1B (66,67), thereby moving the GTPase directly from its complex with eEF1B to its GTP-stabilized complex with aminoacyl-tRNA (the “GSF”). A similar strategy has been proposed for GDP/GTP exchange on eIF2 (68), with eIF2B, a homolog of eEF1B, and initiator tRNA playing the roles of GDS and GSF, respectively.

GTP IS DIFFERENT FROM ITS NONHYDROLYSABLE ANALOGS: ARTIFACTS AND AMBIGUITIES

Hydrolysis deficient analogs of GTP are often used to freeze GTPases in the step just preceding GTP hydrolysis. This is a particularly useful approach when the GTP-bound T form (Scheme 1) is the active molecule in the cycle of the GTPase. However, it has recently been suggested that the active part of the GTPase cycle does not end until inorganic phosphate is released from the GTPase in a GAP-induced reaction. In the cases of EF-G (69) and eIF2 (70), it is GAP-induced release of inorganic phosphate, rather than GTP hydrolysis, that defines the end of the active part of the action cycle. Furthermore, Kotting and colleagues (71) used time-resolved Fourier transform infrared spectroscopy to demonstrate that GTP binding to p21 Ras results in a reaction intermediate after GTP hydrolysis in which 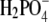is hydrogen-bonded to an eclipsed conformation of the GDP β-phosphate. From this high standard free energy intermediate, 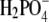may either reform GTP or dissociate in a step that is rate limiting for the complete GTPase reaction. In these and similar cases, where the most important action of the GTPase is carried out after GTP hydrolysis and before phosphate release, analysis of the GTPase frozen in a prehydrolytic step in complex with a GTP analog would miss essential parts of the action cycle.

Another aspect of the replacement of GTP with one of its analogs is that the structures of a GTPase in complex with GTP and a GTP analog may be different. Some GTPases have smaller affinity to GDPNP than to GTP, as exemplified by EF-G (50), RF3 (28), and eRF3 (35). This suggests that also the ratio reflecting the higher affinity of GDPNP binding to the T than to the D form of the GTPase as defined earlier in this article, may be much smaller than the corresponding ratio, 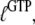for native GTP. We have observed that the affinity of GTP, but not GDPNP, to eRF3 is greatly increased by the presence of eRF1 (Table 1) (35). In terms of our analysis, this means that the effective dissociation constant for GTP binding to eRF3, as defined in Eq. 4, decreases by the addition of eRF1:

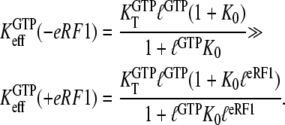(16)

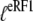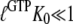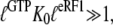Here, is defined according to Eq. 10 as the ratio between the dissociation constants for eRF1 binding to the D and T forms of eRF3. This inequality is readily explained if and so that the following approximations are valid:

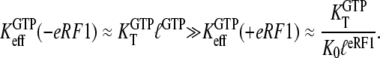(17)

The unchanged affinity of GDPNP to eRF3 upon eRF1 addition, means that

(18)

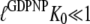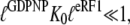Here, by hypothesis, and so that the following approximations are valid:

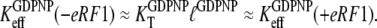(19)

According to Eq. 7, this explanation also implies that eRF3 switches from the D to the T conformation when GDP is swapped for GTP in the presence (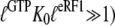 but not absence (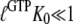) of eRF1. It also implies that eRF3 switches from the D to the T conformation when GDP is swapped for GDPNP neither in the presence (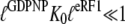) nor in the absence (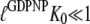) of eRF1.

CONCLUSIONS

At the heart of this work is an equilibrium scheme (Scheme 1) of the conformational propensities of GTPases to be in their inactive D and active T forms. These propensities are determined by the free concentrations of GDP and GTP, the propensity of the GTPase to be in either of its forms when it is bound to GDP, GTP, or free from nucleotide and the presence of cofactors with selective binding to the D and T forms. The scheme also quantifies how differences between GTP on one hand and analogs of GTP on the other may affect the propensity of conformational switching of free as well as cofactor-bound GTPases.

Despite its simplicity, the framework of Scheme 1 and Eq. 10 may clarify a number of hitherto mystifying observations. It suggests, for instance, why bacterial elongation factor EF-G remains in the D form, when its bound nucleotide is changed from GDP to the GTP analog GDPNP (16) or even to native GTP (55) and why the T form of EF-G is only seen in complex with the ribosome (40). It explains in a very similar way why the GTPase eIF5B, when GTP bound, has much higher affinity to the ribosome than when GDP-bound ((72) and J. Lorsch, personal communication), although the GDP and GTP binding forms of free eIF5B are very similar (53). The explanation, we propose, is that free eIF5B, like free EF-G, remains in its inactive D form even when in complex with GTP, but switches conformation in the presence of the ribosome, which, by hypothesis, has higher affinity to the T than to the D form of eIF5B. It accounts for the observation that the crystal structures of GDP- and GDPNP-bound eRF3 are virtually identical (14) without the need to invoke an aberrant, nonclassical mode of operation of this GTPase. It also suggests a simple explanation for why the affinity of GTP to eRF3 increases greatly upon addition of eRF1, whereas the affinity of GDPNP remains virtually unchanged upon eRF1 addition (35).

In all those cases where our theory suggests that the T form of a G-protein will become dominant only in the presence also of other ligands than GTP or when the GTPase is target bound, its prediction of a “classical” mode of operation can be directly tested by high-resolution crystal structures of these complexes. The cryo-EM structure of EF-G in complex with GDPNP on the ribosome is in line with our theory, since it is very different from the free forms of GDPNP- or GTP-bound EF-G; but high-resolution structures are likely to provide more definitive answers.

Another way to test our predictions would be to identify the coexistence of GTP-bound D and T forms of a G-protein. One candidate is elongation factor G in complex with GTP, which may be shifted sufficiently much toward the T form, to allow detection of the coexistence of a major D form and a minor T form. One way to do this experimentally would be to use fluorescence-labeled EF-G and single molecule detection techniques to determine the equilibrium relation and transition rates between the two forms. Similarly, GTP-bound EF-Tu may exist in a major T and a minor D form, and the predicted coexistence of the two forms may be identified by fluorescence techniques as in the case of EF-G.

Yet another way of testing the theory also relates to the absence of a T form for a free G-protein, such as EF-G, eRF3, etc. This may either mean that the free T and D forms are so similar, that they cannot be distinguished by crystallography, or that the GTP-bound free factor remains in the D form, as suggested in this work. If the latter supposition is true, then, e.g., EF-G would enter the pretranslocation ribosome in the same D form, whether GTP or GDP bound, and thus with the same kinetics. When the factor enters GTP-bound, it would subsequently switch conformation to its T form, which could be detected by fluorescence after suitable labeling of the factor. If, in contrast, the factor is GDP-bound, it would remain in that form also when ribosome bound. If the former supposition is true, then the factor would be in the T form already in the free state, and would enter the ribosome with different kinetics than the GDP-bound factor in the D form.

Scheme 1 is based on equilibrium thermodynamics and is, essentially, a concise way to keep track of the difference in standard free energy of the ground states of the D and T forms of GTPases as they pass through the different steps of their cycles. Although the theory in its current form does not predict the rate constants of G-protein cycles, it provides a conceptual framework on which all kinetic considerations have to be based. The scheme also offers a convenient way to classify GTPases according to differences in their modes of operation, i.e., when they switch from their D to their T forms and back again.

Further development of this analysis to account also for the kinetics of GTPase action will greatly benefit from atomic resolution structures of translational GTPases in ribosomal complexes. It is, in particular, the extensive integration of kinetic and structural studies of GTPases that will allow for generalizations at a deeper level of the modes of action of these interesting enzymes.