Balance between Ultrafast Parallel Reactions in the Green Fluorescent Protein Has a Structural Origin

Abstract

The fluorescence photocycle of the green fluorescent protein is functionally dependent on the specific structural protein environment. A direct relationship between equilibrium protein side-chain conformation of glutamate 222 and reactivity is established, particularly the rate of ultrafast proton transfer reactions in the fluorescence photocycle. We show that parallel transformations in the photocycle have a structural origin, and we report on the vibrational properties of responsive amino acids on an ultrafast timescale. Blue excitation of GFP drives two parallel, excited-state deuteron transfer reactions with 10 ps and 75 ps time constants to the buried carboxylic acid side chain of glutamate 222 via a hydrogen-bonding network. Assignment of 1456 cm⁻¹ and 1441 cm⁻¹ modes to ν_sym and assignment of 1564 cm⁻¹ and 1570 cm⁻¹ features to ν_asym of E222 in the 10 ps and 75 ps components, respectively, was possible from the analysis of the transient absorption data of an E222D mutant and was consistent with photoselection measurements. In contrast to the wild-type, measurements of E222D can be described with only one difference spectrum, with the ν_sym mode at 1435 cm⁻¹ and the ν_asym mode at 1567 cm⁻¹, also correlating a large Δν_asym-sym with slow excited-state proton transfer kinetics. Density Functional Theory calculations and published model compound and theoretical studies relate differences in Δν_asym-sym to the strength and number of hydrogen-bonding interactions that are detected via equilibrium geometry and COO⁻ stretching frequency differences of the carboxylate. The correlation of photocycle kinetics with side-chain conformation of the acceptor suggests that proton transfer from S205 to E222 controls the rate of the overall excited-state proton transfer process, which is consistent with recent theoretical predictions. Photoselection measurements show agreement for localized C=O vibrations of chromophore, Q69, and E222 with Density Functional Theory and ab initio calculations placed in the x-ray geometry and provide their vibrational response in the intermediates in the photocycle.

INTRODUCTION

Green fluorescent protein (GFP) from jellyfish Aequorea victoria is a very important marker protein used in a multitude of bioimaging techniques such as reporting on protein expression and trafficking in vivo (1). The photochemical characteristics of GFP arise from highly specific protein-chromophore interactions and are very different when the isolated 4-hydroxybenzylidene-2,3-dimethyl-imidazolinone (HBDI) chromophore is dissolved in liquids, where radiationless decay, associated with rapid twisting motions in the excited state (2,3), is dominant. In GFP, the specific protein environment inhibits these and other rapid deactivation reactions (2–5) and provides specific H-bonding interactions with the HBDI chromophore that are functional in the light-driven reactions of GFP. Fig. 1 shows the H-bonding interaction of the chromophore phenolic oxygen to a water molecule, which in turn is H-bonded to glutamate 222 indirectly via serine 205. It has been established that the proton transfer occurs on a picosecond timescale through this network of H-bonding interactions during the fluorescence photocycle (4–7). This transient proton transfer is fully reversible with reformation of the ground state (Figs. 1 and 2). In addition to the interesting aspects of molecular interactions of electronically excited states, microscopic understanding of the underlying protein-chromophore interactions is important for rational design and alteration of its properties for use in imaging applications. Spectroscopic and kinetic studies of the photocycle of wild-type GFP have shown that it follows the Förster cycle, involving rapid proton transfer (8). The excited-state proton transfer (ESPT) reaction that is triggered by optical excitation of the neutral chromophore at 400 nm is associated with considerably red-shifted fluorescence emission, with the Stokes shift energy corresponding to the reduction in proton affinity of the deprotonated radiative state I* (8). Ultrafast mid-infrared (IR) spectroscopy experiments have identified the buried carboxylate of E222 as the transient proton acceptor from analysis of the hydrogen-deuterium (H/D) exchange effects and the site-specific mutation E222D (4–7). Additionally, the electrostatic rearrangements associated with the rapid proton transfer reaction have been shown to trigger a protein structural response on a picosecond timescale, notably of Q69 in the chromophore-binding site (5,9). The ESPT reaction shows an average H/D kinetic isotope effect of 6 at 298 K, but it is reported to be biphasic both in H₂O (2 and 11 ps) and D₂O (10 and 75 ps) (4,8,10). Whereas transient absorption and fluorescence spectroscopy did not resolve spectral differences between the two parallel ESPT reactions (8,10), the difference mid-infrared spectra corresponding to the 10 ps (A₁*–A) and 75 ps (A₂*–A) components in D₂O did show distinct differences (4).

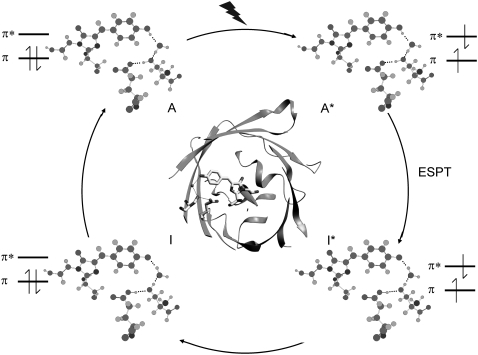
FIGURE 1.

Overview of structural, H-bonding, and electronic changes in the fluorescence photocycle. The phenolic oxygen of the HBDI chromophore is H-bonded indirectly to glutamate 222 via a water molecule and serine 205. Coordinates are taken from PDB 1W7S (5). The electronically excited singlet state of the neutral and anion chromophore, A* and I* respectively, are indicated. ESPT reactions occur during the transition between the A* and I* states that have 10 and 75 ps time constant in D₂O (4,10). Blue excitation with 400 nm light is indicated to create the A* state.

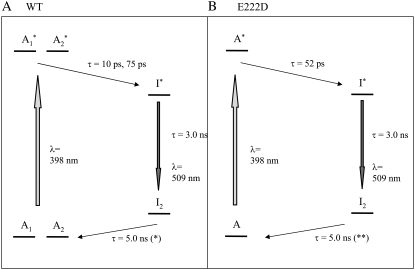
FIGURE 2.

Photocycle scheme for the (A) wild-type and the (B) E222D mutant used for global fitting of the transient absorption data. Note that the I₁ intermediate is not considered here because it does not accumulate to an observable level in the photocycle and is only significant in the pump-dump-probe experiments outlined in reference 10.

In this study, we address the assignments of modes found at different frequencies in the two pathways and propose a structural basis for the parallel proton transfer reactions (vide supra) of populations characterized by different hydrogen-bonding of the excited-state proton acceptor. We also report on photoselection measurements that are extended from those previously reported on selected ground state bands in GFP (7) and HBDI (3) to include the photocycle intermediates. In addition, we apply significant corrections to the results for the finite bleach that occurs with femtosecond-pulsed visible excitation, and we correct reported theoretical calculations of vibrational transition dipole vectors (7) for the interpretation of vibrational anisotropy. Necessary corrections to infrared anisotropy measurements, which has been demonstrated previously to also significantly affect molecular interpretation of carbon monoxide (CO)-binding in myoglobin (11), may be dominated by the finite bleach effect; these corrections, however, can have a contribution from depth-averaging in absorbing samples (11,12). Molecular interpretation is additionally affected, even for relatively localized vibrations such as the C-O stretching mode of heme-bound CO in myoglobin, where bond-stretching causes a dipole reorientation and deviations between the transition dipole moment vector and the corresponding bond vector (13). The photoselection results of GFP provide ultrafast structural information on responsive amino acids E222 and Q69; these results also test existing mode assignments for the ground state proposed from Density Functional Theory (DFT) normal mode calculations in addition to isotope substitution strategies with chromophore model compounds (14,15). Excited-state assignments were previously proposed on the basis of expected bond order changes (4) and, in this study, are evaluated from calculation of frequencies and infrared transition dipole vectors using single excitation configuration interaction (CIS).

MATERIALS AND METHODS

Picosecond transient infrared spectroscopy

Picosecond time-resolved, pump-probe, mid-infrared absorption measurements were performed using the PIRATE facility at the Rutherford Appleton Laboratory (16), essentially as described previously (4). Excitation was with 400 nm, 150 fs pulses from a 1 kHz titanium:sapphire laser at varying energy, 0.1–2 μJ/pulse, focused in a 130-170 μm full width at half-maximum (FWHM) spot. Broadband 150 fs infrared probe pulses generated by difference frequency mixing in type I AgGaS₂, with a 150 cm⁻¹ FWHM at ∼10 nJ/pulse focused in a 100 μm FWHM spot, probed the absorption changes with delays between 2 ps and 2 ns after excitation. The pump and probe beams were focused and overlapped, and their profiles were measured and fitted to a Gaussian profile to estimate the power density. The infrared probe and reference beams were dispersed using spectrometers with 150 lines/mm, 4000 nm blaze gold gratings, and imaged onto 64-element, mercury cadmium telluride photoconductive detectors, which provided a shot-by-shot normalization. The samples were raster-scanned along the X axis and Y axis directions. The E222D mutant of GFP-uv was prepared as described previously (4), used at 4 mM concentration in D₂O, including 5 mM Tris/HCl pD 7.8, and placed between CaF₂ windows with a pathlength of ∼10 μm. A full kinetic data set with excitation at magic angle and delays at 0, 1, 2, 3, 5, 7, 10, 13, 17, 22, 33, 39, 45, 60, 75, 100, 150, 300, 500, 1000, 1500, and 2000 ps after excitation was assembled from multiple samples that collected data from four delays to minimize photodegradation and used minimal scaling using the measurement at 3 ps included in all series. For experiments with the wild-type in D₂O, a sample flow system was used as described previously (4), which had an optical path length of 24 μm, providing an optical density at 400 nm (OD₄₀₀) of 0.176 at 2.4 mM concentration. Measurements were performed with horizontal, vertical, and magic angle orientations of the pump beam relative to the probe beam at 0, 1, 2, 3, 5, 7, 10, 13, 17, 22, 33, 39, 45, 60, 75, 100, 150, 300, 500, 750, 1000, 1250, 1500, 1750, and 2000 ps delay after excitation, between 1775 and 1250 cm⁻¹ in separate, overlapping spectral windows. The extent of polarization of pump and probe beams at the sample were determined to be better than 95%. For polarization-dependent transient absorption measurements, the pump beam was determined to have an approximate Gaussian profile with 170 μm FWHM in both directions and a pulse power of 1.4 μJ. Angles between the vibrational transition dipoles and the optical transition dipole were determined after calculation of the finite bleach, using approaches pioneered for photoselection experiments with myoglobin-CO described in the literature (11,12,17). The measured ensemble averaged anisotropy:

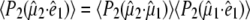(1)

of the infrared absorption with respect to the polarization direction 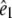of the visible pump pulse contains information on the orientation 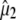of the infrared transition dipole of the vibrational normal mode. Specifically, the second order Legendre polynomial 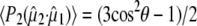yields the angle between and the optical transition dipole 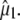For a linear absorber, the optical anisotropy:

(2)

after excitation with an intense pulse is calculated on the basis of the integrated photon flux density and the optical cross section The photolysed fraction 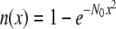is obtained from 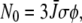where the optical cross section taken to be 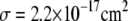at 400 nm (1), 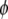= 0.8 is the quantum yield (1), and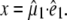

To correct for sample absorption, it is necessary to average over the sample depth. Assuming equal cross section for the ground and excited states, Lim (12) has shown that

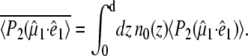(3)

This correction was neglected because transient absorption spectroscopy showed a significant ground state bleach at 400 fs delay after 400 nm excitation (10). In addition, with the observed ground state absorption OD₄₀₀ = 0.176, the photolysis levels used in this study would lead to corrections in the order of ∼1% for an equal excited state cross section, which is considered less then the measurement uncertainty. Although the finite thickness correction is negligible, the correction for finite bleach is significant. In fact, we found it to be larger than expected on the basis of the standard analysis in this section (see below).

Computational details

A model for the side-chain conformation of glutamate 222 and the hydrogen-bonded crystal water Z223 and serine 205 side chain was taken from the GFP_A state x-ray structure determined at 1.8 Å resolution and pH 7.8 from chain A, Protein Data Bank (PDB) 1W7S (5). Carbonyl and amino groups of E222 and S205 were replaced with methyl groups. DFT calculations of the interacting and noninteracting E222 were performed using Gaussian 03 (18) at the B3LYP/6-311+G(2d,2p) level. Geometry optimization was performed including dihedral angle constraints (χ₁ = 62°, χ₂ = 153°, and χ₃ = −145°) (5) for the E222 side-chain conformation. In addition, coordinates of hydrogen-bonded water and Cα and C(=O) main chain atoms of S205 and E222 were frozen. Reported DFT calculations were performed in vacuo and tested with self-consistent reaction field solvent modeling using the polarizable continuum model method, which provided mostly similar results. Geometry optimization and frequency calculation was performed specifying “int=ultrafine” and “opt=verytight” as the keywords for a fine numerical integration grid and tight convergence criteria in Gaussian 03 (18). Geometry optimization and normal mode analysis of the bare 4-hydroxybenzylidene-2,3-dimethyl-imidazolinone (HBDI) chromophore of GFP was performed at the B3LYP/6-311+G(d,p) and HF/6-31G(d) levels for the protonated and anion ground states and at the CIS/6-31(d) level for the first excited state for the protonated and anionic species. The dipole derivative unit vectors for the investigated normal modes calculated with Gaussian 03 and plotted in Gaussview 3.0 were found to be in error. Therefore, dipole derivative vectors presented in this study were computed by a finite difference method from the molecular dipoles with small normal mode displacements, typically < 0.1 kT to either side of the equilibrium geometry. These results corresponded to correct analytical dipole derivatives printed via the iop(7/32=3,7/33=1) option in the log of Gaussian 03. We note that dipole derivative vectors of normal modes of HBDI calculated with Gaussian 98 as recently reported (7) correspond neither with results from finite difference dipole vectors nor with analytical dipole derivative vectors from Gaussian 03 and plotted with Gaussview 03. The optical transition dipole moment was computed for HBDI in vacuum using time-dependent density functional theory (TD-DFT) at the B3LYP/6-311+G(d,p) level.

RESULTS

Transient mid-infrared absorption of the E222D mutant

With 400 nm excitation of the E222D mutant, excited-state H/D (H₂O/D₂O) transfer to D222 occurs (4) (Figs. 1 and 2). Transient absorption data probed at magic angle to the pump beam with delays between 2 ps and 2 ns were collected in two separate ∼150 cm⁻¹ spectral windows between 1650 cm⁻¹ and 1350 cm⁻¹ and interleaved to construct a full kinetic data set. This spectral region covers the infrared absorption of both the antisymmetric (ν_asym) and the symmetric (ν_sym) stretch vibrations of the carboxylate anion side chains of E222 and D222. Measurements of the COOH region at a higher frequency were reported previously (4). The transient difference spectra of the wild-type and the mutant are shown in Fig. 3, with arrows indicating the direction of major changes in absorption with time for comparison.

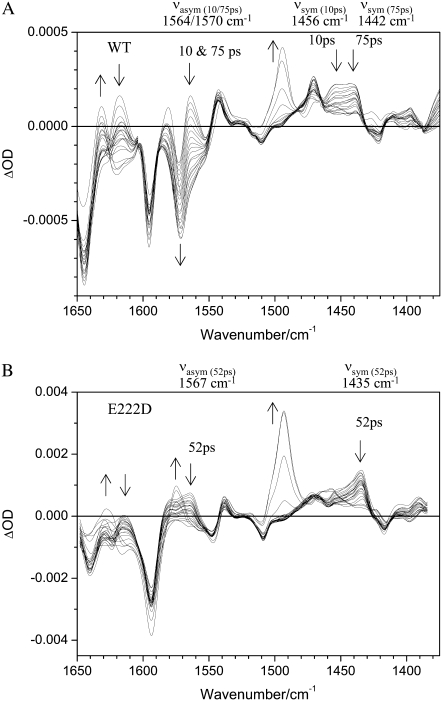
FIGURE 3.

Transient difference absorption changes in the mid-infrared with excitation at 400 nm for (A) wild-type and (B) mutant E222D. (A) Difference absorption relative to the ground state between 1650 cm⁻¹ and 1375 cm⁻¹ with delays between 2 ps and 2 ns of wild-type GFP. Arrows indicate changes with time. The frequencies of the ν_asym and ν_sym modes of E222 are indicated for the 10 ps and 75 ps components for the excited-state deuteron transfer reactions. (B) Difference absorption data with the same delays shown for the E222D mutant. The ν_asym and ν_sym modes of D222 are found at discrete frequencies for the excited state deuteron transfer reaction, which has a 52 ps time constant.

Singular value decomposition according to ΔA = UD(s)V^T of the data set recorded with the E222D mutant produced three relevant spectral components (U) as with the wild-type data. Scaled time traces D(s)V could be fitted with two time constants, providing τ₁ = 52 ps and τ₂ = 1.39 ns (data not shown). Fitting the D(s)V traces with three time constants, τ₁ = 11 ps, τ₂ = 139 ps. and τ₃ = 1.16 ns, did not significantly improve the quality of the fit (data not shown). Moreover, global fitting of the data using three time constants provided very similar spectra for τ₁ and τ₂ in contrast to the wild-type, which has very different spectra associated with the τ₁ = 10 ps and τ₂ = 75 ps components (Fig. 2) (4). Although the ESPT reaction of the E222D mutant may also be biphasic as it is in the wild-type, for the reasons discussed, we considered only a single time constant τ₁ = 52 ps for comparison of the ESPT reaction and τ₂ = 3.0 ns and τ₃ = 5 ns lifetimes for the I* and I₂ states, respectively, as in the wild-type (4,10) (Figs. 2 and 3; Supplementary Material, Fig. S1, Data S1). The fluorescence lifetime of the E222D mutant was determined indirectly from the quantum yield (4). It should be noted that we did not exclude the possibility of structurally different populations in the mutant, but we were unable to resolve any such detail in these data as we could for the wild-type. The I* lifetime of the E222D mutant has been determined indirectly from the steady-state fluorescence quantum yield, which is very close to that of the wild-type (4). The amplitudes that were globally fitted for the I₂ minus A spectrum of the E222D mutant assume a 5 ns time constant, the same as for the wild-type. This time constant was not well determined, with data extending out to 2 ns, and the relative amplitudes of the I₂ product state would be affected if the time constant was significantly different from the wild-type (Fig. 2 B). Global fitting of the wild-type data has been discussed previously and takes into account parallel excited-state deuteron transfer reactions that have 10 and 75 ps time constants (4). A reaction scheme with subsequent 10 and 75 ps phases was rejected on the basis of single wavelength analysis at 1711 cm⁻¹, where only induced absorption due to protonation of E222 is present (4,6). In addition, this model would not be in agreement with transient absorption and fluorescence measurements (8,10).

Visual inspection of the unfitted transient absorption measurements clearly shows the major differences between the wild-type and E222D mutant (Fig. 3), which are also presented in the form of species associated difference spectra (Fig. S1, Data S1). The comparison allows assignment of the ν_asym and ν_sym COO⁻ stretching vibrations of E222, and changes in the position, intensity, and decay are observed. Furthermore, both modes are seen as induced absorptions in the instantaneous spectra, indicating these also belong to the A* state. Measurements of the mutant aid the assignments of these bands and indicate differences in functionality of the carboxylate in the ESPT reactions.

Photoselection experiments on wild-type GFP

To obtain further structural information on assigned protein and chromophore modes, polarization sensitive, transient absorption measurements were performed on the wild-type in D₂O. Using a single sample that was raster-scanned and circulated in a closed pump system to prevent photodegradation, time-resolved IR spectroscopy data were collected with a high signal/noise ratio at horizontal, vertical, and magic angle orientations relative to the polarized probe beam in six overlapping, spectral windows between 1775 and 1250 cm⁻¹. All three data sets were globally fitted using decay constants of τ₁ = 10 ps, τ₂ = 75 ps, τ₃ = 3.0 ns, and τ₄ = 5.0 ns for the A₁*, A₂*, I*, and I₂ states, respectively, as described above (Fig. 2 A) (4), providing the polarization-dependent, species-associated difference spectra. The accuracy of the polarization sensitive measurements is demonstrated by comparing the constructed anisotropy free ((A_‖+ 2A_⊥)/3) species-associated difference spectra with those from measurements at magic angle, showing very good correspondence (Fig. S2, Data S1). For these experiments, excitation was with 1.4 μJ pulses in a 170 μm FWHM spot, from which the optical anisotropy was calculated to be 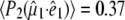and a photolysed fraction n₀ = 0.15, taking into account a Gaussian profile for the pump beam (see Methods section). A separate study of the power density dependence of the isolated transient at 1711 cm⁻¹ was done with 0.21 μJ pulses as lower limit to validate the calculated values of photolysed fraction. Calculated values for 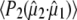decreased systematically with increasing power density due to either nonlinear absorption or an underestimation of the cross section or power density (reported elsewhere). Consequently, 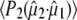at 1.4 μJ pulse energy was empirically adjusted by 1.30 to extrapolate to zero power density. These additional empirical corrections and the finite bleach corrections (see Materials and Methods) are significant, resulting in fundamentally different results compared to reported photoselection measurements of GFP (7) and HBDI (3) that did not address either.

DISCUSSION

Chromophore modes and the ν_asym and ν_sym carboxylate modes in the wild-type and the E222D mutant

The transient absorption in the mid-infrared region of the E222D mutant differs significantly from the wild-type results in selected regions (Fig. 3; Fig. S1, Data S1). The main differences are of absorption changes belonging to COO⁻ modes of E222 at 1570, 1456, and 1442 cm⁻¹. Previously, differences in the intensity and frequency of the COOH stretching modes in the 1710 cm⁻¹ region were reported (4), and our observation of the COO⁻ stretching modes further establishes the assignment to E222 in the wild-type. Additional differences, which are mostly in intensity, of chromophore modes are also observed at 1630 cm⁻¹ (C=C mode; Fig. 3; Fig. S1, C, D, and F, Data S1) and 1470 cm⁻¹ (“phenol 3” mode; Fig. 3; Fig. S1, C, D, and F, Data S1) in the I* state. The intensity differences could arise, in part, from experimental origins and a nonlinear detector readout for strong signals, which does not affect the following analysis.

Directly after excitation in the A* state, induced absorption was observed at 1442 and 1456 cm⁻¹ in the wild-type and at a single frequency, 1435 cm⁻¹, in the corresponding region in the E222D mutant, which is interpreted to be dominated by the ν_sym carboxylate mode (Fig. 3). These features decay concomitantly with ESPT in the wild-type with different time constants: the 1456 cm⁻¹ band associated with a 10 ps time constant and the 1442 cm⁻¹ band with a 75 ps time constant (Figs. 2 and 3). In contrast, the decay of the band at 1435 cm⁻¹ in the E222D mutant can be described with a single time constant of 52 ps (Figs. 2 B and 3 B). This is also reflected in the species-associated difference spectra of the wild-type in the A₁* and A₂* states (Fig. S1, A and B, Data S1; positive bands at 1458 and 1441 cm⁻¹ respectively) and the I* state (Fig. S1 C, Data S1, negative band at 1456 cm⁻¹), and the E222D mutant in the A* state (Fig. S1 E, Data S1; positive band at 1435 cm⁻¹) and I* state (Fig. S1 F, Data S1, negative band at 1435 cm⁻¹). The following discussion focuses on the observation that absorption at 1456 cm⁻¹ decays faster than absorption at 1442 cm⁻¹, which is visually recognized in the untransformed raw data (Fig. 3 A). The biexponential fitting of these data, which results in the decay-associated amplitudes as seen in Fig. S1, Data S1, may alternatively be interpreted and fitted via a distribution of rate constants, which would be a refinement on the analysis that we present in this article. Our interpretation, however, emphasizes the two spectroscopically distinguishable species.

The ν_asym carboxylate mode features are also dramatically changed in the E222D mutant (Fig. 3). In the 1570 cm⁻¹ region, there are both absorption changes of ν_asym and the “phenol 2” mode, as with the ν_sym mode-induced absorption in the A* states, and subsequent decay is seen (Fig. 3; Fig. S1, Data S1), however, with reduced intensity in the E222D mutant compared to the wild-type. It is likely that the phenol 2 mode and the ν_asym mode of E222 become separated in particular in the I* minus A₁* spectrum, with 1578(−) cm⁻¹/1550(+)cm⁻¹ feature and 1564(−) cm⁻¹ bleach in the wild-type ((4); Fig. S1 C, Data S1). The 1570(−) cm⁻¹ bleach in the I* minus A₂* spectrum (Fig. S1 D, Data S1) is very strong and probably obscures contributions of the phenol 2 mode. Similarly, a separation of these modes is observed in the E222D mutant I*–A* spectrum, with 1578(−) cm⁻¹/1547(+) cm⁻¹ and 1567(−) cm⁻¹ features (Fig. S1 F, Data S1). The reduced intensity of the ν_asym mode of D222 is in line with the observed reduced intensity of the corresponding 1713(+) cm⁻¹ transient belonging to protonated D222 in the I* state relative to the corresponding transient in the wild-type of protonated E222 (4).

Assuming changes of the carboxylic acid excited-state proton acceptor only, the changes in the spectra of the E222D mutant support assignment of these features to the ν_sym and ν_asym stretching modes of E222 and D222 in the wild-type and mutant data, respectively. In addition, the relative amplitudes of these features correspond well with the extinction coefficients of ν_asym and ν_sym carboxylate infrared bands (19). Supporting this interpretation, infrared absorption, observed in the neutral and anionic forms of the HBDI chromophore model compound in KBr at 1446 cm⁻¹ and 1445 cm⁻¹, respectively (14,15,20), which has been assigned to a C-C-H in plane deformation mode of the phenol ring, is not strongly responsive to chromophore deprotonation and bond order changes. This mode was also found to be weakly Raman active, and it was reported at 1434 cm⁻¹ and 1439 cm⁻¹ for neutral and anionic HBDI in dimethyl sulfoxide, respectively (15). Thus, it is possible that additional chromophore absorption changes are present in the ν_sym region, but the comparison between the wild-type and E222D mutants indicates it is dominated by the carboxylate mode. The observation that both ν_asym and ν_sym carboxylate bands are A* and I* modes is surprising; it also indicates the possibility of a direct electrostatic effect of the optically excited chromophore in the A* state on the carboxylate group, which is close to van der Waals contact, increasing the cross sections.

The assignment of ν_asym and ν_sym modes at different frequencies in the wild-type ESPT reactions by comparison with the E222D mutant data suggests that different structural populations of the transient proton acceptor underlie the difference between the two parallel photocycle reactions. The Δν_asym-sym differences are 108 cm⁻¹ and 129 cm⁻¹ for the 10 ps and 75 ps components, respectively, which mostly reflects the different frequencies of the ν_sym modes. In the E222D mutant, the Δν_asym-sym difference equals 132 cm⁻¹, also correlating the large value with slow ESPT kinetics (Figs. 2 and 3)

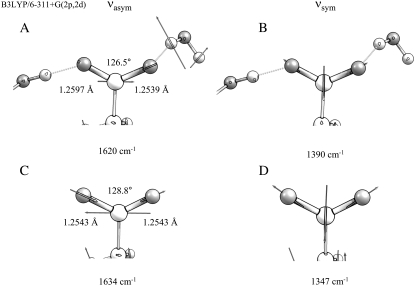
An ab initio study performed at the Hartree-Fock (HF) level of the vibrational frequencies of coordinated carboxylate groups has shown the structural basis leading to changes of the Δν_asym-sym differences (21). In this work, infrared frequencies were calculated for various interacting geometries of the carboxylate anion with coordination to specific solvent molecules and metal ions. Experimentally, it is well established that metal ion coordination of carboxylates leads to reduced Δν_asym-sym differences via both upshifting of the ν_sym mode and downshifting of the ν_asym mode (19,21,22), and calculations indicate that water coordination can have similar effects but with reduced amplitude (21). We note that, in the wild-type and mutant A* minus A difference spectra (Fig. S1, A, B, and E, Data S1), the features assigned to ν_sym and ν_asym modes show upshifts and downshifts, respectively, further supporting their assignment. HF calculations rationalized this observation in terms of bond lengths and angles of the carboxyl group (21). In general, specific interactions were found to lead to reduced equilibrium Φ_OCO bond angles and to a reduced symmetry through different CO bond lengths in asymmetric interacting structures. The frequency splitting is controlled via these equilibrium structure changes and understood from the C-C and C-O stretching couplings (21). DFT calculations performed at the B3LYP 6-311G+(2d,2p) level of a model for E222, including its hydrogen-bonding partners, confirmed these conclusions. The isolated anion in vacuum (in the absence of its hydrogen-bonding partners) led to an optimized geometry with 128.8° Φ_OCO bond angles and 1.2543 Å CO bond lengths (Fig. 4). Harmonic frequency calculations produced 1634 cm⁻¹ and 1347 cm⁻¹ for ν_asym and ν_sym modes, respectively. We note that the frequency calculated for the ν_sym mode is systematically underestimated, as with the HF study (21), and the use of a single diffuse function in the basis set only partially compensates for the inaccuracy of anionic molecule modeling. Including hydrogen-bonding interactions with crystal water Z223 and serine 205 in the x-ray geometry led to an optimized structure with a 126.5° Φ_OCO bond angle and 1.2597 Å and 1.2539 Å CO bond lengths (Fig. 4). Nara et al. (21) proposed an empirical relationship between the Φ_OCO equilibrium bond angle, the δr CO bond length difference and the Δν_asym-sym difference, at the HF/6-31+G(d,p) level as follows:

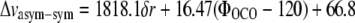(4)

Using this relationship suggests that the 2° Φ_OCO equilibrium bond angle change could account for 39 cm⁻¹ change and the reduced symmetry expressed as the δr CO bond length differences would contribute 9 cm⁻¹. The total Δν_asym-sym difference obtained from the DFT calculations of isolated and interacting glutamate 222, which is 57 cm⁻¹, would therefore be expected to have the largest contribution from the Φ_OCO bond angle change. The DFT calculations appear to support the general conclusions obtained in the HF study (21), relating the Φ_OCO bond angle and symmetry of the carboxylate group to the Δν_asym-sym difference. The coupling with CH wagging motions in the side chain does not strongly influence the frequency of the ν_asym and ν_sym modes, which was also confirmed by computing these values for the two major rotamer conformations (data not shown). These calculations therefore confirm that the asymmetric hydrogen-bonding interactions in GFP directly correlate with a reduced Φ_OCO bond angle and carboxylate symmetry and reduced Δν_asym-sym difference. Functionally, we therefore correlated the fast ESPT reaction with a 10 ps time constant with a more strongly interacting carboxylate group, and we correlated the slow 75 ps phase with a weaker interacting group. From the experimentally determined Δν_asym-sym difference of 21 cm⁻¹ between the two ESPT reactions, the calculations indicate an equilibrium bond angle difference of ∼1°, following arguments of the ab initio study of interacting carboxylate groups (21). This difference in equilibrium conformation is the result of the differences in hydrogen-bonding strength, and the two populations are thus detected via their different COO⁻ stretching frequencies, providing highly resolved structural details in the parallel photoreactions of wild-type GFP. Together, these results suggest that the conformation of the proton acceptor controls the kinetics. This conclusion is consistent with recent predictions (23–25) that proton transfer from S205 to E222 initiates the ESPT reaction, but it is more difficult to reconcile with assumed initiation by proton transfer from the chromophore to the hydrogen-bonded water (26). It was recently argued that the barrier for proton transfer from S205 to E222 that was calculated (23) may be high in view of the observed picosecond kinetics, and alternative models assume extended proton wires and switching mechanisms (27,28).

FIGURE 4.

DFT optimized geometry and frequencies for ν_asym and ν_sym normal modes for isolated and interacting E222 at the B3LYP 6-311+G(2p,2d) level. (A) Bond angle and lengths for a geometry optimized model including hydrogen-bonding interactions to water Z223 and S205. Displacement vectors and calculated frequency of ν_asym are shown. (B) Displacement vectors and frequency of ν_sym for interacting E222. (C) Bond angle and lengths for a geometry optimized model excluding hydrogen-bonding interactions but maintaining dihedral angles taken from the x-ray geometry, and vectors and calculated frequency of ν_asym. (D) Displacement vectors and frequency of ν_sym for isolated E222

Photoselection measurements of ground and excited-state intermediates

Clearly, structural interpretation of the photoselection measurements critically relies on the determination and accuracy of the vectors of both the optical transition dipole and the infrared transition dipoles belonging to the normal modes. In principle, it is possible to obtain orientational information of the optical transition dipole moment from polarized absorption measurements on crystals, which have been reported (29,30). Using P2₁2₁2₁ crystals, a polarization ratio of 1.6 was determined for the neutral state at 400 nm. This provides two solutions at 1.5° and 63.4° (assuming measurement along {100}) and two at 76.0° and −21.3° (assuming measurement along {010}) relative to a molecular reference axis that is in the chromophore plane and connects the OH and O2 chromophore atoms (30). Based on the previously reported experimental dichroism of the 1711 cm⁻¹ transient (7), which provides a value of 6° for the angle α with the reference axis, Shi et al. (30) selected the 1.5° solution as the most likely candidate for 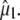Calculation of the optical transition dipole using TD-DFT provided a dipole vector that is rotated 16° relative to the reference axis used by Shi et al. (30) (Fig. 5). We investigated the resulting values for 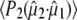using the four possible solutions from the optical crystallography, but we found the best correspondence with experimental values when making the comparison with the dipole vector calculated with TD-DFT, using in particular the E222 COOH, Q69 C=O and chromophore C=O ground state and E222 COO⁻ asymmetric and symmetric bands as the criteria. We note that the 1.5° experimental value adopted by Shi et al. (30) is closest to the TD-DFT vector of the four solutions and additionally provides the best correspondence with experimental values subsequently obtained for 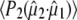(see Table 1). This second argument, however, is valid only for modes excluding the E222 COOH stretching mode, which was used as a selection criterion by Shi et al. (30). In general, the results from TD-DFT appears to fit the measurements well, although the results from optical crystallography (30) are close and also provide reasonable correspondence for a number of modes (Table 1).

FIGURE 5.

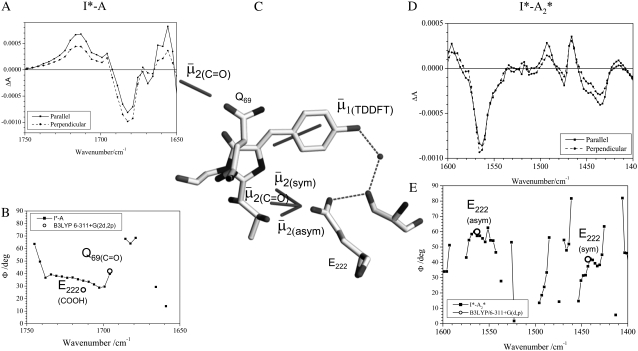
Correspondence of theoretical transition dipole moments of assigned amino acid normal modes with polarization-dependent species associated difference spectra. (A) The 1750–1650 cm⁻¹ region of the polarization dependent I* minus A difference spectrum of the wild-type. COOH and C=O stretching vibrations of E222 and Q69 are assigned at 1711 and 1695 cm⁻¹, respectively. (B) Calculated and experimental angles 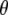in the 1750–1650 cm⁻¹ region of the polarization-dependent I* minus A difference spectrum. (C) Structural arrangement determined in the ground state with coordinates taken from PDB 1W7S (4). The optical transition dipole moment 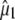obtained from a TD-DFT B3LYP/6-311+G(d,p) calculation is shown as an in-plane vector. The vibrational transition dipole moment vectors 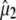from finite difference calculations at the B3LYP/6-311+G(d,p) are placed in the x-ray geometry. (D) The 1600–1400 cm⁻¹ region of the polarization dependent I* minus A₂* difference spectrum of the wild-type. Theoretical and experimental angles 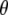in the 1600–1400 cm⁻¹ region of the polarization-dependent I* minus A₂* difference spectrum.

TABLE 1.

Summary of the proposed assignments for vibrational modes belonging to protein and chromophore in the photocycle intermediates of the wild-type as designated in Fig. 1, including angles between 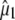and 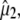comparing proposed experimental with theoretical values of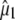

Angle	Frequency (cm−1) 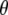(degrees; visible dichroism/TDDFT/experimental IR dichroism)	A1	A1*	A2	A2*	I*	I2
E222	COOH	–	–	–	–	1712	1705
						13/27/33	13/27/33
Q69	C=O	–	1688	–	1685	1695	1695
			28/42/N.A.		28/42/N.A.	28/42/40	28/42/45
1	C=O	1681	1672	1678	1672	1672	1672
		51/66/62	18/33/46	51/66/64	18/33/42	22/37/29	64/79/28
2	C=C	1646	1618	1643	1615	1631/1634	1631/1646
		2/13/13	44/29/51	2/13/13	44/29/64	6/9/53	7/8/57
3	Phenol 1	1596	1581	1596	1578	1587	1578/1581
		11/4/13	40/25/N.A.	11/4/13	40/25/37	40/24/17	10/5/15
E222	COO− (asym)	–	1564	–	1570	–	–
			53/60/52		53/60/60
4	Phenol 2	1572	1564	1572	1567/1570	1547	–
		55/71/22	39/42/52	55/71/32	39/42/60	N.A.
5	C=N & C=C	1553	1541	1553	1544	1525/1541	1539
		25/40/60	24/9/61	25/40/N.A.	24/9/64	21/5/44	2/17/32
6	Phenol 3	1512	1496	1496	1476	1471	1493
		4/12/N.A.	15/0/N.A.	4/12/46	15/0/10	14/1/14	0/15/32
E222	COO− (sym)	–	1456	–	1441	–	–
			39/42/31		39/42/37
7	13C5-sensitive	–	–	–	–	1373	1354
8	Phenol	1275	–	1275	–	1297/1295	1312
		8/6/35		8/6/19		4/11/32	71/86/29

Experimental frequencies and theoretical and experimental values for 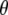using either experimental value of 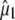(30) (indicated as “visible dichroism”; first value) or calculation of 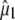at the B3LYP/6-311+G(d,p) level (indicated as “TDDFT”; second value) for the A₁, A₂, and I₂ states and CIS/6-31G(d,p) level for the A₁*, A₂*, and I* singlet states, both relative to theoretical 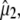calculated at the B3LYP/6-311+G(d,p) level for the A₁, A₂, and I₂ states and CIS/6-31G(d,p) level for the A₁*, A₂*, and I* singlet states. Values for 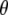obtained experimentally (indicated “experimental IR dichroism”; third value) are listed. Numbering and major mode character are as presented previously (4).

Assignment of 1711, 1695, 1570, and 1450 cm⁻¹ bands to amino acid E222 (COOH), Q69, E222 ν_sym, and E222 ν_asym modes, respectively, have been established in this work and previously (4–6). Good correspondence is found between experimental measurements that are carefully corrected for the finite bleach and empirically for excitation intensity, with theoretical values obtained at the B3LYP/6-311+G(d,p) level by the finite difference method placed in the x-ray geometry (Fig. 5). We note that, with the exception of the E222 (COOH) band, overlap between the chromophore and amino acid bands is likely to lead to further uncertainty in the experimental determination of values for the angles 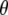between 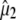and 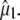Nevertheless, there appears to be good correspondence, particularly for the ν_sym and ν_asym modes of E222, presumably because these bands locally dominate the species-dependent difference spectrum (Fig. 5 D), further strengthening the assignments and conclusions discussed above.

The photoselection measurements further help with assignment, particularly for excited-state modes. Previously, assignments were proposed primarily on the basis of expected bond order changes (4), which have now been confirmed for some modes at the HF and CIS level, although the mode character substantially deviates for some of the chromophore vibrations (data not shown). Here, we present a comparison in Table 1 between experimental (third value in row) and theoretical values for 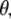using either 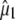as adopted by Shi et al (30) (first value in row) or obtained from TD-DFT (second value). We note that, for the A* and I* excited states due to different normal mode character and single excitation CIS method, the theoretical values for the chromophore will be less reliable.

An excited-state feature where the experimental observation agrees with the theoretical modeling concerns the infrared transition dipole vector of the chromophore C=O mode at 1680 cm⁻¹. This vibration is relatively localized and DFT, HF, and CIS frequency calculations result in similar normal mode character. Calculation of the infrared transition dipole moment vector shows a reduction of the angle for 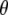in the excited state, as modeled by only the single configuration interaction, by comparison with the ground state at the HF level. The ground state calculation at the HF level, lacking electron correlation, somewhat underestimates the value for 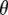compared to calculation at the B3LYP/6-311G(d,p) level, which provides a dipole vector that is close to the C=O bond vector (Table 1) and more closely matches the experimental value. The ground state assignment and measured value for 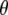are generally in line with those previously reported for the chromophore model compound HBDI (3) and for GFP (7). The downshifted excited-state C=O mode in GFP is in contrast to the broad and kinetically uncoupled upshifted feature at ∼1750 cm⁻¹, proposed to belong to the excited state C=O mode in the solvated and isolated chromophore model HBDI in the neutral state, which clearly displays substantially different excited-state behavior (3). In free HBDI, twisting of the chromophore is proposed as a dominant mechanism for the observed anisotropy changes of the C=O stretching mode (3), whereas mode softening that may contribute to twisting is significantly reduced in the GFP excited-state (31). In intact GFP, assuming no twisting of the chromophore in A*, calculations show that the changed vibrational transition dipole moment vector in A* may arise from small changes in mode mixing, particularly contributions from ring breathing and C=C stretching and potentially from altered molecular dipole response with C=O stretching in A*. Fig. 6 D shows the dipole moments of the C=O stretching mode calculated with HF and CIS in comparison with the experimental values, which shows that the C=O vibration in the A* state is expected to be associated with a reduced value for 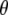and downshifted in frequency relative to the A state. This observation also substantiates the proposed assignment with downshifted frequency at 1672 cm⁻¹, as expected from reduction of the bond order in A*. Furthermore, the long lifetime excludes the contribution of vibrational cooling to the band position, which is not convincingly resolved in the available time-resolved IR spectroscopy data unlike other chromoproteins (32) and probably occurs within 2 ps. These calculations indicate that the observed anisotropy changes may be explained without invoking twisting of the chromophore.

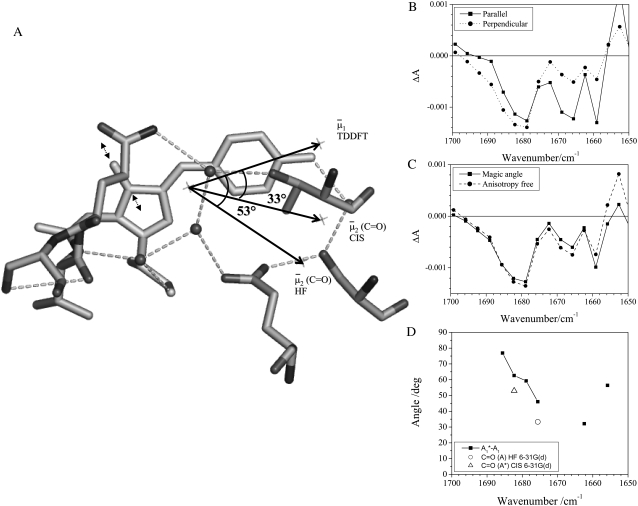
FIGURE 6.

Reorientation of the chromophore C=O vibrational transition dipole moment in the excited state. (A) Orientation and angles between the theoretical optical transition dipole moments 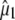and 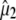for the chromophore C=O vibration in the ground and excited state at the HF/6-31G(d) and CIS/6-31G(d) level, respectively. The general direction of the normal mode displacement is shown with arrows. (B) The 1700–1650 cm⁻¹ region of the polarization dependent A₁* minus A difference spectrum of the wild-type. (C) Reconstructed anisotropy-free ((A_‖+ 2A_⊥)/3) A₁* minus A species-associated difference spectrum and that from measurements at magic angle show good agreement. (D) Theoretical and experimental angles 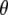in the 1700–1650 cm⁻¹ region of the A₁* minus A difference spectrum.

Further inspection and comparison of theoretical and experimental values highlights a number of closely or reasonably corresponding cases such as the A state C=C mode, the phenol 1 modes, and the A* and I* phenol 3 modes. Clearly, there are also cases where theoretical values do not match experiments for proposed assignments. A number of those can be explained by the inaccuracy of the experimental determination, considering very small difference signals in many cases, and overlapping neighboring bands (Fig. S2, Data S1). However, these reasons cannot explain the differences in all cases, such as the phenol 2 mode in the A states for which the theoretical value is 71° (or 55° using the experimental 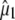) and experimentally a value of 22° was determined, despite an intense and isolated difference band (Table 1; Fig. S2, Data S1).

CONCLUSION

We present a study of the vibrational properties of chromophore and amino acid modes of GFP during the photocycle transitions and focus on the frequency differences between parallel transformations during ESPT. By comparing the transient infrared measurements of the E222D mutant with that of the wild-type, we show that the carboxylate transient proton acceptor group of E222 in the wild-type exists in two different forms that are distinguished by their H-bonding interactions. A direct link between the H-bonding interactions and the rate of ESPT is suggestive of the final hydrogen transfer in the overall concerted process having a measurable level of kinetic control. Apparently, the shorter side chain of D222 in the E222D mutant does not show more than one population within the accuracy of the measurements. The observation that a large frequency splitting Δν_asym-sym in the E222D mutant also correlates with slow ESPT kinetics in the wild-type is additional evidence supporting the interpretation of the frequency differences in the wild-type. Molecular modeling of the E222D mutant suggests that the side chain of D222 is not likely to be present in a rotamer conformation assuming no major additional changes of the immediate environment. The observed ESPT and high ground state population of the neutral A state shows that the electrostatic repulsion between D222 and the chromophore is also sufficiently stabilizing in the mutant. The major conclusion regarding the observed parallel decay channels in the photocycle is that side-chain disorder, which is also present in the ground state (4), is proposed to be related to two populations of the carboxylate of the excited-state proton acceptor that experiences strong and weak hydrogen-bonding interactions and thus different rates of ESPT. The associated fast and slow ESPT reactions provide evidence for observable kinetic control over the photocycle transitions. We conclude that the photoselection study has been most useful for high frequency chromophore modes and the bands belonging to amino acid vibrations, which resolved features in the intermediates of the fluorescence photocycle including those in the singlet excited states A* and I* on an ultrafast timescale.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.