On the Octagonal Structure of the Nuclear Pore Complex: Insights from Coarse-Grained Models

Abstract

The basic structure of the nuclear pore complex (NPC), conserved across almost all organisms from yeast to humans, persists in featuring an octagonal symmetry involving the nucleoporins that constitute the NPC ring. In this article, we seek to understand and evaluate the potential biomechanical reasons for this eightfold symmetry. Our analytical investigation shows that the eightfold symmetry maximizes the bending stiffness of each of the eight NPC spokes while our computational analyses identify the most likely deformation modes, frequencies, and associated kinetic energies of the NPC. These modes have energies close to other published findings using membrane analysis of the nuclear membrane pore opening, and deformation states in agreement with experimental observations. A better understanding of NPC mechanics is essential for characterizing the nucleocytoplasmic transport, which has a central importance in cell biology.

INTRODUCTION

Protein structures called nuclear pore complexes support the perinuclear space between the inner and outer nuclear membranes while controlling all transport between the nucleus and cytoplasm. Nuclear pore complexes (NPCs), protein macroassemblies forming a gating mechanism, regulate cargo transport between the cytoplasm and the nucleoplasm. The nuclear pore complex's vital functionality and intriguing structure continue to motivate extensive studies (1–6). Given the NPC's unique structure and largely mysterious abilities in transporting cargo, attempts have been made to analyze its properties thoroughly (7–10). Little concrete knowledge has been gathered, however, about how the NPC functions, the mechanisms by which it transports cargo, and even the explicit structures of the nucleoporins comprising it. Although a fair amount of understanding exists about the overall transport abilities of the NPC, the mechanics and dynamics of the NPC have remained elusive. For instance, one of the largest, yet most overlooked, characteristic of NPCs is their octagonal cylindrical structures (11,12) composed of some 30 proteins, generally referred to as nucleoporins, or nups.

Owing to the octagonal structure of the nucleoporins and their coassembly, the NPCs have an eightfold rotational symmetry. This symmetry allows for the massive NPC to be built upon a comparatively small number of nucleoporins (13,14), while still maintaining the potential for size distortion and dilation that have been observed experimentally (9). NPCs in yeast and vertebrates differ in size and in detailed components but they possess the same basic architecture (see Fig. 1); the primary structure of the NPC has been evolutionarily conserved. Vertebrate NPCs contain a central framework called the spoke (13,15) complex attached to a cytoplasmic ring and a nucleoplasmic ring (see Fig. 2). Each spoke consists of an inner domain, a central domain and a lumenal domain (3). Yeast NPCs have a mass of ∼60 MDa whereas the vertebrate NPCs have a mass of ∼125 MDa (16). Structural components such as the cytoplasmic ring, nuclear ring, and luminal ring are not present in the yeast NPCs (1). Thus, the spoke complex of a yeast NPC consists of an inner spoke ring, an outer membrane ring, vertical spokes, and a central transporter (16). In both vertebrate and yeast nuclei, the segmented (17) NPC provides a standout or tent pole to preserve the perinuclear space between the inner and outer membranes. NPC densities (18) range from 10 to 60 NPCs/μm² where the largest NPCs with a radius of ∼60 nm are spaced apart by ∼150 nm (see Fig. 3). The transport across the NPCs can be either active or passive in nature. Passive transport occurs by diffusion governed by the concentration gradients for sub-40 kDa molecules (9). The facilitated active transport (for >40 kDa molecules) occurs when karyopherin receptors such as importin-α and importin-β recognize nuclear import signals from the cargo (8,19). The receptors then attach to the cargo and guide the combined structure through the central pore of the NPC by interacting with the phenylalanine-glycine (FG) nucleoporins. When the cargo-receptor unit enters the nucleoplasm, Ran GTP binds to the receptor and cargo is released. A similar process is carried out for the export of the cargo from the nucleus.

FIGURE 1.

(Top) Yeast and vertebrate nuclear pore complexes. Front (a and b) and top (c and d) of yeast and vertebrate (Xenopus) NPCs illustrating the relatively larger size of the vertebrate NPC in the front view and the ubiquitous octagonal shape of both in the top view (Yang et al. (16), Stoffler et al. (41)). The striking octagonal shape (eightfold symmetry) of the NPC is evident. The scale bar is 30 nm. (Bottom) An electron micrograph of a nuclear membrane with two NPCs present (Franke et al. (42)). The scale bar is 100 nm.

FIGURE 2.

Illustration of the NPC showing the central framework surrounded by the double nuclear membrane (7) prepared by D. Stoffler and M. Sanner using a visual programming environment developed at The Scripps Research Institute. The basic framework (15) (modeled herein) is expanded on the right surrounded by four of the eight NPC spokes.

FIGURE 3.

Several NPCs supporting the inner and outer nuclear membranes with spacing between NPCs equal to about three NPC radii. NPC densities range from 10 (yeast) to 60 (vertebrate) NPCs/(μm²). Figure modified from Mazzanti et al. (18).

Both yeast and vertebrate NPCs have eight vertical spokes. Better understanding of the general shape and structure of the NPC may help in unraveling the mechanics behind the NPC's functionality. Furthermore, knowing the rationale behind nature's choice of the octagonal shape may help in conceptualizing innovative designs of structures with similar functionality.

METHODS

To examine the mechanics behind the NPC's functionality, we perform several analyses that include an analytical section analysis on a simple geometric representation of the NPC, a numerical static analysis of a simple cylinder of octagonal segments, and a numerical modal and transient analysis of realistic NPC geometry. The analytical section analysis ultimately produces a transcendental equation whose roots are found symbolically with MATLAB (The MathWorks, Natick, MA). The numerical analyses (static, modal, and transient) are performed with the finite element method and require digital geometry (discretized elements), loads, boundary conditions, and material properties. Fortunately, advances in visualization of the NPC's shape along with its natural symmetry make building realistic geometry reasonably simple to replicate. All of the numerical analyses only call for simple loads and boundary conditions. We are left, however, with having to estimate the material properties for the NPC. In our numerical calculations, we assume an isotropic elastic material with stiffness and density in the order of magnitude of a typical protein, namely actin, for the NPC. By measuring the wave speed through actin, Wagner et al. (20) with densities of protein found by Fischer et al. (21) estimated the following material properties as: density, ρ = 1360 kg/m³, Young's modulus E = 2.2 GPa, and Poisson's ratio ν = 0.4. These values are used for all finite element models herein. To ensure independence of our overall findings to material modeling approach, a different material model was used, namely an incompressible neo-Hookean material (G = 0.8 GPa). The neo-Hookean description allows for finite elastic strains, rather than the small strain theory of a Hookean material, yet the results were qualitatively unchanged. Furthermore, since most proteins including actin are compressible, the Hookean material was ultimately selected.

RESULTS

We speculate that the eight vertical spokes result from a structural requirement to maximize the stiffness of each spoke by distributing the area into an octagonal symmetry to increase the minimum principal moment of inertia and therefore the flexural bending stiffness of the spoke. A computational model was developed based on finite element methods (22) to ascertain that each spoke of the NPC bends about its own neutral axis. The top and bottom of this octagonal hollow cylinder of unconnected segments will move in opposite directions perpendicular to the cylindrical axis. The imposed deformation mode and resulting bending stress distribution in Fig. 4 depict how each segment bends about its own axis. This warrants a closer look at all section properties of the spoke. Looking in the transport direction (top view, Fig. 1), the NPC appears as two concentric rings of smaller and larger radii r and R, respectively. Breaking the annulus into an n-sided polygon, the moment of inertia of each spoke can be determined from the ratio of the radii, and the number of sides, n.

FIGURE 4.

Normalized bending stresses plotted on deformed finite element model (left) of unconnected octagonal segments from NPC central eight-spoke cylinder (right) caused by sway deformation. The bending stress is normalized by dividing all values by the maximum bending stress. The maximum bending stress is proportional to the amount of sway. Instead of an integral cross section, the segmentation of the NPC leads to each spoke extending, twisting, or bending about its own axis that collectively contribute to the structural stiffness of the NPC. In this case, each segment bends about its own neutral axis passing through the each segment's centroid where the bending stress is zero (white line). The top and bottom of the octagonal hollow cylinder of unconnected segments displace in opposite directions perpendicular to the cylindrical axis. Illustration on right modified from Bayliss et al. (17).

From the trapezoidal segment in Fig. 5, the moment of inertia about the x_c axis that passes through the centroid of the area becomes

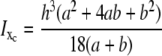(1)

Instead of an integral cross section, the segmentation of the NPC leads to each spoke extending, twisting, or bending about its own axis that collectively contribute to the structural stiffness of the NPC. Using the cross section of the spoke in Fig. 5, the shape of the trapezoid uniquely determined by the number of sides and ratio of radii becomes

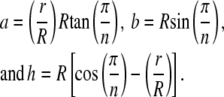(2)

Letting

(3)

the trapezoid shape is found as

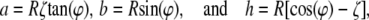(4)

and the trapezoid's moment of inertia becomes

(5)

a function of the annulus radii ratio and the number of segments. Values of I_xc for various values of and 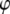are plotted in Fig. 6, which facilitates the visualization of the peak value indicated by a dotted line. The contours are constructed in MATLAB using symbolic algebra. The horizontal hatched area indicates the range of experimentally observed NPC radii ratios, and the vertical hatched area are those rings nearest eight sectors. The transcendental equation,

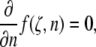(6)

yields the characteristic values of n that maximize I_xc for a given value of 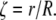The limiting case for 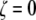is a hexagonal solid structure and as 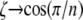the structure becomes a thin circular ring, namely n→∞. The procedure is then applied to the other beam section properties,

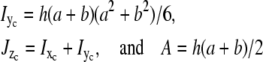(7)

which besides bending, control torsion, 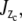and axial or longitudinal extension, A, respectively. The results of the section analysis show the maximizing section values in Fig. 7 along with experimental observations of the prevalent eightfold symmetry; this includes outliers of the nine- and 10-fold symmetries found by Hinshaw and Milligan (11). The eight sectors maximize I_xc for observed NPC radii ratios. Gaps are experimentally observed (panel CF, central framework, Fig. 8) and theoretically introduced by adjusting a and b of the trapezoid as and 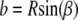where β is some fraction of the sector angle ϕ shown at the lower right of Fig. 7. Although eight sectors maximize I_xc shown in Fig. 7, small changes occur to the maximizing curves (dashed curves) as the gap between the sectors increases. However, changing the gap changes the moments of inertia. As the gap increases from zero 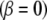(panels NR, nuclear ring moiety, and CR, cytoplasmic ring moiety, Fig. 8) to 50% 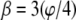(panel CF, Fig. 8), the contour line, I_xc = I_yc, in Fig. 7 migrates upward into the domain of interest (the intersection of the horizontal and vertical hatched areas). Although the eightfold symmetry maximizes the minimum principal moment of inertia for the cross section of a single spoke, it is important to recognize that the NPC is a unified collection of these eight spokes; this circular eightfold symmetry, akin to an eight-legged table, provides support regardless of the direction a cargo (load) might approach. The gap between sectors tends to equate the principal moments of inertia to achieve the best structural support for the least amount of material.

FIGURE 5.

One segment of an n-sided annular polygon contained by the NPC's concentric rings (see panels 1–13 in Fig. 8) forms an isosceles trapezoid whose sections properties can be determined from radii of the concentric rings and the number of segments, n. The subscript “c” refers to those axes that pass through the centroid of the trapezoid. The minimum principal moment of inertia, Ixc, of the segment becomes a key factor in determining the octagonal shape of the central NPC framework.

FIGURE 6.

Contour plot of the moment of inertia, Ixc, for the isosceles trapezoid. Labels A–E refer to various observed NPCs in vertebrate and yeast as listed in Table 2. The dotted line passes through those points where the slope of Ixc equals zero. Horizontal hatched area are observed NPC radii ratios in Table 2; vertical hatched area are those rings nearest eight sectors. The value of Ixc becomes zero as and the trapezoid has no height.

FIGURE 7.

Section properties of the spoke's trapezoid cross section that are maximum for a given number of sectors and radii ratio. Horizontal hatched area are observed NPC radii ratios in Table 2 (solid circles); vertical hatched area are those rings nearest eight sectors. Open circles are nine- and 10-fold geometries rarely (2% ninefold and <0.5% 10-fold) found (Hinshaw and Milligan ((11)) and shown in Fig. 8. The eight sectors maximize Ixc for observed NPC radii ratios. Little change occurs to the curves where partial derivatives with respect to n vanish as the gap between the sectors increases (dashed curves). As the gap increases from zero to 50%, the contour line Ixc = Iyc migrates upward to the middle of the crossing hatched areas. Ixc is less than Iyc below the Ixc = Iyc contour line.

FIGURE 8.

Construction of the finite element model from cross sections through the central framework calculated from the three-dimensional map (Stoffler et al. (10) central image with left panels NR, CF, and CR and right panels 1–13). A two-dimensional finite element mesh overlays the gray section of the central micrograph and is created in the r-z plane. The traced outline in the r-z plane forms this two-dimensional mesh subsequently revolved about the longitudinal axis leaving behind three-dimensional elements. Gaps corresponding to the setting (panel CF) are then created by deleting those element between the spokes. The resulting three-dimensional finite element mesh above the central image is combined with an NPC image (Hinshaw et al. (6)) at the top; it forms a morphed biomechanical image. The octagon of Fig. 7 is superimposed onto the two-dimensional tomography of the central section, panel CF, where the gap between the spokes is largest, 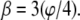The NPC ring cross section's thickness varies over a range of 0.40 < ζ < 0.53 in the bulk of the spokes between horizontal dashed lines marking the inner and outer nuclear membranes. Several two-dimensional maps (panels 1–13) have the white concentric circles with 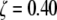or bounding the limits of the observations in Table 2. Though interesting, the nine- and 10-fold symmetry (data outliers in Fig. 7 marked with open circles) found by Hinshaw and Milligan (11) (bottom image) are statistically rare (2% ninefold and <0.5% 10-fold), and as they point out, the nine- and 10-fold symmetries tend to pack into the space designed for the typical eightfold symmetry rather than grow in radius to accommodate the extra segments. Ninefold (a) has and 10-fold (b) has

The simple section analysis does not account for the three-dimensional effects like the taper of the spokes. The benefit and possible biological significance of tapering the spokes in the NPC depend upon the mode of deformation. For example, let's consider a simply supported beam (analogous to the breathing mode) with a transverse load in the center. Tapering the beam to be thicker in the center and thinner at the ends increases the stiffness of the beam and reduces the maximum stresses. Yet the reverse is true for a double cantilever with a transverse end load (analogous to the sway mode). For sway deformation of the double cantilever, this taper reduces stiffness and increases peak stresses. To capture a more realistic geometry, a coarse-grained analysis is constructed from the three-dimensional NPC map motif constructed by Hinshaw and colleagues (6) in Fig. 9 where the lower ring is fixed to prevent rigid body motion (no axial or torsional rigid body motions). Selected premier mode shapes are shown in Fig. 9 with the mode number, frequency, kinetic energy, and mode shape description listed in Table 1. To better quantify the deformation modes, the concept of nodal diameters is used. Nodal diameters (23) connect “nodes” that have no radial displacement during the deformation. For example, an elliptical mode shaped from a circle (oval) would have two nodal diameters connecting the four nodes created where the ellipse crosses the circle. The first 10 mode shapes, corresponding frequencies, and kinetic energies in Fig. 10 and Table 1 illustrate the most likely modes of deformation of the NPC, albeit without surrounding components like the nuclear membranes and other secondary structures shown in Fig. 2. Nuclear membranes with their low stiffness and highly viscous behavior (24,25,) would likely dampen the vibration of the NPC.

FIGURE 9.

Comparing predictions to observations for selected NPC mode shapes, frequencies, and kinetic energies. The contours are of the value of the displacement magnitudes for each mode. The thin line outlines the undeformed shape; the largest displacement magnitude is set to 9 nm to determine the kinetic energy values for all modes. More detail in Table 1 and Fig. 10. (Left) Range of total pore energy computed by Photos et al. (32) agrees with results kinetic energies herein; Beck et al. (12) predict elliptical distortions in NPC from the probability density of the positions of the eight protomers. (Right) Electron micrograph Kiseleva et al. (9) depicts torsional and breathing modes as the Balbiani ring mRNP moves through the NPC enlarging (h and i) and then disappearing (j). Illustration between micrographs of Kiseleva et al. (9) and Panté and Kann (26) show how the 9 nm scale factor was determined from an apparent rotation (torsional mode) of the NPC during transport of the Balbiani ring mRNP, for consistency, this scale factor is used for all modes. Scale bars, 100 nm; Panté and Kann (26) observe side view as intact hepatitis B virus cores crosses the NPC, exciting several modes of deformation, sway in panel D2, and breathing in panel D4.

TABLE 1.

Mode shapes with corresponding frequencies and energies

Mode number	Frequency (GHz)	Kinetic energy (number of kBT)	Mode shape description (see Fig. 10 for plots)
1	0.2804	4,671	1st mode sway
2	0.3327	6,575	1st mode oval, two nodal diameters with rings in phase and same radial displacements
3	0.4519	12,131	1st Mode Ring Torsion, rotating rings with counter rotating rings
4	0.4625	12,707	1st mode oval, two nodal diameters with rings in phase but different radial displacements in each ring
5	0.7747	35,652	3 nodal diameters with rings in phase and same radial displacements
6	0.8279	40,717	1st mode oval invert, two nodal diameters with rings out of phase and different radial displacements
7	1.0784	69,084	1st mode ring torsion, rotating spokes with adjacent pairs in phase
8	1.1701	81,333	2nd mode sway
9	1.2272	89,464	1st mode oval invert, two nodal diameters with rings out of phase and same radial displacements
10	1.2438	91,901	1st mode breathing, 0th nodal diameter

For the number of k_BT, T = 310.15 K and k_B is the Boltzmann constant. Nodal diameters (the number of nodal lines across the diameter of the NPC) connect “nodes” that have no radial displacement during the deformation. For example, an elliptical mode shaped from a circle (oval) would have two nodal diameters connecting the four nodes created where the ellipse crosses the circle. Kinetic energies are computed from a single scaling factor of 9 nm, the maximum displacement magnitude of each mode shape.

FIGURE 10.

First 10 NPC mode shapes. The contours are of the value of the displacement magnitude for each mode. Each frame displays top, front, right end, and isometric projection views. The thin line outlines the undeformed shape; the largest displacement magnitude is set to 9 nm for kinetic energy values. More detail in Table 1.

The modal analysis only determines the displacement amplitudes to within an unknown multiplicative constant; yet, a specific, known measure is preferred. A transient dynamic analysis (using the same model as the modal analysis) with each mode shape as the initial displacement, where the maximum initial displacement is given a specific value, would generate a specific measure of, say, the NPC's kinetic energy. The first mode shape is scaled such that the top ring of the NPC sways 10% of its height (∼9 nm) in the lateral direction. This initial condition excites the first mode shape in the transient analysis, and the top ring begins to sway back and forth relative to the bottom ring with the same frequency of the modal analysis. As the potential (strain) energy of the initially displaced shape converts into kinetic energy, the kinetic energy of the NPC reaches a peak value before being converted back to potential energy. The first mode shape is scaled such that the top ring of the NPC sways 10% of its height (∼9 nm) in the lateral direction. The electron micrographs in Panté et al. (26) implicate the motion of an individual NPC by observing different positions of four different individuals in panels D1–D4 of Fig. 9. In the r-z plane, angle changes of 10° seem reasonable, justifying this 9 nm displacement magnitude for the sway mode. Furthermore, the electron micrographs from Kiseleva et al. (9) suggest that the NPC rotates during Balbiani ring mRNP translocation. Observing the different individual NPCs in panels h, i, and j of Fig. 9 show that a 10° angle of rotation of a single individual NPC may be possible, and with a radius of 50 nm would yield a 9 nm torsional displacement magnitude (inset between electron micrographs of Fig. 9). As a first approximation, we use this 9 nm scaling factor for all modes. Using this single-scale factor for the remaining modes completes the process and these kinetic energies are shown in Table 1 along with their corresponding frequencies and mode shapes.

DISCUSSION

The basic structure of the NPC persists in featuring an octagonal symmetry, conserved throughout organisms, ranging from yeast to humans, involving the nucleoporins that constitute the NPC spokes and rings on both cytoplasmic and nuclear faces. From our analysis, we have demonstrated that the eightfold symmetry is most efficient at maximizing the bending stiffness of each of the eight, large NPC spokes. The reason this becomes important lies in realizing that the NPC is required to transport very large macromolecular cargoes, some of which approach the effective diameter of the core channel itself, quickly without any evidence of phosphorylation, as a direct biological source of energy input. If the NPC were a solid, cylindrical channel in this case, the energy required to push a large cargo complex through the now noncompliant, long cylindrical channel would not only be prohibitively high, but would also present in conjunction with a permanently high entropic barrier preventing even initial inclusion of the cargo. If, in the same case, the NPC was allowed to flex in the modes shown with eight stiff spokes, then the cargo would ideally undergo the minimum amount of contact with the “walls” of the core channel as the NPC inverted (Fig. 11, right, stage 1), dilated (Fig. 11, right, stage 2), and everted (Fig. 11, right, stage 3) to provide a natural biomechanical compliance for the transiting cargo. In this manner, the cargo only has to pass the tightest point (Fig. 11 at stage 2), which would also be the operative entropic barrier, once as opposed to the noncompliant model, where the cargo would continually encounter the tightest point constantly throughout the channel (Fig. 11, noncompliant solid cylindrical model) from the cytoplasm all the way to the nucleoplasm. The advantages of this can also readily be seen in Fig. 12 and the increase in “breathing room” for the cargo being transported versus a standard, solid cylindrical model of the pore. In accordance with this hypothesized mechanism, our analytical section analysis demonstrates that the eightfold symmetry maximizes the bending stiffness of each of the eight NPC spokes whereas our computational analyses (static, modal, and transient) identify the most likely deformation modes, frequencies and associated kinetic energies of the NPC. Further, these modes have energies close to other published findings using membrane analysis of the nuclear membrane pore opening, and physical deformation states in agreement with experimental observations. Understanding the nanomechanical behavior of the NPC via the application of continuum mechanics by finite element methods has a central importance in cell biology. As it stands, this work was spurred in part by the lack of explicit structure of the NPC and the difficulty of pure biological assays on the exact mechanics of transport; one of the significant contributions that we hope to achieve is the validation of a hybrid, biomechanical approach to supercomplexes like the NPC when other methods to develop potential, guided experimentation are otherwise unavailable. A further benefit of this approach is that we are able to justify our views of the biophysical reconformations of the NPC during the nucleocytoplasmic transit process. The application of continuum mechanics by modeling the NPC with finite element methods herein is supported by other physical chemistry, kinetic energy modeling. As an example of this, Yang et al. (27) used a finite element scheme where the polymer was modeled as a rod element capable of self-contact; their results agreed well with other predictions already published using either analytical or numerical approaches. In another case, Bahar and Rader (28) illustrate that experimentally observed motions of proteins can be predicted by coarse-grained (continuum) normal mode analysis. In the case of the nuclear pore complex, by considering the atom as the lower limit of a continuum representing a solid material, the NPC's compact protein structure contains a large number of atoms (125 MDa) fitting the continuum material hypothesis that yields a closed set of partial differential equations approximated by the finite element model used here. Kasas et al. (29) use finite element methods to examine the oscillation of subcellular microtubules via modal analysis. We feel that these data comprise necessary and sufficient conditions as the basis for using finite element analysis, in conjunction with the mathematical treatment of the theory, to reach valid conclusions about the probable deformations the NPC undergoes during biologically relevant processes, i.e., nucleocytoplasmic transport and the transport mechanics. One thing that we have not addressed in this treatment, but would like to in an upcoming future work, is the impact that the FG repeats in the core channel of the NPC have and the role it plays in helping the cargo transit the pore. One of the ways that we postulate the FG repeats interact is to form a “slip channel” for the cargo to slide against for a very short period of time with very high transport velocities. Combined with the temporary formation of a slip channel (Holt et al. (30)) and reconformations of the nuclear pore complex, a large cargo complex can be transported quickly and with little extra effort besides the posttransport step of RanGTP binding to the complex to release the cargo complex from the importin-α/importin-β karyopherin pair. The formation of a slippery channel during the halfway point of cargo transit is, from our preliminary results, quite amenable to rapid nucleocytoplasmic transport. Given the addition of this in the model, we attain results that are quite comparable to currently existing advanced models of the NPC, such as the polymer brush model (C. Wolf and M. R. K. Mofrad, unpublished). Coarse-grained modeling, such as finite element methods, disclose much of the NPC's nanomechanical behavior; this is in contrast to total-complex molecular dynamics of the NPC, since such simulations, even if done per pair of nups, are impractical not only because of the lack of explicit structural data for all the nups, but also because of the overwhelming task of running an explicit simulation. In shedding light on the biomechanical properties of the NPC, we imply, by definition, that the NPC has a structural role in the support of the nuclear envelope as well.

FIGURE 11.

Various states (1–3) of transport of the compliant, eight-spoked NPC on the right compared to the noncompliant, solid cylindrical model of the NPC on the left.

FIGURE 12.

Eightfold segmented NPC is more compliant to the same radial load than a solid cylinder, allowing more room for the cargo to pass easily.

The NPC separates the inner and outer nuclear membrane, keeping the membranes free of shear distortions; hence the NPC stabilizes the perinuclear space. NPCs with interesting nine- and 10-fold symmetry (data outliers in Fig. 7 marked as open circles) are found by Hinshaw and Milligan (11) but they are statistically rare (2% of the NPCs had ninefold symmetry and <0.5% had 10-fold symmetry), and they point out that the nine- and 10-fold symmetries tend to pack into the space designed for the typical eightfold symmetry (see Fig. 8). It is helpful to view the NPC's ring cross section at eye level in the plane of the membrane since there is not just one value of 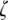as a top view might suggest. Looking closely at cross sections through the central framework (Fig. 8) from Stoffler et al. (10) shows the NPC ring cross-sectional thickness to vary over a range of 0.53 in the bulk of the spoke's span (hatched area) consistent with experimental observations summarized in Table 2 and theoretical predictions in Fig. 7. This range is reasonably constant over the mid span of the spokes, yet the spokes taper as they join both inner and outer rings.

TABLE 2.

Various NPC Sizes

Reference	2r (nm)	2R (nm)	ζ = r/R	Label on Fig. 6
Vertebrate (2)	24.0	60.0	0.40	A
Vertebrate (16)	48.0	94.0	0.51	B
Vertebrate (43)	60	125	0.48	C
Yeast (13)	22.5	48.5	0.46	D
Yeast (16)	49.0	96.0	0.51	E

The maximum of I_xc about the x_c axis (Fig. 5) is determined, not I_x, which would be of all sections about the x axis going through the NPC center as shown in Fig. 5. Optimizing the total section properties of the NPC ring will lead to a solid hollow cylinder, n→∞, not segmented sectors or spokes. A solid hollow cylinder being many times stiffer than the segmented spokes, however, may be overly stiff and not comply with surrounding components. The NPC may be segmented to facilitate transport of large cargos or simply a consequence of the discrete number of proteins available to form the NPC. In both cases, only the section properties of each spoke give rise to the overall stiffness of the NPC, and the eightfold symmetry happens to maximize the weakest link—the minimum principal moment of inertia of a single spoke about its centroid. This holds for both types of NPCs found in vertebrates and yeast. Although their ring structures have different sizes, they both have eight vertical spokes.

The first mode's frequency (0.28 GHz) and kinetic energy (4671 k_BT) agree with total pore energy computed by Photos et al. (32) and this mode qualitatively agrees with observations by Panté and Kann (26) (Fig. 9, panel D2). This lowest energy mode sways where the top and bottom rings move laterally in opposite directions similar to the static computational (finite element) model used in Fig. 4. Due to this sway mode, the NPC acts much like a mechanical lap joint, to stabilize the nuclear envelope, yet is still flexible enough to endure morphological changes of the pore to allow for transport (14). The second mode shape at a slightly higher frequency ovalizes the NPC with its rings in phase with two nodal diameters. Like the sway mode, displacements are in the plane of the nuclear membranes distorting the NPC circular radii into elliptic shapes. Beck et al. (12) suggest that elliptical distortions of the NPC are due to the asymmetry of the eight protomers that form the ring. The third torsional mode where the rings of the NPC counter rotate is the next most likely deformation mode. The sixth mode has enough energy to support two nodal diameters with the rings out of phase similar to a swallowing motion; such a mode is depicted in Fig. 9 (electron micrograph, Kiseleva et al. (9), panels h–j) that could aid the transport of cargos through the central channel. Finally, mode No. 10, the breathing (0th nodal diameter) mode appears, along with mode No. 3 (first torsion), correspond to the electron micrograph showing the dynamics (opening and twisting) of the NPC structure as the Balbiani ring mRNP moves through the NPC under varied levels of calcium and ATP (Rakowska et al. (33)) (Fig. 9, Kiseleva et al. (9), panels h–j). Panté and Kann (26) observed that an intact hepatitis B virus crosses the NPC expanding the central core diameter from 26 nm to 39 nm (Fig. 9, panel D4), an increase of 50% identical to the breathing mode. Realistic cargos would present different principal radii in the plane of the nuclear membrane to the NPC (unlike the gold spheres used by Panté and Kann (26)), and the elliptical two nodal diameter configuration becomes more realistic than the higher energy breathing mode. Although Melcák et al. (34) suggest that circumferential sliding of Nup 58/45 yields a more flexible breathing mode, it would also make the second nodal diameter more flexible as well. Perhaps the rings in the computational analyses herein should have orthotropic rings with a hoop modulus lower than the moduli in the other principal material directions, yet the results presented by Melcák et al. (34) cannot help quantify this reduction in stiffness. Certainly the NPC is made of proteins that are anisotropic in their macroscopic behavior, yet the assumption of an isotropic material is a first-level approximation, given the lack of more accurate information about the NPC's material properties. The anisotropic behavior of the NPC may become more evident with larger displacements caused by transporting larger cargos, although we are not aware of any experimental verification of this. The energy to compress the FG repeats in the central channel and surrounding NPC structure as cargo passes through the NPC depends upon the stiffness of the material and size of the cargo. Larger cargos would need to compress more of the surrounding channel, requiring more energy. Stiffer surroundings would also require more energy for the same size cargo. The structure of the NPC is such to prevent mechanical fluctuations in the normal state of the nuclear membranes, yet still to allow for further expansion to accommodate the transport of large cargo complexes (1,9,35).

For the first three modes of deformation, the kinetic energies are in agreement (4,000 to 12,000 k_BT) with the total pore energy computed by Photos et al. (32). The Derjaguin approximation of a pore (circular opening) in a membrane balances the edge energy of the pore opening with the surface energy of the membrane. Photos et al. (32) modify this energy balance with the free energy contribution of core fibrils comprising the NPC's core granule. This agreement of our finite element transient analysis with the modified Derjaguin's approximation used by Photos et al. (32) supports the results of our analysis for macromolecular protein assemblies; one purpose of the NPC's eightfold symmetry is a benefit for the structural support aspects of the pore. The highest frequencies (1.244 GHz for the breathing mode) are below the 10 GHz frequency limit Creighton (36) established above which all vibrations would occur in the local chemical bonds of the proteins. An experimental estimate of energy comes from Lim et al. (37), where representative worm-like chain models of the modified C-terminal FG domain motifs of NUP153 known as cNUP153 were determined using atomic force microscopy. For small displacement, the chain's stiffness is simply k_BT/(l_pL_C), where the persistence length, l_p, and chain length, L_C, were determined experimentally by Lim et al. for the Kratky-Porod equation (see Eq. 1 and Fig. 1 in Lim et al. (37)). These representative worm-like chains have an average stiffness of 0.0196 k_BT/(nm)². Lim et al. (37) also point out that nearly 30% of the mass of the NPC consists of these types of FG nucleoporins, which translates into ∼625 (60 kDa) cNUP153s. If each FG chain needs to be compressed by say 20 nm to allow transport of 40 nm diameter cargos, the total energy needed becomes the product of the number of FG chains times the work done to compress each chain or,

(8)

which is in the range of the kinetic energy of the first mode of deformation.

Another interesting behavior of the NPC is that it acts as a sort of “entropic gate” in that, for any large cargo to pass, the enthalpy of the pore has to decrease; once this occurs, the Gibbs free energy, 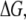drops to the order of k_BT (Rout et al. (38)), which is the diffusion energy allowed for macromolecules, thereby allowing for the distortion of the pore and the “slippage” of the cargo through it, gated only by the internal lattice and configuration of the spokes. Other transport models of the NPC, such as the Brownian diffusion model, do not capture the observed operation of the NPC in situ (Rout et al. (39)). For any macromolecular cargo to get across the NPC, it has to bind to importin-α or importin-β, then manage to bind to the NPC ring and/or the lattice granule at the core of the central channel; after which, it simply traverses the pore (Rout et al. (39)). An important event for transport is that the FG nups have to make a clear path for the cargo, unless there are very strong phobic interactions between the cargo and the fibrils; otherwise energy is required in the form of active facilitated transport to push the cargo through the lattice. However, the NPC is never phosphorylized at any time during the entire transport process until the cargo binds to the basket on the nucleoplasmic side and the macromolecule is unbound by GTP binding to the cargo complex (Rout et al. (39)). Furthermore, experiments have shown that the directionality of the NPC is fully reversible and only controlled by the RanGDP/RanGTP gradient across the nuclear envelopes i.e., cytoplasmic and nucleoplasmic sides, respectively (Rout et al. (39)). Hence, the transport not only requires no active, direct input of energy, in the form of phosphorylation, but is also easily reversible (Zhong et al. (40)). The aforementioned properties are not compatible with a simple channel, composed of a core lattice of FG nup fibrils, where the complex must push its way through. Such a simplistic description, however, falls short of describing the pore characteristics in that it cannot achieve the experimentally measured speeds of NPC transport or the reversibility of a given NPC transport event. The model of the NPC we have described thus far, however, abides by these properties in addition to the slip-flow modeling of transport through the central channel where the Knudsen number, a key dimensionless number that is used to delineate and characterize molecular flow, can be controlled to favor very rapid molecular slip-flow (C. Wolf and M. R. K. Mofrad, unpublished). The entropy for the NPC, in the various modal analysis states, can be calculated stochastically and can be shown to vary with the different configurational states of the nuclear pore membrane glycoprotein 210 (GP210) spoke nups.

CONCLUSION

Mechanics and scaling arguments were used here to propose a reason for the eightfold symmetry (octagonal shape) of nuclear pore complexes. We suggest, based on the theoretical treatment used in this article, that a high flexural stiffness of the vertical spokes is desirable for the normal functioning of the NPCs. Indeed the octagonal shape maximizes the minimum principal moment of inertia of each spoke's cross section about the centroid of the isosceles trapezoidal area bounded by the octagonal angle, 2π/n where n = 8, and the inner and outer radii of the NPC. In addition, this higher bending stiffness is also desirable when the NPCs change their conformation to respond to signals. Although analytical methods show that the octagonal shape maximizes the bending stiffness, numerical methods identify the most likely modes of NPC deformation and estimate the kinetic energies of the NPC. The breathing and torsional modes resulting from the modal analysis are observed by Kiseleva et al. (9), and the kinetic energies (first three modes) are significantly close to other published findings using a modified Derjaguin's approximation by Photos et al. (32) and experimental observations by Lim et al. (37), confirming the approach used herein. Insight into modes of NPC deformation and corresponding kinetic energies enhance our understanding of nucleocytoplasmic exchange. Influencing what the NPC transports and controlling what payload can and cannot enter the cell's nucleus promises vastly improved gene-transfection and gene-therapy methods in the near future.