Rapid calculations of time-harmonic nearfield pressures produced by rectangular pistons

Abstract

A rapid method for calculating the nearfield pressure distribution generated by a rectangular piston is derived for time-harmonic excitations. This rapid approach improves the numerical performance relative to the impulse response with an equivalent integral expression that removes the numerical singularities caused by inverse trigonometric functions. The resulting errors are demonstrated in pressure field calculations using the time-harmonic impulse response solution for a rectangular source 5 wavelengths wide by 7.5 wavelengths high. Simulations using this source geometry show that the rapid method eliminates the singularities introduced by the impulse response. The results of pressure field computations are then evaluated in terms of relative errors and computational speeds. The results show that, when the same number of Gauss abscissas are applied to both approaches for time-harmonic pressure field calculations, the rapid method is consistently faster than the impulse response, and the rapid method consistently produces smaller maximum errors than the impulse response. For specified maximum error values of 10% and 1%, the rapid method is 2.6 times faster than the impulse response for pressure field calculations performed on a 61 by 101 point grid. The rapid approach achieves even greater reductions in the computation time for smaller errors and larger grids.

I. INTRODUCTION

The impulse response approach popularized by Stepanishen¹ and derived by Lockwood and Willette for a rectangular source² provides a general method for calculating the nearfield of uniformly excited acoustic radiators with exact closed-form expressions. This approach defines the impulse response for each spatial coordinate as the response to an impulse velocity evaluated across the surface of a vibrating piston. The expression for the impulse response is convolved with the time derivative of the piston velocity, and the result describes the pressure output as a function of time. For pressure fields produced by time-harmonic excitations, the simulated field is directly proportional to the Fourier transform of the impulse response. Impulse response solutions are available for transducers with a wide variety of shapes, including standard circular,¹ rectangular,^2,3 and spherical shell⁴ geometries. The impulse response is also applicable to simulations of transducers with nonuniform surface excitations.^5,6

Unfortunately, acoustic field computations with the impulse response sometimes encounter numerical difficulties.⁷ These numerical problems arise in response to rapid changes in the impulse response in regions above the edge of the piston. Numerical problems in these regions are typically addressed with high sampling rates. By increasing the number of samples and compensating for the increased frequency content of the impulse response, the computation time is therefore also increased.

With a new rapid integral formulation, the numerical problems with impulse response calculations are solved for uniformly excited rectangular pistons. In time-harmonic numerical calculations, the edge artifacts are eliminated when analytically equivalent integrals are derived and singularities are subtracted from the equivalent integrals. The equivalent integral improves the numerical performance both in the neighborhood of the edge and throughout the nearfield. The improved performance is demonstrated in numerical calculations which show that the integrals with the subtracted singularities converge much more quickly than integrals that evaluate the impulse response. Comparisons between these two methods show that the impulse response produces larger numerical errors and requires more computation time. Thus, the rapid formulation simultaneously reduces the computation time and decreases the numerical error relative to the impulse response.

II. THEORY

The impulse response formulation for a rectangular radiator is derived from the time-domain Green’s function analysis presented in Lockwood and Willette,² which defines the steady-state acoustic field produced by a rectangular radiator for a time-harmonic excitation as

$$p(x,y,z;t)=-j\omega \rho \upsilon e^{j\omega t}H(x,y,z;k).$$ (1)

In Eq. (1), ω is the excitation frequency in radians per second, ρ is the density of the medium, υ is a constant normal velocity evaluated at the surface of the rectangular radiator, k is the wavenumber, and H(x,y,z;k) is the Fourier transform of the impulse response. The center of the rectangular radiator is the origin of the spatial coordinates (x,y,z), and the positive z direction is defined by the normal evaluated at the center of the rectangular source. When computed in terms of the wavenumber k for a rectangular radiator with lateral dimensions s × l, the Fourier transform of the impulse response evaluated directly above one corner is

$$\begin{array}{l}{H}_{s,l}(z;k)=-\frac{1}{2\pi }(\frac{j\pi }{2k}[e^{-jk\sqrt{z^2+s^2+l^2}}-e^{-jkz}]\hfill \\ -{\displaystyle {\int }_{\sqrt{z^2+s^2}}^{\sqrt{z^2+s^2+l^2}}{\cos }^{-1}}\left\{\frac{s}{\sqrt{{\beta }^2-z^2}}\right\}{e}^{-jk\beta }d\beta \hfill \\ -{\displaystyle {\int }_{\sqrt{z^2+l^2}}^{\sqrt{z^2+s^2+l^2}}{\cos }^{-1}}\left\{\frac{l}{\sqrt{{\beta }^2-z^2}}\right\}{e}^{-jk\beta }d\beta ).\hfill \end{array}$$ (2)

After applying the change of variables τ= β/c and replacing the wavenumber k with ω/c, where c represents the speed of sound, this expression is equivalent to that presented in Lockwood and Willette.² In Eq. (2), the subscripts s and l contain the lengths of the lateral dimensions of the rectangular radiator measured in the x and y directions, respectively. The notation H_s,l(z;k) emphasizes that the expression in Eq. (2) is only valid along the normal evaluated at the corner of each rectangular subelement. Therefore, this expression is only evaluated as a function of the z coordinate and the wavenumber k.

At all other field coordinates, the Fourier transform of the impulse response is determined by superposition according to the approach presented in Lockwood and Willette.² The superposition approach, which is adopted here, subdivides a rectangular radiator into four smaller rectangles whenever the (x,y) coordinates of the field point fall within the lateral (x,y) extent of a rectangular radiator that defines the z axis in the direction of the element normal. In Fig. 1, the source is divided into four smaller rectangles that share a corner at (x₀,y₀) for all points satisfying |x| < a and |y| < b, where the element half-width is defined by a and the element half-height is defined by b. After the rectangular source is subdivided into subelements labeled 1, 2, 3, and 4, the sum of the individual contributions in front of the common corner point is then evaluated above the common corner of the four sources. Thus, the contributions of the four rectangular subelements are superposed and the Fourier transform of the total impulse response is evaluated as

$$H(x,y,z;k)={\displaystyle \sum _{i=1}^4\pm H_{s_i,l_i}(z;k).}$$ (3)

In Eq. (3), the subscripts of s and l specify the subelement number as in Fig. 1. The sign of each contribution in Eq. (3) depends on the location of the field coordinate (x,y,z) relative to the outer boundary of the source. Four contributions are added together where |x| < a and |y| < b, and, in general, when |x| > a and/or |y| > b, two contributions are added and two more are subtracted. The exceptions to these rules occur wherever only one equality (either |x| = a or |y| = b) is satisfied, in which case only two rectangular sources are superposed. Where |x| = a and |y| = b, the field coordinate is located directly over a corner of the rectangular source so Eq. (2) is applied directly.

FIG. 1.

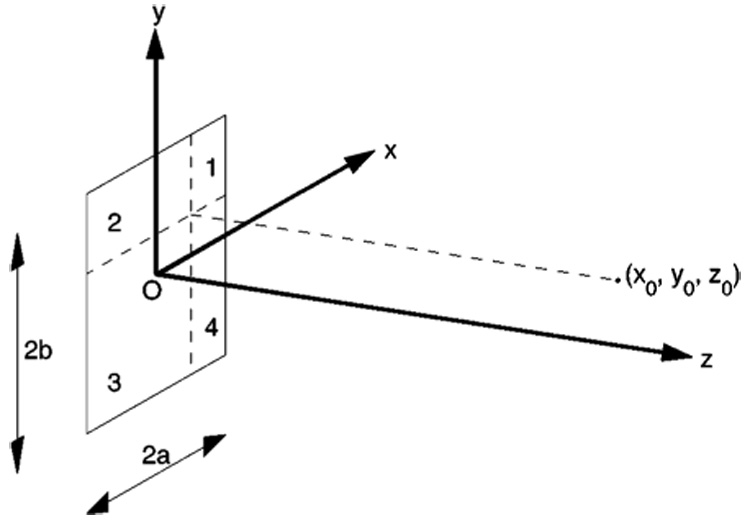
Definition of coordinate axes and rectangles for superposition calculations. The center of the element defines the origin (O) of the coordinate system, and the vertices of the rectangular radiator are specified by the intersections of the lines x = ±a and y = ±b. The z axis is coincident with the element normal. In this coordinate system, the borders of the rectangles defining the subelements required for superposition calculations are specified by the lines x = x₀, y = y₀, x = ±a, and y = ±b. All of these lines are located in the z = 0 plane. The rectangles defined by these boundaries share a common corner at (x₀,y₀), and the Fourier transform of the impulse response at (x₀,y₀,z₀) is determined by superposing the results for rectangles that share the vertex (x₀,y₀).

III. METHODS

The numerical performance of the integral presented in Eq. (2) is improved in three steps. The first improvement is obtained after equivalent integrals are derived and a singularity is subtracted from each integrand. The resulting equivalent analytical expression demonstrates superior numerical properties relative to the impulse response in terms of both computation time and numerical error. The second improvement further reduces the computation time by isolating repeated calculations that are unique to the new integral expression. Instead of evaluating the same expression repeatedly, values are computed once and then stored in memory for subsequent evaluations. The third step consolidates certain integrals that share the same integrand and a common upper or lower integration limit. After all of these steps are combined, the resulting integrals are evaluated with Gauss quadrature and normalized numerical errors are computed.

A. Equivalent integral formulation

When the integrals in Eq. (2) are evaluated numerically, the results are hampered by poor convergence characteristics. For these two integrals, the numerical convergence is limited by the slope of the integrand, which is dominated by the inverse cosine term in Eq. (2). The inverse cosine term produces slopes that are particularly large in all locations where x≈a and/or y≈b. These large slopes cause considerable difficulty when standard quadrature techniques (trapezoidal rule, Simpson’s rule, Newton–Cotes formulas, Romberg integration, Gauss quadrature, etc.) are employed. The numerical problems encountered by Eq. (2) motivate the derivation of an equivalent formulation that avoids excessive slopes within the integrand.

An equivalent integral is obtained from the first integral in Eq. (2) after ${\text{cos}}^{-1}(s/\sqrt{{\beta }^2-z^2})$ is replaced with ${\text{tan}}^{-1}(\sqrt{{\beta }^2-z^2-s^2}/s)$ and then the order of integration is exchanged as follows:

$$\begin{array}{l}{\displaystyle {\int }_{\sqrt{z^2+s^2}}^{\sqrt{z^2+s^2+l^2}}{\cos }^{-1}}\left\{\frac{s}{\sqrt{{\beta }^2-z^2}}\right\}{e}^{-jk\beta }d\beta \hfill \\ ={\displaystyle {\int }_{\sqrt{z^2+s^2}}^{\sqrt{z^2+s^2+l^2}}\left[{\displaystyle {\int }_0^{\sqrt{{\beta }^2-z^2-s^2}}\frac{s}{{\sigma }^2+s^2}d\sigma }\right]e^{-jk\beta }d\beta }\hfill \\ ={\displaystyle {\int }_0^l\left[{\displaystyle {\int }_{\sqrt{{\sigma }^2+z^2+s^2}}^{\sqrt{l^2+z^2+s^2}}{e}^{-jk\beta }}d\beta \right]}\frac{s}{{\sigma }^2+s^2}d\sigma .\hfill \end{array}$$ (4)

After the innermost integral is evaluated, the same procedure is repeated for the second integral in Eq. (2). The two resulting integral expressions are then inserted into Eq. (2), and the result is

$$H_{s,l}(z;k)=\frac{j}{2\pi k}\left(\frac{\pi }{2}{e}^{-jkz}-s{\displaystyle {\int }_0^l\frac{e^{-jk\sqrt{z^2+{\sigma }^2+s^2}}}{{\sigma }^2+s^2}d\sigma }-l{\displaystyle {\int }_0^s\frac{e^{-jk\sqrt{z^2+{\sigma }^2+l^2}}}{{\sigma }^2+l^2}d\sigma }\right).$$ (5)

Equation (5) is analytically equivalent to the integral expression in Eq. (2).

In Eq. (5), a singularity is encountered in each integrand whenever s or l approaches zero. The singularity arises if the corresponding integrand is evaluated at or near the lower limit. When the singularity is encountered in this location, the denominator becomes very small, and therefore the quotient becomes very large. This singularity is easily eliminated when a series expansion is evaluated for the numerator of each integrand.⁸ The resulting term, e^−jkz, is then subtracted from and added to the numerator of each integrand. The term that is subtracted from each numerator is retained for numerical calculations, and the term that is added to each numerator is evaluated analytically. This yields

$$H_{s,l}(z;k)=-\frac{j}{2\pi k}\left(s{\displaystyle {\int }_0^l\frac{e^{-jk\sqrt{z^2+{\sigma }^2+s^2}}-e^{-jkz}}{{\sigma }^2+s^2}d\sigma +l{\displaystyle {\int }_0^s\frac{e^{-jk\sqrt{z^2+{\sigma }^2+l^2}}-e^{-jkz}}{{\sigma }^2+l^2}d\sigma }}\right).$$ (6)

Thus, an expression that is analytically equivalent to the impulse response is obtained, and by subtracting the singularity from the numerator of each integrand, the numerical conditioning of each integrand is further improved.

B. Shared integrands

In the region where |x| > a and |y| > b, superposition dictates that contributions from two subelements are added and two subelements are subtracted according to Eq. (3). When these responses are superposed, integrals sharing a common integrand are combined to improve numerical performance. In this region, the pairs (s₁, l₁) and (s₂, l₂) are defined as the sides of the smallest and largest rectangles such that s₁ = |x| − a, l₁ = |y| − b, s₂ = |x| + a, and l₂ = |y| + b, where a is half of the element width and b is half of the element height defined in Fig. 1. The Fourier transform is then evaluated as H(x,y,z;k) = H_s1,l1(z;k) + H_s2,l2(z;k) − H_s1,l2(z;k) − H_s2,l1(z;k). Ordinarily, this would require the evaluation of two integrals for each subelement, resulting in a total of eight integral evaluations; however, combining the limits for shared integrands reduces the number of integrals from eight to four. Two of the four integrals are evaluated from s₁ to s₂, and the two remaining integrals are evaluated from l₁ to l₂.

Combining integrals that share integrands reduces the total number of integrals evaluated, and this in turn decreases the computation time. The combined integrals also improve the accuracy of the computed acoustic field, since each integral is evaluated over a smaller range of values as specified by the limits. This approach is applicable whenever two terms share the same integrands, which occurs where |x| > a and/or |y| > b. If only one of these two inequalities is satisfied, then two pairs of integrals are combined. The computation times and numerical errors are simultaneously reduced whenever either one or two pairs of integrals are combined.

C. Gauss quadrature

Each integral is evaluated numerically with Gauss quadrature.⁸ The Gauss quadrature rule was obtained from the FORTRAN routine GRULE.⁸ The Gauss rule computes the abscissas g_i and weights w_i of the n point Gauss–Legendre integration rule for the interval [−1,1] in two iterations for double precision accuracy. The abscissas are then converted with a linear mapping function⁹ that is defined for an arbitrary interval [u,υ]. The mapping function is defined for the abscissas as

$${\sigma }_i=\frac{\upsilon -u}{2}{g}_i+\frac{\upsilon +u}{2}$$ (7)

and the Gauss weights w_i are scaled by (υ−u)/2. Gauss quadrature is applied in all of the simulation results presented here.

D. Repeated calculations

In Eq. (6), the limits of integration and the denominator of each integral are independent of the z coordinate. Furthermore, the same limits of integration are repeated in certain integrals, and certain expressions are repeatedly evaluated within the same integral. These features of Eq. (6) are exploited for numerical calculations with careful bookkeeping. If the field coordinate system is defined parallel to the planes where x = 0 or y = 0 (or both, as in the coordinate system of Fig. 1), the terms in the numerator and denominator containing σ² + l² and/or σ² + s² are computed once and then stored in memory for calculations using subsequent values of the z coordinate. This option is not available with the impulse response, which updates the limits of integration and recomputes the integrand with each new value of x, y, and z. Furthermore, the abscissas appear in Eq. (6) only as square terms, and this is exploited by squaring the mapping function in Eq. (7), yielding

$${\sigma }_i^2=\frac{{(\upsilon -u)}^2}{4}{g}_i^2+\frac{{\upsilon }^2-u^2}{2}{g}_i+\frac{{(\upsilon +u)}^2}{4}.$$ (8)

Thus, the squared Gauss abscissas $g_i^2$ are evaluated in advance, and the values for ${\sigma }_i^2$ are then determined from the linear combination of precomputed Gauss abscissas g_i and squared Gauss abscissas $g_i^2$. Additional simplifications are possible when the lower integration limit is zero, as in Eq. (6), allowing the reduction of Eq. (8) to (υ²/4)(g_i+1)², which is an expression that is further accelerated by precomputing (g_i+1)². Precomputed values of $g_i^2$ are available for both Eq. (2) and Eq. (6); however, in Eq. (2), the integrand contains both squared (β²) and unsquared (β) abscissas, and the impulse response requires additional time to calculate both of these terms.

E. Error calculations

The spatial distribution of numerical errors in the computed acoustic field is obtained after the absolute value of the difference between two beam patterns is computed and the result is normalized. This error calculation, when presented in a mesh plot, highlights the regions where singularities are encountered. The error η(n,z) describes the normalized difference between a complex pressure field, P(x,z), and a reference beam pattern, P_ref(x,z). The normalization factor is defined here as the maximum absolute value of the reference beam pattern P_ref(x,z). This scalar normalization factor was selected to prevent division by zero and to avoid exaggerating the error values where the field amplitudes are relatively small. The spatially varying error η(x,z) is thus defined as

$$\eta (x,z)=\frac{|P(x,z)-P_{\text{ref}}(x,z)|}{{\text{max}}_{x,z}|P_{\text{ref}}(x,z)|},$$ (9)

and the maximum error is then

$${\eta }_{\text{max}}=\frac{{\text{max}}_{x,z}|P(x,z)-P_{\text{ref}}(x,z)|}{{\text{max}}_{x,z}|P_{\text{ref}}(x,z)|}.$$ (10)

Thus, plots of η(x,z) show the spatial distribution of error values, and η_max condenses all of the errors for each pressure field calculation into a single value.

IV. RESULTS

An example of a simulated beam pattern produced by a rectangular piston is presented in Fig. 2. This rectangular piston, which has a width of 2a = 5λ and a height of 2b = 7.5λ, is equivalent to that simulated in Fig. 13 of Lockwood and Willette² with an aspect ratio b/a = 1.5 and half-width a = 2.5λ. In Fig. 2, the acoustic field is evaluated in the half-plane defined by y = 0 and x ⩾ 0, which is located across the middle of the rectangular piston in the height direction and halfway across the face of the radiating piston in the width direction.

FIG. 2.

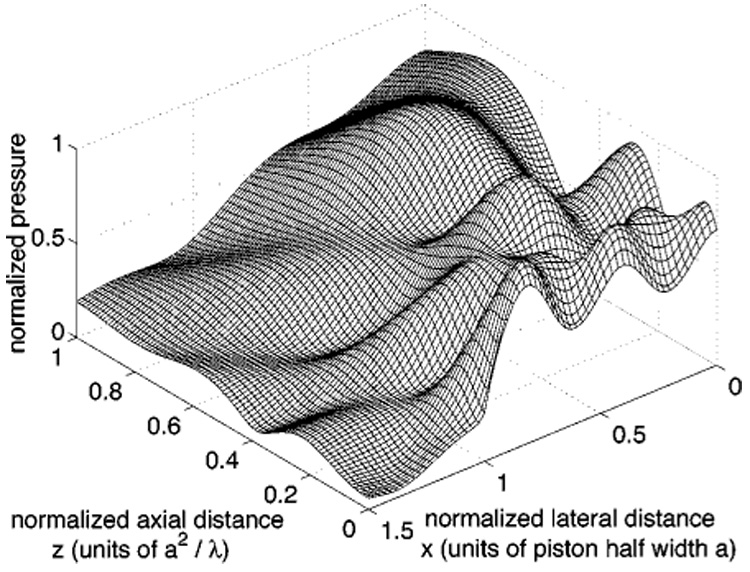
Simulated time-harmonic pressure field for a 5λ wide and 7.5λ high rectangular source. The wavelength of the acoustic excitation is represented by λ, so the element half width is 2.5λ, and the aspect ratio is b/a = 1.5. This simulated pressure distribution, which serves as the reference for subsequent error calculations, is obtained when Eq. (2) is evaluated with 200 000-point Gauss quadrature for each of the subelements and then superposed according to Eq. (3).

The half-plane in Fig. 2 is obtained when Eq. (2) is superposed with the appropriate choice of signs in Eq. (3). In this figure, Eq. (2) is evaluated with 200 000-point Gauss quadrature. This result is demonstrated as a reference because the maximum normalized error between this beam pattern and other beam patterns that are computed with a greater number of Gauss abscissas is η_max ≈ 10⁻¹⁵. Larger errors are encountered if the Fourier transform of the impulse response in Eq. (2) is obtained using a substantially smaller number of Gauss abscissas. When the 200 000-point Gauss quadrature results using Eq. (2) are compared with 200 000-point Gauss quadrature applied to the rapid integral expression in Eq. (6), the mesh plots are indistinguishable, and the value of η_max for each is ≈ 10⁻¹⁵. In other words, the impulse response in Eq. (2) and the analytically equivalent formulation in Eq. (6) have converged to the same value at all points in space when each integral is evaluated with 200 000-point Gauss quadrature.

A. Spatial error distribution

Figure 3 shows the normalized difference η(x,z) between the reference beam pattern in Fig. 2, which was computed with 200 000-point Gauss quadrature, and the Fourier transform of the impulse response described by Eq. (2) evaluated with 9-point Gauss quadrature. In Fig. 3, the spatial error distribution η(x,z) consists of a peak value near the edge coordinates of the rectangular source (x,z) = (a,0) and a numerical artifact that begins near the location of the peak error value and continues out in the +z direction indefinitely along the line x/a = 1. The artifact is barely noticeable on either side of the line x/a = 1 in the nearfield region for calculations using fewer Gauss abscissas because the errors that the impulse response encounters elsewhere in the field are initially very large. Once the integrand is sufficiently sampled, the edge artifact emerges, and for the 5λ × 7.5λ rectangular source geometry considered here, the edge artifact becomes evident in this nearfield grid only when the impulse response is evaluated with nine or more Gauss abscissas.

FIG. 3.

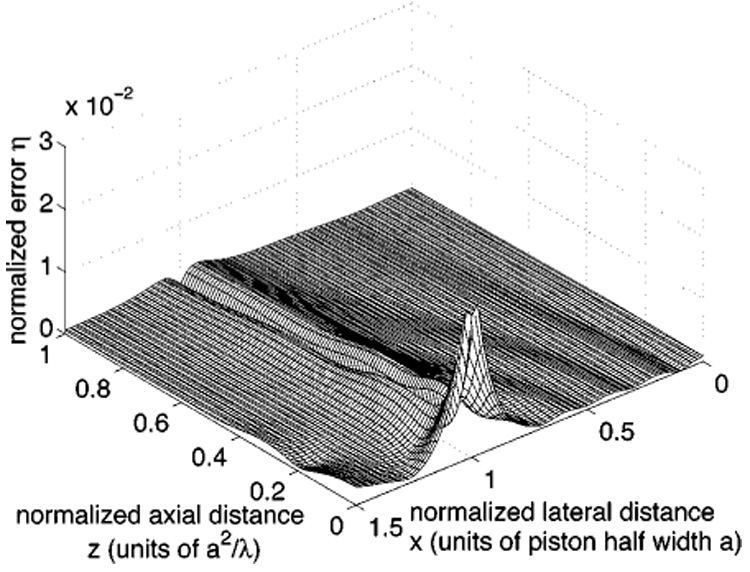
Normalized difference between the reference beam pattern in Fig. 2 and the results of 9-point Gauss quadrature applied to the impulse response calculation in Eq. (2). A peak error value of 2.4×10⁻² is indicated at the edge of the rectangular source. A numerical artifact, located on both sides of the line x/a = 1, also extends across the mesh. If the number of Gauss abscissas is increased, the peak error in the neighborhood of z = 0 disappears, but the remaining errors on either side of the line x/a = 1 are only diminished slightly. The remaining errors that start near each edge of the source and continue outward in the +z direction beyond the far edge of the mesh are produced by the inverse cosine terms in the impulse response.

Figure 4 contains the normalized difference between the reference beam pattern in Fig. 2 and the results of 9-point Gauss quadrature applied to the rapid integral expression in Eq. (6). Throughout the computed field, the error values in Fig. 4 are smaller than those encountered in Fig. 3, suggesting that the rapid formulation converges more quickly than the impulse response. Figure 2 also shows that the rapid approach eliminates the singularity in the impulse response that was demonstrated in Fig. 3 along the line x/a = 1. Although some numerical errors remain in Fig. 4 near z = 0, these are confined to a small region next to the face of the rectangular source. The spatial error distribution in Fig. 4 is representative of that obtained with four or more Gauss abscissas. As the number of Gauss abscissas increases, the error rapidly decreases everywhere in the pressure grid.

FIG. 4.

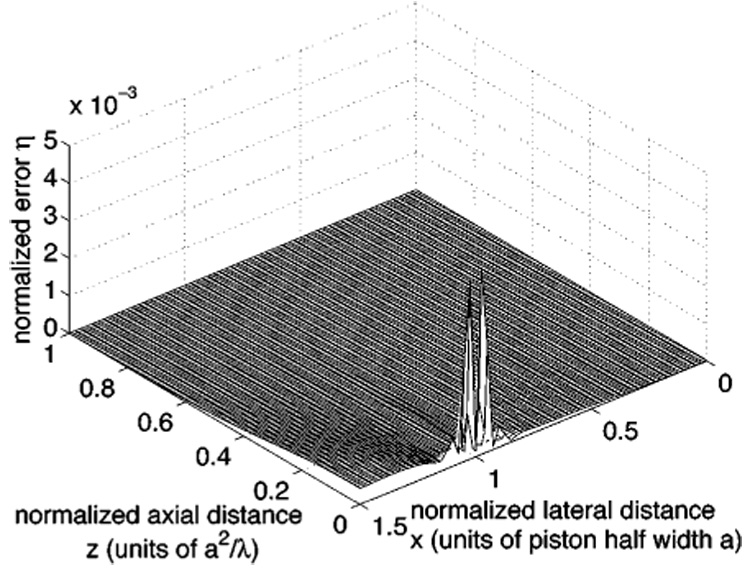
Normalized difference between the reference beam pattern in Fig. 2 and the results of 9-point Gauss quadrature applied to the rapid formulation in Eq. (6). At the edge of the rectangular source, the peak error value reaches 5.0×10⁻³, which is smaller than the error computed with the same number of Gauss abscissas demonstrated in Fig. 3 for the impulse response. Furthermore, the numerical artifact on both sides of the line x/a = 1 in Fig. 3 is eliminated by subtracting the singularity in Eq. (6). As the number of Gauss abscissas is increased, the computed error values throughout the field are rapidly reduced.

B. Error values and computation times

Figure 5 and Figure 6 contain a summary of the errors calculated and times measured when results using the impulse response in Eq. (2) and the rapid formulation in Eq. (6) are evaluated numerically. In Fig. 5 and Fig. 6, the errors and run times are evaluated as the number of Gauss abscissas increases from 1 to 200. The computations are performed on an 800 MHz Intel Pentium III personal computer running the Red Hat Linux operating system version 7.1. On this computer, all simulations are run sequentially with the intent of maintaining similar load conditions for outside processes. Each simulation is written in the C programming language. All simulation routines, including those involving Eq. (2), apply every available numerical acceleration technique.

FIG. 5.

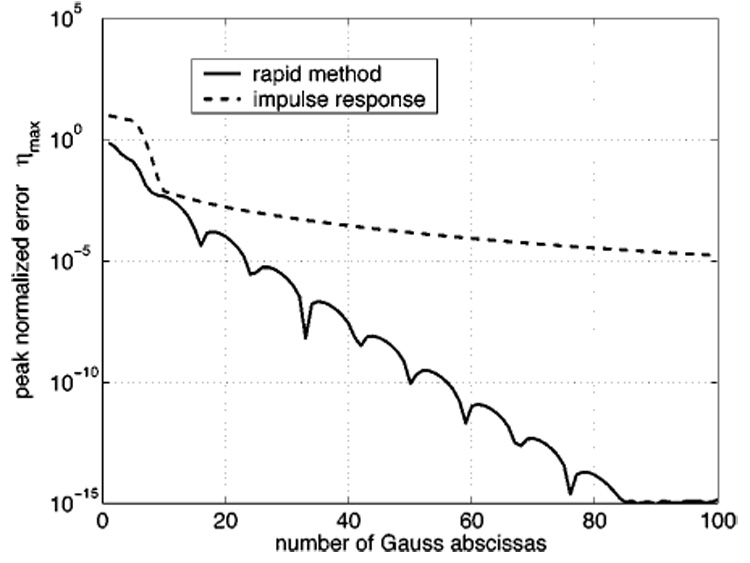
Comparison of the maximum normalized errors η_max obtained from the rapid approach (solid line) and the impulse response (dashed line) as a function of the number of Gauss abscissas. This figure shows that, for the source and grid geometry evaluated here, the maximum error η_max computed with the rapid approach is consistently smaller than that obtained with the impulse response. With the rapid formulation in Eq. (6), the computed errors at individual grid locations are also typically smaller than those calculated with the impulse response.

FIG. 6.

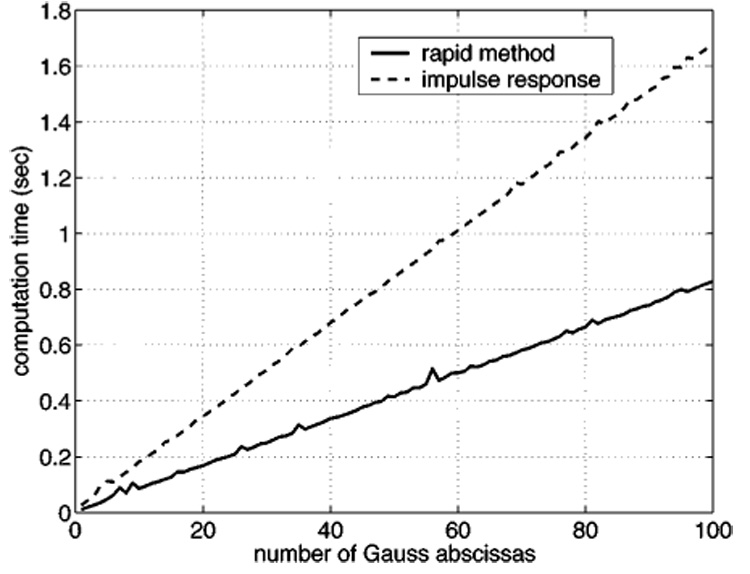
Comparison of measured computation times required for simulations of a 5λ×7.5λ rectangular source using results obtained from the impulse response in Eq. (2), indicated with a dashed line, and the rapid formulation Eq. (6), indicated with a solid line, as a function of the number of Gauss abscissas. This result, along with the result of Fig. 5, shows that the rapid formulation in Eq. (6) simultaneously reduces the errors and the run times relative to those obtained with the impulse response.

Figure 5 demonstrates that the peak errors obtained from the rapid integral expression in Eq. (6) are consistently smaller than those computed using the impulse response in Eq. (2). In Fig. 5, the reference beam is again defined in Fig. 2 as the result of 200 000-point Gauss quadrature applied to Eq. (2), and the maximum error is computed with Eq. (10). Figure 5 shows that the impulse response converges slowly at first, then accelerates over a short range until the singularity near the line x/a = 1 is encountered. The impulse response again converges slowly once the singularity is observed. Figure 5 also demonstrates that the rapid formulation in Eq. (6) achieves a consistent reduction in the error as the number of Gauss abscissas increases and that no singularity is present along the line x/a = 1.

Figure 6 shows that the computation time is linearly proportional to the number of Gauss abscissas. Figure 6 indicates that, for a 61 by 101 point rectilinear grid layout and a 5λ wide by 7.5λ wide rectangular source, the computation time required for calculations using the rapid integral formulation in Eq. (6) is only half that required for the impulse response. This comparison, which is evaluated independent of the respective maximum error values, only considers the time required to evaluate each expression for a certain number of Gauss abscissas applied to this grid and source geometry.

If these computation time comparisons are normalized with respect to the peak error values, the rapid formulation demonstrates even better performance. For example, the rapid integral method of Eq. (6) first achieves a peak error value below 10% with six Gauss abscissas, and the impulse response in Eq. (2) first reaches a peak error less than 10% with nine Gauss abscissas. After the computation time for the rapid method using six Gauss abscissas is divided into the computation time for the impulse response using nine Gauss abscissas, the result indicates that the rapid approach is 2.6 times faster than the impulse response for an error value target of 10%. Likewise, the peak error calculated for the impulse response drops below 1% with ten Gauss abscissas, and the peak error for the rapid method falls below the same peak error target with eight Gauss abscissas. This yields a ratio of computation times equal to 2.6, so the rapid approach is 2.6 times faster for a desired peak error of 1%. A peak error value of 0.1% is reached when 25 Gauss abscissas are applied to the impulse response, and this same error is achieved when only 14 Gauss abscissas are applied to the rapid method. The quotient of the two run times is again evaluated, and the result indicates that the rapid approach is 3.6 times faster for a peak error of 0.1%. The computation times and peak errors are functions of the source and grid geometry, so some variations in these values are expected as the input parameters change.

V. DISCUSSION

A. Computation times

Although the overall structure of the routines tested for Eq. (2) and Eq. (6) was generally the same, certain features of the integrals in Eq. (6) are responsible for the shorter run times achieved by the rapid formulation for the same number of Gauss abscissas. This result is demonstrated in Fig. 6. The impulse response in Eq. (2) contains an inverse trigonometric function, and evaluating the inverse cosine term in Eq. (2) requires more computation time than division by a second order polynomial in Eq. (6). Other inverse trigonometric functions such as inverse sine and inverse tangent are also slower than division by a second-order polynomial. If any of these inverse trigonometric functions are applied to pressure calculations using the impulse response approach, then the rapid method is consistently faster, even if the pressure is only evaluated at a single point.

After each integral sharing an appropriate common integrand is combined for Eq. (2) and Eq. (6), a reduction in the computation time is achieved for both methods. Additional reductions in the computation time are realized for the rapid method when the shared terms in Eq. (6) are exploited. The expressions σ² + s² and σ² + l² appear twice in Eq. (6), but each is only evaluated once and then stored in memory for subsequent calculations. The values of s and l remain unchanged as the computational grid is traversed in the +z direction for a constant value of (x,y), and this allows the repeated use of the stored values for σ² + s² and σ² + l². The value of e^−jkz is also computed once for each value of z in the computational grid and then stored. When the corresponding z value is encountered in the evaluation of Eq. (6), the stored value for e^−jkz is inserted. Individually, each step reduces the computation time somewhat, but by combining all of these steps, the rapid method achieves a significant overall time savings.

For both the impulse response and the rapid method, the Gauss weights and abscissas are calculated in advance and stored in a file. These are the only values that remain unchanged as the grid and source geometries are varied, and these are the only values that are common to both pressure field calculation methods. These values are loaded prior to each calculation, so the time required to calculate the Gauss parameters is not included in Fig. 6. However, the Gauss weights and abscissas are the only values that are calculated in advance. After the complete mesh of pressure field values is calculated for a certain number of Gauss abscissas, all values in memory are cleared, and the next calculation starts from scratch. Therefore, each time value shown in Fig. 6 includes the time required for a complete pressure field calculation along with all of the associated overhead. In other words, by clearing memory after each pressure field mesh is calculated, each time value shown in Fig. 6 for a certain number of Gauss abscissas represents the computation time that is required for an entire mesh of pressure field values calculated from start to finish.

Although the rapid method reduces the computation time by factors of 2.6, 2.6, and 3.6 relative to the impulse response for 10%, 1%, and 0.1% peak errors, respectively, this result is specific to the grid and source geometry shown in Fig. 1 and Fig. 2. Other grid and source geometries can either reduce or increase the relative computation time. A smaller decrease in the computation time is expected for reduced grid sizes, whereas the rapid method is significantly faster when applied to larger three-dimensional (3D) grids. A larger grid enables more shared calculations, and this in turn reduces the computation time required for the rapid method.

Computations of pressure fields on very large 3D grids are commonly performed in simulation studies of ultrasound phased arrays designed for thermal therapy. These ultrasound phased arrays consist of hundreds or thousands of independent elements, and the computed 3D pressure grid can reach hundreds of wavelengths on each side. Computations of the pressure fields generated by ultrasound therapy arrays include a substantial nearfield component. These calculations are also very time-intensive. Simulations of thermal therapy arrays and other large phased array systems will benefit greatly from the fast computation times and small numerical errors achieved by the rapid pressure field calculation method in Eq. (6).

B. Numerical errors

The numerical errors in Fig. 3–Fig. 5 are caused by the aliasing or undersampling of each integrand. The primary source of aliasing in pressure field calculations using the impulse response is the inverse cosine function in Eq. (2). The inverse cosine term produces slopes that are particularly large where x/a ≈ 1 and/or y/b ≈ 1, and, in these regions, finite sampling rates amplify aliasing problems caused by the impulse response. The inverse tangent function encounters the same aliasing problems in these regions. In fact, the errors shown in Fig. 3 are produced by every pressure field calculation formula that uses inverse trigonometric functions. Along the line x/a = 1 in the y = 0 plane, the numerical errors are particularly severe in Fig. 3. As indicated by the result in Fig. 3, large slopes even cause numerical problems for Gauss quadrature, which provides additional samples near the upper and lower limits of integration. In the two-dimensional result shown in Fig. 3, the numerical errors produced by the impulse response are concentrated along a line tangent to the edge of the rectangular source, and in three dimensions, these errors are adjacent to the planes tangent to the edge of the source. The tangents to the four edges of the rectangular source are defined by x = ±a and y = ±b in the coordinate system described in Fig. 1, so the errors produced by the impulse response are found immediately adjacent to these four planes. In two-dimensional pressure fields, the errors are observed along lines as demonstrated in Fig. 3.

Equation (6) eliminates these errors by subtracting a term from the numerator of each integrand, therefore avoiding problems that are otherwise encountered when each denominator grows small. Thus, the singularity disappears after the e^−jkz term is subtracted in Eq. (6). The numerical error in Eq. (6) is generally dominated by the frequency components in the complex exponential term $e^{-jk\sqrt{z^2+{\sigma }^2+s^2}}$ in the integrand. If this complex exponential term is adequately sampled, then aliasing problems are avoided, and the numerical solution to Eq. (6) converges quickly as demonstrated in Fig. 5. A similar complex exponential term e^−jkβ in Eq. (2) also influences the convergence of the impulse response. If the e^−jkβ term is adequately sampled, aliasing problems are reduced in most locations away from the line at x/a = 1 (or in 3D calculations, the planes x = ±a and y = ±b). Near x/a = 1, the impulse response requires a substantial number of additional samples to reduce the effects of aliasing introduced by the cos⁻¹ term in Eq. (2).

These results suggest that the rapid method is better suited for calculations of the time-harmonic pressure field produced by a rectangular source than the impulse response. Results obtained with Eq. (2) occasionally achieve a smaller maximum error for the same number of Gauss abscissas in a limited number of locations for some restricted combinations of source and grid geometries; however, Eq. (6) produces significantly smaller errors in the vast majority of acoustic field calculations. Furthermore, computation times are consistently shorter with the rapid approach. Whenever the measured computation times are compared for the same maximum error, the rapid method is consistently faster than the impulse response.

C. Circular sources

Similar solutions for the time-harmonic fields generated by a circular piston are presented by Archer-Hall et al.¹⁰ and Hutchins et al.¹¹ The solution in Ref. 10 applies a cylindrical coordinate system with a movable origin¹ to the solution of the Kirchhoff integral. These manipulations convert a double integral into a simplified single integral, and the resulting expression is similar to Eq. (6). The solution presented by Hutchins et al.¹⁰ begins by deriving the velocity potential for a circular piston driven by a time-harmonic excitation. The velocity potential is expressed as a double integral containing Bessel functions, and this result is simplified using Hankel transform tables. When the best features of the Archer-Hall et al.¹⁰ and Hutchins et al.¹¹ solutions are combined,¹² the resulting single integral expression is similar to Eq. (6).

D. Other integration techniques

Gauss quadrature,⁹ when applied to the integrals presented herein, consistently produces more accurate results in less time than other standard integration procedures, including the trapezoidal rule, Simpson’s rule, and Newton–Cotes rules. These integration techniques were tested extensively on Eq. (2) and Eq. (6) for a fixed number of abscissas, and Gauss quadrature was retained after superior numerical accuracy was clearly established for these two integral formulations. Similar tests were also performed with an adaptive Romberg integration scheme, and the adaptive scheme failed to consistently converge within the specified tolerance, especially when applied to Eq. (2). Thus, Gauss quadrature is the preferred numerical integration scheme for Eq. (2) and Eq. (6).

E. Future work

Further numerical improvements are still possible for time-harmonic simulations of the nearfield pressure produced by a rectangular piston. Future studies will include considerations of spatial sampling,^13–15 which changes the number of abscissas required as a function of the piston geometry and the field coordinates. If the number of Gauss abscissas is allowed to vary spatially in a scheme that maintains sufficient sampling rates for each integrand, then the computation time will be reduced while the computed pressure fields maintain a specified maximum error. This is achieved with a grid sectoring scheme for circular pistons,¹² and similar results are expected for rectangular sources.

VI. CONCLUSION

Numerical singularities in the impulse response were identified and eliminated for a time-harmonic excitation applied to a rectangular source. These singularities, which emanate from the edges of a rectangular source, result from the large slopes produced by the inverse trigonometric functions in the impulse response. The numerical problems caused by these singularities are removed by substituting equivalent integral expressions and exchanging the order of integration in each. Further improvements are achieved by subtracting the singularity from each integrand, by exploiting repeated expressions, and by combining integrals which share integrands and a single common limit. The resulting expressions are evaluated with Gauss quadrature. The results show that the rapid approach in Eq. (6), when evaluated numerically, consistently outperforms the impulse response in Eq. (2) in terms of both computation time and numerical error. In calculations of the pressure field produced by the 5λ × 7.5λ rectangular source shown in Fig. 2, the rapid approach is 2.6 times faster than the impulse response for maximum specified errors of 10% and 1%. Even greater reductions in the computation time are achieved by the rapid approach relative to the impulse response as the maximum specified error is reduced and as the size of the computational grid is increased.