TROSY in triple-resonance experiments: New perspectives for sequential NMR assignment of large proteins

Abstract

The NMR assignment of ¹³C, ¹⁵N-labeled proteins with the use of triple resonance experiments is limited to molecular weights below ∼25,000 Daltons, mainly because of low sensitivity due to rapid transverse nuclear spin relaxation during the evolution and recording periods. For experiments that exclusively correlate the amide proton (¹H^N), the amide nitrogen (¹⁵N), and ¹³C atoms, this size limit has been previously extended by additional labeling with deuterium (²H). The present paper shows that the implementation of transverse relaxation-optimized spectroscopy ([¹⁵N,¹H]-TROSY) into triple resonance experiments results in several-fold improved sensitivity for ²H/¹³C/¹⁵N-labeled proteins and approximately twofold sensitivity gain for ¹³C/¹⁵N-labeled proteins. Pulse schemes and spectra recorded with deuterated and protonated proteins are presented for the [¹⁵N, ¹H]-TROSY-HNCA and [¹⁵N, ¹H]-TROSY-HNCO experiments. A theoretical analysis of the HNCA experiment shows that the primary TROSY effect is on the transverse relaxation of ¹⁵N, which is only little affected by deuteration, and predicts sensitivity enhancements that are in close agreement with the experimental data.

In the standard protocol for protein structure determination by NMR spectroscopy, sequence-specific resonance assignment plays a pivotal role (1). Several different assignment strategies are available, and one of the established procedures for obtaining sequential assignments (2) involves uniform ¹³C/¹⁵N labeling and delineation of heteronuclear scalar couplings with triple-resonance experiments (3–7). In these experiments, the transfer of magnetization along networks of scalar-coupled spins includes long delays during which ¹³C and ¹⁵N magnetization evolve in the transverse plane. Fast transverse relaxation during these delays and during ¹H acquisition, limits the application of triple-resonance NMR experiments with larger proteins. For experiments that exclusively correlate ¹H^N, ¹⁵N, and ¹³C, the situation has been improved by ²H-labeling of the ¹³CH_n moieties, which eliminates dipolar ¹³C relaxation by the directly attached protons (8) and reduces ¹H^N line broadening by dipole–dipole (DD) coupling with remote protons. However, uniform deuteration also imposes stringent limitations on the structural information that can be obtained by NMR (8,9) and does not significantly reduce ¹⁵N relaxation during the delays when this spin is in the transverse plane. Here, we propose to extend the application of triple-resonance experiments by using the principle of transverse relaxation-optimized spectroscopy (TROSY) (10). TROSY suppresses transverse relaxation in ¹⁵N–¹H^N moieties by constructive use of interference between dipole–dipole coupling and chemical shift anisotropy (CSA) (10) and thus results in improved sensitivity of triple-resonance experiments by minimizing ¹⁵N transverse relaxation during ¹⁵N evolution periods and ¹H^N transverse relaxation during detection. Because part of the gain achieved with TROSY stems from the reduced T₂ relaxation rate of ¹⁵N, TROSY will benefit triple-resonance experiments with deuterated as well as protonated proteins. In this paper, we present experimental schemes for the implementation of TROSY in the amide proton-to-nitrogen-to-α carbon correlation (HNCA) and amide proton-to-nitrogen-to-carbonyl carbon correlation (HNCO) experiments, which correlate the ¹⁵N–¹H(i) group with ¹³C^α(i) and ¹³C^α(i − 1), and with ¹³CO(i − 1), respectively (11, 12). For a quantitative evaluation of the sensitivity gain that can be achieved, we compare [¹⁵N, ¹H]-TROSY-HNCA with conventional HNCA (13).

METHODS

Triple-resonance experiments use coherence transfers along a network of scalar coupled ¹⁵N, ¹³C, and ¹H spins (3–7). Thereby, coherence transfer from ¹⁵N to either ¹³C^α or ¹³CO requires long delays due to the small ¹J(¹⁵N, ¹³C^α)- and ¹J(¹⁵N, ¹³CO)-coupling constants. Because the ¹⁵N magnetization is in the transverse plane throughout these transfer periods, the ¹⁵N chemical shift evolution is recorded in a constant-time (ct) fashion during the magnetization transfer (14, 15), and relaxation of ¹⁵N due to DD coupling with the directly bound ¹H^N and to ¹⁵N CSA leads to severe loss of coherence. Using the TROSY principle (10), transverse relaxation during these critical ¹⁵N evolution periods can be efficiently suppressed. Similarly, ¹H^N transverse relaxation during detection due to ¹H^N CSA and to DD coupling with ¹⁵N can be suppressed with the use of TROSY.

In the following product operator analysis (16) of the [¹⁵N, ¹H]-TROSY-HNCA experiment (Fig. 1), we describe the ¹³C magnetization (C) with Cartesian operators, whereas for the ¹H^N (H) and ¹⁵N (N) magnetizations single-transition operators (17) are used. For both ¹³C/¹⁵N- and ²H/¹³C/¹⁵N-labeled proteins, the ¹H as well as the ¹⁵N steady–state magnetizations are used at the outset, and the density matrix after the first insensitive nuclei enhanced by polarization transfer (INEPT) step at time point b in Fig. 1 becomes

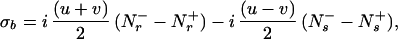1

where the constant factors u and v represent the relative magnitudes of the steady–state ¹H and ¹⁵N magnetizations (18, 19), and the single-transition operators N_r^± and N_s^± represent the ¹⁵N magnetization associated with the rotating frame transition frequencies ω_s^N = ω^N + πJ_HN and ω_r^N = ω^N − πJ_HN, respectively (20). Only the N_s⁻ and N_s⁺ terms are transferred to detectable magnetization after the single transition-to-single transition polarization transfer (ST2-PT) element (18) (time points e–f in Fig. 1). During the ct period T/2 between time points b and c, the N_s^± spin operators evolve due to the ¹⁵N chemical shift and the J-couplings to the two neighboring α-carbons, ¹³C^α(i) and ¹³C^α(i − 1). The resulting antiphase terms N_s^± C_z^α(i) and N_s^± C_z^α (i − 1) are converted to multiple-quantum coherences by the 90° (¹³C^α) pulse at time point c. During t₂, these terms evolve due to the ¹³C^α chemical shift because carbonyl carbons and deuterons or protons are decoupled (Fig. 1). The 90° (¹³C^α) pulse at time point d completes the ¹³C^α evolution period. During the second half of the ct ¹⁵N evolution period, the N_s^± C_z^α (i) and N_s^± C_z^α (i − 1) terms again evolve due to the ¹⁵N chemical shift (21),

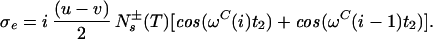2

Two signals in the ¹³C(t₂) dimension exhibit the intraresidual correlation ω₁(¹⁵N_i)/ω₂(¹³C_i^α) modulated by cos(ω^C(i)t₂) and the sequential correlation ω₁(¹⁵N_i)/ω₂(¹³C_i−1^α) modulated by cos(ω^C(i − 1)t₂). Transverse ¹⁵N relaxation during the ct period T = 1/¹J_NC^α is given by (see Appendix):

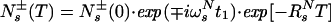3

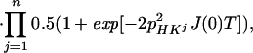where the term pHKj2J(0) represents the relaxation of 15N due to DD interactions of 1HN (H) with remote protons Kj (see Appendix) and RsN is the 15N relaxation rate due to DD coupling with 1HN and to 15N chemical shift anisotropy CSA. Auto- and cross-relaxation terms due to 13Cα–15N and 13CO–15N DD coupling were neglected because they contribute <10% to the overall relaxation rate of 15N (see Appendix). The ST2-PT element (18) (Fig. 1, e-f) transfers the magnetization from 15N to 1HN (Ns+ → Hs−), resulting in the following coherence being acquired during t3:

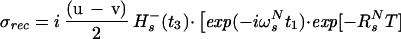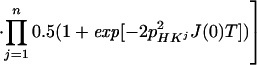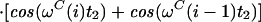4

In Eq. 4, the transition H_s⁻ is associated with the resonance frequency ω_s^H = ω^H + πJ_HN, and the ¹H^N relaxation is given by Eq. 5 (10):

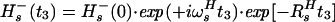5

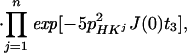where R_s^H is the ¹H^N relaxation rate due to DD coupling with ¹⁵N and to ¹H^N CSA (10).

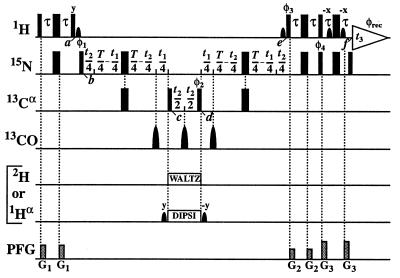
Figure 1.

Experimental scheme for the [¹⁵N, ¹H]-TROSY-HNCA experiment. The radio-frequency pulses on ¹H, ¹⁵N, ¹³C^α, ¹³CO, ²H, and ¹H^α are applied at 4.7, 118, 56, 177, 3.6, and 4.7 ppm, respectively. Narrow and wide black bars indicate nonselective 90° and 180° pulses. Sine bell shapes on the lines marked ¹H and ¹H^α indicate selective 90° pulses. On the line marked ¹³CO, three selective 180° pulses are applied off-resonance with a duration of 120 μs and a Gaussian shape. The line marked PFG indicates the durations and amplitudes of pulsed magnetic field gradients applied along the z-axis: G₁: 800 μs, 15 G/cm; G₂: 800 μs, 9 G/cm; and G₃: 800 μs, 22 G/cm. The delays are τ = 2.7 ms and T = 44 ms. The phase cycle is: φ₁ = {y, −y, −x, x}; φ₂ = {4x, 4(−x)}; φ₃ = {−y}; φ₄ = {−y}; φ_rec = {y, −y, −x, x, −y, y, x, −x}, with all other radio-frequency pulses applied with phase x. A phase-sensitive spectrum in the ¹⁵N(t₁) dimension is obtained by recording a second FID for each t₁ value, with φ₁ = {y, −y, x, −x}, φ₃ = {y} and φ₄ = {y}, and data processing as described by Kay et al. (41). Quadrature detection in the ¹³C^α(t₂) dimension is achieved by the States-TPPI method (42) applied to the phase φ₂. The use of water flip-back pulses (43) at times a and e ensures that the water magnetization stays aligned along +z throughout both the ct period T and the data acquisition period t₃. Residual transverse water magnetization is suppressed immediately before data acquisition (44). The scheme is used for two alternative experiments. For ²H-labeled proteins, ²H-decoupling during t₂ is achieved with WALTZ-16 composite pulse decoupling (45) at a field strength of γB₂ = 2.5 kHz. For measurements with protonated proteins, selective ¹H^α-decoupling during the ¹³C^α(t₂) evolution period is applied instead, using a DIPSI-2 decoupling scheme (46) with γB₂ = 0.51 kHz. The two selective pulses on the water resonance before and after DIPSI-2 ensure the correct treatment of the water during the subsequent t₁ and t₂ evolution periods.

EXPERIMENTAL PROCEDURES

NMR spectra were recorded with two 23-kDa globular proteins, i.e., uniformly ²H/¹³C/¹⁵N-labeled gyrase-23B (95% H₂O/5% D₂O, pH 6.5 at 20°C) (22–24) and uniformly ¹³C/¹⁵N-labeled FimC (90% H₂O/10% D₂O, pH 5.0 at 20°C) (25). A Bruker DRX-750 spectrometer equipped with four radio-frequency channels was used. Data processing included zero-filling and sine bell filtering (26), using the program prosa (27), and the spectra were analyzed with xeasy (28). For gyrase-23B and FimC at 20°C, the isotropic rotational correlation time, τ_c, was estimated from the T₁/T₂ ratio of the backbone ¹⁵N nuclei (29) to be 15 ns.

RESULTS

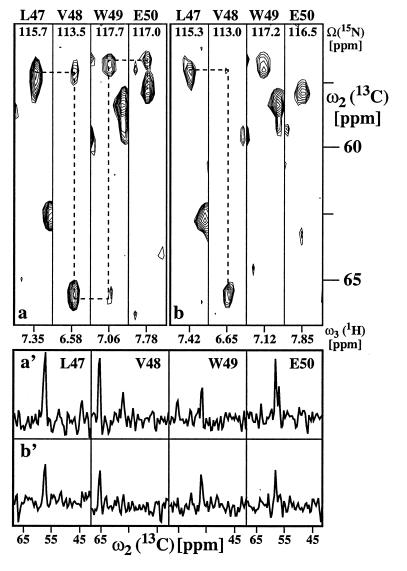
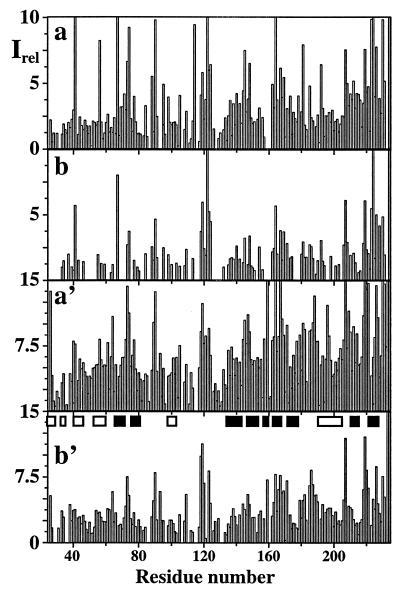
The pulse sequence of Fig. 1 was applied with ²H/¹³C/¹⁵N-labeled gyrase-23B (22–24) and ¹³C/¹⁵N-labeled FimC (25). Fig. 2a shows [ω₂(¹³C), ω₃(¹H)] strips from a three-dimensional (3D) [¹⁵N, ¹H]-TROSY-HNCA spectrum of gyrase-23B, and Fig. 2b shows the corresponding strips from a conventional HNCA experiment (13) recorded with identical conditions. Using TROSY, all sequential ¹H^N-¹³C^α connectivities could be identified, as indicated by the broken lines (Fig. 2a), whereas with conventional HNCA no reliable sequential assignment was possible (Fig. 2b). A more quantitative assessment of the gain in signal-to-noise is afforded by the cross sections in Fig. 2a′ and b′. Data of this type were collected in Fig. 3 for the complete sequence of gyrase-23B. In [¹⁵N, ¹H]-TROSY-HNCA (Fig. 3a), nearly all sequential cross peaks were present with sufficient intensity to allow sequential assignments, which was feasible only for a fraction of the sequence when conventional HNCA is used (Fig. 3b). TROSY also yielded greatly increased intensities of the intraresidual correlation peaks [ω₁(¹⁵N_i)/ω₂(¹³C_i^α)/ω₃(¹H_i^N)] (Fig. 3a′ and b′). In line with theoretical considerations (10), the highest sensitivity gains were obtained for the immobilized core of the protein, with values of 2.9 for the α-helices and 3.4 for the β-sheets. The average sensitivity gain for sequential and intraresidual correlation peaks of the entire protein was 2.4-fold.

Figure 2.

Comparison of a [¹⁵N, ¹H]-TROSY-HNCA recorded with the scheme of Fig. 1 and b conventional HNCA (13) using ¹H DIPSI-2 decoupling with γB₂ = 3.13 kHz during t₁ and t₂, and ¹⁵N WALTZ-16 decoupling with γB₂ = 1.6 kHz during acquisition. Both experiments were recorded with a 1 mM solution of uniformly ²H/¹³C/¹⁵N-labeled gyrase-23B. 26(t₁) × 32(t₂) × 512(t₃) complex points were accumulated, with t_1max(¹⁵N) = 21.7, t_2max(¹³C^α) = 6.4, and t_3max(¹H) = 48.7 ms. Fifty-six scans per increment were acquired, resulting in a total measuring time of 38 h per 3D spectrum. Corresponding [ω₂(¹³C),ω₃(¹H)] strips from the two 3D experiments centered about the ¹H^N chemical shifts were taken at the ¹⁵N chemical shifts of residues 47–50. Because no decoupling during t₁ and t₃ is used in TROSY, the amide ¹H^N and ¹⁵N resonances in a are shifted in both dimensions by ≈45 Hz relative to the corresponding resonances in b. The sequence-specific assignments are indicated at the top by the one-letter amino acid symbol and the residue number in the amino acid sequence. In both spectra, dashed lines indicate sequential connectivities that could be reliably identified (see text). (a′ and b′) cross sections along the ω₂(¹³C) dimension through the four [ω₂(¹³C),ω₃(¹H)] strips at the ω₃(¹H) positions indicated at the bottom in a and b, respectively, where the complete chemical shift range acquired in the ω₂(¹³C) dimension is plotted.

Figure 3.

Plots of the relative signal intensities, I_rel, along the amino acid sequence of uniformly ²H/¹³C/¹⁵N-labeled gyrase-23B (1 mM protein concentration in 95% H₂O/5% D₂O at pH 6.5 and T = 20°C). (a) Sequential correlation peaks (ω₂(¹³C_i−1^α)/ω₃(¹H_i^N)) in [¹⁵N, ¹H]-TROSY-HNCA. (b) Same as a measured with conventional HNCA (13). (a′) Intraresidual correlation peaks (ω₂(¹³C_i^α)/ω₃(¹H_i^N)) in [¹⁵N, ¹H]-TROSY-HNCA. (b′) Same as a′ measured with conventional HNCA. Both spectra were recorded with the same experimental conditions and processed identically, as described in the text. The α-helical and β-sheet regions in the x-ray structure of gyrase-23B (22) are identified in b′ by open and filled bars, respectively.

Measurements corresponding to those in Figs. 2 and 3 also were performed with uniformly ¹³C/¹⁵N-labeled FimC in order to evaluate the performance of [¹⁵N, ¹H]-TROSY-HNCA with protonated proteins. The experimental scheme of Fig. 1 was used with ¹H^α decoupling. The average sensitivity enhancement for the entire protein was 1.5-fold, with a sensitivity gain of 1.7 for the regular secondary structures, which in FimC consist exclusively of β-sheets.

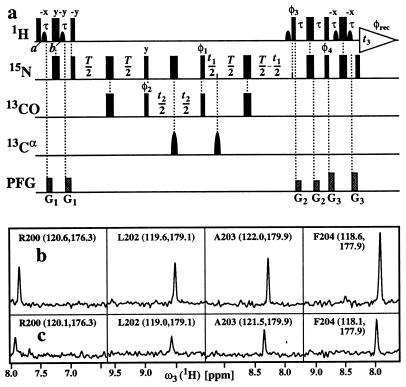
The pulse scheme of the [¹⁵N, ¹H]-TROSY-HNCO experiment (Fig. 4a) was applied to ²H/¹³C/¹⁵N-labeled gyrase-23B with identical conditions to those described for the HNCA experiment in Fig. 2. As an illustration of the results obtained, Fig. 4b and c compares corresponding cross-sections from [¹⁵N, ¹H]-TROSY-HNCO and conventional HNCO (30). From a corresponding data set to Fig. 3, the average gain in sensitivity for the entire protein was found to be 2.4-fold, with values of 2.5 and 2.9 for the α-helices and the β-sheets, respectively.

Figure 4.

(a) Experimental scheme for the [¹⁵N, ¹H]-TROSY-HNCO experiment. All experimental parameters and the phase cycle are the same as in the [¹⁵N, ¹H]-TROSY-HNCA scheme of Fig. 1. (b and c) Show, respectively, cross sections along the ω₃(¹H) dimension through four peaks of the 3D [¹⁵N, ¹H]-TROSY-HNCO spectrum and the conventional 3D HNCO spectrum (30) of uniformly ²H/¹³C/¹⁵N-labeled gyrase-23B (1 mM protein concentration in 95% H₂O/5% D₂O at pH 6.5 and T = 20°C). 26(t₁) × 30(t₂) × 512(t₃) complex points were accumulated, with t_1max (¹⁵N) = 10.8, t_2max(¹³CO) = 12.0, and t_3max(¹H) = 48.7 ms. Eight scans per increment were acquired, resulting in a total measuring time of 7 h per 3D spectrum. At the top of each panel, the sequence-specific assignment is indicated by the one-letter amino acid symbol and the residue number in the amino acid sequence, and the ω₁(¹⁵N) and ω₂(¹³CO) chemical shifts are indicated in parentheses.

DISCUSSION

The HNCA and HNCO measurements (Figs. 2–4) showed that significant improvement of triple resonance experiments can be achieved by suppression of transverse ¹⁵N and ¹H^N relaxation with TROSY. In this section, the origins of the enhanced sensitivity of [¹⁵N, ¹H]-TROSY-HNCA are further analyzed.

In Eq. 5, the ¹H^N relaxation can be represented by a single exponential, with the rate constant

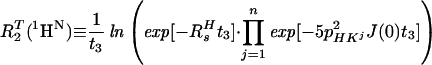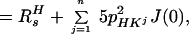6

where R₂^T(¹H^N) denotes the transverse ¹H^N relaxation rate in [¹⁵N, ¹H]-TROSY-HNCA. To a good approximation for the molecular size range of interest, the ¹⁵N relaxation in [¹⁵N, ¹H]-TROSY-HNCA (Eq. 3) may similarly be represented by a single exponential decay, with the rate constant R₂^T(¹⁵N):

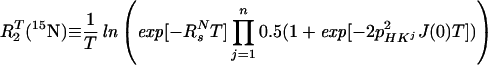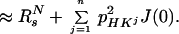7

The approximation of Eq. 7 assumes that pHKj2J(0)T ≪ 1, which is satisfied for commonly used ct periods, T, over the τc range 1–80 ns. For the conventional HNCA experiment, corresponding transverse relaxation rates, R2C(15N) and R2C(1HN), were evaluated as the average of the relaxation rates in the individual components of the 15N and 1HN doublets, respectively. Using Eqs. 6 and 7 for a 23-kDa protein with τc = 15 ns at 750 MHz, and the corresponding formalism for conventional HNCA, one predicts for the protonated protein that TROSY yields 2.9-fold and 1.5-fold reductions of the 15N and 1HN relaxation rates, respectively, when compared to conventional HNCA (Table 1). For conventional HNCA, one expects further that deuteration reduces the 1HN relaxation rates 2.5-fold and 1.6-fold for β-sheets and α-helices, respectively, and that deuteration yields only a small reduction, by less than a factor 1.3, of the 15N relaxation rate. For [15N, 1H]-TROSY-HNCA, deuteration has approximately the same absolute effects on R2T(15N) and R2T(1HN), but because of the greatly reduced RsN and RsH rates the relative improvement is larger, i.e., up to 6.5 for 1HN and up to 2.9 for 15N (Table 1).

Table 1.

Transverse ¹H^N and ¹⁵N relaxation rates predicted for a 23-kDa protein at 750 MHz in [¹⁵N, ¹H]-TROSY-HNCA and in conventional HNCA^*

	TROSY-HNCA		HNCA		Gain†
	R2T(15N)[s−1]	R2T(1HN) [s−1]	R2C(15N) [s−1]	R2C(1HN) [s−1]	AT/AC
Isolated 15N–1HN group	3.0	3.2	20.9	20.3	8.0
β-sheet 13C/15N-labeled‡	10.6	41.1	28.5	58.2	1.8
α-helix 13C/15N-labeled§	8.7	31.5	26.6	48.6	2.0
β-sheet 2H/13C/15N-labeled¶	3.7	6.3	21.6	23.5	4.7
α-helix 2H/13C/15N-labeled‖	5.0	13.2	22.9	30.3	2.9

^*15N and ¹H^N relaxation rates were calculated using Eqs. 6 and 7, respectively, as described in the text. The values listed for conventional HNCA are the average relaxation rates of both components of the ¹⁵N and the ¹H^N doublets, given by R_s^N and R_r^N, and by R_s^H and R_r^H, respectively. The following parameters were used: r_HN = 1.04 Å (39), Δσ_N = 155 ppm, Δσ_H = 15 ppm, Θ_N = 15°, Θ_H = 10° (40), and τ_c = 15 ns. 

^†A^T and A^C are the relative signal intensities obtained with [¹⁵N, ¹H^N]-TROSY-HNCA and conventional HNCA. The ratio A^T/A^C was calculated with Eq. 8, using T = 52 ms. 

^‡Remote protons considered are ¹H^N (i − 1), ¹H^N (i + 1), ¹H^N (j), ¹H^α (i), ¹H^α (i − 1), ¹H^α (j), ¹H^β (i), and ¹H^β (i − 1) at distances of 4.3, 4.3, 3.3, 2.8, 2.2, 3.2, 2.5, and 3.2 Å, respectively, which are typical for an antiparallel β-sheet [i is the observed residue, (i − 1) and (i + 1) the sequential neighbors, and j indicates a long-range contact across the β-sheet (2)]. 

^§Remote protons are ¹H^N (i − 1), ¹H^N (i + 1), ¹H^N (i − 2), ¹H^N (i + 2), ¹H^α (i), ¹H^α(i − 1), ¹H^α(i − 2), ¹H^α(i − 3), ¹H^α(i − 4), and ¹H^β(i) at distances of 2.8, 2.8, 4.2, 4.2, 2.6, 3.5, 4.4, 3.4, 4.2, and 2.5 Å, respectively, which are typical for an α-helix (2). 

^¶Remote protons are ¹H^N (i − 1), ¹H^N (i + 1), and ¹H^N (j) at 4.3, 4.3, and 3.3 Å (2). 

^‖Remote protons are ¹H^N (i − 1), ¹H^N (i + 1), ¹H^N (i − 2), and ¹H^N (i + 2) at 2.8, 2.8, 4.2, and 4.2 Å (2). 

We calculated a theoretical sensitivity gain for [¹⁵N, ¹H]-TROSY-HNCA relative to conventional HNCA by using Eq. 8,

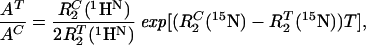8

where A^T and A^C are the peak amplitudes in corresponding [¹⁵N, ¹H]-TROSY-HNCA and conventional HNCA experiments, respectively. The amplitudes are linearly proportional to the ¹H^N relaxation rates, whereas the dependence on the ¹⁵N transverse relaxation rates is exponential because of the ct evolution in the ¹⁵N dimension (15). For a 23-kDa protein, Eq. 8 predicts an 8-fold sensitivity gain for the hypothetical isolated ¹⁵N–¹H^N moiety. When allowing for DD coupling with remote protons, the gain for β-sheets and α-helices amounts to 4.7 and 2.9 in deuterated proteins and to 1.8 and 2.0 in protonated proteins, respectively. Sensitivity gains measured for the ²H/¹³C/¹⁵N-labeled gyrase-23B were 3.4 for β-sheets and 2.9 for α-helices, and for ¹³C/¹⁵N-labeled FimC, a gain of 1.7 was measured for the β-sheet regions. These experimental data are in good agreement with the theoretical predictions (Table 1).

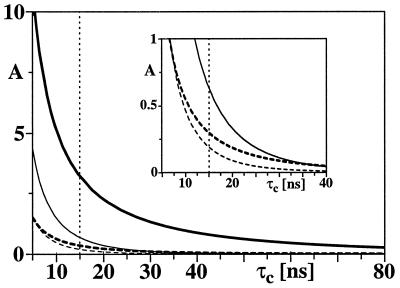
The sensitivity gain (Eq. 8) depends on the molecular size. Fig. 5 shows the relative peak amplitudes calculated for [¹⁵N, ¹H]-TROSY-HNCA (bold lines) and for conventional HNCA (thin lines) as a function of the rotational correlation time, using the parameters listed in Table 1. The thick and thin solid lines indicate the peak intensities for ¹⁵N–¹H^N moieties located in β-sheet regions of a ²H/¹³C/¹⁵N-labeled protein. The dashed lines show the corresponding intensities expected for a ¹³C/¹⁵N-labeled protein. The rapid decrease of the peak amplitude with increasing molecular size limits the application of the conventional HNCA experiment to much smaller proteins than [¹⁵N, ¹H]-TROSY-HNCA (Fig. 5). Actually, for deuterated proteins similar peak amplitudes are expected for τ_c = 15 ns with HNCA and τ_c = 50 ns with [¹⁵N, ¹H]-TROSY-HNCA. For τ_c values above 15 ns, [¹⁵N, ¹H]-TROSY-HNCA with protonated proteins is predicted to yield similar sensitivity as conventional HNCA with deuterated proteins (see Fig. 5).

Figure 5.

Relative signal amplitudes, A, calculated during the ct ¹⁵N evolution and ¹H acquisition periods for [¹⁵N, ¹H]-TROSY-HNCA (thick lines) and conventional HNCA (thin lines) at a magnetic field strength of 750 MHz for variable isotropic rotational correlation times, τ_c, in the range from 5 to 80 ns, which corresponds to protein sizes in H₂O solution at 20°C from ≈7 kDa at τ_c = 5 ns to ≈260 kDa at τ_c = 80 ns. The solid and dashed lines represent the signal amplitudes, A, for a ¹⁵N–¹H^N moiety in a β-sheet of a deuterated and a protonated ¹³C/¹⁵N-labeled protein, respectively (see Table 1 for the parameters used). (Inset) An expanded plot for the range of A from 0 to 1. The dotted vertical line indicates the τ_c value of 15 ns estimated for the 23-kDa proteins gyrase-23B and FimC.

Similar results to those obtained here with [¹⁵N, ¹H]-TROSY-HNCA are predicted for the use of [¹⁵N, ¹H]-TROSY with other triple-resonance experiments that use coherence pathways with ct ¹⁵N evolution periods. For HNCO this is born out by the experiment in Fig. 4, and similar results have been obtained for HN(CO)CA (15), HNCACB (31, 32), and HN(CO)CACB (7,33) (M.S., G.W., K.P., H.S., and K.W., unpublished results). Overall, the present investigation predicts that TROSY-type triple-resonance experiments (Figs. 1 and 4) will be applicable for the assignment of significantly larger proteins than the corresponding conventional triple-resonance experiments. The predictions of Fig. 5 may serve as a platform for estimating the feasibility of resonance assignments and the instrument time needed for particular proteins in the size range 10–250 kDa. Thereby, one has to take into account that these curves can only provide a general guideline, since the CSA parameters may be somewhat variable in the individual amino acid residues (34–38).

ABBREVIATIONS

ct

constant-time

DD

dipole–dipole

CSA

chemical shift anisotropy

HNCA

amide proton-to-nitrogen-to-α carbon correlation

HNCO

amide proton-to-nitrogen-to-carbonyl carbon correlation

ST2-PT

single transition-to-single transition polarization transfer

TROSY

transverse relaxation-optimized spectroscopy

3D

three-dimensional

Appendix

The transverse ¹⁵N relaxation rate is calculated for a four-spin system H-N-C-K representing the backbone atoms ¹H^N, ¹⁵N, and ¹³C^α and a remote proton K, with scalar couplings ¹J_HN, ¹J_NC, and J_KN. ¹³CO, which is not considered (see below), would be treated in the same way as ¹³C^α. The following single spin transition basis operators (47) were selected to evaluate the transverse relaxation of the ¹⁵N single-quantum coherences that evolve in [¹⁵N, ¹H]-TROSY-HNCA:

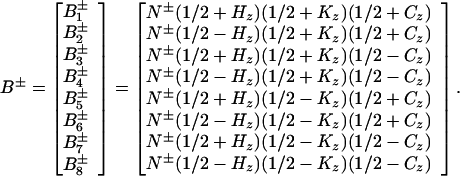A1

In this basis, the Liouville matrix in the rotating frame has the diagonal form given by Eq. A2:

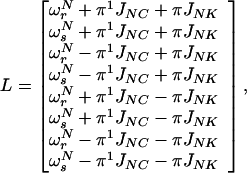A2

with ω_r^N = Ω^N − Ω₀ + π¹J_HN and ω_s^N = Ω^N − Ω₀ − π¹J_HN, where Ω₀ is the reference frequency and Ω^N the Larmor frequency of N. In calculating the relaxation matrix, Γ, the DD interactions H-N, N-C, C-K, and H-K, the CSA of H and N, and all cross-correlation terms between these relaxation interactions are taken into account. Not included are the very small N-C DD interactions (48). In the slow-tumbling approximation, only terms in J(0) need to be retained:

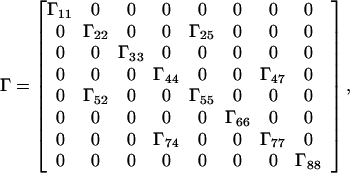A3

where the Γ_ii represent the relaxation rates of individual transitions of the N multiplet. Γ₂₅, Γ₅₂, Γ₄₇, and Γ₇₄ represent the cross-relaxation between different nondegenerate transitions of the N multiplet with resonance frequencies separated by π¹J_HN. The individual relevant matrix elements are:

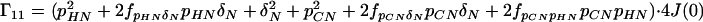A4

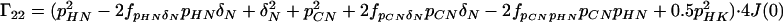A5

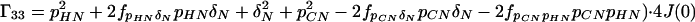A6

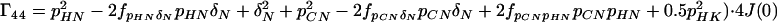A7

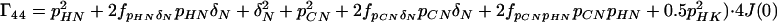A8

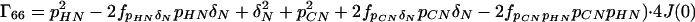A9

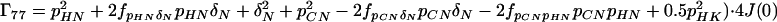A10

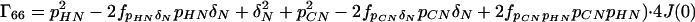A11

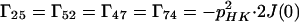A12

f_ki = 0.5(3cos²Θ_kl − 1), p_ij = (2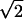r_ij³)⁻¹ћγ_iγ_j and δ_N = (3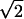)⁻¹ γ_NB₀Δσ_N, where ћ is the Planck constant divided by 2π, Θ_kl the angle between the unique tensor axes of the interactions k and l, γ_i the gyromagnetic ratio of spin i, r_ij the distance between the spins i and j, B₀ the polarizing magnetic field, and Δσ_N the difference between the axial and perpendicular principal components of the ¹⁵N chemical shift tensor, which is assumed to be axially symmetric. Numerical calculations using Eqs. A4–A12 showed that the terms (p_CN² ± 2f_pCNδNp_CNδ_N ± 2f_pCNpHNp_CNp_HN)⋅4J(0) contribute <10% to the overall relaxation of ¹⁵N and can be neglected. This applies for both ¹³C^α and ¹³CO. The Eqs. A2 and A3 show that there is no interference between the group of basis operators B₁^±, B₃^±, B₆^±, and B₈^± and the other four basis operators. Thus, for these operators, the time evolution can be calculated individually, resulting in single-exponential relaxation determined exclusively by interactions within the H-N spin subsystem. Because of the pairwise linkage of B₂^± with B₅^±, and of B₄^± with B₇^±, the relaxation of the corresponding transitions is in general biexponential. However, since Γ_ij ≪ π¹J_HN (i ≠ j) the off-diagonal elements can be neglected, so that a single-exponential decay is obtained for all basis operators:

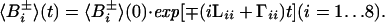A13

The sum of the operators B₂^±, B₄^±, B₆^±, and B₈^± represents the magnetization of the TROSY ¹⁵N multiplet component, so that the transverse ¹⁵N magnetization at time t can be described by:

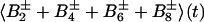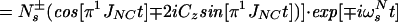A14

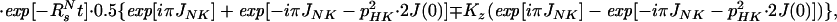where N_s^± = N^± (1/2 − H_z) and R_s^N = (p_HN² − 2f_pHNδNp_HNδ_N + δ_N²)⋅4J(0). Eq. A14 can be further simplified by assuming that J_NK = 0. Furthermore, since N^± K_z does not result in an observable signal, the evolution of the ¹⁵N magnetization can be described by A15:

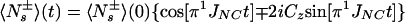A15

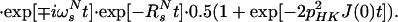This treatment can be expanded to n mutually noninteracting remote protons, K¹, K², …, Kⁿ, resulting in Eq. A16:

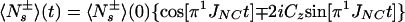A16

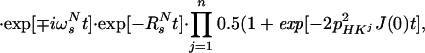Eq. A16 was used for the derivation of Eq. 3 in the main text.