Safety For Whom? The Effects of Light Trucks on Traffic Fatalities*

Abstract

Light trucks have doubled their share of the vehicle fleet from 1980 to 2004. This paper examines the effects of this increase on traffic safety, combining estimates from a state-level panel data set with an accident-level micro data set. The results suggest that a one percentage point increase in light truck share raises annual traffic fatalities by 0.34 percent, or 143 deaths per year. Of this increase, approximately one-fifth accrue to the light trucks’ own occupants, and the remaining four-fifths accrue to the occupants of other vehicles and pedestrians. Using standard value of life figures, the implied Pigovian tax is approximately 3,850 dollars per light truck sold. Overall, light trucks pose a significant hazard to other users of the highway system but on average provide no additional protection to their own occupants.

1 Introduction

Over the course of two decades light truck sales have increased from 16.4 percent of light vehicles sales in 1980 to 50.0 percent of light vehicles sales in 2005 (Davis and Diegel, 2007). This sales growth has induced a corresponding shift in vehicle fleet composition that continues today. The commercial success of these vehicles is due in part to the fact that many consumers associate them with occupant safety because of their high mass and rugged image (Bradsher, 2002). Indeed, previous research has suggested that a heavier vehicle fleet is a safer vehicle fleet (Crandall and Graham, 1989). Nevertheless, the net effect of light trucks on traffic fatalities – the leading cause of death for persons under the age of 40 – is ambiguous.

It is well-established in the highway safety literature that additional vehicle mass can improve own-occupant outcomes in the event of an accident, all other things being equal (Evans and Frick, 1993; Evans and Frick, 1994). However the safety benefits of additional mass in multi-vehicle collisions come at the cost of greater external risk to the occupants of other vehicles. The net effect of additional vehicle mass on traffic fatalities can therefore be minimal (Evans, 2001).¹ Furthermore, light trucks possess several unique features that may make them more dangerous both to their own occupants and to others. Relatively poor braking and maneuverability make them difficult to handle, and a high center of gravity increases the risk of rollover. Stiff frames and high ground clearance make them more likely to ride up over car bumpers and penetrate passenger compartments. Because of these distinct characteristics, and because the increased popularity of light trucks has coincided with a deceleration in traffic fatality reductions, the question of how light trucks impact traffic safety has attracted significant attention (Hakim, 2003a).

To measure the effects of light trucks on traffic fatalities, I first estimate the net effect of vehicle fleet composition on traffic fatalities using a unique state-level panel data set spanning 24 years. I then use a random sample of police-reported accidents to estimate the effects of light trucks on their own occupants and on other roadway users when an accident occurs. The risks that light trucks impose upon their own users I define as ‘internal’ risks; the risks that light trucks impose upon other vehicles and pedestrians I define as ‘external’ risks.² This distinction is important for policy – rational consumers will account for increased internal risk when making their purchasing decisions, but they will not account for increased external risk unless corrective taxes are in place.³ I combine the results from the state-level and accident-level estimation strategies to determine an important unknown parameter: the relative crash rate of light trucks as compared to cars. Using this parameter, I estimate the total internal and external effects of shifting the vehicle fleet composition from cars towards light trucks.

Previous analyses using accident-level micro data have shown that, in the event of an accident, light trucks pose a greater hazard to other vehicles than do cars (Joksch, 1998; Toy and Hammitt, 2003; White, 2004). In particular, White (2004) uses a random sample of all police-reported accidents to demonstrate that when an accident occurs, light trucks impose significant externalities on other cars, trucks, and pedestrians. However, a vehicle can be hazardous for two distinct reasons: it can inflict more damage when a crash occurs, and it can be more likely to have a crash. Accident-level data alone cannot identify the relative crash rate of light trucks as compared to cars.⁴ White (2004) therefore reports a wide range of possible internal, external, and total effects using different plausible values of the relative crash rate parameter.

An alternative approach is to use county- or state-level data to estimate the effect of vehicle fleet composition on total traffic fatalities. Coate and VanderHoff (2001) use four years of state-level data to measure the effect of light trucks on traffic fatalities; they cannot control for unobserved state effects and find inconsistent results across different specifications. However, with state-level data alone it is impossible to disaggregate the net fatality effect into its internal and external components. Gayer (2004) addresses this issue by combining micro-level data on fatal accidents with cross-sectional state-level data. Several creative identifying assumptions allow him to calculate the total internal and external fatality effects of light trucks, but his estimated effects exceed the largest effects reported in White (2004) by a factor of ten or more.

This paper confronts the contradictions in the previous literature by combining updated micro-level estimates from police-reported accident data with new state-level estimates that control for unobserved state heterogeneity.⁵ It also provides much more precise estimates of the total, external, and internal fatality effects of light trucks than has previously been possible. The paper is organized as follows. Section 2 describes the data. Section 3 presents an empirical model and results for the net effect of vehicle fleet composition on traffic fatalities using state-level panel data. Section 4 presents an empirical model and results for the internal and external effects of light trucks on fatalities. Section 5 concludes. The results suggest that a one percentage point increase in the light truck share of the vehicle fleet increases annual traffic fatalities by approximately 143.⁶ Of this increase, approximately 79 percent are external fatalities, and the remaining 21 percent are internal fatalities. These estimates appear robust to a variety of concerns, including reverse causality, unobserved state trends, and driver selection by vehicle type.

2 Data and Descriptive Statistics

I define light trucks as pickup trucks, sport utility vehicles, and vans with a gross vehicle weight of under 10,000 pounds. Both the Federal Highway Administration (FHWA) and the National Highway Traffic Safety Administration (NHTSA) apply this definition to identify light trucks in the data sets that this study uses (U.S. Department of Transportation, 2000).⁷ Table 1 presents information on the average weight, size, and performance of the top 10 selling cars and top 10 selling light trucks in 2000 and 2005. Popular light trucks are approximately 50 percent heavier and 10 percent longer than popular cars, though these differentials narrow over time. Average height-to-width ratio – an important determinant of stability – is 15 percent higher for light trucks than for cars (lower is more stable), and light trucks have inferior braking distance and emergency handling relative to cars. Average horsepower-to-weight ratio – a good proxy for acceleration –is higher for cars than for light trucks. Overall, the mass differential suggests that light trucks should be more protective of their own occupants and more damaging to other vehicles occupants in multi-vehicle crashes. The braking, stability, and handling characteristics, however, imply that light trucks are more difficult to control than cars, which, ceteris paribus, could lead to more accidents.

Table 1.

Vehicle Characteristics

Vehicle Type, Year	Weight (lbs)	Length (feet)	Height/Width (ratio)	Ground Clearance (inches)	Braking Distance (feet)	Emergency Handling (mph)	HP/Weight (HP/100 lbs)
Top 10 Cars, 2000	2,829	15.3	0.81	5.5	141	Good	4.6
Top 10 Trucks, 2000	4,523	17.1	0.93	7.4	146	Fair	3.7
Top 10 Cars, 2005	3,031	15.6	0.82	5.5	141	50.4	4.9
Top 10 Trucks, 2005	4,484	17.1	0.93	7.7	147	46.9	4.6

Notes: All car-truck differences are statistically significant except HP/Weight ratio in 2005 and Braking Distance in 2000 and 2005. Data come from Consumer Reports, Ward’s Automotive, Edmunds, and The New York Times. Consumer Reports changed its rating system for the emergency handling maneuver between 2000 and 2005 from a discrete index (Poor, Fair, Good, Very Good, Excellent) to a continuous index (mph).

I use two distinct data sets to estimate the effects of light trucks on traffic fatalities. The first data set is a state-level panel data set from the FHWA Highway Statistics Series (U.S. Department of Transportation, 2004). The data include information on traffic fatalities, vehicle registrations, vehicle miles traveled, and licensed drivers.⁸ I supplement this information with demographic, state policy, and weather data from the U.S. Census, the Current Population Survey, NHTSA, and the National Oceanic and Atmospheric Administration. These data span from 1981 to 2004.

The second data set is a random sample of police-reported accidents. These data come from NHTSA’s General Estimates System (GES).⁹ The data include information on injuries and fatalities, vehicle type, geographic location, weather conditions, use of safety equipment, and driver and occupant characteristics. For analytic purposes, I decompose this data set into five sub-samples: two-vehicle crashes involving at least one car, two-vehicle crashes involving at least one light truck, single-vehicle crashes, crashes involving motorcycles, and crashes involving pedestrians or pedalcyclists. These data span from 1996 to 2004.

Table 2 presents summary statistics for the two data sets. There was a mean of 881 annual fatalities per state during the sample period, and the light truck share of the vehicle fleet averaged close to 30 percent.¹⁰ 47 continental states are included in the analysis; Oklahoma is excluded because it is missing data for some years. The accident-level data set includes data on 454,014 accidents.¹¹ Of these accidents, 5,717 involve at least one fatality, and approximately 47 percent of them involve at least one light truck.

Table 2.

Summary Statistics

Variable	Mean	Std. Dev.
State Panel Data Set
Traffic fatalities	880.8	876.6
Fatalities per 100,000 persons	18.4	6.2
Light truck share	0.296	0.114
Sample period	1981–2004
Number of states	47
Observations	1,128
Accident-Level Data Set
Average number of vehicles	1.80	0.66
Percent involving light trucks	0.470	0.499
Fatal accidents	5,717
Total accidents	454,014
Sample period	1996–2004

Notes: Panel means are across state-time observations; they do not equal national means across time.

3 State-Level Results

3.1 Results

The popularization of the sport utility vehicle has resulted in strong growth in light truck sales over the past 15 years. After recovering from the oil price shocks of the early 1980s, light truck sales accounted for 25.3 percent of new vehicle sales in 1985. Market share gains continued through 1990, when light truck market share reached 30.2 percent. Growth then accelerated, and by 2005 light trucks constituted 50 percent of new vehicle sales. Table 3 reports market share by type of light truck from 1980 to 2005. Virtually all the growth in light truck share since 1990 has come from SUVs. From 1990 to 2005, the combined market share of pickup trucks and vans fell 1.2 percentage points (5 percent), while market share of SUVs increased 20.7 percentage points (370 percent). This rapid growth in market share provides an opportunity to examine the relationship between traffic fatalities and light truck share across different states over time.

Table 3.

Market Share by Vehicle Type

Variable:	1980	1985	1990	1995	2000	2005
Car Share	83.5	74.7	69.9	62.1	55.0	49.9
Pickup Truck Share	12.7	14.4	14.6	15.0	15.7	15.8
Van Share	2.0	5.8	10.0	10.9	10.2	7.9
SUV Share	1.7	5.1	5.6	12.0	18.9	26.3

Notes: Columns may not sum to 100 due to rounding. Source: Davis and Diegel (2007).

The total number of traffic fatalities, including pedestrians and pedalcyclists, is specified as a function of the light truck share of a state’s vehicle fleet and a set of observed and unobserved variables:

$$E[F_{st}\mid {\mathit{LTS}}_{st},{\mathit{POP}}_{st},X_{st},{\gamma }_t,{\alpha }_s]=exp[\beta {\mathit{LTS}}_{st}+ln({\mathit{POP}}_{st})+X_{st}\delta +{\gamma }_t+{\alpha }_s]$$ (1)

F_st represents the number of traffic fatalities in state s during year t, LTS_st is the percentage of vehicle registrations that are light trucks, POP_st is state population (the scale variable), and γ_t and α_s are unobserved year and state effects respectively. The vector X_st includes per capita beer consumption, indicators for primary and secondary safety belt laws, share of vehicle miles traveled that are on rural roadways, percent of licensed drivers under 25, percent of licensed drivers over 70, rural and urban speed limits, the unemployment rate, share of the population with a college degree, share of the population under 18, measures of rainfall and snowfall, and quadratic time trends for each Census Division.

Because the dependent variable takes on integer values, I use a negative binomial regression model for estimation purposes.¹² To account for unobserved state and year effects, I include indicators for both states and years in all regressions.¹³ The strength of the negative binomial model is that it is unbiased if the conditional mean is correctly specified. In that sense, it is no less robust than least squares, and it may provide a better approximation of the conditional expectation function. In theory, the standard errors could still be sensitive to the maximum likelihood assumptions, but experimentation with bootstrapped standard errors produced estimates of similar size to the analytic standard errors. Nevertheless, I also present results for linear regressions to verify that the conclusions are not overly sensitive to the estimation procedure.

Columns (1) through (4) of Table 4 present results for the negative binomial models. The regressions are weighted by state population, and the standard errors are clustered at the state-level to correct for within-state serial correlation (Bertrand et al., 2004). Column (1) reports results from the preferred specification, which contains a full set of controls. The coefficient of 0.344 on the light truck share variable is statistically significant and implies that a one percentage point increase in light truck share is associated with a 0.34 percent increase in total traffic fatalities. The scale variable – population – has a coefficient somewhat below one (0.79), but it is not significantly different than one. Although not reported in the table, other control variables have coefficients with signs in the expected directions. Beer consumption has a positive and significant coefficient, while primary belt laws, secondary belt laws, and the unemployment rate have negative and significant coefficients.¹⁴

Table 4.

Effect of Light Trucks on Traffic Fatalities

Variable:	(1)	(2)	(3)	(4)	(5)	(6)
Light truck share	0.344 (0.109)	0.362 (0.150)	0.461 (0.254)	0.420 (0.373)	0.291 (0.113)	0.297 (0.153)
Population	0.79 (0.12)	0.96 (0.09)	0.69 (0.35)	0.66 (0.18)	0.82 (0.12)	0.94 (0.09)
Controls	Full Set	Base Set	Full Set	None	Full Set	Base Set
Estimation method	Neg Bin	Neg Bin	Neg Bin	Neg Bin	WLS	WLS
Sample period	1981–2004	1981–2004	1996–2004	1981–2004	1981–2004	1981–2004
Observations	1,128	1,128	423	1,128	1,128	1,128

Notes: Parentheses contain standard errors clustered by state. All regressions include state and year effects and are weighted by state population.

Column (2) reports results from a specification containing a base set of controls: population, beer consumption, safety belt laws, unemployment, rural mileage, and weather. The coefficient on light truck share (0.362) remains positive and statistically significant. Column (3) reports results from the preferred specification when the sample is limited from 1996 to 2004. This specification is of interest because the accident-level data set covers the years from 1996 to 2004. The coefficient on light truck share (0.461) is marginally significant (z = 1.81) and somewhat higher than the coefficient in column (1), but the difference is not statistically significant. Column (4) reports results from a specification that controls only for population, year effects, and state effects. The light truck share coefficient of 0.420 is similar in magnitude to the coefficient in the preferred specification, but the standard error has increased to the point at which the result is no longer statistically significant.

Columns (5) and (6) in Table 4 present weighted linear regression models that are directly analogous to the negative binomial models in columns (1) and (2). As in columns (1) and (2), the light truck share coefficients in columns (5) and (6) are positive and significant, although they have decreased in magnitude by 15 to 18 percent.¹⁵ Nevertheless, the linear regressions generate estimates that are similar to the negative binomial regressions.

A causal interpretation of the estimate from the preferred specification, 0.344, implies that that the 21.8 percentage point increase in light truck share from 1981 to 2004 has increased traffic fatalities by approximately 2,900 deaths in 2004. However, there are several reasons to doubt that the coefficient reported in column (1) represents an estimate of the causal effect of light trucks on traffic fatalities. In particular, issues including reverse causality, measurement error in the light truck series, changes in vehicle miles traveled, and unobserved changes in traffic fatality rates may affect the coefficient estimate.

3.2 Potential Issues in Causal Interpretation

3.2.1 Reverse Causality

Many consumers equate light trucks with superior occupant protection. It is therefore possible that light truck sales are partially driven by the fatality rate itself; consumers may switch to vehicles that they perceive to be safer when the accident rate rises. I explore this possibility with a Granger causality test that examines the relationship between traffic fatalities and new vehicle sales.

Using sales data, I check whether light truck sales respond to changes in the state traffic fatality rate. Columns (1) through (4) of Table 5 present the results from regressions of the light truck share of vehicle sales on contemporaneous and lagged values of traffic fatalities per capita, as well as a full set of controls.¹⁶ Column (1) specifies both the truck share variable and the fatality variables in levels. Column (2) changes the fatality variables to logs. Column (3) specifies both the truck share variable and the fatality variables in logs. Column (4) changes the fatality variables to levels. Column (5) estimates the preferred traffic fatalities specification, equation (1), for the same time period as columns (1) through (4).¹⁷ If the positive coefficient on light truck share in the original regressions is due to the endogeneity of light truck sales, then the regressions in columns (1) through (4) should show an even stronger relationship between light truck sales and fatalities per capita than the regression in column (5). However, I find the opposite pattern. None of the fatality coefficients is statistically significant, and the sum of the fatality coefficients is never significantly different than zero.¹⁸ A joint test of the fatality variables fails to reject in all four columns, producing p-values of 0.907, 0.967, 0.327, and 0.713 respectively. In comparison, the light truck share coefficient in column (4) has a p-value of 0.002. It is therefore unlikely that the positive coefficient on light truck share is due to the endogeneity of light truck sales.

Table 5.

Reverse Causality

	(1)	(2)	(3)	(4)	(5)
Dependent variable	Truck Sales Share	Truck Sales Share	Log Truck Sales Share	Log Truck Sales Share	Log Fatalities
Light truck share					0.335 (0.099)
Fatality variables specification	Levels	Logs	Logs	Levels
Fatalities per capita	0.024 (0.039)	−0.003 (0.008)	−0.013 (0.026)	0.115 (0.128)
Fatalities per capita (t-1)	−0.008 (0.033)	−0.004 (0.007)	−0.022 (0.018)	−0.059 (0.092)
Fatalities per capita (t-2)	0.008 (0.038)	−0.001 (0.007)	−0.002 (0.019)	0.046 (0.111)
Fatalities per capita (t-3)	0.018 (0.037)	−0.001 (0.007)	−0.017 (0.020)	0.028 (0.101)
Sum of fatality coefficients	0.042 (0.059)	−0.009 (0.013)	−0.054 (0.032)	0.130 (0.141)
Joint test p-val	0.907	0.967	0.327	0.713
Sample period	1984–2001	1984–2001	1984–2001	1984–2001	1984–2001
Observations	846	846	846	846	846

Notes: Parentheses contain standard errors clustered by state. All regressions include a full set of controls, state and year effects, and are weighted by state population.

3.2.2 Measurement Error and Changes in Vehicle Miles Traveled

Measurement error is present in the light truck registration series, which is based on data reported by state authorities. Because not all states register vehicles on the same time frame, the Federal Highway Administration adjusts the series to make them comparable across states. These adjustments are imperfect, introducing a degree of error into the series. In general this measurement error should attenuate the coefficient on the light truck variable, biasing it towards zero.¹⁹ The direction of the bias therefore implies that, if anything, the estimated coefficient on the light truck share variable is too conservative.

Of greater concern is the possibility that vehicle miles traveled within a state may be positively correlated with a state’s light truck share. To explore this possibility, I include the log of total vehicle miles traveled as a scale variable in addition to population. The results from this specification are presented in column (2) of Table 6. The coefficient on light truck share is close to the original preferred specification, displayed in column (1). It increases slightly in magnitude, from 0.344 to 0.371, and it remains positive and statistically significant (z = 2.94).²⁰ Furthermore, a regression of log vehicle miles traveled on light truck share and a full set of controls produces a negative coefficient of -0.063 with a t-statistic of −0.51. I therefore find no evidence of a positive relationship between vehicle miles traveled and light truck share.

Table 6.

Measurement Error and Unobserved State Trends

Variable:	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Light truck share	0.344 (0.109)	0.371 (0.126)	0.496 (0.160)	0.515 (0.152)	0.550 (0.171)	0.297 (0.367)	0.449 (0.171)
Population	0.79 (0.12)	0.49 (0.14)	1.33 (0.29)	1.62 (0.31)	1.34 (0.22)	0.52 (0.16)	1.44 (0.15)
VMT		0.35 (0.09)
New vehicle share					0.253 (0.165)
State time trends	No	No	Yes	Yes	Yes	No	No
Sample period	1981–2004	1981–2004	1981–2004	1981–2001	1981–2001	1981–1989	1990–2004
Observations	1,128	1,128	1,128	987	987	423	705

Notes: Dependent variable in all regressions is traffic fatalities. Parentheses contain standard errors clustered by state. All regressions include a full set of controls (minus Census Region time trends in Columns 3 through 6), state and year effects, and are weighted by state population.

3.2.3 Unobserved Changes in Determinants of Traffic Fatality Rates

All models include state effects to control for unobserved differences across states that are constant over time. Nevertheless, unobserved factors that affect traffic fatalities and change over time may be correlated with light truck share growth. Specifically, traffic fatalities depend upon three factors: roadway conditions, vehicle technology, and driver characteristics.²¹ Any unobserved factor that affects the coefficient on light truck share should therefore operate through one of these three channels.

It is possible that states which had greater levels of growth in their light truck share experienced less favorable demographic changes or road improvements than states with lower levels of growth in their light truck share. To check for this possibility, I perform several tests. First, I include a set of state time trends in the regression. The results from this regression are presented in column (3) of Table 6. Comparing column (1) of Table 6, which has no state time trends, with column (3), which includes state linear time trends, reveals that the light truck share coefficient increases by 44 percent and remains statistically significant. This suggests that geographic trends that are correlated with light truck purchases are not upwardly biasing the coefficient on light truck share.

Nevertheless, the technology of a state’s vehicle fleet could plausibly be correlated with light truck share in a manner that would not be accounted for by time trends. In particular, because the growth in light truck share is a recent phenomena, states which have a higher rate of turnover in their vehicle fleets will have more light trucks. All other things being equal, these states will also have a younger, and potentially safer, vehicle fleet. Therefore, it is possible that vehicle fleet average age could be biasing the light truck share coefficient, though the bias should be downward.

Table 6 presents evidence showing that the level of technology in a state’s vehicle fleet is not downwardly biasing the coefficient on light truck share. Column (4) reports a regression of traffic fatalities on light truck share and a full set of controls and state and time effects.²² Column (5) presents the same regression, but also includes as a control the ratio of vehicle sales over the past five years divided by total registered vehicles. The light truck share coefficient is 7 percent higher in column (5), suggesting that there is no downward bias from excluding the level of technology in a state’s vehicle fleet.

A final specification test takes advantage of the fact that most of the growth in light truck share came after 1989, with the ‘invention’ of sport utility vehicles. Although the timing of this invention may be endogenous, it applied equally across all states. Furthermore, there is no reason to believe that changes in underlying state demographic characteristics were substantially more pronounced during the 1990s than during the 1980s.²³ For example, the interstate mobility rate – an important measure of how quickly state populations are changing – rose only slightly between the 1981–1989 period and the 1990–2004 period, from 3.0 percent to 3.2 percent (U.S. Census Bureau, 2006). However, the rate of growth in light truck share was 4.5 times higher post-1990 than in the 1980s. From 1981 to 1989, light truck share grew by an average of 0.29 percentage points per year, but from 1990 to 2004 light truck share grew by an average of 1.30 percentage points per year. The popularization of sport utility vehicles in 1990, with the release of the Ford Explorer, could therefore be conceptualized as a natural experiment which inflated the magnitude of changes in the light truck fleet.²⁴ If demographic trends are correlated with changes in light truck share, and these trends do not become sharply more pronounced in the 1990s relative to the 1980s, then the light truck share coefficient post-1989 should be substantially lower in magnitude than the light truck share coefficient pre-1990.

Columns (6) and (7) of Table 6 present regressions that test whether the light truck share coefficient falls after 1989. In column (6), the sample is restricted to the period from 1981 to 1989. In the column (7), the sample is restricted to the period from 1990 to 2004. The 1981–1989 light truck share coefficient is estimated at 0.297 while the 1990–2004 light truck share coefficient is estimated at 0.449, suggesting that unobserved state trends are not driving the light truck share coefficient.²⁵

The results from state-level panel data suggest that a 10 percentage point increase in light truck share raises traffic fatalities by approximately 3.4 percent, or 1,430 deaths per year. This reduced-form estimate, however, gives no insight about the specific mechanisms generating the additional fatalities. Fatalities may increase because light trucks crash more often than cars (the extensive margin), or because light trucks are more dangerous than cars in multi-vehicle collisions, or because light trucks are more dangerous to their own occupants in single-vehicle collisions (the intensive margins). The state-level results combine all of these potential effects (and others). The next section examines accident-level data in order to discriminate between these possibilities and determine how much of the additional risk is borne by the occupants of the new light trucks and how much is borne by the occupants of other vehicles and pedestrians.

4 The Internal and External Distribution of Fatalities

4.1 Aggregate-Level Estimates

Section 3 presents state-level panel data results that quantify the effect of light trucks on total traffic fatalities but do not reveal how many of these fatalities accrue to new light truck occupants and how many accrue to other users of the roadway system. One way to estimate this breakdown is to compare the overall fatality rates of light trucks and cars. For example, column (3) in Table 4 indicates that between 1996 and 2004, a one percentage point increase in light truck share raised fatalities by approximately 0.34 percent. During the same period, the occupant fatality rate for recent light trucks was 6.8 percent higher than for recent cars (Insurance Institute for Highway Safety, 2007; Ward’s Automotive Yearbook, 1994–2004).²⁶ If light trucks posed no additional risk to other roadway users, and if the marginal driver switching from a car to a light truck increased her fatality rate by 6.8 percent, then a 1 percentage point increase in light truck share would raise total traffic fatalities by 0.068 percent. This increase in fatalities would accrue exclusively to the occupants of new light trucks, so this figure represents an estimate of the internal fatality risk of light trucks. The remainder of the 0.344 percent total increase in traffic fatalities – 0.276 percent – represents an estimate of the external fatality risk, or the risk to other roadway users. Therefore, aggregate fatality rates suggest that internal fatalities account for approximately 20 percent of the total fatality increase and external fatalities account for the remaining 80 percent.

However, using aggregate statistics to estimate the breakdown of internal and external fatalities may generate misleading estimates if the average light truck or car driver is not representative of the marginal light truck or car driver. In particular, Bradsher (2002) notes that the sport utility vehicle buyers tend to come from the safest group of drivers on the road: middle-aged, affluent men and women. If the marginal consumer, who is indifferent between a car and a light truck, is a safer driver than the average car buyer, then her fatality rate in a car will be lower than the average fatality rate of car drivers. In that case, using aggregate fatality rates to calculate the internal versus external fatality breakdown will underestimate the number of internal fatalities and overestimate the number of external fatalities. To address this problem, I examine accident-level micro data from the GES data set.

4.2 Empirical Framework

A vehicle can be more dangerous because it crashes more often or because, when it crashes, it causes more damage (either to other vehicles or to its own occupants). The former mechanism I refer to as the participation margin, and the latter mechanism I refer to as the intensity margin. The fatality process therefore operates through both participation in accidents and the intensity of accidents. For a vehicle of type k, the probability of participation is that vehicle’s collision rate, $p_k^{c\cdot }$.²⁷ For a vehicle of type k, the average intensity of an accident is the probability of a fatality in the event of an accident, $p_k^{f\cdot \cdot }$. The contribution of a vehicle to the total number of traffic fatalities therefore equals the sum of the vehicle’s participation rates in various types of accidents times its fatality rates in those types of accidents. A vehicle of type k increases expected internal fatalities by

$$E[I{F}_k]=p_k^{cs}\cdot p_k^{\mathit{fsi}}+p_k^{cl}\cdot p_k^{\mathit{fli}}+p_k^{ch}\cdot p_k^{\mathit{fhi}}$$ (2)

where IF_k are internal fatalities, $p_k^{cs}$ is the vehicle’s collision involvement rate in single-vehicle collisions, $p_k^{\mathit{fsi}}$ is the vehicle’s internal fatality rate in the event of a single-vehicle collision, and $p_k^{\cdot l\cdot }$ and $p_k^{\cdot h\cdot }$ are the same quantities for multi-vehicle collisions involving light vehicles (i.e., cars and light trucks) and multi-vehicle collisions involving heavy trucks respectively. The subscript c refers to collision risk, f refers to fatality risk, i refer to internal, l refers to light vehicles, and h refers to heavy trucks. In this analysis, k takes on two values, cars or light trucks.

A vehicle of type k increases expected external fatalities by

$$E[E{F}_k]=p_k^{cl}\cdot p_k^{\mathit{fle}}+p_k^{cm}\cdot p_k^{\mathit{fme}}+p_k^{cp}\cdot p_k^{\mathit{fpe}}$$ (3)

where EF_k are external fatalities, $p_k^{cl}$ is the vehicle’s collision involvement rate in multi-vehicle collisions, $p_k^{\mathit{fle}}$ is the external fatality rate in other vehicles in the event of a multi-vehicle collision, and $p_k^{\cdot m\cdot }$ and $p_k^{\cdot p\cdot }$ are the same quantities for light vehicle collisions involving motorcycles and pedestrians respectively.²⁸ Note that to compare cars and light trucks, we must calculate both equations (2) and (3) separately for k = ‘cars’ and k = ‘light trucks’. We can then compare IF_cars to IF_{light trucks} and EF_cars to EF_{light trucks}.²⁹

To estimate fatality rates in the event of an accident – the $p_k^{f\cdot \cdot }$ terms in equations (2) and (3) – I apply a methodology implemented in White (2004) to the accident-level micro data. I examine the five types of accidents contained in equations (2) and (3) separately: two-vehicle collisions involving at least one car, two-vehicle collisions involving at least one light truck, single-vehicle collisions, two-vehicle collisions involving a motorcycle, and collisions involving a pedestrian or pedalcyclist.³⁰ For each accident type, I estimate a logit regression that specifies the probability of fatalities as a function of vehicle, driver, and accident characteristics.

For two-vehicle collisions, I define one vehicle as the vehicle being struck. If the accident involves two vehicle types, then the struck vehicle is by default the vehicle type of that data set (e.g., for two-vehicle collisions involving at least one car, the struck vehicle is always a car). If the accident involves two vehicles of the same type (i.e., two cars or two light trucks), then one of the vehicles is randomly assigned to be the struck vehicle. The remaining vehicle I designate as the striking vehicle. The dependent variable is the presence of a fatality in struck vehicle, and the variable of interest is a dummy variable that takes a value of one if striking vehicle is a light truck. For single-vehicle collisions, the dependent variable is the presence of a fatality in the single vehicle, and the variable of interest is a dummy variable indicating whether the vehicle involved in the accident is a light truck. For collisions involving pedestrians, the dependent variable codes whether a pedestrian died, and the variable of interest is a dummy variable indicating whether the striking vehicle is a light truck.

All regressions are weighted so that the sample is representative of the population of accidents. Controls include the number of occupants inside the struck vehicle, vehicle model year, a dummy variable for heavy trucks, and dummy variables for medium cities, large cities, safety belt use (or helmet use, for motorcycles), rain, snow, fog, darkness, weekdays, negligent driving, drivers under the age of 21, drivers over the age of 60, interstate highways, divided highways, male drivers, young male drivers, and years.

4.3 Accident-Level Results

The first column of Table 7 reports the logit regression coefficient on the dummy variable indicating whether the striking vehicle is a light truck. In single-vehicle collisions, the striking vehicle and the struck vehicle are one and the same. In pedestrian or pedalcyclist collisions, the ‘struck vehicle’ is the pedestrian or pedalcyclist. The second column reports the probability of a fatality in the struck vehicle conditional on the vehicle type of the striking vehicle (light truck or car). When the striking vehicle is a light truck, the probability is calculated as the weighted average of the predicted logit regression probabilities taken across all accidents in which the striking vehicle is a light truck. When the striking vehicle is a car, this probability is equal to the weighted average of the predicted logit regression probabilities taken across the same set of observations, but the light truck indicator for the striking vehicle is set to zero. The probability comparison therefore fixes the covariates at the values associated with light truck drivers.³¹ The third column reports the sample size for each data set.

Table 7.

Predicted Probabilities of Fatality in Struck Vehicle

	Logit Results	Fatality Probability	Sample
Two-vehicle crashes w/cars			190,791
Striking veh. is light truck	0.486 (0.135)	0.00178
Striking veh. is car		0.00110
Two-vehicle crashes w/light trucks			117,549
Striking veh. is light truck	0.684 (0.221)	0.00137
Striking veh. is car		0.00070
Single-vehicle crashes			118,069
Veh. is light truck	0.191 (0.073)	0.00891
Veh. is car		0.00741
Crashes w/motorcycles			3,191
Striking veh. is light truck	0.728 (0.189)	0.07245
Striking veh. is car		0.03773
Crashes w/pedestrians or pedalcyclists			15,990
Striking veh. is light truck	0.663 (0.105)	0.04342
Striking veh. is car		0.02451

Notes: For single-vehicle crashes, the ‘struck vehicle’ is the single vehicle involved in the crash. For pedestrian or pedalcyclist crashes, the ‘struck vehicle’ is the pedestrian or pedalcyclist. Parentheses contain standard errors. All regressions include controls and are weighted by sampling weights.

The first set of rows in Table 7 presents results for two-vehicle collisions involving cars. The results indicate that light trucks pose a significant hazard to cars in the event of a collision. The light truck coefficient is positive and highly significant (z = 3.59). The probability of a fatality in the struck vehicle increases by 62 percent if the striking vehicle is a light truck rather than a car, from approximately 0.0011 to 0.0018. The magnitude of this effect is consistent with the results of previous accident-level studies, including Toy and Hammitt (2003), Gayer (2004), and White (2004).

The second set of rows in Table 7 presents results for two-vehicle collisions involving light trucks. These results indicate that light trucks also pose a significant hazard to other light trucks in the event of a collision. The light truck coefficient is positive and significant (z = 3.09). The probability of a fatality in the struck vehicle increases by 97 percent if the striking vehicle is a light truck rather than a car, from approximately 0.0007 to 0.0014. In fact, the probability of fatalities in a collision involving two light trucks is estimated to be 24 percent higher than in a collision involving two cars. Nevertheless, a comparison of the fatality probabilities in these rows with the fatality probabilities in the first set of rows reveals that, for their own occupants, light trucks are safer than cars in the event of a multi-vehicle collision. In multi-vehicle collisions, light trucks therefore reduce internal fatalities at the expense of additional external fatalities.

The third set of rows in Table 7 reports results for single-vehicle collisions. The light truck coefficient is again positive and significant (z = 2.62). The probability of a fatality in a single-vehicle collision increases by 20 percent, from approximately 0.0074 to 0.0089, when the vehicle is a light truck rather than a car. This fatality rate differential matches the injury rate differential from controlled crash tests quite closely, increasing our confidence in the results.³² Some of the increased lethality may be due to increased rollover risk in light trucks; a logit regression with a rollover event as the dependent variable returns a light truck coefficient of 0.72 (z = 40.53).

The fourth and fifth sets of rows in Table 7 report results for two-vehicle collisions involving motorcyclists and single-vehicle collisions involving pedestrians or pedalcyclists. Light trucks increase the risk of fatalities in motorcycle collisions by 92 percent, from approximately 0.0377 to 0.0725 (z = 3.85 in the logit regression). They increase the probability of fatalities in pedestrian or pedalcyclist collisions by 77 percent, from approximately 0.0245 to 0.0434 (z = 6.33 in the logit regression).

Overall, light trucks pose a significant hazard to other vehicles in the event of a collision. Depending on the type of accident, the risk of fatality to others (or to themselves, in single-vehicle collisions) increases by 20 to 97 percent. However, these estimates may not be interpretable as causal effects in the traditional sense (e.g., Rubin, 1974).

4.4 Interpretation

Expected fatalities for a given vehicle type are a function of both participation in accidents and the intensity of accidents. The probability of participation is the collision rate, or the $p_k^{c\cdot }$ terms in equations (2) and (3). The intensity of accidents is the probability of a fatality in the event of a collision, or the $p_k^{f\cdot \cdot }$ terms in equations (2) and (3). The fatality rates presented in the subsection above are estimates of intensity and are therefore conditional upon the event of an accident. However, Angrist (2001) notes that when the probability of participation is a function of intensity, estimates of intensity conditional on participation do not have a causal interpretation.

In this case, the primary issue is that light trucks may positively affect collision rates. If so, the conditional-on-collision difference in fatality rates between cars and trucks need not equal the difference in fatality rates between cars and trucks in a series of controlled crash tests. This discrepancy occurs because the set of accidents in which trucks are participating is different than the set of accidents in which cars are participating. Measuring the causal effect of crash intensity on fatalities requires us to observe cars participating in all the accidents in which trucks participate. Nevertheless, because the goal is to measure the distribution of external and internal fatalities rather than the causal effect of intensity on fatalities, the accident-level estimates are still useful. Equations (2) and (3) must hold because they are identities, even if the $p_k^{f\cdot \cdot }$ terms do not have a causal interpretation.

Since we are tabulating internal and external fatalities, it is irrelevant whether the increased fatality risk from light trucks arises because they are more dangerous in the same collision or because their characteristics cause them to enter into more dangerous collisions. Still of concern, however, is the possibility that driver characteristics of light trucks and cars are different and that these differences may affect fatality rates in the event of a collision.³³

This concern is mitigated by two facts. First, controlling for a wide range of covariates, as is done in Table 7, does not strongly affect the results. This implies that differences in observable driver characteristics are not responsible for the fatality rate differential between cars and light trucks. Second, the fatality estimates for single-vehicle collisions match the results of controlled crash tests (the analog of a randomized controlled trial) remarkably closely. Using government crash test data for all vehicles tested between 1993 and 2004, I compute the average frontal crash test rating for cars and for light trucks.³⁴ The average frontal crash test rating for cars during this period implies a 0.155 probability of serious injury, while the average frontal crash test rating for light trucks implies a 0.184 probability of serious injury. These figures indicate that the probability of serious injury in a single-vehicle frontal collision is 18 percent higher for light trucks than for cars.³⁵ In comparison, the figures presented in the third set of rows in Table 7 imply that the probability of a fatality in a single-vehicle collision is 20 percent higher for light trucks than for cars. The experimental crash test results therefore match the regression estimates very closely, indicating that driver selection is unlikely to be biasing the regressions.

To compute collision rates, I examine the five types of collisions involving light duty vehicles (i.e., cars and light trucks) in the data set: single-light vehicle, two-light vehicles, light vehicle-heavy truck, light vehicle-motorcycle, and light vehicle-pedestrian. Table 8 reports the annual collision rate for each type of collision; this rate is calculated by dividing the total number of collisions of each type (taken from the GES data set used in Section 4.3) by the total number of registered light vehicles.³⁶ Two-light vehicle collisions are the most common, occurring at an annual rate of 0.034 per vehicle, and light vehicle-motorcycle collisions are the least common, occurring at an annual rate of 0.00015 per vehicle.

Table 8.

Annual Per Light Vehicle Collision Rates

Collision Type:	Annual Rate
Two light vehicles	0.03393
Single light vehicle	0.00781
Light vehicle and heavy truck	0.00141
Light vehicle and motorcycle	0.00015
Light vehicle and pedestrian or pedalcyclist	0.00056

Notes: Rates are over 1996–2004 period.

I first calculate the internal fatality effects of replacing 2.1 million light trucks with cars (one percent of the vehicle fleet) assuming that the collision rate of these vehicles remains unchanged. This is equivalent to changing the $p_k^{f\cdot \cdot }$ terms in equation (2) while leaving the $p_k^{c\cdot }$ terms unchanged.³⁷ There are three types of collisions involving internal fatalities: single-light vehicle, two-light vehicles, and light vehicle-heavy truck. Consider the internal fatality risk from single-vehicle accidents. The change in fatal crashes from switching 2.1 million light trucks to cars is the single-vehicle collision rate times the difference in fatality risk between cars and light trucks in single-vehicle collisions times 2.1 million (0.00781 · (0.0074–0.0089) · 2.1 million).

The collision rate (0.00781) comes from Table 8, while the fatality risks (0.0074 and 0.0089) come from Table 7. The resulting number is multiplied by 1.15, as each fatal collision results in approximately 1.15 fatalities (White, 2004). The product, reported at the top of the first column in Table 9, implies that the switch would decrease single-vehicle collision fatalities by 28 per year if the collision rate remains unchanged. The two-light vehicle and light vehicle-heavy truck internal fatality changes are computed in a similar manner.³⁸ The fifth row in Table 9 totals the internal effects. The replacement of 2.1 million light trucks with cars is expected to increase internal fatalities by 4 deaths per year if the collision rate remains unchanged.

Table 9.

Changes in Internal and External Fatalities from Replacing 2.1 Million Light Trucks with Cars

	(1)	(2)
Ratio of Light Truck Collision Rate to Car Collision Rate	1.00	1.13
Internal Effects:
Single-vehicle collisions	−28	−48
Two-vehicle collisions	33	21
Light vehicle-heavy truck collisions	−1	−4
Total Internal Deaths	4	−31
External Effects:
Two-vehicle collisions	−57	−71
Collisions with motorcycles	−11	−14
Collisions with pedestrians/pedalcyclists	−22	−27
Total External Deaths	−91	−112
Net Effect:	−87	−143

Notes: Numbers may not sum exactly due to rounding.

I then calculate the external fatality effects of replacing 2.1 million light trucks with cars (one percent of the vehicle fleet) assuming that the collision rate of these vehicles remains unchanged. This is equivalent to changing the $p_k^{f\cdot \cdot }$ terms in equation (3) while leaving the $p_k^{c\cdot }$ terms unchanged. There are three types of collisions that result in external fatalities: two-light vehicles, light vehicle-motorcycle, and light vehicle-pedestrian. Consider the external fatality risk from light vehicle-pedestrian accidents. The change in fatal crashes from switching 2.1 million light trucks to cars is the light vehicle-pedestrian collision rate times the difference in fatality risk between cars and light trucks in light vehicle-pedestrian collisions times 2.1 million (0.00056 · (0.0245 – 0.0434) · 2.1 million). The collision rate (0.00056) comes from Table 8, while the fatality risks (0.0245 and 0.0434) come from Table 7. The result, reported in the third row of the first column in Table 9, implies that the switch would decrease pedestrian fatalities by 22 per year if the collision rate remains unchanged. The two-light vehicle and light vehicle-motorcycle external fatality changes are computed in a similar manner.³⁹ The second-to-last row in Table 9 totals the external effects. The replacement of 2.1 million light trucks with cars is expected to decrease external fatal crashes by 91 per year if the collision rate remains unchanged.

The sum of the internal and external effects, reported in the last row of Table 9, is 4 − 91 = −87, indicating that reducing the light truck share by one percentage point will reduce annual traffic fatalities by 87. However, estimates from the preferred state-level specification over the same sample period imply that a one percent reduction in light truck share should reduce annual traffic fatalities by 0.34 percent, or approximately 143. The discrepancy between these two estimates − 87 and 143 – implies that the collision rate of drivers who switch from light trucks to cars does not remain constant. Not only are light trucks more dangerous in collisions, but they must be more likely to enter into a collision.

What collision rate differential between cars and light trucks can explain the discrepancy between the accident-level results and the state-level results? The second column in Table 9 reports the internal and external effects of replacing 2.1 million light trucks with cars under the assumption that the light truck crash rate is 13 percent higher than the car crash rate.⁴⁰ This is equivalent to assuming that each of the $p_k^{c\cdot }$ terms in equations (2) and (3) is 13 percent higher for light trucks than for cars. This figure of 13 percent is implied by the data if we assume that the collision rate differential between light trucks and cars is constant across collision types; it is the unique crash rate differential that equalizes the state-level and accident-level estimates of total traffic fatalities.⁴¹

The estimates in the second column of Table 9 suggest that reducing the light truck share of the vehicle fleet by one percentage point reduces internal fatalities by 31 deaths per year and reduces external fatalities by 112 deaths per year.⁴² Therefore, external fatalities account for approximately 79 percent of the total change in traffic fatalities, and internal fatalities account for the remaining 21 percent. These estimates are similar to the breakdown based on aggregate fatality rates presented at the beginning of the section. Furthermore, the ratio of internal to external deaths is not very sensitive to variations in the relative pedestrian collision rate between cars and light trucks. For example, if cars and light trucks have the same pedestrian collision rate (rather than trucks having a collision rate that is 13 percent higher), then external fatalities account for 77 percent of the change in traffic fatalities. If light trucks have a pedestrian collision rate that is 25 percent higher than cars, then external fatalities account for 81 percent of the change in traffic fatalities.

A final complication pertains to the sampling frame. Because accidents only enter the data set if they are reported to the police, less severe accidents are less likely to enter the data set. If light trucks cause accidents to be more severe, then multi-vehicle or pedestrian accidents involving light trucks will be more likely to enter the data set. This over-representation would reduce the estimated risk that light trucks pose in a given collision and increase the estimated collision rate for light trucks. However, the potential scale of this bias is limited. Simulations reveal that if the true fatality risk differential between cars and light trucks (conditional on an accident occurring) is 20 percent higher than estimated, the external fatality share changes only 3 percentage points, from 79 percent to 82 percent. Alternatively, minor single-vehicle collisions involving large pickup trucks may be less likely to be reported because these vehicles are involved in rugged work and have already accumulated a number of dents. This underreporting would cause single-vehicle light truck collisions to appear more dangerous than they are. I experiment with reducing the risk of fatalities in single-vehicle collisions involving light trucks by 10 percent.⁴³ Under this assumption, the external fatality share changes only 3 percentage points, from 79 percent to 82 percent. Nevertheless, because of the potential sampling frame biases, the estimate that external fatalities account for 79 percent of the total change in traffic fatalities should be viewed as a lower bound.

The results in Table 9 and the estimates at the beginning of the section demonstrate that light trucks are a hazard not only to other drivers and pedestrians, but to their own occupants as well. The increase in internal fatality risk is due in part to the higher estimated collision rate for light trucks. A variety of factors may contribute to this increased collision rate. First, light trucks generally have poor handling and braking in comparison to cars. Furthermore, their height relative to the roadway causes drivers to perceive themselves to be traveling slower than they are (Rist, 2001). However, the first column in Table 9 shows that even if light trucks had the same collision rate as cars, their occupants would enjoy little additional protection on average, perhaps because of the increased rollover risk.

4.5 Dynamic Implications

Several recent trends have the potential to affect this paper’s estimates. First, the composition of the light truck fleet itself is changing. Manufacturers have developed smaller SUVs and “crossover vehicles,” such as the Honda CR-V and the Toyota RAV4. They have also implemented some changes that make SUVs more “crash compatible” with cars (Hakim, 2003b). On the other hand, larger pickups and SUVs have become increasingly popular. From 1995 to 2005, the percentage of SUVs classified as large grew from 12.7 percent to 45.4 percent, and the percentage of pickup trucks classified as large grew from 56.1 percent to 89.8 percent (Davis and Diegel, 2007). To explore the net effect of these changes, Figure 1 graphs the coefficients from a logit regression that models the probability of a fatality in a multi-vehicle collision as a function of whether the striking vehicle was a light truck, as in Table 7. However, instead of a single light truck indicator, the regression contains 24 light truck indicators, one for each model year from 1981 to 2004.⁴⁴ Figure 1 plots how these light truck coefficients evolve from year to year. Although each coefficient is estimated with substantial error, there appears to be a slight upward trend as the model years progress. This suggests that the composition of light trucks is not becoming safer to cars over time.

Figure 1.

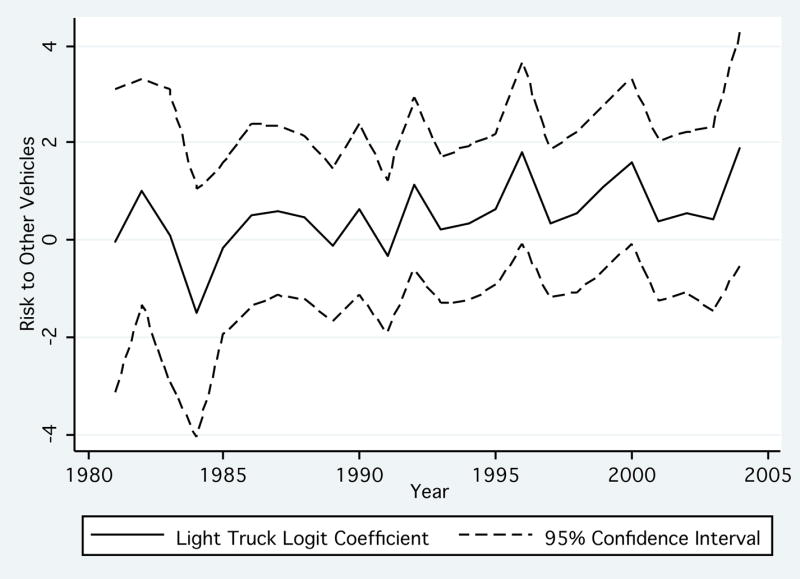
Light Truck Risk By Model Year

Another important development is the rise in gasoline prices over the past several years. Rising gasoline prices should reduce demand for light trucks, lowering the total external costs of light trucks. However, the external cost of the marginal light truck could potentially grow, since a given truck is now increasingly likely to hit a car rather than another truck. A cross-country regression of light truck share on average gasoline price, using data from the United States, Great Britain, Germany, France, and Japan, predicts that a one dollar increase in gasoline prices lowers light truck share by 10 percentage points (t = −3.7).⁴⁵ This relationship is likely confounded by differences in geography, urbanization, and culture, so I interpret the estimate as an upper bound on the causal effect of gasoline prices on light truck share.

Real gasoline prices increased by $1.03 in the United States from 2002 to 2006, potentially reducing light truck share by up to 10.3 percentage points in the long run (U.S. Department of Energy 2007). How might this affect the external risk of the marginal light truck? Some multi-vehicle collisions that previously involved the marginal light truck hitting another light truck will now involve the marginal light truck hitting a car. The estimates in Table 7 indicate that the fatality risk from being struck by a light truck changes from 0.00137 − 0.00070 = 0.00067 when riding in a light truck to 0.00178 − 0.00110 = 0.00068 when riding in a car.⁴⁶ The external risk of the marginal light truck should therefore be unaffected. Total external fatalities attributable to light trucks, however, could drop by 20 percent if long run light truck share decreases from 50 percent (the 2005 market share) to 40 percent.⁴⁷

5 Conclusion

This paper analyzes the effects of light trucks on traffic fatalities by combining state-level and accident-level data sets. The results suggest that a one percentage point increase in the light truck share of the vehicle fleet increases annual traffic fatalities by approximately 0.34 percent, or 143 deaths per year. Of these deaths, approximately one-fifth accrue to the occupants of the new light trucks, while the remaining four-fifths accrue to the occupants of other vehicles, pedestrians, and pedalcyclists. Light trucks therefore pose a significant cost to other users of the highway system, but do not appear to provide any additional protection to their own occupants. Using standard value of life estimates of seven million dollars per life (Viscusi and Aldy, 2003), a vehicle life-span of fifteen years, and a real discount rate of three percent, the implied Pigovian tax is approximately 3,850 dollars per light truck sold. At current sales rates, such a tax would generate over 30 billion dollars of revenue each year. Although rising gasoline prices may mitigate the increase in light truck share, they are unlikely to reduce it to pre-2000 levels. Interpreted on a larger scale, the results suggest that the 21 percentage point increase in light truck share from 1981 to 2004 currently results in as many as 2,900 additional traffic fatalities per year. This estimate may partially explain why, despite advances in safety technology, the annual number of traffic fatalities in the United States has increased by over 10 percent from 1992 to 2005, rising from 39,250 to 43,200.