Limited internal friction in the rate-limiting step of a two-state protein folding reaction

Abstract

Small, single-domain proteins typically fold via a compact transition-state ensemble in a process well fitted by a simple, two-state model. To characterize the rate-limiting conformational changes that underlie two-state folding, we have investigated experimentally the effects of changing solvent viscosity on the refolding of the IgG binding domain of protein L. In conjunction with numerical simulations, our results indicate that the rate-limiting conformational changes of the folding of this domain are strongly coupled to solvent viscosity and lack any significant “internal friction” arising from intrachain collisions. When compared with the previously determined solvent viscosity dependencies of other, more restricted conformational changes, our results suggest that the rate-limiting folding transition involves conformational fluctuations that displace considerable amounts of solvent. Reconciling evidence that the folding transition state ensemble is comprised of highly collapsed species with these and similar, previously reported results should provide a significant constraint for theoretical models of the folding process.

A fundamental aspect of the folding of proteins is that an extended and highly disordered polymer chain must collapse to form a compact, globular protein. The folding of larger (≥100 residues), multidomain proteins appears to occur via one or more significantly populated, compact, partially folded intermediate (1). In contrast, the folding of smaller, single domain proteins usually occurs in a concerted fashion accurately modeled as a simple, two-state process lacking well populated intermediate states (e.g., see refs. 2–4). Despite significant recent debate (e.g., see refs. 1 and 5–7), the relationship of chain collapse to the rate-limiting steps of two-state and multistate protein folding remains unclear.

The kinetic barriers that define protein folding rates remain incompletely understood (8). Theoretical models of the process have implicated diffusive chain motions as the rate limiting step in folding, and several groups have suggested that the viscosity dependence of folding rates might serve a useful probe of the rate limiting conformational changes (9–11). Recently, Jacob et al. (12) have investigated the effects of viscosity-increasing cosolvents on the rapid (k_f > 1,000 s⁻¹) refolding of the Bacillus cold shock protein (cspB). They demonstrated that the folding rate of cspB is strongly affected by the presence of these agents and concluded that “collapse of the polypeptide chain occurs in the rate-limiting event of its folding” (12). To further characterize the rate-limiting conformational changes that define two-state protein folding kinetics, we have investigated, both experimentally and by integration of the diffusion equation for a simple barrier crossing problem, the effects of a viscogenic agent on the refolding of the 62-residue IgG binding domain of peptostreptococcal protein L (protein L).

Protein L is a small, single domain protein lacking disulfide bonds, proline residues, prosthetic groups or other factors that might produce complicated, multiphasic folding kinetics (13). Previous evidence, including mono-exponential refolding kinetics, the exponential denaturant dependence of refolding and unfolding rates, the equivalence of thermodynamic properties derived from kinetic and equilibrium experiments, and the equivalence of refolding kinetics as characterized by using a number of independent biophysical probes all indicate that the folding of protein L is well described as a simple, two-state process (3). We report here the effects of changing solvent viscosity on the kinetics of this apparently two-state protein folding reaction.

MATERIALS AND METHODS

Recombinant protein L was expressed with a histidine tag in Escherichia coli, was purified as described, and was used without cleavage of the affinity tag (3). The presence of the affinity tag and the lower ionic strength used in this study may account for some of the slight discrepancies between the values reported here and those reported previously (3, 14). All experiments were conducted at 22.5 ± 1.0°C in 50 mM sodium phosphate, pH 7.0 (phosphate) or in phosphate plus guanidine hydrochloride (GuHCl) and glucose at the appropriate concentrations. All materials used were reagent grade or better.

The effects of glucose on the stability of protein L were determined by GuHCl denaturation (Fig. 1). Equilibrium unfolding was monitored by following ellipticity at 220 nm with a Hamilton automatic titrator coupled to an Aviv 62DS spectropolarimeter (Aviv Associates, Lakewood, NJ). Samples were preequilibrated for 60–90 s before measurements. All solutions were made volumetrically to a protein L concentration of 18 μM. Data were fitted to Eq. 2, with reported confidence limits representing estimated fitting errors.

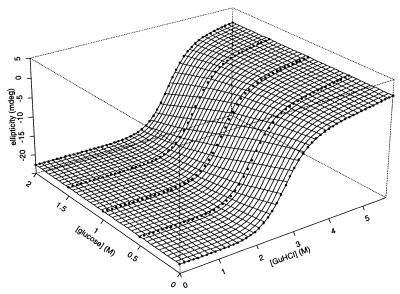
Figure 1.

The equilibrium unfolding of protein L as a function of glucose and GuHCl. The circles denote the far UV (220 nm) CD signal of protein L at various cosolvent concentrations. The surface represents a fit to a model assuming a simple, linear relationship between the relative free energy of folding and the concentration of each cosolvent (see Eq. 2 in the text). The quality of this fit (r² = 0.98) is significant evidence that, over these concentration ranges, the effects of GuHCl and glucose on protein L stability are both linear and additive. Conditions are 50 mM phosphate buffer (pH 7.0) at 22.5°C.

Kinetic refolding and unfolding were monitored by tryptophan fluorescence with excitation at 280 nm and detection >310 nm in a Biologic SFM-4 stopped-flow fluorimeter (Biologic, Grenoble, France). Protein L in phosphate plus 0–7 M GuHCl was unfolded or refolded by dilution with phosphate buffer containing various concentrations of GuHCl to final protein L concentrations of 7–30 μM. For studies at increased viscosity, glucose was included in all buffers at the appropriate concentrations. Sums of 4–6 kinetic traces were collected at each solvent condition and were analyzed by using a Pade–Laplace fitting algorithm. Control experiments using free tryptophan indicated that reasonably accurate mixing ratios were achieved even at very high solvent viscosities (data not shown). Intrinsic folding rates, the extrapolated rate at 0 M GuHCl (Fig. 2; k_in), were calculated by using a fit of the equation

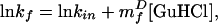1

with error bars representing estimated fitting errors. At all glucose concentrations investigated, lnk_f is a linear function of GuHCl concentration (r² > 0.95). The full data set (Fig. 3) was fitted to Eq. 3, with confidence limits representing estimated fitting errors. Isostability refolding kinetics (Fig. 4) were collected at −3.0 kcal⋅mol stability by using combinations of glucose and GuHCl determined from equilibrium stability data (Fig. 1). Reported values represent the average of five sets of three experiments each, with error bars representing the SDs of these averages. Each set was collected at a unique syringe mixing ratio (final GuHCl and glucose concentrations constant) to minimize systematic mixing errors. The constant GuHCl concentration (0.636 M) folding data reported represent the averages and SDs of triplicate measurements.

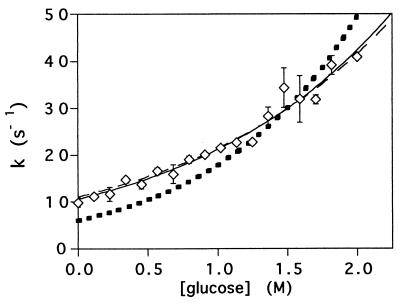
Figure 2.

The intrinsic (extrapolated to 0 M GuHCl) refolding rates of protein L over a range of glucose concentrations are well fitted (r² = 0.96) by a simple exponential function at and below 2 M glucose. The significant deviation >2 M glucose, which corresponds to >35% sugar by weight, suggests that the folding mechanism of protein L is altered under these conditions.

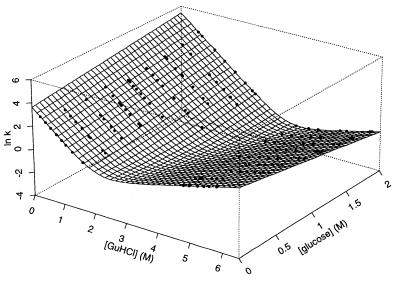
Figure 3.

The relaxation (refolding and/or unfolding) rates of protein L at >130 combinations of GuHCl and glucose concentrations are well fitted by a simple, two-state model (Eq. 3) with kinetic GuHCl refolding and unfolding m values of −2.08 M⁻¹ and 0.91 M⁻¹, respectively, kinetic glucose refolding and unfolding m values of 0.81 M⁻¹ and −1.17 M⁻¹, respectively, and intrinsic refolding and unfolding rates of 37 s⁻¹ and 0.02 s⁻¹, respectively. The close correlation between the equilibrium folding parameters of protein L derived from these values and from values obtained from the fit of Fig. 1 (described in the text) indicates that the folding kinetics of protein L are two state over the range of conditions used here.

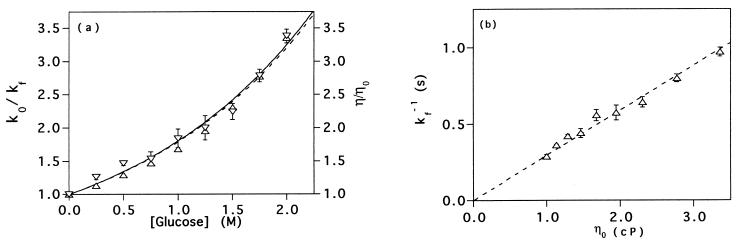
Figure 4.

(a) The refolding time constant of protein L at various glucose concentrations relative to the time constant in the absence of glucose (k₀/k_f; up triangles). The GuHCl concentration was varied from 1.1 to 2.4 M to maintain a constant native state stability of −3 kcal⋅mol. The solid line represents a least squares fit of these data to a single exponential (coefficient = 0.58 ± 0.01; r² = 0.987). The calculated relative viscosities of the solutions (down triangles) also have been fitted to a simple exponential (dashed line; coefficient = 0.59 ± 0.01; r² = 0.982). The close correspondence between the two curves strongly suggests that the reduction in the refolding rate of protein L as glucose concentration increases reflects changes in solvent viscosity. (b) A plot of refolding time constants versus relative solvent viscosity is well fitted by a simple, proportional relationship (r² = 0.985) with a proportionality constant of 0.29 ± 0.01 s⋅cP⁻¹.

The viscosities (η) of various glucose or GuHCl solutions were calculated by fitting empirical literature values (15, 16) to sixth order polynomials. Glucose- and GuHCl-induced changes in viscosity were added in the manner of Kawahara and Tanford (15). The contribution of GuHCl to solvent viscosity in mixed solvent systems is negligible below 3 M GuHCl.

All fits were ordinary least squares, performed by using s-plus (MathSoft, Seattle) (Figs. 1 and 3) or kaleidagraph (Abelbeck Software, Reading, PA) (Figs. 2, 4, and 5). Numerical integrations of equation 13 (Fig. 6) were performed by using mathematica (Wolfram Research, Urbana, IL). Confidence limits on numerical values represent estimated fitting errors. Correlation coefficients (r) represent Patterson r values for single dimensional fits or information coefficients (the Patterson r value of the observed vs. predicted values) for multidimensional fits (Figs. 1 and 3).

Figure 5.

The refolding rates of protein L at 0.636 M GuHCl and a range of glucose concentrations are well fitted by a simple kinetic model (solid line; r² = 0.97) assuming an inversely proportional relationship to solvent viscosity and a linear relationship between the free energy barrier and glucose concentration. The predicted kinetic m_f^S value thus obtained (1.3 ± 0.1 M⁻¹) is very similar to the value (1.2 M⁻¹) obtained independently by assuming the true θ value is the viscosity-corrected θ_glucose value (see text). Fixing m_f^S at 1.2 M⁻¹ (see text for justification) and introducing an internal friction term, ξ, to the model produces an equivalently good fit (dashed line; r² = 0.97) and predicts an insignificant internal friction (−0.1 ± 0.2 cP). Fixing m_f^S at 1.2 M⁻¹ and fixing the internal friction at 4 cP [the internal friction observed for a conformational change in myoglobin; (32)] produces a significantly poorer fit (dotted line; r² = 0.79). See text for a full description of the various kinetic models.

Figure 6.

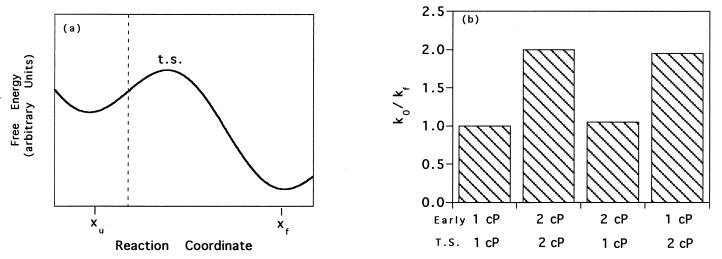
(a) Numerical simulations of diffusive barrier crossing in a simple potential described by sin(x) − x indicate that it is the diffusive nature of motions at or near the transition state that are monitored by the experiments described in this paper. The native and unfolded states are indicated by x_f and x_u, respectively. (b) The dependence of folding time constants viscosity. From the left, the histograms represent relative reaction time constants when viscosity is fixed at 1 cP over the folding path, is fixed at 2 cP, is 2 cP before the barrier (to the left of the dotted line in Fig. 4a), or is 2 cP at the barrier (to the right of the dotted line in Fig. 4a). The near equivalence of the second and fourth bars indicates that the viscosity dependence of motions at or near the transition state is the primary determinant of the viscosity dependence of protein folding rates.

RESULTS

The experimental determination of the solvent viscosity dependence of protein folding rates would appear straightforward, but it is not. Viscogenic cosolvents invariably alter solvent properties other than viscosity and, in doing so, alter the net stability of the native state and the free energy barrier to folding (17). We have used two methods to distinguish viscosity-specific effects from cosolvent-induced changes to the free energy barrier. Our first approach was the isostability technique, in which refolding rates are monitored under cosolvent conditions producing equivalent equilibrium stabilities (12, 18, 19). This assumes that the effect of cosolvents on the stability of the native state parallels effects on the transition state. Although there exists evidence supporting this assumption (17–20), we also have tested specifically its applicability to viscosity dependence studies; if viscosity is the mechanistic agent underlying changes in isostability refolding rates, then the rates will be related more directly to solvent viscosity than to cosolvent concentration or other solution properties. Our second approach was to analyze kinetic data by using physically plausible models that explicitly and independently treat the effects of glucose on viscosity and on the transition state barrier.

Thermodynamics.

Polyhydric, viscogenic cosolvents increase the stabilities of proteins (17, 21). Equilibrium unfolding data for protein L collected over the ranges 0–2 M glucose and 0–6 M GuHCl are well fitted to a simple model in which the free energy of unfolding of protein L is linearly related to both GuHCl and glucose concentrations:

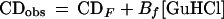2

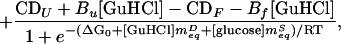where CD_obs is the observed circular dichroism signal at 222 nm, CD_F and CD_U are the signals arising from fully native and fully unfolded material, respectively, B_f and B_u reflect the sensitivity of the native and unfolded signals to GuHCl, ΔG₀ reflects the relative free energy of unfolding in the absence of cosolvents, m_eq^D and m_eq^S (the equilibrium m values) reflect the sensitivity of the unfolding free energy to GuHCl and glucose, respectively, R is the gas constant, and T is the temperature in Kelvin. The excellent fit (r² = 0.98) of equilibrium unfolding circular dichroism (CD) data to Eq. 2 (represented by the surface in Fig. 1) suggests that the relative free energy of unfolding for protein L is well described as a simple, linear function of GuHCl and glucose: ΔG = ΔG₀+ m_eq^D[GuHCl] + m_eq^S[glucose] where ΔG₀ = −5.0 ± 0.3 kcal·mol⁻¹, m_eq^D = 1.87 ± 0.11 kcal⋅mol⁻¹M⁻¹, and m_eq^S = −1.0 ± 0.1 kcal⋅mol⁻¹M⁻¹. The GuHCl m value is in excellent agreement with previous reports (1.85 in ref. 3; 1.7 ± 0.1 in ref. 22), and the glucose m value is similar to those reported for the sugar-induced stabilization of other proteins (e.g., see refs. 23 and 24). GuHCl denaturation curves fitted at individual glucose concentrations do not produce any systematic trend in m_eq^D and produce ΔG values that are well described (r² = 0.98) as a linear function of glucose concentration (data not shown), suggesting that m_eq^D and m_eq^S are constant under the conditions used. Taken together, these data suggest that the effects of glucose and GuHCl on protein L stability are both linear and additive. This result is consistent with previous studies of the additivity of the effects of denaturants and stabilizing agents (e.g., see refs. 19 and 25).

Kinetics.

Agents that stabilize proteins usually increase the rates with which they fold. Consistent with this observation, the refolding rate of protein L increases exponentially with increasing glucose concentration up to 2 M, at which the protein refolds six times more rapidly than in water (Fig. 2). At glucose concentrations >2 M, the refolding rate of protein L decreases, suggesting that the folding mechanism may be altered at very high cosolvent concentrations. Although no clear rationalization for such a mechanistic change is forthcoming, 2 M glucose is >35% sugar by weight and thus is a rather nonphysiological solvent. A similar change in mechanism might explain the anomalous, and otherwise difficult to rationalize (12), refolding kinetics reported for cspB at high (e.g., >2 M glucose) cosolvent concentrations (Fig. 5B of ref. 12).

The refolding and unfolding rates of protein L at >130 glucose and GuHCl concentrations are well fitted (r² = 0.97) by a simple, two-state model (Fig. 3). The fit of data collected over the ranges 0–2.0 M glucose and 0.3–6.3 M GuHCl to the equation

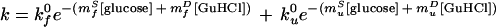3

provides intrinsic (in the absence of cosolvents) refolding and unfolding rates (k_f⁰ and k_u⁰) of 37 s⁻¹ and 0.02 s⁻¹, respectively. From this fit, we also obtain apparent kinetic m values for both glucose (m_f^S = 0.81 M⁻¹ and m_u^S = −1.17 M⁻¹) and GuHCl (m_f^D = −2.08 M⁻¹ and m_u^D = 0.91 M⁻¹). These kinetic parameters can be used to estimate the equilibrium folding thermodynamics of protein L: ΔG₀ = −4.4 ± 1.2 kcal⋅mol⁻¹, m_eq^D = 1.8 ± 0.3 kcal⋅mol⁻¹M⁻¹, and m_eq^S = 1.2 ± 0.2 kcal⋅mol⁻¹M⁻¹. The close correspondence between these values and values obtained from equilibrium unfolding experiments (above) provides strong evidence that protein L folds and unfolds via a simple, two-state mechanism over the range of conditions used (2).

The effects of sugars and denaturants on the equilibrium stabilities of proteins have been shown to be proportional to the change in solvent-accessible surface area that occurs on folding (21, 26). By analogy, the ratio m_f/(m_f − m_u) (θ) should, for both glucose and GuHCl, reflect the fraction of surface area buried in the native state that also is buried in the folding transition state. However, the θ values obtained from the fit of Fig. 3 differ significantly: θ_glucose = 0.41 ± 0.05, and θ_GuHCl = 0.69 ± 0.09 [in excellent agreement with previously reported values (3, 14)]. A similar discrepancy has been reported for the two-state folding of acylphosphatase, which exhibits θ values of 0.42 and 0.80 for glucose and urea, respectively (23). The origin of this discrepancy is discussed below.

Isostability Folding.

Under isostability conditions, the refolding rate of protein L decreases as glucose concentration increases. This effect is readily apparent in data collected at GuHCl cosolvent concentrations producing a net stability of −3.0 kcal⋅mol⁻¹ (Fig. 4). The rate changes appear to be closely and inversely related to changes in solvent viscosity and not caused by other, specific interactions with glucose or to a systematic error in the assumptions inherent in the isostability correction. Empirical measurements indicate that the relative viscosity (η/η₀, where η₀ is the solvent viscosity in the absence of cosolvents) of solutions in the range 0–2 M glucose is well fitted by a simple exponential function with an exponential coefficient of 0.58 ± 0.01 M⁻¹ (r² = 0.987) (Fig. 4a). If refolding rates are inversely proportional to solvent viscosity under isostability conditions, then a plot of the relative refolding time constant (k₀/k_f, where k₀ is the refolding rate in 0 M glucose at a stability of −3 kcal⋅mol⁻¹) vs. glucose concentration should fit an exponential function with this coefficient. A fit of these data to an exponential function produces a coefficient of 0.59 ± 0.01 M⁻¹ (r² = 0.982) (Fig. 4a). The coincidence of these two values suggests that the dependence of the protein L refolding rate on glucose concentration is caused by the viscogenic properties of the cosolvent, and none of the other solution properties of glucose that we have investigated, including density, osmolarity, water activity, or dielectric constant (15, 16, 27, 28) reproduce this relationship (data not shown). Under isostability conditions refolding time constants (k_f⁻¹) are extremely well fitted (r² = 0.985) by a simple, proportional relationship to solvent viscosity with a proportionality constant of 0.29 ± 0.01 seconds per centipoise (cP; 1 P = 0.1 Pa s). A similar, proportional relationship is reported for the viscosity dependence of the isostability refolding time constants of cspB over a similar range of solvent viscosities (inset of figure 5A of ref. 12).

Kinetic Modeling.

More than 50 years ago, Kramers described a detailed diffusion model of chemical reactions (29). In the limit of low viscosity, where Brownian forces do not alter substantially the energy of the reactants during the course of the reaction, the model predicts that rates will increase with increasing viscosity. Consistent with this, computer simulations conducted at viscosities orders of magnitude lower than that of water exhibit increasing folding rates with increasing η (10). In contrast, in the limit of high viscosity, Kramers’ model predicts that reaction rates are inversely proportional to η. Because of the considerable exchange of energy between polymer molecules and the solvent, the folding of real proteins is almost certainly in this over-damped, high viscosity regime (10, 30).

Several groups have published extensions of Kramers’ theory to describe the conformational dynamics of less than fully hydrated species in the high viscosity regime (e.g., see refs. 31–33). These extensions include an “internal friction” or “internal viscosity” term, ξ, corresponding to the friction between adjacent structural elements of the protein. The reaction rate then is given by an equation of the general form

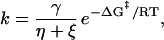4

where η is solvent viscosity, γ is a proportionality constant with units of cP⋅s⁻¹, and ΔG‡ is the free energy barrier. For protein folding as a function of glucose concentration, which affects both ΔG‡ and η, we have

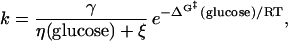5

where η(glucose) and ΔG‡ (glucose) are the solvent viscosity and the relative transition state free energy as functions of glucose concentration. From Fig. 4a, we see that, over the range 0–2 M glucose, η is well approximated as η₀e^{0.58[glucose]}, where η₀ is the viscosity of the buffer in the absence of cosolvents (1.00 cP; ref. 21). Assuming that, like that of the native state (Fig. 1), the relative free energy of the transition state is linearly related to glucose concentration, Eq. 5 can be rewritten as

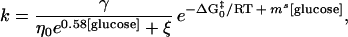6

where ΔG₀^‡ is the relative transition state free energy in the absence of glucose and m^S is the true kinetic glucose m value. For the simplest case, in which the internal friction is negligible, we can rewrite Eq. 6

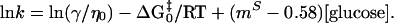7

From this equation, we see that lnk_f and lnk_u are linear functions of glucose concentration with slopes of

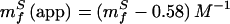8

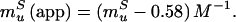9

The fit of Fig. 3 provides values for m_f^S(app) = 0.81 M⁻¹ and m_u^S(app) = −1.17 M⁻¹. Using these values and Eqs. 8 and 9, we can calculate the true kinetic glucose m values, m_f^S and m_u^S, as 1.39 M⁻¹ and −0.59 M⁻¹, respectively, and also can obtain a “viscosity corrected” θ_glucose,

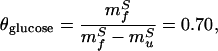10

which is well within experimental error of the value of θ_GuHCl derived fully independently (0.69 ± 0.09 above and 0.70–0.75 in refs. 3 and 14) from GuHCl-based measurements. The close correspondence of these values suggests that the discrepancy between glucose- and GuHCl-based estimates of transition state compactness (see above) arises entirely from the viscogenic effects of glucose and provides further evidence both for the compactness of the protein L folding transition state and for an inversely proportional relationship between folding kinetics and solvent viscosity.

[It should also be noted that the effect of GuHCl on solvent viscosity will cause θ_GuHCl to slightly overestimate transition state compactness, but, with an exponential coefficient of 0.07 M⁻¹ (15)—versus 0.58 M⁻¹ for glucose—the effect is small. In a related manner, because of the temperature dependence of the viscosity of water, ΔcP_f/ΔcP_eq slightly underestimates transition state compactness. These effects may explain a previously noted, systematic discrepancy between ΔcP and denaturant-based measures of transition state conformation (23, 34).]

Evidence for the negligible contribution of internal friction to the folding kinetics of protein L also is provided by fits of Eq. 6, which, for convenience, can be rewritten as follows:

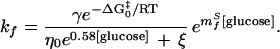11

With three variables (ξ, m_f^S, and γe^{−ΔG₀‡/RT}), Eq. 11 is constrained poorly by refolding data (Fig. 5) and produces a ξ of 2 ± 35 cP. To more tightly constrain ξ, m_f^S can be fixed by assuming that the θ_GuHCl and viscosity-corrected θ_glucose values represent the true θ value:

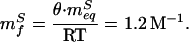12

This value of m_f^S produces an excellent fit of refolding data (solid line in Fig. 5; r² = 0.97) and a tightly constrained estimate for ξ of −0.1 ± 0.2 cP. Consistent with this, fixing ξ at 0 cP (which reproduces Eq. 6) and allowing m_f^S to float also produces an excellent fit of the data (dashed line in Fig. 5; r² = 0.97) with a predicted m_f^S (−1.3 ± 0.1 M⁻¹) effectively indistinguishable from the value derived above. Assuming that ξ = 4 cP [the internal friction observed for a conformational change in myoglobin (32)] produces a significantly poorer fit (dotted line in Fig. 5; r² = 0.79). These results provide evidence, independent of the isostability approach, that, under the conditions used, the refolding of protein L is in the high viscosity limit with a rate that is inversely proportional to solvent viscosity with a small or nonexistent internal friction contribution to the rate limiting step.

Simulations.

The results of our experimental investigations motivated us to investigate which aspects of the folding process are probed by changing solvent viscosity. This can be performed by integration of the diffusion equations for a simple barrier crossing problem (Fig. 6a) by using a viscosity term, η(x), that varies along the reaction coordinate, x:

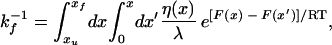13

where x_u and x_f represent the unfolded and native states, λ is a proportionality constant, and F(x) is the energy as a function of the reaction coordinate (29, 35). Integration of this equation with viscosity held constant over the reaction coordinate simulates the experiments conducted above and produces the expected linearity of k_f⁻¹ with viscosity (Fig. 6b). In a previous study (12), it was suggested that the viscosity dependence of protein folding reflects the contribution of chain collapse to the folding barrier. To quantitatively test which aspects of the folding reaction are probed by these experiments, we have conducted two further simulations in which the viscosity term is altered discontinuously midway between the unfolded and transition states. As demonstrated in Fig. 6b, the viscosity at the transition state is the primary determinant of the rate, and the dependence on the viscosity at early, low energy states populated en route to the transition state is negligible.

DISCUSSION

How might the solvent viscosity dependence of protein folding be interpreted? The numerical simulations (Fig. 6) indicate that changing solvent viscosity monitors the motions of conformations energetically near the transition state, rather than the large scale diffusive motions required to form a collapsed transition state. Although the viscosity dependence observed for protein L folding is not inconsistent with a collapse-limited reaction mechanism, the results of our simulations are not consistent with the claim that viscosity-dependent folding kinetics directly demonstrate that “the compaction of the polypeptide chain occurs in the rate-limiting step of folding (12).”

A small number of studies of the viscosity dependencies of protein conformational changes have been reported. Haas et al. (31) have used a modification of Kramers’ theory (similar to Eq. 4) to fit the end-to-end diffusion kinetics of polyglycine chains ranging from 4 to 10 residues. They report that the dynamic behavior of the fully hydrated, 10-residue chain is inversely dependent on solvent viscosity and appears to involve motions that displace bulk solvent. In contrast, the dynamic behavior of a four-residue chain is dominated by an internal friction and is affected relatively less by changing solvent viscosity. A similar approach has been used to model the solvent viscosity dependence of the rate of ligand dissociation-induced conformational changes in myoglobin (32). This study demonstrated that, for the relatively small structural rearrangements of a compact, solvent-excluded, native protein, an internal friction approximately four times that of water dominates the reaction rate under physiological solvent conditions and solvent displacement plays a relatively minor role in limiting the rate of conformational change.

The simple, proportional relationship between isostability refolding time constants and relative viscosity (Fig. 4), the close correspondence between θ_GuHCl and the viscosity-corrected θ_glucose (Eq. 10), and the excellent fit of the glucose dependence of protein L folding rates to a simple model based on Kramers’ theory (Fig. 5) all indicate that the rate-limiting transition in the folding of protein L does not exhibit a significant internal friction component. This suggests that the rate-limiting conformational change in the folding of this protein more closely resembles the diffusion through bulk solvent of the end-to-end dynamics of a fully solvated polypeptide chain than the structural rearrangements of a collapsed protein.

Although consistent with some theoretical models of folding (9–11), a rate-limiting folding transition involving conformational fluctuations that displace considerable amounts of solvent is in contrast to results indicating that folding transition states appear to be rather compact species. As described above, 70% of the solvent-accessible surface area buried in the native state of protein L is buried in its folding transition state, and, thus, the folding of protein L might be expected to exhibit a significant internal friction. The solvent viscosity dependence of cspB folding similarly appears to lack an appreciable internal friction contribution (12, 16). This result is all the more surprising because cspB is thought to form the most highly collapsed transition state of any protein characterized to date; it is reported that ≈90% of the change in solvent accessible surface area occurs at or before the transition state (12). Thus, barrier-crossing fluctuations that displace significant amounts of solvent may be a general property of two-state protein folding reactions that progress via even very compact transition states.

ABBREVIATIONS

cspB

Bacillus cold shock protein

GuHCl

guanidine hydrochloride

protein L

IgG binding domain of peptostreptococcal protein L

CD

circular dichroism

cP

centipoise