Thermodynamics of the Hydroxyl Radical Addition to Isoprene

Abstract

Oxidation of isoprene by the hydroxyl radical leads to tropospheric ozone formation. Consequently, a more complete understanding of this reaction could lead to better models of regional air quality, a better understanding of aerosol formation, and a better understanding of reaction kinetics and dynamics. The most common first step in the oxidation of isoprene is the formation of an adduct, with the hydroxyl radical adding to one of four unsaturated carbon atoms in isoprene. In this paper we discuss how the initial conformation of isoprene, s-trans and s-gauche, influences the pathway to adduct formation. We explore the formation of pre-reactive complexes at low and high temperatures, which are often invoked to explain the negative temperature dependence of this reaction’s kinetics. We show that at higher temperatures the free energy surface indicates that a pre-reactive complex is unlikely, while at low temperatures the complex exists on two reaction pathways. The theoretical results show that at low temperatures all eight pathways possess negative reaction barriers, and reaction energies that range from −36.7 to −23.0 kcal·mol⁻¹. At temperatures in the lower atmosphere, all eight pathways possess positive reaction barriers that range from 3.8 to 6.0 kcal·mol⁻¹, and reaction energies that range from −28.8 to−14.4kcal·mol⁻¹.

Introduction

Because of its great importance, isoprene (2-methyl-l,3-butadiene) and its oxidation reactions have been studied for many decades. ^{1–20,21–51} Isoprene is produced by plants under heat stress, and it has been suggested that isoprene protects plant membranes from thermal shock.⁵² Approximately 500 teragrams of isoprene are emitted into the atmosphere annually,⁵³ and consequently, the process of isoprene oxidation has significant effects on atmospheric chemistry. In a warming Earth, isoprene emission will increase and so will its atmospheric concentration. Isoprene oxidation by the hydroxyl radical leads to ozone formation in the troposphere.^34,53,54 Consequently, a more complete understanding of this reaction will lead to better models of regional air quality, a better understanding of aerosol formation and a better understanding of reaction kinetics and dynamics.

There are numerous articles that discuss the possibility of hydroxyl radical addition to all four unsaturated carbons of isoprene,^{11,23–25,29,34,39,44,49,51,55–57} and experimentalists have found supportive evidence for formation of all four adducts.²⁴ A subject of debate has been the relative importance of the four possible adducts.^{11,24,25,28,39,41,51} Since each adduct has a different chemical structure, different oxidative pathways lead to different end products through subsequent reaction steps.^28,55,58 As such, it is valuable to know the adducts that are most prevalent in the troposphere. To make this assessment, it is necessary to consider the conformations of isoprene before reacting with the hydroxyl radical because their positions on the hypersurface may affect the oxidative pathway the reaction follows.⁴⁰

In addition, experimental rate constants for the hydroxyl radical addition to isoprene show an unusual temperature dependence, with a negative temperature dependence at room temperature and a positive temperature dependence at lower temperatures.^{1,21,24,27,28,31,35,38,44,46,55,58,59,60–62} The negative temperature dependence has been explained as resulting from a flat reaction potential energy surface in this region, due to the formation of a pre-reactive complex whose energy is lower than the separated reactants.⁶³

Previous computational studies have examined the potential energy surface for the hydroxyl radical addition to isoprene’s s-trans conformation, almost exclusively reporting electronic or zero-point corrected electronic energies with a few studies reporting enthalpy of reactions.^24,25,39,51 A single computational study, that provided BHandHLYP/6-311G**//BHandHLYP/6-311G** and PMP2/cc-pVTZ//MP2/6-311G** energies, investigated the role of isoprene’s s-gauche conformation in the reaction.⁵⁶ Missing from this body of research is a discussion of how this reaction behaves on the free energy surface. In this paper, we present the computed pathways for the hydroxyl radical addition to isoprene’s s-trans and s-gauche conformations at each of its four unsaturated carbons. Each pathway starts with the separated reactants, proceeds through a pre-reactive complex and transition state, and ends in the formation an adduct. Optimized geometries and thermal corrections are provided at the BHandHLYP/6-311G** theory level, while electronic energies were computed at the CCSD(T)/aug-cc-pVDZ and BD(T)/aug-cc-pVDZ levels; the BD(T) theory was essential for eliminating the instabilities that arise in determining amplitudes in the wave function. The BD(T) calculations, which do not suffer from spin contamination, are a novel aspect of this work and yield the most reliable energies for the isoprene-hydroxyl radical system to date. We present E_zpv, H°_298K, G°_298K and E_a for each of the eight pathways. Included in the discussion is how the potential energy surfaces are affected by entropy at tropospheric temperatures, focusing on the pre-reactive complexes and reaction barriers. The results have universal utility for similar reactions.

Methods

Selecting a suitable theory level for the reaction of the hydroxyl radical with isoprene is not trivial. Two related issues are the problem of spin contamination and accurate calculation of the energetics and structures of open-shell transition-state systems. Total spin is denoted as <S²>, where <S²> = s(s+1) and s is the number of unpaired electrons. Generally, if the difference in the calculated spin operator from the expected value of the total spin, <S²>, is within 10% then the results can be trusted.⁶⁴ For a doublet, <S²> = 0.75, so the 10% range encompasses 0.675 to 0.825. In an unrestricted (u) Møller-Plesset calculation (MP2), spin contamination of higher energy spin states can become incorporated in the wavefunction because the wavefunction is no longer an eigenfunction of the total spin;^64–66 Unrestricted MP2 calculations on the isoprene-hydroxyl radical system suffer from severe spin contamination, and all of our efforts to use uMP2 with different basis sets on the radicals studied in this work were not fruitful (data not shown). Although ab initio electronic structure programs such as Gaussian⁶⁷ have ways of resolving spin contamination problems, such as annihilating the first higher spin state that appears in the contaminated wave function and then calculating projected energies,^68–71 these subroutines do not improve geometries or frequencies since the annihilated wave function is not used in any subsequent SCF calculations.⁶⁶ In contrast, spin contamination in density functional theory (DFT) calculations is not well defined and spin projection should not be used.^72–75 The single reference methods that are least susceptible to spin contamination are the coupled cluster theories uCCSD, uQCISD, and the Brueckner Doubles’ uBD(T) perturbative approach.⁷¹

The second problem involves the accurate calculation of transition-state structures and energies for open-shell systems. DFT has been found to be more accurate for transition-state geometries and reaction path energies than for absolute energies,^76–84 and any particular DFT method should be benchmarked for a particular reaction before it can be trusted for accurate determination of barrier heights.^66,79,85 Truhlar and co-workers examined the ability of electronic structure methods to model transition states when the unrestricted wave functions show significant spin contamination.⁸⁶ They concluded that quadratic configuration and coupled cluster methods, with unrestricted reference states, provided good approximations to transition-state geometries, while connected triples are needed for reliable saddle-point energies. Besides spin contamination, we have the potential problem of non-dynamical electron correlation, which arises when different determinants have similar weights because of frontier orbital degeneracy. Coupled-cluster theory⁸⁷ generally makes a good estimation of electron correlation energy, with CCSD being a popular theory that includes all single and double excitations.⁶⁶ One measure of the multireference character of CCSD is the T₁ diagnostic,⁸⁸ which is the T₁ operator (for all single excitations over all the occupied and virtual orbitals) in coupled cluster theory, and a value above 0.02 is grounds for caution when interpreting CCSD results.⁶⁶ Adding the effects of triple excitations through perturbation theory and a singles/triples coupling term defines the CCSD(T) method.^66,89 It is possible for large singles amplitudes to result in instability in the perturbation theory estimate, and one way to eliminate that instability is the change of HF orbitals to Brueckner orbitals, which requires that the singles amplitudes in the CCSD cluster operator be zero.⁶⁶

Considering the above issues, all reactants, pre-reactive complexes, transition-state, and adducts structures were optimized at the unrestricted and restricted BHandHLYP/6-311G** level of theory as appropriate, followed by harmonic frequency calculations to verify stationary points. Several researchers have shown uBHandHLYP, with a variety of basis sets, to be an appropriate theory level for studying radical reactions.^{39,56,90–93} A conformer search around isoprene’s central bond was performed to determine stationary points along this degree of freedom, followed by single-point calculations on each stationary point at the CCSD(T)/aug-cc-pVDZ, CCSD(T)/aug-cc-pVTZ, and BD(T)/aug-cc-pVDZ levels of theory.^94–97 The uBHandHLYP/6-311G** optimized radical species had spin contamination within the 10% range from the expected value.⁶⁴ Subsequent single-point calculations were performed at the uCCSD(T)/aug-cc-pVDZ and uBD(T)/aug-cc-pVDZ levels of theory. Enthalpies and free energies were obtained by combining the unrestricted or restricted BHandHLYP frequency data with the corresponding CCSD(T) and BD(T) electronic energies.

Pre-reactive complex geometries were found using IRC calculations to connect eight different transition states to prior points on the reaction coordinate. These structures were optimized using a reaction coordinate step size of 0.01 amu^1/2 Bohr, and calculating the second derivative at every point (keywords opt=stepsize=1,calcall). All calculations were performed using Gaussian 03.⁶⁷

Results

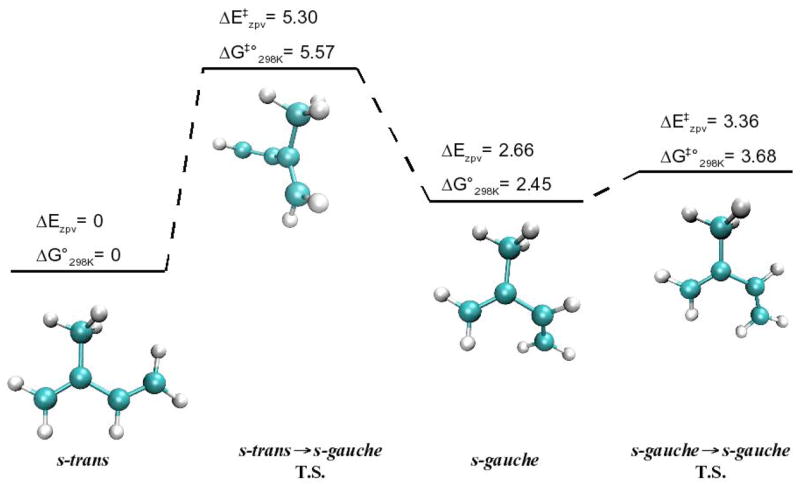
Table 1 provides the relative energies for each stationary point along the potential energy surface for the rotation about isoprene’s single bond. The conformational search yielded two stable gas-phase conformations; one conformer is an s-trans structure with a 180° torsion angle along the carbon backbone, and the other is an s-gauche conformer with a 41° torsion angle. The s-trans conformer is the most stable at 0 and 298.15 K, with the s-gauche lying 2.7 (E_zpv), 2.8 (H°_298K) and 2.5 (G°_298K) kcal·mol⁻¹ higher in energy at the CCSD(T)/aug-cc-pVTZ level. As Figure 1 shows, the rotational barriers for the s-trans s-gauche transition are 5.3 (E^‡_zpv), 5.0 (H^‡°_298K) and 5.6 (G^‡°_298K) kcal·mol⁻¹, while the rotational barriers between the two s-gauche conformers, whose transition state is the s-cis conformer, are 0.7 (E^‡_zpv), 0.2 (H^‡°_298K) and 1.2 (G^‡°_298K) kcal·mol⁻¹. Based on a Boltzmann distribution calculation using the relative E_zpv values, the s-trans conformer will have 100% abundance at 10 K; similarly, using the relative G°_298K values, the s-gauche conformers will an approximate abundance of 3.2% at 298 K.

Table 1.

BHandHLYP/6-311G**, CCSD(T)/aug-cc-pVDZ, CCSD(T)/aug-cc-pVTZ and BD(T)/aug-cc-pVDZ Changes in Energy.¹

	ΔEzpv2	ΔH298°	ΔG298°
	s-gauche minima3
BHandHLYP/6-311G**	2.67	2.77	2.46
CCSD(T)/aug-cc-pVDZ	2.62	2.72	2.41
CCSD(T)/aug-cc-pVTZ	2.66	2.76	2.45
BD(T)/aug-cc-pVDZ	2.63	2.73	2.42
	s-trans → s-gauche transition state barrier3
BHandHLYP/6-311G**	5.48	5.17	5.75
CCSD(T)/aug-cc-pVDZ	4.99	4.68	5.26
CCSD(T)/aug-cc-pVTZ	5.30	4.99	5.57
BD(T)/aug-cc-pVDZ	5.01	4.70	5.28
	s-gauche → s-gauche transition state barrier4
BHandHLYP/6-311G**	0.80	0.34	1.33
CCSD(T)/aug-cc-pVDZ	0.73	0.27	1.27
CCSD(T)/aug-cc-pVTZ	0.70	0.24	1.23
BD(T)/aug-cc-pVDZ	0.73	0.27	1.27

¹Energies computed using BHandHLYP/6-311G** optimized geometries. All values are in kcal·mol⁻¹.

²Zero-point vibration corrected electronic energy.

³Energies are relative to isoprene’s global minima, the s-trans conformation.

⁴Energies are relative to isoprene’s s-gauche conformation.

Figure 1.

Figures 2 and 3 display the BHandHLYP geometries for reactants, pre-reactive complexes, transition states and products for isoprene’s s-trans and s-gauche conformers reacting with the hydroxyl radical. Figure 4 displays the potential energy and free energy hypersurfaces along the reaction coordinate that connects the reactants, the pre-reactive complexes, the transition states and the final products for the reaction of the hydroxyl radical with carbon one of isoprene’s s-trans conformer.

Figure 2.

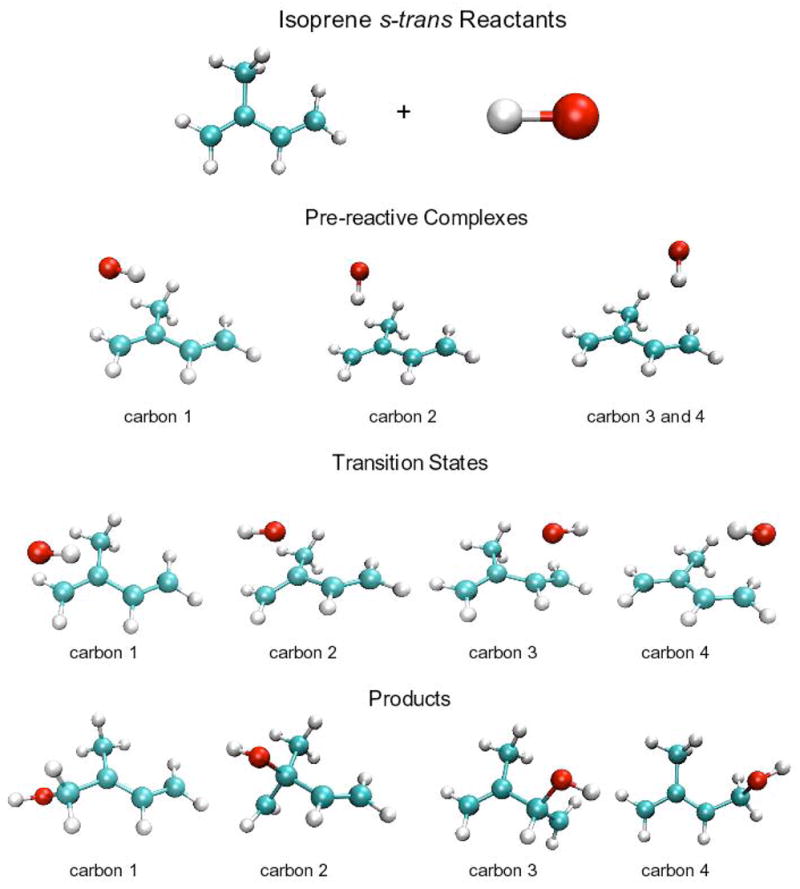
Figure 3.

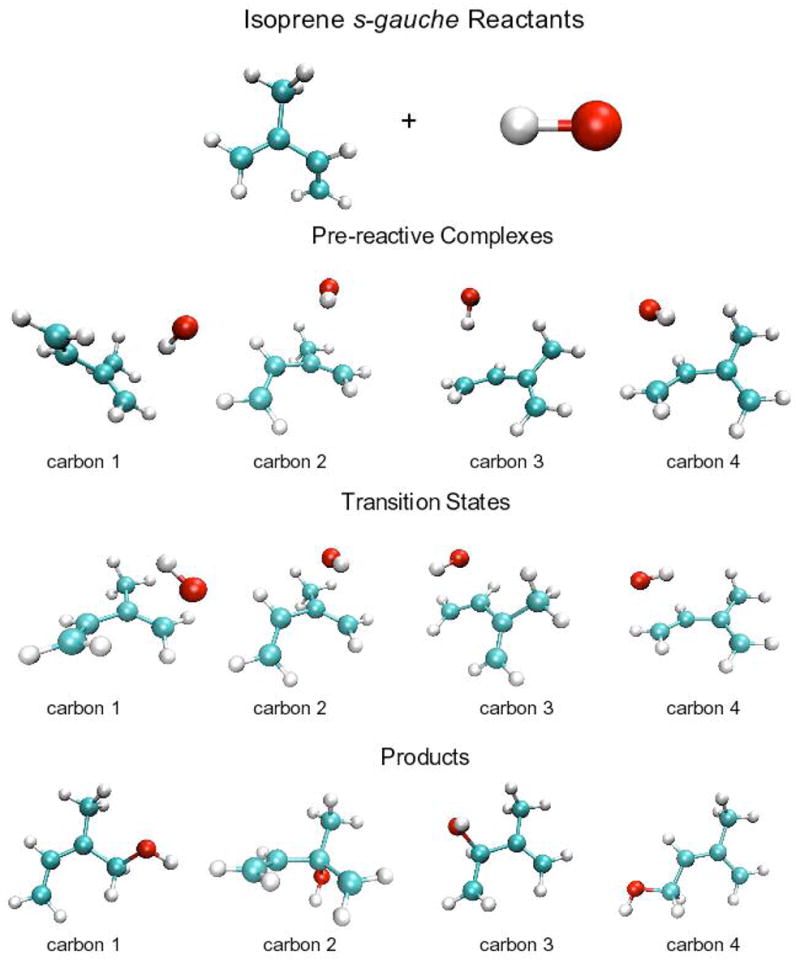
Figure 4.

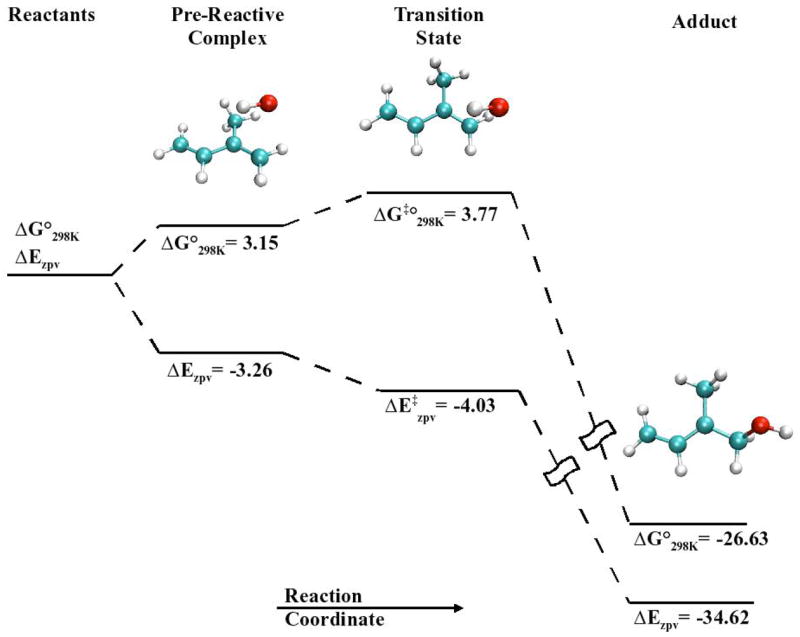
Tables 2–4 provide the thermodynamic details of the potential energy surface for each of the eight pathways, as exemplified in Figure 4 for a single pathway. These pathways are represented by C_n^d, where “n” and “d” indicates the carbon atom undergoing addition and the isoprene conformation, respectively. For example, The C₁¹⁸⁰ pathway represents the addition of the hydroxyl radical to the first carbon of s-trans isoprene (Figure 2), while the C₂⁴¹ pathway represents the addition of the hydroxyl radical to the second carbon of s-gauche isoprene (Figure 3). Table 2 contains the CCSD(T) and BD(T) energies for the transition from reactants to pre-reactive complexes for the eight different reaction pathways. Table 3 contains the activation energies for the transition from reactants to the transition state, while Table 4 contains the energies for the overall reaction from reactants to the eight adducts.

Table 2.

CCSD(T)/aug-cc-pVDZ and BD(T)/aug-cc-pVDZ Changes in Energy from Reactants to Pre-reactive Complexes.¹

Pathway	ΔEzpv2	ΔH298°	ΔG298°	ΔEzpy2	ΔH298°	ΔG298°
	CCSD(T)			BD(T)
C1180	−3.13	−3.10	3.28	−3.26	−3.23	3.15
C2180	−3.16	−3.24	3.31	−3.16	−3.24	3.31
C3180	−2.41	−2.58	4.55	−2.93	−3.11	4.02
C4180	−2.41	−2.58	4.54	−2.93	−3.11	4.02
C141	−2.78	−2.97	4.23	−2.93	−3.12	4.08
C241	−3.29	−3.24	3.26	−3.32	−3.28	3.22
C341	−2.80	−2.99	4.22	−3.01	−3.20	4.01
C441	−2.70	−2.87	4.16	−2.73	−2.90	4.13

¹Energies computed using BHandHLYP/6-311G** optimized geometries. All values are in kcal·mol⁻¹.

²Zero-point vibration corrected electronic energy.

Table 4.

CCSD(T)/aug-cc-pVDZ and BD(T)/aug-cc-pVDZ Energies of Reaction, relative to reactants.¹

Pathway	ΔEzpv2	ΔH298°	ΔG298°	ΔEzpv2	ΔH298°	ΔG298°
	CCSD(T)			BD(T)
C1180	−34.25	−35.09	−26.25	−34.62	−35.46	−26.63
C2180	−23.26	−24.23	−14.33	−23.49	−24.46	−14.55
C3180	−22.84	−23.72	−14.26	−23.02	−23.90	−14.44
C4180	−32.15	−33.14	−23.73	−32.54	−33.52	−24.11
C141	−36.27	−37.29	−27.82	−36.66	−37.68	−28.21
C241	−26.26	−27.30	−17.20	−26.43	−27.47	−17.37
C341	−24.29	−25.28	−15.68	−24.46	−25.45	−15.85
C441	−35.42	−36.21	−28.41	−35.81	−36.60	−28.80

¹Energies computed using BHandHLYP/6-311G* * optimized geometries. All values are in kcal·mol⁻¹.

²Zero-point vibration corrected electronic energy.

Table 3.

CCSD(T)/aug-cc-pVDZ and BD(T)/aug-cc-pVDZ Energies of Activation, relative to the reactants.¹

Pathway	ΔEZPV‡2	ΔH298°‡	ΔG298°‡	Ea3	ΔEZPV‡2	ΔH298°‡	ΔG298°‡	Ea3
	CCSD(T)				BD(T)
C1180	−3.30	−3.95	4.50	−2.76	−4.03	−4.67	3.77	−3.48
C2180	−2.19	−3.04	6.38	−1.85	−2.74	−3.59	5.83	−2.40
C3180	−1.71	−2.51	6.54	−1.33	−2.23	−3.04	6.01	−1.85
C4180	−3.08	−3.88	5.01	−2.69	−3.79	−4.58	4.31	−3.39
C141	−3.42	−4.19	4.77	−3.01	−4.01	−4.79	4.17	−3.60
C241	−3.96	−4.94	4.84	−3.76	−4.47	−5.45	4.33	−4.27
C341	−2.86	−3.85	5.69	−2.67	−3.47	−4.46	5.08	−3.28
C441	−2.38	−3.12	5.34	−1.93	−3.09	−3.83	4.63	−2.64

¹Energies computed using BHandHLYP/6-311G** optimized geometries. All values are in kcal·mol⁻¹.

²Zero-point vibration corrected electronic energy.

³Calculated using Transition State Theory where E_a = ΔH°^‡ + 2RT.

Discussion

Isoprene’s Conformation

BHandHLYP/6-311G** reproduces the experimental known gas-phase geometry³ of the s-trans conformation reliably, with a bond distance RMSD of 0.015Å and an angle RMSD of 1.3°. This agreement is acceptable for the closed shell isoprene geometry considering this theory level has previously been determined appropriate for radical species.^{39,56,90–92} The relative stability of the two isoprene conformations, as determined by CCSD(T)/aug-cc-pVTZ (H°_298K=2.8) and BD(T)/aug-cc-pVDZ (H°_298K=2.7), is in decent agreement with the most recent experimental finding that the s-gauche conformer is enthalpically less stable by 2.46 kcal·mol^−1.98 Our computed s-gauche population at 298K (3.2%) is also in agreement with the experimental approximation of 4.7%.³ Our CCSD(T)/aug-cc-pVTZ computed rotational energy barriers (G^‡°_298K=5.6 & 3.4 kcal·mol⁻¹) agree with early experimental values of 5.8 kcal·mol⁻¹ (s-trans s-gauche) and 3.4 kcal·mol⁻¹ (s-gauche s-gauche), which are Raman values that were refined using an ab initio method.⁹⁹ Other experimental free energy values for the s-trans s-gauche barrier are 3.67 and 3.9 kcal·mol^−1.98,100 A further computational investigation on the rotational barrier height is warranted, but is beyond this paper’s interest of exploring the isoprene-hydroxyl radical reaction.

The relatively high s-trans s-gauche barrier, regardless if the value is 3.67 or 5.6 kcal·mol⁻¹, indicates that the two conformers will not be in rapid equilibrium, but rather in a long-lived statistical equilibrium at 298K. Therefore, at any given time we would expect that 3% of the isoprene molecules will be in the s-gauche conformation in the lower atmosphere and will be available to react with the hydroxyl radical.

Methodology Evaluation

We tested the multireference character of uCCSD, uCCSD(T) and uBD(T) by computing the T₁ diagnostic for the C₁¹⁸⁰ pathway. The T₁ diagnostic for the transition state was 0.037, indicating a potential problem. For the formation of the transition state from the separated reactants, uCCSD/aug-cc-pVDZ yield an activation free energy that was a ~2 kcal·mol⁻¹ higher than the corresponding uCCSD(T)/aug-cc-pVDZ results; thus, the inclusion of perturbative triples had a significant effect on the free energy of activation. Switching to uBD(T)/aug-cc-pVDZ lowered the electronic (E^‡_zpv) and free energy (G°^‡_298K) of activation by another 0.73 kcal·mol⁻¹, and coupled with the T₁ diagnostic indicates that the HF reference in the uCCSD calculation is poor.¹⁰¹ This is supported by Table 3, where the uBD(T) method lowers the activation energies for each pathway, in comparison to the uCCSD(T) method, by an average of −0.62 kcal·mol⁻¹. The pre-reactive complexes show that the uBD(T) energies lower the interaction energies relative to the uCCSD(T) values by an average of 0.09 kcal·mol⁻¹, with the exception of the C₃¹⁸⁰ and C₄¹⁸⁰ pathways’ pre-reactive complexes whose uBD(T) energies are energetically lower by 0.53 kcal·mol⁻¹. The use of the uBD(T) adduct energy lowers the reaction energies by an average of 0.29 kcal·mol⁻¹, in comparison to the uCCSD(T) values, with the C₁ and C₄ adducts for both isoprene conformations possessing lower energies by 0.39 kcal·mol⁻¹. Thus, the quality of the uCCSD(T) energies is questionable when a radical species is present in the calculation, and for the remainder of the discussion we will refer to BD(T) results.

Pre-reactive Complex

Pre-reactive van der Waals complexes, such as the radical OH···CH₄ and OH··· acetylene complexes, have been observed in low-temperature molecular beams.^102–115 Thus, we know through spectroscopy that pre-reactive complexes can form at low temperatures and pressures, and can lead to products by passing through a transition state that connects the pre-reactive complex to the addition product. Less amenable to experiment is the detection of pre-reactive complexes at the higher pressures and temperatures common in the atmosphere. As we will soon show, these higher pressures and temperatures suggest that free energy considerations matter most in determining the stability of pre-reactive complexes.

Spangenberg and coworkers infer that a pre-reactive complex forms in the hydroxyl radical addition to isoprene, based on their kinetic data.⁴⁴ Francisco-Márquez and coworkers predicted four pre-reactive complexes for isoprene, two for each isoprene conformation, using BHandHLYP and MP2 theories with the 6-311G** basis set.^39,56 Their pre-reactive complexes, when isoprene is in the s-trans conformation, have a E_zpv of −2.80 and −2.99 kcal·mol⁻¹ (BHandHLYP) and −3.30 and −3.49 kcal·mol⁻¹ (MP2) relative to the reactants, and lie below the transition state. We were able to locate seven pre-reactive complexes that are minima on all eight pathways using the BHandHLYP theory, with reaction barriers in both the forward and reverse directions. However, at the BD(T) theory level the electronic energy barrier in the forward direction disappears in all pathways, except for the C₂¹⁸⁰ and C₃¹⁸⁰ pathways,¹ because the transition states possess more negative relative E_zpv energies relative to the pre-reactive complexes (see next section). For these barrierless pathways, we envision the potential energy surface guiding the collisions of isoprene and the hydroxyl radical, quickly passing through the pre-reactive complexes’ transition state regions to form the adducts. However, to date there has not been an experimental finding of any pre-reactive complex for this reaction. The C₂¹⁸⁰ and C₃¹⁸⁰ pathways possess 0.4 and 0.7 kcal·mol⁻¹ transition-state energy barriers relative to their pre-reactive complexes, and present likely candidates for trapping in a low temperature gas-phase experiment.

Since pre-reactive complexes are formed as a result of coloumbic interactions between the two molecules, the formation of the pre-reactive complex will be favorable in terms of electronic energy, but the proximity of two molecules together will decrease the entropy of the system. At 298 K, the contribution of entropy in this reaction is an appreciable effect and needs consideration. As a result of the molecular complex formation, where two molecules behave as one, three translational and three rotational degrees of freedom are lost and the overall entropy of the system is decreased. The BD(T) results in Table 2 show that while the pre-reactive complexes reside below the reactants’ potential (E_zpv) and enthalpic (H₂₉₈°) energies, they are not minima on the free energy (G₂₉₈°) hypersurfaces at 298 K. The fundamental equations, H=E_tot+RT and G=H-TS,² reveal that at low temperatures the free energy will be quite close to the potential energy, but as the temperature increases the free energy will deviate from the potential energy (Figure 4). This causes the pre-reactive complexes to no longer be minima on the free energy surfaces. As shown in Table 2, the relative free energy of the pre-reactive complex along all pathways resides above the reactants’ energies, with values ranging from 3.2 to 4.1 kcal·mol⁻¹.

Transition State

The isoprene’s s-gauche conformer provides lower activation energies (E_a) for all pathways than those for the s-trans conformer, with the exception of the C₄¹⁸⁰ pathway. Results in Table 2 show theoretical evidence for hydroxyl radical addition to all four unsaturated carbons of isoprene. At the low temperatures found in a molecular beam, all pathway barriers (ΔE^‡ zpv) are favorable with negative values, with the C₂⁴¹ barrier being lowest by 0.5 kcal·mol⁻¹. This agrees with the results found by Greenwald and coworkers, who found negative transition-state barriers for the each of the s-trans pathways (i.e. C_1–4¹⁸⁰ pathways) using roQCISD(T)/6-311++G**//B3LYP/6-311++G** electronic energies that have been corrected for basis set effects.⁵¹ Francisco-Márquez and coworkers, using BHandHLYP and MP2 energies employing the 6-311G** basis set, also found negative transition-state barriers for the C₁¹⁸⁰ and C₄¹⁸⁰ pathways, but positive barriers for the C₂¹⁸⁰ and C₃¹⁸⁰ pathways. The two positive barriers are likely due to the inadequacy of these theories to describe the radical character of the transition state.

At room temperature all barrier values (ΔG^‡_298K) become positive, with pathways C₁¹⁸⁰ possessing the lowest barrier by 0.4 kcal·mol⁻¹. The C₁⁴¹, C₄¹⁸⁰ and C₂⁴¹ pathways have the next lowest barriers, with values that are within 0.16 kcal·mol⁻¹ of each other; this difference is likely to be within the error bars of the BD(T) calculations, and they should be considered equivalent pathway barriers after the C₁¹⁸⁰ barrier. The addition of the hydroxyl radical to carbons two and three have smaller barriers when isoprene is in the s-gauche conformation, with C₂⁴¹ and C₃⁴¹ barriers that are 1.5 and 0.9 kcal·mol⁻¹, respectively, lower than the corresponding s-trans pathway barrier. Surmounting the reaction barrier appears feasible at each unsaturated carbon, considering that the C₁¹⁸⁰, C₄¹⁸⁰, C₁⁴¹, C₂⁴¹, C₃⁴¹ and C₄⁴¹ pathways barriers are within 1.3 kcal·mol⁻¹ of each other, a conclusion also arrived at in a previous study.⁵⁶

Product

Adduct production is favored for all eight pathways, as seen in Table 4. The BD(T) reaction energies for adduct formation are more negative than the CCSD(T) values by an average of 0.3 kcal·mol⁻¹, with C₁ and C₄ pathway adducts possessing the greatest difference of 0.4 kcal·mol⁻¹. Adduct formation is favored along the four C₁ and C₄ pathways, by a minimum of 6.1 kcal·mol⁻¹ with respect to the C₂ and C₃ pathways. This is consistent with twenty previous calculations whose ΔH₂₉₈° and ΔE reaction energies for pathway C₁¹⁸⁰ range from −31.5 to −47.7 kcal·mol⁻¹ (average = −39.6), for C₂¹⁸⁰ range from −13.4 to −32.1 (average = −26.2), for C₃¹⁸⁰ range from −14.6 to −31.7 (average = −25.6), and for C₄¹⁸⁰ range from −29.6 to −45.0 kcal·mol⁻¹ (average = −37.1).^{24,25,39,51,56} In regards to isoprene’s s-gauche conformation, Francisco-Marquez and coworkers determined PMP2/cc-pVTZ//MP2/6-311G** and BHandHLYP/6-311G(d,p)//BHandHLYP/6-311G(d,p) reaction energies along the C₁⁴¹:C₂⁴¹:C₃⁴¹:C₄⁴¹ pathways, with values of −44.7:−27.3:−26.6:−42.8 and −38.0:−21.0:−20.7:−36.1 kcal·mol⁻¹, respectively.⁵⁶ Our ΔE_zpv reaction energies fall within the range of previously reported C¹⁸⁰ pathway reaction energies, while being significantly lower than the average value of those calculations. A notable difference is seen for the C₁⁴¹ and C₄⁴¹ pathways, whose ΔE_zpv reaction energies are more positive than Francisco-Marquez and coworkers’ values. Considering all C¹⁸⁰ and C⁴¹ pathways, the most exothermic reaction follows the C₁⁴¹ pathway, which is more negative by 0.9, 2.0 and 4.1 kcal·mol⁻¹ relative to the C₄⁴¹, C₁¹⁸⁰, and C₄¹⁸⁰ pathways, respectively. However, based on the Boltzmann distribution at low temperatures, there should be very little if any s-gauche conformation available for reaction with the hydroxyl radical, making these pathways unlikely.

At atmospheric temperatures, the adducts along the C₁¹⁸⁰, C₄¹⁸⁰, C₁⁴¹ and C₄⁴¹ pathways are still favored according to our ΔG°_298K values, by a minimum value of 6.7 kcal·mol⁻¹ with respect to the C₂ and C₃ pathways. However, the reaction is, in general, less exothermic by an average of 8.4 kcal·mol⁻¹. Considering all pathways, the most exothermic reaction now follows the C₄⁴¹ pathway, which is more negative by 0.6, 2.5 and 4.7 kcal·mol⁻¹ relative to the C₁⁴¹, C₁¹⁸⁰ and C₄¹⁸⁰ pathways, respectively.

Conclusions

The first step in the atmospheric oxidation of isoprene consists of the formation of an adduct, with the hydroxyl radical adding to one of four carbon atoms on isoprene. We have shown that the use of MP2 and CCSD(T) theory is inappropriate when studying this reaction due to the reference wave function of the radical species; instead the use of Brueckner doubles with connected triples provides energies that are more trustworthy.

We were able to locate seven pre-reactive complexes that are minima on all eight pathways using the BHandHLYP theory, with reaction barriers in both the forward and reverse directions. These barriers disappear at the BD(T) theory level, with the exception of the C₂¹⁸⁰ and C₃¹⁸⁰ pathways, which present likely candidates for trapping in a low-temperature gas-phase experiment. For the barrierless pathways, we envision the potential energy surface guiding the collisions of isoprene and the hydroxyl radical such that it quickly passes through pre-reactive complexes and transition-state regions to form the adducts. At temperatures in the lower atmosphere, all pre-reactive complexes are no longer minima on the free energy surfaces; all transition state barrier values become positive, with the lowest to highest pathway energy barrier ordering being C₁¹⁸⁰<C₁⁴¹<C₂⁴¹=C₄¹⁸⁰<C₄⁴¹<C₃⁴¹<C₂¹⁸⁰<C₃¹⁸⁰, spanning an energy range from 3.8 to 6.0 kcal·mol⁻¹.

Considering all pathways, the most to least exothermic pathway for adduct formation at low temperatures is C₁⁴¹<C₄⁴¹<C₁¹⁸⁰<C₄¹⁸⁰≪C₂⁴¹<C₃⁴¹<C₂¹⁸⁰<C₃¹⁸⁰, spanning an energy range from −36.7 to −23.0 kcal·mol⁻¹. At higher temperature the order remains the same except C₄⁴¹ become more exothermic than C₁⁴¹, and the temperatures range from −28.8 to −14.4 kcal·mol⁻¹. Thermodynamically, the initial conformation of isoprene has a direct effect on which pathway the hydroxyl radical addition to isoprene reaction follows. Based on a Boltzmann distribution of isoprene, the C¹⁸⁰ pathways are most likely at low temperatures while all eight C¹⁸⁰ and C⁴¹ pathways are feasible at higher temperatures.