Dynamic weighting in Monte Carlo and optimization

Abstract

Dynamic importance weighting is proposed as a Monte Carlo method that has the capability to sample relevant parts of the configuration space even in the presence of many steep energy minima. The method relies on an additional dynamic variable (the importance weight) to help the system overcome steep barriers. A non-Metropolis theory is developed for the construction of such weighted samplers. Algorithms based on this method are designed for simulation and global optimization tasks arising from multimodal sampling, neural network training, and the traveling salesman problem. Numerical tests on these problems confirm the effectiveness of the method.

Metropolis Algorithm

Metropolis et al. (1) introduced the fundamental idea of Monte Carlo simulation of a system x by the (computer-simulated) evolution of a Markov process whose stationary distribution at equilibrium is the same as the Boltzmann distribution f(x) = (1/z) exp{−U(x)/t}. Here t is the temperature, U(⋅) is the energy of the system, and z is a normalizing constant. The transition from a current state x to a new state x′ is obtained as follows. First, draw y from a proposal transition function T(x → y) and compute the Metropolis ratio

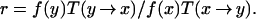If r > 1 then y is accepted as the new state, otherwise, accept y with probability r. If y is not accepted, set the new state x′ to be the old state x. This generates a series of states x_i, i = 1, 2, … . , which, after the system has equilibrated, can be regarded as correlated samples from the Boltzmann distribution. The expectation of any state function can be estimated by the sample average of the corresponding function values.

This method is currently one of the most versatile tools in scientific computation. It is indispensable in simulations tasks in statistical mechanics (2), and it plays an important role in protein folding (3), multiple sequence alignment (4), and chip design and machine learning (5).

A serious limitation of the Metropolis method is the inability of the system to escape from deep local energy minima. For the system to do this, it must move from a state of low energy to a state of much higher energy. However, the expected waiting time for such a move is roughly exponential in the energy difference. Thus there is a waiting time dilemma: either to wait forever in a deep local energy minimum or to have an incorrect equilibrium distribution.

One approach to avoid getting trapped by local minima is motivated by the fact that it is easier to escape from such traps if the system is at a higher temperature. In the method of simulated annealing (5), the system evolves according to the Metropolis rule, but the temperature is slowly reduced according to an “annealing scheme” from a high initial value to very low values as the simulation proceeds. However, unless the decrease of temperature is impractically slow, simulated annealing is still prone to be trapped by local minima, and recent attempts to exploit temperature variation have emphasized treating the temperature t as a dynamic variable that coevolves with the original system state x. Usually t takes value in a finite set t₁ > t₂ > … > t_k−1 > t_k, and the augmented system has a state vector (t, x) following an augmented Boltzmann density of the form α_if_i(x) where f_i is the density of the original system at temperature t_i, and α_i is a tunable constant. The Metropolis algorithm can again be used in the simulation of this augmented system. After reaching equilibrium, one selects only those augmented states with t = t_k and accepts the corresponding system state x as a sample value. This “simulated tempering” method had been applied successfully to the simulation of random field Ising models (6).

Sampling a Complexity Ladder

By considering a ladder of k temperatures, simulated tempering simultaneously simulates from k related systems with different levels of complexity. There is no reason why the different levels of complexity have to be generated by varying the temperature, and different ladders of complexity have been suggested in specific applications (7). A fruitful approach to construct the ladder is the sequential build-up approach (8). In this approach we think of approximating the original system by a system with a reduced number of degrees of freedom. The reduced system is again approximated by a system with a further reduced degree of freedom, until we reach a system of a manageable size. The augmented system now has a state vector (i, x_i) where i is the indicator for the complexity level and the dimension of x_i increases as i increases.

If the augmented system can move up and down the complexity ladder freely according to the Metropolis rule, then satisfactory results will be obtained for the highest complexity system. In practice, however, this is not easy to achieve. A major difficulty concerns the choice of k, the number of levels in the complexity ladder. Because the performance of the method depends on how freely the augmented system can move from one end of the complexity ladder to the other end, one must make sure that the waiting time for such a traversal of the ladder is not too large. Even in the ideal situation when the system behaves like a symmetric random walk along the ladder, the expected waiting time for a traversal is of order k². This puts a severe limit on how many levels of complexity we can afford to employ. On the other hand, unless we employ many levels, there will be large probability barriers between adjacent levels in the augmented system, making it practically impossible to accept transitions between certain levels according to the Metropolis rule. Thus, although the idea of sampling a complexity ladder is conceptually attractive, its usefulness is still severely limited by the waiting time dilemma.

Dynamic Importance-Weighting

The approach we propose as a way out of the waiting time dilemma can be described in loose terms as follows: If necessary, the system may make a transition against a steep probability barrier without a proportionally long waiting time. To account for the bias caused by such a transition, we compute an importance weight and record it along with the sampled state vector. At equilibrium, estimates for expectations are obtained by the importance-weighted average of the sampled values, rather than the simple average as in the Metropolis method.

In general, the importance weight w associated with a state x is itself a dynamic variable and may affect the next transition for the augmented system (w, x). Note that here x may already include other auxiliary variables such as the temperature variable in a simulated tempering setup. Unlike simulated tempering, however, the transition rule for this augmented system can no longer be obtained by the Metropolis method, because we do not have a specification of a target equilibrium distribution for (w, x). Instead, we propose to use invariance with respect to importance-weighting (IWIW, defined below) as a principle for designing valid transition rules. Let f(x) be a target density for the system x. A joint density g(w, x) is called correctly weighted if ḡ(x) = ∫ g(w, x)w dw as a function of x is proportional to f(x). A transition rule for the system (w, x) is said to satisfy IWIW if the joint density of (w, x) after a one-step transition remains correctly weighted whenever the initial joint density is correctly weighted. If we have independent identically distributed samples (w₁, x₁), (w₂, x₂), … . , (w_n, x_n) from a correctly weighted joint density, then the weighted average [of a state function h(x) over the sample]

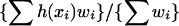will converge to the expectation of h(x) under the target density f.† IWIW is simply a requirement that the transition rule preserves this nice property for the joint density. We have designed many transition rules that satisfy IWIW exactly or approximately. The following are some useful examples.

(i) Type-R transitions. Draw y from a proposal transition function T(x → y) and compute the usual Metropolis ratio r. Let θ be an arbitrary function of (x, w), and a = wr/(wr + θ). With probability a, set x′ = y and w′ = wr/a, otherwise set x′ = x and w′ = w/(1 − a).

(ii) Type-Q transitions. Draw y from a proposal transition function T(x → y) and compute the usual Metropolis ratio r. Let θ as in (i) and u be an independent random variable uniformly distributed in [0, 1]. The computation of (y, r, u) is called a trial. The trial is said to be a success if u is less than a = min(1, wr/θ). Perform such a trial. If it is a success, set x′ = y, w′ = wr/a. If it is a failure, set x′ = x, w′ = w/q where q = 1 − p is the conditional probability of rejection of a proposal. If (1/q) is unknown, we can use an unbiased estimate of it based on further independent trials.

(iii) Type-M transitions. Draw x′ from an invariant transition function K(x → x′) and then set w′ = w. The resulting transition (w, x) → (w′, x′) then satisfies IWIW. Here by an invariant transition K(x → x′) we mean a transition function that leaves the target density f(x) unchanged after a one-step transition. Thus, if we apply a series of Metropolis transitions or Gibbs transitions on the state vector x and leave the weight w unchanged, then the result satisfies IWIW.

Type-M and type-R moves are exactly IWIW, but type-Q moves are only approximately so. However, in actual use, a type-Q move does not seem to produce any noticeable bias. When θ > 0, the weights in type-R and type-Q transitions have a tendency to increase if there are frequent rejections, and this eventually enables the sampler to escape from a deep local minimum. Thus, besides being essential for the computation of weighted estimates, the importance weights also facilitate faster mixing of the Markov chain. It is often necessary to alternate different types of moves (and different values of θ) in the same process to achieve efficient and stable mixing. Type-M moves are mainly used for transitions within a given complexity level, and type-R and type-Q moves are mainly used for transitions across complexity levels.

We usually perform the operations of stratification and trimming on the importance weights before computing the weighted estimate of the expectation of any state function h(x). First the sample points are stratified according to the value of the function h(x). The strata are of roughly the same size and within each stratum the variation of h(x) is small. The highest k% (usually k = 1) of the weights within each stratum are then trimmed to be the value of the (100 − k)th percentile of the weights within that stratum. In our experience, these operations induce negligible bias in the weighted estimate but can reduce its variance substantially. Note that the trimmed weights depend on the function of interest.

Multimodal Sampling

We test the methods on the following bimodal density:

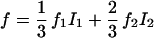where f₁ and f₂ are density functions on [−100, 100]⁹ having the following form:

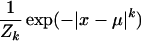and I₁ is the indicator function of the set {x₁ < 0}, I₂ is the indicator of {x₁ ≥ 0}. Here Z_k is a normalizing constant and k = 2 and 1.5 for f₁ and f₂, respectively. The centers of f₁ and f₂ are at −10 and 10, respectively, for the first coordinate, and at the origin for the 8 remaining coordinates. We will see that simulated tempering, which is normally a powerful method, turns out to be ineffective on this problem.

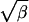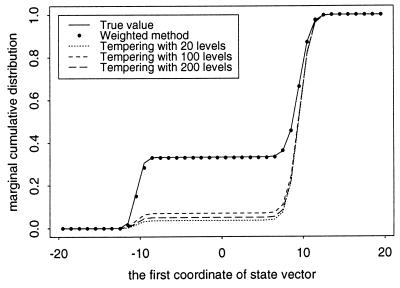
In applying simulated tempering in this example, we have used complexity ladders with 20, 100, and 200 levels. For each ladder, β = 1/t increases from a low value of 0.00001 to a high value of 1 geometrically by a constant ratio. The proposal function in each level is a multivariate normal distribution centered at the current position with covariance matrix σI, where σ = 0.05/ for the low-β levels and σ = 1.25/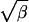 for the medium and high-β levels. Starting from the origin, we run simulated tempering until 4000 samples are obtained at β = 1. The results averaged over 50 independent runs are plotted in Fig. 1. Clearly the ratio of the two components is not estimated correctly. Although so many levels are used, simulated tempering fails in the simulation.

Figure 1.

Simulation from a bimodal distribution in nine-dimensional space. The two modes are separated along the first coordinate by a large region of almost zero probability. The cumulative distribution of the first component is presented together with estimates of it obtained by the weighted method and by the simulated tempering method with various temperature ladders. The mass due to the left mode is 0.333, which is well estimated only by the weighted method.

We also applied dynamic importance weighting to this example. The complexity ladder used is the same as the 20-levels (temperature) ladder used in simulated tempering. The proposal function is the same as that used by simulated tempering. Type-R transition is used for jumps between levels. After one new level is reached, 50 type-M transition steps are made within the same level. Starting from the origin, we run the weighted method until we reach β = 1 one thousand times. Averaging over 10 independent runs, we can obtain the correct estimation of the distribution (Fig. 1), with respect to both the relative weights of the component densities and the distributional shape within each component. The computation time used by the weighted method is about the same as that used by simulated tempering with 100 levels.

Training of Neural Networks

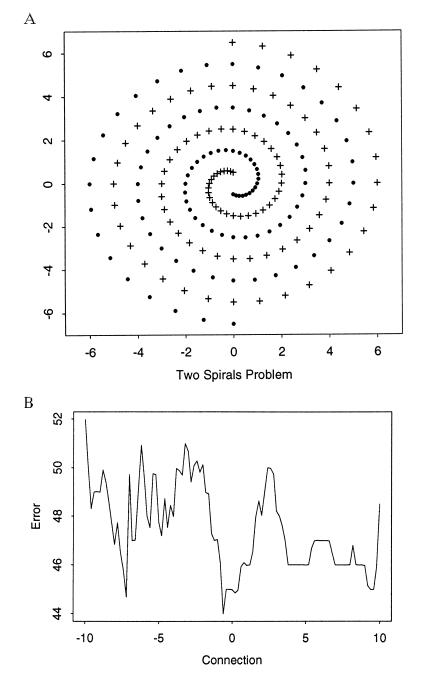
In a multilayer network, each unit (node) in a hidden layer independently processes the values fed to it by units in the preceding layer and then presents its output to units in the next layer for further processing. The output of any unit, except that of an input node, is a sigmoidal transform of the connection-weighted sum of its inputs. In supervised learning, there is a sample of training cases where, in addition to input values, ideal output values are also available. “Learning” is accomplished by choosing the connection strengths to make the network outputs match the ideal outputs as closely as possible on the training data. Currently, the most popular learning algorithm is the back-propagation algorithm and its variants (9). It is known, however, that back-propagation can fail badly in some situations. A famous example is the two-spiral problem shown in Fig. 2A, where conjugate gradient back-propagation learning with a layer of as many as 60 hidden units still yielded training errors larger than 4% (10). We have applied dynamic importance weighting to train a three-layer (25 hidden units) network for the two-spiral problem with 192 training cases. We used the sum of squares of fitting errors as the energy function, and sampled on a complexity scale of 4 temperatures. Because our objective was global optimization rather than sampling, the samples obtained at the lowest temperature were then subjected to further local iterative refinement by a conjugate-gradient-based search. Table 1 compares the performances of our weighted sampler, simulated annealing, and back-propagation. It is clear that the latter two essentially failed for this problem. Their poor performance is not too surprising when one examines Fig. 2B, where the energy around a particular local mode is plotted as a function of one of the connection strengths (with the other connection strengths fixed). The picture is typical of plots of this nature and it illustrates the extreme roughness of the energy landscape. Remarkably, the importance-weighted Markov process appears to have sampled the connections efficiently even in the face of such a complex energy landscape. We have also achieved perfect training with a 2–14-4–1 network. Thus, contrary to common belief, our results show that a standard multilayer feedforward architecture is capable of producing a classification rate better than that given by “cascade-correlation networks” which utilize “short-cut” connections (11).

Figure 2.

(A) The two-spirals problem. The 192 training cases correspond to the 192 points. For each case the two input values are the x and y coordinates of the point, and the ideal output value is either 0 or 1, depending on which spiral the point lies on. (B) Profile of the error surface corresponding to variation in one connection with the remaining connections at fixed values.

Table 1.

Performance comparison

Statistic	Weighted method	Simulated annealing	Back-propagation
Mean	14.9204	28.4318	47.7964
SD	3.3766	2.1833	0.4512
Minimum	6.016	25.5978	43.6813
Error number	6	33	81

For each method, the same network structure (2-25-1) and amount of computation time are used. Repeated random startings are used for simulated annealing and back-propagation. The mean, SD, and minimum are summary statistics of the energy of the configurations found by each method. The error number is the minimum number of misclassified training cases (of 192) attained by that method. 

Traveling Salesman Problem (TSP)

The TSP is the problem of finding the shortest tour through a set of J cities of specified locations so that each is visited once and only once. It is perhaps the most well known member of the class of NP-complete problems [hardest problems among those verifiable in polynomial time]. There are a number of large TSPs, some of them having known optimal answers, that can serve as challenging tests for newly proposed combinatorial optimization methods (ref. 12; see also the Website ftp://ftp.iwr.uniheidelberg.de/pub/tsplib).

To apply dynamic weighting to the TSP, we first create an ordering for the “sequential build-up” of the set of cities. This is done by starting with a randomly selected city and then adding cities one by one, and each time the city to add is the one having the maximum separation from the set of already ordered cities. This ordering can be achieved in low-order polynomial time. We then consider a sequence of TSPs of increasing level of complexity. At the lowest level we have a TSP with the first m₀ (m₀ = 15, for example) cities in the build-up ordering. At the next lowest level we add a block of the next m cities to get a slightly larger TSP. The block size m depends on the size of the full set and the number of levels we want to employ on the complexity ladder. In this way we build up a ladder of complexity consisting of TSPs on increasing subsets of the cities. Typically we use between 15 and 25 levels, and usually the size (I) of the TSP at the highest level of the ladder is still much smaller than the size J of the original TSP. In the numerical tests I is between 0.2J and 0.4J. We think of the I-city problem as an approximation to the J-city problem, in the sense that a good tour for the former can be regarded as an outline for the “global shape” of good complete tours for the latter problem. A natural approach is to generate such “global shapes” with probabilities reflecting the chance that they will lead to good complete tours, and then try to produce the complete tours by local refinement. Thus our global search strategy consists of two steps. First the I-city tours are sampled from a Boltzmann distribution with tour length as the energy. For each I-city tour generated this way, we use a greedy algorithm to insert the remaining cities, one by one according to the build-up order, until all J cities are added to the tour. In the sampling step, to add a city to a tour, consider the 15 (say) nearest neighbors on the tour to the city and sample a new path through these 16 cities. This new path when connected to the rest of the tour outside the neighborhood will then give a new tour. The new path is sampled from a distribution designed to mimic the local Boltzmann distribution whose energy is equal to the path length. To add a block of m cities to the tour, the cities are added one by one as described. An accept/reject decision is made after all m cities are added, and an importance weight is computed accordingly. Deletions of cities from a tour follow a similar procedure. All transitions are cross-level transitions. There is no Lin-type (13) uphill moves between the cross-level jumps because we want to see whether good performance can be achieved without such traditional heuristics. The final greedy fill-in of the remaining J − I cities is done by using sequential branch and bound search over a series of small (15 cities) path spaces.

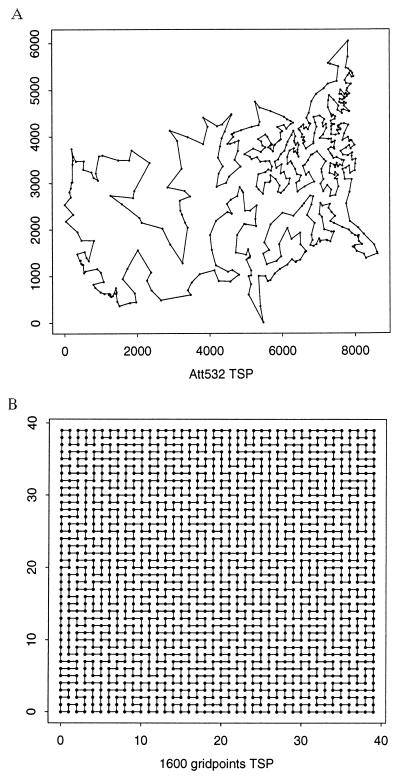
Fig. 3 presents the solutions found on two large TSPs: att532 and grid1600. The computation time is 4h and 10h respectively on an Ultrasparc I. For att532, our solution has an excess of 0.002 over the exact optimum. This is much better than reported solutions from other heuristic search methods except that of a special version of the genetic algorithm [with a mutation based on the very powerful Lin–Kernighan (14) moves] which gave a comparable excess. Our solution is exact for the grid1600 problem, which has not been solved by other heuristic search methods.

Figure 3.

(A) Our best solution for a 532-cities TSP. The tour length is 27,744, whereas the exact minimum is 27,686. (B) One of the exact minimal tours we found for a 1,600-cities problem.

Conclusion

We have introduced the importance weight as a dynamic variable into Markov-chain-based Monte Carlo methods. The condition of invariance with respect to importance weighting is proposed as a principle to guide the construction of the Markov transition rules. The dynamically weighted sampler can explore very rough energy surfaces more efficiently than the classical Metropolis sampler. Basically, the proposed scheme allows a trade-off between the length of the waiting time (to equilibrium) and the variability of the weights. Weighting is especially effective when used to facilitate cross-level jumps in a complexity ladder. In this paper we have outlined the basic theory and have provided numerical examples to demonstrate its utility. Further efforts will be needed to clarify the limiting behavior of the weighted process and to understand the optimal trade-off between the variability of the weights and the ease of relaxation.

ABBREVIATIONS

IWIW

invariance with respect to importance-weighting

TSP

traveling salesman problem