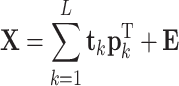Metabolomics approach for determining growth-specific metabolites based on Fourier transform ion cyclotron resonance mass spectrometry

Abstract

Fourier transform ion cyclotron resonance mass spectrometry (FT-ICR/MS) is the best MS technology for obtaining exact mass measurements owing to its great resolution and accuracy, and several outstanding FT-ICR/MS-based metabolomics approaches have been reported. A reliable annotation scheme is needed to deal with direct-infusion FT-ICR/MS metabolic profiling. Correlation analyses can help us not only uncover relations between the ions but also annotate the ions originated from identical metabolites (metabolite derivative ions). In the present study, we propose a procedure for metabolite annotation on direct-infusion FT-ICR/MS by taking into consideration the classification of metabolite-derived ions using correlation analyses. Integrated analysis based on information of isotope relations, fragmentation patterns by MS/MS analysis, co-occurring metabolites, and database searches (KNApSAcK and KEGG) can make it possible to annotate ions as metabolites and estimate cellular conditions based on metabolite composition. A total of 220 detected ions were classified into 174 metabolite derivative groups and 72 ions were assigned to candidate metabolites in the present work. Finally, metabolic profiling has been able to distinguish between the growth stages with the aid of PCA. The constructed model using PLS regression for OD₆₀₀ values as a function of metabolic profiles is very useful for identifying to what degree the ions contribute to the growth stages. Ten phospholipids which largely influence the constructed model are highly abundant in the cells. Our analyses reveal that global modification of those phospholipids occurs as E. coli enters the stationary phase. Thus, the integrated approach involving correlation analyses, metabolic profiling, and database searching is efficient for high-throughput metabolomics.

Electronic supplementary material

The online version of this article (doi:10.1007/s00216-008-2195-5) contains supplementary material, which is available to authorized users.

Introduction

Comprehensive metabolomics is clearly distinct from conventional metabolism studies in that it addresses whole cellular activities rather than just focusing on enzymes, reactions, or metabolites. Over the past decade methods that offer both high resolution and sensitivity for the measurement of a vast number of metabolites have been established and two major approaches, targeted and nontargeted metabolomics studies, have been developed in metabolome studies [1, 2]. Targeted metabolomics plays a crucial role in understanding the primary effects of genetics alternations based on restricted information of a class of metabolites, and analytical procedures often need to include processes for identification and quantification of selected metabolites. Only recent advances in mass spectrometry have allowed nontargeted metabolomics, which is intended for unbiased analyses such as mapping metabolite profiles in the whole cellular processes in given organisms.

Fourier transform ion cyclotron resonance mass spectrometry (FT-ICR/MS) is the best MS technology for obtaining exact mass measurements owing to its great resolution and accuracy [3, 4], and several outstanding FT-ICR/MS-based metabolomics strategies have been reported [5–10]. Development of a general scheme for FT-ICR/MS-based metabolic profiling, with the aid of its potential for the high resolution measuring power together with ion signal intensity information, should thus make a significant contribution to metabolomics studies. To attain the purpose of and to understand the cell system based on the components of metabolites, we apply chemometrics and bioinformatics approaches to FT-ICR/MS data. Among a variety of metabolomics strategies, FT-ICR/MS offers a unique opportunity in nontargeted metabolomics studies owing to its extreme accuracy (below 1 ppm) in the mass measurement. Thus, chemical formulas and molecular identities of metabolites can be predicted with the aid of high precision mass spectrometry (MS) data and can also be easily linked to reported metabolites.

Metabolomics research currently confronts a problem associated with high-throughput data acquisition technologies including chromatography-coupled mass spectrometry (MS) and FT-ICR/MS which have facilitated simultaneous detection and quantification of a large number of metabolite-derived peaks without metabolite assignment [11]; a very similar situation has arisen in genomics research in that technologies for determination of the nucleotide sequence in the whole genome has progressed without annotations of gene functions [12]. Progress in annotation of metabolites in metabolomics can bridge the gap between the data and their biological interpretation. The problem with annotation of metabolites is that there is only a piece of information about peaks corresponding to precise molecular weight for metabolite-derived ions in MS, but when we measure quantities of ions in a time series experiment, metabolite-derived ions such as isotope ions and multivalent ions could be categorized by correlations between ions originated from identical metabolites, which can lead to more precise annotation of ions. Thus, correlation analysis of ions may be a powerful approach to annotation of metabolites in metabolomics.

In the present study, we propose a procedure for metabolite annotation using the data obtained from FT-ICR/MS by taking classification of metabolite-derived ions into consideration. Here, we perform the nontargeted comprehensive analysis of metabolomics for the time series measurements in Escherichia coli, and discuss a metabolic profiling scheme on the basis of FT-ICR/MS analyses furnished with a bioinformatics scheme including data preprocessing, classification of ions originated from identical metabolites, and supervised and unsupervised learning algorithms for metabolomics.

Experimental

Strains and growth conditions

The strain used in this study was E. coli K-12 W3110. An aliquot (8 ml) of an overnight liquid culture of W3110 in LB medium at 37 °C was inoculated into in 2 l LB (pH 7.4) medium in a 3-l jar fermenter. Cells were grown continuously at 37 °C for ca. 12 h, adjusting the agitation speed to 300 rpm with fixed 2 l min⁻¹ air flow rate. Growth was monitored by measuring the optical density at 600 nm (OD₆₀₀).

Sample preparation

A culture medium was passed through a 0.45-μm-pore-size filter (Durapore Membrane, Millipore). Residual E. coli cells on the filter were washed with Milli-Q water and then plunged into 2 ml methanol [13]. After sonication for 1 min, the methanol solution was kept at 4 °C for ca. 20 h. The solution was then filtered through disposable membrane filter units (DISMIC-13JP, ADVANTEC), evaporated, and stored at −80 °C until use. Upon FT-ICR/MS analysis, the extracts were dissolved in 50% (v/v) acetonitrile/water. A set of 2,4-dichlorophenoxy acetic acid ([M−H]⁻ = 218.96212), ampicillin ([M−H]⁻ = 348.10235), 3-[(3-cholamidopropyl)dimethylammonio]propanesulfonic acid ([M−H]⁻ = 613.38920), and tetra-N-acetylchitotetraose ([M−H]⁻ = 829.32078) were used as the internal mass calibrants (IMCs) in the negative ion mode analysis.

FT-ICR/MS conditions

Mass analysis was done in the negative ion mode using an IonSpec Explorer FT-ICR/MS (IonSpec) equipped with a 7-T actively shielded superconducting magnet. Ions were generated from an ESI source with a fused silica needle of 0.005-inch i.d. Samples were infused using a Harvard syringe pump model 22 at a flow rate of 0.5 to 1.0 μl min⁻¹ through a 100-μl Hamilton syringe. All the experimental events were controlled using Omega8 software (IonSpec). Briefly, the potentials on the electrospray emitters were set to −3.0 kV for the negative electrosprays. The base pressure in the source region was approximately 5 × 10⁻⁵ torr (1 torr = 133.3 Pa). For the negative electrosprays, sample solutions were prepared in 50% (v/v) acetonitrile/water with 0.1% (v/v) of ammonium hydroxide. Ionized metabolites were accumulated for a period of 2,500–5,000 ms in a hexapole ion trap/guide and transferred through a radiofrequency-only quadrupole into the FT-ICR cell in the superconducting magnetic field, where they were again trapped. The direct current potentials in the negative ion mode analyses were 2 V during the ion accumulation and −2 V for the ion transfer into the FT-ICR cell. These ions trapped in the hexapole were extracted for transfer into the FT-ICR cell. In the negative ion modes, the potentials on the extraction plate were −12 V during the ion trapping and were reversed to 2 V for the extraction. The base pressure in the analyzer region was set to approximately 4 × 10⁻¹⁰ torr. ESI-MS spectra were acquired over the m/z range 55–1,000 from 1,024,000 independent data points. MS/MS analyses were done using the sustained off-resonance irradiation SORI-CID methods [14, 15]. SORI Rf was set at 0.5–1.5 V, and the N₂ collision gas was used with a 400-ms pulse.

FT-ICR/MS data processing and data analyses

The first requirement for the success of metabolomics is the ability to mine the generated data and to perform reliable and comparative analysis. To attain this, we have developed a bioinformatics scheme (DrDMASS+) consisting of four stages: (i) peak correction, (ii) multivariate data processing, (iii) unsupervised learning such as principal component analysis (PCA) and batch-learning SOM (BL-SOM), and (iv) supervised learning such as partial least squares (PLS) regression. DrDMASS+ and its instruction manual are freely available at http://kanaya.naist.jp/DrDMASSplus/.

• (i)Peak correction. Though FT-ICR/MS affords extremely high resolution m/z values, analytical data fluctuations are generally associated with the m/z values at the three or four decimal places level. So, initially, appropriate m/z values must be estimated from the observed m/z values. The experimental m/z values of the IMCs were fixed to their theoretical values, and the m/z error calibration data were reflected in the m/z compensation for all other ion species in each spectral scan.
• (ii)Multivariate data processing. After compensating m/z values, ion peak matching among ten independent scans was done for repeated identifiable m/z values. The threshold levels of ion appearance frequencies were freely adjustable. The intensity values of repeatedly observed ions were converted into percentage values of total ion intensity. Thus, metabolomics data from a single biological sample consisted of averaged m/z values with intensity information from ten spectral scans.
• (iii)Unsupervised learning. PCA is a multivariate method to project a distribution of data points in a multidimensional space into a space of fewer dimensions and BL-SOM is a method to classify such data points into groups (grids) accommodating similar decrease/increase patterns [16, 17].
• (iv)
  Supervised learning. PLS is a method for linearly relating a data matrix X (M × N) to a vector y (M × 1) where M and N represent the number of samples and parameters, respectively. The PLS model is represented by Eqs. (1) and (2).

  1

2

Here, p _k and q _k are called the loading vector of X, and the coefficient of y for the kth component, respectively. L is the number of components and t _k is a score vector for the kth component. E (M × N) and e (M × 1) represent the residual matrix and vector, respectively. The number of PLS components, L, is determined to maximize a predicted correlation coefficient (R _pred) by leave-one-out cross-validation for each component according to Eq. (3):

3

Here, y _obs is an experimental y value, y _pred is a predicted y value, and _obs is the mean of y _obs. The PLS equations (Eqs. (1) and (2)) can also be transformed into a linear form represented by Eq. (4) [18]:

4

Here, b is a regression coefficient vector and its elements are represented by b _j (j = 1,2,...,N).

DPClus

DPClus is a graph clustering software that can extract densely connected clusters using an algorithm that is based on density and periphery tracking of clusters [19]. It is also necessary to provide a value of minimum density we allow for the generated clusters (d), a minimum value for cluster property that determines the nature of periphery tracking (cp _in), and a minimum number of objects that we want in a cluster. DPClus is freely available at http://kanaya.naist.jp/DPClus/.

Species–metabolite relationship database

We have accumulated the information of 41,644 species–metabolite pairs encompassing 21,118 metabolites and 13,094 species in the KNApSAcK database (as of 1 February 2008) [20]. Information on metabolites in the database can be searched by metabolite name, organism, molecular weight, molecular formula, and mass spectral data taking the ionization modes ([M+NH₄]⁺, [M+Na]⁺, [M+K]⁺, [M+H]⁺, and [M−H]⁻) into consideration. Furthermore, the KNApSAcK package installed in the user’s computer provides tools for analyzing their own datasets of mass spectra provided the files that contain the data are prepared according to the program’s instructions. This database system and its online manual are freely available at http://kanaya.naist.jp/KNApSAcK/.

Results and discussion

Data processing of FT-ICR/MS: from data acquisition to assessment of cellular conditions according to metabolite composition

The concept of FT-ICR/MS data processing from data acquisition of a time series experiment to describe cellular conditions from exponential to stationary growth phase by metabolites consists of five steps (Fig. 1). Time series experiments are a popular method for studying a wide range of biological systems. In bacteria, there are a few reported papers which comprehensively analyzed bacteria intrametabolites [21]. However, to our knowledge there are no papers about bacteria which address total intrametabolic profiling. In order to elucidate intrametabolite profiling in a whole cell, we performed the time series experiment in E. coli (Fig. 1a). Samples were collected at 135, 150, 170, 190, 250, 420, 480, and 720 min postinoculation (which correspond to T1, T2, T3, T4, T5, T6, T7, and T8, respectively), and metabolites were extracted, and measured by FT-ICR/MS. FT-ICR/MS raw data were processed for differential metabolomics according to the peak correction and peak matching of the DrDMASS+ program. We selected m/z values whose appearance frequencies were higher than 50% among ten scans. Thus, differential metabolomics was studied in terms of corrected m/z values with average signal intensities of reproducible ions from ten independent spectral data. The observed m/z values for ions individual measurements in the time series experiment were calibrated with those of internal standards [8]. Peak matchings were carried out to make a matrix consisting of intensities for m/z values and time points (Fig. 1b) utilizing a metabolomics platform, based on FT-ICR/MS incorporating the metabolite profiling tool DrDMASS+. After the processing step, 220 independent ions were detected in the negative ion mode analysis. Thus, our time series data matrix consists of intensities of 220 independent ions corresponding to metabolites for eight measurement points.

Fig. 1.

Data processing scheme consisting of five steps. a Time series experiments in E. coli. The growth curve shows eight time points (135, 150, 170, 190, 250, 420, 480, and 720 min postinoculation corresponding to T1, T2, T3, T4, T5, T6, T7, and T8, respectively), at which samples were taken, and metabolites were extracted, and measured by FT-ICR/MS. b Data structure after data preprocessing by DrDMASS+ including peak correction and peak matching. M and s shows the number of detected ions and samples, respectively. c Classification of ions into metabolite derivative groups by DPClus based on the correlations between detected ions. d Annotation of ions by searching metabolite databases (KNApSAcK and KEGG). e Assessment of cellular conditions according to metabolite composition by using multivariate analyses

There are many ions originated from identical metabolites, i.e., isotope ions and multivalent ions. If detected ions are classified into identical metabolite-derived ion groups, we can use further information for annotating chemical structures in metabolites because isotope pattern allows us to estimate the number of carbons in molecular formulas for metabolites, and the real number of metabolites included in samples can also be estimated. This step was carried out by DPClus software (Fig. 1c). After classification of ions into specific metabolite derivative groups, we performed annotation of ions as metabolites using public natural compound databases, KNApSAcK [20] and KEGG [22–24] (Fig. 1d), and cellular conditions were characterized by the composition of metabolites using two approaches, supervised and unsupervised learning. Cellular condition could be assessed by the metabolite composition using principal component analysis (PCA), and the relationship between cell densities and the metabolite composition, reflecting transition from exponential to stationary phases, could be understood by using partial least squares (PLS) regression (Fig. 1e). Marker metabolites significant in exponential and stationary growth were determined using PLS regression.

Classification of ions into metabolite derivative groups

The difference of m/z value between isotope ions originated from carbon atom (1.0033 u) is a clue for determining whether or not the ions are originated from identical metabolites. Furthermore, ions, originated from identical metabolites, occurring in different ion valence are also detected. Isotope intensity pattern of a metabolite in an MS chart can serve as a powerful additional constraint for removing wrong elemental composition candidates [25]. When intensities of ions are correlated to each other in a time series experiment, those ions would be expected to be originated from an identical metabolite. Tautenhahn et al. [26] successfully combined highly correlated pairs of mass signals in LC-MS to chemical relation hypothesis groups. Thus, taking into consideration the differences of m/z values for ions and correlation of time series profiles of ions, isotope ions can be classified into metabolite derivative groups, which lead to estimation of molecular formula of metabolites. To attain this, we visualized all correlations in a time series experiment between ions. Pairwise ion–ion correlations were calculated by Pearson’s correlation coefficient (r) [27]. We extracted a set of 742 unique binary relations involving 148 ions by the threshold r ≥ 0.9 (p < 2.3 × 10⁻³, n = 8) and visualized this by using the graph-clustering method called DPClus. Out of total 220 detected ions, 72 ions do not show significant correlation with other ions. Figure 2 shows the configuration of the 742 relations including 148 ions assigned to 11 isolated clusters (ID = 1 to 11). Two largest isolated subgraphs consisting of 43 and 28 ions, respectively, can be characterized by six clusters (ID = 1−1 to 1−6) and three clusters (ID = 2−1 to 2−3), of size > 2, which are all complete graphs where an edge connects every pair of distinct vertices within the same cluster. Ions assigned to multiple complete subgraphs are depicted by blue nodes. Relations between ions and cluster IDs are listed in the Electronic supplementary material (Table S1).

Fig. 2.

Correlation analyses based on the graph clustering. A graph sharing correlation between ions and densely connected clusters. Each boxed black number (1–11) corresponds to a cluster ID detected by the graph clustering. Each node corresponds to an ion with m/z value indicated. The colors of nodes represent the ions within a cluster (green), the common ions among clusters (blue), and the other ions (silver). The intracluster edges are green and intercluster on the other edges are orange. The thick blue broken circles show the clusters 1–1, 1–2, 1–3, 1–4,5, 1–6, 2–1, 2–2, and 2–3. The red dotted circles show isotope ions. PG1–PG10 are shown in red. M-1to M-17 near the nodes are the identities of ions which have candidates according to the KNApSAcK search: M-1, dTDP-L-rhamnose; M-2, BE 32030B; M-3, ADP-L-glycero-beta-D-manno-heptopyranose; M-4, octanoic acid; M-5, dTMP; M-6, UDP-D-glucose, UDP-D-galactose; M-7, UDP-N-acetyl-D-mannosamine, UDP-N-acetyl-D-glucosamine; M-8, dTDP; M-9, kinamycin A, kinamycin C; M-10, ATP, dGTP; M-11, omega-cycloheptanenonanoic acid; M-12, oleic acid, cis-11-octadecanoic acid, omega-cycloheptylundecanoic acid; M-13, adenosine 3′,5′-bisphosphate, ADP, dGDP; M-14, NAD; M-15, UDP; M-16, NADH; M-17, antibiotic MI 178–34F18A2, antibiotic MI 178–34F18C2

We assume that ions which belong to the same cluster and have appropriate m/z difference of ¹³C and certain valences could be considered to have originated from identical metabolites. Initially, to determine isotopic ion pairs, we searched ion pairs under conditions that the ion pairs have not only correlation with each other but also appropriate m/z difference for certain k-valence, i.e., M⁻+H⁺ = 2M²⁻+2H⁺ = ... = kM^k−+kH⁺. Furthermore, to determine ion pairs originated from identical metabolites, our search was extended to ions other than isotope ions. Thus, 19 metabolite derivative groups consisting of multiple ions including isotope and multivalent ions were identified (Fig. 2, surrounded by red broken lines). In total, 148 ions were classified into 102 metabolite derivative groups which include isotope ions and multivalent ions.

Annotation of ions

The concept of metabolite annotation comprises mass spectral annotation and biological metadata annotation including description of actual experimental conditions that help unravel the biological role of metabolites by their changes in levels in response to genetic and environmental perturbation [28, 29]. In the present study, we use the term ‘metabolite annotation’ to describe a procedure of providing chemical characterization to individual metabolite-derived ions; thus our annotation procedure can be classified as a mass spectral annotation, which is important for interpretation of cellular conditions according to metabolite compositions. There are two distinct ways to provide metabolite annotation: an exhaustive computation of all chemically possible isomeric structures or a query of databases for known natural compounds. In the present study, we annotated ions based on the latter method using additional evidence of chemical information such as MS/MS fragmentations. Three publicly available databases concerning natural products are PubChem [30], KEGG, and KNApSAcK. The PubChem database is comprised of records for over 19.6 million compounds with over 11 million unique structures including small molecules, particularly diagnostic and therapeutic agents. In our study, ions are natural compounds and it is better to search the databases that contain natural products. In KEGG, the metabolic pathways are constructed by interspecies gene relations such as orthologs and paralogs, so metabolite–species relations can be obtained via information of enzymes. The KEGG database focuses on metabolites related to known metabolic pathways and includes around 13,000 metabolites. On the other hand, the relationships between metabolites and their biological origins have been addressed systematically in the KNApSAcK database, which has accumulated 41,644 records (species–metabolite pairs) encompassing 21,118 metabolites and 13,094 species (as of 1 February 2008). The total number of secondary metabolites for which molecular structures have been elucidated is estimated to be 50,000 [31]. So, around 42% of metabolites have been compiled in the database and this is considered to be enough for searching candidates including species information. As the first stage, we searched metabolites in two databases (KEGG and KNApSAcK) by molecular weights estimated from m/z values for ions.

Isotope patterns allow us to estimate the number of carbons in molecular formulas for metabolites because natural compounds on earth reflect the natural abundance of stable elemental isotopes, such as ¹³C (which is found at approximately 1.07% of the most frequent isotope ¹²C) [32]. The abundance of isotope ions is dependent on the actual elemental composition and can therefore serve as a powerful filter in calculating unique elemental compositions from mass spectral data [33]. In view of rigorous atomic mass, mass differences between isotopes of atoms are not identical, e.g., mass differences between ¹H and ²H, ¹²C and ¹³C, and ¹⁴N and ¹⁵N are 1.0063 u, 1.0033 u, and 0.9970 u, respectively. Several software methods calculate isotope patterns of compounds based on the assumption that mass differences of atomic isotopes for different atoms can be considered to be identical [34]. Because of the extent of high resolution in FT-ICR/MS, we cannot neglect the isotope differences, i.e., it could be possible to separately detect each isotope ion containing ²H, ¹³C, ¹⁵N and so on. But intensities of isotope compounds with isotope atoms other than ¹³C would be too small to consider, because the probability of ions containing ²H, ¹⁵N, and so on is much lower compared with ions containing ¹³C. So assuming that an isotope ion M+1 is derived from only ¹³C, a relative ratio of M (¹²C) and M+1 (¹³C) separated by the difference (1.0033 u) of m/z values for two peaks can allow us to estimate how many carbon atoms a compound should contain without prior information about the structure. In addition to this, MS/MS fragmentation patterns provide structural information of metabolites, so we performed MS/MS analysis for the five peaks corresponding to m/z = (A) 662.1037, (B) 719.4868, (C) 733.5056, (D) 747.5183, and (E) 761.5293.

In ion A, the intensity of m/z = 662.1037 is highly correlated with those of m/z value 663.1080 in cluster 6, so those would be isotope ions, i.e., m/z = 662.1037 (M) and m/z = 663.1080 (M+1) because of the difference 1.0043. The number of carbon atoms estimated by the intensity ratio of 662.1037 to 663.1080 was in the range of 19 and 21 at the 99% confidence interval of the t test (Table 1). We got 845 possible molecular formulas consisting of six types of atoms (C, H, O, N, P, and S) in the range of ±0.01 for an ion with m/z = 662.1037. After reducing candidates that do not have the estimated number of carbon atoms, we could get 92 possible candidates, i.e., about 89% candidate molecular formulas could be considered to be not true. The candidate metabolite for ion A according to the KNApSAcK search (no hits in KEGG database) is nicotinamide adenine dinucleotide (NAD) (C₂₁H₂₇N₇O₁₄P₂), and ions obtained from MS/MS analysis (m/z = 540.0782, 328.0532) for ion (A) are consistent with the fragmentation pattern of NAD (Fig. 3a), i.e., fragmentation ions with m/z = 540.0782 and 328.0532 could be assigned to ([C₁₅H₂₀N₅O₁₃P₂]⁻) [theoretical m/z = 540.0533] and ([C₁₀H₁₁N₅O₆P]⁻) [theoretical m/z = 328.0447], respectively. Thus, we annotated the ions corresponding to m/z = 662.1037 and 663.1080 in cluster 6 as NAD and also m/z = 331.0586 in cluster 6 as a doubly charged ion ([M−2H]²⁻) of NAD.

Table 1.

Summary of reduction of candidates using the isotope pattern in ions in MS/MS analyses

Ion ID	Cluster ID	Monoisotope (M)	Isotope (M+1)	Difference	Number of candidates±0.01	Estimated carbon number	Number of estimated candidates	Element ratio	Candidate	Actual number of carbon atoms
A	6	662.1037	663.1080	1.0044	845	19–21	92	90	NAD	21
B	1	719.4868	720.4917	1.0048	146	36–40	33	33	PG1	38
C	2	733.5056	734.5087	1.0032	167	38–44	34	34	PG2	39
D	1	747.5183	748.5227	1.0044	175	39–40	12	12	PG3	40
E	2	761.5293	762.5340	1.0047	219	28–60	102	102	PG4	41

M ‘monoisotope’ column corresponds to [M−H]⁻ in the negative ion mode analysis

Fig. 3.

MS/MS analyses of the five ions in the negative ion mode analysis. [M−H]⁻ corresponds to the detected ion. a Fragmentation pattern and chemical structure of nicotinamide adenine dinucleotide (NAD) ion with m/z = 662.1037. b–e Fragmentation patterns of phosphatidylglycerols 1–4 (PG1–PG4) ions with m/z = 719.4868, m/z = 733.5056, m/z = 747.5183, and m/z = 761.5293. R₁ and R₂ correspond to fatty acids

Next, we annotated four selected monoisotope ions m/z = (B) 719.4868, (C) 733.5056 (D) 747.5183, and (E) 761.5293. Though the candidate metabolites could not be obtained by the database search, fragmentation ions for those were obtained by MS/MS analyses in Fig. 3b–e. In the MS/MS spectrum corresponding to the ion with m/z = (B) 719.4868 (Fig. 3b), two peaks for fragment ions (e.g., m/z = 253.2181 and 255.2337) could be assigned to an unsaturated fatty acid (C₁₆H₃₀O₂) [theoretical m/z = 253.2167 ([R₂O]⁻)] and a saturated fatty acid (C₁₆H₃₂O₂) [theoretical m/z = 255.2324 ([R₁O]⁻)], indicating that the ion with m/z = 719.4868 is a phosphatidylglycerol (PG). All ions (B–E) possess some common identifiable peaks (e.g., m/z = 255.2337, 391.2260, 465.2628, and 483.2735 in Fig. 3b), suggesting that they are similar types of molecules, i.e., four ions, B–E, referred to as PG1 to PG4, respectively, would be different types of PGs summarized in Fig. 4a. The numbers of carbon atoms estimated at the 99% confidence interval of the t test were also true for all four ions, suggesting that identification of isotope ions based on the graph clustering and estimating the number of carbon atoms by the confidence interval of the t test could also be reliable to reduce the number of candidate molecular formulas. We also checked the effect of other constraints for reducing candidates, i.e., using element ratio constraints (H/C 0.2−3.1, O/C 0–1.2, N/C 0–1.3, P/C 0–0.3, and S/C 0–0.8) [25], but there was no impact after reducing by the t test (element ratio column in Table 1), suggesting that if we get the isotope pattern data for a metabolite in a time series, the relative ratio of isotope ions (M and M+1) can efficiently narrow down candidate molecular formulas even without other constraints. Though incorporating chromatographic separation systems into the FT-ICR/MS system is helpful to estimate the relative ratio of isotope ions and also to predict the candidate molecular formula of unknown ions in a single measurement, time series data set can also ensure the possibility of candidate molecular formulas from a statistical perspective, i.e., the confidence interval of the t test.

Fig. 4.

Summary of phosphatidylglycerols detected in this study. a Molecular structures of PG1–PG4 determined by MS/MS analyses. Chemical structures in left, middle, and right columns correspond to substructure X₁, X₂, and X₃ of phosphatidylglycerols, respectively. b Relation of mass differences among PG1 to PG10. PG xx:y headgroups, xx total number of carbons in the fatty acid chains, y number of double bonds, c cyclopropane, CFA cyclopropane fatty acid formation, US unsaturation. Theoretical Δ(CH₂)₂, CFA, and US are 28.0313, 14.0157, and 2.0157, respectively

It has been reported that PGs are composed of various molecular species [35]. In the present study, another six metabolite derivative groups can be annotated as PGs by following three ‘rules’ in fatty acid metabolism (Fig. 4b): (1) Cyclopropane fatty acid (CFA) formation occurs as one of the modifications of phospholipids [36, 37]. A mass difference of 14.0157 corresponding to CFA was obtained in five pairs of PGs (PG1 and PG2, PG3 and PG4, PG5 (m/z = 691.4588) and PG6 (m/z = 705.4757), and PG7 (m/z = 745.5045) and PG8 (m/z = 759.5242), and PG9 (m/z = 773.5375) and PG10 (m/z = 787.5556)). (2) An elongation process occurs in fatty acids [38], i.e., a mass difference of 28.0313 u corresponds to one cycle of two-carbon addition in fatty acid biosynthesis, which was obtained in six pairs of PGs (PG5 and PG1, PG1 and PG3, PG7 and PG9, PG6 and PG2, PG2 and PG4, and PG8 and PG10). (3) A desaturation process, i.e., a mass difference of 2.0157 was obtained in two pairs of PGs (PG3 and PG7, and PG4 and PG8). So, annotation of PG5 to PG10 could be validated by enzyme reactions in lipid metabolism.

We searched the other 174 ions using KNApSAcK, and obtained 163 metabolite candidates from the search of the entire metabolite inventory in the database. Based on the species–metabolite relationship and MS/MS analyses above, we were finally able to assign 33% of 220 detected ions to candidate metabolites. If we restrict the search to only bacteria–metabolite relations of the KNApSAcK database, then we find 26 ions are related to 38 metabolites (Table 2). Out of these, there is only one whose candidates have different molecular formulas. The other 25 ions correspond to unique elemental compositions, suggesting that the information of species–metabolite relationship is efficient to extract useful lists of candidate metabolites. In this study, the percentage of ions annotated to metabolite candidates is much higher than that in the case of a plant reported by Nakamura et al. (10% of peaks in Arabidopsis thaliana) [9].

Table 2.

Summary of candidates for ions based on KNApSAcK search using bacteria–metabolite relationship

Detected m/z a	Theoretical m/z	Molecular formula	Exact mass	Error	Candidate	Species
72.9878	73.9951	C2H2O3	74.0004	0.0053	Glyoxylic acid	Escherichia coli
143.1080	144.1153	C8H16O2	144.1150	0.0003	Octanoic acid	Escherichia coli
253.2137	254.2210	C16H30O2	254.2246	0.0036	omega-Cycloheptanenonanoic acid	Alicyclobacillus acidocaldarius
253.2185	254.2258	C16H30O2	254.2246	0.0012	omega-Cycloheptanenonanoic acid	Alicyclobacillus acidocaldarius
281.2444	282.2516	C18H34O2	282.2559	0.0042	Oleic acid	Escherichia coli
		C18H34O2	282.2559	0.0042	cis-11-Octadecanoic acid	Lactobacillus plantarum
		C18H34O2	282.2559	0.0042	omega-Cycloheptylundecanoic acid	Alicyclobacillus acidocaldarius
297.2410	298.2482	C18H34O3	298.2508	0.0026	alpha-Cycloheptaneundecanoic acid	Alicyclobacillus acidocaldarius
297.2467	298.2540	C18H34O3	298.2508	0.0032	alpha-Cycloheptaneundecanoic acid	Alicyclobacillus acidocaldarius
297.2516	298.2589	C18H34O3	298.2508	0.0081	alpha-Cycloheptaneundecanoic acid	Alicyclobacillus acidocaldarius
321.0506	322.0579	C10H15N2O8P	322.0566	0.0013	dTMP	Escherichia coli K12
346.0570	347.0643	C10H14N5O7P	347.0631	0.0012	AMP	Escherichia coli
		C10H14N5O7P	347.0631	0.0012	3′-AMP	Escherichia coli
		C10H14N5O7P	347.0631	0.0012	dGMP	Escherichia coli
401.0168	402.0241	C10H16N2O11P2	402.0229	0.0012	dTDP	Escherichia coli
402.9962	404.0035	C9H14N2O12P2	404.0022	0.0013	UDP	Escherichia coli
426.0237	427.0310	C10H15N5O10P2	427.0294	0.0016	Adenosine 3′,5′-bisphosphate	Escherichia coli
		C10H15N5O10P2	427.0294	0.0016	ADP	Escherichia coli
		C10H15N5O10P2	427.0294	0.0016	dGDP	Escherichia coli
454.0391	455.0464	C20H19Cl2NO7	455.0539	0.0075	Antibiotic MI 178–34F18A2	Actinomadura spiralis MI178–34F18
		C20H19Cl2NO7	455.0539	0.0075	Antibiotic MI 178–34F18C2	Actinomadura spiralis MI178–34F18
458.1112	459.1185	C15H22N7O8P	459.1267	0.0083	Phosmidosine B	Streptomyces sp. strain RK-16
495.1039	496.1112	C24H20N2O10	496.1118	0.0006	Kinamycin A	Streptomyces murayamaensis sp. nov.
		C24H20N2O10	496.1118	0.0006	Kinamycin C	Streptomyces murayamaensis sp. nov.
505.9908	506.9981	C10H16N5O13P3	506.9957	0.0023	ATP, dGTP	Escherichia coli
547.0756	548.0829	C16H26N2O15P2	548.0808	0.0020	dTDP-L-rhamnose	Escherichia coli
565.0503	566.0576	C15H24N2O17P2	566.0550	0.0025	UDP-D-glucose	Escherichia coli
		C15H24N2O17P2	566.0550	0.0025	UDP-D-galactose	Escherichia coli
606.0775	607.0848	C17H27N3O17P2	607.0816	0.0032	UDP-N-acetyl-D-mannosamine	Escherichia coli
		C17H27N3O17P2	607.0816	0.0032	UDP-N-acetyl-D-glucosamine	Escherichia coli
618.0897	619.0970	C17H27N5O16P2	619.0928	0.0042	ADP-L-glycero-beta-D-manno-heptopyranose	Escherichia coli
662.1037	663.1109	C21H27N7O14P2	663.1091	0.0018	NAD	Escherichia coli
664.1095	665.1168	C21H29N7O14P2	665.1248	0.0080	NADH	Escherichia coli
741.4729	742.4801	C32H62N12O8	742.4814	0.0012	Argimicin A	Sphingomonas sp.
786.4712	787.4785	C41H65N5O10	787.4731	0.0054	BE 32030B	Nocardia sp. A32030
853.3166	854.3239	C41H46N10O9S	854.3170	0.0069	Argyrin G	Archangium gephyra Ar 8082
		C45H56Cl2N2O10	854.3312	0.0073	Decatromicin B	Actinomadura sp. MK73–NF4
		C39H50N8O12S	854.3269	0.0030	Napsamycin C	Streptomyces sp. HIL Y–82,11372

^aValues correspond to the [M−H]⁻ ion in the negative ion mode analysis

Cellular conditions assessed according to metabolite composition

Figure 5 shows (a) the growth curve, (b) the number of ions detected in each time point, and (c) expression profiles of metabolites in clusters 1–5. The number of ions detected in each cluster decreases toward T6 and after that increases toward T8, suggesting that after the exponential phase, composition of metabolites in E. coli would be largely changed at T6.

Fig. 5.

a Growth curve. b Time series change of total number of detected ions in each time point. c Average expression profiles of ions in clusters 1–5. Error bars shows standard deviation in each time point

Ions in clusters 5 and 3 correspond to ion accumulation in T2 and T3 at the exponential phase (Fig. 5c), respectively, suggesting that these metabolites would be necessary only at certain cell states. A candidate for the ion with m/z = 281.2444 in cluster 5 obtained by KNApSAcK searching is oleic acid (M-12 in Fig. 2; error of m/z = 0.0042) which is a precursor of phospholipids and has one double bond, suggesting that biosynthesis of fatty acid with double bond might occur in the exponential but not stationary phase, and other ions in cluster 5 would be compounds in a pathway related to fatty acid biosynthesis.

Candidates for the ion with m/z = 565.0503 (M-6) in cluster 3 are UDP-D-glucose and UDP-D-galactose. Candidates for the ion with m/z = 606.0775 (M-7) are UDP-N-acetyl-D-mannosamine and UDP-N-acetyl-D-glucosamine, which are precursors of lipopolysaccharides (LPS) [39], suggesting that LPS biosynthesis would occur only in the exponential phase and relate to abundances of UDP-D-glucose and UDP-D-galactose, and other ions in cluster 3 would be compounds related to LPS biosynthesis. A candidate for the ion with m/z = 143.1080 in cluster 3 is octanoic acid (M-4), which is the direct precursor of a vitamin, lipoic acid, and is also an exponential phase-specific metabolite. E. coli contains a pool of octanoic acid which can act as a substrate for lipoate ligase during lipoate starvation of a lipoic acid auxotroph [40]. The accumulation of octanoic acid at stage T3 would be needed in the exponential phase to prepare biosynthesis of vitamins. Ions in cluster 4 correspond to ion accumulation in T7 at the stationary phase (Fig. 5c), suggesting that ions in cluster 4 would be compounds related to the stationary phase.

According to profiles in Fig. 5c, clusters 1 and 2 are exponential and stationary phase specific, respectively. It is well known that phospholipid production decreases dramatically at the stringent response [41, 42], and the bulk of CFA synthesis occurs as cultures enter the stationary phase of growth [38]. Those facts are consistent with the structures of PG2, PG4, PG6, PG8, and PG10 in cluster 2 being CFA forms of PG1, PG3, PG5, PG7, and PG9 in cluster 1, respectively. In addition to this, CFA synthesis occurs in a broad range of phosphatidylglycerols after T5. Thus, cellular conditions of E. coli could be explained in terms of the composition of metabolites.

Unsupervised learning such as PCA and BL-SOM makes it possible to examine metabolic phenotyping of seedlings treated with different herbicidal chemical classes for pathway-specific inhibitions [8] and accurate classification of genes based on time series expression profiles which led to the prediction of gene functions [5, 6, 43]. Figure 6a shows the PCA projection of measurement points in time series data. The proportions, that is, percent variances to total variance, are 94.3% and 2.4% for the first and second principal components (PC1 and PC2), respectively. So the first two principal components, which can explain 96.7% of total variance, are enough to examine the differences in eight time points. The distribution of eight time points in the first two PCs as shown in Fig. 6a implies that time points are clearly classified into two groups, an early group consisting of T1, T2, T3, T4, and T5, and a late group consisting of T6, T7, and T8, suggesting that the different growth stages could be represented by the metabolomics data. The former and latter roughly correspond to exponential and stationary phases in the growth curve of E. coli. This result shows that the metabolite profile in E. coli seems to be totally shifted from T5 to T6, which is also consistent with the transient point in the number of detected ions in Fig. 5b.

Fig. 6.

PCA and PLS analyses. a Plot of eight time points using the first two PCs and b intensity of regression coefficients when the PLS model equation is transformed into a linear regression-like formula. The metabolites written in red are reported metabolites in E. coli. The metabolites written in black are reported metabolites in other bacteria species

To directly relate composition of metabolites to cellular conditions, we applied partial least squares (PLS) regression to the metabolite profiling data. PLS regression provides a quantitative model to estimate the cellular conditions based on the composition of metabolites. So in the present study, we focused on the PLS model to estimate cellular conditions from exponential to stationary phase based on intensities of m/z values in FT-ICR/MS and examined quantitative differences of metabolites based on the PLS model. Growth of bacteria can be generally monitored by measuring the optical density at 600 nm (OD₆₀₀). A linear model for estimating the OD₆₀₀ values according to the metabolite quantities in individual time points provides the useful information associated with quantitative differences of the metabolite between exponential and stationary phases. To attain this, we conducted PLS regression, which is applicable when the number of independent variables is very large compared with the number of samples. Using Eq. (4) the OD₆₀₀ value can be directly estimated from the corresponding intensity vector of m/z values. When the ion has a positive value of a regression coefficient by PLS regression, its ion’s level should increase from exponential to stationary phase because the optical density is saturated in the highest level of the growth curve. We got the best linear model in PLS regression with one component (R _pred = 0.94). The Pearson’s correlation between the observed and predicted OD₆₀₀ values is r = 0.97, suggesting that our constructed model would work well, and is informative to clarify the relation between a growth stage and metabolite profile. Next, we plotted the regression coefficients of each ion determined by using the proposed model in order to elucidate which metabolite is important for estimating the OD₆₀₀ values (Fig. 6b). The ions with negative and positive coefficients contribute to the constructed model, negatively and positively, and are dominant in exponential and stationary phase, respectively. Four ions (PG1, m/z = 719.4868; PG2, m/z = 733.5056; PG3, m/z = 747.5183; PG4, m/z = 761.5293) which were analyzed by MS/MS analysis as described above had the highest coefficients. Other annotated six ions (PG5, m/z = 691.4588; PG6, m/z = 705.4757; PG7, m/z = 745.5045; PG8, m/z = 759.5242; PG9, m/z = 773.5375; PG10, m/z = 787.5556) also had higher coefficients, suggesting that PLS analysis could extract stage-specific metabolites efficiently. Thus, the observed behavior of metabolites is highly reflected in the regression coefficients of the PLS model and the interpretation of the coefficients is fairly consistent with the transition of metabolites from exponential to stationary phase.

Conclusions

This study presents a metabolomics approach to analyze growth-specific metabolites of bacteria, based on the FT-ICR/MS platform. Correlation analyses can make it possible to predict unknown molecular structure using isotope ratios by way of grouping metabolite derivative ions. Though 1-ppm mass accuracy alone is insufficient for unique elemental composition assignment [33], integrated analysis based on information of isotope relation, fragmentation patterns by MS/MS analysis, and co-occurring metabolites can makes it possible to annotate ions as metabolites and estimate cellular conditions based on metabolite composition. PCA revealed the differences between the growth stages on the basis of 220 independent metabolites, suggesting that metabolic profiling is a useful method for distinguishing the growth stages. Using PLS regression we constructed a linear relationship between OD₆₀₀ values and metabolite profiles. High correlation between predicted and observed OD₆₀₀ values certifies the correctness of the linear model. Our analyses reveal that global CFA formation of PGs occurs as E. coli enters the stationary phase from the exponential phase. The results indicate that nontargeted metabolomics based on direct-infusion FT-ICR/MS is useful for analyzing the responses of biological systems to a variety of changes. Our integrated methodology is applicable to metabolic studies involving other organisms.

Electronic supplementary material

Below is the link to the electronic supplementary material.