Evolution of flowering decisions in a stochastic, density-dependent environment

Abstract

Demography is central to both ecology and evolution, and characterizing the feedback between ecology and evolution is critical for understanding organisms' life histories and how these might evolve through time. Here, we show how, by combining a range of theoretical approaches with the statistical analysis of individually structured databases, accurate prediction of life history decisions is possible in natural density-regulated populations undergoing large fluctuations in demographic rates from year to year. Our predictions are remarkably accurate and statistically well defined. In addition, we show that the predicted trait values are evolutionarily and convergence stable and that protected polymorphisms are possible.

Ecology and evolution are intimately related as patterns of births and deaths determine fitness, the currency of evolution, and also how populations change through time (1, 2). Understanding the feedback between evolutionary and ecological processes is therefore of fundamental importance when attempting to predict life history traits and how these might vary through time. The feedback is made explicit in the study of adaptive dynamics (3) in which the current population state determines which novel mutants can invade. By explicitly deriving selection pressures from ongoing observable ecological interactions, this approach allows the quantitative prediction of life histories, but it has rarely been applied to natural populations. Here we show how combining the adaptive dynamics framework with recent advances in the modeling of size-structured populations and long-term individually structured field studies allows quantitative prediction of life history phenomena.

At the heart of an adaptive dynamics model is an ecological model describing the performance of individuals and how they interact. In addition to this, some form of tradeoff function is required to describe the costs and benefits of different life history tactics. Given this information, we can then use tools from adaptive dynamics to predict the traits organisms should possess, in the terminology of adaptive dynamics these are evolutionarily singular strategies, and determine the stability properties of the predicted trait values. In particular we are interested in whether the predicted trait values are: (i) evolutionarily stable, which would then render the population immune to invasion by new mutants; and (ii) convergence stable, which ensures the gradual approach to the predicted trait values through a series of mutations (3). In addition to this, we can also look for the existence of protected polymorphisms about the predicted trait values, i.e., combinations of trait values that can coexist.

Given the power of the adaptive dynamics approach, it is perhaps surprising that there have been very few attempts to apply these techniques to natural populations (2, 4, 5). The difficulty lies in constructing a realistic ecological model describing how individuals interact, characterizing the relevant tradeoffs, and estimating appropriate parameters. Monocarpic plants, in which reproduction is fatal, are ideal systems for the application of these ideas because: (i) long-term individually structured datasets are available and these allow the performance of individuals to be quantified (6–8); (ii) individual performance (the probability of survival, growth rate, seed production, etc.) is size-dependent and size is straightforward to measure in the field (7, 8); (iii) density dependence acts primarily through seedling establishment (7–9); and (iv) reproduction is fatal and so the cost of reproduction is known. There is also known to be a genetic basis to size at flowering (10, 11).

Here we use data from Carlina vulgaris and Carduus nutans, two monocarpic perennials native to Europe, which reproduce only by seed. Carlina has no seed bank (7) whereas Carduus has a long-lived seed bank (12). In both studies individuals were followed through time allowing individual variation in growth, survival, and reproduction to be quantified (6–9). In both species demographic rates are size-dependent and vary from year to year (see Materials and Methods). For monocarpic plants a key trait is the flowering strategy, which describes how the probability of flowering varies with plant size. Specifically we describe this by using a logistic regression,

where β₀ and β_s are the fitted intercept and slope, respectively, and x is plant size on a log scale. For both species, the probability of flowering varies gradually with plant size reflecting some constraint or else a decision to flower made some time between censuses. We therefore imposed gradual size dependence by fixing β_s at its estimated value and characterized the flowering strategy using β₀ (see ref. 13 for further discussion). Decreasing β₀ reduces the probability of flowering, and consequently the average size at flowering increases.

In a constant environment, characterizing the best strategy is straightforward because a plant should delay reproduction until seed production this year equals that expected next year (14, 15). Once this size or age is attained, individuals should flower. In the field, however, things are much more complicated as a result of spatial and temporal stochasticity in the environment. The long-term evolutionary outcome will reflect these complexities. Therefore, to construct a realistic ecological model we used density-dependent stochastic integral projection models, because these allow: (i) efficient parameterization of the size-dependent demography using a series of regression models; and 2) temporal variation and density dependence in demographic rates; see Materials and Methods for a description of the models.

With a parameterized ecological model, we can then use tools from stochastic demography to characterize the fitness of rare mutant flowering strategies. This is given by the long-term stochastic growth rate of the mutant's flowering strategy in an environment set by the resident flowering strategy (16). In this way we capture how flowering strategies affect each other's fitness and can describe patterns of invasibility between different strategies. To summarize this information we use pairwise invasibility plots (pips) a graphical tool from adaptive dynamics (3). Construction of the pips is described in Materials and Methods.

Results

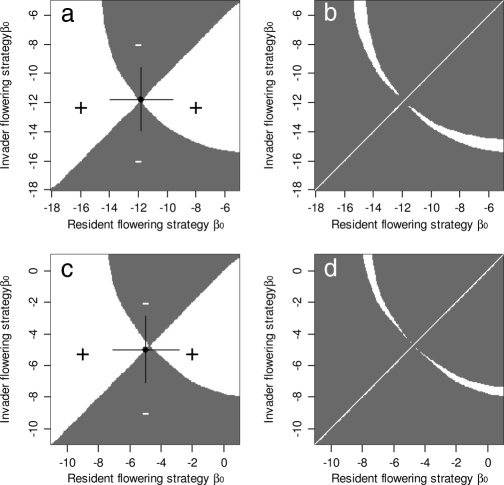
The pips for both species are shown in Fig. 1 a and c. Areas where the strategy on the y axis can invade the strategy on the x axis are shown in white; where it cannot and will go extinct are shaded. On the diagonal crossing the graph from bottom left to top right, the resident's strategy is equal to the invaders', and therefore both have zero stochastic growth rates. The intersection of this diagonal with the line separating areas with positive and negative growth rates represents the singular strategy, x*. Several conclusions about the evolutionary dynamics emerge: for both species: (i) the vertical line through x* is entirely in the shaded area, indicating that the singular strategy, x*, cannot be invaded, and is therefore evolutionarily stable (ES); (ii) the area immediately above the main diagonal to the left, and below the main diagonal to the right is white, indicating that any resident strategy can be invaded by a mutant closer to the singular strategy, x*, which therefore has convergence stability; (iii) the horizontal line through x* is entirely within the white area, indicating that x* can always spread through the population when initially rare; (iv) protected polymorphisms occur when two strategies x and y can mutually invade each other. This set of strategies can be identified by taking the mirror image of the pip along its main diagonal and then overlaying the two graphs. Sets of strategies forming protected polymorphisms occur in areas of overlapping positive stochastic growth rates. For both species, this set is non-zero indicating that protected polymorphisms can occur (Fig. 1 b and d). In all cases, the polymorphic strategies consist of a small and large flowering strategy, which lie on opposite sides of the ES strategy. The small flowering strategy can be thought of as a high-risk strategy that allows the population to increase rapidly when conditions are favorable, but as a result of its short generation time cannot effectively average stochastic variation in the environment. The large flowering strategy in contrast is a low-risk strategy with the opposite properties. Combining the information in the pips (Fig. 1 a and c) with the geometry of the coexistence boundaries (Fig. 1 b and d) allows the evolutionary stability of the protected polymorphisms to be determined (17). For both species the singular strategy is convergence stable and the angle between the two coexistence boundaries is narrower than 90°; so the protected polymorphisms lack evolutionary stability. Note, for both species the singular strategy is very close to that observed in the field.

Fig. 1.

Graphical analysis of evolutionary dynamics. (a and c) Flowering strategy pairwise invasibility plots for Carlina (a) and Carduus (c). Shaded areas represent unsuccessful invasion of the resident strategy (x axis) by an invading strategy (y axis). The solid point and horizontal and vertical lines indicate the observed flowering intercepts and their 95% confidence intervals. (b and d) Graphs obtained by overlaying the pip with its mirror image. Areas in white represent areas of coexistence.

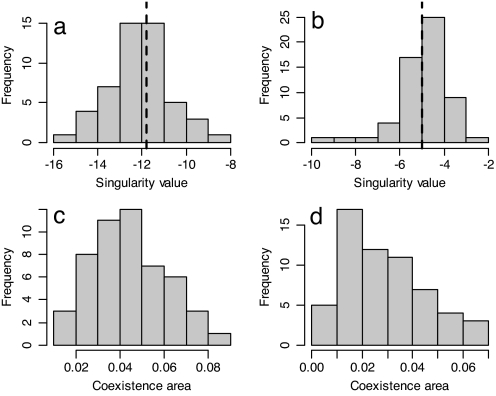
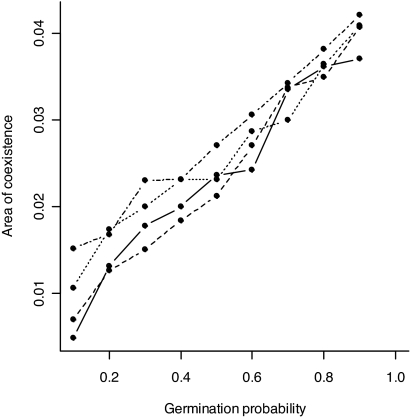
To explore whether the results are robust to estimation errors, we performed a bootstrapped analysis; see Materials and Methods for details. This analysis demonstrates that the singularities are well defined and not significantly different from those observed in the field (Fig. 2 a and b). In both species, the area of coexistence was greater than zero for all of the bootstrapped parameter sets (Fig. 2 c and d) indicating that uncertainty in parameter estimation does not affect the qualitative prediction that protected polymorphisms are possible. For both species, we have little quantitative information on the probabilities of seed germination (g) and death (d) and so a sensitivity analysis was performed; see Materials and Methods for details. Increasing the probability of seed germination increased the range of strategies that can form protected polymorphisms (Fig. 3). Increasing the probability of seed death, d, had a similar although smaller effect. These effects are a consequence of increasing germination (or seed death) resulting in less efficient averaging of the environment so making the small, high-risk flowering strategy more risky and allowing a wider range of large, low-risk flowering strategies to coexist.

Fig. 2.

Robustness analysis. (a and b) Distribution of the evolutionary singularities obtained from the 50 bootstrapped parameter combinations in Carlina (a) and Carduus (b). Dashed lines are the estimated intercepts from statistical models fitted to the data. (c and d) Distribution of the area of coexistence obtained for each bootstrapped parameter combination for Carlina (c) and Carduus (d).

Fig. 3.

Relative area of coexistence of different flowering intercepts β₀ for Carlina for different values of the germination (g), and seed death probability, d = 0.01 (full line), d = 0.05 (dashed line), d = 0.1 (dotted line), and d = 0.2 (dashed-dotted line). Relative area was taken as the ratio of the area of coexistence divided by the total area of parameter space considered (Fig. 1). Coexistence increases with g and marginally increases with d. Irregularities are due to numerical rounding. The same pattern is obtained for Carduus (data not shown).

Discussion

The existence of protected polymorphisms about the predicted flowering strategy was completely unexpected and provides a possible mechanism contributing to the maintenance of genetic diversity, and indeed, several selection experiments have demonstrated that natural populations harbor substantial genetic variance for flowering size (10, 11). However, it must be emphasized that the protected polymorphisms observed in Carduus and Carlina are not ES; flowering strategies intermediate between strategies forming a protected polymorphism can invade and so in the long-term genetic variability is unlikely to be maintained by this mechanism unless genetic constraints prevent the populations achieving the singular strategy. This might occur if some genes, for example, the FRIGIDA gene important in vernalization (18), which influences flowering, have large effects making it difficult to produce intermediate flowering sizes. In this situation, it may be impossible to produce precisely the ES strategy, and so alternative strategies on either side of the ES strategy will persist.

These results can also be viewed from a species perspective and illustrate how different species might coexist solely as a result of differences in their flowering strategy. The mechanism underpinning the coexistence of different strategies or species is the relative nonlinearity of competition, which occurs because the nonlinear responses to the shared competitive conditions (i.e., density dependence in seed recruitment) are sufficiently different (19).

We suspect that in many field systems where traits that influence population growth rate are affected by fluctuations in the environment, coexistence of different life history strategies may occur via relative nonlinearity of competition. In particular, it seems likely that the patterns of protected polymorphisms observed in Carlina and Carduus will be observed in other systems with similar life histories and for other traits that influence the rates at which populations respond to fluctuations in the environment. For example, in a theoretical study, Ellner (20) showed that coexistence of high- and low-germination strategies was possible because of relative nonlinearity of competition; preliminary analysis suggests this also occurs in Carduus, which has a long-lived seed bank. Ellner also conjectured that similar results would be found for seed size, growth-survival trade-offs, and reproductive effort. In each case, the strategy capable of rapid population growth under favorable conditions (i.e., small seeded, rapid growth, high reproductive effort) suffers most when conditions are unfavorable. The results presented here are in agreement with this conjecture.

The construction of pips using stochastic, density-dependent structured population models may seem like a rather complicated way to study evolution. However, this approach allows us to quantify how changes in trait values influence fitness taking the entire life cycle into account, in a realistic environment that includes both the effects of density dependence and temporal variation in demography. Simple optimization approaches assume evolution maximizes some measure of population growth; however, even in a constant environment, this may not be valid (21). In variable environments, models with and without density dependence can produce diametrically opposite predictions over large areas of biologically reasonable parameter values (22), clearly indicating the importance of density dependence when attempting to make predictions about natural systems. Other approaches such as selection analysis (23) are much simpler but unfortunately may make erroneous predictions, especially for traits such as flowering size, where there is likely to be an “invisible fraction” problem (24), i.e., mortality selection that occurs before the trait is expressed. For example, in most monocarpic plants, including Carlina and Carduus, seed production, a measure of lifetime reproductive success, increases with flowering size (15). A selection analysis of flowering size would therefore conclude there is substantial directional selection of flowering size, even when, as in Carlina and Carduus, there is none.

Our approach is, of course, only as good as the data used to parameterize the models, and in particular, if important selection pressures are not included in the model then it is unlikely to allow accurate quantitative prediction. Conversely one cannot assume that because a model produces reasonable predictions that all of the important processes have been included. For example different selection pressures might cancel each other's effects (8, 9) making the predictions of a simple model accurate even when important selection pressures have been ignored.

Our results indicate that prediction of trait values and characterization of their evolutionary stability properties is possible in the field, through careful analysis of long-term individually structured data and the application of new modeling techniques. Furthermore, we have shown that our results are statistically robust. Extending this approach to other systems with more complex life histories and patterns of density dependence will be challenging, as will the integration of ideas and methods from quantitative genetics. However, increasing dialogue between ecologists and evolutionary biologists will allow the ecological theatre in which evolution is played out to be understood and should bring these challenges within reach.

Materials and Methods

Here, we describe application of adaptive dynamics techniques to evolutionary dynamics of flowering size for two field systems: namely Carduus nutans, and Carlina vulgaris. To construct the pairwise invasibility plots (pips) central to adaptive dynamics, we use stochastic density-dependent integral projection models (IPM) to describe the dynamics of a resident population (9, 25) and characterize the fitness of rare mutant strategies using the stochastic growth rate (9, 16, 25).

Population Biology of Carlina vulgaris and Carduus nutans.

To parameterize the IPMs, we need to describe how demography (growth, survival, fecundity) varies with plant size. In Carlina, size was measured as length of the longest leaf, whereas in Carduus, we used the mean radius (based on two measurements), and this was converted to rosette area, assuming the plants are circular. Annual changes in log plant size were described by a regression model of the form y = a_g + b_gx where x and y are plant size this year and next year, and a_g and b_g are the fitted intercept and slope, respectively. To explore yearly fluctuations in growth, we fitted “year” as a fixed effect; allowing a_g to vary between years. The year effect was significant for both species (P < 0.01), and the effect of log size (b_g) was significant for Carlina (P < 0.001) but not for Carduus (P > 0.05). For both species, survival probability, s(x), was modeled as a logistic regression, including year as a fixed effect to capture yearly variation in survival not related to plant size. In both species, the year effects were significant (P < 0.01) and survival increased significantly with log size for both species (P < 0.01). Flowering probability was modeled by using a logistic regression and increased significantly with log size for both species (P < 0.01), the fitted model was

where β₀ is the intercept, β_s the size-specific slope, and x a measure of plant size depending on the species. For both species the probability of flowering varies gradually with plant size reflecting some constraint or else a decision to flower made some time between censuses. We therefore imposed gradual size dependence by fixing β_s at its estimated value and characterized the flowering strategy by using β₀ (see ref. 13 for further discussion). Seed production was described by using allometric relationships of the form seeds = exp(A + Bx) for both species. The distribution of seedling size, f_d(y), on a log scale for both species was well-described by a normal distribution.

In Carlina, total yearly seed production was highly variable but showed no relationship with the number of seedling recruits that appeared in monitored quadrats the following year (7). In Carduus there was no relationship between seed bank density in quadrats and the observed number of seedling recruits (9). Recruitment is therefore limited by the availability of microsites allowing successful seedling establishment, i.e., density dependence operates through seedling establishment.

No data were available to parameterize germination and seed death from these populations; however extensive field studies indicate that Carlina does not form a seed bank, whereas Carduus forms a long-lived seed bank. In keeping with this, we set the probability of seed death, d, equal to 0.2 in both species and the probability of germination, g, to 0.2 in Carduus and 0.99 in Carlina.

Structured Dynamics in a Stochastic Environment.

To describe the dynamics of a resident flowering strategy and estimate the fitness of invading strategies we used IPMs parameterized from field data (25, 26). In these models the size distribution of the established plant population is described by a density function n(x, t), where n(x, t)dx is the number of individuals in the size range [x, x + dx], and an additional state variable S(t) is used to track the number of seeds in the seed bank in year t. The model takes the form,

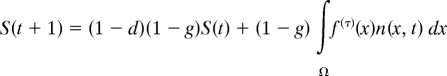where d and g are the probability of seed death and germination, respectively, f^(τ)(x) the expected seed production of size x plants, p^(τ)(y, x) describes the growth of individuals from size x to size y, f^(τ)(y, x) is the expected number of recruits of size y produced by size x plants before the action of density dependence, p_e(t) is the probability of seedling establishment, and f_d(y) is the size distribution of seedling recruits. τ defines the type of environment, in terms of growth, survival, and recruitment, experienced in year t, and f^(τ)(x), p^(τ)(y, x), and f^(τ)(y, x) are referred to collectively as the kernel functions. Details of how the kernel functions are related to the fitted demographic functions, described above, are given in Table 1. The seed bank equation is made up of two parts: those seeds that remain in the seed bank, plus the seeds produced this year, which remain dormant. The established plant population, n(y, t + 1), is made up of three parts: plants that establish from the seed bank, established plants that survive and grow, plus seeds produced this year that germinate and establish; see ref. 9 for details of model construction.

Table 1.

Summary of the functions used to construct the integral projection models.

Kernel function	Component functions	Fitted functions	Variable parameter
p(y, x) = s(x)[1 − pf(x)]g(y, x)	Survival	logit(s) = m0 + msx	m0
	Flowering	logit(pf) = β0 + βsx
	Growth	g(y, x) ∼ N(ag + bgx, σg2)	ag
f(x) = s(x)pf(x)fn(x)	Seed production	fn = exp(A + Bx)
f(y, x) = fd(y)f(x)	Seedling size	fd ∼ N(μsd,σSD2)

The probabilities of survival (s) and flowering (p_f) are described by logistic regressions, and for survival, the intercept (m₀) varies from year to year. Growth is described by a linear regression y = a_g + b_gx and so is conditional on size this year, x; size next year, y, follows a normal distribution with mean a_g + b_gx and variance σ_g². The variance (σ_g²) is estimated from scatter about the regression line. The intercept of the fitted relationship (a_g) varies from year to year and only in Carlina is growth size-dependent (b_g &sup1; 0). The distribution of seedling size (f_d) follows a normal distribution with mean and variance estimated from the data. Parameter values are given in refs. 7 and 9.

The yearly variation in the model was generated by sampling independently from the n − 1 different year types, τ (τ = 1, 2, 3, … n − 1) corresponding to the n years observed in the data, i.e., each year type is associated with the temporally varying parameter vector, including the year specific survival and growth intercepts, and the number of recruits observed the following year, denoted R(τ + 1). The observed number of recruits is treated as a parameter in the models because density dependence acts on recruitment (see below), and we assume the number of microsites suitable for recruitment varies from year to year. These parameters can be summarized by a vector θ(τ) = (m₀(τ), a_g(τ), R(τ + 1)). By using θ(τ) and the temporally invariant parameters defined in Table 1 we can construct the kernel functions for a year t corresponding to year type τ. Because seedling establishment is density dependent, the probability a seed establishes is given by

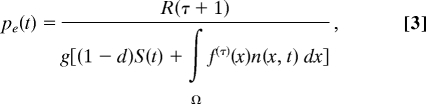where the term on the bottom is the total number of seeds that germinate. To simulate the model, we draw τ independently at random and then construct the kernel functions and calculate p_e(t). By using these we can then use standard numerical methods to solve Eq. 2, see (9) Appendix B for details. This corresponds to the matrix selection approach to constructing stochastic matrix models (27) and can be thought of as a nonparametric bootstrap from the set of estimated kernel functions.

Fitness of Invading Genotypes.

To construct the pips we need to calculate the fitness of rare mutant flowering strategies. In a variable environment, such as we have for both species, fitness is determined by the invasion exponent, ϑ, defined by

where N_t is the total population size at time t (16). The number ϑ is equal to the stochastic growth rate of an invading mutant population in the environment set by the resident, i.e., ϑ = log λ_s and so if ϑ is negative the invader will go extinct. We assume the invader and resident experience the same sequence of environments and only differ in their flowering strategy, and so all seedlings compete on an equal footing for the available microsites. To estimate ϑ we assume the invader is rare and so its density has no effect on its population growth rate. We then generate a time series (5000 years) for the resident population consisting of the year type τ₁, τ₂, …, τ₅₀₀₀ and the probability of establishment (p_e^R(1), p_e^R(2), …, p_e^R(5000)). This defines the environment in which we estimate ϑ. We calculate ϑ by iterating the model for the invader, using the resident time series for τ and replacing p_e(t) in Eq. 2 by p_e^R(t). The maximum likelihood estimator of the invader growth rate, ϑ, is then given by

where N_t is the total population size at time t. Ellner and Rees (25) prove that for a wide class of stochastic integral projection models, including those considered here, the stochastic growth rate exists and may be computed by using Eq. 5.

Construction of the Pips.

To obtain the pips we estimated the stochastic growth rate for rare invading flowering strategies by using a wide range of invading and resident strategies (3). For each resident flowering strategy, β₀, we calculated the stochastic growth rate of rare alternative flowering strategies. This allows us to characterize the invader-resident combinations where invasion is possible. Pips assume the population is either asexual, or made up of completely selfing diploids. However, Turelli et al. (28) have shown that conditions for protected polymorphisms in a haploid system extend to a system of diploids with complete or incomplete dominance.

Capturing Uncertainty in Parameter Estimates.

To verify that results are robust to uncertainty in parameter estimation, we bootstrapped the data. Specifically, for regressions incorporating year effects (growth and survival) we sampled the data within years with replacement. For regressions without year effects (seed allometries, probability of flowering) and the mean and variance of seedling size we sampled the entire data set with replacement. In both species we sampled the number of seedling recruits observed per quadrat in each year with replacement, and took the total to obtain the bootstrapped estimate of recruits observed in that year. We then reran the analysis to obtain pips for each bootstrapped parameter set. For each species we generated 50 bootstrapped datasets.

To explore whether the presence of protected polymorphisms depended on the assumed probabilities of germination and death we constructed pips by using a range of probabilities of seed death (d ∈ {0.01, 0.05, 0.1, 0.2}) and germination (g ∈ {0.1, 0.2, …, 0.9, 0.99}) and calculated the area of coexistence.