Application of a polarizable force field to calculations of relative protein–ligand binding affinities

Abstract

An explicitly polarizable force field based exclusively on quantum data is applied to calculations of relative binding affinities of ligands to proteins. Five ligands, differing by replacement of an atom or functional group, in complexes with three serine proteases—trypsin, thrombin, and urokinase-type plasminogen activator—with available experimental binding data are used as test systems. A special protocol of thermodynamic integration was developed and used to provide sufficiently low levels of systematic error along with high numerical efficiency and statistical stability. The calculated results are in excellent quantitative (rmsd = 1.0 kcal/mol) and qualitative (R² = 0.90) agreement with experimental data. The potential of the methodology to explain the observed differences in the ligand affinities is also demonstrated.

The ability to accurately calculate the binding affinity, or equivalently binding free energy, of a ligand for a protein would be highly useful in the field of drug design for lead selection and optimization. Although screening and docking methods (1, 2) have been successful in filtering large chemical databases, they cannot provide definitive calculations of binding energy because of the simplified scoring functions used and the restricted number of states tested. Hence, more accurate calculations have generally been based on molecular mechanics models (3, 4). In these methods the required properties of statistical ensembles are determined by molecular dynamical or Monte Carlo simulations of systems by using a physically grounded description of interactions between particles. The theoretical thermodynamic foundation of such methods is clear, simple, and well established (5).

Despite these advantages, as well as initial optimism and long development, only a limited number of successful simulations have been published during the past decade (e.g., refs. 6–14; for review of early results, see refs. 3 and 4). In part, this is explained by many methodological difficulties that must be overcome, especially in accurate and efficient description of long-range interactions and adequate sampling of the conformational space. Major efforts devoted to solving these problems have resulted both in partial success (15, 16) and the recognition of some principal limitations. Notably, several theoretically based techniques have been developed, such as umbrella sampling, the concept of potential of mean force, and artificial restraining potentials, which restrict or decompose the conformational space and simplify adequate sampling (e.g., 11, 17–20).

The other principal problem has been the quality of the model potentials or force fields (FFs) used to describe atom–atom interactions. The most questionable point in this respect is the role of nonadditive effects, particularly electronic polarizability. Widely used FFs such as MMFF (21), AMBER (22), OPLS (23), CHARMM (24), and GROMOS (25) are not explicitly polarizable but rather include polarizability implicitly in their parameterization. Under restricted simulation conditions such an approach can be justified, as confirmed by reasonable solvation free energies calculated with the aid of these FFs (see, e.g., ref. 26). However, data on solvation of small molecules and properties of uniform organic liquids are, in fact, the major part of the training set used for parameterization of such FFs. Thus, it is unreasonable to expect that predictions from a nonpolarizable FF will be equally (and universally) accurate in other environments, for example, in a very nonuniform protein-active site. For this reason polarizable versions of the mentioned FFs are currently under active development (27–29), but their applications to macromolecules of biological importance have been very limited (30, 31).

In this article, we present the methodology and results of calculation of relative binding affinities in protein–ligand systems with our general-purpose quantum mechanical polarizable force field (QMPFF) (32–36). QMPFF is fitted exclusively to ab initio quantum mechanical (QM) data on molecular properties and intermolecular interactions without reference to condensed phase data. The key point of the parameterization procedure is the separate fitting of the four basic components of intermolecular energy in dimers (electrostatics, exchange, induction, and dispersion) to the corresponding QM counterparts, which is essential for FF transferability. Here, we use the functional form of the latest QMPFF version, QMPFF3, which has been shown (34–36) to be successful at describing properties of biologically relevant organic molecules and their interactions in gas, liquid, and solid phases. It should be stressed that in the present simulations the FF was used “as is” and without any tuning of the parameters and/or functional form to the solvent–protein–ligand system being studied.

To assess the application of QMPFF3 to binding free-energy calculations, we use the data of Katz et al. (37, 38) on affinities of a set of related ligands (Fig. 1) to three serine proteases frequently considered as therapeutic targets: trypsin, thrombin, and urokinase-type plasminogen activator (uPA). The data have several features that make it challenging and valuable as a test set. First, the molecules are related to a real drug design problem, the search for new uPA inhibitors. Second, although the protein sites are similar and are relatively rigid (37–39), the binding affinities of the ligands are diverse. Some ligands have similar affinities despite being more structurally disparate, whereas other affinities are very different despite small structural modifications in the respective ligands, and moreover, the affinity differences change significantly from protein to protein. Third, some modifications in the ligands have unusual consequences, for example, change from an imidazole to indole scaffold leads to an increase in affinity contrary to expectations (38). Fourth, the data are sufficiently detailed to allow their step-by-step comparison with calculations for cycling mutations, which provide a useful check on errors. Finally, crystallographic structures of almost all of the complexes are known, so the accuracy of ligand–protein conformations obtained in the course of the simulations can be verified.

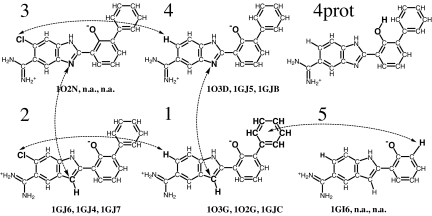
Fig. 1.

Inhibitors of serine proteases from ref. 37 and 38 used as a test system. Arrows show simulated mutations. Note that four of the mutations form a closed cycle, 1 → 2 → 3 → 4 → 1. The PDB codes (40) of the corresponding complexes with trypsin, thrombin, and uPA are also shown if they exist. According to ref. 37, the 1GJC complex contains ligand 1, but the 1GJC files from the PDB contain ligand 4. Thus, the complex of uPA with ligand 1 was obtained by substituting the corresponding nitrogen of ligand 4 by a CH group without change of coordinates of any other atoms. Ligands are shown as they are in complexes: with deprotonated phenyl oxygen (38). In solution the ligands will be largely protonated at this site as shown for ligand 4 in the upper right corner.

Materials and Methods

To determine relative binding affinities ΔΔG_A→B ≡ ΔG_B − ΔG_A, where ΔG_A and ΔG_B are the binding free energies of ligands A and B to the protein, we use the traditional thermodynamical cycle (3, 4), which expresses the desired difference as the difference of the free-energy changes resulting from two alchemical mutations between the ligands made in the bound state and in solution, respectively: ΔΔG_A→B = ΔΔG_A→B^site − ΔΔG_A→B^water. To calculate mutation free-energy differences, we applied the method of Multiconfiguration Thermodynamic Integration (41). Because of a number of the method refinements, as described in detail in the first six sections of SI Text, we found 1 ns of productive MD trajectory per mutation to be sufficient.

Supporting Information.

For further details, see SI Text, Figs. S1–S27, and Tables S1–S5.

Results

The inhibitors considered in the present work are shown in Fig. 1. To reveal the role of the FF, we performed the same simulations under the same protocol but with two FFs: our QMPFF3 (36) and MMFF (21), the Merck molecular mechanics FF. We chose MMFF for comparison because, like QMPFF, it is based on ab initio quantum data, although the underlying model is less physical in that it does not account for electron polarization, the diffuse character of the electron clouds, atomic quadrupoles, and so on. Both FFs were implemented in our in-house molecular dynamics package AlgoMD (33). Calculated results for free-energy differences associated with each mutation in water and each protein site by using both FFs are presented in Table 1. In this and other tables, the standard statistical errors are shown in parentheses in units of the last digit(s). More detailed information on the results is given in supporting information (SI) Text, dH/dλ Graphs for All Simulated Systems.

Table 1.

Free-energy changes for simulated mutations (kcal/mol)

Mutation	Trypsin	Thrombin	uPA	Water*
Results of simulations by using QMPFF3 force field
1→2	5.3 (3)	8.1 (3)	4.0 (2)	3.2 (2)
2→1	−5.6 (3)	−7.7 (2)
2→3	1.9 (3)	0.7 (3)	2.2 (3)	0.2 (4)
3→4	−6.8 (3)	−7.9 (4)	−5.0 (2)	−4.6 (2)
4→3		7.9 (2)
4→1	−0.7 (3)	−1.2 (3)	−0.8 (2)	1.3 (3)
1→5†	−4.0 (4)	−5.7 (5)	−4.3 (4)	−7.7 (5)
Results of simulations by using MMFF force field
1→2	−3.2 (3)	2.6 (3)	−1.8 (2)	−4.3 (2)
2→3	−6.2 (2)	−7.4 (2)	−5.1 (2)	−5.7 (2)
3→4	3.6 (2)	−1.0 (3)	2.0 (2)	5.0 (2)
4→3	−3.9 (2)
4→1	5.7 (2)	5.5 (2)	4.5 (2)	5.0 (2)
1→5†	−28.3 (4)	−36.4 (9)	−27.8 (4)	−28.9 (4)

*With account for correction on different charge states of the ligands in complexes and in solution as described in SI Text, Thermodynamical Cycle Approach When Ligands Are in Different Charged States in Different Environments.

^†With account for NVT-NPT correction as described in SI Text, Introduction of NVT-NPT Correction.

The level of statistical error depends on the length of the trajectory used for the data accumulation and the number of intermediate steps, and therefore determines the computational costs of the simulation. In our investigation we took the view that striving for statistical errors much smaller than those expected from the FF is pointless. That decision implies a choice of the protocol parameters providing a level of statistical error of ≈0.3–0.7 kcal/mol depending on the severity of the mutation.

It should be noted that effects of a single mutation presented in Table 1 cannot be directly compared in different FFs. In any FF the energy of a molecule is defined only with respect to some reference state, so the energy usually has no physical meaning. For this reason the effect of a single mutation also has no physical meaning. In contrast, when calculating the difference between the effects of a mutation in two environments, say in vacuo and in water or in water and a protein site as presented in Table 2, the contribution of these reference constants cancels and the result can be compared with experimental solvation or binding energies or predictions of another FF.

Table 2.

Binding free-energy differences for all simulated mutations (kcal/mol)

FF/Mutation	1→2	2→3	3→4	4→1	1→5
Trypsin
QMPFF3	2.1 (4)	1.7 (5)	−2.2 (4)	−2.0 (5)	3.7 (7)
MMFF	1.1 (4)	−0.5 (2)	−1.4 (3)	0.7 (3)	0.6 (6)
exp.*	1.3	1.2	−1.4	−1.1	2.4
Thrombin
QMPFF3	4.9 (4)	0.5 (5)	−3.3 (5)	−2.5 (5)	2.0 (7)
MMFF	6.9 (4)	−1.7 (3)	−6.0 (4)	0.5 (3)	−7.5 (11)
exp.*	2.8, 3.1†	0.2, 0.4†	−1.4, −1.8†	−1.6, −1.7†	1.6
uPA
QMPFF3	0.8 (3)	2.0 (5)	−0.4 (3)	−2.1 (4)	3.4 (7)
MMFF	2.5 (3)	0.6 (3)	−3.0 (3)	−0.5 (3)	1.1 (6)
exp.*	−1.0, 0.1†	2.5, 3.2†	−0.4, −0.9†	−1.1, −2.4†	2.2

*Values according to ref. 38.

^†Values according to ref. 37.

In simulations with QMPFF3, all components of the system—protein, water, and ligand—are polarizable. Determination of atomic parameters was done within the general QMPFF3 scheme (36); no special or modified parameters were used for the simulations presented here. Below we discuss some features of the results in more detail with primary attention to the QMPFF3 results.

Stability of the Results.

To be sure that the results are statistically stable we performed a special analysis described in detail in SI Text, Analysis of Statistical Stability of the Results. In particular, the protein structure was followed by the dynamics of rmsd of “site” atoms (the amino acids having any atom within 8 Å of the ligand and left unfixed; see SI Text, Overview of Methods, for details). In simulations with both FFs, after a pronounced increase of rmsd as a result of the thermalization, the rmsd then approached a stable plateau, with approximately the same plateau level reached no matter which structure was used to start, crystallographic or molecular dynamics (MD) equilibrated. This means that the observed rmsd represents only the thermal fluctuations rather than some structural change of the site.

Statistical saturation of calculated dG/dλ and ΔG values was checked by using the block-averaging approach (42) and tracing the dynamics of running and sliding averages. The analysis revealed the presence of a time-varying component with characteristic time of ≈10–20 ps and variation amplitude of up to 10 kcal/mol in dG/dλ and ≈1–2 kcal/mol in ΔG. Reliable averaging of this component generally requires at least 50–100 ps of data accumulation, justifying our choice of the length of the productive trajectory per each intermediate mutation step (100 ps).

In general, our analysis demonstrated statistical reliability of all simulations performed with QMPFF3. The MMFF results were also statistically reliable whenever the ligand pose was stable. However, in thrombin, MMFF simulations starting from the crystallographic pose have difficulty reproducing the configurations of ligands 1–4 in the region of the S1′ site. The terminal aryl group of these ligands situated initially in this site is pushed into solvent where it moves freely without finding a stable configuration. It is interesting that this instability is avoided if one starts the simulation from the protein structure prepared as described in SI Text, Overview of Methods, using the QMPFF3 force field, because QMPFF3 is able to flip a protein lysine (LYS60F) to make a favorable interaction with the ligand aryl group. Thus, QMPFF3 finds a stable configuration that also preserves stability in MMFF, whereas MMFF cannot find this configuration itself. Here, we give only the stable result for MMFF simulations of the thrombin complexes. Other cases are discussed in detail in SI Text, Analysis of Statistical Stability of the Results.

The statistical stability does not guarantee that the results are free from systematic errors resulting from incomplete sampling of the thermodynamical state. Such errors could manifest themselves by variations of results when initiating calculations from slightly different configurations. There are no general ways to characterize and reveal these errors, but here we consider two approaches to reveal possible systematic effects. First, we compare the ligand poses predicted by the simulation with crystallographic ones. If the pose is not reproduced, any quantitative agreement of binding free energy with experiment should be considered as coincidental. Mutations 1 → 2 and 3 → 4 are the most demanding in this respect, because the initial and final ligand poses in these cases are substantially different. Fig. 2 shows that QMPFF almost perfectly predicts the pose of ligand 2 via simulation of the 1 → 2 mutation starting from the pose of ligand 1. (Also the pose of ligand 1 is well reproduced starting from the pose of ligand 2 in the simulation of the back mutation 2 → 1. The situation with 3 → 4 and 4 → 3 mutations is similar.)

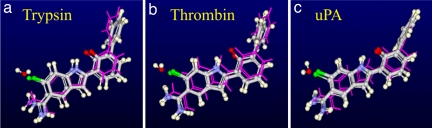
Fig. 2.

Comparison of the simulated pose of the ligand 2 (thick sticks and balls) as obtained by mutation in trypsin (a), thrombin (b), and uPA (c) starting from ligand 1 (thin magenta sticks) with the crystallographic pose of ligand 2 (balls and sticks). A structural water present in the complex with ligand 1 and displaced by ligand 2 is also shown (at upper left of the ligands). The atom color code is: gray, carbon; white, hydrogen; blue, nitrogen; red, oxygen; green, chlorine.

Second, we measure how close the free-energy difference is to zero, as calculated over a cycle of mutations simulated independently. The simplest type of such a cycle is the forward-and-back mutation. We performed several simulations of this type (see Table 1) and in all cases the difference of the results was within one standard deviation. A stricter test of this type of stability is the convergence of the cycle over four consecutive mutations (Fig. 1). The total duration of all of the runs used in the four mutations composing the cycle is ≈5 ns. The mutations together can be considered as one complex mutation simulated in a long run (0.5 ns in each intermediate point) with a known exact theoretical result of zero ΔG. For this reason it is reasonable to expect that systematic effects from the long-scale dynamics and imperfect sampling in any single calculation will show up as imperfect cycle closure. For all three proteins and water, the difference of calculated closure of the cycles (i.e., ΔG_1→2 + ΔG_2→3 + ΔG_3→4 + ΔG_4→1) from ideal (i.e., 0) was within statistical error (Table 3).

Table 3.

Clockwise closure of mutation cycle shown in Fig. 1 (kcal/mol)

FF	Trypsin	Thrombin	uPA	Water
QMPFF3	−0.3 (6)	−0.3 (6)	0.4 (5)	0.1 (5)
MMFF	0.1 (4)	−0.3 (5)	−0.4 (4)	0.0 (3)

Errors here and in Table 2 are obtained from errors of the individual mutation steps given in Table 1 considered as statistically independent.

Finally, we analyzed the stability of our methodology with respect to parameters of the calculation protocol that are somewhat arbitrary. Comparing results obtained with different values of these parameters, we found typical differences in ΔG values of ≈0.1 kcal/mol, which is obviously within the expected accuracy of the method (for details see SI Text, dH/dλ Graphs for All Simulated Systems).

Relative Binding Affinities.

Calculated results for differences of binding free energies or equivalently relative binding affinities are compiled in Table 2 and in graphical form in Fig. 3. Statistical characteristics of the relation between calculations and experiment (37, 38) are shown in Table 4. As can be seen, the results obtained with the QMPFF3 FF are well correlated with the experimental data. The correlation is approximately the same for each protein and for the whole set of data. Thus, the results essentially reproduce all qualitative changes of the affinities of different ligands to different proteins.

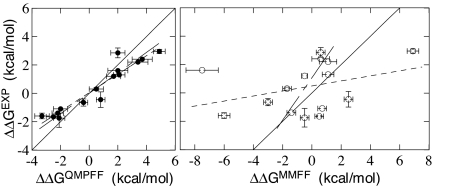
Fig. 3.

Comparison of experimental and calculated relative binding affinities. (Left, filled points) Results obtained with the QMPFF3 force field. (Right, open points) Results obtained with the MMFF force field. The solid line is the diagonal x = y, the horizontal bars show the statistical errors, the vertical bars show the experimental uncertainty derived from the data of refs. 36 and 37. Dashed lines show linear fits derived considering the calculated points as a function of the experimental ones (long dashes), and vice versa (short dashes). Agreement of the two fits for QMPFF3 demonstrates a high level of correlation in this case (see Table 4). Similarly, low correlation for MMFF is indicated by the substantial discrepancy in slope of the fits.

Table 4.

Mean deviations (〈dev〉), rmsd values (kcal/mol), and correlation coefficients between groups of results and corresponding experimental data

	Trypsin	Thrombin	uPA	Trypsin + uPA	All
QMPFF
〈dev〉	0.2	0.0	0.3		0.2
rmsd	0.9	1.2	0.9		1.0
R2	0.998	0.98	0.81		0.90
MMFF
〈dev〉	−0.4	−1.9	−0.3	−0.3	−0.9
rmsd	1.4	5.0	2.1	1.8	3.2
R2	0.23	0.17	0.11	0.13	0.12

The slope of the straight-line fit of relative binding affinities calculated with QMPFF3 to those determined experimentally is ≈1.4 and not the value of 1.0 expected for perfect agreement. This is caused mainly by a small but somewhat uniform overestimation of the binding energy difference for 1 → 2 mutations and similar underestimation for 3 → 4 mutations. According to our analysis, the major reason for this may be a simplified description of torsions in the initial version of the QMPFF3 force field used here. Because of the high-level description of nonbonded interactions, we found it possible to obtain good accuracy of torsion energy profiles with torsion parameters dependent only on the types of the two central atoms. Clearly such a simplified representation cannot be perfect. In particular, we find that the QMPFF3 parameters underestimate the barrier for coplanar positioning of the amidine group (terminal NH₂-C-NH₂) with the adjacent aromatic ring by ≈1–1.5 kcal/mol in comparison with the ab initio quantum value. [The latter was calculated by using our in-house AlgoQMT software (43, 44) at the MP2/TZ* level, the same level as in QM calculations used for the QMPFF3 parameterization in ref. 36.] In-site poses of ligands 2 and 3 correspond to a favorable relative orientation of amidine group and aromatic ring, whereas the in-site poses for ligands 1 and 4 are unfavorable with coplanarity of these groups. In water the amidine group is in a favorable conformation in all of the ligands. Thus, correction for the underestimation of the torsional barrier by QMPFF3 will subtract ≈1–1.5 kcal/mol from the 1 → 2 mutation and similarly add this value to the 3 → 4 mutation, in accordance with the observed tendency.

Over all of the comparisons, the rmsd from experiment is 1.0 kcal/mol, which is about the accuracy of the experimental data themselves, as can be deduced from comparison of results from refs. 37 and 38 (see Table 2). This level of accuracy provides the possibility to rationalize the differences in the effect of the same mutation for different proteins (see next section) and potentially help in the ligand optimization process.

Results obtained with the MMFF FF show almost no correlation with experiment for the whole set, as well as for the separate proteins, although some of the values almost precisely match the experimental values. Thus, it can be argued that in the later case some kind of the error cancellation is occurring. It should be stressed that we use identical protocols for both FFs, and the details of the methodology do not obviously favor one FF over the other. Moreover, as shown in the preceding section, the methodology provides stable results in all respects. Thus, the problems found with the MMFF force field are not caused by any methodological errors, such as inadequate sampling, but apparently represent the inadequacies of the force field itself.

Role of the Structural Water.

A potential advantage of calculating relative binding affinities via simulation, as opposed to experiment, in addition to determining whether a proposed modification to a ligand will be favorable before going to the trouble of synthesizing it, is the ability of simulation to explain the mechanism of affinity changes. Understanding the mechanism may in turn suggest modifications that produce further improvement. To exemplify the possibilities of our method in this respect, we discuss below the reasons for different relative binding affinities of ligand 1 and ligand 2 for different proteins.

Mutations 1 → 2 (as well as 4 → 3) in all proteins result in expulsion of a molecule of structural water. This molecule is situated in the complexes with ligands 1 and 4 deep inside the protein pocket and bridging the ligand with the protein site. (To obtain an idea of the water position, see water 619 in the 1O2G pdb complex.) In complexes with ligands 2 and 3 the water molecule is thermodynamically unfavorable and is not observed in the crystallographic structures. However, in the simulations starting from the complex with ligand 1 (or 4) the water molecule, being highly buried, cannot actually reach the bulk water because of limited simulation time. Indeed, because the water molecule is situated between the protein and ligand, its passage to the bulk requires detachment of the whole ligand. Calculations of binding energy from simulations that sample multiple bindings and detachments of the ligand are far beyond present computational capabilities. To overcome this problem, we have developed a special treatment of the structural water molecule, including it in the general mutation scheme. Theory and details of the approach are presented in the SI Text, Protocol of Simulation of Mutations Resulting in Structural Water Expulsion.

It should be noted that the decision to conduct the mutations 1 → 2 (and 4 → 3) with expulsion of the structural water should not be based only on the respective x-ray structures, which might be wrong in this respect or might not be available in other cases. The analysis presented below demonstrates how this decision could be made a priori and exemplifies the contribution of bridging water molecules to overall binding affinity.

Partial effects of a mutation, that is, the effects caused by separate atomic groups or interactions, depend on a particular alchemical path and for this reason are not meaningful (3). To avoid this difficulty we subdivide the discussed mutations into two steps, each of which has a physical meaning. In the first step the molecule of structural water is decoupled from the complex and moved to the bulk water without changing the ligand. The complex of ligand 1 partially “dried” in this way is completely stable and represents one of its physically possible states. If the cost of the water expulsion is negative, the dried complex is more favorable and would be the major state of the complex in solution. However, a positive effect means an increase of the stability of the bound complex by a water bridge between the protein and ligand. Note that such a calculation with the modified ligand (in this case, ligand 2) can be done to decide whether the water should be removed as a result of the mutation. Alternatively one can compare which mutation—with or without water expulsion—would be more favorable. Indeed, we used this approach to validate the necessity for water displacement, and it could also be used in the case of mutated ligands for which the x-ray structure of the complex is unknown.

As the second step, the mutation from ligand 1 to ligand 2 in the dried complex is simulated to estimate the role of the intermolecular interactions in the affinity differences. The results of the two steps are presented in Table 5. Note that the combined effect of the drying step and the mutation step is equivalent to the effect of the single mutation from ligand 1 to ligand 2 including water displacement presented in Table 2. In this way, we incidentally obtained another closed mutation cycle (1 → 1dried → 2dried → 1) to further verify the stability of the methodology.

Table 5.

Relative binding free energies in mutations involving structural water replacement obtained with QMPFF3 force field (kcal/mol)

Mutation	Trypsin	Thrombin	uPA
1→1dryed	3.4 (3)	4.8 (3)	0.5 (2)
1dryed→2dryed	−0.8 (3)	−0.2 (3)	0.0 (3)
1→2dryed*	2.1 (4)	4.9 (3)	0.8 (3)
cycle closure	0.5 (6)	−0.3 (5)	−0.3 (5)

*Results for 1→2dryed are taken from Table 2.

It is clear that the mutation from ligand 1 to ligand 2, viewed as a separate process taking place in the dried site, is slightly favorable and has approximately the same effect for all proteins. In contrast, the water displacement is unfavorable in all cases and very sensitive to the particular protein environment. Hence, the water is responsible for almost all of the difference in binding affinity between proteins observed experimentally. This interpretation is not trivial and differs from that made based only on the experimental results and difference of the structures of the S1 sites (37).

The results of this section exemplify the influence of structural water on ligand binding, which has been increasingly discussed in the literature (e.g., ref. 45), and underlines the critical necessity of accounting for this effect to reproduce relative binding affinities accurately. More generally, the analysis demonstrates the value of the presented simulations for correct interpretation of experimental data, which is of major importance for effective ligand optimization.

Discussion and Conclusion.

It is surprisingly difficult to assess the current state of the art in protein–ligand free-energy calculations. Unquestionably, a number of impressively accurate results have been published for both relative and more recently absolute binding free-energy calculations (6–14), with a general trend toward increased ambition and accuracy as computer power and theoretical understanding have increased. However, it is equally true that binding affinity calculations by simulation methods are not widely used in the pharmaceutical industry (3) and have not yet had the same impact that simpler docking and scoring methods and general molecular modeling have had. In part, the methods used by academic experts and a few companies may be too time-consuming and specialized for the average industrial computational chemist. Moreover, a widespread feeling that the excellent results obtained in certain cases may not be generally replicable in other cases, especially when the experimental answer is not known beforehand to guide method development, may also be contributing to the slow uptake of the technology into everyday drug design practice.

In this work we have investigated whether a polarizable, transferable FF fitted exclusively to high-level QM data is advantageous in providing adequate results in MD simulations of protein–ligand binding. For this purpose we applied our methodology to complexes with serine proteases, which relate to an actual drug design problem. However, these proteins are known to have relatively rigid sites that reduce convergence and sampling problems as well as other issues of the MD protocol and allow us to concentrate on the role of the FF. The recently introduced ab initio force field QMPFF3 was used, because it had demonstrated high accuracy and transferability in crystal and liquid simulations (34–36) as a result of its strong physical basis and explicit polarizability. It is important to repeat that QMPFF3 was fitted only to QM data for a set of small molecules and their multimers and was in no way tuned for the systems being analyzed here.

The results presented in this article, in particular, comparison with the widely used molecular mechanics force field MMFF, show that a transferable quantum mechanically modeled FF such as QMPFF3 can indeed be important for accurate free-energy calculations. In the system analyzed, the calculated relative binding affinities using QMPFF3 are in good quantitative agreement with experiments for the whole dataset. They provide correct qualitative conclusions on the relative tightness of the protein–ligand complexes and are able to predict subtle differences between effects of the same mutation for different proteins. Moreover, analysis of the remaining deviations of the current results from experiment suggests that further improvement is possible by refining the torsion component of our FF to more closely reproduce ab initio QM results, which will be done in future versions of QMPFF (36).

As mentioned above MMFF was chosen for comparison because, like QMPFF, it was parameterized from ab initio QM data. Of course, it could be argued that MMFF may not be the best possible nonpolarizable FF and the results obtained by using some other FF might be better. However, we would like to stress again that all MMFF predictions (except for one outlying point for thrombin) are in a reasonable range and some are even perfect: it is only by considering the whole set that one can conclude that the FF is inadequate in the system studied. Such a situation represents exactly what can be expected if a FF is accurate in systems close to those used for its training but is restricted in its transferability to other systems. This idea is supported by a more detailed consideration of the results obtained in ref. 13. In this investigation, the authors used the CHARMM force field fitted specially for protein simulations. Nevertheless, although all calculated absolute affinities presented in table 3 of ref. 13 are in the experimental range, a considerable achievement, they still say nothing regarding the relative tightness of the protein–ligand complexes, because the computational-experimental correlation coefficient is R² = 0.0063.

To allow the use of a polarizable FF with reasonable computational efficiency, a special mutation protocol based on Multiconfiguration Thermodynamic Integration was applied. Appropriate choice of the alchemical path (the manner of parameter switching) allows simulation of the whole mutation in one step with only a few windows for the alchemical parameter. To make the protein calculations computationally effective, a suitable method of periphery fixation was developed and validated. For the same reason, a cutoff approach was used while we attempted to avoid known artifacts by appropriate discharging of the protein periphery. By combining these and other ideas (all methods used are described in detail in SI Text), and despite the use of a more computationally intensive polarizable FF, it was possible to simulate each mutation in only 49–60 h (9–15 h with MMFF) on a cluster of 10 microprocessors, avoiding any need for a supercomputer or even for a large cluster. Although we attempted to minimize the impact of the necessary approximations on accuracy by extensive validation, as described in the SI Text, further testing of our methodology and FF is highly desirable, by applying it to a diverse set of protein–ligand complexes including those involving larger alchemical transformations.

The good quantitative agreement with experiment seen here and the ability to distinguish differences in mutation effects for different ligands and different proteins provides a possibility to use our methodology to rationalize the ligand optimization procedure. An example of such a rationalization was given by demonstrating the role of structural water replacement in some of the considered mutations. Understanding why certain alterations increase binding affinity is critical in suggesting new ligands, which can then be tested by MD simulation before chemical synthesis. Thus, the current investigation is a step toward the realization of the long-standing hope to use modern free-energy calculation methodologies in practical drug design.