Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Jul 1.
Published in final edited form as: J Exp Child Psychol. 2007 Nov 26;100(3):225–233. doi: 10.1016/j.jecp.2007.10.003

Quantity Representation in Children and Rhesus Monkeys: Linear versus Logarithmic Scales

Michael J Beran 1, Julie S Johnson-Pynn 2, Christopher Ready 3
PMCID: PMC2492577  NIHMSID: NIHMS55751  PMID: 18022633

Abstract

The performance of 4- and 5-year-old children and rhesus monkeys was compared using a computerized task for quantity assessment. Participants first learned two quantity anchor values and then responded to intermediate values by classifying them as either similar to the large anchor or the small anchor. Of primary interest was an assessment of where the point of subjective equality (PSE) occurred for each species across four different sets of anchors to determine whether the PSE occurred at the arithmetic mean or the geometric mean. Both species produced PSEs that were closer to the geometric mean for three of four anchor sets. This indicates that monkeys and children access either a logarithmic scale for quantity representation or a linear scale that is subject to scalar variability, both of which are consistent with Weber’s law and representation of quantity that takes the form of analog magnitudes.

Keywords: Quantity Judgments, Representational Scale, Children, Monkeys, Bisection Task

The quantity discriminations made by many species are restricted in their accuracy on the basis of the ratio between those sets (e.g., Barth, Kanwisher, & Spelke, 2003; Beran, 2007; Beran, Taglialatela, Flemming, James, & Washburn, 2006; Brannon, Cantlon, & Terrace, 2006; Brannon & Terrace, 2000; Call, 2000; Cantlon & Brannon, 2006; Huntley-Fenner, 2001). Comparisons with larger ratios (as determined by dividing the smaller quantity by the larger quantity) lead to lower performance levels, even when the distance between sets is constant (e.g., 8 versus 10 is more difficult than 2 versus 4). This suggests that an analog magnitude system produces discriminable representations of sets, and this system is consistent with Weber’s law, which states that discrimination of sets becomes more difficult for a fixed difference as the magnitude of those sets increases.

Evidence for discrimination performance being modulated by Weber’s Law comes from differing sources. One task, used primarily with nonhuman primates, involves judgments between two sets of items (e.g., Beran, 2004; Brannon & Terrace, 2000; Call, 2000; Cantlon & Brannon, 2006; Judge, Evans, & Vias, 2005). This task also sometimes is used with human children (e.g., Brannon & Van de Walle, 2001; Feigenson, Carey, & Hauser, 2003). The second task is the bisection task that has been used extensively with rats and pigeons (e.g., Emmerton & Renner, 2006; Fetterman, 1993; Meck & Church, 1983; Roberts, 2005, 2006) and occasionally with nonhuman primates and human children (e.g., Beran, Smith, Redford, & Washburn, 2006; Droit-Volet, Clement, & Fayol, 2003; Jordan & Brannon, 2006a, 2006b). In the bisection task, two anchor values (e.g., smallest set size and largest set size) are established through training, and then a larger range of values, including intermediate values, are presented. This task provides an important assessment of how quantity is represented because one can establish the point of subjective equality (PSE) at which there is indifference between classifying a stimulus as similar to the small anchor or large anchor.

Knowing where the PSE falls is important in discerning how quantity is represented (Roberts, 2005). One possibility is that these representations are linear. A second possibility is that the scale for representation is linear, but with an increase in the variability of the discrimination proceeding in step with increases in the magnitude of the quantity itself (e.g., scalar variability; Gallistel & Gelman, 1992; Gibbon, 1977; Meck & Church, 1983). A third alternative is that these representations are logarithmic, so that differences between sets with larger magnitudes are more pronounced compared to smaller sets despite the fact that the actual quantitative differences themselves are identical and the variability of the discrimination is constant (Dehaene, 2003; Roberts, 2005). If the PSE falls near the arithmetic mean, this establishes that the scale is linear. If the PSE falls near the geometric mean (the square root of the product of the anchor values), the interpretation is slightly more complicated. This outcome may suggest that the representation is logarithmic with larger values more compressed in their relative spacing compared to smaller values, although it also can reflect a linear scale in which the represented distance between each successive quantity is equal (see Gibbon, 1981; Roberts, 2005).

To date, only two studies have been conducted with human children using the bisection task, with conflicting results. Droit-Volet et al. (2003) presented sequential sets of stimuli to 5-year-old and 8-year-old children and found that the PSE fell near the arithmetic mean. Jordan and Brannon (2006a), however, presented 6-year-old children with static sets of stimuli using a variation of the matching-to-sample paradigm and found that PSEs for two different sets of anchors both were near the geometric mean (a finding that matched a similar test given to rhesus monkeys; Jordan & Brannon, 2006b). Thus, data from human children have offered conflicting evidence of where the PSE falls for bisection tasks. In addition, there are very few direct comparisons of the performance of children and nonhuman animals on the identical tasks designed to assess numerical or quantitative skills (but see Cantlon & Brannon, 2006; Jordan & Brannon, 2006a). Typically, data from nonhuman animals indicate that the PSE falls nearer to the geometric mean (e.g., Emmerton & Renner, 2006), suggesting that representations of quantity are scalar in nature or that there is logarithmic compression of those representations.

We presented rhesus monkeys and human children with the identical computerized bisection task. We tested children who were slightly younger than those in previous studies, we used more anchor values with each participant, and our bisection task differed from previous studies as the response choices were symbolic stimuli rather than analog stimuli matching the sample array. This last modification was necessary because we wanted to avoid having monkeys and children focus on specific properties of the response choices. Instead, we wanted to use consistent, arbitrary labels for the two response classes. Our aim was to assess whether bisection occurred nearer the geometric or arithmetic means for these two species and to compare our results to the previous conflicting studies that also used the bisection method with children.

Methods

Participants

Nineteen human children were tested. There were 11 females and 8 males. The mean age of the children was 54 months (SD = 5.10 months, range 47 months to 65 months). These children all were enrolled at a child development center affiliated with an institution of higher learning in the Southeastern United States. All children were voluntary participants whose parents granted consent prior to the experiment. Children were tested individually, and each child was scheduled to participate in four separate sessions.

Seven adult male rhesus monkeys (Macaca mulatta) were tested, and they ranged in age from 3 years to 21 years (mean = 10 years). All monkeys were trained prior to this experiment to respond to computer generated stimuli using joysticks, and these animals had participated in some previous experiments in which they choose the larger of two sets of analog stimuli (e.g., Beran, 2007). However, only two of the monkeys had ever participated in a bisection task similar to the one used here (Beran et al., 2006).

Apparatus

Trials were presented to the monkeys on a Compaq DeskPro with an attached 17-inch color monitor. Joystick responses were made with a Gravis GamePad Pro digital joystick mounted vertically to the cage. The test program was written in Visual Basic for Windows. When feedback was available for responses (see below), correctly completed trials were automatically rewarded by the computer with single 94 mg Bio-Serv food pellets through use of an automated pellet dispenser (for details, see Richardson et al., 1990). Children completed the experimental program on a Toshiba laptop computer. Children responded through key presses rather than joystick responses.

Design and Procedure

Children and monkeys worked on highly similar computer programs that were modified only slightly for the two species. At the beginning of each session, participants learned the relevant anchor values for that session. The four sets of anchors that were used were 1 and 9, 1 and 16, 2 and 18, and 3 and 12. Each participant was assigned the anchors in a random order.

A to-be-judged array of white dots appeared in the top center of a black screen. The non-overlapping circles had randomly chosen radii (10–20 pixels) and randomly chosen positions to provide for a large number of possible configurations for each quantity. Some of these circles were colored fully in white whereas others were unfilled. We used this manipulation because it resulted in trials of the same quantity including a wide range of illumination levels to help dissociate illumination and quantity (see Beran et al., 2006). At the bottom of the screen, a white letter “L” was on the left side of the screen, and a white letter “M” was on the right side of the screen.

The participant’s task was to decide whether an array’s quantity most closely matched the small anchor or the large anchor designated for the session. During the training phase of each session, all presented sets of dots exactly matched either the small anchor or the large anchor. If the quantity matched the small anchor, the correct response was the “L” stimulus. If the quantity matched the large anchor, the correct response was the “M” stimulus. The monkeys made a response by moving a red cursor to a response letter through hand manipulation of a joystick. Children made a response by pressing one of two keys on either the right or left side of the keyboard. Each key was covered with a different colored sticker to prevent children from pressing any other keys. For monkeys, a correct response produced a food pellet, ascending melodic tones, and the next trial after a 1 s inter-trial interval. An error brought a blank screen, a 1 s buzz tone, and then the next trial after a 20 s inter-trial interval. For the children, a correct response produced a funny noise (such as giggling, laughing, or cheering) and a bright smiling cartoon face in the center of the screen, and the next trial after a 1 s inter-trial interval. An error brought an unhappy cartoon face and some variation of an annoying sound (such as a gong or crash sound). All of the children’s trials were initiated by the experimenter through key presses when a child indicated his or her willingness to continue. There was no timeout period for incorrect responses for the children, and the inter-trial interval varied in relation to the attention level of the child.

One methodological difference between species pertained to the number of trials completed. Because we wanted each child to participate in four sessions (one with each set of anchors), we tried to keep the sessions short so that children would agree to participate over multiple days. Therefore, children produced between 100 and 150 trials in a single session. Rhesus monkeys, however, had continuous access to the task for several hours each day, and the mean number of trials completed by the monkeys was 5,635 trials. However, both species were given the same training criterion with each set of anchors (7 of 10 trials correct) prior to moving to the test phase.

Children also were partially instructed as to the task requirements. They were told they should pay attention to what was on the screen and try to decide which key went with each set. However, children were not explicitly told the anchor values, and none of the instructions given to the children explicitly indicated that the task was quantitative or numerical in nature. Finally, to prevent overt counting responses, children were required to respond as fast as they could, and trials were cleared from the screen and not scored after a 5-s interval without a response from the child. Fewer than 5% of the trials were excluded because of this temporal criterion as children responded very quickly (typically within about 2 s). As there was no expectation that the monkeys could count the arrays of the dots, this temporal criterion was not used with them. Monkeys also responded very quickly (usually in less than 2 s).

During the test phase, the majority of trials for both species consisted of one of the anchor quantities, and feedback was always presented for these trials. However, on approximately one quarter of the trials the participant was presented with a randomly selected intermediate quantity. On these trials, there was no feedback given to either species after a response. Rather, the screen was cleared and the next trial was presented immediately.

The PSE was established for each set of anchors using the best fit equation and determining the theoretical quantity at which 50% of trials were labeled as the small anchor and 50% as the large anchor. The Weber fraction for each species and each set of anchor values was determined by calculating the ratio of one half the difference between the theoretical quantity at which the “L” was selected on 25% of the trials and at which the “L” was selected on 75% of the trials and the PSE (as in Jordan & Brannon, 2006a). For example, if 25% of the trials with sets of four items were classified with the “M” response and 75% of the trials with sets of 10 items were classified with the “M” response, and the PSE was established to be 6, the Weber fraction would be .50.

Results

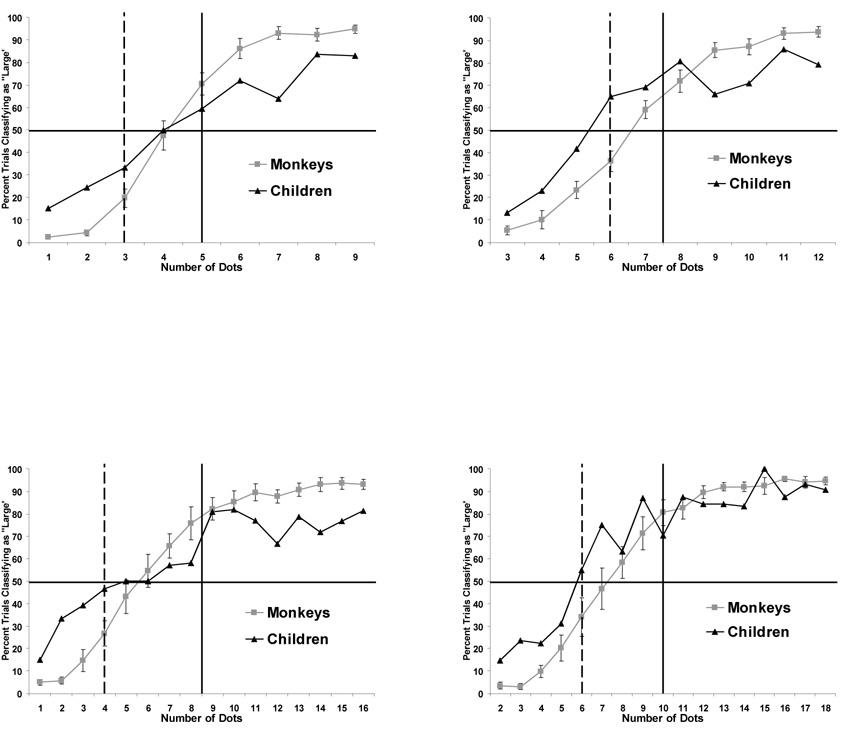
Figure 1 presents the percentage of trials on which participants responded to sets of a given quantity with the “M” response. The monkey values are the means for the group of animals. Because human children completed so few trials at each anchor set compared to the monkeys, and because most of those trials did not involve intermediate quantities, all responses from children were combined so that a sufficiently large corpus of data would be available for presentation and statistical analysis. Therefore, all trials from the children are represented in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Percentage of responses that were to the “M” stimulus as a function of the true quantity of dots presented. Data are presented separately for each species, and each graph shows performance for a different set of anchors. The horizontal line shows the 50% level. The dashed vertical line shows the geometric mean, and the continuous vertical line shows the arithmetic mean for each set of anchors. Bars on the monkey lines show standard errors of the mean. All data are presented for children because of the small number of probe trials.

For each set of anchors, we established a best-fit line for the monkeys’ performance and the children’s performance. The PSE values and Weber fractions from these best-fit lines are presented in Table 1. In all cases except for one, the best fit was logarithmic. The exception was for the anchors 1 and 9, for which a linear fit accounted for the greatest percentage of variance in performance for both species.

Table 1.

Best fit line outcomes for children and monkeys regarding variance accounted for, the point of subjective equality (PSE), and the Weber fraction for each set of anchors

Anchors Arithmetic Mean Geometric Mean Best Fit R2 PSE Weber fraction
1 and 9 5.0 3.0
  Children Linear .945 4.57 .62
  Monkeys Linear .913 4.51 .41
1 and 16 8.5 4.0
  Children Logarithmic .902 4.45 .87
  Monkeys Logarithmic .929 4.95 .65
2 and 18 10.0 6.0
  Children Logarithmic .895 5.53 .49
  Monkeys Logarithmic .939 6.75 .49
3 and 12 7.5 6.0
  Children Logarithmic .875 5.72 .38
  Monkeys Logarithmic .955 6.30 .34
Open in a new tab

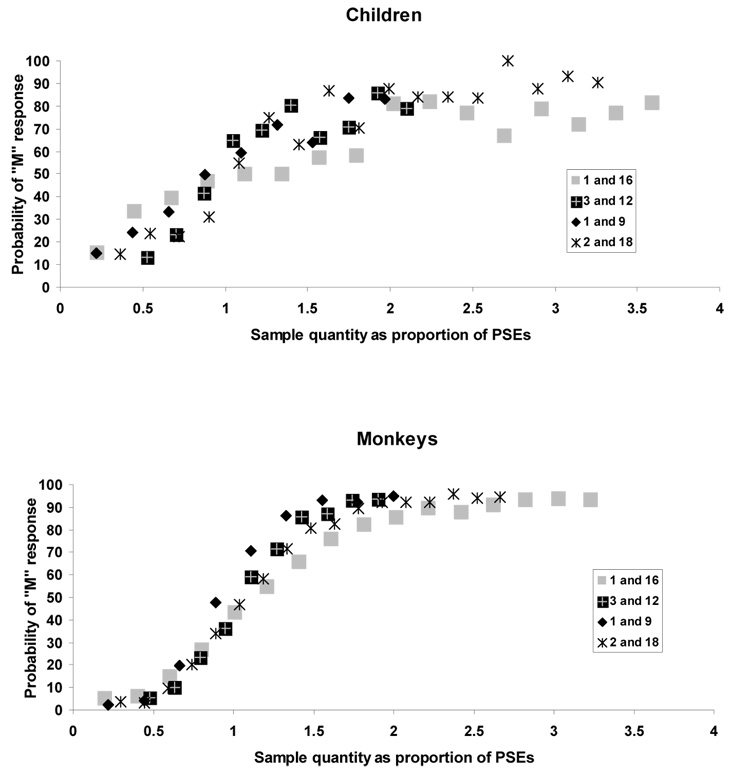
Figure 2 presents performance for each species across all anchor values that are normalized as a proportion of the PSEs. This allows an examination of the extent to which these psychophysical functions overlap (as in Jordan & Brannon, 2006a). For the rhesus monkeys, an Analysis of Covariance with the normalized anchor values as the covariate and the percent of trials classified as closer to the larger anchor as the dependent variable indicated that the regression lines for each pair of anchors were not significantly different from each other, F (3, 47) = 1.97, p = .13. However, the lines were different for the data from children, F (3, 47) = 3.04, p = .038.

Figure 2.

Figure 2

Open in a new tab

The percentage of “M” responses across all sets of anchor values for each species. Individual set sizes are normalized as a proportion of the PSE for each set of anchor values. This allows a direct comparison across different anchors values in terms of how often each specific quantity was classified as closer to the larger anchor value.

Discussion

The performance of the monkeys and the children showed some similarities and some differences. The PSE values for the children fell near the geometric mean for three out of four anchor values. These data were consistent, in general, with Weber’s law. This means that children were representing the quantities either linearly with scalar variance or logarithmically. These data from 4- and 5-year-old children match those of Jordan and Brannon (2006a) with 6-year old children. Our data and those of Jordan and Brannon (2006a) differ from those reported from 5- and 8-year-old children (Droit-Volet et al., 2003) that indicated that the PSE for children fell closer to the arithmetic mean (see Jordan and Brannon, 2006, for some suggestions as to how differences in methodology may have contributed to these different outcomes). The children in our study produced a wider range of Weber fractions than did those in the Jordan and Brannon (2006a) study, and this may have been the result of the younger age of the children we tested, although it may also have been the result of the small number of probe trials that we could present. Therefore, future studies will need to better demonstrate the consistency of the Weber fraction across quantity ranges, as well as further lower the minimum age of the children tested. Our study also demonstrates that presenting symbolic response options for this type of bisection task does not change the general nature of responding by young children while also allowing for the removal of potentially distracting response stimulus features (such as their element arrangement, density, etc.).

Overall, the data from the monkeys were better fit as logarithmic functions, although monkey PSEs were closer to the arithmetic means compared to the children’s PSEs for two of the anchor sets (3:12 and 2:18; Figure 1). Jordan and Brannon (2006a, 2006b) reported that the psychophysical functions were superimposed for the two anchor sets they presented to monkeys and children. This was true as well for our monkeys although the functions were different for the children primarily as a result of the 1 and 9 anchor set.

Both species’ best-fit lines for the data with the 1 and 9 anchors were linear. Those data looked more like the data reported by Droit-Volet et al. (2003) and differ from the other anchor sets we used. What might account for the difference with this one set of anchors? Because this set contained the smallest quantities, it may have encouraged more of an enumerative strategy, which in turn may have activated a linear representation. Siegler and Booth (2004) have suggested that children may use multiple forms of representation when dealing with large numbers and small numbers of items, and that may be the case here as well. In addition, they suggested that the form of representation also shifts with development, from logarithmic during preschool years to a mix of logarithmic and linear representations, and then to a linear representation during the school years. Thus, a mix of representations is not without precedent.

The PSE data for both species complements the data reported by Jordan and Brannon (2006a, 2006b) by also showing that monkeys and children represent quantity either linearly with scalar variance or logarithmically. The underlying representation of the presented quantities may be logarithmic (Dehaene, 1997; Roberts, 2005) where smaller quantities are represented with a greater distance between them whereas larger quantities are more compressed in their representation. Thus, the same absolute difference between quantities would become increasingly smaller on a log scale of representation as quantity increased in general. However, the underlying representation instead may be linear if variability is scalar and increases in proportion to the size of the number (Meck & Church, 1983; Roberts, 2005). Although we cannot differentiate between linear representations with scalar variability or logarithmic representations by these two species, the data do indicate that performance is constrained by Weber’s law for both species, although perhaps to somewhat different degrees. Further investigations, including those with additional species and younger children, are needed to better discern the form of a potentially phylogenetically widespread mechanism for representing quantity.

Acknowledgements

Michael J. Beran, Language Research Center, Georgia State University; Julie S. Johnson-Pynn, Department of Psychology, Berry College; Christopher Ready, Department of Psychology, Berry College.

This research was supported by National Institute of Child Health and Human Development Grant HD-38051 and by Grant BCS-0634662 from the National Science Foundation.

Address correspondence to Michael Beran at: Language Research Center, Georgia State University, P.O. Box 3965, Atlanta, GA 30302; e-mail to mjberan@yahoo.com.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Contributor Information

Michael J. Beran, Georgia State University

Julie S. Johnson-Pynn, Berry College

Christopher Ready, Berry College.

References

  1. Barth H, Kanwisher N, Spelke E. The construction of large number representations in adults. Cognition. 2003;86:201–221. doi: 10.1016/s0010-0277(02)00178-6. [DOI] [PubMed] [Google Scholar]
  2. Beran MJ. Chimpanzees (Pan troglodytes) respond to nonvisible sets after one-by-one addition and removal of items. Journal of Comparative Psychology. 2004;118:25–36. doi: 10.1037/0735-7036.118.1.25. [DOI] [PubMed] [Google Scholar]
  3. Beran MJ. Rhesus monkeys (Macaca mulatta) enumerate sequentially presented sets of items using analog numerical representations. Journal of Experimental Psychology: Animal Behavior Processes. 2007;33:42–54. doi: 10.1037/0097-7403.33.1.42. [DOI] [PubMed] [Google Scholar]
  4. Beran MJ, Smith JD, Redford JS, Washburn DA. Rhesus monkeys (Macaca mulatta) monitor uncertainty during numerosity judgments. Abstracts of the Psychonomic Society. 2005;10:60–61. [Google Scholar]
  5. Beran MJ, Taglialatela LA, Flemming TJ, James FM, Washburn DA. Nonverbal estimation during numerosity judgements by adult humans. Quarterly Journal of Experimental Psychology. 2006;59:2065–2082. doi: 10.1080/17470210600701171. [DOI] [PubMed] [Google Scholar]
  6. Brannon EM, Cantlon JF, Terrace HS. The role of reference points in ordinal numrical comparisons by rhesus macaques (Macaca mulatta) Journal of Experimental Psychology: Animal Behavior Processes. 2006;32:120–134. doi: 10.1037/0097-7403.32.2.120. [DOI] [PubMed] [Google Scholar]
  7. Brannon EM, Terrace HS. Representation of the numerosities 1–9 by rhesus macaques (Macaca mulatta) Journal of Experimental Psychology: Animal Behavior Processes. 2000;26:31–49. doi: 10.1037//0097-7403.26.1.31. [DOI] [PubMed] [Google Scholar]
  8. Brannon EM, Van de Walle GA. The development of ordinal numerical competence in young children. Cognitive Psychology. 2001;43:53–81. doi: 10.1006/cogp.2001.0756. [DOI] [PubMed] [Google Scholar]
  9. Call J. Estimating and operating on discrete quantities in orangutans (Pongo pygmaeus) Journal of Comparative Psychology. 2000;114:136–147. doi: 10.1037/0735-7036.114.2.136. [DOI] [PubMed] [Google Scholar]
  10. Cantlon JF, Brannon EM. Shared system for ordering small and large numbers in monkeys and humans. Psychological Science. 2006;17:401–406. doi: 10.1111/j.1467-9280.2006.01719.x. [DOI] [PubMed] [Google Scholar]
  11. Dehaene S. The neural basis of the Weber-Fechner law: A logarithmic mental number line. Trends in Cognitive Sciences. 2003;7:145–147. doi: 10.1016/s1364-6613(03)00055-x. [DOI] [PubMed] [Google Scholar]
  12. Droit-Volet S, Clement A, Fayol M. Time and number discrimination in a bisection task with a sequence of stimuli: A developmental approach. Journal of Experimental Child Psychology. 2003;84:63–76. doi: 10.1016/s0022-0965(02)00180-7. [DOI] [PubMed] [Google Scholar]
  13. Emmerton J, Renner JC. Scalar effects in the visual discrimination of numerosity by pigeons. Learning and Behavior. 2006;34:176–192. doi: 10.3758/bf03193193. [DOI] [PubMed] [Google Scholar]
  14. Feigenson L, Carey S, Hauser MD. The representations underlying infants' choice of more: Object files versus analog magnitudes. Psychological Science. 2002;13:150–156. doi: 10.1111/1467-9280.00427. [DOI] [PubMed] [Google Scholar]
  15. Fetterman JG. Numerosity discrimination: Both time and number matter. Journal of Experimental Psychology: Animal Behavior Processes. 1993;19:149–164. [PubMed] [Google Scholar]
  16. Gallistel CR, Gelman R. Preverbal and verbal counting and computation. Cognition. 1992;44:43–74. doi: 10.1016/0010-0277(92)90050-r. [DOI] [PubMed] [Google Scholar]
  17. Gibbon J. Scalar expectancy theory and Weber's law in animal timing. Psychological Review. 1977;84:279–325. [Google Scholar]
  18. Huntley-Fenner G. Children's understanding of number is similar to adults' and rats': Numerical estimation by 5–7-year-olds. Cognition. 2001;78:B27–B40. doi: 10.1016/s0010-0277(00)00122-0. [DOI] [PubMed] [Google Scholar]
  19. Jordan KE, Brannon EM. A common representational system governed by Weber's law: Nonverbal numerical similarity judgments in 6-year-olds and rhesus macaques. Journal of Experimental Child Psychology. 2006a;95:215–229. doi: 10.1016/j.jecp.2006.05.004. [DOI] [PubMed] [Google Scholar]
  20. Jordan KE, Brannon EM. Weber’s Law influences numerical representations in rhesus macaques (Macaca mulatta) Animal Cognition. 2006b;9:159–172. doi: 10.1007/s10071-006-0017-8. [DOI] [PubMed] [Google Scholar]
  21. Judge PG, Evans TA, Vyas DK. Ordinal representation of numeric quantities by brown capuchin monkeys (Cebus apella) Journal of Experimental Psychology: Animal Behavior Processes. 2005;31:79–94. doi: 10.1037/0097-7403.31.1.79. [DOI] [PubMed] [Google Scholar]
  22. Meck WH, Church RM. A mode control model of counting and timing processes. Journal of Experimental Psychology: Animal Behavior Processes. 1983;9:320–324. [PubMed] [Google Scholar]
  23. Richardson WK, Washburn DA, Hopkins WD, Savage-Rumbaugh ES, Rumbaugh DM. The NASA/LRC Computerized Test System. Behavior Research Methods, Instruments, and Computers. 1990;22:127–131. doi: 10.3758/bf03203132. [DOI] [PubMed] [Google Scholar]
  24. Roberts WA. How do pigeons represent numbers? Studies of number scale bisection. Behavioural Processes. 2005;69:33–43. doi: 10.1016/j.beproc.2005.01.005. [DOI] [PubMed] [Google Scholar]
  25. Roberts WA. Evidence that pigeons represent both time and number on a logarithmic scale. Behavioural Processes. 2006;72:207–214. doi: 10.1016/j.beproc.2006.03.002. [DOI] [PubMed] [Google Scholar]
  26. Siegler RS, Booth JL. Development of numerical estimation in young children. Child Development. 2004;75:428–444. doi: 10.1111/j.1467-8624.2004.00684.x. [DOI] [PubMed] [Google Scholar]

RESOURCES