Ion-Nanotube Terahertz Oscillator

Abstract

We report the intriguing dynamics of a potassium ion interacting with a 16 Å carbon nanotube. The ion induces a strong dielectric response in the nanotube wall that can be described through a self-consistent tight-binding method. The polarization of the nanotube was found to play a critical role in the ion-nanotube interaction, which exhibits a low access barrier of only 1.05 kcal/mol and a deep, attractive well with a depth of about 30 kcal/mol. An ion bound in the nanotube is predicted to oscillate at a frequency of about 0.4 terahertz, dragging the electrons of the nanotube along. Besides its appealing nature in low-dimensional physics, such nano-oscillator may serve as a room temperature terahertz wave detector.

Confined in one-dimensional carbon nanotubes (CNTs), molecules exhibit dynamics not observed in bulk systems [1–3]. Such CNT-confined systems have been proposed both as nanoelectromechanical devices such as ultrafast memory units [1] or gigahertz oscillators [2], and as templates that mimic biological channels [3–5]. Most theoretical investigations presently are either of the computationally cheap classical molecular dynamics (MD) type [3–5] or of the computationally expensive ab initio MD type [6, 7], lacking a simple, efficient, and accurate description of the electronic degrees of freedom for CNTs. Recently, both classical and semi-empirical approaches were proposed to address this problem by, for example, including the curvature induced static dipole moment [8], recalibrating atomic partial charges of the CNT from density functional theory (DFT) calculations [9], and incorporating the dielectric response of CNTs through solving the Lippmann-Schwinger equation [10], or through a Hamiltonian approach [11]. It has been demonstrated that [9] the self-consistent π-electron tight-binding (TB) approach shows excellent agreement with DFT results.

In this work, we studied a potassium ion (K⁺) interacting with an open-ended 12-section (6,6) carbon nanotube as shown in Fig. 1a. The CNT is 15.6 Å long and 8.3 Å in diameter with both ends saturated by hydrogen atoms. The structure of the CNT was constructed by folding a graphite layer into a hollow cylinder with C-C and C-H bond lengths fixed at 1.44 Å and 1.09 Å, respectively.

FIG. 1.

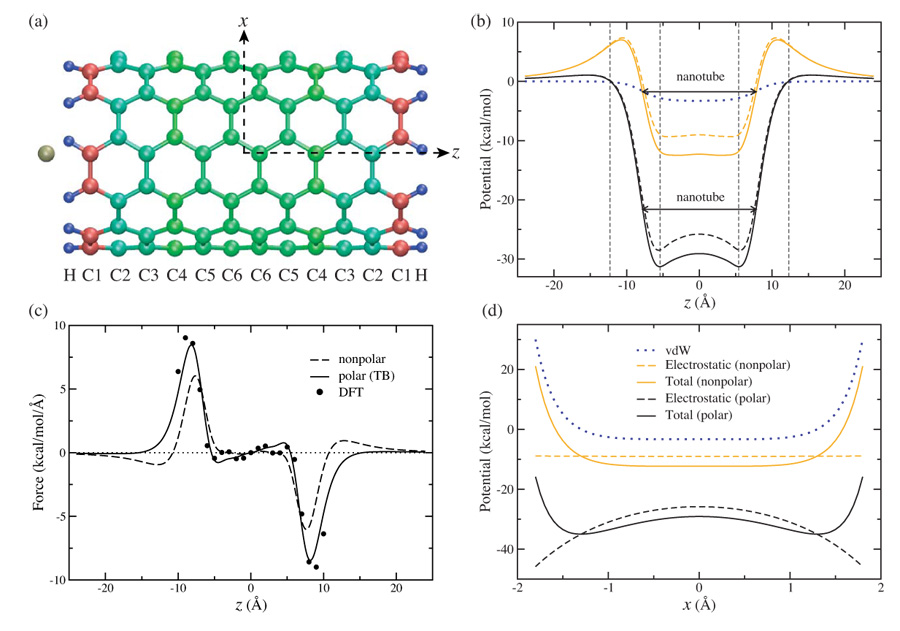
(color online). Structure and energetics of the nano-oscillator. (a) Front view of the nano-oscillator. The nanotube is colored according to initial atomic partial charges q₀. Blue (H): positive; red (C1): negative. (b) Interaction energies between the potassium ion and the nanotube along the z-axis. The intervals used for the numerical fitting of the total potential to V (z) = c₀+c₂ z² are indicated by dashed lines (see text). (c) Force acting on the ion positioned along the z-axis. Comparison is made between a nonpolarizable nanotube model (dashed line), a polarizable nanotube model (solid line), and DFT calculations (solid circles). (d) Same as (b), but along the x-axis.

The K⁺-CNT complex was divided into a quantum mechanical region (the CNT), and a classical particle (the K⁺ ion). The interaction potential $V(\overrightarrow{R})$ consists of van der Waals (vdW) and electrostatic terms,

$$V(\overrightarrow{R})={\displaystyle \sum _i{V}_{\mathrm{L}\mathrm{J}}(|\overrightarrow{R}-{\overrightarrow{r}}_i|)+{\displaystyle \sum _i\frac{Q[q_{0i}+\delta q_i(\overrightarrow{R})]}{|\overrightarrow{R}-{\overrightarrow{r}}_i|}}},$$ (1)

where Q and $\overrightarrow{R}$, respectively, are the charge and coordinates of the K⁺ ion. The summation index, i, runs through each atomic site of the CNT. The vdW interaction was described by the Lennard-Jones potential V_LJ(r) = 4.0 ε [(σ/r)¹² − (σ/r)⁶] with parameters taken from the CHARMM27 force field [12, 13], i.e., ε_KH = 0.043749 kcal/mol, ε_KC = 0.078039 kcal/mol, σ_KH = 2.7473 Å, and σ_KC = 3.3464 Å. The initial atomic partial charges q_0i were determined from DFT calculations on an isolated CNT [9] as q₀(H)= 0.138308 e, q₀(C1)= −0.176750 e, q₀(C2)= 0.032725 e, q₀(C3)= 0.023788 e, q₀(C4)= −0.022954 e, q₀(C5)= 0.006498 e, and q₀(C6)= −0.001615 e.

Due to the presence of the ion, the CNT becomes polarized. It is well-known that infinitely long armchair CNTs are metallic [14], and their π-electrons can effectively screen out external fields [15, 16]. Limited by the finite length, both the parallel and perpendicular dielectric constants are around 5 for the CNT segment under study [9]. In this work, the dielectric response of the CNT is described through a self-consistent TB Hamiltonian [9, 11], which allows one to compute the induced charges of the CNT due to an external field. To efficiently incorporate the polarization effect into MD simulations, the instantaneous atomic partial charges of the CNT are updated constantly as the sum of the bare charges, q₀, and the induced charges, δq.

As one can see from Fig. 1b, the axial motion of the ion is dominated by the electrostatic interactions. Coulomb interaction due to the static charges q₀ is attractive inside the CNT and repulsive outside, a feature resulting from the dipole fields created by the slightly positively charged H atoms and negatively charged C1 atoms at the ends of the CNT. Without considering the polarization effect of the CNT, the access barrier amounts to 7.02 kcal/mol, which would make it extremely difficult for a K⁺ ion to enter the CNT at room temperature (1k_BT = 0.59 kcal/mol, with k_B the Boltzmann constant and T = 298K).

However, the dielectric response of the CNT has a significant effect on the interaction potential profile. By applying the self-consistent TB approach [9, 11], one can quantify the attraction of a K⁺ ion by the polarizable CNT. As a result, the potential curve for the ion is nearly flat outside the CNT with a maximum of only 1.05 kcal/mol, and becomes strongly attractive inside the CNT with a minimum at about −30 kcal/mol. Compared to the nonpolarizable model, the edge of the central potential energy well becomes much steeper, and the double-well feature becomes pronounced with two minima separated by about 10.8 Å as shown in Fig. 1b and 1c. The lowered access barrier enables the K⁺ ion to enter the CNT spontaneously at room temperature, and the deep well traps the ion firmly. Since the underlying mechanism is dominated by the Coulomb interaction, trapping is insensitive to the exact values of vdW parameters, which are usually not known accurately. Thus, our suggestion is force field independent and should also apply to monovalent cations other than potassium.

In the radial direction x, the ion is confined within a few Å around the origin, where the Coulomb potential caused by q₀ is nearly constant (Fig. 1d). As the ion departs from the z-axis, the electrostatic potential is lowered by δq, while the vdW potential increases rapidly. Due to the interplay of these three contributions, the total potential exhibits a low local maximum at the origin and a minimum at a radial distance of about 1.3 Å.

To evaluate the quality of the suggested description, we performed a series of single point DFT calculations to determine the force acting on the ion positioned along the z-axis (Fig. 1c). The calculations were carried out using the B3LYP/6–31G* [17] model implemented in the Gaussian 03 package [18]. Except for the case that the ion is located at the origin, where the K⁺-CNT complex has a D_6d symmetry, the remainder of the calculations assumed a C_6υ symmetry. Despite the simplicity of the proposed TB model, such as the point charge approximation, exclusion of σ-electrons, lack of exchange and correlation terms, and negligence of charge transfer between CNT and ion, one notes a remarkable agreement between the forces calculated from the DFT treatment and the suggested model. This indicates that the semi-empirical quantum mechanical description of the CNT electrons, combined with a classical MD simulation of the ion, captures the essence of the ion motion in the CNT.

More details of the potential field are revealed from the contour plot on the x-z plane in Fig. 2a. At the origin O, the potential has a local maximum. Along the path from O via P to one of the minima Q, the change in the potential is about 8.4 kcal/mol as shown in Fig. 2b. In the x-y plane, the potential field can be constructed by taking advantage of the six-fold rotational symmetry of the system. For radial distances of less than 2 Å, however, the potential is found to be of nearly cylindrical symmetry.

FIG. 2.

(color online). Energy map. (a) Contour plot of the total interaction energy in the x-z plane. The energy minimum, V_min = −37.48 kcal/mol, is located at Q = (1.30, 0, 5.80)Å. Color codes for values of the interaction energy given in units of kcal/mol are defined in the side bar. (b) Energy profile along the path O→P→Q→O, as indicated by the dashed line in (a) with P = (0, 0, 5.80)Å.

One can estimate the oscillation frequency of the K⁺ ion from the total interaction potential shown in Fig. 1b. The harmonic component of the potential was extracted from a quadratic expansion, V (z) = c₀ + c₂ z². The region in which the potential curve exhibits its dominant slope, i.e., 5.4 Å ≤ |z| ≤ 12.3 Å was selected for the fitting to ensure a positive c₂, which is obtained as 0.31 kcal/mol/Ų. The oscillating frequency is estimated as $f\approx \sqrt{2c_2/M}/2\pi =0.41$ terahertz (THz), where M = 39.09 amu is the mass of the K⁺ ion.

To investigate the dynamics of the K⁺-CNT complex, we simulated the system for 4.84 ps employing the polarizable CNT model [9, 11] in a microcanonical ensemble with the CNT frozen at its ideal geometry. At each integration time step (2 fs), the electric field of the ion was regarded as an external perturbation in the TB Hamiltonian, and the induced charges δq_i of CNT were evaluated by relaxing the CNT to its TB Born-Oppenheimer surface. Since the CNT is fixed throughout the simulation, δq_i depend only on the position of the K⁺ ion, $\overrightarrow{R}$. The force is the total derivative of the potential in Eq. (1),

$$\overrightarrow{F}(\overrightarrow{R})=-{\displaystyle \sum _i\overrightarrow{\nabla }{V}_{\mathrm{L}\mathrm{J}}(|\overrightarrow{R}-{\overrightarrow{r}}_i|)}+{\displaystyle \sum _i\left[\frac{Q(q_{0i}+\delta q_i(\overrightarrow{R}))(\overrightarrow{R}-{\overrightarrow{r}}_i)}{|\overrightarrow{R}-{\overrightarrow{r}}_i{|}^3}-\frac{Q\overrightarrow{\nabla }\delta q_i(\overrightarrow{R})}{|\overrightarrow{R}-{\overrightarrow{r}}_i|}\right]},$$ (2)

where the last term is a correction term that explicitly accounts for the dependence of δq_i on $\overrightarrow{R}$. During the MD simulation, this term was computed numerically at each integration time step.

At the beginning of the simulation, a K⁺ ion was released with zero initial velocity on the z-axis at (0, 0,−8.803) Å, 1.0 Å away from one end of the CNT. Attracted by the potential well, the ion began to oscillate. During the simulation, the ion finished two complete oscillation cycles with a frequency of 0.43 THz as shown in Fig. 3a, consistent with the estimate given above. The motion of the ion naturally drags the electrons of the CNT to oscillate at the same frequency. The total energy of the ion, a sum of potential energy and kinetic energy, was conserved throughout the simulation with a peak deviation of 0.02% (Fig. 3b). According to Fig. 1d and Fig. 2, points on the z-axis correspond to local potential maxima on the cross sections of the CNT. Small perturbations in the radial direction can cause the ion to move off the z-axis, which may lead to a deviation in the axial oscillation frequency. In order to examine the uncertainty in the oscillation frequency, the K⁺ ion was placed off the z-axis at (1.4, 0,−8.803) Å at the beginning of a second simulation. It was found that the axial oscillation of the ion is accompanied by fluctuations in the cross section of the CNT, resulting in a slight decrease of the oscillation frequency by 5%.

FIG. 3.

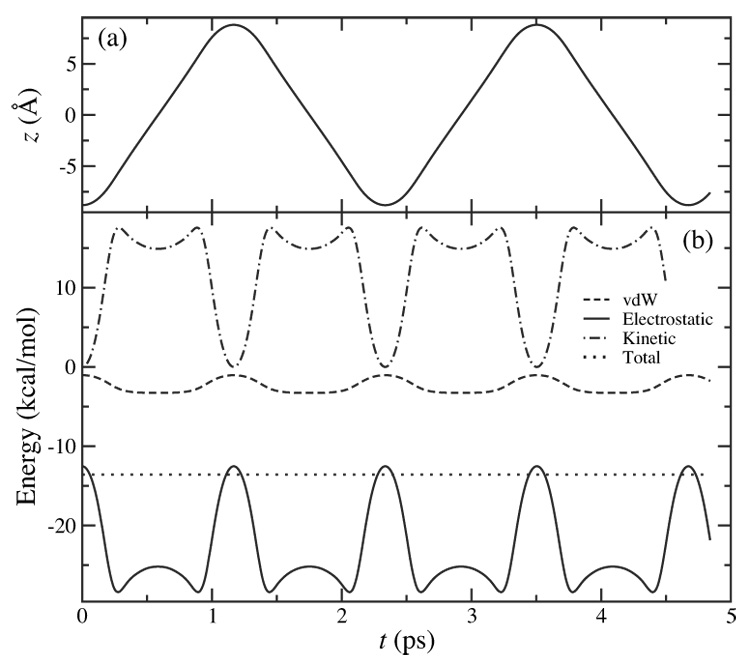
Dynamics of the nano-oscillator. (a) Oscillating motion of the K⁺ ion. (b) Energy constancy of the oscillator during the simulation. The simulation length is 4.84 ps with an integration time step of Δt = 2 fs. The same results were obtained for Δt = 1 fs.

Energy dissipation, e.g., through the phonon modes of the CNT, should damp the oscillation observed in the above quantum mechanical / molecular mechanical simulations. Investigations on coaxial multi-walled CNTs [2, 19, 20] show a small friction force in the order of 10⁻¹⁵ ~ 10⁻¹⁴ N per atom between CNTs in contact. In addition, studies of fast moving charged particles on a two-dimensional surface [21] or along a one-dimensional channel [22,23] suggest that excitation of surface-plasmons is responsible for energy losses of the particles. Hence, a complete characterization of the nano-oscillator requires knowledge of the vibrational modes as well as of the dynamic dielectric response function of the CNT. Work in this direction is in progress.

Terahertz optics is an emerging field with promising applications including material characterization, tomographic imaging, as well as chemical and biological sensing [24, 25]. Presently, development of THz technologies is hindered by difficulties in the generation and detection of THz electromagnetic fields. The nano-oscillator identified here may serve as a THz wave detector which can operate at room temperature.