The degree of nonlinearity and anisotropy of blood vessel elasticity

Abstract

Blood vessel elasticity is important to physiology and clinical problems involving surgery, angioplasty, tissue remodeling, and tissue engineering. Nonlinearity in blood vessel elasticity in vivo is important to the formation of solitons in arterial pulse waves. It is well known that the stress–strain relationship of the blood vessel is nonlinear in general, but a controversy exists on how nonlinear it is in the physiological range. Another controversy is whether the vessel wall is biaxially isotropic. New data on canine aorta were obtained from a biaxial testing machine over a large range of finite strains referred to the zero-stress state. A new pseudo strain energy function is used to examine these questions critically. The stress–strain relationship derived from this function represents the sum of a linear stress–strain relationship and a definitely nonlinear relationship. This relationship fits the experimental data very well. With this strain energy function, we can define a parameter called the degree of nonlinearity, which represents the fraction of the nonlinear strain energy in the total strain energy per unit volume. We found that for the canine aorta, the degree of nonlinearity varies from 5% to 30%, depending on the magnitude of the strains in the physiological range. In the case of canine pulmonary artery in the arch region, Debes and Fung [Debes, J. C. & Fung, Y. C.(1995) Am. J. Physiol. 269, H433–H442] have shown that the linear regime of the stress–strain relationship extends from the zero-stress state to the homeostatic state and beyond. Both vessels, however, are anisotropic in both the linear and nonlinear regimes.

In solving any surgical problems of a blood vessel, physicians need to know the mechanical properties of the blood vessels. In devising any strategy to heal or remodel an artery, we must know the stress and strain in the vessel (1–8). To determine the stress and strain, we must know the constitutive equations of the materials (1, 4, 5, 7, 9). To determine the constitutive equation, we must know the zero-stress state of the material (10, 11). The constitutive equation of the blood vessel wall has been studied by Bergel, Patel, Vaishnav, Fung, Hayashi and many others (see refs. 1, 2, 5, 8, and 12 and references therein). Conventionally, tests were done on cannulated excised straight segments of blood vessels by longitudinal stretching and circumferential distension with internal pressure. Fung (13, 14) summarized the experimental viscoelastic results by describing the arterial wall as pseudo-elastic, which has the characteristics that its hysteresis is essentially independent of frequency over a wide range of 5 to 6 decades. This pseudo-elasticity is explained by a stress-relaxation function that has a continuous relaxation spectrum. For pseudo-elastic bodies, the loading and unloading curves are repeatable in cyclic testing, hence each can be treated as an elastic curve. Aorta is pseudo-elastic, and its hysteresis is small (∼5%). Until 1983, however, it was not known that the zero-stress state of the aorta (or more precisely, the state of zero stress-resultants and stress-moments) is not an unloaded tube, but is an open sector (10, 11). Thus, all pre-1983 data and most newer ones were not referred to the correct zero-stress state. On the other hand, newer data that refer to the zero-stress state have been limited to uniaxial strain variations (15, 16). Hence, a new beginning on biaxial tests has to be made.

In this article, biaxial tests were used to resolve a controversy on whether the stress–strain relationship is linear in the physiological range, and whether the vessel wall is biaxially isotropic (2, 17). We used our biaxial testing machine to obtain data on canine thoracic aorta and established a constitutive equation that resolves these questions. Our method is to fit the data with the stress–strain relationship derived from a strain energy function that is a sum of two parts: one part yielding a linear stress–strain relationship and the other part yielding a nonlinear one. The material constants in the strain energy function are determined from the experimental data. The in vivo values of the strains are determined by separate experiments. With this stain energy function, we can define a degree of nonlinearity parameter, which represents the fraction of the nonlinear strain energy in the total strain energy per unit volume. With the degree of nonlinearity known for any given sets of in vivo strains, the significance of the nonlinearity of vessel wall elasticity on nonlinear dynamics phenomena such as the formation of solitary waves (solitons) in arteries can be evaluated.

METHODS

The thoracic aortas of five mongrel dogs weighing 25.1 ± 7.5 (SD) kg were used. The animals at normal physiological condition were anesthetized with pentobarbital at 30 mg/kg, heparinized with 40 kU, and then killed with an overdose of 125 mg/kg of pentobarbital. Immediately thereafter, their chests were opened and the main aortas were excised. The aortas were maintained in Krebs solution at 4°C, buffered to pH 7.4, and bubbled with 95% O₂/5% CO₂. A segment about 3-cm long was cut from the thoracic region between the 4th and 7th branch of costal arteries. A radial cut was made in the dorsal position of the segment. The segment sprang open into a sector, relieving the residual stress. The opening angles were found to be 77.0° ± 18.8°.

To measure its dimensions, the specimen was taken out of the Krebs solution and placed on a glass plate. Since the specimen at the zero-stress state was very soft, its weight and the surface tension of saline were sufficient to bend it into a flat slab on the glass. The longitudinal and circumferential dimensions of the specimen were read at four different locations with a ruler. The wall thickness was measured at 9 points using a tissue micrometer. Averaging was carried out in each dimension. The overall dimensions of the specimen was approximately 3.0 × 3.0 × 0.18 cm.

Four staples were applied onto each edge of the specimen so that pieces of silk thread can be used to connect the specimen to four platforms that were connected to force transducers and loading mechanism. A rectangular mark of dimensions 0.5 × 0.5 cm was painted onto the central portion of the specimen on the smooth intimal surface using a black water-resistant ink from a Sharpie pen. The painted frame was used as a target to measure strains.

Mechanical testing of the arterial specimens was done in a testing machine called TRIAX, which was developed in our own laboratory. In the TRIAX machine, a specimen can be stretched biaxially. The stretching forces are measured with force transducers and the deformations of the central portion of the specimen are measured optically without touching, thus avoiding the edge effect as much as possible. This gives us a direct and accurate measurement of the stress and strain in the testing specimen. Biaxial testing had been reported on such soft tissues as the skin (5, 18), the lung parenchyma (20–22), the pulmonary artery (23), and the pericardium (19). The accuracy of the instrument has been reported in these references.

Briefly, the test specimen was bathed in Krebs solution in a compartment at room temperature, with the target mark facing up. There were four platforms: two along the x axis and two in the perpendicular direction, y. Each pair of the platforms could be moved at an equal rate in opposite directions through a servomotor. The force in each direction was measured by a force transducer attached to one of the platforms and controlled through a feedback circuit. The deformation of the specimen was monitored by two video cameras: one for the x direction and the other for the y direction. The dimensions of the painted rectangular mark were measured by a pair of Video Dimensional Analyzers, the output of which was recorded in a computer that calculated the strains in two perpendicular directions. Since the target mark occupied only a small central portion of the specimen, the edge effect caused by the staples was minimized. If the shape of the rectangular target did not change during the course of the experiment, then the stresses and strains in the target area were regarded as uniformly distributed.

Tests were done either in a force mode, in which the forcing function was controlled, or in a deformation mode, in which the strain and strain rate were controlled. A computer (NEC Equity III+) controlled the operation of the machine and collected the data. As a specimen was mounted onto the machine, a small preload (about 3% of the maximum load) was applied on each axis of the specimen. Then the force distributing platforms were adjusted manually until no force was detected in the silk threads. The dimensions of the rectangular target at this stage were read and chosen as the reference state for strain measurements.

In protocol 1, forces in both x (circumferential) and y (longitudinal) directions were simultaneously cycled from the preload to the maximum load (loading) and back to the preload (unloading) in a triangular wave form at 0.05 Hz. Forces and dimensional changes of the target in both directions were recorded simultaneously. In protocol 2, the force in the longitudinal direction was held at 4 or 5 constant levels; at each level, the force in the circumferential direction was cycled from the preload to the maximum load and back to the preload in the triangular wave form at 0.05 Hz. In protocol 3, the force in the longitudinal direction was cycled at 0.05 Hz while the force in circumferential direction was held at 4 or 5 constant levels. Hence, the two-dimensional strain domain was effectively covered by the experimental trajectories. At each testing, data were read after at least 10 cycles of loading and unloading for the purpose of preconditioning. The sampling rate for data collection was 5 Hz.

The stretch ratios λ_θθ and λ_zz, in the circumferential and longitudinal directions, respectively, are defined as the ratios of the current dimension of the target to its dimension at the reference state in corresponding directions (4). The Lagrangian stresses T_θθ and T_zz are defined as the force divided by the corresponding initial cross-sectional area (4).

We obtained a large number of experimental curves illustrated in Figs. 1 and 2. We seek to consolidate these curves into a mathematical formula. We found that the arterial specimens have very small hysteresis, and the concept of pseudoelasticity (13, 14) applies. The loading curve and unloading curves are repeatable in cyclic loading and do not differ much. Hence, each can be treated as an elastic curve. We collected data on the loading process. In the two-dimensional case, the relevant Kirchhoff’s stresses and Green’s strains in the longitudinal and circumferential directions are S_zz, S_{θθ and} E_zz, E_θθ, respectively, and the shear stress S_θz = S_zθ, and shear strain E_θz = E_zθ. The strain-energy function is a function of the strains E_θθ, E_zz, E_θz, and E_zθ. In view of the experimental data illustrated in Figs. 1 and 2, we propose the following strain-energy function:

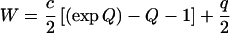1

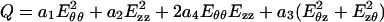1a

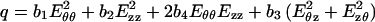1b

where E_θθ and E_zz are related to the stretch ratios λ_θθ and λ_zz by (3):

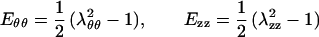2

and c, a₁, a₂, a₃, a₄, b₁, b₂, b₃, and b₄ are material constants. The unit of c, b₁, b₂, b₃, and b₄ are those of stress, whereas a₁, a₂, a₃, and a₄ are nondimensional. It is known (3) that the derivatives of the strain energy function are the Kirchhoff stresses:

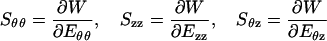3

S_θθ and S_zz are related to the Lagrangian stresses T_θθ and T_zz by the relations:

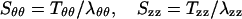4

The Kirchhoff stresses S_θθ and S_zz derived from Eqs. 1 and 3 are:

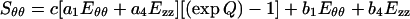5

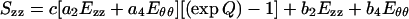5a

Shear was studied by Deng et al. (24), but was zero in the present study, hence a₃ and b₃ are irrelevant in the present experiment. When the strains E_θθ and E_zz and stresses S_θθ, S_zz were calculated from the experimental data on one hand and formulas Eqs. 1a–c, 5a, and 5b on the other hand, we can minimize the sum of squared errors:

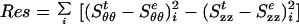6

and determine the unknown constants c, a, and b. In Eq. 6, the superscripts t and e represent the theoretical and experimental values of the Kirchhoff stresses, respectively, and the sum is carried out over all the experimental data points in all three protocols for each specimen. A computational scheme based on the nonlinear least squares method was developed for the minimization, using an NAG subroutine E04FDF (Numeric Algorithms Group).

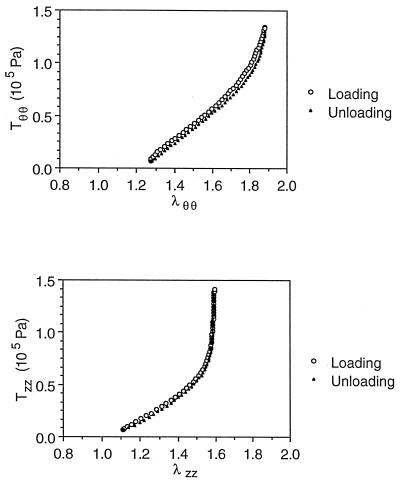
Figure 1.

The stress–strain curves recorded in protocol 1 for specimen No. 27. Open circles denote the loading curve and solid triangles denote the unloading curves. The unloading curve differs very little from the loading curve so that the hysteresis can be neglected. The linear region is rather long.

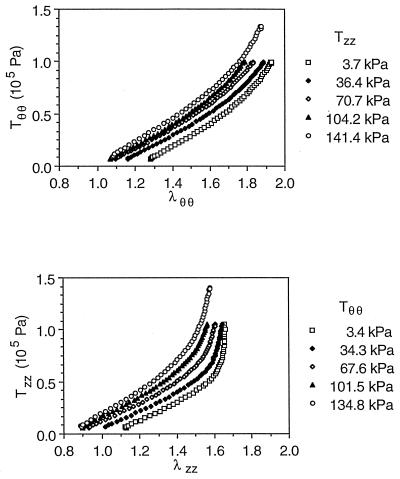
Figure 2.

The stress–strain relationships recorded in protocols 2 and 3 for specimen No. 27 when the stress is cycled in one direction and kept constant in the transverse direction. Only the loading curves are plotted.

The goodness of a curve fitting is indicated by a high correlation coefficient (R), which is defined by the formula:

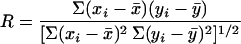7

in which x_i are the theoretical values, y_i are the corresponding experimental values, x̄ and ȳ are the mean values of x_i and y_i, respectively, and i ranges over all the experimental data points in the summation.

RESULTS

Typical experimental results of T_θθ vs. λ_θθ and T_zz vs. λ_zz for protocol 1 showed very little hysteresis (Fig. 1). The relatively linear regions were remarkably long, up to λ_θθ = 1.7 and λ_zz = 1.5. In these relatively linear regions, both curves had roughly equal slopes. Between λ_zz = 1.5 and 1.6, T_zz became nonlinear and increased rapidly. T_θθ became obviously nonlinear between λ_θθ=1.7 and 1.8, and increased much more slowly as compared with λ_zz.

The experimental results of the same specimen for protocols 2 and 3 (Fig. 2) have similar trends as those from protocol 1. The stress–strain curve shifted upwards when the stress in the transverse direction was kept at a higher level. The collection of experimental curves is presented in Zhou (25).

These experimental curves were fit with the theoretical formulas Eqs. 1–5. On applying Eqs. 1 and 5 to the present experimental results, we obtained the values of the unknown constants c, a₁, a₂, a₄, b₁, b₂, and b₄ listed in Table 1. It is found that the absolute values of a₄ are one or two orders of magnitude smaller than a₁ and a₂, whereas its sign is positive in some cases, and negative in others. Hence, we propose a simplification by dropping a₄ altogether. By letting a₄ = 0, the material constants were calculated again and the results are listed in Table 1.

Table 1.

Material constants of the strain-energy function given by Eq. 1 determined from the curves of loading process of the canine thoracic aorta by a nonlinear least error squares method

Specimen No.	22	23	24	27	28	Mean	S.D.
All coefficients of Eq. 1*
c (kPa)	3.734	1.896	8.287	0.812	81.63	19.27	31.28
a1	1.132	1.215	0.667	0.904	0.243	0.832	0.351
a2	2.265	2.564	0.921	3.118	0.573	1.888	0.977
a4	−0.0515	0.1116	−0.1085	−0.1279	0.0041	−0.0344	0.0863
b1 (kPa)	43.54	74.91	16.69	33.43	37.52	41.22	19.06
b2 (kPa)	44.99	76.04	17.84	39.81	38.92	43.52	18.73
b4 (kPa)	14.37	22.83	8.603	10.95	9.715	13.29	5.15
With a4 set to zero
c (kPa)	4.712	1.123	6.903	1.199	72.38	17.26	27.64
a1	1.001	1.327	0.559	0.712	0.259	0.772	0.367
a2	2.084	2.594	0.907	2.760	0.606	1.790	0.878
a4	0.0	0.0	0.0	0.0	0.0	0.0	0.0
b1 (kPa)	44.25	45.09	25.13	34.17	37.45	37.22	7.31
b2 (kPa)	44.88	46.96	21.88	39.24	38.96	38.38	8.82
b4 (kPa)	13.56	15.61	3.528	10.04	9.919	10.53	4.11

*Except for a₃, b₃, which were not tested. 

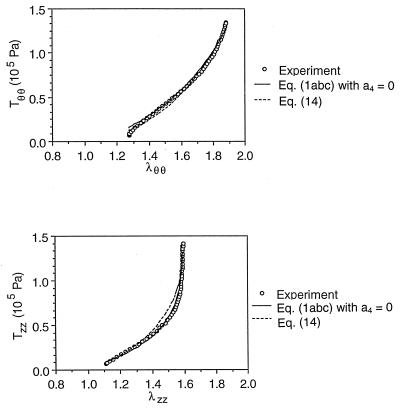
The theoretically predicted relationship between the Lagrangian stress and the stretch ratio is compared with the experimental results for protocol 1 in Fig. 3. The solid lines are calculated on the basis of the strain energy function given by Eq. 1a with a₄ = 0. The fitting is excellent throughout the entire strain range. The correlation coefficient computed according to Eq. 7 is greater than 0.95 in every case, including those in protocols 2 and 3 (data not shown). We also found that the theoretically predicted stress–strain curves do not show noticeable difference with or without dropping a₄ in Eqs. 5a and 5b, i.e., the correlation coefficients are all greater than 0.95.

Figure 3.

Comparison between the theoretical and experimental loading stress–strain curves. The experimental curves are the same as in Fig. 1. The theoretical curves are calculated based on Eqs. 1a–c with a₄ = 0 (solid lines) and Eq. 14 (dashed lines). Good agreements are observed for both strain energy functions with Eqs. 1 a–c presenting a better fit.

Next, we determine the range of in vivo stress and strain values. The stress and strain of the thoracic aorta in physiological conditions are calculated as follows: the in situ longitudinal stretch ratio of the canine thoracic aorta was about 1.3 (see ref. 26). The internal blood pressure varied from 80 mmHg (diastolic) to 120 mmHg (systolic). Let L_θ and H denote the circumference and the thickness of the vessel wall at the zero-stress state, respectively. Let r and h be the mid-wall radius and the thickness of the vessel, respectively, at a physiological pressure p. The incompressibility of the vessel wall, λ_rrλ_θθλ_zz = 1, where λ_rr is the stretch ratio in the radial direction, yields (4):

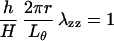8

The internal pressure p results in a hoop stress σ_θθ in the wall. By Laplace law (4),

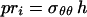9

where r_i is the inner radius of the vessel at the internal pressure. The Cauchy stresses σ_θθ and σ_zz are related to the Kirchhoff stress S_θθ and S_zz by (3)

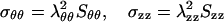10

Combining Eqs. 8–10, we obtain, approximately, by treating r_i as r,

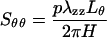11

L_θ and H were measured at the beginning of the testing. So, for a given physiological pressure p and a stretch ratio λ_zz, the stress S_θθ is calculated from Eq. 11. Then, by solving the nonlinear equation (5a), the strain E_θθ is obtained. S_zz follows from Eq. 5b. Hence, the stresses (S_θθ and S_zz or σ_θθ and σ_zz) and strains (E_θθ and E_zz or λ_θθ and λ_zz) in the physiological conditions are computed. The results show that, for five specimens, the circumferential stretch ratios are 1.566 ± 0.107(SD), 1.673 ± 0.106(SD), and 1.759 ± 0.107(SD) at internal pressures 80 mmHg, 100 mmHg, and 120 mmHg, respectively. Thus, it is seen that, in physiological condition, the thoracic aorta operates in the range of nonlinear circumferential stress–strain relationship.

The Degree of Nonlinearity and Anisotropy.

With the results above, we can define a degree of nonlinearity (DNL), as the fraction of the nonlinear strain energy in the total strain energy:

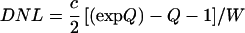12

where W is given by Eq. 1a. It is clear by Eqs. 1b and 1c that Q and q are both of the second order in the strain components, whereas the numerator in Eq. 12 is of the fourth order in the strains because, by a power series expansion, the nonlinear strain energy is given by:

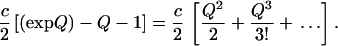13

Hence when the strains E_θθ, E_zz, E_zθ all tend to zero, the DNL tends to zero as rapidly as the fourth power of the strains. DNL is finite when some strain components are finite. Table 3 shows the values of the degree of nonlinearity, DNL, and the total strain energy per unit volume, W, for specific values of the circumferential stretch ratio λ_θθ and longitudinal stretch ratio λ_ZZ. These results are calculated by using Eq. 2 for strains, using Eqs. 1b and 1c for Q and q, with Table 1 for the constants c, a₁… , b₁… , Eq. 1a for W, and Eq. 12 for DNL. The trend of the degree of nonlinearity is shown in Table 3. In the physiological range, λ_ZZ lies in 1.3–1.5, and λ_θθ lies in 1.4–1.8. Thus if λ_ZZ = 1.3 and λ_θθ is 1.6, the degree of nonlinearity is 13.5%. If λ_ZZ = 1.4 and λ_θθ = 1.8, then the degree of nonlinearity is 29.2%. Note in Table 3 the non-monotonic behavior of DNL at finite E_zz when E_θθ tends to zero. This can be verified by Eq. 12.

Table 3.

The total strain energy per unit volume (W) and the degree of nonlinearity (DNL) of canine aorta calculated according to the material constants given in Table 1

Circumf. stretch ratio	λθθ	1.0	1.2	1.4	1.6	1.8
Circumf. strain	Eθθ	0.0	0.22	0.48	0.78	1.12
Strain energy per unit volume, W
Long. stretch ratio	λzz = 1.0	0.000	0.906	4.296	12.441	29.085
	λzz = 1.2	0.962	2.408	6.659	15.680	33.920
	λzz = 1.3	2.495	4.279	9.070	19.000	39.000
	λzz = 1.4	5.268	7.454	12.980	24.290	47.210
Degree of nonlinearity, %
Long. stretch ratio	λzz = 1.0	0.00	0.66	3.27	8.99	19.74
	λzz = 1.2	3.46	2.87	5.16	10.34	20.79
	λzz = 1.3	8.44	6.89	8.32	13.47	23.85
	λzz = 1.4	16.06	13.68	14.24	18.97	29.20

DNL = 100 × nonlinear strain energy/total strain energy. 

The experimental results give answer to the question of anisotropy or isotropy of the canine aorta also. In the nonlinear regime, the material is not isotropic because the constants a₁ and a₂ in Tables 1 and 2 are unequal. The constant a₂ is more than twice as large as a₁, consistent with the observation that the longitudinal stress–strain curve turns nonlinear at a smaller strain and has a steeper nonlinear region than the circumferential stress–strain curve does (Figs. 1 and 2). In Mohan and Melvin (27) and Zhou (25), the anisotropy of the strength of blood vessel wall (failure characteristics) is discussed. In the linear regime, it is well known (4) that an isotropic elastic material is characterized by two, and only two, material constants. The results given in Table 1 show that three material constants b₁, b₂ and b₄, plus a shear modulus G that was not measured, are necessary to characterized aorta in the linear regime. Thus, the aorta is in general anisotropic. The shear modulus is discussed in the following section.

Table 2.

Material constants of the strain-energy function given by Eq. 14 determined by a nonlinear least errors method from the whole set of experimental results.

Specimen no.	22	23	24	27	28	Mean	SD
c (kPa)	120.2	126.0	49.6	153.6	172.9	124.5	42.0
a1	0.320	0.289	0.338	0.175	0.200	0.264	0.065
a2	0.451	0.397	0.441	0.314	0.292	0.379	0.065
a4	0.0681	0.0727	0.0099	0.0406	0.0390	0.0461	0.0227

The constant a₃ is related to shear and is not tested in this experiment. 

DISCUSSION

First, let us compare our strain energy function given in Eq. 1 with other strain energy functions in the literature. Note first that the strain energy function given in Eq. 1 is a special case of a formula given by Tong and Fung (28), which includes linear and nonlinear terms, as well as shear strain and a group of third-order terms in Q. After examining the application of the formula to experimental data on skin, Tong and Fung (28) concluded that the third order terms contribute little to the improvement of accuracy of the stress–strain law, and recommended dropping them in further mathematical modeling of soft tissue mechanics. The shear term has been shown to be correct in representing the results of torsion experiments of blood vessels by Deng et al. (24), who used the results to evaluate the shear modulus, G, of the arterial wall. On specializing the formula in (28) to blood vessel and emphasizing the linear and nonlinear terms, we get Eq. 1.

If we delete q from Eq. 1 and retain the term that is linear in Q, then we obtain a strain-energy function

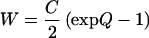14

which was adopted by Fung et al. (29). When Eq. 14 was applied to the experimental data obtained by the present experiment, and the coefficients c, a₁, a₂, a₄ were determined by Marquart’s algorithm (29), we obtained the results given in Table 2. An illustration of the curve fitting is shown by the dotted curves in Fig. 3. It is seen that the fitting is very good, but not as good as that of Eq. 1. The correlation coefficient of S_θθ and E_θθ is greater than 0.95 in every case, but the correlation of S_zz and E_zz lies between 0.86 and 0.97. But Eq. 14 is much simpler than Eq. 1. Only four constants are needed for Eq. 14, whereas seven constants are needed for Eq. 1 (a₃, b₃ being irrelevant in the present case because shear or torsion are not considered). Furthermore, Fung (30) has shown that a strain-energy function given by Eq. 14 can be inverted to obtain a complementary energy function, which is a function of stress components. How to invert a strain energy function given by Eq. 1 is still unknown. Hence, for practical purposes of analyzing blood vessels in vivo, Eq. 14 is recommended.

In the literature, there are several other strain energy functions for the blood vessel. Patel and Vaishnav (31) and Vaishnav et al. (32) used polynomials. The difficulties with the polynomial form are too many constants and instability of experimental determination of the constants as discussed in ref. 29. Demiray et al. (33) introduced a strain energy function consisting of a polynomial plus an exponential term in the form W = q + c expQ, while considering the vessel as an orthotropic membrane. Demiray and Erbay (34) used the same approach to describe the abdominal aorta; Demiray et al. (35) assumed isotropy. These forms can be expected to offer good fit to experimental data. However, if isotropy is assumed a priori, then it cannot be used to test anisotropy. The expression expQ includes terms describing linear elasticity, whereas the expression (expQ)-Q-1 contains only nonlinear terms. Hence, Eq. 1a assures a clear separation of linear and nonlinear elasticity terms. The alternative exponential forms of strain energy function cannot lead to a clear cut definition of the degree of nonlinearity as Eq. 12 does.

Chuong and Fung (36) showed how the exponential strain energy function can be used in three-dimensional case; and Chuong and Fung (37) worked out the effect of residual stresses.

The issue of isotropy should be discussed further. In all specimens we tested, the values of b₁ and b₂ are about equal. Some authors seize upon the equality of the Young’s modulus in two perpendicular directions to claim that the material is isotropic. This, of course, may or may not be true. In classical theory of elasticity, it is shown (4) that for an isotropic material the shear modulus (G) must be derivable from the Young’s modulus (E) and Poisson’s ratio (ν) according to the equation G = E/(2+2ν). The shear modulus of arterial wall was not measured in the present experiment. Deng et al. (24), however, have measured the shear modulus of blood vessels with a combined torsion, inflation, and stretching experiment. They have shown that the shear modulus of rat arteries does not obey the relation G = E/(2+2ν); hence, the arterial wall is not isotropic.

A similar case exists in Debes and Fung (23) who have used the same TRIAX biaxial testing machine to study the stress–strain relationship of the canine pulmonary artery at the arch region, for which the zero-stress state is approximately a flat sheet. Data on the stress–strain relationship of the pulmonary artery at the arch region can be fitted by a linear constitutive equation, Eq. 1a with c = 0, from the zero-stress state to the in vivo homeostatic condition and well beyond it in the physiological region. A similar equality of b₁ and b₂ was found for the pulmonary artery. But since b₃ and b₄ are additional independent constants, the tissue cannot be said to be isotropic. The anisotropy is explained by considering a composite material like a fabric. Let the weave and warp be made of the same material and of the same size and spacing. Then the Young’s modules in the directions of the weave and warp are the same. But the shear modulus would depend on how the fibers are cemented together. If the contact points were lubricated the shear modulus would approach zero. If the contact points were glued the shear modulus would depend on the spacing and the bending rigidity of the fibers. Hence, the shear modulus is an independent variable which does not obey the relation G = E/(2+2v) in general. Hence, the fabric is anisotropic in general.

This study was made on excised blood vessel specimens with the material treated as uniform throughout the wall thickness. It is desirable to study the vessel in vivo and with the wall treated as layers of endothelium, intima, and media (smooth muscle cells) and adventitia (fibrous tissues). A method to do this has been presented by Fung and Liu (38).

CONCLUSION

The experimental results from biaxial tests of canine aortas and a strain energy function given by Eq. 1a fit each other very well. Eq. 1a separates the strain energy function of linear elasticity and nonlinear elasticity into two terms, with which a “degree of nonlinearity” can be defined by Eq. 12. The aorta wall is not isotropic. In the linear regime, anisotropy is revealed by the existence of more than two independent material constants. In the nonlinear regime, anisotropy is revealed by the significant difference between the constants related to the longitudinal and circumferential directions. Finally, with regard to the strain energy function, we found that a simpler form given by Eq. 14 fits all the experimental data on thoracic aorta quite well.