Statistics in Brief: The Importance of Sample Size in the Planning and Interpretation of Medical Research

Abstract

The increasing volume of research by the medical community often leads to increasing numbers of contradictory findings and conclusions. Although the differences observed may represent true differences, the results also may differ because of sampling variability as all studies are performed on a limited number of specimens or patients. When planning a study reporting differences among groups of patients or describing some variable in a single group, sample size should be considered because it allows the researcher to control for the risk of reporting a false-negative finding (Type II error) or to estimate the precision his or her experiment will yield. Equally important, readers of medical journals should understand sample size because such understanding is essential to interpret the relevance of a finding with regard to their own patients. At the time of planning, the investigator must establish (1) a justifiable level of statistical significance, (2) the chances of detecting a difference of given magnitude between the groups compared, ie, the power, (3) this targeted difference (ie, effect size), and (4) the variability of the data (for quantitative data). We believe correct planning of experiments is an ethical issue of concern to the entire community.

Introduction

“Statistical analysis allows us to put limits on our uncertainty, but not to prove anything.”—Douglas G. Altman [1]

The growing need for medical practice based on evidence has generated an increasing medical literature supported by statistics: readers expect and presume medical journals publish only studies with unquestionable results they can use in their everyday practice and editors expect and often request authors provide rigorously supportable answers. Researchers submit articles based on presumably valid outcome measures, analyses, and conclusions claiming or implying the superiority of one treatment over another, the usefulness of a new diagnostic test, or the prognostic value of some sign. Paradoxically, the increasing frequency of seemingly contradictory results may be generating increasing skepticism in the medical community.

One fundamental reason for this conundrum takes root in the theory of hypothesis testing developed by Pearson and Neyman in the late 1920s [24, 25]. The majority of medical research is presented in the form of a comparison, the most obvious being treatment comparisons in randomized controlled trials. To assess whether the difference observed is likely attributable to chance alone or to a true difference, researchers set a null hypothesis that there is no difference between the alternative treatments. They then determine the probability (the p value), they could have obtained the difference observed or a larger difference if the null hypothesis were true; if this probability is below some predetermined explicit significance level, the null hypothesis (ie, there is no difference) is rejected. However, regardless of study results, there is always a chance to conclude there is a difference when in fact there is not (Type I error or false positive) or to report there is no difference when a true difference does exist (Type II error or false negative) and the study has simply failed to detect it (Table 1). The size of the sample studied is a major determinant of the risk of reporting false-negative findings. Therefore, sample size is important for planning and interpreting medical research.

Table 1.

Type I and Type II errors during hypothesis testing

Truth	Study findings
	Null hypothesis is not rejected	Null hypothesis is rejected
Null hypothesis is true	True negative	Type I error (alpha) (False positive)
Null hypothesis is false	Type II error (beta) (False negative)	True positive

For that reason, we believe readers should be adequately informed of the frequent issues related to sample size, such as (1) the desired level of statistical significance, (2) the chances of detecting a difference of given magnitude between the groups compared, ie, the power, (3) this targeted difference, and (4) the variability of the data (for quantitative data). We will illustrate these matters with a comparison between two treatments in a surgical randomized controlled trial. The use of sample size also will be presented in other common areas of statistics, such as estimation and regression analyzes.

Desired Level of Significance

The level of statistical significance α corresponds to the probability of Type I error, namely, the probability of rejecting the null hypothesis of “no difference between the treatments compared” when in fact it is true. The decision to reject the null hypothesis is based on a comparison of the prespecified level of the test arbitrarily chosen with the test procedure’s p value. Controlling for Type I error is paramount to medical research to avoid the spread of new or perpetuation of old treatments that are ineffective. For the majority of hypothesis tests, the level of significance is arbitrarily chosen at 5%. When an investigator chooses α = 5%, if the test’s procedure p value computed is less than 5%, the null hypothesis will be rejected and the treatments compared will be assumed to be different.

To reduce the probability of Type I error, we may choose to reduce the level of statistical significance to 1% or less [29]. However, the level of statistical significance also influences the sample size calculation: the lower the chosen level of statistical significance, the larger the sample size will be, considering all other parameters remain the same (see example below and Appendix 1). Consequently, there are domains where higher levels of statistical significance are used so that the sample size remains restricted, such as for randomized Phase II screening designs in cancer [26]. We believe the choice of a significance level greater than 5% should be restricted to particular cases.

Power

The power of a test is defined as 1 − the probability of Type II error. The Type II error is concluding at no difference (the null is not rejected) when in fact there is a difference, and its probability is named β. Therefore, the power of a study reflects the probability of detecting a difference when this difference exists. It is also very important to medical research that studies are planned with an adequate power so that meaningful conclusions can be issued if no statistical difference has been shown between the treatments compared. More power means less risk for Type II errors and more chances to detect a difference when it exists.

Power should be determined a priori to be at least 80% and preferably 90%. The latter means, if the true difference between treatments is equal to the one we planned, there is only 10% chance the study will not detect it. Sample size increases with increasing power (Fig. 1).

Fig. 1A–C.

The graphs show the distribution of the test statistic (z-test) for the null hypothesis (plain line) and the alternative hypothesis (dotted line) for a sample size of (A) 32 patients per group, (B) 64 patients per group, and (C) 85 patients per group. For a difference in mean of 10, a standard deviation of 20, and a significance level α of 5%, the power (shaded area) increases from (A) 50%, to (B) 80%, and (C) 90%. It can be seen, as power increases, the test statistics yielded under the alternative hypothesis (there is a difference in the two comparison groups) are more likely to be greater than the critical value 1.96.

Very commonly, power calculations have not been performed before conducting the trial [3, 8], and when facing nonsignificant results, investigators sometimes compute post hoc power analyses, also called observed power. For this purpose, investigators use the observed difference and variability and the sample size of the trial to determine the power they would have had to detect this particular difference. However, post hoc power analyses have little statistical meaning for three reasons [9, 13]. First, because there is a one-to-one relationship between p values and post hoc power, the latter does not convey any additional information on the sample than the former. Second, nonsignificant p values always correspond to low power and post hoc power, at best, will be slightly larger than 50% for p values equal to or greater than 0.05. Third, when computing post hoc power, investigators implicitly make the assumption that the difference observed is clinically meaningful and more representative of the truth than the null hypothesis they precisely were not able to reject. However, in the theory of hypothesis testing, the difference observed should be used only to choose between the hypotheses stated a priori; a posteriori, the use of confidence intervals is preferable to judge the relevance of a finding. The confidence interval represents the range of values we can be confident to some extent includes the true difference. It is related directly to sample size and conveys more information than p values. Nonetheless, post hoc power analyses educate readers about the importance of considering sample size by explicitly raising the issue.

The Targeted Difference Between the Alternative Treatments

The targeted difference between the alternative treatments is determined a priori by the investigator, typically based on preliminary data. The larger the expected difference is, the smaller the required sample size will be. However, because the sample size based on the difference expected may be too large to achieve, investigators sometimes choose to power their trial to detect a difference larger than one would normally expect to reduce the sample size and minimize the time and resources dedicated to the trial. However, if the targeted difference between the alternative treatments is larger than the true difference, the trial may fail to conclude a difference between the two treatments when a smaller, and still meaningful, difference exists. This smallest meaningful difference sometimes is expressed as the “minimal clinically important difference,” namely, “the smallest difference in score in the domain of interest which patients perceive as beneficial and which would mandate, in the absence of troublesome side effects and excessive costs, a change in the patient’s management” [15]. Because theoretically the minimal clinically important difference is a multidimensional phenomenon that encompasses a wide range of complex issues of a particular treatment in a unique setting, it usually is determined by consensus among clinicians with expertise in the domain. When the measure of treatment effect is based on a score, researchers may use empiric definitions of clinically meaningful difference. For instance, Michener et al. [21], in a prospective study of 63 patients with various shoulder abnormalities, determined the minimal change perceived as clinically meaningful by the patients for the patient self-report section of the American Shoulder and Elbow Surgeons Standardized Shoulder Assessment Form was 6.7 points of 100 points. Similarly, Bijur et al. [5], in a prospective cohort study of 108 adults presenting to the emergency department with acute pain, determined the minimal change perceived as clinically meaningful by patients for acute pain measured on the visual analog scale was 1.4 points. There is no reason to try to detect a difference below the minimal clinically important difference because, even if it proves statistically significant, it will not be meaningful.

The meaningful clinically important difference should not be confused with the effect size. The effect size is a dimensionless measure of the magnitude of a relation between two or more variables, such as Cohen’s d standardized difference [6], but also odds ratio, Pearson’s r correlation coefficient, etc. Sometimes studies are planned to detect a particular effect size instead of being planned to detect a particular difference between the two treatments. According to Cohen [6], 0.2 is indicative of a small effect, 0.5 a medium effect, and 0.8 a large effect size. One of the advantages of doing so is that researchers do not have to make any assumptions regarding the minimal clinically important difference or the expected variability of the data.

The Variability of the Data

For quantitative data, researchers also need to determine the expected variability of the alternative treatments: the more variability expected in the specified outcome, the more difficult it will be to differentiate between treatments and the larger the required sample size (see example below). If this variability is underestimated at the time of planning, the sample size computed will be too small and the study will be underpowered to the one desired. For comparing proportions, the calculation of sample size makes use of the expected proportion with the specified outcome in each group. For survival data, the calculation of sample size is based on the survival proportions in each treatment group at a specified time and on the total number of events in the group in which the fewer events occur. Therefore, for the latter two types of data, variability does not appear in the computation of sample size.

Example

Presume an investigator wants to compare the postoperative Harris hip score [12] at 3 months in a group of patients undergoing minimally invasive THA with a control group of patients undergoing standard THA in a randomized controlled trial. The investigator must (1) establish a statistical significance level, eg, α = 5%, (2) select a power, eg, 1 − β = 90%, and (3) establish a targeted difference in the mean scores, eg, 10, and assume a standard deviation of the scores, eg, 20 in both groups (which they can obtain from the literature or their previous patients). In this case, the sample size should be 85 patients per group (Appendix 1). If fewer patients are included in the trial, the probability of detecting the targeted difference when it exists will decrease; for sample sizes of 64 and 32 per group, for instance, the power decreases to 80% and 50%, respectively (Fig. 1). If the investigator assumed the standard deviation of the scores in each group to be 30 instead of 20, a sample size of 190 per group would be necessary to obtain a power of 90% with a significance level α = 5% and targeted difference in the mean scores of 10. If the significance level was chosen at α = 1% instead of α = 5%, to yield the same power of 90% with a targeted difference in scores of 10 and standard deviation of 20, the sample size would increase from 85 patients per group to 120 patients per group. In relatively simple cases, statistical tables [19] and dedicated software available from the internet may be used to determine sample size. In most orthopaedic clinical trials cases, sample size calculation is rather simple as above, but it will become more complex in other cases. The type of end points, the number of groups, the statistical tests used, whether the observations are paired, and other factors influence the complexity of the calculation, and in these cases, expert statistical advice is recommended.

Sample Size, Estimation, and Regression

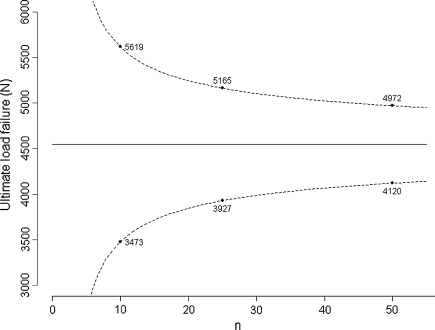
Sample size was presented above in the context of hypothesis testing. However, it is also of interest in other areas of biostatistics, such as estimation or regression. When planning an experiment, researchers should ensure the precision of the anticipated estimation will be adequate. The precision of an estimation corresponds to the width of the confidence interval: the larger the tested sample size is, the better the precision. For instance, Handl et al. [11], in a biomechanical study of 21 fresh-frozen cadavers, reported a mean ultimate load failure of four-strand hamstring tendon constructs of 4546 N under loading with a standard deviation of 1500 N. Based on these values, if we were to design an experiment to assess the ultimate load failure of a particular construct, the precision around the mean at the 95% confidence level would be expected to be 3725 N for five specimens, 2146 N for 10 specimens, 1238 N for 25 specimens, 853 N for 50 specimens, and 595 N for 100 specimens tested (Appendix 2); if we consider the estimated mean will be equal to 4546 N, the one obtained in the previous experiment, we could obtain the corresponding 95% confidence intervals (Fig. 2). Because we always deal with limited samples, we never exactly know the true mean or standard deviation of the parameter distribution; otherwise, we would not perform the experiment. We only approximate these values, and the results obtained can vary from the planned experiment. Nonetheless, what we identify at the time of planning is that testing more than 50 specimens, for instance 100, will multiply the costs and time necessary to the experiment while providing only slight improvement in the precision.

Fig. 2.

The graph shows the predicted confidence interval for experiments with an increasing number of specimens tested based on the study by Handl et al. [11] of 21 fresh-frozen cadavers with a mean ultimate load failure of four-strand hamstring tendon constructs of 4546 N and standard deviation of 1500 N.

Similarly, sample size issues should be considered when performing regression analyses, namely, when trying to assess the effect of a particular covariate, or set of covariates, on an outcome. The effective power to detect the significance of a covariate in predicting this outcome depends on the outcome modeled [14, 30]. For instance, when using a Cox regression model, the power of the test to detect the significance of a particular covariate does not depend on the size of the sample per se but on the number of specific critical events. In a cohort study of patients treated for soft tissue sarcoma with various treatments, such as surgery, radiotherapy, chemotherapy, etc, the power to detect the effect of chemotherapy on survival will depend on the number of patients who die, not on the total number of patients in the cohort. Therefore, when planning such studies, researchers should be familiar with these issues and decide, for example, to model a composite outcome, such as event-free survival that includes any of the following events: death from disease, death from other causes, recurrence, metastases, etc, to increase the power of the test.

Discussion

The reasons to plan a trial with an adequate sample size likely to give enough power to detect a meaningful difference are essentially ethical. Small trials are considered unethical by most, but not all, researchers because they expose participants to the burdens and risks of human research with a limited chance to provide any useful answers [2, 10, 28]. Underpowered trials also ineffectively consume resources (human, material) and add to the cost of healthcare to society. Although there are particular cases when trials conducted on a small sample are justified, such as early-phase trials with the aim of guiding the conduct of subsequent research (or formulating hypotheses) or, more rarely, for rare diseases with the aim of prospectively conducting meta-analyses, they generally should be avoided [10]. It is also unethical to conduct trials with too large a sample size because, in addition to the waste of time and resources, they expose participants in one group to receive inadequate treatment after appropriate conclusions should have been reached. Interim analyses and adaptive trials have been developed in this context to shorten the time to decision and overcome these concerns [4, 16].

We raise two important points. First, we explained, for practical and ethical reasons, experiments are conducted on a sample of limited size with the aim to generalize the results to the population of interest and increasing the size of the sample is a way to combat uncertainty. When doing this, we implicitly consider the patients or specimens in the sample are randomly selected from the population of interest, although this is almost never the case; even if it were the case, the population of interest would be limited in space and time. For instance, Marx et al. [20], in a survey conducted in late 1998 and early 1999, assessed the practices for anterior cruciate ligament reconstruction on a randomly selected sample of 725 members of the American Academy of Orthopaedic Surgeons; however, because only ½ the surgeons responded to the survey, their sample probably is not representative of all members of the society, who in turn are not representative of all orthopaedic surgeons in the United States, who again are not representative of all surgeons in the world because of the numerous differences among patients, doctors, and healthcare systems across countries. Similar surveys conducted in other countries have provided different results [17, 22]. Moreover, if the same survey was conducted today, the results would possibly differ. Therefore, another source for variation among studies, apart from sampling variability, is that samples may not be representative of the same population. Therefore, when planning experiments, researchers must take care to make their sample representative of the population they want to infer to and readers, when interpreting the results of a study, should always assess first how representative the sample presented is regarding their own patients. The process implemented to select the sample, the settings of the experiment, and the general characteristics and influencing factors of the patients must be described precisely to assess representativeness and possible selection biases [7].

Second, we have discussed only sample size for interpreting nonsignificant p values, but it also may be of interest when interpreting p values that are significant. Significant results issued from larger studies usually are given more credit than those from smaller studies because of the risk of reporting exaggerating treatment effects with studies with smaller samples or of lower quality [23, 27], and small trials are believed to be more biased than others. However, there is no statistical reason a significant result in a trial including 2000 patients should be given more belief than a trial including 20 patients, given the significance level chosen is the same in both trials. Small but well-conducted trials may yield a reliable estimation of treatment effect. Kjaergard et al. [18], in a study of 14 meta-analyses involving 190 randomized trials, reported small trials (fewer than 1000 patients) reported exaggerated treatment effects when compared with large trials. However, when considering only small trials with adequate randomization, allocation concealment (allocation concealment is the process that keeps clinicians and participants unaware of upcoming assignments. Without it, even properly developed random allocation sequences can be subverted), and blinding, this difference became negligible. Nonetheless, the advantages of a large sample size to interpret significant results are it allows a more precise estimate of the treatment effect and it usually is easier to assess the representativeness of the sample and to generalize the results.

Sample size is important for planning and interpreting medical research and surgeons should become familiar with the basic elements required to assess sample size and the influence of sample size on the conclusions. Controlling for the size of the sample allows the researcher to walk a thin line that separates the uncertainty surrounding studies with too small a sample size from studies that have failed practical or ethical considerations because of too large a sample size.

Appendix 1

The sample size (n) per group for comparing two means with a two-sided two-sample t test is

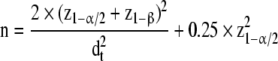where z_1−α/2 and z_1−β are standard normal deviates for the probability of 1 − α/2 and 1 − β, respectively, and d_t = (μ₀ − μ₁)/σ is the targeted standardized difference between the two means.

The following values correspond to the example:

• α = 0.05 (statistical significance level)

• β = 0.10 (power of 90%)

• |μ₀ − μ₁| = 10 (difference in the mean score between the two groups)

• σ = 20 (standard deviation of the score in each group)

• z_1−α/2 = 1.96

• z_1−β = 1.28

Therefore:

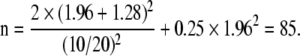Two-sided tests which do not assume the direction of the difference (ie, that the mean value in one group would always be greater than that in the other) are generally preferred. The null hypothesis makes the assumption that there is no difference between the treatments compared, and a difference on one side or the other therefore is expected.

Appendix 2

Computation of Confidence Interval

To determine the estimation of a parameter, or alternatively the confidence interval, we use the distribution of the parameter estimate in repeated samples of the same size. For instance, consider a parameter with observed mean, m, and standard deviation, sd, in a given sample. If we assume that the distribution of the parameter in the sample is close to a normal distribution, the means, x_n, of several repeated samples of the same size have true mean, μ, the population mean, and estimated standard deviation,

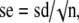1

also known as standard error of the mean, and

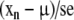2

follows a t distribution. For a large sample, the t distribution becomes close to the normal distribution; however, for a smaller sample size the difference is not negligible and the t distribution is preferred. The precision of the estimation is

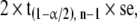3

and the confidence interval for μ is the range of values extending either side of the sample mean m by

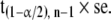4

For example, Handl et al. [11] in a biomechanical study of 21 fresh-frozen cadavers reported a mean ultimate load failure of 4-strand hamstring tendon constructs of 4546 N under dynamic loading with standard deviation of 1500 N. If we were to plan an experiment, the anticipated precision of the estimation at the 95% level would be

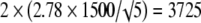5

for five specimens,

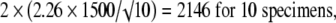6

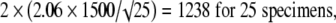7

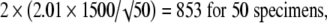8

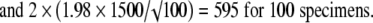9

The values 2.78, 2.26, 2.06, 2.01, and 1.98 correspond to the t distribution deviates for the probability of 1 − α/2, with 4, 9, 24, 49, and 99 (n − 1) degrees of freedom; the well known corresponding standard normal deviate is 1.96. Given an estimated mean of 4546 N, the corresponding 95% confidence intervals are 2683 N to 6408 N for five specimens, 3473 N to 5619 N for 10 specimens, 3927 N to 5165 N for 25 specimens, 4120 N to 4972 N for 50 specimens, and 4248 N to 4844 N for 100 specimens (Fig. 2).

Similarly, for a proportion p in a given sample with sufficient sample size to assume a nearly normal distribution, the confidence interval extends either side of the proportion p by

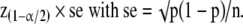10

For a small sample size, exact confidence interval for proportions should be used.