An MCMC algorithm for haplotype assembly from whole-genome sequence data

Abstract

In comparison to genotypes, knowledge about haplotypes (the combination of alleles present on a single chromosome) is much more useful for whole-genome association studies and for making inferences about human evolutionary history. Haplotypes are typically inferred from population genotype data using computational methods. Whole-genome sequence data represent a promising resource for constructing haplotypes spanning hundreds of kilobases for an individual. In this article, we propose a Markov chain Monte Carlo (MCMC) algorithm, HASH (haplotype assembly for single human), for assembling haplotypes from sequenced DNA fragments that have been mapped to a reference genome assembly. The transitions of the Markov chain are generated using min-cut computations on graphs derived from the sequenced fragments. We have applied our method to infer haplotypes using whole-genome shotgun sequence data from a recently sequenced human individual. The high sequence coverage and presence of mate pairs result in fairly long haplotypes (N50 length ∼ 350 kb). Based on comparison of the sequenced fragments against the individual haplotypes, we demonstrate that the haplotypes for this individual inferred using HASH are significantly more accurate than the haplotypes estimated using a previously proposed greedy heuristic and a simple MCMC method. Using haplotypes from the HapMap project, we estimate the switch error rate of the haplotypes inferred using HASH to be quite low, ∼1.1%. Our Markov chain Monte Carlo algorithm represents a general framework for haplotype assembly that can be applied to sequence data generated by other sequencing technologies. The code implementing the methods and the phased individual haplotypes can be downloaded from http://www.cse.ucsd.edu/users/vibansal/HASH/.

Cataloging human genetic variation, and understanding its phenotypic impact, is central to understanding the genetic basis of disease. This genetic variation is present in the form of single nucleotide polymorphisms (SNPs), insertions/deletions, inversions, translocations, copy number variations, etc. The abundance of SNPs in the human genome and the development of high-throughput genotyping technologies have made SNPs the marker of choice for understanding human genetic variation and performing disease association studies. The HapMap project (The International HapMap Consortium 2005, 2007) has genotyped more than 3 million common SNPs in 269 individuals from four human populations. With the availability of commercial genotyping chips that can read more than 100,000 SNPs spread across the human genome, the potential of whole-genome association studies for finding disease-related variants has been realized (Easton et al. 2007; Helgadottir et al. 2007; McPherson et al. 2007; Sladek et al. 2007; The Wellcome Trust Case Control Consortium 2007).

Current genotyping methods determine the two alleles at an individual SNP and are unable to provide information about haplotypes, the combination of alleles present at multiple SNPs along a single chromosome. Haplotypes observed in human populations are a result of shuffling of ancestral haplotypes through recombination and contain much more information about human genetic variation than genotypes. In the absence of molecular methods for determining haplotypes, haplotypes are inferred computationally from SNPs genotyped in a sample of individuals from a population (Clark 1990; Excoffier and Slatkin 1995; Stephens et al. 2001; Niu et al. 2002; Stephens and Donnelly 2003). Haplotypes inferred from the HapMap genotypes have been used for making various inferences about human evolutionary history, e.g., estimate the fine-scale distribution of recombination events and identify genes that show signs of positive selection (The International HapMap Consortium 2005; Sabeti et al. 2007). The HapMap haplotypes have proven to be invaluable for whole-genome association studies in multiple ways. To reduce cost, disease association studies are performed using a subset of SNPs in the human genome. The HapMap haplotypes are useful for evaluating the power of these subsets to detect association at the untyped SNPs in human populations. Further, the haplotype data have also been used for fine-scale mapping of variants identified in association studies (Gudmundsson et al. 2007) and for improving the power of whole-genome association studies (Pe’er et al. 2006; Marchini et al. 2007; Zaitlen et al. 2007).

Nonetheless, there are some limitations of using haplotypes reconstructed from population data. All haplotype phasing methods, explicitly or implicitly, exploit linkage disequilibrium (LD), the correlation of alleles at physically proximal SNPs in the human genome. In short regions of the genome, high LD reduces the number of distinct haplotypes, allowing these methods to piece together haplotypes for an individual. Therefore, the accuracy of haplotypes is reduced in regions with low levels of LD. In general, population data from unrelated individuals do not contain enough information to reliably estimate the haplotypic phase between distant markers (>100 kb). Accurate long-range haplotypes may prove useful for finding multiple genetic variants that contribute to complex diseases. To obtain such haplotypes, additional information such as family data is invaluable. For example, the presence of trios in two of the HapMap populations (CEU and YRI) has allowed the inference of highly accurate haplotypes. This in turn has been proven to be informative for detecting copy neutral variation such as inversions (Bansal et al. 2007). However, family data are hard to obtain for every population sample.

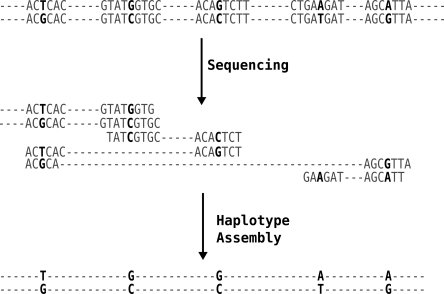
The availability of full diploid genome sequences for a large number of individuals would be ideal for obtaining a comprehensive understanding of all forms of genetic variation and especially useful for finding rare genetic variants associated with disease. Advancements in sequencing technology are driving down the cost of sequencing, and it should be possible to completely sequence many human individuals in a few years (Shaffer 2007; Schuster 2008). Whole-genome sequence data from a single individual represent an alternate resource from which the two haplotypes can potentially be determined. Each sequence read represents a fragment of a chromosome. A read that spans multiple variant sites can reveal the combination of alleles present at those sites on that chromosome. Using the overlaps at heterozygous sites between a collection of reads, one can potentially assemble the two haplotypes for a chromosome (for an illustration, see Fig. 1). This “haplotype assembly” represents a different computational challenge in comparison to genome sequence assembly, where one uses the sequence overlap between reads (ignoring the variant sites) to piece together a haploid genomic sequence.

Figure 1.

Illustration of how haplotypes can be assembled from sequenced reads. Each read is a fragment of one of the two chromosomes. Reads that share an allele at a common variant can be inferred to come from the same chromosome and joined together. Reads that differ at a particular variant can be inferred to come from different chromosomes and similarly extend the two haplotypes.

Haplotype assembly refers to the problem of reconstructing haplotypes from a collection of sequenced reads given a genome sequence assembly. A more challenging problem is to separate out the two haplotypes during the sequence assembly process itself. This has recently been done for some small, highly polymorphic genomes (Vinson et al. 2005) but remains difficult to accomplish for large eukaryotic genomes such as humans. Large eukaryotic genomes include many repetitive sequences, and a sequence assembly must therefore distinguish between two (almost identical) instances of a sequence that lie on the same chromosome as well as separating the chromosomes. The haplotype assembly problem may seem easier, but the objectives are different. By working with a reference sequence, one can focus on obtaining highly accurate haplotypes and estimating their reliability rather than just obtaining “a single” haplotype assembly. Also, as many individuals in a population are sequenced, it is computationally more efficient to generate a reference assembly once and assemble haplotypes for each of the individuals.

For haplotype assembly to be feasible, one requires a high sequence coverage (sufficient overlaps between reads) and reads that are long enough to span multiple variant sites. Given the level of polymorphism in the human genome (∼0.1%), single shotgun reads (∼8,001,000 base pairs long) at 5–8× coverage would result in short haplotype segments. However, paired ends or mate pairs (pair of sequenced reads derived from the same shotgun clone) provide linkage information that can substantially increase the length of inferred haplotypes. Even with mate pairs, it is not possible to link all variants on a chromosome. A haplotype assembly for a diploid genome is a collection of haplotype segments or disjoint haplotypes. In the absence of errors in sequenced reads, the correct haplotype assembly is unique and is not difficult to derive. Errors in reads increase the space of possible solutions, making this problem computationally challenging. The problem of finding the haplotype assembly that optimizes a certain objective function (e.g., minimize the number of conflicts with the sequenced reads) has been explored from a theoretical perspective (Lippert et al. 2002; Rizzi et al. 2002; Halldorsson et al. 2003; Bafna et al. 2005) and has been shown to be computationally intractable for gapped reads (e.g., mate pairs). A statistical method was proposed (Li et al. 2004) for reconstructing haplotypes from sequenced reads aligned to a reference genome. The method is based on inferring local haplotypes using a Gibbs sampling approach and joining these local haplotypes using overlaps. This method has recently been extended (Kim et al. 2007) to include polymorphism detection as part of the haplotype reconstruction pipeline, and applied to the genome of Ciona intestinalis.

Recently, Levy et al. (2007) sequenced the complete diploid genome of a single human individual. Approximately 32 million sequenced reads (from clone libraries of various lengths) were used to generate a genome assembly referred to as HuRef. More than 4.1 million genomic variants were detected by identifying heterozygous alleles within the sequenced reads and through comparison of the HuRef assembly with the NCBI version 36 human genome assembly. Of these, 1.8 million heterozygous variants were used for haplotype assembly. The presence of paired-end sequences or mate pairs with different insert sizes (ranging from 2–40 kb) increases the length of the haplotype segments that can be inferred but also results in links between physically distant variants. As mentioned earlier, there are no efficient algorithms for haplotype assembly in the presence of mate pairs, and statistical methods for haplotype assembly (Li et al. 2004; Kim et al. 2007) that start by inferring short local haplotypes are not particularly suited for the HuRef data. A simple greedy heuristic was implemented to build haplotypes incrementally starting from single reads (see Methods) (Levy et al. 2007). More than 70% of the 1.8 million heterozygous variants used for haplotype assembly were assembled into haplotypes that cover at least 200 variants. In addition, 1.5 Gb of the genome could be covered by haplotypes longer than 200 kb in length. Comparison of sequenced reads to the reconstructed haplotypes showed that 97.4% of the variant calls are consistent with the haplotype assembly. Notwithstanding the reasonable accuracy of the haplotype assembly for HuRef, the greedy strategy represents a relatively simple approach for this problem. It incrementally reconstructs a single haplotype assembly and does not attempt to find a haplotype assembly that is optimal under a probabilistic or combinatorial model. In Levy et al. (2007), we had briefly mentioned that it is possible to obtain a more accurate haplotype assembly using Markov chain Monte Carlo (MCMC) methods and had implemented one such algorithm. In this article, we describe a novel MCMC algorithm, HASH (haplotype assembly for single human) for haplotype assembly. The MCMC approach represents a natural way to search the space of possible haplotypes to find likely haplotype reconstruction(s) and also allows us to estimate the reliability of the reconstructed haplotypes. The transitions of the Markov chain underlying our algorithm are determined using the graph structure of the links between the variants and are not restricted to be local.

Results on the HuRef sequence data demonstrate that the haplotypes reconstructed using HASH are more consistent with the sequenced fragments than the haplotypes obtained using the greedy heuristic. By use of haplotypes sampled by the MCMC algorithm, we estimate that the HuRef haplotypes have a switch error rate of 0.9%. By using simulations, we also demonstrate that our MCMC algorithm can reconstruct haplotypes to a high degree of accuracy and determine which variant calls are likely to be incorrect. Based on comparison to population haplotypes from the HapMap project, we estimate a switch error rate of ∼1.1% for the HuRef haplotypes inferred using HASH. In comparison, the switch error rate for the haplotypes reconstructed using the greedy heuristic is 3.1%. Although we describe results using data from whole-genome Sanger sequencing of a human individual, our methods are valid for performing haplotype assembly from sequenced reads generated using any sequencing technology as long as the polymorphism rate for the sequenced organism and the length of sequenced reads allow the linking of multiple variants. They are also applicable to inferring haplotypes using short haploid sequences from other sources (for example, see Konfortov et al. 2007).

Methods

We assume that a list of genetic variants such as SNPs, short insertions/deletions, etc., is available. A list of polymorphic variants can be generated while sequence assembly is performed or can be obtained from a database of genetic variants such as dbSNP (Sherry et al. 2001). We restrict ourselves to variants that have been identified to be heterozygous in the genome of the individual under consideration, as homozygous variants are uninformative about phasing of other variants. Note that certain variants that are truly heterozygous in the genome may be reported as homozygous, as both alleles are not sampled a sufficient number of times during sequencing.

Each sequenced read is mapped to the reference genomic sequence to obtain the alleles it has at each of the heterozygous sites. For a variant, reads with sequence matching the consensus sequence are assigned as 0, while those not matching are assigned as 1. Paired-end reads from the same clone that map to the assembly in the expected orientation and whose physical separation is within the expected range are represented as a single fragment. Mated reads that show some inconsistency in orientation or distance are split into two separate fragments. Note that these aberrant mapping pairs might represent chimeric errors but also heterozygous structural variation in the HuRef genome; Levy et al. (2007) describe some of these variations. Here, we ignore this additional information.

Haplotype likelihood

Formally, each fragment i is represented by a ternary string X_i ∈ {0, 1, −}ⁿ, where the − corresponds to the heterozygous loci not covered by the fragment. The complete data can be represented by a fragment matrix X with m rows and n columns, where each row represents a fragment and each column corresponds to a variant site. Corresponding to each variant call X_i[j], we have an error probability q_i[j], which denotes the probability that the variant call is incorrect. As q_i[j] cannot be estimated from the fragment data, we use quality scores s_i[j] that usually accompany sequence data. For example, the quality scores might be obtained using phred (Ewing and Green 1998). Sequence quality scores are integer values related to the error probabilities as

For SNPs, s_i[j] describes the quality value for the allele call; for multibase variants, s_i[j] is the lowest of the quality values for the base calls in the variant; for the case of a gap (insertion/deletion), s_i[j] corresponds to the lower of the two quality values on either side of the gap. If information about the sequencing quality values is not available or for performing simulations, we assume a uniform error probability q_i[j] = 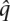for all variant calls. In what follows, we will assume that q is available and fixed.

Let H = (h, h) represent the unordered pair of haplotypes, where h is a binary string of length n and h is the bitwise complement of h; i.e., h[j] = 1 − h[j]. The problem of reconstructing the most likely pair of haplotypes given the fragment data (known) is given by

However, we are interested in sampling H from a probability distribution. By using Bayes’ rule, we can write

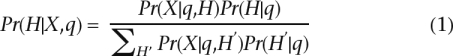Assuming a uniform prior on the space of haplotypes, we have

We assume that the variant calls for a fragment X_i are independent of each other. Therefore,

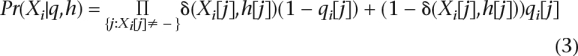where δ(X_i[j],h[j]) = 1 if X_i[j] = h[j] and 0 otherwise. Assuming that each fragment is randomly generated from one of the two haplotypes, we can write

Finally, Pr(X_i|q,H) can be computed as a product over fragments (assuming that fragments are independently generated):

In the remainder of this paper, we will refer to Pr(X|H,q) as a distribution over H for notational convenience.

MCMC algorithm

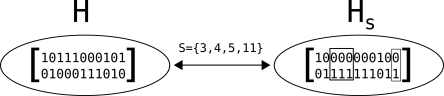
Instead of computing the most likely solution, it is potentially more useful to sample from the posterior distribution of haplotypes. As the number of possible haplotypes grows exponentially with the number of variants, we construct a Markov chain to sample from the posterior distribution of H given the fragment matrix X and the matrix of error probabilities q. The states of the Markov chain correspond to the set of possible haplotypes. Transitions of the Markov chain are governed by subsets S of columns of the fragment matrix X. Specifically, each transition is of the form: H → H_S, where H is the current state (haplotype pair) and H_S is a new haplotype pair created by “flipping” the values of the columns in S. Figure 2 illustrates how H_S is derived from H. For columns not in S, such as column 1, H and H_S are identical. However, columns in S = {3, 4, 5, 11} are flipped in H_S.

Figure 2.

Illustration of how H_S can be derived from a haplotype pair H and a subset S of the columns of the fragment matrix.

If Γ = {S₁, S₂, . . . , S_k} is a collection of subsets of columns of X, then for each state H, there are k + 1 possible moves to choose from, including the self-loop. The Markov chain in state H chooses a subset S_i ∈ Γ and moves to the new state H_Si with a certain probability. The transition probabilities are chosen to ensure that they satisfy the detailed balance conditions. The MCMC algorithm is described as follows.

• Initialization: Choose an initial haplotype configuration H⁽⁰⁾.

• Iteration: For t = 1, 2, . . . obtain H^t+1 from H^t as follows:

1. With probability 1/2, set H^t+1 = H^t

2. Otherwise, sample a subset S from Γ with probability (1/|Γ|)

3. With probability min [1,(Pr(X|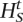,q)/Pr(X|H^t,q))], set H^t+1 = 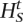. Otherwise, set H^t+1 = H^t

Our algorithm uses the Metropolis update rule (Metropolis et al. 1953) and is completely specified by the fragment matrix X, the matrix q of error probabilities, and the collection of subsets Γ. We denote the corresponding Markov chain as ℳ(X, q, Γ) or simply by ℳ(Γ), whenever X and q are implicit. Note that Step 1 of the above algorithm, which represents a self-loop probability of 1/2, is added to ensure aperiodicity that is required for analysis of the mixing time of the Markov chain (Randall 2006). In practice, it is not essential and can be removed as most Markov chains are indeed aperiodic.

Choosing Γ

A natural choice for Γ is Γ₁ = {{1},{2}, . . . , {n}}. We can show that a Markov chain ℳ (X, q, Γ) is ergodic and has the desired posterior distribution Pr(X|H,q) if Γ₁ ⊆ Γ (for proof, see Supplemental material). Indeed, ℳ(Γ₁) was proposed by Churchill and Waterman (1992) for a related problem. However, we prove theoretically that the mixing time of ℳ(Γ₁) grows exponentially with d, the depth of coverage, for a representative family of examples (for proof, see Supplemental material). This implies that it may take an inordinately long time before the chain ℳ(Γ₁) is sampling from the posterior distribution.

Supplemental Figure S1 illustrates this point empirically and also provides insight for an improved algorithm. The fragment matrix X(n, d) has n columns, with each pair of adjacent columns linked by d fragments. X(n, d) admits two equally likely haplotype configurations H₁ and H₂, which differ by a single flip of half of the columns. Nevertheless, the time to move from H₁ to H₂ increases exponentially with d (see Supplemental Fig. S1). For d = 5, the expected time is ∼10 million steps, (increasing for smaller values of q). However, by augmenting Γ slightly, by adding the subset S₁..._n/2 (columns 1 to n/2), the mixing time reduces to being polynomial in n and d. The proof of this assertion requires advanced techniques based on the notion of graph conductance and coupling arguments (V. Bafna and V. Bansal, unpubl.; available at http://www.cse.ucsd.edu/users/vibansal/HASH/). Our analysis on this family suggests the following iterative strategy: When a current Markov chain ℳ(Γ) has converged to a local optimum, use the current haplotype and the fragment matrix X to identify “bottlenecks” to rapid convergence. Next, add subsets S to Γ that eliminate these bottlenecks, and continue. As described below, we use a recursive graph partitioning strategy to identify bottlenecks to convergence.

A graph-partitioning approach

We construct an undirected weighted graph G(X) with each column of the fragment matrix as a separate node of this graph and an edge between two nodes if there is some fragment that covers both columns. The weight of an edge between two columns is the number of fragments that cover both columns. A cut in G(X) is simply a subset S of vertices, with weight equal to the sum of weights of the edges going across the cut. A minimum-cut (min-cut) is a cut with minimum weight in the graph G(X). From the perspective of the Markov chain, a cut represents a subset of variants, and a cut with low-weight represents a good candidate to include in Γ. We partition the graph G(X) into two pieces S and S using a simple min-cut algorithm (Stoer and Wagner 1994) and add the two subsets S, S to Γ. We apply the same procedure recursively to the two induced subgraphs G(S) and G(S), adding two new subsets to Γ every time we compute a new cut. The recursive graph-partitioning approach ensures that Γ includes Γ₁ and has n additional subsets. A formal description of the graph-partitioning algorithm is given in the Supplemental material.

Information about the variant calls in the fragment matrix can be used for assigning weights to the edges in G(X). This is potentially more informative than just using the number of fragments. Consider the example fragment matrix in Supplemental Figure S1. The subset S₁..._n/2 is a good candidate for Γ, not only because the cut corresponding to this subset has low weight (two edges) but also because the two fragments linking this subset of columns to the rest of the matrix are inconsistent with each other. We have developed a scheme that assigns weights to the edges of G(X) based on the consistency of a haplotype pair H with the fragment matrix. A fragment adds 1 to the edge weight between two columns if the phase suggested by the fragment is consistent with the current haplotype assembly. If not, it contributes −1 to the edge weight. Hence, a cut with low or negative weight corresponds to a subset of columns whose current phase with respect to the rest of the columns is inconsistent with the fragment matrix. This scoring scheme is fully described in the Supplemental material, and we denote the graph partitioning algorithm for computing Γ as WeightedGraphPartitioning(X, H). In Figure 3, we give an example of the graph G(X) and illustrate the recursive graph partitioning method for computing Γ.

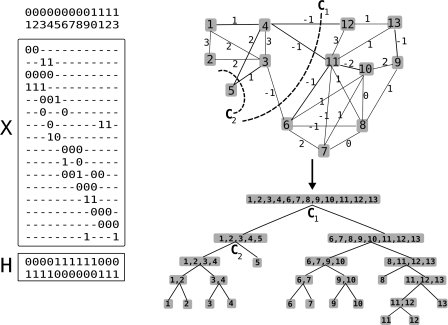
Figure 3.

Illustration of the recursive graph-partitioning algorithm for computing Γ. The weighted graph G(X) derived from the fragment matrix X and a haplotype pair H is shown on the top right. The tree structure below demonstrates the recursive partitioning of the columns of X using min-cut computations in the graph G(X). The first cut (C₁), partitions the columns of X into two subsets: S = {1, 2, 3, 4, 5} and S = {6, 7, 8, 9, 10, 11, 12, 13}. The second cut (labeled C₂), further partitions the subset S into two smaller subsets: {1, 2, 3, 4} and {5}. Γ is obtained from the subsets labeling the nodes of the tree (except the root node).

The recursive graph-partitioning approach for constructing Γ is greatly motivated by the nature of the sequencing data that we have analyzed. Supplemental Figure S2 shows an example of a fragment matrix from chromosome 22 of HuRef. Shotgun sequencing leads to nonuniform sampling of variants creating “weak” links in the fragment matrix that the graph-partitioning approach can exploit to construct Γ.

The complete MCMC algorithm

The collection of subsets Γ computed using the weighted graph-partitioning approach is dependent upon the haplotype pair H. As we sample haplotypes with greater likelihood, it is potentially useful to update Γ. The complete algorithm, which we call “HASH” (short for haplotype assembly for single human), is as follows:

HASH(X,q)

1. Set Γ⁽⁰⁾ ← Γ₁.

2. Set H⁽⁰⁾ at random or otherwise.

3. For t = 1, 2, . . .

   • (a) Let H^(t) = ℳ(Γ^(t−1), X, H^(t−1), c) be the haplotype obtained after running ℳ(Γ^(t−1)) for c × n steps (c ≈ 1000).

   • (b) Compute Γ^(t) = WeightedGraphPartitioning(X, H^(t)).

4. Set Γ ← Γ^(t) and discard all previous samples.

5. Run the chain ℳ(Γ) initialized with H^(t) for ∼10⁶ × n steps.

Steps 1-3 in the above algorithm represent a Γ determination phase where we start from a haplotype H⁰ and Γ initialized to Γ₁. We run the Markov chain for a certain number of steps (c × n, where c ∼ 1000) and then compute a new Γ using the current haplotype pair. This is repeated until we see no improvement in the likelihood of the best haplotype sampled by the Markov chain. After this initial Γ determination phase, we run the Markov chain initialized using the current haplotype and the final Γ for ∼10⁶ × n steps. The samples used to make inference about the posterior distribution are drawn only from this Markov chain. For drawing samples from ℳ(Γ), we discard the first 10,000 × n samples and thin the chain every 1000 × n steps.

Results

HuRef sequence data

The HuRef genome assembly (Levy et al. 2007) represents the sequence of a single human individual using traditional Sanger sequencing technology. It was derived from ∼32 million reads and has a sequence coverage of 7.5. Using the HuRef sequenced reads and comparison between the HuRef genome assembly and the NCBI reference genomic sequence, a list of potential DNA variants was compiled. These variants are not restricted to SNPs but also include short insertions/deletions, etc. The sequenced reads were mapped to the HuRef assembly to determine the alleles at each variant. For each sequenced read, the sequencing quality values were used to assign an error probability for the variant sites. After applying various filters to define a set of reliable heterozygous variants, there were ∼1.8 million heterozygous variants for the 22 autosomes (for details, see Levy et al. 2007).

To illustrate the coverage and connectivity of the sequenced fragments, we present some statistics for chromosome 22, which has 24,967 heterozygous variants. For this chromosome, the fragment matrix had 103,356 rows, where each row corresponds to a DNA fragment from one of the two copies of the chromosome. Hence, paired-end reads (sequenced ends of clones) are represented as a single row; 18,119 of these fragments correspond to such paired-end reads. About half of the fragments (53,279) link two or more variants and therefore are potentially useful for haplotype assembly. These 53,279 fragments correspond to 173,084 variant calls (about seven calls per variant) in the fragment matrix. By using the overlap between these fragments, the chromosome can be partitioned into 609 disjoint haplotypes (in addition to 921 isolated variants) of varying lengths, the largest of which links 1008 variants. In terms of the actual physical distance spanned by haplotypes, the N50 haplotype length (length such that 50% of the variants are contained in haplotype segments of the given length or greater) is ∼350 kb. Note that a haplotype segment does not link all variants it spans (for an illustration of a haplotype segment, see Supplemental Fig. S2). Even if haplotype length is measured in terms of the number of variants linked, the N50 length is ∼400 variants.

The importance of paired-end reads for haplotype assembly can be gauged from the comparison of the distribution of the number of variants among haplotypes of different sizes for (1) reads including paired-end information versus (2) unpaired reads (see Supplemental Fig. S3). If we ignore the paired ends and split them into separate fragments, the linkage between the variants, and consequently, the haplotype block sizes are greatly reduced. The number of disconnected haplotypes increases to 4378 with no haplotype having more than 100 variants.

Performance of HASH on simulated data

To test the performance of HASH, we generated simulated data with varying error rates as follows: First, the fragment matrix X was modified to make it perfectly consistent with a particular haplotype. Next, to simulate an error rate of ε (0 ≤ ε ≤ 0.1), each variant call in the fragment matrix was “flipped” (changed from 0 to 1 or vice versa) independently with probability ε. For this modified fragment matrix, we know the true haplotypes and also the variant calls that are correct (those that were not flipped) and those that are incorrect (the ones that were flipped during simulations). Therefore, we can assess the performance using two different criteria: (1) the distance of the reconstructed haplotypes from the true haplotypes and (2) the ability to predict which variant calls are incorrect.

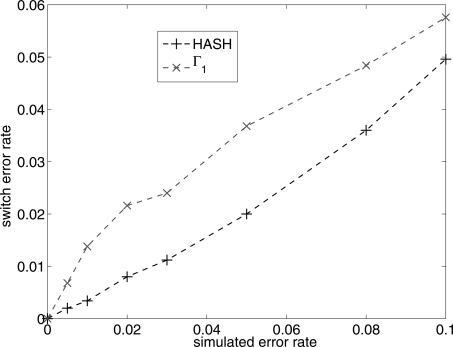
In Figure 4, we plot the average switch distance of the maximum likelihood reconstructed haplotypes from the true haplotypes as a function of ε. Average switch distance or switch error rate (Lin et al. 2002) is defined as the fraction of positions for which the phase between the two haplotypes is different relative to the previous position. The switch error rate increases roughly linearly with increasing error rate and is (∼2×) lower for HASH than for the MCMC algorithm with Γ1. This is expected given the slow convergence of the Markov chain with Γ1. The switch error rate for the greedy heuristic (Levy et al. 2007) is also high in comparison with HASH (data not shown).

Figure 4.

Comparison of the switch error rate for the algorithm HASH and the MCMC algorithm with Γ₁. The Y-axis is the average switch distance of the reconstructed haplotypes from the true haplotypes. The X-axis (simulated error rate) is the fraction of variant calls in the fragment matrix that were flipped.

By using an MCMC procedure, one can estimate the posterior error probability for each variant call in the fragment matrix. Given a haplotype pair H = (h, h), let Z_i(H) denote the probability that fragment X_i is sampled from h. Denote ε_i[j, h] = 1 if X_i and h disagree at position j. Finally, let ε_i[j] = 1 to denote that X_i[j] is called incorrectly, and ε_i[j] = 0 otherwise. Then, the posterior error probability can be computed as follows:

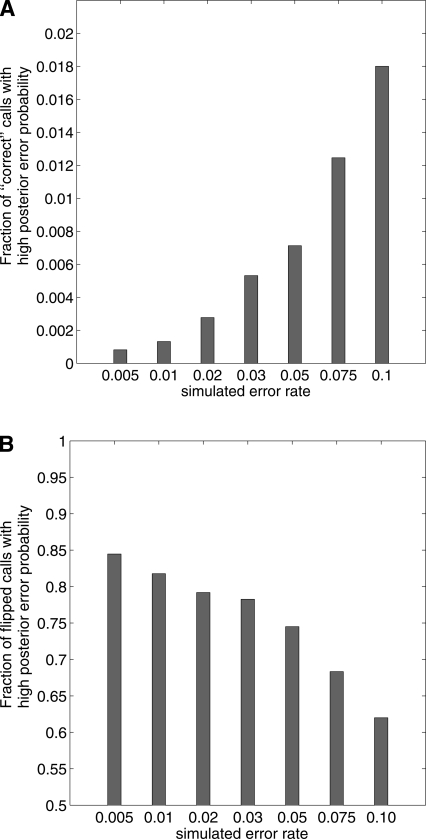
Here π_H = Pr(X|H, q) is a probability distribution over H. See Supplemental material for a complete description. We compare the posterior error probability for the “correct” variant calls with those for the “incorrect” variant calls to demonstrate that our algorithm HASH can predict the incorrect variant calls. In Figure 5A, we plot the false-positive rate (fraction of correct variant calls that had a posterior error probability greater than 0.5) for different values of ε. For an error rate of 0.02, the fraction of incorrect variant calls with a high posterior error probability (>0.5) is ∼80%. In Figure 5B, we plot the true-positive rate (fraction of flipped base calls that had a posterior error probability of >0.5). Increasing the cutoff value for the posterior error probability reduces both the true-positive rate and the false-positive rate. For an error rate of 0.02, 65% of the incorrect (or flipped) variant calls have a posterior error probability greater than 0.95, while only 0.015% of the correct variant calls have such a high posterior error probability.

Figure 5.

Fraction of variant calls with a posterior error probability of ≥0.5 using the HASH algorithm for different values of ε. (A) False-positive rate, given by the fraction of “correct” variant calls with high posterior error probabilities. (B) True-positive rate, given as the fraction of “flipped” variant calls with high posterior error-probability.

The plots suggest that the error in reconstruction is very low for typical sequencing errors, but increases with increasing error rate. Also, our measure for estimating accuracy is (perhaps, overtly) conservative. For example, if there is a single call for a variant and this variant call is flipped, it is not possible to reconstruct the true haplotype or predict that this variant call is incorrect. Flipping a variant call affects not only the posterior error probability of that variant call but also the error probability of variant calls that cover the same column. Therefore, increasing the error rate is expected to increase the number of “correct” variant calls with a high posterior error probability. Also, if the error rate is large and the number of fragments covering each variant is small, it may not be possible to reconstruct the true haplotype exactly from the mutated fragment matrix.

HASH versus other MCMC algorithms

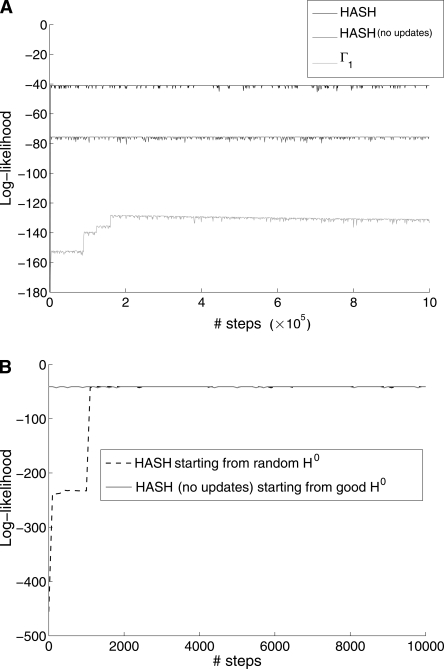
Our goal in devising HASH is to enable the Markov chain to move out of local optima and transition to haplotypes with greater likelihood. We compared the performance of HASH against two other MCMC algorithms: (1) ℳ(Γ₁), the Markov chain with Γ₁, and (2) ℳ(Γ) where Γ was computed once using the recursive graph-partitioning on G(X). Recall that HASH is similar to algorithm 2 except that Γ is updated iteratively. For this, we used data from chromosome 22 and looked at the maximum-likelihood haplotype pair sampled by each algorithm. The results shown are for a block with ∼200 columns from chromosome 22 (see Fig. 6A). In each case, the Markov chain was initialized with a random haplotype pair. As expected, HASH dominates both in the likelihood of the sampled solution and in the speed with which the solution is reached. ℳ(Γ₁) gets stuck in a local optima and will take a prohibitively large number of steps to sample the maximum likelihood solution.

Figure 6.

Results of running the MCMC algorithm with different Γ on a fragment matrix with n = 200 columns (from chromosome 22 of HuRef genome). (A) A comparison of the HASH algorithm against two other MCMC algorithms: (1) ℳ(Γ₁) and (2) ℳ(Γ) where Γ was computed using the recursive graph-partitioning algorithm G(X). All algorithms were initialized with a random haplotype pair. (B) Comparison of HASH algorithm initialized with a random haplotype against ℳ(Γ) (graph-partitioning) initialized with a good haplotype. Note that we are zooming in on the first 10,000 steps in the iteration.

In Figure 6B we zoom in on the “Γ update” phase of the HASH algorithm for the above example. The HASH algorithm was initialized with a completely random haplotype. We observe that the likelihood of the best haplotype sampled by the HASH algorithm after a few updates to Γ is identical to that of the Markov chain with the graph-partitioning-based Γ started from a good quality solution. Although the results shown in Figure 6 are for one particular example, they are similar for all data sets (data not shown). The two results combined show that the sample space has many locally optimal solutions that one could be trapped in, but dynamic updates to the Markov chain architecture, as described by HASH, allow for rapid convergence, increasing the likelihood of sampling the globally optimum solution.

Haplotypes for HuRef

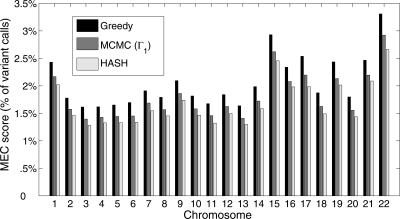
We compared the most likely haplotype assembly obtained using HASH with the greedy haplotype assembly (Levy et al. 2007) for each of the 22 autosomes of the HuRef individual. HASH was run independently on each of the disjoint haplotype blocks for a chromosome. For each chromosome, we compared the haplotype assembly against the fragment matrix and computed the MEC (minimum error correction) score (Bafna et al. 2005), defined as the minimum number of variant calls in the fragment matrix that need to be modified for every fragment to perfectly match one of the two haplotypes. The MEC score represents a parsimonious estimate of the discordance between the haplotypes and the fragment matrix. A more detailed formulation of the MEC score is given in the Supplemental material. In Figure 7, we compare the MEC scores for three different methods: Greedy heuristic (Levy et al. 2007), MCMC algorithm with Γ₁, and HASH. The haplotype assembly derived using HASH has a lower MEC score for each chromosome, reflecting the greater accuracy of the haplotypes. For chromosome 22, the MEC score for HASH was 20% lower than the greedy algorithm. Note that the MEC score is not expected to be zero, even for the true haplotypes, due to errors in base-calling.

Figure 7.

The percentage of variant calls that are inconsistent with the best haplotype assembly for three different methods: Greedy heuristic (Levy et al. 2007), MCMC algorithm with Γ₁ and the HASH algorithm for the 22 autosomes of HuRef.

We also compared the log-likelihood of the haplotype assemblies for the greedy algorithm and HASH. The log-likelihood was computed using the sequencing quality values to estimate the q matrix. We found that the log-likelihood for the haplotypes reconstructed using HASH was consistently higher than that of the greedy haplotypes, indicating that the haplotypes are significantly more accurate. For example, the log-likelihood of the greedy haplotype assembly for chromosome 22 (summed over all disjoint haplotypes) was −15683.4. In comparison, the most likely haplotype assembly using the HASH algorithm had a log-likelihood of −11,944.25 (a reduction of 23.8%).

We compared the posterior error probabilities for each variant call against the sequencing quality values. To allow an unbiased comparison, the HASH algorithm was run using uniform error probabilities estimated from the greedy haplotypes (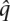 = fraction of inconsistent variant calls). For chromosome 22, 2.26% of variant calls (3919/173,804) had a posterior error probability greater than 0.5. For variant calls with low sequencing quality values (q ≥ 0.01), 4.2% (1203/28,532) had a high posterior error probability. From Supplemental Figure S4, we can see that the fraction of variant calls with a high posterior probability increases with increase in the error probability (or decrease in sequencing quality value). This correlation between high posterior error probabilities and low sequencing quality values represents an independent confirmation of the quality of the reconstructed haplotypes and also indicates that some of the inconsistencies between the reconstructed haplotypes and the fragments are a result of sequencing error.

Estimating accuracy of HuRef haplotypes

The HuRef haplotypes obtained using HASH are highly consistent with the sequenced fragments and have a low MEC error rate (see Fig. 7). However, we also want to be able to estimate the absolute accuracy of the HuRef haplotypes. The absolute accuracy can be expressed in terms of the “switch error rate” (Lin et al. 2002) or the fraction of adjacent pairs of variants whose phase in the HuRef haplotypes is incorrect. We have computed two independent estimates of the switch error rate: one based on the haplotypes samples generated by our MCMC algorithm and another through comparison of the HuRef haplotypes to the population haplotypes from the HapMap project.

Switch error estimates using samples from the MCMC algorithm

We used the haplotypes sampled by the algorithm HASH to estimate the reliability of the phase between adjacent pairs of variants in a haplotype segment. For a pair of adjacent variants (i, j), if we denote the two alleles at each site by 0 and 1, there are two possible haplotype pairs: (00, 11) and (01, 10). Based on haplotypes sampled by the Markov chain, the switch error probability for a pair (i, j) was estimated as the fraction of times the less frequent haplotype pair was observed. See Supplemental Figure S2 for a plot of switch error probabilities for a haplotype segment from HuRef. The switch error rate for a chromosome can be approximated as the average of the switch error probabilities for adjacent pairs. For chromosome 22 of HuRef, the switch error rate was estimated to be 0.009 using 1000 samples.

Switch error rate based on comparison to HapMap haplotypes

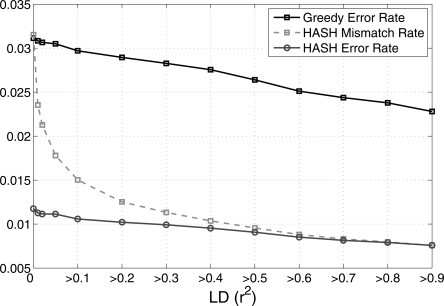
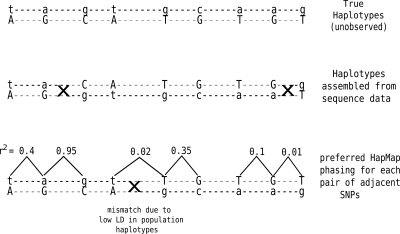
One of the benefits of inferring haplotypes from sequence data is that the local accuracy of the haplotypes is unlikely to be affected by the level of LD in a region. This also presents the opportunity of using LD in population data to detect switch errors in the HuRef haplotypes. For a pair of variants that are in strong LD in population data, the correct HuRef phasing is expected to match the more likely population based phasing. If the inferred HuRef phasing does not match the preferred population phasing, one can infer a switch error with some probability (the probability value depends upon the strength of LD between the pair of variants). We use this idea to empirically estimate the switch error rate of the HuRef haplotypes. As the HuRef individual is of Caucasian origin, we have used the haplotypes from the CEU population in the HapMap project (www.hapmap.org) for this comparison. We identified the subset of SNP variants in HuRef that were also genotyped in the HapMap project. For each pair of adjacent SNPs in this subset, there are two possible haplotype phasings: (00, 11) and (01, 10). Let f₀₀, f₁₁, f₀₁, and f₁₀ represent the frequencies of the four haplotype pairs in the HapMap CEU sample. If (f₀₀ × f₁₁) > (f₀₁ × f₁₀), the pair (00, 11) is defined to be the preferred HapMap phasing. Otherwise, (01, 10) is the preferred HapMap phasing. For a pair of adjacent HapMap SNPs in the HuRef haplotypes (that were part of the same haplotype segment), the phasing of the HuRef individual is compared to the preferred HapMap phasing for that pair. The mismatch rate is defined as the fraction of pairs for which the HuRef phasing does not match the preferred HapMap phasing. In Figure 8, we plot the mismatch rate of the HuRef haplotypes for chromosome 22 (estimated using HASH) as a function of LD (measured using r²). The mismatch rate is lowest for pairs with high levels of LD (0.008 for pairs with r² > 0.8) and increases to 0.031 for all pairs. The mismatch rate for pairs with high levels of LD can mainly be attributed to switch errors in the HuRef haplotypes. For pairs of SNPs with low LD, mismatches between the HuRef haplotypes and the preferred HapMap phasing can represent switch errors or chance mismatches (for an illustration, see Fig. 9). To correctly estimate the error rate, we first compute an expected mismatch rate for the HapMap haplotypes as follows: for every pair of adjacent SNPs, we sample one of the two haplotype pairs ([00, 11] or [01, 10]) based on the haplotype frequencies in the HapMap haplotypes. The expected mismatch rate is the fraction of pairs for which the sampled pair mismatches the preferred HapMap phasing. The expected mismatch rate is an estimate of the mismatch rate for a haplotype pair with no switch errors. For a particular value of r², we define the “adjusted mismatch rate” as the mismatch rate minus the expected mismatch rate. The adjusted mismatch rate represents an estimate of the switch error rate of the HuRef haplotypes that is corrected for variation in LD in the HapMap haplotypes. We observe that the adjusted mismatch rate for HASH (Fig. 9) is nearly independent of LD, ranging from 0.011 for all pairs to 0.0078 for pairs of SNPs with r² > 0.8. The adjusted mismatch rate for the greedy heuristic is almost three times that of HASH, providing the strongest proof of the greater accuracy of the haplotypes inferred using HASH.

Figure 8.

Mismatch rate and the “adjusted mismatch rate” (error rate) of the HuRef haplotypes estimated by comparison with the CEU HapMap haplotypes. The error rate is plotted as a function of r², i.e., computed for all pairs of adjacent SNPs with r² greater than a certain value.

Figure 9.

Comparison of haplotypes assembled using sequence data with the preferred HapMap phasing for each pair of adjacent SNPs inferred from the HapMap haplotypes. For three pairs of adjacent SNPs, the phase of the sequence-based haplotypes mismatches the preferred HapMap phasing (indicated by crosses). The first pair shows strong linkage disequilibrium (r² = 0.95), and therefore, the mismatch is more likely to represent a switch error in the sequence-based haplotypes. For the second pair of SNPs, the sequence-based haplotypes are correct and the mismatch is due to low LD between the SNP pair. For the third pair, LD is again low and the mismatch is due to a switch error in the sequence-based haplotypes.

Both internal and external estimates indicate that the switch error rate of the HuRef haplotype assembly is ∼0.01. The switch error rate for HapMap individuals from the CEU and YRI samples has been estimated to be 0.0053 and 0.0216, respectively (Marchini et al. 2006). The haplotypes for these individuals have been inferred using a combination of trio and population information. The increased error-rate for YRI is due to lower levels of LD in the Yoruban population. Switch error rates for haplotypes inferred without trio information are typically much higher (0.054 for CEU individuals). An advantage of inferring haplotypes using sequence data is that the error rates are expected to be independent of the ancestry of the individual. Moreover, since the switch errors are distributed independent of LD, the error rate could be reduced further by incorporating LD information from population data in the haplotype assembly.

Discussion

With the rapid development of new sequencing technologies (Bentley 2006) comes the promise of individualized sequencing, wherein the complete genomic sequence of individuals will be available. In the past few years, next-generation sequencing technologies have drastically reduced the cost of sequencing complete genomes (for a comparison of three next-generation sequencing methods, see Mardis 2008). Many individual genomes have been sequenced (Levy et al. 2007; Wheeler et al. 2008), and hundreds of human individuals are proposed to be sequenced in the future (Kaiser 2008). As shown by Levy et al. (2007), whole-genome Sanger sequencing in the presence of paired ends allows one to reconstruct accurate and long haplotypes. In general, haplotype assembly is feasible when the sequenced fragments are long enough to cover multiple variants and the sequence coverage is high enough to overcome base-calling error. Most of the next-generation sequencing technologies have the ability to generate paired-end sequences which is crucial for haplotype assembly. Although the read lengths are typically shorter than those for Sanger sequencing, continued enhancements in technology are improving the read lengths; e.g., 454 Life Sciences (Roche) read lengths have increased from 100 bp to over 400 bp (Schuster 2008). In the future, third-generation technologies could deliver reads several thousand base pairs long (Korlach et al. 2008; von Bubnoff 2008).

Haplotype assembly from sequenced reads of an individual genome has several advantages over haplotypes obtained by computationally phasing SNP genotypes from a population. First, the accuracy of the phasing is not limited by regions of low LD, and it is possible to recover very long haplotypes spanning several hundred kilobases. Second, it is possible to assemble “complete” haplotypes linking alleles at all variants such as SNPs, insertion/deletions, etc., that are heterozygous in the individual. Third, the accuracy of haplotypes inferred from genotype data depends a great deal on the knowledge of ancestry of the individual, while haplotype assembly from sequence data does not require knowledge of the population of origin of the individual. It is important to note that these two approaches for inferring haplotypes are complementary to each other. As individual genomes are sequenced, population data could be combined with sequence data to obtain longer and more accurate haplotypes for an individual. LD from population data could be used to determine the phase between variants that are not linked by sequenced reads, while sequence data could be used to infer haplotypes across regions of low LD. The highly accurate haplotypes generated by the HapMap project for the CEU and YRI samples could prove especially useful for improving the quality of haplotypes assembled using individual sequencing.

In this article, we have described a MCMC algorithm for haplotype assembly that samples haplotypes given a list of all heterozygous variants and a set of sequenced reads mapped to a genome assembly. Our emphasis has been on describing how a particular choice of moves for the Markov chain enables it to sample the haplotype space more efficiently than a naive Markov chain. We have shown that haplotypes reconstructed using HASH are much more consistent with the sequenced reads than haplotypes inferred using a greedy heuristic. Comparison of the HuRef haplotypes to the HapMap haplotype data suggests that the error rate of haplotype reconstruction using HASH is low (∼1.1%) and independent of the local recombination rate. Instead, simulations show that the error rate depends upon the sequencing error and depth of coverage. As technologies improve, the cost and error rates will improve further, increasing the power and accuracy of haplotype assembly.

There are several aspects of our approach to haplotype assembly that could be investigated further. In our approach, we assume that a list of variants generated from the sequenced reads is available. Detection of SNPs and variant sites from sequencing data is a challenging problem in itself, and one can possibly integrate the variant detection phase with the estimation of haplotypes. This approach has recently been adopted (Kim et al. 2007) and can have certain advantages for genomes whose variant sites are not well characterized. Our framework considers only heterozygous variants for haplotype assembly. In Levy et al. (2007), a variant was called as heterozygous if at least 20% of the reads (minimum of two reads) supported the minor allele. This stringent criteria results in miscalling of heterozygous sites as homozygous. It is possible to add the alleles for such sites to the two haplotypes assembled using the remaining sites. An alternative approach would be to use all variants for the estimation of haplotypes. Our model for haplotype likelihood considers each variant call independently. One can incorporate more complex error models where all the variant calls for a read are erroneous, e.g., as a result of the read being incorrectly mapped, or some of the variant sites do not represent real polymorphic variants, e.g., paralogous SNPs. The HASH framework is independent of the likelihood model and can be easily adapted for such models.

Finally, we note that there are some novel aspects of our MCMC algorithm, HASH. We have shown, both empirically and theoretically, that a simple Markov chain with local moves, i.e., a chain in which all transitions are between haplotypes that differ in a single column, is unable to sample the haplotype space efficiently. We have proposed a Markov chain with nonlocal moves that allows transition between haplotypes that differ in multiple columns. The transition matrix of this Markov chain is determined by min-cut computations on an associated graph derived from the sequenced reads. Moreover, the Markov chain architecture is dynamically updated periodically, to escape local minima.