Auditory Cortex Phase Locking to Amplitude-Modulated Cochlear Implant Pulse Trains

Abstract

Cochlear implant speech processors transmit temporal features of sound as amplitude modulation of constant-rate electrical pulse trains. This study evaluated the central representation of amplitude modulation in the form of phase-locked firing of neurons in the auditory cortex. Anesthetized pigmented guinea pigs were implanted with cochlear electrode arrays. Stimuli were 254 pulse/s (pps) trains of biphasic electrical pulses, sinusoidally modulated with frequencies of 10–64 Hz and modulation depths of −40 to −5 dB re 100% (i.e., 1–56.2% modulation). Single- and multiunit activity was recorded from multi-site silicon-substrate probes. The maximum frequency for significant phase locking (limiting modulation frequency) was ≥60 Hz for 42% of recording sites, whereas phase locking to pulses of unmodulated pulse trains rarely exceeded 30 pps. The strength of phase locking to frequencies ≥40 Hz often varied nonmonotonically with modulation depth, commonly peaking at modulation depths around −15 to −10 dB. Cortical phase locking coded modulation frequency reliably, whereas a putative rate code for frequency was confounded by rate changes with modulation depth. Group delay computed from the slope of mean phase versus modulation frequency tended to increase with decreasing limiting modulation frequency. Neurons in cortical extragranular layers had lower limiting modulation frequencies than did neurons in thalamic afferent layers. Those observations suggest that the low-pass characteristic of cortical phase locking results from intracortical filtering mechanisms. The results show that cortical neurons can phase lock to modulated electrical pulse trains across the range of modulation frequencies and depths presented by cochlear implant speech processors.

INTRODUCTION

The cochlear implant is a highly successful neural prosthesis that can restore hearing to severely and profoundly deaf people. Most present-day implant users receive stimulation in the form of amplitude-modulated electrical pulse trains (Wilson et al. 1991; Zeng et al. 2004). In such a stimulation strategy, the sound waveform is processed by a bank of band-pass filters. The envelope of each filter output is used to amplitude modulate a constant-rate pulse train, which is delivered to a particular electrode in an implanted electrode array. Spectral information about sound is transmitted by the band-pass filter operation leading to activation near the tonotopically appropriate cochlear place. Information about the temporal envelope of sounds is transmitted by the modulation of the pulse trains. If envelope information is to be used for speech recognition, that information must in some way be transmitted to the auditory cortex. This study examined the transmission of envelope information from a cochlear implant to the auditory cortex in an animal model.

Envelope frequencies useful for speech recognition in both normal-hearing listeners and cochlear implant users range from ∼2 to 16 Hz or higher (Drullman et al. 1994; Fu and Shannon 2000; Rosen 1992; Shannon et al. 1995; Van Tasell et al. 1987; Xu and Zheng 2007; Xu et al. 2005); estimates of the upper value of that range varies among studies, extending as high as 50 Hz in the scheme proposed by Rosen (1992). Envelopes carry cues pertinent to manner of articulation, voicing, vowel identity, and prosody (reviewed by Rosen 1992). Envelope sensitivity in cochlear implant users is qualitatively similar to that of normal-hearing listeners (Busby et al. 1993; Cazals et al. 1994; Richardson et al. 1998; Shannon 1992). Psychophysical thresholds for detection of electrical pulse-train modulation are as low as −40 dB (1% modulation) for modulation frequencies ≤100 Hz. Critical features of speech waveforms, after envelope extraction and logarithmic compression, appear at the output of a cochlear implant speech processor with modulation depths as low as −30 to −14 dB (3–10% modulation; Geurts and Wouters 2001; Snyder et al. 2000; Wilson et al. 1991).

Neurons throughout the normal auditory system can phase lock (i.e., fire in synchrony) with amplitude-modulated sounds (reviewed by Joris et al. 2004; Langner 1992). The upper frequency cut-off for neural phase locking decreases at successively higher levels of the auditory pathway. In the guinea pig, neurons phase lock to modulator frequencies of nearly 1,000 Hz in the dorsal cochlear nucleus (Zhao and Liang 1997), >200 Hz in the inferior colliculus (Rees and Palmer 1989), and up to ∼200 Hz in the medial geniculate body (MGB) (Creutzfeldt et al. 1980). In the auditory cortex, most reports of phase locking to click trains or to amplitude modulated sounds have indicated that driven spike rates peak at “best modulation frequencies” around 8–10 Hz and that little phase locking to modulated sounds is observed for modulation frequencies above ∼20 Hz (Creutzfeldt et al. 1980; Eggermont 1991, 1994, 1998, 2002; Gaese and Ostwald 1995; Schreiner and Urbas 1988).

The observations of limited cortical phase locking in most studies prompt the question of how temporal envelope frequencies relevant to speech, roughly 2 to as high as 50 Hz, are represented in the auditory cortex. One possibility is that temporal information is recoded at some level of the auditory pathway in a form not requiring phase locking. Another possibility is that temporal information is represented explicitly by phase locking in the cortex but that phase locking to frequencies above ∼20 Hz has been missed in previous studies because of some aspect of the stimulus or the analysis. Even if phase-locking at frequencies up to ∼50 Hz reaches thalamic-recipient neurons of the primary auditory cortex, it is not clear whether high-frequency phase locking is maintained through intracortical processing and reaches the neurons that project out of area A1 to other cortical and subcortical targets. This study focuses on amplitude-modulation frequencies in the upper end of the range of envelope frequencies relevant to speech recognition and contrasts cortical phase locking between granular (i.e., thalamic-recipient) and extragranular laminae of the cortex.

Another unknown is the sensitivity of cortical neurons to stimuli presented at shallow modulation depths. With a few exceptions (Liang et al. 2002), studies of cortical phase locking to stimulus envelopes have used click trains or, in the case of sinusoidally modulated tones, 100% modulation depths. It is difficult to extrapolate from such studies to the range of modulation depths that are available in the amplitude-compressed speech that is presented to a cochlear implant user. For that reason, this study tests modulation depths as low as 1%, corresponding to the lowest modulation depths that can be detected by human subjects (Busby et al. 1993; Cazals et al. 1994; Galvin and Fu 2005; Pfingst et al. 2007; Richardson et al. 1998 Shannon 1992).

The results show robust phase locking in the auditory cortex across the range of modulation frequencies and modulation depths relevant to speech recognition by cochlear implant users. This report quantifies the basic characteristics of cortical phase locking, including differences among cortical laminae and an unexpected nonmonotonic dependence on modulation depth, and contrasts rate and temporal codes for modulation frequency. Preliminary results have been presented in abstracts (Middlebrooks 2005; Middlebrooks and Lee 2004). Modulation sensitivity as a function of stimulus parameters relevant to speech processor design is quantified elsewhere (Middlebrooks 2008).

METHODS

Overview

Data collection consisted of extracellular spike recordings from the auditory cortex of anesthetized guinea pigs in response to acoustical and electrical cochlear stimulation presented to the ear contralateral to the cortical recording site. Experiments were controlled by a Windows-based personal computer interfaced with System 3 hardware from Tucker-Davis Technologies (TDT; Alachua, FL). Custom software was written as MATLAB scripts (The MathWorks, Natick, MA). Experiments were conducted in a sound-attenuating chamber. Each animal was studied first in a normal-hearing condition using acoustic tones presented from a calibrated loudspeaker placed ∼20 cm from the animal's left ear. Based on cortical responses to tones, the recording probe was positioned in cortical area A1 in an area in which neurons had mid- to high-frequency characteristic frequencies, and the probe was fixed in place. The animal was deafened bilaterally, a stimulating electrode array was implanted in the scala tympani of the left cochlea, and cortical responses to electrical cochlear stimuli were studied.

Animal preparation

All experiments with animals were conducted with approval of the University of Michigan Committee on Use and Care of Animals. Data were obtained from 20 pigmented guinea pigs of either sex, ranging from ∼500 to 1,000 g in weight. Animals were premedicated with atropine sulfate (0.1 mg/kg, im) and were anesthetized with a mixture of ketamine (40 mg/kg, im) and xylazine (10 mg/kg, im). Additional doses of ketamine were given throughout the experiment to maintain an areflexive state. Animal preparation typically lasted ∼2 h, followed by ∼12–16 h of data collection. The animal's right cochlea was ablated with a carbide burr to eliminate auditory responses to the animal's breathing sounds and other acoustic input.

A micropositioner was used to insert a multisite cortical recording probe (NeuroNexus Technologies, Ann Arbor, MI), one per animal, into the right auditory cortex through a small hole in the dura. In each experiment, preliminary mapping of characteristic frequencies identified cortical area A1 on the basis of the rostro-lateral to caudo-medial gradient of low-to-high characteristic frequencies. In three animals, the recording probe was oriented approximately parallel to the cortical surface, ∼0.5–1.0 mm deep, aligned with the tonotopic characteristic-frequency gradient. In the remaining 17 animals, the probe was oriented approximately perpendicular to the cortical surface, aligned with radial cell columns. Characteristic frequencies measured from the radial penetrations were relatively constant at all recording depths in each animal and ranged among animals from 6 to 32 kHz (mean, 14.6 kHz). That high-frequency range was chosen because it corresponds to the tonotopic location of the cochlear implants, which lay in the basal half of the basal turn of the cochlea. The low-frequency region of area A1 was avoided intentionally. Neurons in the low-frequency region can show phase locking to the fine structure of acoustic tones in the range of 60–250 Hz (Wallace et al. 2002), but the low-frequency region of the cochlea is not stimulated selectively by cochlear implant electrodes, either in this animal model or, presumably, in humans. After the recording probe was at its intended position relative to the tonotopic map, it was fixed in place.

The left tympanic bulla was opened to expose the round window and the basal turn of the cochlea. The left cochlea was deafened by intrascalar infusion of neomycin sulfate, which is toxic to cochlear hair cells (Nuttall et al. 1977). In our experience with other guinea pigs (unpublished data), that procedure reliably results in a >80-dB elevation of thresholds for the cochlear compound action potential within <10 min.

Cochlear electrical stimulation

The cochlear stimulating electrode array was a six- or eight-electrode animal version of the Nucleus 22 banded electrode array (Cochlear, Englewood, CO). Like the human version, it consisted of platinum electrodes on a silicone-elastomer carrier. The electrodes were 0.4-mm-diam bands, 0.3 mm in length, spaced 0.75 mm, center-to-center. The electrode array was implanted in the left scala tympani through a small cochleostomy drilled with a diamond burr. The electrode array was inserted as far as possible into the scala tympani, occupying roughly the basal half of the basal turn of the cochlea. The cochlear electrode array was fixed in place throughout each experiment.

Cochlear electrical stimuli were generated by a custom eight-channel optically isolated current source that was capacitatively coupled to the electrodes with an output time constant of 3 ms. The current source was controlled by a multi-channel 16-bit D/A converter (TDT model RV8 or RX8; output rate 48,828 samples/s). Stimuli were presented in a monopolar configuration. The active electrode was a single intrascalar electrode, and the return electrode was a wire inserted in a neck muscle. Typically, the most apical electrodes had the lowest electrode threshold for cortical activation (Bierer and Middlebrooks 2002), so one of the two most apical electrodes was used as the active electrode.

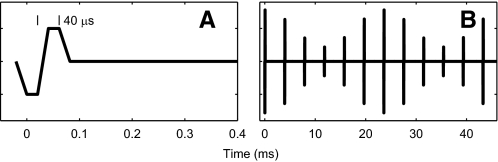
Electrical stimuli were modulated 600-ms trains of biphasic pulses, initially cathodic, 41 μs/phase (Fig. 1). Pulse trains were presented at repetition periods of 1.2 s. The pulse trains had a carrier rate of 254.313 pulses/s (pps; written as 254 for convenience in presentation); higher carrier rates were tested elsewhere (Middlebrooks 2008). The carrier rate of 254 pps is close to the 250-pps rate that is used in the SPEAK strategy that has been widely used in clinical cochlear implant speech processors (Skinner et al. 1994). Although newer processors can accommodate faster rates, rates of ∼250 pps often are prescribed by audiologists.

FIG. 1.

Stimulus waveforms. A: individual electrical pulses were biphasic, initially cathodic, charge balanced, and 40 μs per phase. The trapezoidal appearance of the waveform reflects the 48,828 samples/s output rate. B: sinusoidally amplitude-modulated pulse trains had pulse rates of 254 pulses/s (pps). The example shows a modulation frequency of 42.4 Hz and modulation depth of −5 dB.

Base current levels generally were set to 2, 4, and 6 dB above that the spike threshold for an unmodulated pulse train threshold. Currents in modulated pulse trains ranged above and below the base current level. Pulse trains were sinusoidally amplitude modulated by the function 1 + msin(2πf_mt), where m is the modulation index (ranging from 0 to 1) and f_m is the modulation frequency (in Hz). Starting modulator phases of 0, π/2, and π radians were tested, and all gave equivalent results. The modulation depth is represented in decibels as 20 log10(m). Modulation depths tested routinely ranged from −40 (1% modulation) to −5 dB (56.2% modulation) in 5-dB steps. Tested modulation frequencies were as high as 63.58 Hz, which was 1/4 of the carrier frequency. Earlier experiments tested modulation frequencies at even 10-Hz multiples (e.g., 10, 20, etc.) whereas later experiments tested multiples of 21.19 Hz, which was an integer fraction of the 254-pps carrier pulse rate. No difference in phase locking was observed between those conditions and, in summary statistics, the data from 21.19-, 42.39-, and 63.58-Hz modulators were grouped with the data from 20-, 40-, and 60-Hz modulators, respectively. In six animals, we also tested unmodulated pulse trains that varied parametrically in pulse rate.

Blocks of trials consisted of parametric variations of base current level, modulator frequency, and modulator depth. The order of stimuli was randomized such that every combination of parameters was tested once, and every combination was tested again in a different random order, and so on until each combination of stimuli had been repeated 20 times.

Cortical recording and spike sorting

The cortical recording probe consisted of a single silicon-substrate shank, 15 μm thick and 100 μm wide, tapering to ∼15 μm in width. Along the shank were 16 iridium-plated recording sites, 177 or 413 μm² in area, centered at 100- or 150-μm intervals. Neural waveforms were recorded simultaneously from the 16 sites using a TDT RA16 or RX5 system consisting of parallel headstages, amplifiers, 16-bit digitizers, and digital signal processors. Waveforms were digitized at a sample rate of 24,414 samples/s, low-pass filtered, resampled at 12.2 kHz, and stored on computer disk. Neural spikes were detected on-line for monitoring of the experiment, but all reported data analysis used spikes that were isolated off-line from the stored neural waveforms.

Electrical artifact from the cochlear stimulus could be detected by the cortical recording probe and potentially could have contaminated neural spike detection. Such contamination was eliminated using a sample-and-hold function that was programmed into the recording path. Immediately before the onset of each electrical pulse, the function sampled the present values of the 16 neural waveforms and held the outputs at those levels for 143.4 μs, which encompassed both phases of the 40-μs/phase biphasic pulse and a brief recovery time for the amplifier. The sample and hold resulted in a loss of data during ∼3.6% of each period of the 254-pps pulse train. Any residual artifact resulting from the release of the sample-and-hold function typically was eliminated by the denoising procedure described below. In a few instances in which the artifact could not be eliminated entirely, or in test cases in which the artifact-reject procedure was disabled intentionally, artifact propagated to the cortical recording site with a delay of <2 ms. The short latency of the artifact made it easy to distinguish from cortical neural activity, which showed a latency of >7 ms, as described in results.

The following procedure was used to identify stimulus-evoked spikes based on off-line analysis of the stored neural waveforms. First, a denoising procedure was applied to the waveforms to attenuate signals that were correlated among the 16 recording channels (Bierer and Anderson 1999). Such signals to be attenuated included far-field slow-wave potentials, artifact that remained from the sample-and-hold function, and any other electrical interference. Second, the denoised waveforms were interpolated to 48.8-kHz time resolution using Fourier interpolation. Third, a range of peak-to-trough (or trough-to-peak) times was selected (typically 150–350 μs), and the distribution of peak-to-trough amplitudes of spikes fitting those time criteria was displayed. Based on visual inspection of that distribution, a range of amplitudes was selected that isolated a single unit or, more often, included a small number of unresolved units. Finally, the entire set of waveforms was processed to isolate spikes that fit specified ranges of peak-to-trough times and amplitudes. The data set consisted of 61 well-isolated single units, characterized by discrete distributions of peak-to-trough amplitudes, and 206 unresolved recordings of 2 or more units. This report will use the terms “units” or “unit activity” to indicate both single- and multiunit recordings from a single recording site and “isolated single unit” to indicate the well-isolated single units. A small number of units appeared as outliers in distributions of first-spike latency and/or limiting pulse rates. Those units with latencies <7 ms and/or phase locking to pulse rates >80 pps were interpreted to be from thalamocortical fibers and were eliminated from further analysis.

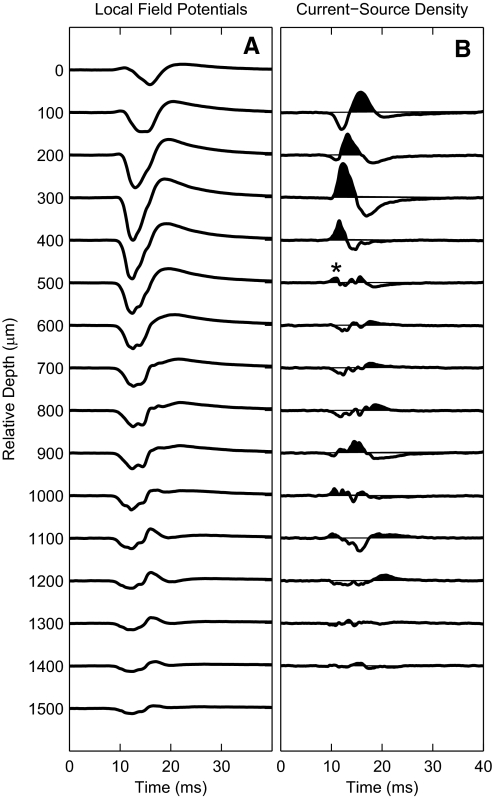
Current source density analysis was used as a functional measure of the depth of recording sites relative to cortical laminae (Müller-Preuss and Mitzdorf 1984); this procedure was used only for the 17 animals in which recording probes were aligned with radial cell columns. Low-pass-filtered local field potentials elicited by single electrical pulses or acoustic clicks were recorded simultaneously at each of the 16 recording sites (Fig. 2A). The current-source density is proportional to the second spatial derivative of the field potentials. In Fig. 2B, current sinks are shown as upward deflections, filled, and current sources as downward deflections. A current sink consistently was observed in the superficial depths, decreasing in latency over a few hundred milliseconds of increasing depth. In eight animals, recording sites were marked with electrolytic lesions, and postmortem tissue was fixed by immersion in buffered aldehydes, cryostat sectioned, and Nissl stained. Histological reconstruction showed that the deepest site at which the short-latency current sink was present (Fig. 2, *) coincided in depth with the transition from lamina III to IV, corresponding to the major depth of termination of thalamocortical fibers. That physiologically defined depth was used as a reference for examination of laminar specificity of response properties; i.e., it appears as zero relative depth in Fig. 10.

FIG. 2.

Use of current-source density analysis to identify cortical depths. A: local field potentials recorded at 16 sites at 100-μm intervals along a single silicon-substrate probe oriented parallel to radial cell columns. B: current-source density traces derived from the 2nd spatial (i.e., depth) derivative of the potentials in A. Current sinks are drawn upward and are filled. *Deepest site at which the short-latency sink was present, which in histological reconstruction tended to lie at the border of laminae III and IV.

FIG. 10.

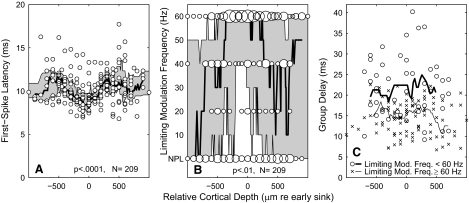
Laminar dependence of 1st-spike latency, limiting modulation frequency, and group delay. Cortical depths are stated relative to the depth of the shortest-latency current sink evident in current-source density analysis. Shading in Fig. 10, A and B, indicates the interquartile ranges, and continuous lines in A–C represent medians. Those ranges and medians were computed by values within a 21-point sliding window. A: symbols represent 1st-spike latencies of individual single- or multiunit recordings. Latencies varied significantly with cortical depth (P < 0.0001, ANOVA; depths grouped in steps of 300 μm). B: the area of each circle is proportional to the number of recordings showing a particular limiting modulation frequency (rounded to the nearest 20 Hz) at a particular cortical depth (rounded to the nearest 50 μm). Limiting modulation frequency varied significantly with cortical depth (P < 0.01, Kruskal-Wallis nonparametric ANOVA). NPL, for “no phase locking,” indicates units for which no significant phase locking was observed at any tested modulation frequency or depth. A nonparametric test was selected because of those NPL points and because of the coarse sampling of modulation frequencies. Limiting modulation frequencies were assigned at the modulation depth that gave the highest value. C: symbols represent group delays of individual single- or multiunit recordings. O and X represent units for which the limiting modulation frequency was <60 or ≥60 Hz, respectively, and thick and thin lines represent the median values of those respective populations.

Data analysis

Stimulus base current levels were specified relative to neural thresholds for electrical stimulation. Thresholds were based on a signal-detection analysis (Green and Swets 1966; Macmillan and Creelman 2005) of trial-by-trial spike counts measured in response to brief pulse trains varied in current in 1-dB steps; the analysis is detailed in Middlebrooks and Snyder (2007). Thresholds generally were stable within ∼1 dB throughout the durations of recording sessions.

The strength of phase locking of cortical spikes to the modulator waveform was represented by the vector strength (Goldberg and Brown 1969). The vector strength and mean phase were obtained by expressing spike times relative to the phase of the modulator, representing each spike as a unit vector with orientation given by that phase, and computing the sum of the unit vectors. The vector strength was given by the length of the resultant vector divided by the number of vectors. It could range from 0 (no phase locking) to 1 (all spikes at identical phase); spike probability exactly following the sine modulator waveform would yield a vector strength of 0.5. Modulation gain (in dB) was computed as 20 log10 (2r/m), for response vector strength r and stimulus modulation depth m (Rees and Palmer 1989). The statistical significance of the vector strength was evaluated by the Rayleigh test of circular uniformity (Mardia 1972) at the level of P < 0.001. The mean phase was given by the orientation of the resultant vector. The mean phase lag tended to increase linearly with increasing modulator frequency, as shown in results. The slope of the best-fitting phase-versus-frequency line gave the group delay, D = Δφ/2πΔf, for mean phase lag (φ) in radians and modulator frequency (f) in Hertz; group delay was computed only from data points showing significant vector strength at at least two tested frequencies, one of which was ≥20 Hz. Cortical units tended to respond to the onset of a pulse train with a temporally compact burst of spikes, regardless of the modulating waveform. That onset burst tended to produce an erroneous impression of high vector strength. For that reason, all computations of vector strength and mean phase were based only on spikes occurring between 100 and 600 ms after the onset of the pulse train, well after the onset burst.

RESULTS

General characteristics of cortical phase locking

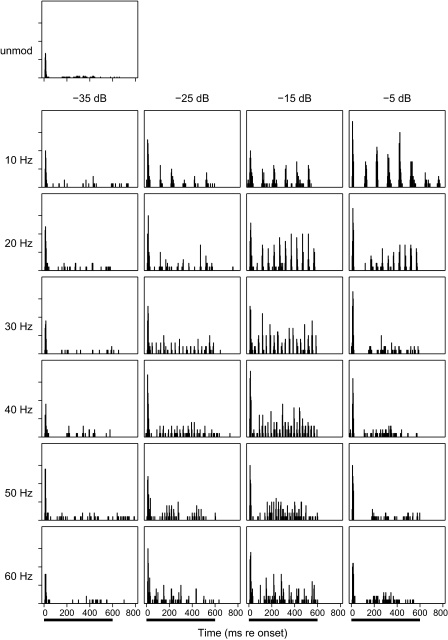
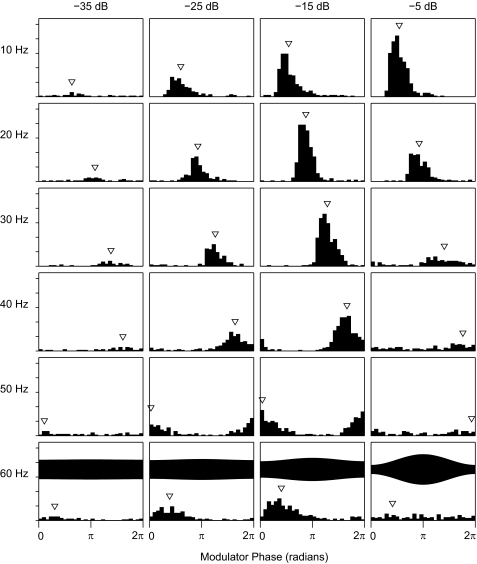
The phase-locking characteristics of one well-isolated single unit are shown in Figs. 3, 4, 5, and 8A. Those figures all show data from the same unit to permit comparison across various data representations; those particular data were collected using base current levels of ±282 μA, 1 dB above the spike threshold for an unmodulated pulse train. Like nearly all studied units, this unit responded to the onset of an unmodulated 254-pps pulse train with a robust burst of spikes followed by little or no tonic firing (Fig. 3, top panel). In contrast, modulated pulse trains tended to produce a burst of spikes at stimulus onset, a ∼50- to 100-ms period of reduced firing, and periodic tonic firing lasting throughout the duration of the pulse train. Figure 3 shows poststimulus time histograms for various modulation frequencies and depths. At the 10- and 20-Hz modulation frequencies, the periodic tonic cortical firing can be seen at modulation depths at least down to −25 dB, fading at −35 dB. At higher modulation frequencies, the tonic firing by this unit was greatest at intermediate modulation depths (i.e., −15 dB), decreasing at higher and lower modulation depths. At the −15-dB depth, one can see the frequency of the periodic cortical firing increasing with modulation frequency ≤50 Hz. For the 60-Hz modulator in this example, one can see a periodicity in the response at ∼14 Hz, which likely represents phase locking to the difference frequency derived from the 254-Hz pulse train and a multiple of the 60-Hz modulator, i.e., ∼254 pps –(4 × 60 Hz) = ∼14 Hz. That ∼14-Hz periodicity was not present in tests (in other guinea pigs) of responses to a 63.58-Hz modulator, which is an integer factor of the carrier pulse rate.

FIG. 3.

Poststimulus time histograms of responses of a well-isolated single unit to electrical stimulation. Top left panel: response to an unmodulated 254-pps pulse train. All other panels show responses to sinusoidally modulated pulse trains presented at a base current level 1 dB above the threshold for an onset response to an unmodulated train. Panels are arranged by modulation frequency (ordered by rows as indicated) and modulation depths (ordered by columns). The solid bars at the bottom indicate the 600-ms duration of the pulse trains. Ticks on the vertical axis represent 0.5 spikes per 3-ms time bin summed across 20 trials.

FIG. 4.

Period histograms of the responses shown in Fig. 3. Spike times occurring 100–600 ms after stimulus onset are binned according to modulator phase, π/15-radian per bin. Arrowheads indicate mean phase. Panels are arranged by modulation frequency (rows) and modulation depth (columns). Ticks on the vertical axis represent 1 spike per bin, 30 bins per period, summed across 20 trials. The bottom row of panels shows 1 period of the stimulus envelope for each modulation depth; the shown phase is arbitrary.

FIG. 5.

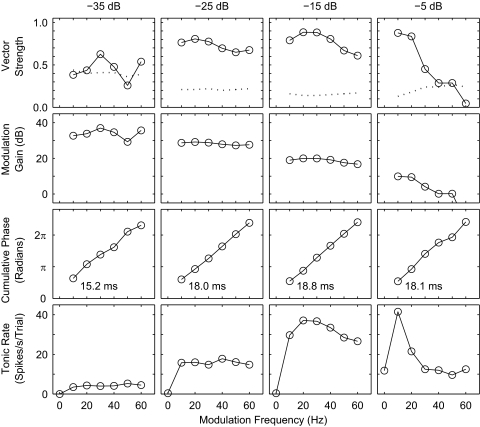
Phase-locking measures from the responses shown in Figs. 3 and 4, plotted as a function of modulation frequency. Panels are arranged by modulation depth (columns). All data are based on spikes occurring 100–600 ms after stimulus onset (i.e., onset response in the initial 100 ms is omitted). Plots in the top 3 rows (vector strength, modulation gain, and cumulative phase) are based on vector addition. Numbers in the 3rd row indicate group delay, computed from the slopes of the phase-vs.-frequency plots. The 4th row, tonic rate, plots the mean number of spikes per trial in the 100- to 600-ms postonset time period. Modulation frequencies of 0 (bottom row) indicate responses to unmodulated pulse trains.

FIG. 8.

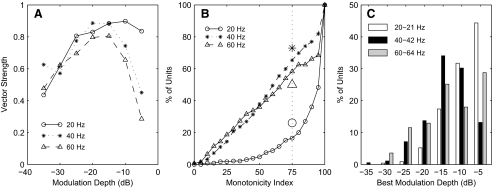
Nonmonotonic dependence of vector strength on modulation depth. A: vector strength as a function of modulation depth for the unit shown in Figs. 3–5. The parameter is modulation frequency. B: cumulative distribution of monotonicity index across recording sites at which vector strength was significant at 1 or more modulation depths. Monotonicity index is the vector strength at the deepest modulation tested (i.e., −5 dB) as a percentage of the greatest vector strength across all tested depths. The dotted line indicates a 75% criterion for nonmonotonic depth dependence. Large symbols show the percentage of isolated single units showing monotonic indices ≤75. C: distribution of modulation depths producing the greatest vector strengths. n = 229.

The phase-locked periodic firing of units was evident in period histograms, which show spike counts on a time scale expressed as phase of the modulating sine function (Fig. 4). The bottom row of panels also shows one period of the stimulus envelope for each modulation depth. In nearly all of the panels, the modulation gain was substantially greater than unity in that the depth of modulation of spike probability was greater than the depth of modulation of the stimulus waveform. A stimulus modulation depth of −25 dB, for instance, corresponds to only 5.6% modulation of the stimulus, whereas the illustrated period histograms for those modulation depths show nearly 100% modulation of the neural spike counts. In each panel, an arrowhead identifies the mean phase of the response, computed from the vector sum of spikes as described in methods. The lag of the mean phase relative to the modulator tended to increase with increasing modulator frequency, as expected based on a constant delay in the neural pathway from the ear to the cortex.

Figure 5 quantifies several characteristics of the phase locking of this representative unit as a function of modulation frequency. The top row of panels shows the vector strength of phase locking (solid lines and circles). Dotted lines show the Rayleigh criterion for statistically significant phase locking at the level of P < 0.001. This unit is typical of many units in that the Rayleigh criterion was higher at the shallowest (−35 dB) modulation depth than at greater depths because the spike rate was reduced at the shallow depth. This unit showed significant phase locking at all illustrated frequencies at depths −25 and −15 dB. At the greatest modulation depth (−5 dB), the vector strength was greatest at 10 Hz and declined sharply with increasing modulation frequency. The decline in vector strength with increasing frequency was much less prominent at modulation depths of −25 and −15 dB; the trend was inconsistent at −35 dB.

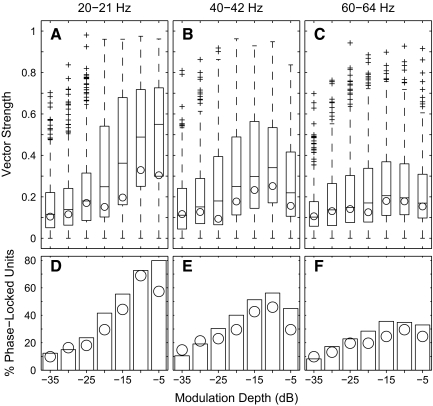
The distributions of vector strength across the sample population are shown in the top panels of Fig. 6; as noted in methods, data collected for 21-, 42-, and 64-Hz modulators are grouped with data for 20, 40, and 60 Hz. The box plots show the distributions across all single- and multiunit recordings, and the circles indicated the medians of the single-unit values. Vector strengths varied widely among units, which can be explained in part by the dependence of vector strength on depth in the cortex, considered in a later section. The distributions largely mirror the characteristics demonstrated by the single unit represented in Fig. 5. Vector strength tended to decline with increasing modulation frequency. Vector strength increased monotonically with increasing modulation depth at the low modulation frequency, whereas, at the higher modulation frequencies, vector strength often declined at the greatest modulation depth. These distributions include vector strengths of all units, irrespective of whether the vector strength was significant. The bottom row of panels in Fig. 6 shows the percentage of units that showed significant phase locking (Rayleigh test, P < 0.001) under various stimulus conditions. At 20-Hz modulation, the percentage of phase-locked units increased monotonically with increasing modulation depth. At higher modulation frequencies, however, the percentage declined slightly at the greatest depths.

FIG. 6.

A–C: distribution of vector strengths across the unit sample. Panels indicate data from modulation frequencies of 20–21, 40–42, and 60–64 Hz, as indicated. Every vector strength is shown, regardless of statistical significance. In each panel, each box and whiskers represents the distribution of vector strengths at 1 modulation depth: horizontal lines indicate 25th percentile, median, and 75% percentile, whiskers indicate ranges of data within 1.5 times the interquartile range, and plus signs indicate outlying points. Circles indicated the medians values for isolated single units. D–F: percentage of vector strengths at each modulation depth that were significant according to a Rayleigh test (P < 0.001). The bars represent the population of all single- and multiunits (n = 267), and circles represent isolated single units (n = 61).

The second row of panels in Fig. 5 shows modulation gain for the representative unit, which reflects the modulation of the cortical response divided by the modulation of the stimulus waveform (see methods). Gains were positive for nearly all illustrated modulation depths and frequencies. A gain of 20 dB, for example, indicates that the temporal modulation of spike probability in the period histogram is 10 times greater than the amplitude modulation of the stimulus. There is a steady decrease in modulation gain associated with increasing modulation depth, largely because the range of vector strengths (the numerator in the gain computation) covers only a factor of ∼2, whereas the modulation depths (the denominator) range over a factor of ∼32. Comparable levels of modulation gain were observed across the sampled population of 267 units. For example, modulation gain across all units and all tested modulation frequencies averaged 4.2 ± 4.1 dB at the −5-dB modulation depth and 32.4 ± 3.5 dB at the −35-dB depth.

The third row of panels in Fig. 5 shows the cumulative mean phase lag of responses relative to the modulator phase. The data tend to follow straight lines, particularly for modulation depths of −25 and −15 dB, at which the vector strength was most consistently high. The slopes of the best-fitting phase-versus-frequency lines give the group delay between the phase of the stimulus modulating waveform and the phase of the period histograms. Slopes were computed by linear regression of all the points that showed significant vector strength; the group delay is indicated by the number in each panel. Group delays typically were fairly constant across modulation depths. In the example, delays ranged from 18.0 to 18.8 ms except for the value of 15.2 ms for depth −35 dB, which probably reflects an imprecise group delay measurement caused by the smaller number of significantly phase-locked points at that depth.

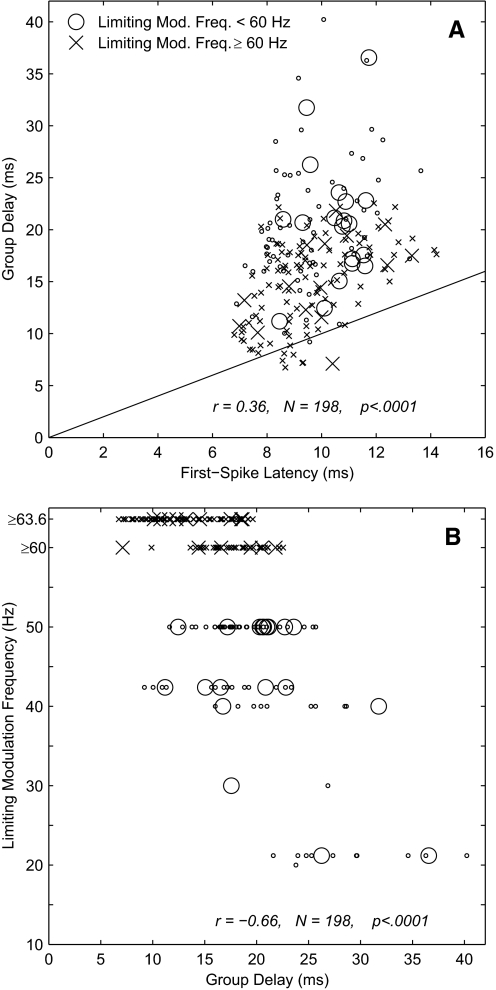
Across all tested units, group delays exhibited a significant positive correlation with first-spike latencies measured from responses to unmodulated waveforms (r = 0.36, P < 0.0001, n = 198; r = 0.35, P < 0.05, n = 34 for single units), although almost all the group delays were longer than the first-spike latencies (Fig. 7A). Group delays tended to segregate according to the highest modulation frequency at which units showed significant phase locking (the limiting modulation frequency). Units with limiting modulation frequencies ≥60 Hz tended to show short group delays. Most of those 117 units had group delays ≤20 ms [14.9 ± 4.1 (SD) ms; n = 113; indicated by X in Fig. 7A]. Conversely, units with limiting modulation frequencies <60 Hz tended to show longer group delays (20.5 ± 6.0 ms, n = 85; indicated by O). The relationship between limiting modulation frequency and group delay is plotted in Fig. 7B. The correlation between those two measures was as follows: r = −0.66, P < 0.0001, n = 198 (r = −0.60, P < 0.0005, n = 34 for single units). Note that this analysis understates the number of units with limiting modulating frequencies ≤21 Hz because group delays could not be computed in cases in which the modulation frequencies were tested in 20- or 21-Hz intervals and units failed to phase lock to frequencies >21 Hz. Including units for which group delay could not be computed, 113 had limiting frequencies ≥60 Hz and 154 had limiting frequencies <60 Hz. There also was a weak but significant negative correlation between limiting modulation frequency and first-spike latency (r = −0.45, P < 0.0001, n = 267).

FIG. 7.

A: group delay vs. 1st-spike latency. Group delay was computed from the slope of the best-fitting mean-phase-vs.-modulation-frequency line. Group delay was computed only for single- or multiunit recordings for which vector strengths were significant for ≥2 modulation frequencies, at least 1 of which was ≥20 Hz. Each value represents the base current level and modulation depth that yielded significant vector strengths at the maximum number of modulation frequencies, with the highest level and deepest depth selected in case of ties. First-spike latencies were computed from responses to unmodulated pulse trains and were given by the median latency of the first spike computed across all trials eliciting ≥1 spike. B: limiting modulation rate vs. group delay. Limiting modulation rate was the maximum tested modulation rate at which the vector strength was significant. In both panels, O and X represent units for which the limiting modulation frequency was <60 or ≥60 Hz, respectively. Large symbols represent isolated single units, and small symbols represent multiunit recordings.

The observation of physiologically reasonable group delays confirms that the observed phase locking of cortical neurons was not contaminated by artifact from the electrical stimulus. In a few instances in which artifact could not be avoided, and in test cases in which the artifact-reject system was disabled intentionally, measured group delays were <2 ms. Those cases were excluded from further analysis.

The bottom row of panels in Fig. 5 shows mean tonic spike rates of the example single unit. These spike rates exclude the onset burst during the first 100 ms after stimulus onset, and each of these plots includes a datum at 0 Hz, representing the tonic response to the unmodulated pulse train. The frequency dependence of spike rates of this unit tended to parallel the frequency dependence of vector strength in that a sharp decline in rate with increasing frequency was evident at the −5 dB modulation depth and was less pronounced at lower modulation depths. This unit was fairly typical in that its spike rates decreased with decreases in modulation depth, even between depths at which there was negligible change in vector strength (i.e., between −15 and −25 dB).

At the greatest modulation depth tested, −5 dB, most units tended to show maximum spike rates and vector strengths at modulation frequencies of 10 Hz; frequencies <10 Hz were not routinely tested. For instance, of 126 units tested with modulation frequencies as low as 10 Hz, 71% showed maximum spike rates for the 10-Hz modulator, whereas only 10, 8, and 12% of units showed maximum spikes elicited by modulation frequencies of 20, 40, and 60 Hz, respectively. Peak responses to a 10-Hz modulator or 10-pps pulse rate likely reflect an interaction of the extrinsic stimulus with the intrinsic alpha rhythm of the cortex (Eggermont 1992; Gaese and Ostwald 1995; Kenmochi and Eggermont 1997). Consistent with that notion, neurons often showed a periodic discharge following the offset of a 10-Hz stimulus. An example can be seen in Fig. 3 in the 10-Hz, −5-dB panel, in which two discrete bursts of spikes at 100-ms intervals follow the offset of the 600-ms stimulus. Among the neurons that were tested at 10 Hz, 18.5% showed significant continuing 10-Hz periodic spike patterns (P < 0.001, Rayleigh test) in the interval 20–200 ms after the offset of a 10-Hz modulated pulse train, whereas no units showed 20-, 40-, or 60-Hz periodicity after 20-, 40-, or 60-Hz stimuli. Most of the detailed analysis in this paper used modulator frequencies of 20 Hz and higher, which tended not to engage intrinsic cortical rhythms.

Nonmonotonic sensitivity to modulation depth

Phase locking to higher frequencies (e.g., 40 and 60 Hz) often was weak at very low modulation depths, strengthened with increasing modulation depth, and weakened again at the greatest modulation depths. For example, vector-strength data from the single unit shown in Figs. 3–5 are plotted in Fig. 8A as a function of modulation depth. For this unit, strong phase locking to 20 Hz persisted at the greatest modulation depths, but vector strengths for phase locking to 40 and 60 Hz at a depth of −5 dB dropped to about one half or less of the maximum value. The dependence of vector strengths on modulation depth was compared across units by computing a “monotonicity index,” which was the vector strength at −5-dB modulation depth expressed as a percentage of the maximum vector strength observed across all depths. Indices of 100% indicate units that showed a monotonic increase in vector strength with increasing modulation depth, and smaller indices indicate nonmonotonic depth dependence with phase locking that declined at the maximum depth. The cumulative distribution of the monotonicity index across the sample population is shown in Fig. 8B; the population at each frequency includes only units showing significant phase locking at that frequency. At a modulation frequency of 20 or 21 Hz, only 17% of the population (26.1% of single units) had monotonicity indices <75%, indicating that vector strengths of most units increased essentially monotonically with increasing modulation depth. At modulation frequencies of 40–64, however, ∼60% of units had monotonicity indices ≤75%, indicating a nonmonotonic dependence on modulation depth. Figure 8C shows that the greatest tested modulation depths, −5 or −10 dB, usually produced the maximum vector strength for modulation depths of 20–21 Hz but that maximum vector strengths often were produced at shallower depths at 40–64 Hz.

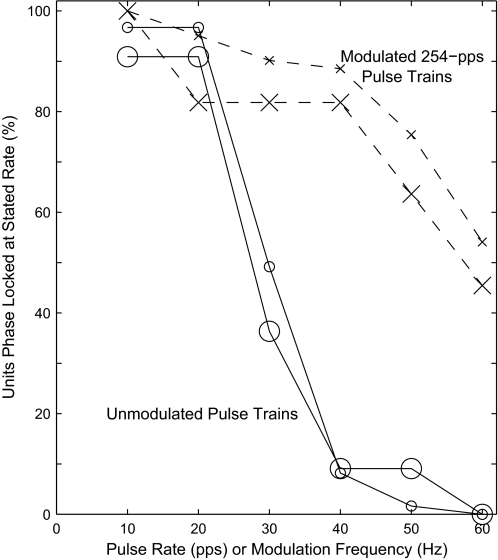
The results presented to this point have represented responses to a constant 254-pps pulse train modulated at various frequencies and depths. We also evaluated phase-locked responses to unmodulated pulse trains that varied in pulse rate from 10 to 60 pps. One could regard these relatively low-rate pulse trains as showing modulation effectively deeper than that produced by 100% modulation by a sine function. In six animals (61 single- and multiunit sites), we compared cortical phase locking to these unmodulated pulse trains with phase locking to modulated 254-pps pulse trains. In both conditions, we determined the maximum pulse rate or modulation frequency that produced significant cortical phase locking (Rayleigh test, P < 0.001); these are referred to as the limiting pulse rate and limiting modulation frequency, respectively. Most units phase locked to higher frequencies in response to the modulated 254-pps pulse trains than to the unmodulated pulses. This is shown in the form of a cumulative distribution in Fig. 9. Few neurons phase locked to unmodulated pulse rates of 40 pps or higher, whereas 54% of the 61 neurons phase locked to modulation frequencies as high as 60 Hz; that percentage is 42.3% across the overall population of 267 units for which limiting modulation frequencies were measured.

FIG. 9.

Cumulative distribution of units significantly phase locked to unmodulated pulse trains varying in pulse rate or to modulated 254-pps pulse trains varying in modulation frequency. The modulation frequency for each unit was the highest value computed across all tested modulation depths. Small symbols represent the 61 single- and multiunits (in 6 guinea pigs) that were tested both with unmodulated and modulated pulse rates in 10-pps steps of pulse rate and 10-Hz steps of modulation frequency, and large symbols represent only the 11 isolated single units.

The spike rates in response to unmodulated pulse trains resembled those to modulated trains in that, in both cases, spike rates generally were greatest for pulse rates or modulation frequencies around 10 pulses or modulation cycles per second. In response to unmodulated pulse trains, 57 of 61 units (93%) showed maximum spike rates for the 10-pps rate. Of those 57 units, 40 (70%) also responded with more than half-maximal spike rates to 20-pps stimuli.

Laminar dependence of phase locking

The strength of phase locking to modulated 254-pps pulse trains or to unmodulated lower-rate pulse trains varied according to the depth of units in the cortex. As described in methods, current source density analysis was used as a functional means of identifying the depth corresponding to the highest density of thalamic afferents, and that depth will be taken as the origin of a relative depth scale. In Fig. 10A, symbols represent first-spike latencies of individual single- or multiunit recordings,. First-spike latencies showed a minimum near the 0 μm, confirming that neurons with short first-spike latencies tend to correspond in laminar depth with the short-latency current sink in current-source-density plots (P < 0.0001, ANOVA, depths grouped with 300-μm resolution). The across-trial SD of first-spike latencies for each unit was small, averaging 1.92 ± 1.21 ms across 209 units, with 95% of units showing SD <4 ms. There was a weak but significant tendency for the SD of first-spike latencies to increase with laminar distance from the thalamic input layers, i.e., with distance from relative cortical depth = 0 (r = 0.23, P < 0.001, n = 209).

Limiting modulation frequencies also varied significantly with cortical depth. In Fig. 10B, data are grouped in 50-μm steps of cortical depth and 20-Hz steps of limiting modulation frequency. Areas of circles are proportional to the number of units at each combination of cortical depth and limiting modulation frequency, and shading indicates the range between 25th and 75th percentiles. The 75th percentile extended to 60 Hz at most depths, indicating that >25% of units at most depths showed significant phase locking to the highest frequency that was tested. The 25th percentile and median showed a sharp dependence on cortical depth. More than 75% of neurons located near the thalamic input layers phase locked to 40 Hz and >50% phase locked to 60 Hz. The limiting modulation frequency fell off rapidly in supra- and infragranular layers. That suggests that if information about high modulation frequencies is propagated into noninput layers (and out of cortical area A1), that information either is carried by phase locking in a reduced population of neurons or is re-coded in some form that is not evident as phase locking.

Group delay did not vary systematically with cortical depth. In Fig. 10C, X and O plot the group delay of units that did or did not, respectively, phase lock to modulation frequencies ≤60 Hz. At any particular range of cortical depths, units with lower limiting modulation frequencies tended to have longer group delay (consistent with the data in Fig. 7), and the percentage of units with long group delays was somewhat higher in extragranular layers (consistent with Fig. 10B). Nevertheless, neither the units with high (P = 0.21, n = 95) nor low (P = 0.57, n = 49) limiting modulation frequency showed a significant dependence of group delay on cortical depth. Units with low limiting modulation frequencies are under-represented in this plot, because 65 of the 114 units with low limiting modulation frequencies did not phase lock to a high enough frequency to permit computation of group delay; those units tended to lie in extragranular layers. That probably accounts for the lack of significant correlation of group delay with cortical depth across the population of all units with measurable group delays (P = 0.33, n = 144).

Signaling of modulation frequency by spike timing and rate

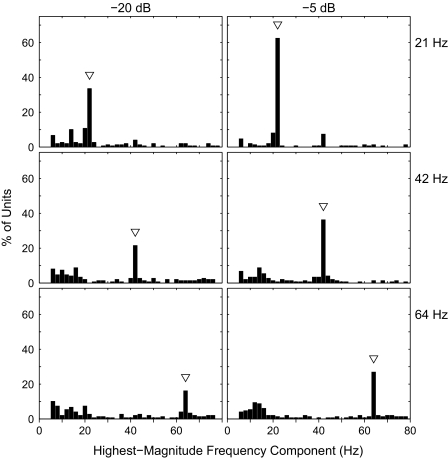
We compared the ability of cortical neurons to signal the frequency of a modulated pulse train either by a measure of the timing of spikes or by frequency-specific spike rates. The temporal measure was based on the poststimulus time histograms of units, each averaged across 20 repetitions of each stimulus condition. For each unit and each stimulus frequency, the poststimulus time histogram was transformed to the frequency domain with a discrete Fourier transform and the power spectrum was computed; the power spectrum of the poststimulus time histogram is equivalent to the spectrum of the autocorrelogram of the histogram (Oppenheim and Schafer 1989). For each unit and stimulus frequency, the highest-magnitude frequency component in the spectrum was identified. This was done for 120 units in nine animals that were tested with modulation frequencies of 21, 42, and 64 Hz. Figure 11 shows the distribution across units of maximum-magnitude frequency components for the three tested frequencies and for two modulation depths. In all conditions, the most commonly identified frequency component was the one equal to the stimulus frequency; these are regarded as “correct” identifications. At the −5-dB depth, for instance the percentage of correct frequency identifications was highest for the 21-Hz stimulus and decreased with increasing stimulus frequency. This is consistent with the decrease in the percentage of neurons that phase locked to higher frequencies, particularly in extragranular layers. With a decrease in modulation depth from −5 to −20 dB, there was a decrease in the percentage of correct identifications, consistent with the decrease in the percentage of units phase locked to the −20-dB depth. Nevertheless, the decrease in accuracy was in the form of increased scatter of incorrect identifications—there was no systematic bias in errors. In this sample of units, phase locking of cortical neurons signaled modulation frequency accurately across a considerable range of modulation depth.

FIG. 11.

Signaling of modulation frequency by neural spike periodicity. Each panel plots the distribution among neurons of the highest-magnitude frequency component in an autocorrelation analysis of firing patterns. In each panel, an arrowhead indicates the modulation frequency. Panels are arranged by modulation frequency (rows) and modulation depth (columns). n = 120.

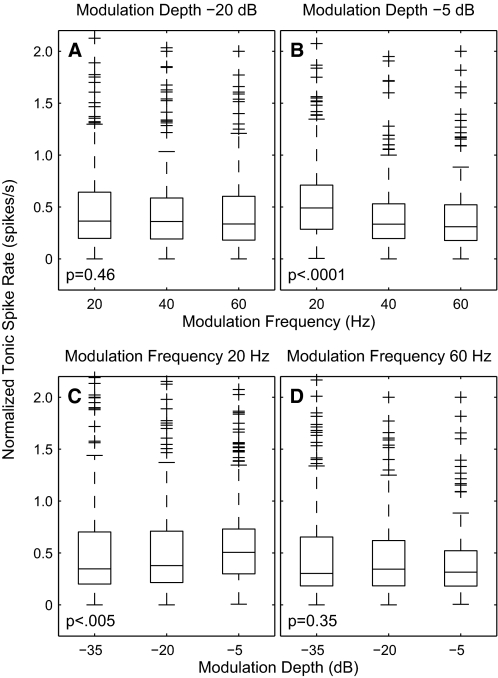
In response to modulated pulse rates, mean tonic spike rates (i.e., omitting the 1st 100 ms of responses) varied both with modulation frequency and with depth, as shown for an isolated single unit in Fig. 5. That unit was fairly typical in that it showed substantial changes in spike rate between modulation depths at which there was little change in vector strength (i.e., compare the columns showing modulation depths of −25 and −15 dB). Also, the dependence of spike rate on modulation frequency could differ depending on the modulation depth. Figure 12 shows the distribution of spike rates across the sample population (n = 267). The tonic spike rate for each unit (the rate during 100–600 ms after stimulus onset) is shown normalized by a constant equal to that neuron's onset rate (the rate during 0–100 ms) to an unmodulated 254-pps pulse train. The effect of modulation frequency on spike rate is shown for modulation depths of −20 (Fig. 12A) and −5 dB (Fig. 12B). At the shallower depth, the distribution across the sample showed no significant dependence on modulation frequency. At the deeper modulation, the distribution showed a small but significant decrease in spike rate with increasing modulation frequency. The effect of modulation depth on spike rate is shown for modulation frequencies of 20 (Fig. 12C) and 60 Hz (Fig. 12D). At the lower modulation frequency, the distribution of spike rates increased significantly with increasing modulation depths. At the higher frequency, however, there was no significant dependence of spike rate on depth.

FIG. 12.

Distribution of tonic spike rates as a function of modulation frequency and depth. Data from modulation frequencies of 21, 42, and 64 Hz were combined with data from 20, 40, and 60 Hz, respectively. For each unit, tonic spike rates in the interval 100–600 ms after stimulus onset were normalized by the onset response (in the interval 5–30 ms) to an unmodulated pulse train. Base current levels were 4 dB above the threshold for the onset response for each unit. Characteristics of the box and whisker plots are as described for Fig. 6. The statistical tests were Kruskal-Wallis ANOVA. A and B: distributions of normalized tonic spike rates as a function of modulation frequency at depths of −20 (A) and −5 dB (B). C and D: distributions of normalized tonic spike rates as a function of modulation depth at frequencies of 20 (C) and 60 Hz (D).

DISCUSSION

Relation to previous studies

The study by Schreiner and Raggio (1996) is the most directly related to this study. Those investigators tested cortical multiunit responses to cochlear implant stimuli consisting of unmodulated pulse trains that varied in rate from 2 to 38 pps. The analysis relied on the “stimulus-locked firing rate,” which was the firing rate measured in a window 10–30 ms in length, beginning 5 ms after each electrical pulse. Stimulus-locked firing rates typically peaked at pulse rates averaging 7–8 pps, and stimulus-locked firing rates were reduced to one half at pulse rates averaging 12–14 pps. In the present data set, 70% of units showed half-maximal tonic spike rates persisting to unmodulated pulse rates of 20 pps, although that spike-rate measure counted all spikes regardless of timing. The preferred measures of stimulus-synchronized cortical responses in this study were limiting pulse rate (for unmodulated pulse trains) or limiting modulation frequency (for modulated 254-pps pulse trains), which are based on vector strength. By those measures, about one half of cortical units in this data set were synchronized to 30-pps unmodulated pulse trains, and nearly one half were synchronized to pulse trains modulated at 60 Hz.

Snyder et al. (2000) have explored phase-locked responses of neurons in the cat's inferior colliculus to cochlear implant stimulation. Most neurons showed low-pass sensitivity to unmodulated pulse rates, with the limiting rate averaging 104 pps. In response to 100%-modulated pulse trains, the limiting modulation frequency for 100% modulation depth averaged 42.2 Hz, but the distribution extended to 220 Hz. In the present study, nearly one half of the cortical neurons phase locked to modulator frequencies of 60 Hz. It is surprising to find higher limiting modulation rates in the cortex than in the inferior colliculus. One possible explanation is that phase locking in the inferior colliculus might have been suppressed by the 100% modulation depth that was used. Another possible explanation is that Snyder et al. avoided electrical artifacts by restricting analysis to inferior colliculus neurons giving the highest-amplitude spikes. That might have biased their sample to neurons with lower limiting phase-locked rates. In this study, an artifact-rejection procedure enabled recordings from a broader sample of units.

Cortical phase locking has been addressed in numerous previous studies using acoustical stimulation with clicks or modulated tones. Across most studies, phase locking to acoustical and electrical stimulation are similar in many respects. Best modulation frequencies in both conditions are ∼5–15 Hz (Eggermont 1991, 1994, 1998, 2002; Gaese and Ostwald 1995; Schreiner and Raggio 1996; Schreiner and Urbas 1988). Several studies have shown that best modulation frequencies in the cortex tend to correlate with intrinsic cortical rhythms, either spontaneous spindle frequencies or oscillatory rebounds following the offset of stimulation (Eggermont 1992; Gaese and Ostwald 1995; Kenmochi and Eggermont 1997). Similarly, neurons in this study often showed oscillatory responses at ∼10 Hz in response to pulse trains that were presented at pulse rates well above the rate to which the neuron could phase lock. Studies using acoustic stimulation in anesthetized preparations have reported low-pass or band-pass dependence of cortical phase locking on stimulus rate, with limiting rates around 20 Hz or lower (Creutzfeldt et al. 1980; Eggermont 1991, 1994, 1998, 2002; Gaese and Ostwald 1995); a median value of 25.1 Hz was reported by Lu and Wang (2000) for anesthetized cats. Limiting rates generally were higher in this study using electrical stimulation. In this study, 97% of units tested with unmodulated pulse trains showed limiting rates of 20 pps or higher, and 49% showed phase locking at 30 pps or higher.

One caveat in interpreting these results, and those of the majority of previous studies, is that data were collected under conditions of general anesthesia, which is known to influence the temporal firing patterns of cortical neurons. For instance, anesthesia tends to reduce the trial-by-trial variance in first-spike latencies (Ter-Mikaelian et al. 2007) and to increase the stimulus-related information carried by first-spike latencies (Mickey and Middlebrooks 2003). Reports of the effects of anesthesia on cortical phase locking are mixed. Several reports have concluded that anesthesia impairs phase locking. That is, phase locking to sounds extends to higher frequencies in unanesthetized preparations (Anderson et al. 2006; Liang et al. 2002; Lu et al. 2001; Ribaupierre et al. 1972; Steinschneider et al. 1998). In contrast, Ter-Mikaelian et al. (2007) showed in gerbils that anesthesia tended to enhance cortical phase locking to modulation frequencies greater than ∼20 Hz. Clearly, additional study of cortical phase locking under unanesthetized conditions is needed.

Sensitivity to modulation frequency and depth

One of the goals of this study was to explore the upper end of the range of modulation frequencies that might elicit phase-locked activity in cortical neurons. About one half of the tested cortical neurons exhibited significant phase locking across the ∼2-to ∼50-Hz range of modulation frequencies that carry information for speech recognition by cochlear implant users. Normal-hearing listeners can detect sinusoidal modulation of broadband noise at modulation depths as low as approximately −25 dB (Viemeister 1979), and cochlear implant users can detect modulation of electrical pulse trains at depths of approximately −40 dB (Busby et al. 1993; Galvin and Fu 2005; Pfingst et al. 2007; Shannon 1992). A likely explanation for the greater modulation sensitivity observed with electrical stimulation derives from the extremely limited dynamic range of electric hearing. At a modulation depth of −35 dB, for instance, the range of amplitudes from minimum to maximum is 0.31 dB, which is a sizeable fraction of the dynamic range of electric hearing, yet is below the just-noticeable difference for sound pressure level. Moreover, modulation sensitivity with cochlear implants might be enhanced by the enhanced across-fiber synchrony that is observed under conditions of electrical stimulation. That speculation is consistent with the observation that relatively widespread cochlear electrical stimulation using a monopolar configuration promotes greater modulation sensitivity than does stimulation with a more-restricted bipolar configuration (Middlebrooks 2008).

There have been few previous studies of the effects of modulation depth on phase locking of cortical units. One exception is a study of responses to amplitude-modulated acoustic tones in auditory cortex of unanesthetized marmosets (Liang et al. 2002). A subset of the studied units tested over limited ranges of modulation depths showed generally monotonic increases in firing rate with modulation depth increasing from 20–50 to 100%. Eggermont (1994) compared phase locking to acoustic noise modulated with 25, 50, 75, and 100% modulation depths. Modulation depths of 50% and higher produced similar temporal modulation transfer functions. In that study, modulation depths <50% rarely evoked phase locking to the modulating waveform. Krishna and Semple (2000) studied responses in the gerbil inferior colliculus to tones varying in modulation frequency and depth. Most of their units showed monotonic increases in response rate with increasing modulation depth. Thresholds for phase-locked responses were as low as ∼10% modulation (−20 dB). The present study examined phase locking systematically to modulation depths as low as 1% modulation (−40 dB). As shown in Fig. 6, significant phase locking often was seen at depths as low as −35 dB; modulation thresholds as low as −40 dB were shown using a more sensitive measure introduced elsewhere (Middlebrooks 2008). Similarly, Litvak et al. (2001) showed phase locking of auditory nerve fibers to electrical pulse trains modulated with a depth of −40 dB.

A novel finding of this study was the nonmonotonic dependence of vector strength (and spike rate) on modulation depth. Most units showed vector strength increasing monotonically with increasing modulation depth for modulation frequencies up to ∼20 Hz, but the majority of units showed a nonmonotonic dependence of vector strength on depth for higher modulation frequencies. Moreover, the results for unmodulated pulse trains can be interpreted as parallel to the modulation results if one regards these relatively low-rate pulse trains as showing modulation effectively deeper than that produced by 100% modulation of a high-rate carrier. That is, nearly all units showed significant phase locking to pulse trains at rates ≤20 pps, and the percentage of phase-locked units declined sharply at higher pulse rates. It remains to be tested whether nonmonotonic depth dependence is limited to cochlear implant stimulation or whether it also is seen with acoustic stimulation. The nonmonotonic depth dependence observed in this study combined with the use of click-train or 100%-modulated stimuli in nearly all previous studies might account for the many observations, particularly in anesthetized animals, that phase locking in the auditory cortex is largely absent at rates >20 Hz (Creutzfeldt et al. 1980; Eggermont 1991, 1994, 1998, 2002; Gaese and Ostwald 1995; Schreiner and Urbas 1988).

A tentative hypothesis to explain the nonmonotonic dependence of phase locking on modulation depth is that a strongly modulated stimulus could elicit tightly synchronized periods of intracortical inhibition, somewhat shorter than the 50- to 100-ms period of inhibition that was observed following the initial excitatory response to the onset of nearly all suprathreshold stimuli. Recovery from inhibition in somewhat <50 ms would permit phase-locked responses to modulation frequencies of 20 Hz or lower but would suppress responses to higher modulation frequencies. Hypothetically, inhibition produced by stimuli with shallower modulation depth would be weaker in magnitude or quicker to recover, thereby permitting phase locking to higher modulation frequencies. That hypothesis remains to be tested.

Temporal and rate codes for modulation frequency

A goal of this study was to evaluate the cortical representation of the modulation frequencies of cochlear implant stimuli in the frequency range relevant to speech reception, i.e., up to ∼50 Hz. One can consider two general forms of representation: temporal codes, in which the timing of features of stimulus envelopes are mirrored in the timing of cortical spikes, and rate codes, in which the spike rates of neurons vary systematically with stimulus frequency. The results showed the feasibility of a temporal code based on the phase-locking of cortical neurons. Significant phase locking to modulation frequencies ≤60 Hz was observed in nearly all units recorded in thalamic afferent layers and in no less than 25% of units recorded in extragranular layers. An analysis based on autocorrelation (Fig. 11) showed that the frequency of phase locking of many neurons corresponds closely to the stimulus modulation frequency across a considerable range of modulation depths. A reduction in modulation depth from −5 (56%) to −20 dB (10%) resulted in some increase in the scatter of responses but produced no systematic change in the frequency signaled by the phase-locking firing patterns of neurons. Presumably the frequency signal in the population would have been even more salient if the analysis had been restricted only to the population of phase-locked units. The significance of the apparent loss of phase locking in some 75% of units in extragranular layers is unclear. One possibility is that temporal information is transformed within those layers to an as-yet-unidentified nontemporal code by which information is transmitted to other cortical and noncortical areas. According to that scheme, the phase-locked units in those layers might be interneurons and some or all of the non–phase-locked neurons would be the projection neurons. An alternative possibility is that temporal information is restricted to specialized pathways and that the non–phase-locking neurons are part of a pathway specialized for one or more functions for which stimulus envelope frequency is irrelevant or for which phase locking is a liability.

These results are not consistent with a straightforward model in which modulation frequency in the range of 10–60 Hz is signaled by the spike rate of cortical neurons. A sizeable majority of units has best modulation frequencies ∼10 Hz. That indicates that modulation tuning of spike rates is not a likely candidate for representation of modulation frequencies in the range of 20–60 Hz. The tonic spike rates of single neurons can vary with modulation frequency, such that a change in spike rate might signal a change in modulation frequency, but spike rates and the frequency dependence of spike rates are confounded by changes in modulation depth. The spike rates of the single unit plotted in Fig. 5, for instance, varied by a factor of ∼2 between modulation depths of −25 and −15 dB, whereas vector strength was essentially constant over that range. Similar characteristics are seen in the distribution of spike rates across the entire sample of units (Fig. 12). One must leave open the possibility that different conclusions might be reached in a future study in unanesthetized animals. Nevertheless, these results show that the sensitivity of cortical neurons to modulation frequency is so confounded by modulation-depth sensitivity that the modulation-frequency information carried by spike rates is essentially uninformative.

Cochlear implant users report increases in perceived pitch corresponding to increases in the rate of unmodulated pulse trains to rates as high as 300 pps (Geurts and Wouters 2001; Kong et al. 2004; McKay et al. 1994; Xu et al. 2002; Zeng 2002). Based on the present results, it seems highly unlikely that discriminations of such high pulse rates rely on phase-locked activity in the auditory cortex. No data are available for electrical stimulation in unanesthetized primates, but the acoustic click data in unanesthetized marmosets (Liang et al. 2002) indicate that only ∼20% of cortical neurons phase lock to 128-cps click trains and only a handful phase lock to 256 cps. Evidence for an alternative, non–phase-locked, representation of pulse rate comes from the work of Lu et al. (2001) in the auditory cortex of unanesthetized marmosets. Those investigators described a class of “nonsynchronized” units that showed spike rates that increased with increases in acoustic click rates beginning at rates of 50 cps/s or higher. If such a rate code exists for electric hearing, it could conceivably account for rate-pitch perception in cochlear implant users. In this study, ∼30% of units showed tonic non–phase-locked responses that generally increased in spike rate with increases in pulse rates above ∼50 pps, but that effect was not robust and showed considerable trial-by-trial variation (data not shown). One presumes that the low tonic rates observed in this study were at least partially caused by the use of anesthetic. Future studies in unanesthetized animals are needed to test whether nonsynchronized tonic spike rates could signal rate pitch in electric hearing.

Low-pass filtering of modulation

The highest phase-locked frequencies in the auditory cortex are considerably lower than those observed in the subcortical auditory pathway. Phillips (1989) considered and rejected the hypothesis that this low-pass characteristic of phase locking results from the accumulated temporal imprecision of transmission across the multiple synapses in the path from ear to cortex. Contrary to an imprecision hypothesis is the observation that the trial-by-trial SD in first-spike latencies in the cortex is less than the temporal periods of frequencies to which cortical neurons phase lock. In this study, for instance, the SD of first-spike latencies averaged <2 ms. If imprecision in transmission through the auditory pathway were the limiting factor in phase locking, a SD of 2 ms would yield period histograms with about two thirds of spikes falling within a 4-ms range. That would predict strong phase locking to 125-pps pulse trains, which was never observed. Similarly, imprecision in intracortical transmission cannot account for observations that the percentage of neurons showing phase locking to modulation frequencies of 60 Hz is reduced in extragranular layers. Across all layers, 95% of units had an SD in first-spike latencies <4 ms, which should support strong phase locking to 60 Hz or higher.

In this study, group delays computed from the mean phases of period histograms showed a strong inverse correlation with limiting modulation frequencies. Units with limiting frequencies of 60 Hz or higher tended to have short group delays, no more than a few milliseconds longer than their first-spike latencies; those units will be referred to here as “all-pass” units. That the group delays of all-pass units showed so little additional delay relative to their first-spike latencies suggests that those units were subject to little or no intracortical filtering. All-pass units were found in greatest percentage in the thalamic afferent laminae, but no fewer than 25% of units recorded in all lamina were all-pass. That latter observation suggests that all-pass phase locking is transmitted unfiltered to subpopulations of units throughout the depth of cortical area A1. Units with limiting rates <60 Hz tended to show group delays substantially longer than their first-spike latencies; those will be referred to as “low-pass” units. Low-pass units showed a weak but significant tendency to have longer first-spike latencies. The negative correlation of limiting rate or frequency with first-spike latency suggests that low-pass units are one or more synapses removed from the thalamic-recipient neurons. Nevertheless, the group delays of low-pass units are too long to be accounted for by a few excitatory feed-forward synapses. Rather, the long group delays point to intracortical inhibitory processes as shaping low-pass modulation transfer functions cutting off below 60 Hz.

Eggermont (1999) has modeled group delay as the sum of a simple transmission delay from the ear to the cortex (represented by the 1st-spike latency) plus a “temporal filter delay” reflecting intracortical synaptic mechanisms. In his data set consisting of responses to unmodulated acoustical click trains in cat cortical area A1, filter delays of various units formed two groups. About two thirds of units had filter delays averaging 1.3 ms, and one third of units had delays averaging 13.4 ms. In the present study, all-pass units had temporal filter delays (computed as group delay minus 1st-spike latency) averaging 5.3 ± 3.6 ms, and low-pass units had temporal filter delays averaging 10.7 ± 5.8 ms; again, the filter delay for low-pass units is probably underestimated because many low-pass units did not have measurable group delays. Based on the similarities of filter delays, the all-pass and low-pass units of this study seem to correspond to Eggermont's short- and long-delay units, respectively. The percentage of low-pass units was greater in this study (56%) than in Eggermont's study (∼1/3). The higher proportion of low-pass units might reflect a species difference (guinea pig vs. cat) or that Eggermont attempted to record from middle cortical layers (reported as depths of 600–1,200 μm below the cortical surface), whereas this study sampled a broader range of depths.

Concluding remarks

The existing literature on phase-locked responses in the auditory cortex is based primarily on responses to acoustic stimuli, either unmodulated clicks or 100%-modulated sinusoids. The general impression conveyed by that literature is that phase locking in the cortex cuts off at modulation frequencies of ∼20 Hz or lower and that the failure to phase lock to higher frequencies is a result of imprecise feed-forward transmission at thalamo-cortical and intracortical synapses and/or some sort of persistent intracortical inhibition. This study explored a broader range of modulation frequencies and modulation depths, using cochlear implant stimulation. Tests of the sensitivity of phase locking to modulation depth showed that the deepest modulation tended to suppress phase locking, perhaps accounting for the failure of previous studies to show phase locking at rates above ∼20 Hz. Indeed, this study showed cortical phase locking up to ≥64 Hz, extending somewhat beyond the range of modulation frequencies needed for speech recognition with cochlear implants. Examination of the relationships among laminar depth of neurons, limiting modulation frequency, first-spike latencies, and group delays lead us to reject the hypothesis that phase-locking to high modulation frequencies (i.e., >20 Hz) is merely “lost” within the cortex because of accumulated effects of multiple imprecise synaptic links. Instead, the results suggest that high modulation frequencies are low-pass filtered within the cortex, perhaps as a consequence of recoding in some as-yet unidentified form. Forthcoming data extend these findings by quantifying modulation detection thresholds as a function of electrical stimulus parameters that are important for cochlear implant speech processor design (Middlebrooks 2008).

GRANTS

This work was supported by National Institute for Deafness and Other Communication Disorders Grants RO1 DC-04312 and P30 DC-05188.