Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2007 May 15;274(1619):1715–1721. doi: 10.1098/rspb.2007.0415

Host community structure and the maintenance of pathogen diversity

Caroline Buckee 1,*,†, Leon Danon 2,†, Sunetra Gupta 1
PMCID: PMC2493584  PMID: 17504739

Abstract

Community structure has been widely identified as a feature of many real-world networks. It has been shown that the antigenic diversity of a pathogen population can be significantly affected by the contact network of its hosts; however, the effects of community structure have not yet been explored. Here, we examine the congruence between patterns of antigenic diversity in pathogen populations in neighbouring communities, using both a deterministic metapopulation model and individual-based formulations. We show that the spatial differentiation of the pathogen population can only be maintained at levels of coupling far lower than that necessary for the host populations to remain distinct. Therefore, identifiable community structure in host networks may not reflect differentiation of the processes occurring upon them and, conversely, a lack of genetic differentiation between pathogens from different host communities may not reflect strong mixing between them.

Keywords: community structure, pathogen diversity, host network structure

1. Introduction

Many important pathogens, including Neisseria meningitidis, the causal agent of bacterial meningitis, the influenza virus and the malaria parasite (Plasmodiuin falciparum), exhibit high levels of antigenic diversity. Theoretical models have been developed to try to understand the factors leading to the evolution and maintenance of antigenic diversity (Dietz 1979; Castillo-Chavez et al. 1989; Gupta et al. 1996, 1998; Andreasen et al. 1997; Gog & Swinton 2002; Gomes et al. 2002). Many such models assume that immunity to one strain will confer partial immunity to other similar strains. Models incorporating multiple loci show that high levels of cross-immunity can lead to the polarization of the pathogen population, with subsets of strains that do not share antigenic determinants stably dominating the population (Gupta et al. 1996, 1998). Within this framework, intermediate levels of cross-immunity can cause strains to oscillate in dominance, showing chaotic behaviour under certain conditions, whereas low cross-immunity allows all strains to coexist independently.

Understanding how contacts between neighbouring communities of hosts affect the dynamics of pathogens is critical for controlling the diseases they cause, since most human populations are structured into communities, from the scale of the family group to towns, cities and countries. Recent advances in the field of complex networks and, particularly, in relation to community structure, provide a natural framework to study these effects (Strogatz 2001; Albert & Barabási 2002; Newman 2003; Dorogovtsev et al. 2003). Models of the spread and evolution of infectious diseases on social networks have shown that local clustering of hosts can alter the transmission dynamics of an epidemic and change the evolutionary selection pressures on traits such as virulence and infectious period (van Baalen 2002; Eames & Keeling 2003; Read & Keeling 2003, 2006; Kiss et al. 2006). It has also been shown that in a highly structured spatial setting, strong cross-immunity can lead to local selection for different subsets of strains in neighbouring clusters of hosts, thereby increasing the overall diversity of the pathogen population (Buckee et al. 2004). None of these models has explored social networks with community structure, however. Here, we explicitly incorporate separate host communities with the aim of determining how varying levels of interaction between them affects the separation of antigenic profiles of pathogen populations.

Many epidemiological models have explored the effects of the strength of coupling between metapopulations on disease dynamics (Bartlett 1957; Rohani et al. 1999; Grenfell et al. 2001; Xia et al. 2004). These models explore transmission on different spatial scales (Bartlett 1957; Grenfell et al. 2001; Xia et al. 2004) and the effects of metapopulation structure on the eradication of disease through vaccination (Rohani et al. 1999). The effects of spatial separation on the genetic structure of natural populations have also been extensively studied by ecologists (reviewed in Harrison & Hastings 1996). Reduced gene flow between geographically or genetically separate communities can lead to genetic differentiation between subpopulations, and an increase in overall genetic diversity as a result of local differences in allelic frequencies (Levin 1988; Barton & Hewitt 1989; Mallet & Barton 1989; Kruuk et al. 1999; Molofsky et al. 1999). The majority of these ecological models focus on the balance between dispersal and selection required for two populations to remain genetically distinct.

Here, we develop a series of models that explore the effects of community structure on the maintenance of antigenic diversity within pathogen species. Like the ecological models discussed above, we investigate the balance between the separation of host communities and the level of immune selection necessary for the maintenance of antigenically distinct pathogen subpopulations. In the context of pathogen genetics, reduced dispersal between subpopulations in ecological models is analogous to the reduced transmission occurring between different communities of hosts. We show that distinct community structure in the host population is insufficient to maintain the separation between profiles of pathogen antigenic diversity.

2. Deterministic metapopulation model

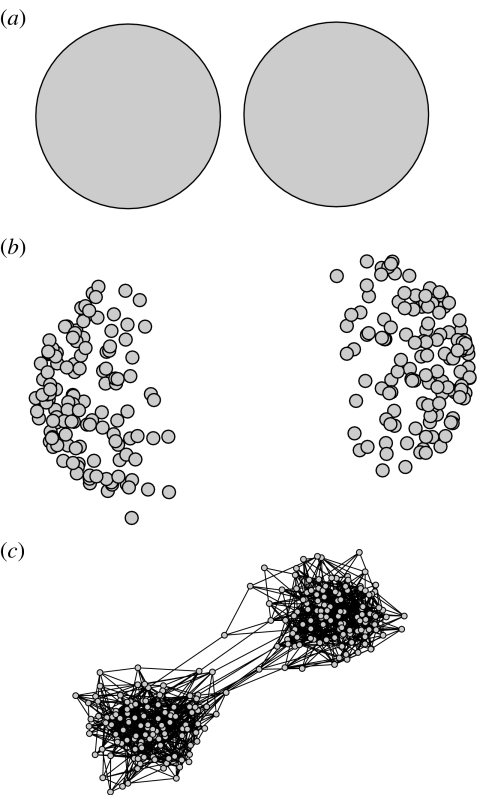
First, a metapopulation version of the Gupta et al. (1996, 1998) model of strain dynamics was developed, incorporating two linked populations. Each community was defined by its own set of three differential equations, shown below, and linked by the coupling term, α, which was incorporated into the force of infection for each strain, ic. Strains were defined by their antigenic determinants, i, and their community, c (figure 1a). The equations, shown below, were set up in a two-locus two-allele framework, such that four strains were possible, each sharing alleles with two other strains.

Figure 1.

Figure 1

Open in a new tab

Schematics of the three approaches. (a) The deterministic model with two communities. (b) Random-mixing stochastic model separated into two communities. (c) Static network model with quenched disorder.

Hosts exposed to one strain gained protection to all strains sharing alleles with that strain (the subset i′, including itself), depending on the level of cross-immunity, γ. In the absence of cross-immunity (γ=0), therefore, hosts exposed to one strain gained no protection to other strains with common alleles, while under complete cross-immunity (γ=1), they gained full protection to these strains. Note that cross-immunity in this case acted to reduce transmission rather than block infection.

dzicdt=λic(1−zic)−μzic,dwicdt=∑i′cλic(1−wic)−μwic,dxicdt=λic(1−wic+(1−γ)(wic−zic))−σxic.

Here, zic is the proportion of the population immune to strain ic; wic is the proportion non-susceptible to any strain sharing alleles with strain ic; and xic is the proportion infected with strain ic. The coupling term was embedded within the force of infection, λic, as follows:

λic=β(xic+αxic′),0≤α≤1,

where ic′ are strains from the other community with the same antigenic determinants and β is the transmission coefficient, which was the same for each strain. Since the strength of coupling covaried with R0 in this formulation of λ, we explored different forms of this coupling term. For example, we assessed the model output for the entire range of parameters assuming λic=β((1−α)xic+αxic′). However, the precise form appeared to make little difference to the outcome of the model, so the original formulation was used for simplicity. The parameters σ and μ are the rate at which hosts lose infectiousness and the death rate, respectively. The equations were examined numerically, and in order to identify the effects of coupling and explore the stability of neighbouring communities with different equilibria, the two communities were seeded with two discordant strains having non-overlapping antigenic repertoires. It was assumed that the duration of infectiousness (1/σ) was short when compared with the average lifespan (1/μ), and immunity was lifelong. Parameters were assigned such that the basic reproductive ratio R0 (here, βic/σ) or the average number of secondary cases resulting from a primary infection in a completely susceptible host population (Anderson & May 1991), was the same for every strain.

We observed from the results of this model that for lower levels of cross-immunity, all strains could coexist within both the communities at the same prevalence, so metapopulation structure had no identifiable effect. However, the effects of metapopulation structure of the system became evident at higher levels of cross-immunity. Two stable equilibria resulted, depending on the initial conditions:

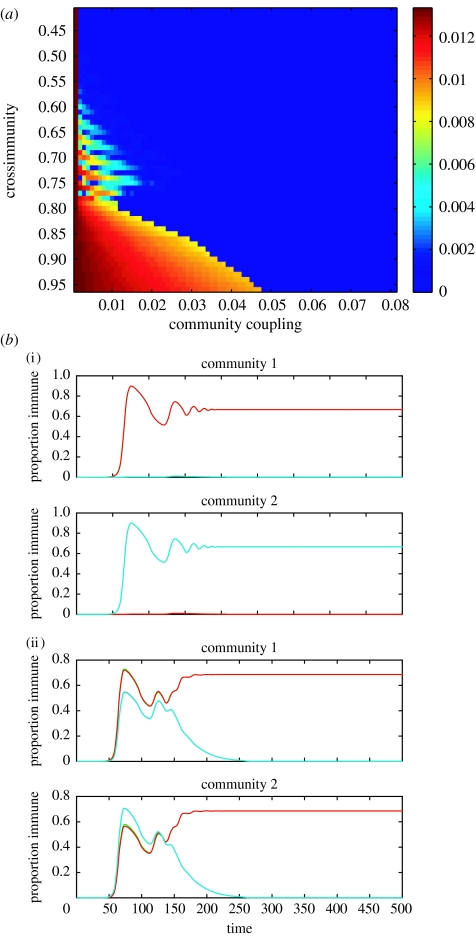
  1. For initial strain prevalences above an extremely low threshold (here 0.0001), the two communities maintained separate dynamics when they were weakly coupled. Here, different subsets of strains dominated each community, each subset being a pair of discordant strains (i.e. sharing no alleles), and this separation required higher levels of connectedness (α) between communities as the level of cross-immunity (γ) increased. As cross-immunity declined, essentially lowering competition between strains for hosts, ‘synchronization’ of antigenic profiles (whether stable or oscillatory) occurred at much lower levels of connectedness. Figure 2a shows the relationship between the two parameters, α and γ, with the colouring indicating the difference in prevalence of the same antigenic strain in the two communities; the dark blue space shows where the two communities are behaving as a single population. For levels of cross-immunity resulting in oscillatory dynamics, the coupling between communities had a similar effect, with the communities maintaining asynchronous oscillations of discordant subsets of strains at very low coupling (α<0.015). This effect can be observed as a light striped area in figure 2a between γ=0.6 and 0.8. Again, at higher levels of coupling, the two communities showed identical oscillatory dynamics, shown in dark blue. Other studies of multiple strain systems have also shown that synchronized dynamics between strains are sensitive to biological parameters such as transmission rate (Kamo & Sasaki 2002; Rohani et al. 2003), and often become unstable when stochasticity is introduced.

  2. The second equilibrium occurred for extremely low initial prevalences of the seeded strains (dominant strains seeded at 0.0001 or less). Here, the relationship between cross-immunity and coupling was qualitatively the same as the previous equilibrium, but in this case, the two communities became homogeneous at even lower levels of α (α=0.0014 when γ=1, see figure 2a; in an equivalent figure for the second equilibrium, only the x-axis would be altered). It would appear that this second equilibrium resulted from the inability of different dominant subsets to establish themselves in either community before the system equilibrated. As mentioned before, the maintenance of different discordant pairs of pathogen strains in the two communities required increasing levels of cross-immunity as the coupling between them strengthened.

Figure 2.

Figure 2

Open in a new tab

(a) The relatizonship between community coupling, immune selection and pathogen antigenic profiles for the deterministic model. The colour shows the difference in prevalence of the same strains in the two different communities for different levels of coupling (α) and cross-immunity (γ), with dark blue corresponding to total synchrony and dark red representing an extreme of asynchrony. Note the region of oscillatory dynamics between γ=0.6 and 0.8. Here, parameter values were as follows: β=0.3, σ=0.1, μ=0.002. (b) The dynamics of different strains within the two communities for different levels of coupling under strong cross-immunity. Communities 1 and 2 are seeded with discordant subsets of strains (here, one subset is represented by the red line and another by the blue line, since both strains within each subset are found at the same prevalence). (i) When cross-immunity is strong and α is very low (above: α=0.001, γ=0.9), the communities remain separate such that each community is dominated by the subset of strains it was seeded with. (ii) When cross-immunity is strong and α is relatively high (below: α=0.05, γ=0.9), on the other hand, the communities synchronize rapidly such that both are dominated by the same subset of strains. Other parameter values were as follows: β=0.3, σ=0.1 and μ=0.002.

Figure 2b shows examples of simulations of the deterministic model where cross-immunity was strong and coupling between communities was either above or below the threshold required for pathogen synchronization. Above, extremely low coupling between communities mean that the different subsets can be maintained at equilibrium in each community. Below, on the other hand, both communities are dominated by the same subset of strains at equilibrium because the separation between host communities is insufficient to prevent competition between the strains.

3. Stochastic models with community structure

As in the deterministic model, the pathogen strains were defined by two immunodominant genetic loci, each with two alleles, and by two communities, giving eight possible pathogen strains. Infected hosts could infect other hosts in the population depending on the transmission coefficient and the population structure, and this probability was the same for all strains. Upon infection, hosts remained infectious for a certain period of time before becoming immune to the infecting strain for a further period in an allele-specific manner. The duration of infectiousness and immunity were defined as the inverse of the probability that a host lost infectiousness or immunity at each time-step. Immunity to one pathogen strain meant that the host was partially immune to any pathogens with common alleles, dependent on the level of cross-immunity, γ. As in Buckee et al. (2004), cross-immunity was modelled assuming that a host's vulnerability (v) to infection depended on the extent to which the infecting strain shared antigenic determinants with strains in the host's immune memory (as in the deterministic framework). Here, the fraction of identical antigens f was converted into a vulnerability of infection between 0 and 1, such that v=(1−f1/γ)γ, and γ was a positive number between 0 and 4 scaling the level of cross-immunity (see Buckee et al. (2004) for details). The probability of a host becoming infected with a strain was therefore a product of the host's vulnerability and the transmissibility of the strain. Co-infection of the same host by two different strains could lead to a recombination event between them, and the probability of recombination was equal for each locus. Hosts infected with two strains could therefore transmit a new strain that was a hybrid of these two ‘parent’ strains. Mutation, modelled as the random switching of alleles at each locus with a defined probability, was also included so that all possible strains could be generated following the seeding of the host population. Again, the two communities were seeded with different subsets of non-overlapping strains.

In the first stochastic model, the host population was divided into two communities each with Nc=256 hosts, as shown in figure 1b. In a single time-step, each host could infect other hosts within the same community with a probability pin, assuming that the destination host did not already have any immunity to the infecting strain. In addition, a host in community i could infect hosts from community c with a probability pout (figure 1b). For the communities to remain distinguishable in this case, pin must be greater than pout. This stochastic version was designed as an intermediate between the mean field model described above and the network model below, with pout being equivalent to α, and will be referred to hereafter, as the random-mixing stochastic model. The motivation for this intermediate model was the observation that, in ecological literature, exotic species invading a new community (analogous to different subset of strains) have a higher probability of successful invasion once spatial clustering occurs around an ‘entry point’ (Korniss & Caraco 2005). We predicted that the static links between two hosts could create this kind of situation and change the qualitative outcome of the model.

In addition to the above, a network version with quenched disorder was implemented (figure 1c); networks were randomly generated, static for the course of each simulation and hosts were neither added nor removed. In contrast to the random-mixing stochastic case, here the contact structure was defined at the beginning of each simulation, and infectious hosts were only able to infect predefined neighbours. Hosts had on average ztot=10 links, zin of which were to hosts within the same community and zout to hosts in the other community. To be able to compare directly with the above approach, zin was set to Ncpin and zout to Ncpout. Note that it is not necessarily the case that the host communities can be distinguished for zin>zout, since both are average values. In any particular realization, this number will fluctuate and a host may find itself better connected with the ‘wrong’ community. To determine how community structure within the host population was affected by values of zin and zout, we used the ‘fast’ algorithm for identifying communities within networks (Newman 2004) to evaluate our simulated populations.

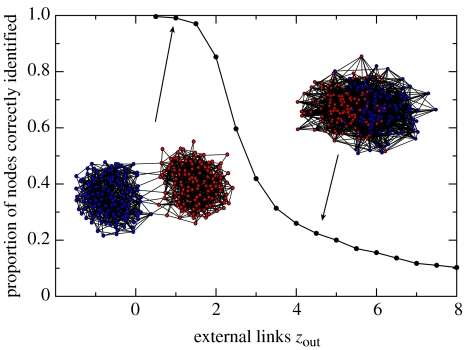
To get an idea of how the algorithm works, consider a network in which each node has been assigned to a community (i.e. the network has been ‘partitioned’) in some arbitrary way. This partition has an associated value of modularity Q, defined in Newman & Girvan (2004) as the difference between the number of links between nodes within each community and the expected number of links for the same communities in a randomized network. Joining any two neighbouring partitions would produce a change in modularity, ΔQ, which will be large if they share many links and small if they share few links. Starting with each node in the network defined as its own community, we successively join pairs of communities that share many links (those that produce the highest ΔQ) until an optimum modularity is reached. We can use the algorithm to evaluate the level of community structure in our simulated populations by simply counting the number of nodes that are correctly identified as belonging to a community for each value of zout. The result of this exercise is shown in figure 3, where communities in which ztot=10 for each host remain very well defined for values of zout up to 3.

Figure 3.

Figure 3

Open in a new tab

Relationship between zout and identifiable community structure. Network structure here is represented as the proportion of nodes correctly identified by the community identification algorithm as a function of zout. The communities remain very well defined for values of zout up to 3.

4. Comparing deterministic and stochastic (random mixing and network) formulations

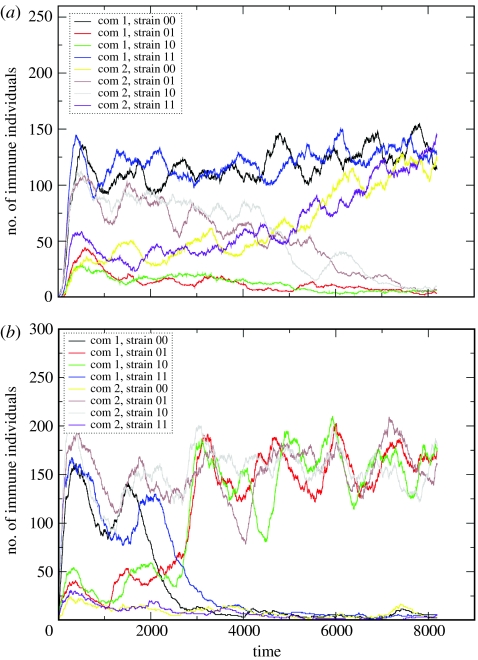
Both the random-mixing and network models showed similar dynamics to the deterministic systems for different levels of cross-immunity, with all strains coexisting when cross-immunity was low, oscillations occurring at moderate levels, and the domination of non-overlapping subsets of strains at high levels. Figure 4 shows an example of a network simulation in which the two communities begin with different dominant subsets, but make a sudden transition to both communities having the same dominant strains. The time taken to make this transition was significantly negatively correlated with the level of connectivity between the two communities (R2=−0.362, p<0.00001), as might be expected, but not with the level of cross-immunity. Synchronization of antigenic profiles could also occur without either community previously establishing dominant subsets.

Figure 4.

Figure 4

Open in a new tab

Number of immune individuals against time, with the two communities being seeded with different discordant sets. (a) For the random-mixing stochastic model, where γ=4, zout=1.0 and (b) for the static network implementation, with γ=4 and zout=0.5. In both cases, the dominance of the different discordant sets is established in the communities. After a number of steps, one discordant set becomes dominant in the whole population.

To compare the antigenic profiles in different communities within the stochastic frameworks, we used a population-level metric of diversity (Buckee et al. 2004) based on the Shannon–Weaver diversity index (Shannon & Weaver 1949). When cross-immunity was high, the within-community diversities were expected to be relatively low. If both the communities were dominated by the same subsets of strains, then the overall diversity would also be low. Conversely, when different dominant strains were maintained in each community, the overall population showed high diversity, since all strains existed at more or less the same prevalence overall. Thus, the diversity of individual communities could be compared with that of the overall population, with the difference between local and global diversities being analogous to the difference in prevalence of the same strains in different communities for the deterministic model.

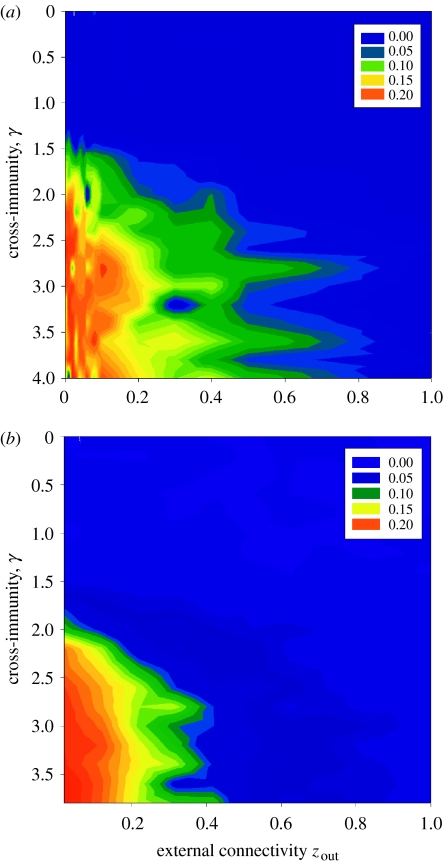
Figure 5 shows the effects of cross-immunity and community separation on the pathogen population for the random-mixing (figure 5a) and the network (figure 5b) models. The figures are in the same format as figure 2, but use the difference between the diversity of the overall population and individual communities as a measure of the homogeneity of the pathogen population across the two communities. Although it is not straightforward to calibrate parameters between the different models, it appeared that the random-mixing and network models behaved equivalently to the deterministic model. Interestingly, the random-mixing version was slightly noisier than the network version. Both stochastic models showed similar qualitative outcomes to the first equilibrium of the deterministic model (figure 2a), with stronger cross-immunity allowing for separate pathogen dynamics in the two communities at higher levels of connectivity. The quantitative differences between α and zout are approximately 10-fold in the transition from separate communities to one large population. There appeared to be no second equilibrium, however, and the prevalence of seeded strains had no impact on the outcome of the models.

Figure 5.

Figure 5

Open in a new tab

Relationship between cross-immunity and connectivity in the stochastic models. For both models, the colours represent the absolute difference between the individual communities' diversity and the diversity of the population as a whole. Results of the (a) random-mixing stochastic model and (b) network model.

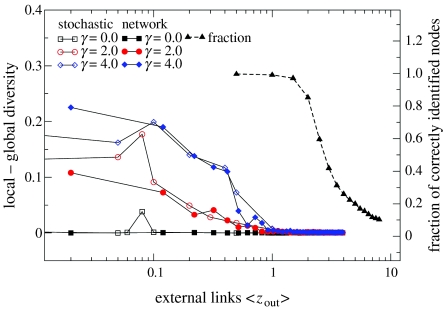
Pathogen dynamics became synchronized between communities at values of zout at which host communities in both stochastic models were still extremely well defined. Indeed, the host communities homogenized at a value of zout an order of magnitude above that necessary for the pathogen populations to become identical. Figure 6 shows this key finding from the study; the synchronization of pathogen dynamics is shown in comparison with the homogenization of the host community networks. Note the logarithmic scale on the x-axis. For the random-mixing case, pathogens in the two communities showed identical structuring and dynamics within a few time-steps for values of pout>0.001. Similarly, for the static network case, the pathogens in the two communities behaved essentially as one population after a short time for zout>0.5 (equivalent to pout>0.001 in the random-mixing model), whereas the communities of hosts remained highly differentiated until zout rose above approximately 3. Thus, identifiable community structure in the host network can only lead to antigenic differences between their pathogen populations at extremely low values of zout.

Figure 6.

Figure 6

Open in a new tab

A comparison of pathogen dynamics and host community structure from the stochastic models. Black triangles represent host community structure (figure 3), identifying the proportion of nodes correctly identified by the community identification algorithm (on the right-hand y-axis) as a function of zout (on the x-axis). The communities remain very well defined for values of zout up to 3. The dynamics of the pathogen populations are shown in blue, red and black squares (for cross-immunity or γ=0), circles (for γ=2) and diamonds (for γ=4, which is equivalent to 1 in the deterministic framework). The y-axis in this case corresponds to the local diversity minus the global diversity, which is indicative of homogeneous dynamics in the two communities if equal to zero. Note that zout in the network model cannot be zero or the network would be disconnected.

5. Discussion

Our main finding is that when there is strong cross-immunity, community structure can stably maintain diverse subsets of pathogen strains within neighbouring communities, but only if the connectivity between them is extremely low. Community structure therefore appears to have little effect upon the diversity of the pathogen population unless the communities are very well defined. Thus, a lack of antigenic differentiation between pathogen subpopulations in different host communities is not necessarily indicative of strong ties between them. Conversely, differences in antigenic profiles of pathogen populations may not reflect distinct community structure among hosts, but rather some other process such as the adaptation to varied local environments.

The relationship between cross-immunity and connectivity was qualitatively the same for all the three models, with the degree of cross-immunity required to maintain separate subsets of antigenic types in different host communities increasing with community connectivity. However, even when cross-immunity was strong, the overall pathogen population quickly became homogeneous with respect to the dominant strains at very low levels of connectivity. This occurred even when communities were initially dominated by different subsets of strains, and therefore could not be attributed to the lack of initial establishment of these strains within each community. The large discrepancy between the community connectivity required for host as compared to pathogen population homogenization generally suggests that the widespread identification of community structures in real social networks may not imply similar structuring of dynamic processes occurring upon them.

With the exception of very isolated communities, these models show that pathogen populations occurring within most communities of hosts are not likely to exhibit substantial differentiation in their antigenic repertoires. This may explain the global distribution of antigenic combinations observed for species such as Neisseria meningitidis, which have been shown to be structured into stable antigenic types by high levels of cross-immunity (Gupta et al. 1996; Urwin et al. 2004). In the context of our models, the stability of these antigenic types over wide areas does not necessarily imply high levels of mixing among host populations, but can be explained by strong immune selection even when links between neighbouring communities are very weak. It would be interesting to compare the distribution of antigen genes with that of the housekeeping genes of N. meningitidis, which do display geographical differentiation between different countries of Europe (Jolley et al. 2005). Our models suggest that genes that are under immune selection should not show the same level of differentiation.

Acknowledgments

This research was supported by EPSRC (C.B.) and the Generalitat de Catalunya (L.D.).

References

  1. Albert R, Barabási A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002;74:47–97. doi:10.1103/RevModPhys.74.47 [Google Scholar]
  2. Anderson R.M, May R.M. Oxford University Press; Oxford, UK: 1991. Infectious diseases of humans: dynamics and control. [Google Scholar]
  3. Andreasen V, Lin J, Levin S.A. The dynamics of cocirculating influenza strains conferring partial cross-immunity. J. Math. Biol. 1997;35:825–842. doi: 10.1007/s002850050079. doi:10.1007/s002850050079 [DOI] [PubMed] [Google Scholar]
  4. Bartlett M.S. Measles, periodicity and community size. J. R. Stat. Soc. A. 1957;120:48–70. [Google Scholar]
  5. Barton N.H, Hewitt G.M. Adaptation, speciation and hybrid zones. Nature. 1989;341:497–503. doi: 10.1038/341497a0. doi:10.1038/341497a0 [DOI] [PubMed] [Google Scholar]
  6. Buckee C.O, Koelle K, Mustard M.J, Gupta S. The effects of host contact network structure on pathogen diversity and strain structure. Proc. Natl Acad. Sci. USA. 2004;101:10 839–10 844. doi: 10.1073/pnas.0402000101. doi:10.1073/pnas.0402000101 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Castillo-Chavez C, Hethcote H.W, Andreasen V, Levin S.A, Liu W.M. Epidemiological models with age structure, proportionate mixing, and cross-immunity. J. Math. Biol. 1989;27:233–258. doi: 10.1007/BF00275810. doi:10.1007/BF00290636 [DOI] [PubMed] [Google Scholar]
  8. Dietz K. Epidemiologic interference of virus populations. J. Math. Biol. 1979;8:291–300. doi: 10.1007/BF00276314. [DOI] [PubMed] [Google Scholar]
  9. Dorogovtsev S.N, Goltsev A.V, Mendes J.F, Samukhin A.N. Spectra of complex networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2003;68(Pt 2):046 109. doi: 10.1103/PhysRevE.68.046109. [DOI] [PubMed] [Google Scholar]
  10. Eames K.T, Keeling M.J. Contact tracing and disease control. Proc. R. Soc. B. 2003;270:2565–2571. doi: 10.1098/rspb.2003.2554. doi:10.1098/rspb.2003.2554 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gomes M.G, Medley G.F, Nokes D.J. On the determinants of population structure in antigenically diverse pathogens. Proc. R. Soc. B. 2002;269:227–233. doi: 10.1098/rspb.2001.1869. doi:10.1098/rspb.2001.1869 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gog J.R, Swinton J. A status-based approach to multiple strain dynamics. J. Math. Biol. 2002;44:169–184. doi: 10.1007/s002850100120. doi:10.1007/s002850100120 [DOI] [PubMed] [Google Scholar]
  13. Grenfell B.T, Bjornstad O.N, Kappey J. Travelling waves and spatial hierarchies in measles epidemics. Nature. 2001;414:716–723. doi: 10.1038/414716a. doi:10.1038/414716a [DOI] [PubMed] [Google Scholar]
  14. Gupta S, Maiden M.C, Feavers I.M, Nee S, May R.M, Anderson R.M. The maintenance of strain structure in populations of recombining infectious agents. Nat. Med. 1996;2:437–442. doi: 10.1038/nm0496-437. doi:10.1038/nm0496-437 [DOI] [PubMed] [Google Scholar]
  15. Gupta S, Ferguson N, Anderson R. Chaos, persistence, and evolution of strain structure in antigenically diverse infectious agents. Science. 1998;280:912–915. doi: 10.1126/science.280.5365.912. doi:10.1126/science.280.5365.912 [DOI] [PubMed] [Google Scholar]
  16. Harrison S, Hastings A. Genetic and evolutionary consequences of metapopulation structure. Trends Ecol. Evol. 1996;11:180–183. doi: 10.1016/0169-5347(96)20008-4. doi:10.1016/0169-5347(96)20008-4 [DOI] [PubMed] [Google Scholar]
  17. Jolley K.A, Wilson D.J, Kriz P, McVean G, Maiden M.C. The influence of mutation, recombination, population history, and selection on patterns of genetic diversity in Neisseria meningitidis. Mol. Biol. Evol. 2005;22:562–569. doi: 10.1093/molbev/msi041. doi:10.1093/molbev/msi041 [DOI] [PubMed] [Google Scholar]
  18. Kamo M, Sasaki A. The effect of cross-immunity and seasonal forcing in a multi-strain epidemic model. Physica D. 2002;165:228–241. doi:10.1016/S0167-2789(02)00389-5 [Google Scholar]
  19. Kiss I.Z, Green D.M, Kao R.R. The effect of contact heterogeneity and multiple routes of transmission on final epidemic size. Math. Biosci. 2006;203:124–136. doi: 10.1016/j.mbs.2006.03.002. doi:10.1016/j.mbs.2006.03.002 [DOI] [PubMed] [Google Scholar]
  20. Korniss G, Caraco T. Spatial dynamics of invasion: the geometry of introduced species. J. Theor. Biol. 2005;233:137–150. doi: 10.1016/j.jtbi.2004.09.018. doi:10.1016/j.jtbi.2004.09.018 [DOI] [PubMed] [Google Scholar]
  21. Kruuk L.E, Baird S.J, Gale K.S, Barton N.H. A comparison of multilocus clines maintained by environmental adaptation or by selection against hybrids. Genetics. 1999;153:1959–1971. doi: 10.1093/genetics/153.4.1959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Levin B.R. Frequency-dependent selection in bacterial populations (and discussion) Phil. Trans. R. Soc. B. 1988;319:459–472. doi: 10.1098/rstb.1988.0059. doi:10.1098/rstb.1988.0059 [DOI] [PubMed] [Google Scholar]
  23. Mallet J, Barton N. Inference from clines stabilized by frequency-dependent selection. Genetics. 1989;122:967–976. doi: 10.1093/genetics/122.4.967. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Molofsky J, Durrett R, Dushoff J, Griffeath D, Levin S. Local frequency dependence and global coexistence. Theor. Popul. Biol. 1999;55:270–282. doi: 10.1006/tpbi.1998.1404. doi:10.1006/tpbi.1998.1404 [DOI] [PubMed] [Google Scholar]
  25. Newman M.E. Mixing patterns in networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2003;67:026126. doi: 10.1103/PhysRevE.67.026126. [DOI] [PubMed] [Google Scholar]
  26. Newman M.E. Fast algorithm for detecting community structure in networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;69:066133. doi: 10.1103/PhysRevE.69.066133. [DOI] [PubMed] [Google Scholar]
  27. Newman M.E, Girvan M. Finding and evaluating community structure in networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2004;69:026113. doi: 10.1103/PhysRevE.69.026113. [DOI] [PubMed] [Google Scholar]
  28. Read J.M, Keeling M.J. Disease evolution on networks: the role of contact structure. Proc. R. Soc. B. 2003;270:699–708. doi: 10.1098/rspb.2002.2305. doi:10.1098/rspb.2002.2305 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Read J.M, Keeling M.J. Disease evolution across a range of spatio-temporal scales. Theor. Popul. Biol. 2006;70:201–213. doi: 10.1016/j.tpb.2006.04.006. doi:10.1016/j.tpb.2006.04.006 [DOI] [PubMed] [Google Scholar]
  30. Rohani P, Earn D.J, Grenfell B.T. Opposite patterns of synchrony in sympatric disease metapopulations. Science. 1999;286:968–971. doi: 10.1126/science.286.5441.968. doi:10.1126/science.286.5441.968 [DOI] [PubMed] [Google Scholar]
  31. Rohani P, Green C.J, Mantilla-Beniers N.B, Grenfell B.T. Ecological interference between fatal diseases. Nature. 2003;422:885–888. doi: 10.1038/nature01542. doi:10.1038/nature01542 [DOI] [PubMed] [Google Scholar]
  32. Shannon C.E, Weaver W. University of Illinois Press; Urbana, IL: 1949. The mathematical theory of communication. [Google Scholar]
  33. Strogatz S.H. Exploring complex networks. Nature. 2001;410:268–276. doi: 10.1038/35065725. doi:10.1038/35065725 [DOI] [PubMed] [Google Scholar]
  34. Urwin R, Russell J.E, Thompson E.A, Holmes E.C, Feavers I.M, Maiden M.C. Distribution of surface protein variants among hyperinvasive meningococci: implications for vaccine design. Infect. Immun. 2004;72:5955–5962. doi: 10.1128/IAI.72.10.5955-5962.2004. doi:10.1128/IAI.72.10.5955-5962.2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. van Baalen M. Dilemmas in virulence management. In: Dieckman U, Metz J.A.J, Sabelis M.W, Sigmund K, editors. The adaptive dynamics of infectious diseases: in pursuit of virulence management. Cambridge University Press; Cambridge, UK: 2002. pp. 60–69. [Google Scholar]
  36. Xia Y, Bjornstad O.N, Grenfell B.T. Measles metapopulation dynamics: a gravity model for epidemiological coupling and dynamics. Am. Nat. 2004;164:267–281. doi: 10.1086/422341. doi:10.1086/422341 [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES