Segmentation of Electron Tomographic Data Sets Using Fuzzy Set Theory Principles

Abstract

In electron tomography the reconstructed density function is typically corrupted by noise and artifacts. Under those conditions, separating the meaningful regions of the reconstructed density function is not trivial. Despite development efforts that specifically target electron tomography manual segmentation continues to be the preferred method. Based on previous good experiences using a segmentation based on fuzzy logic principles (fuzzy segmentation) where the reconstructed density functions also have low signal-to-noise ratio, we applied it to electron tomographic reconstructions. We demonstrate the usefulness of the fuzzy segmentation algorithm evaluating it within the limits of segmenting electron tomograms of selectively stained, plastic embedded spiny dendrites. The results produced by the fuzzy segmentation algorithm within the framework presented are encouraging.

1 Introduction

Understanding of biological processes is greatly facilitated by structural information. Transmission electron microscopy (TEM) has become an essential technology for the study of three-dimensional (3D) structural information of biological machines and can be used to observe specimens at a wide range of resolution, from hundreds of angstroms to atomic resolution (Jiang and Chiu, 2007; Lučić et al., 2005; Nogales et al., 1998; Renault et al., 2006). TEMs allow the study of specimens using relatively small amounts of biological preparation (Chiu, 1993) and cryo-technology (Dubochet et al., 1988) enables imaging of biological machines in near-native conditions.

For most practical purposes, TEM images of biological specimen can be considered two-dimensional (2D) projections of the object under study. Unfortunately, the images produced by a TEM are corrupted projections of biological specimens. Physical limitations and properties of TEMs, the high sensitivity of biological material to electron radiation, and the need to use low-dose electron beams contribute to the production of degraded images (Frangakis and Förster, 2004; Lučić et al., 2005; Marco et al., 2004; McIntosh et al., 2005). As a consequence, the images usually need to be post-processed to correct aberrations and to improve the signal-to-noise ratio (SNR) prior to interpretation.

The most interesting use of the information obtained by a TEM is the production of 3D density functions that approximate the spatial electron-density distribution associated with the preparation of the biological specimen under study, a process commonly known as reconstruction. A reconstruction is carried out by a computer algorithm that requires 2D projections of the specimen from different directions, in a similar fashion as the various tomographic techniques in medicine (Herman, 1980; Natterer and Wübbeling, 2001). The reconstructed density function is generally corrupted by noise and artifacts that are consequences of residual errors in the processing of the projected images, errors inherent to the reconstruction algorithms, and missing information in the collection of data (Frangakis and Förster, 2004; Lučić et al., 2005; Marco et al., 2004; McIntosh et al., 2005; Subramaniam, 2005).

Electron tomography (a method that produces reconstructions using projected images acquired from of single and unique biological specimens that are tilted along one or two axis perpendicular to the optical axis of the electron microscope) allows the study of biological specimens in their natural environment covering the intermediate resolution range of 5-20 nm, permitting the study of specimens such as molecular assemblies, small organelles, isolated cellular structures, tissue sections, and entire prokaryotic cells (Bajaj et al., 2003; Baumeister, 2002; Frangakis and Förster, 2004; Sali et al., 2003).

Because the reconstructed density function is typically an imprecise approximation to the biological preparation, it is generally necessary to apply methods to improve its quality and to carry out its analysis (Frangakis and Förster, 2004; Lučić et al., 2005; Marco et al., 2004; McIntosh et al., 2005; Subramaniam, 2005). In particular, it is of special interest to define the extent of the density function that best approximates the electron-density distribution associated with only the biological specimen under study. The extraction, isolation or identification of meaningful regions of the density function is an operation that is commonly referred to as segmentation. This operation is often required for analyzing, visualizing and manipulating meaningful information in a reconstructed density function. In fact, segmentation is one of the most prolific fields of research in robot vision and medical imaging (Fu and Mui, 1981; Haralick and Shapiro, 1985; Lohmann, 1998; Pal and Pal, 1993; Udupa and Herman, 1999).

Segmentation algorithms developed for other imaging domains generally do not yield satisfying results. Despite development efforts that specifically target electron tomography (Bajaj et al., 2003; Bartesaghi et al., 2005; Frangakis and Hegerl, 2002; Sandberg and Brega, 2007; Volkmann, 2002) manual segmentation continues to be the preferred method in electron tomography (Marsh et al., 2001). Unfortunately, manual segmentation suffers from user bias, non-reproducibility, and operator fatigue. Moreover, it forces the user to evaluate the object of interest in 2D rather than in 3D (Higgins et al., 1992; Singh et al., 1998; Udupa and Herman, 1999). Also, for density functions produced by modern electron tomographic methods, a manual segmentation usually requires many hours of user time.

Here we introduce to the field of electron tomography a segmentation method (Herman and Carvalho, 2001) based on fuzzy set theory (Bandemer and Gottwald, 1995; Rosenfeld, 1979, 1983; Zadeh, 1965) (for the sake of simplicity, we refer to this method as fuzzy segmentation). The reason for selecting the fuzzy segmentation method is the extent of successful experience using segmentation techniques based on fuzzy set theory in the medical imaging community (Dellepiane et al., 1996; Dellepiane and Fontana, 1995; Nyul and Udupa, 2000b; Udupa et al., 2001; Udupa and Saha, 2003). In particular, in (Carvalho et al., 2002) this method was used to yield good segmentations from noisy reconstructed density functions produced by positron emission tomography (an imaging modality characterized by low resolution and SNR). Because the images and reconstructions produced in EM frequently have a low SNR, the results produced by the fuzzy segmentation algorithm with PET data lead us expect a good performance in this field too.

In spite of the amount of research on segmentation methods in biomedicine there still is a lack of a standard protocol to evaluate their results. Nevertheless, there is agreement on the need of validating the results with some “ground truth” (Chalana and Kim, 1997; Udupa et al., 2002a; Warfield et al., 2004; Yoo et al., 2000). Calculated density functions (phantoms) and manual segmentation of experimental data by domain experts are the most common methods to generate the ground truth. While phantoms are extremely useful for evaluating image processing methods, this approach often fails to accurate model the full range of phenomena occurring in the imaging process (e.g., the breakdown of linearity for thick specimens in EM) and, consequently, there is always the need of carrying out final tests on real data. Hence, interactive delineation of the objects of interest has often been used to compare the results of segmentation algorithms and this is the approach we followed for this work. In order to account for the aforementioned drawbacks of manual segmentation, we follow a statistical protocol where several expert operators would produce multiple segmentations, both manual and automatic, for a collection of several reconstructions. This allows an assessment of manual segmentation performance and thus a more meaningful comparison with the results of the automatic segmentation.

2 Methods

2.1 Manual Segmentation Technique

Segmentation is considered manual when a human operator carries out both the task of recognizing the objects of interest on an image and the task of delineating the extent of those objects with the help of a computer interface. The computer interface that we used for carrying the manual segmentation follows a traditional approach (Udupa, 1982; NCMIR, 2002) in which the user has a graphical interface that displays the orthogonal planes of a reconstruction one by one and permits the placing and editing of marks in every image plane. The marks are joined by straight lines in such a way that the user can create 2D contours that enclose regions in any slice. By moving along all the slices, the user can create a stack of 2D contours that enclose the objects of interest. This implementation of the manual segmentation can either produce the surface defined by the 2D contours, a procedure carried out by creating a 3D Delaunay triangulation (Delaunay, 1934), or produce a data set containing the voxels enclosed by the user-delineated 2D contours.

2.2 Multi-Object Fuzzy Segmentation

In spite of the corrupting processes during imaging, imaged objects typically appear as cohesive entities with imprecise boundaries. Fuzzy segmentation attempts to measure such connectedness among elements of imaged objects (Udupa and Saha, 2003). Since the connectedness of the elements making up imaged objects is imprecise, fuzzy sets theory provides an appropriate mathematical framework to model such a concept.

In fuzzy set theory, sets have imprecise boundaries and membership to a fuzzy set is a matter of degree. A fuzzy set is defined by assigning to every possible element a value that represents the degree to which the element resembles the concept represented by the fuzzy set. Such assignment of values is made through a membership function that typically has a codomain equal to the closed interval [0, 1] of real numbers. In such a range, a value of 1 indicates full membership to a fuzzy set and a value of 0 indicates nonmembership. It is important noticing that the success of modeling with fuzzy set theory critically depends on the construction of appropriate membership functions.

In fuzzy segmentation it is assumed that the properties defining a voxel (to be precise, the density function sampled at such location) as a member or nonmember of an object change smoothly. Furthermore, in accordance to fuzzy set theory, the degree of membership to an object can be determined by a membership function indicating the degree of certainty that a given voxel belongs to an object. Fuzzy segmentation locally measures this relation between any two adjacent voxels with a fuzzy spel affinity. This function is typically reflexive and transitive. Some authors also impose symmetry (Udupa and Saha, 2003; Udupa and Samarasekera, 1996). Nonetheless, there are few restrictions on the definition of fuzzy voxel affinity for adjacent voxels and the function can be defined based on the problem at hand. In practice it is a function of two consecutive voxels and their density values (Saha et al., 2000; Udupa and Saha, 2003; Udupa and Samarasekera, 1996; Udupa et al., 1997). In this work the locality of a fuzzy spel affinity refers to the insistence that the function be zero if the two voxels are not adjacent. For this presentation voxels are represented by a discrete vector c̄ which is a 3-tuple (c₁, c₂, c₃) whose components belong to ℤ. Furthermore, voxels will be arranged over the simple cubic grid but the same algorithm can be easily extended to voxels in other grids (Herman and Carvalho, 2001; Udupa and Saha, 2003). Since reconstruction algorithms produce a subset of the simple cubic grid, we consider the pair of voxels {c̄, d̄} to be adjacent if the distance between them is either (a) 1 or (b) less or equal to $\sqrt{2}$ (the so-called face and face-edge adjacencies, respectively). For geometrical reasons, it is common practice that the voxels in the background have face-edge adjacencies only and those in the foreground have face adjacency (Herman, 1998).

Nonetheless, it has been recognized that the function defining the fuzzy affinity should consider object features and homogeneity, and it has the following general form (Carvalho et al., 1999; Herman and Carvalho, 2001; Saha et al., 2000; Udupa and Saha, 2003; Udupa and Samarasekera, 1996; Udupa et al., 1997):

$$\psi \left(\overline{c},\overline{d}\right)={\psi }_A\left(\overline{c},\overline{d}\right)f\left({\psi }_H\left(\overline{c},\overline{d}\right),{\psi }_O\left(\overline{c},\overline{d}\right)\right),$$ (1)

where ψ_A is an adjacency relation between voxels c̄ and d̄. The component ψ_O measures the degree of similarity of intensity features to expected object features, and the component ψ_H measures the degree of intensity homogeneity.

In particular, we have selected the following form of fuzzy affinity that has produced good results in previous studies

$$\psi \left(\overline{c},\overline{d}\right)={\psi }_A\times [w_O{\psi }_O\left(\upsilon \left(\overline{c}\right)+\upsilon \left(\overline{d}\right)\right)+w_H{\psi }_H\left(\left|\upsilon \left(\overline{c}\right)-\upsilon \left(\overline{d}\right)\right|\right)],$$ (2)

where υ (c̄) is the value of the density function at voxel c̄, and 0.5 is the typical choice for the weights w_O and w_H. Typically, the adjacency relation ψ_A is symmetric and has the following form ${\psi }_A\left(\overline{c},\overline{d}\right)=\{\begin{array}{cc}1,& \left(\overline{c},\overline{d}\right)\in \rho \\ 0,& \mathrm{otherwise}\end{array}$. In our case, the binary relation ρ is represented by either the face ((c̄,d̄) ∈ ω ⇔ ‖c̄−d̄‖ = 1) or face-edge ((c̄,d̄) ∈ β ⇔ 1 ≤ ‖c̄−d̄‖ ≤ 1) adjacencies. In the case for the functions ψ_O and ψ_H, common choices (Carvalho et al., 2005; Herman and Carvalho, 2001; Saha et al., 2000) are

$$\begin{array}{ccc}{\psi }_O\left(x\right)=e^{-\frac{{\left(\frac{1}{2}x-m_O\right)}^2}{2{\sigma }_O^2}}& \text{and}& {\psi }_H\left(x\right)\end{array}=e^{-\frac{{\left(x-m_H\right)}^2}{2{\sigma }_H^2}}.$$ (3)

The variables m_O and σ_O are assumed to be the mean and standard deviation of the sum $\frac{1}{2}\left(\upsilon \left(\overline{c}\right)+\upsilon \left(\overline{d}\right)\right)$, and m_H and σ_H are, in turn, assumed to be the mean and standard deviation of |υ (c̄) − υ (d̄)|.

It is possible to represent a fuzzy relation with a graph in which the nodes of the graph are the elements, the voxels in this case, and the values of the fuzzy relation are the weights or “strengths” of the edges of the graph. Since we are working with a non-symmetric fuzzy spel affinity, the graph would be directed and the nodes will have in- and out-degrees equal to the number of neighbors in their respective voxels. In such representation, a chain is a sequence (c̄⁽⁰⁾, …, c̄^(L)) of nodes, for 1 ≤ l ≤ L, and a link is a pair of adjacent nodes {c̄^(l−1), c̄^(l)}. The strength of a chain is determined by the strength of its weakest link or edge. Two nodes (i.e., voxels) that are joined by a chain are connected. Finally, the fuzzy connectedness between any pair of voxels is the strength of the strongest chain between them (Saha and Udupa, 2001; Udupa and Samarasekera, 1996).

The purpose of any of the fuzzy segmentation algorithms is to efficiently compute the fuzzy connectedness of every voxel in a reconstruction to sets of seed voxels (Herman and Carvalho, 2001; Nyul and Udupa, 2000a; Udupa and Saha, 2003; Udupa et al., 2002b; Udupa and Samarasekera, 1996). These seed voxels represent points in the reconstruction that certainly belong to objects to be segmented (i.e., they have connectedness equal to 1) and, traditionally, they are manually selected by an operator. However, in those circumstances where enough a priori information about the density functions is available it is possible to automatize the seed selection process, such as in (Garduño, 2002). One of the important assumptions behind the fuzzy segmentation approach we are presenting is that knowledgeable humans are better at recognizing the whereabouts of objects within a density function, whereas computers typically outperform humans at delineating those objects. This assumption is reflected in the selection of the sets of seed voxels.

In this work, we implemented and tested the algorithm presented in (Herman and Carvalho, 2001), that is based on the concepts in (Udupa and Samarasekera, 1996) but allows for every object to have its own definition of fuzzy affinity and its own set of seed voxels. A detailed discussion of the different algorithms is beyond the scope of this manuscript and can be found in (Carvalho et al., 2005; Herman and Carvalho, 2001; Saha et al., 2000; Udupa and Saha, 2003; Udupa et al., 2002b; Udupa and Samarasekera, 1996). In this multi-object segmentation method each object is defined as the set of voxels that are connected in a stronger way to one of the seeds of that object than to any of the seeds of the other objects. The most computationally expensive task in determining the object boundaries based on the seeds is the calculation of the multiple fuzzy connectedness of all the voxels to the seed voxels by means of finding the strongest chain between a voxel and one or more seed voxels. For this task a greedy algorithm is used to efficiently create a segmentation of the reconstruction.

The general theory of the algorithm allows for dealing with an arbitrary number of objects, but for the sake of simplicity we discuss the case when the density functions are segmented into two objects: the biological specimen and its background. With both the foreground and the background we associate a set of seeds, denoted by S₁ and S₂, respectively. Both S₁ and S₂ are subsets of a reconstruction and their union is nonempty. In the tests performed here, the seeds are selected manually by the user using a graphical interface that allows the user to create, or modify, a set of seeds for every object of interest. What we wish to produce is two connectedness functions σ₁ (for the foreground) and σ₂ (for the background) such that, for every point c̄ in a reconstruction (a) σ₁ (c̄), σ₂ (c̄) ∈ [0,1] (i.e., both σ₁ and σ₂ define fuzzy sets (Pal and Majumder, 1997; Zimmermann, 1996)), (b) every point in the reconstruction is either in the foreground, in the background, or both, and (c) the only way a point c̄ in the reconstruction can be in both the foreground and the background is if σ₁ (c̄) = σ₂ (c̄). Such a pair (σ₁,σ₂) corresponds to what has been defined as a 2-segmentation in (Herman and Carvalho, 2001) and we refer to as a fuzzy segmentation. It is important to notice that since all the voxels in a reconstruction belong to either fuzzy object in the segmentation, then σ_i > 0.

Furthermore, every link {c̄,d̄} in the foreground has a strength ψ₁ (c̄,d̄) and every link {c̄,d̄} in the background has strength ψ₂ (c̄,d̄) such that ψ₁ (c̄,d̄), ψ₂ (c̄,d̄) ∈ [0,1]. Such a pair (ψ₁, ψ₂) corresponds to what has been defined as a 2-fuzzy graph in (Herman and Carvalho, 2001).

It can be assumed that for any set of seeds (S₁,S₂, …,S_M) and link strengths (ψ₁,ψ₂, …ψ_M) there is one and only one fuzzy segmentation consistent with them (Herman and Carvalho, 2001). In this work we use a greedy, and hence efficient, algorithm that receives as input seeds (S₁,S₂, …,S_M) and link strengths (ψ₁,ψ₂, …,ψ_M) and produces as output the unique fuzzy segmentation (σ₁,σ₂, …,σ_M) consistent with them. For a detailed discussion of the algorithm and its performance, we refer to (Carvalho et al., 2002) and (Herman and Carvalho, 2001). Other algorithms have a “robustness” property, which guarantees that seeds selected at different times by an operator produce the same result (Udupa et al., 2002b) but have some drawbacks that the algorithm used in this work does not; for a discussion of the behavior of both algorithms see (Carvalho et al., 2005).

2.3 Comparison of Segmentation Methods

There have been recent attempts to evaluate the results of different segmentation algorithms by (Chalana and Kim, 1997; Udupa et al., 2002a; Warfield et al., 2004) by producing “ground truth” from manual delineations produced by expert operators. The ground truth can then be used to compare the outputs of computer-based segmentation algorithms. Clearly, it is necessary to take into account the discrepancies between users and between the decisions made by a single user over time. Such a behavioral approach assumes that the density function υ is an approximation to a well-known biological structure; we utilized data from selectively stained, plastic embedded spiny dendrites (Andersen, 1999; Sosinsky and Martone, 2003). For testing, we obtained ten reconstructions, in the range of 1 × 10⁸ voxels, each of which was manually segmented by one expert user. In addition, we used a smaller reconstruction with three delineations done by two independent experts. The ten reconstructions served as ground truth for the segmentations produced by the algorithm in Section 2.2 and the three manual delineations served to measure the precision among expert operators and the possible variance of the ground truth produced from their delineations. We used the affinity functions introduced in equations in (2) and (3) for all tests.

The fuzzy algorithm has only a few parameters that will determine the outcome of its results. One such parameter is the adjacency of voxels in every class. As we mentioned in Section 2.2, in the case of the simple cubic grid, it has been shown that objects should have face adjacency and the background should have face-edge adjacency (Herman, 1998); however, when the fuzzy segmentation algorithm is executed, having two different adjacencies for distinct objects may be difficult for operators (when there are many classes in an object may be difficult to decide what classes represent the background and which the foreground). Hence, we carried out experiments with two adjacencies (face and face-edge for the foreground and background, respectively) and with a single adjacency (face adjacency). Consequently, the number of links used for calculating the mean and standard deviation for the affinity function ψ will be 66|S₁| and 6|S₂| for the face-edge and face adjacencies, respectively (we represent both the cardinality of a set and the magnitude of a vector by | • |).

Since the results from the fuzzy segmentation algorithm produce reconstructions with voxels in a range of values (0,1] it is possible to obtain several results by thresholding the fuzzy segmentation. This property of the fuzzy segmentations allows for adjusting the result to approximate better the object of interest. However, we do not threshold the results produced by the fuzzy segmentation; after processing we consider all the values in the resulting segmentations as equal to one for only those voxels inside the foreground objects and zero for the rest.

The process of object recognition, carried out by the operators during seed selection, is an important factor that determines the outcome of the segmentation algorithm. Consequently, two operators were trained on how to use the graphical software that allows to place and modify seed points on the reconstructions.

For the evaluation of the precision of the fuzzy segmentation algorithm we measured the proportion of discordance between segmentations using the following measure (Jaccard, 1901)

$$\mathrm{precision}=\frac{\left|O_i\cap O_j\right|}{\left|O_i\cup O_j\right|},$$ (4)

where O_i and O_j, for i ≠ j, represent two different segmentations. This operation provides a simple way to measure the level of agreement between operators, for both manual delineations and fuzzy segmentations.

To compare the accuracy of the fuzzy segmentation algorithm, we followed two approaches. The first, suggested by Udupa et al. (Udupa et al., 2002a), measures the sensitivity (true positive findings) and specificity (true negative findings) of the segmentations as compared to the ground truth, see Fig. 1. Similarly to (Udupa et al., 2002a), we define the sensitivity as follows

Fig. 1.

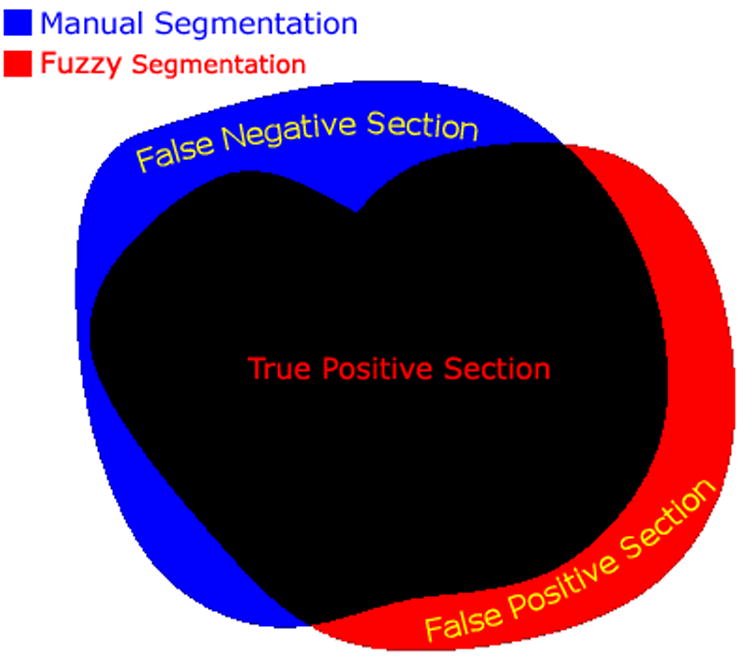
The accuracy of a segmentation algorithm can be described by the percentage of voxels correctly classified as inside of the object (TPF or sensitivity), the fraction of voxels falsely classified as outside the object (FNF), and the fraction of voxels falsely classified as inside the object (FPF or 1-specificity).

$${\mathrm{TPF}}_{i,j}=\frac{|O_{i,j}\cap O_i^g|}{\left|O_i^g\right|},$$ (5)

which, for the reconstruction i, TPF represents the overlap of the fuzzy segmentation created by the observer j to that of the gold standard. Similarly, we measure the fraction of voxels falsely identified as belonging to the object by

$${\mathrm{FPF}}_{i,j}=\frac{\left|\left(O_{i,j}\cup O_i^g\right)-O_i^g\right|}{\left|O_i^g\right|},$$ (6)

where the difference between segmentation results is voxelwise. The specificity of the fuzzy segmentation is measured by the overlap of true negative findings. However, it is typically more interesting to find the fraction of voxels falsely identified as not belonging to the object. Such a measure is computed by

$${\mathrm{FNF}}_{i,j}=\frac{\left|\left(O_{i,j}\cup O_i^g\right)-O_{i,j}\right|}{\left|O_i^g\right|}.$$ (7)

It is important to notice that the aforementioned measures are complementary in such a way that it is possible to find the sensitivity by calculating 1 − FNF and the specificity by computing 1 − FPF.

In (Warfield et al., 2004) Warfield et al. propose a method that computes a Maximum-Likelihood estimate of the underlying “true segmentation” based on a collection of segmentations. The algorithm produces a measure of quality for each segmentation as sensitivity and specificity. The data are incomplete since there is no knowledge of the ground truth, but there is an observable function of the complete data (i.e., the operators' segmentations). We can represent the complete data as (D, T), where D is a N × R matrix representing R segmentations (every column of the matrix D represents a segmentation of N voxels), and T is a N × 1 matrix representing the unknown ground truth. We can further define the probability mass function of the complete data as ρ (D, T|p̄,q̄), where p̄ and q̄ are R-dimensional vectors representing the sensitivity and specificity, respectively. The goal is to find the sensitivity and specificity of every operator that maximize the probability mass function:

$$\left(\overline{p}\prime ,\overline{q}\prime \right)=arg\underset{\overline{p},\overline{q}}{max}\rho \left(D,T|\overline{p},\overline{q}\right).$$ (8)

The above Maximum-Likelihood problem is solved by the Expectation-Maximization method (Dempster et al., 1977; Moon, 1996). As a final result, the method in (Warfield et al., 2004) produces an estimate of the ground truth, contained in the matrix T, and estimates for the sensitivity, in p̄, and the specificity, in q̄, for all the operators. It is important to note that this method requires a prior probability function that describes the likelihood of a voxel be classified as part of the object. It is clear that this probability function affects the result of the method. Here we use the manual segmentations to provide an estimate of the prior probability function by computing the fraction of voxels making up the object in every reconstruction.

3 Results and Discussion

The time required by the operators to manually segment each of the 10 reconstructions varied between 16 to 20 hours. In the case of the fuzzy segmentation software, the operators first created files containing seed points with two classes only; representing the foreground and the background. However, after a first execution of the software, in most of the cases the visual inspection of the results indicated that the outcome was not good enough and the files of seed voxels were modified to either change the seed points or to add new classes to account for artifacts that a two-class approach could not handle, see Fig. 2. In general, this process resulted in up to three executions of the fuzzy segmentation software. The original selection of seed voxels took the operators an average of 20 minutes, posterior modifications took around 10 minutes. An execution of the fuzzy segmentation software took up to 20 minutes (on a single-AMD Opteron™ Processor 250 machine at 2.4 GHz with 11.6 Gb and running under Linux) for the largest reconstruction (320 × 864 × 236 voxels) with 3 classes. Nonetheless, in our experiments the operators never executed the software more than three times. In general, operators were satisfied, judged by visual inspection, with the results produced by the software. Due to the large size of the reconstructions we only present results for reconstruction number 9 in figure Fig. 3.

Fig. 2.

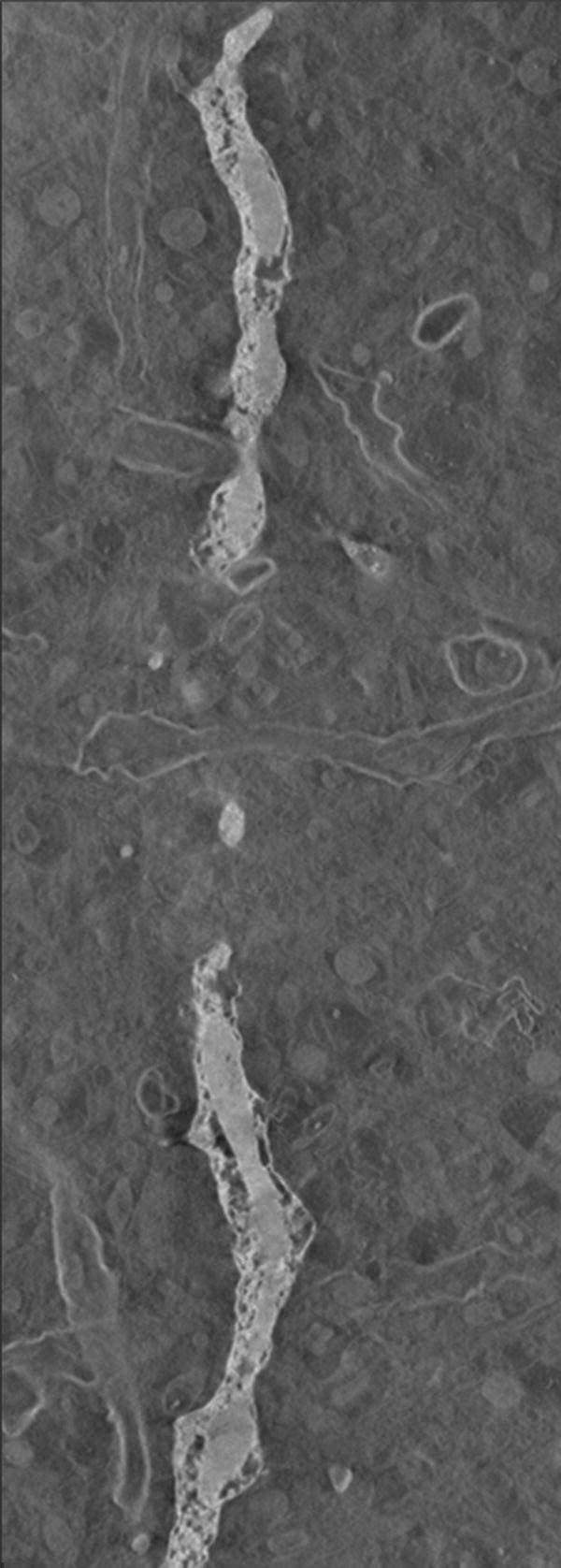
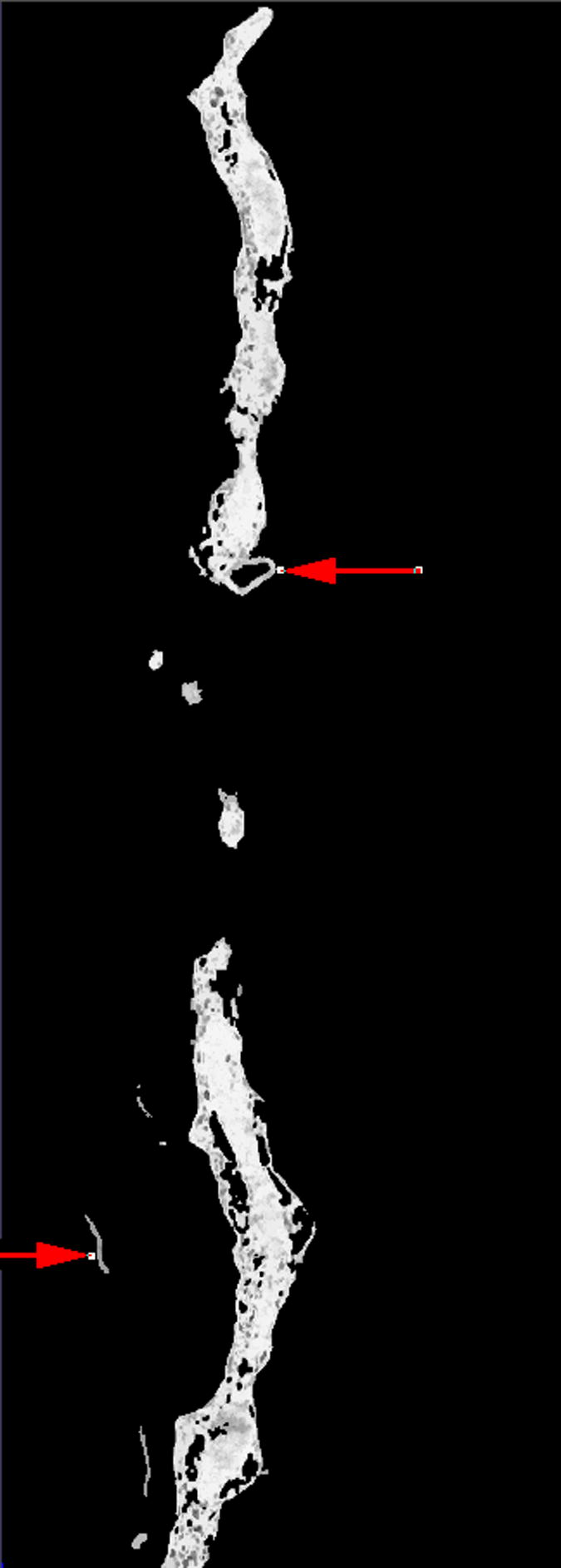
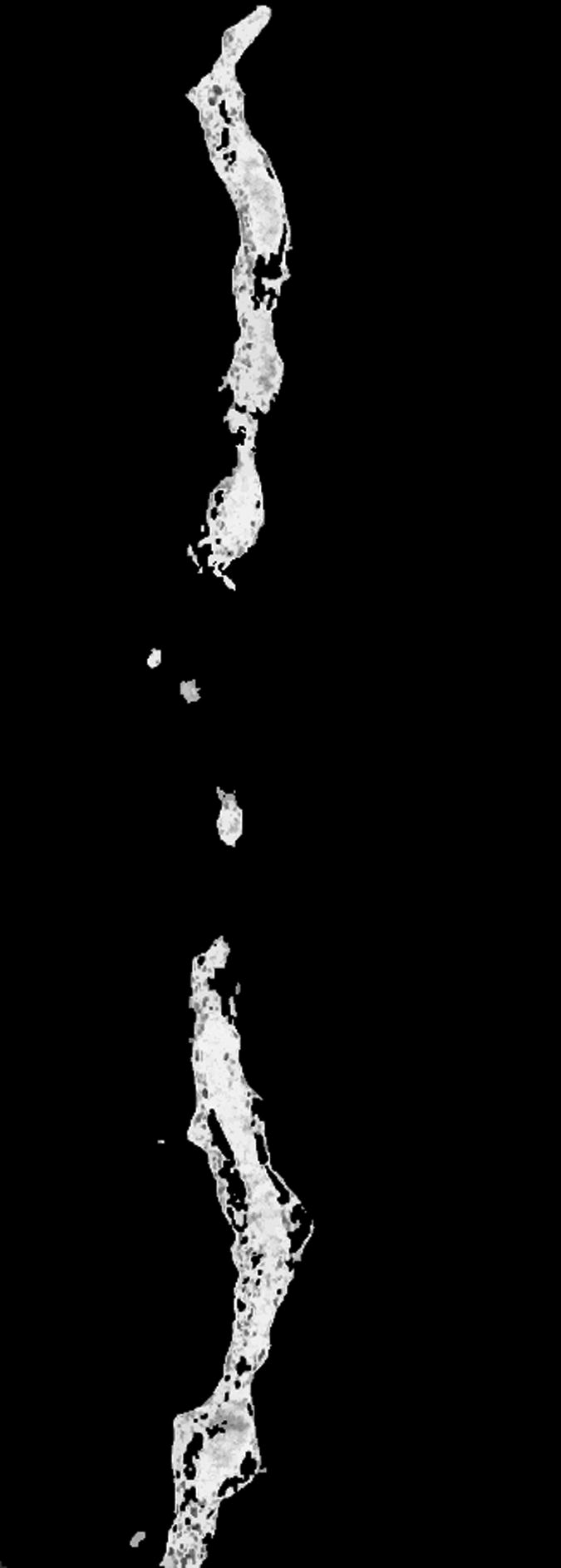
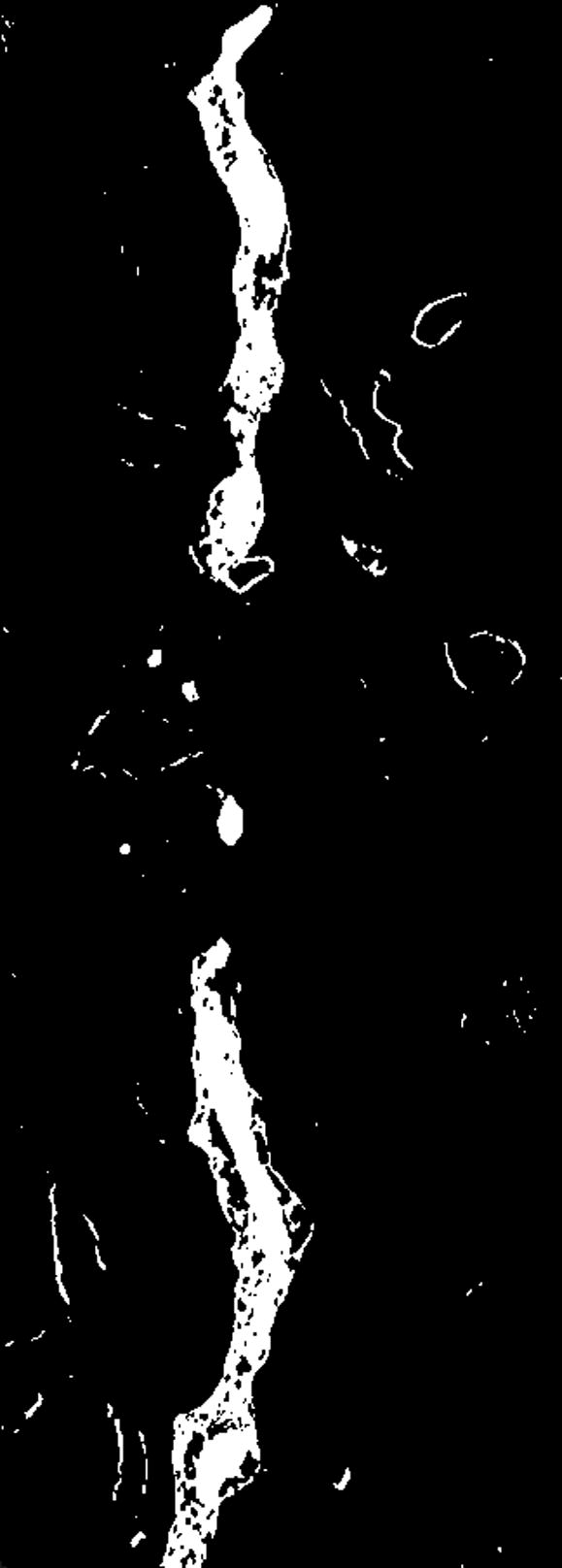
For our experiments we used reconstructions from selectively stained, plastic embedded spiny dendrites (Andersen, 1999; Sosinsky and Martone, 2003) (a well-known biological structure). The operators initially created two sets of seed points corresponding to the foreground and background, respectively. However, after inspecting the results it became obvious that either new object classes or new seed points were necessary. Image (a) shows a plane of the reconstruction number 2 where artifacts are visible. Image (b) presents the result, at the same plane as (a), of using two classes where some of the artifacts were classified as objects (pointed by red arrows). Image (c) presents the final result, at the same plane as (a), in which three classes were used (two foreground classes and background) and no artifacts were included. Image (d) shows a thresholded version of the reconstruction in (a) at an appropriate threshold. Finally, (e) shows the manual delineation for such a plane.

Fig. 3.

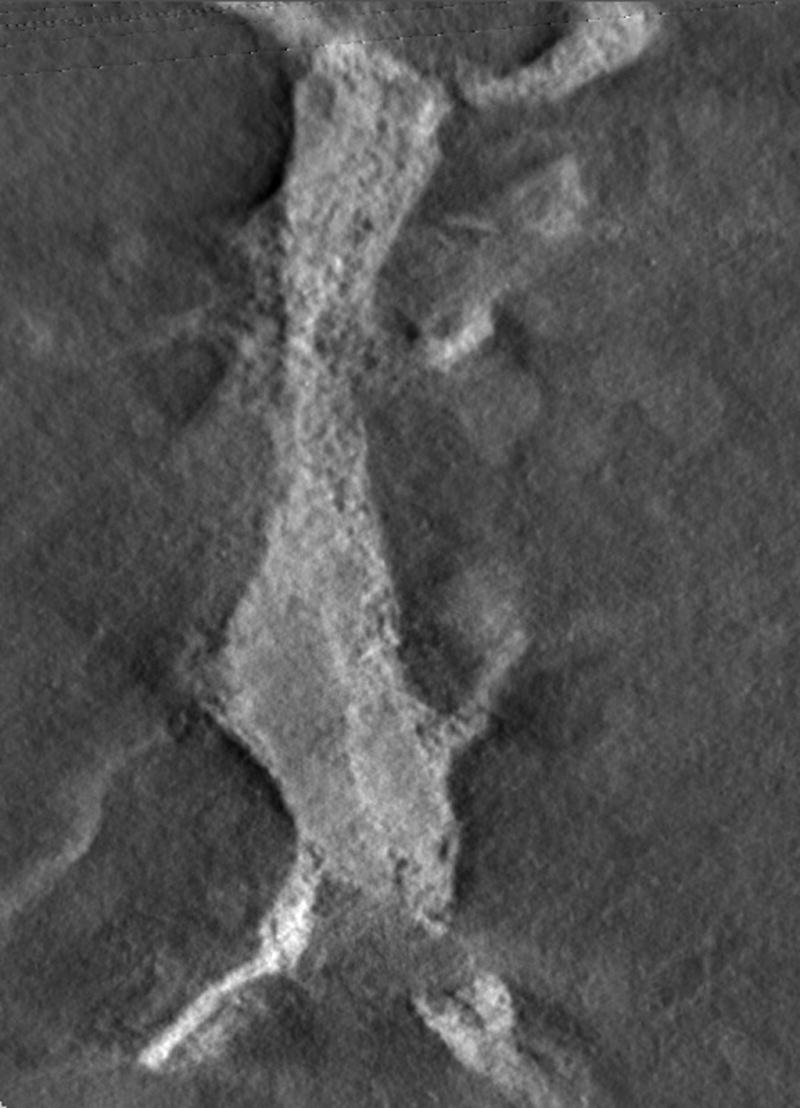
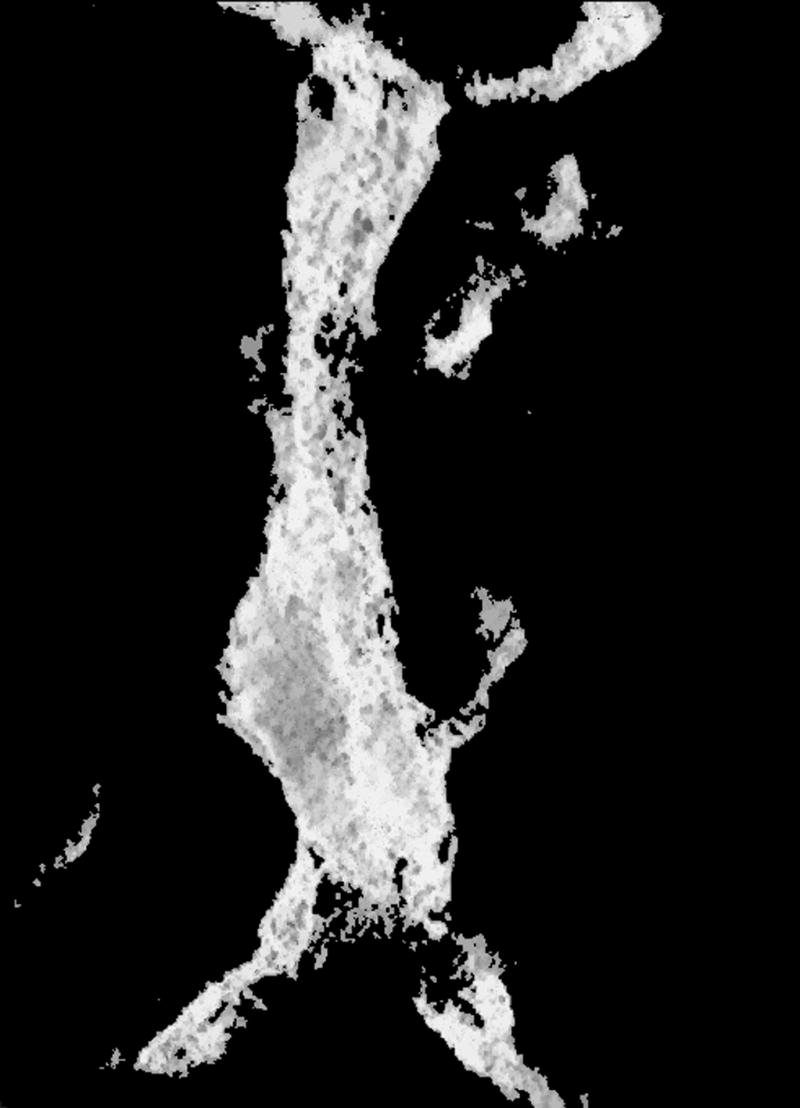
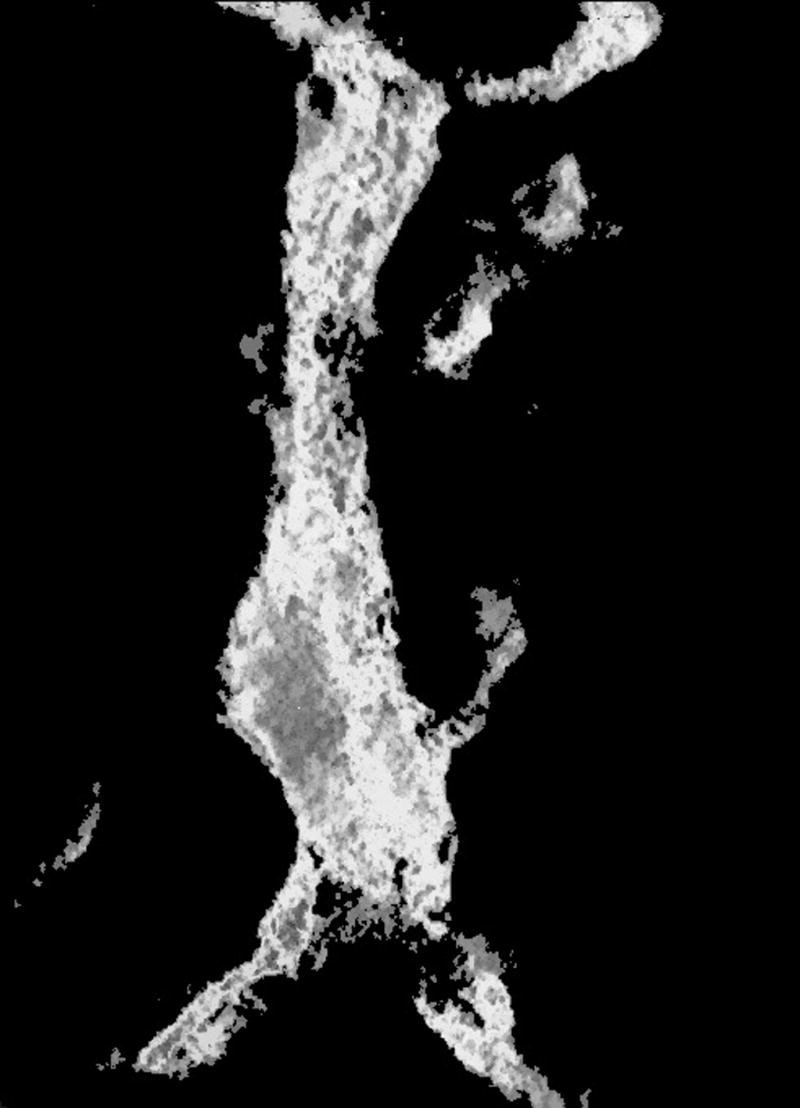
Visualization of the same plane for (a) the original reconstruction number 9, (b) the result obtained by thresholding the reconstruction, (c) the result obtained by the first operator, and (d) the result obtained by the second operator.

3.1 Quantitative Results

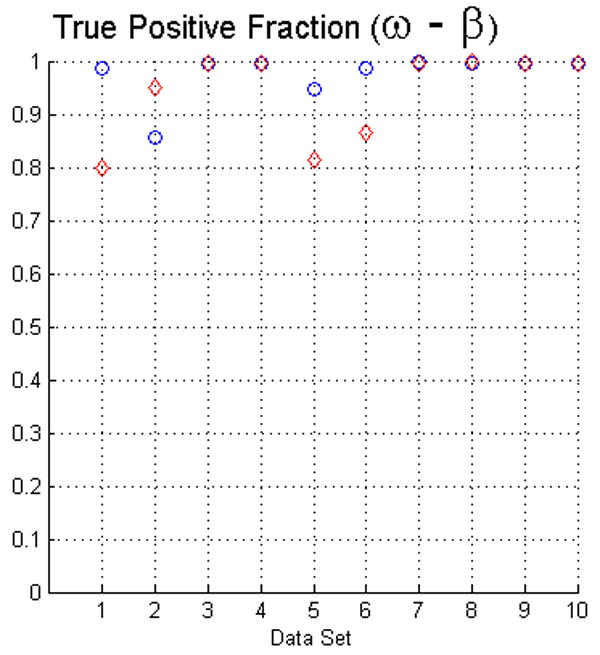
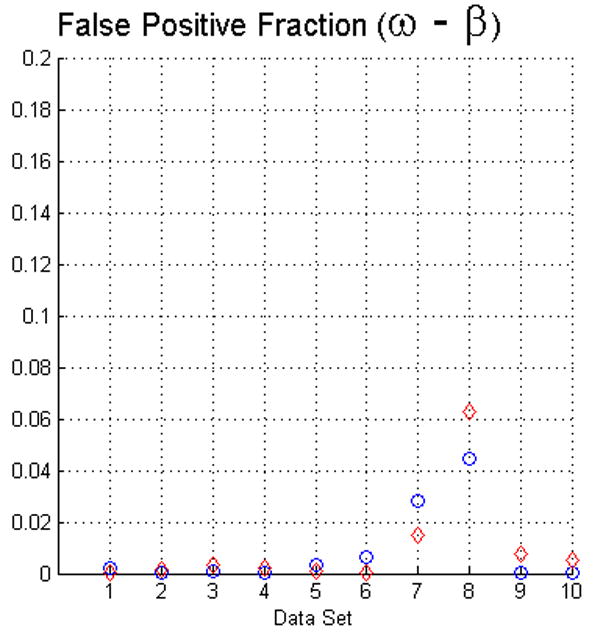
The fact that operators used visual inspection to validate the results yielded by the fuzzy segmentation software is not sufficient as a measure of quality. Thus, as we described in Section 2 we used two evaluation methods. For measuring the true positive and false positive fractions we first used equations (5) and (6). The results of such evaluation with face-edge (β) and face (ω) adjacencies for the background are presented in the upper and lower rows of Fig. 4, respectively.

Fig. 4.

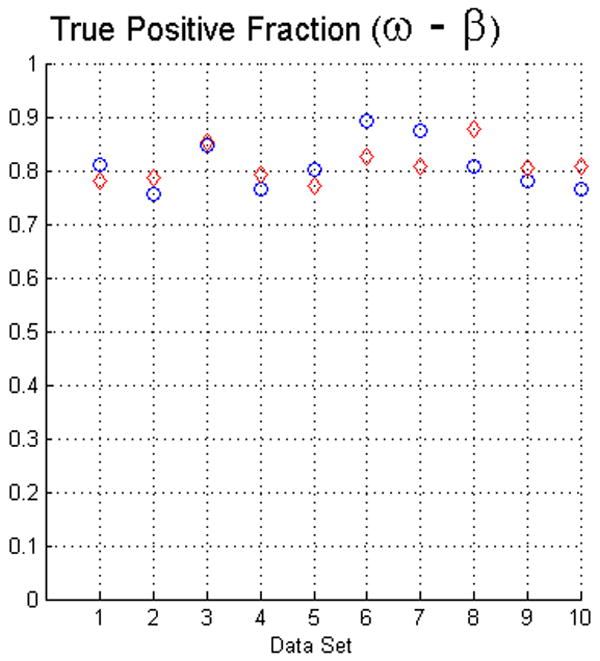
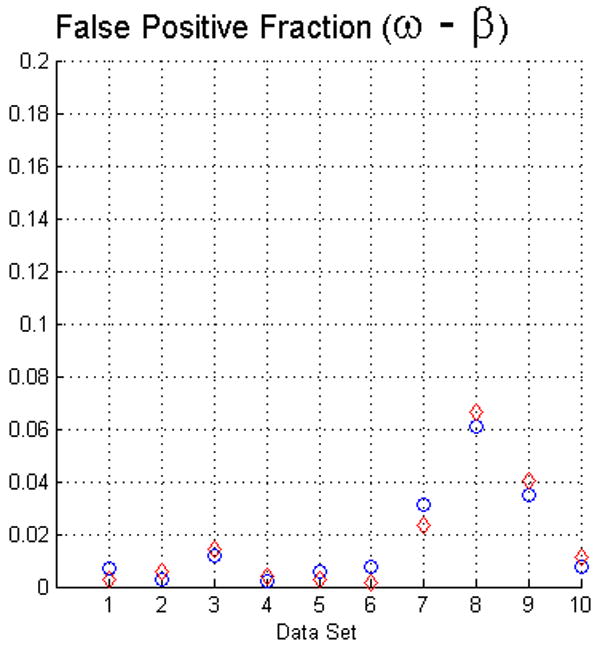
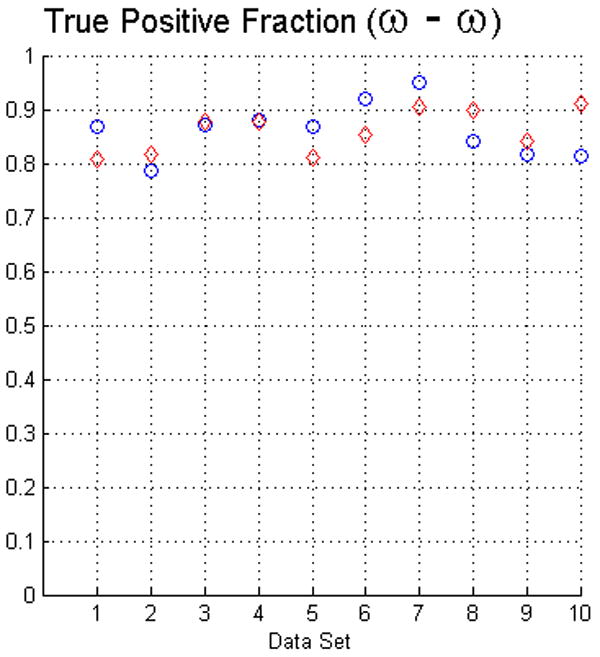
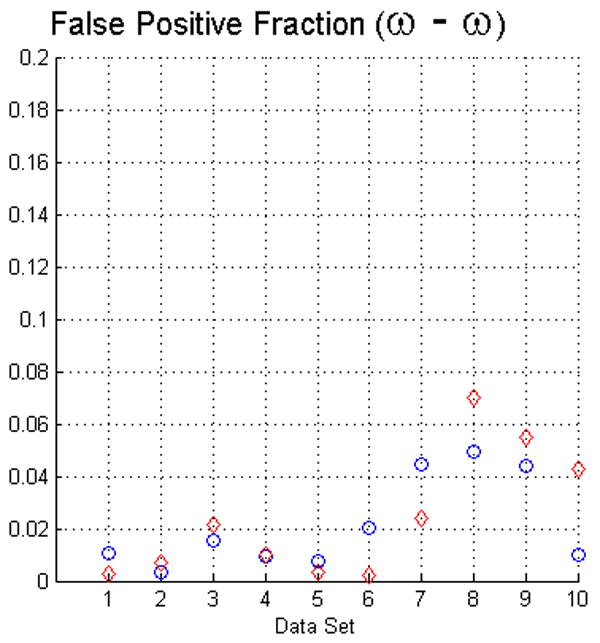
The plots in this figure represent the true-positive and false-positive fractions, produced by equations (5) and (6). The upper row represents the results for face (ω) and face-edge (β) adjacencies for foreground and background classes, respectively. The bottom row represents the results for foreground and background classes using face (ω) adjacency. The diamonds and circles represent the results for the first and second operators, respectively.

The analysis of the ten reconstructions suggests that the software is capable to produce high specificity, except for reconstruction number 8 where we found difficult to reduce the selection of part of the background. In general, the software does not abundantly overestimate the extent of the objects of interest. This measure also agrees with the visual inspection carried out by the operators for their final results, for example see Fig. 3.

On the other hand, we observed that in many circumstances the quantitative results suggested that the software “underestimated” the objects of interest, as compared to the manual delineations. This is in part due to the fact that the automatic segmentation is more “accurate” in the sense that it preserves gaps and holes in the reconstruction. Human operators tend to ignore these features and generate, on the whole, a more compact segmentation (see Fig. 2). Whether the holes should be considered part of the object or not is an open question. Despite these differences, the software had a sensitivity of at least 80%. Finally, our evaluation suggests that the use of the same adjacency for all the classes produces better results (in particular, it increased the sensitivity to above the 80% in almost all the cases).

For measuring the true positive and false positive fractions of voxels in the objects we also used the STAPLE method (Warfield et al., 2004). The results of such evaluation, using the same criteria of Fig. 4, are presented in Fig. 5. Interestingly, this approach confirms that the fuzzy segmentation algorithm has high specificity since the results for the false positive fraction are very similar in both evaluation methods. In contrast, the sensitivity is higher following this evaluation. Such a result is encouraging but it has to be taken carefully. Since this method requires of initialization parameters in order to compute the Expectation-Maximization, the maxima shown may not correspond to the global maxima. We computed the prior probability from the manual delineations, and we initialized the specificity and sensitivity vectors to 0.9 as recommended in (Warfield et al., 2004).

Fig. 5.

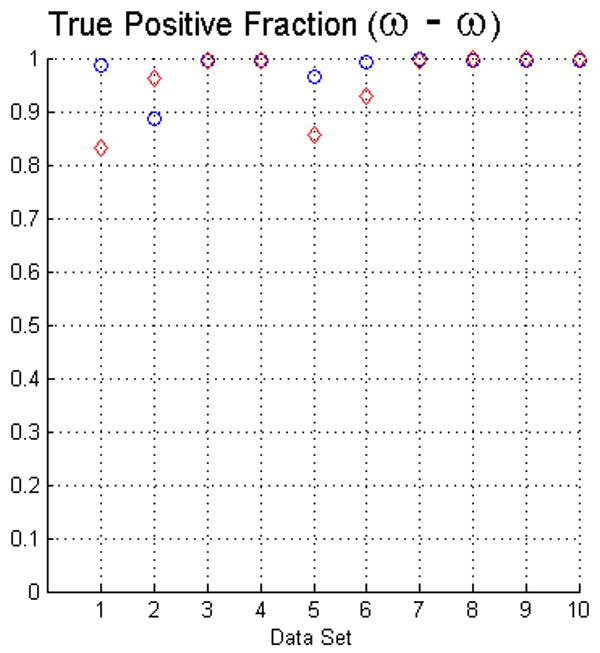
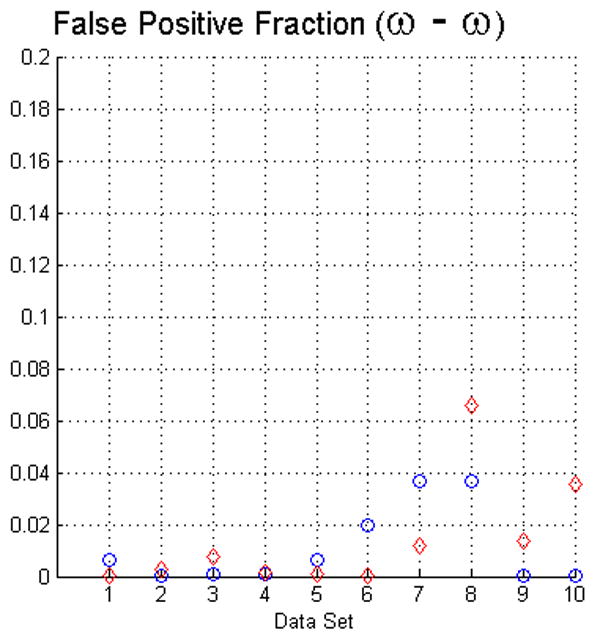
The plots in this figure represent the true positive and false positive fractions, produced by the STAPLE method (Warfield et al., 2004). The upper row represents the results for face (ω) and face-edge (β) adjacencies for foreground and background classes, respectively. The bottom row represents the results of using face (ω) adjacency for both foreground and background objects.

3.1.1 Precision

As suggested by Udupa et al. (Udupa et al., 2002a), the evaluation of a segmentation algorithm is not complete without accounting for the accuracy of the method. Hence, we measure the precision among operators by using the results for three manual delineations that were obtained from the smaller data set. The precision between manual delineations was 84.92% in average and it was as low as 83.99%. Interestingly, the three operators had large disagreements among them in the same region of the reconstruction. Three operators segmented the same object and we created an average of such delineations (Fig. 6). This averaged data set has a fuzzy property since a value of 1 implies total agreement by all the operators and a different value represents the level of disagreement between operators. The overall precision between manual delineations was 84.92% in average and was as low as 83.99%.

Fig. 6.

Manual delineation suffers from user bias and non-reproducibility, this is demonstrated in these images. Three operators segmented the same object and we created an average of such delineations. The darker the gray level value, the more disagreement between operators. We can see that in this case, expert operators greatly disagreed in what should be included in an object.

Since the fuzzy segmentation requires of user intervention, we believe that variation in the way humans take decisions is the most important factor for producing similar results. Furthermore, the way the software calculates the statistics necessary for computing the connectivity and affinity between voxels is based on the number and position of seed points selected by the operators. In order to measure precision in our tests for fuzzy segmentation, we followed two approaches.

The first approach is intended to see how sensitive the algorithm is to variation of seed points by measuring the precision for segmentations created by the operators' selected seed points and segmentations created by randomly modified seed points. The experiments consisted in taking the original seed points for each dataset and randomly modifying them. Clearly, it is necessary to verify that a seed in the foreground does not leave the boundaries of the object; the same is valid for the seed points in the background. Therefore, for each dataset, we used its gold standard dataset to restrict the space in which a seed could be modified. For every seed point we search for the closest boundary. Such a search produces a distance that determines a sphere in which the seed point can be modified. Later, every seed point is randomly modified within its respective sphere. For each dataset, we created ten sets of modified seed points and calculated the precision of the respective segmentation results to the segmentation produced by the original seed points using Eq. (4), see Fig. 7.

Fig. 7.

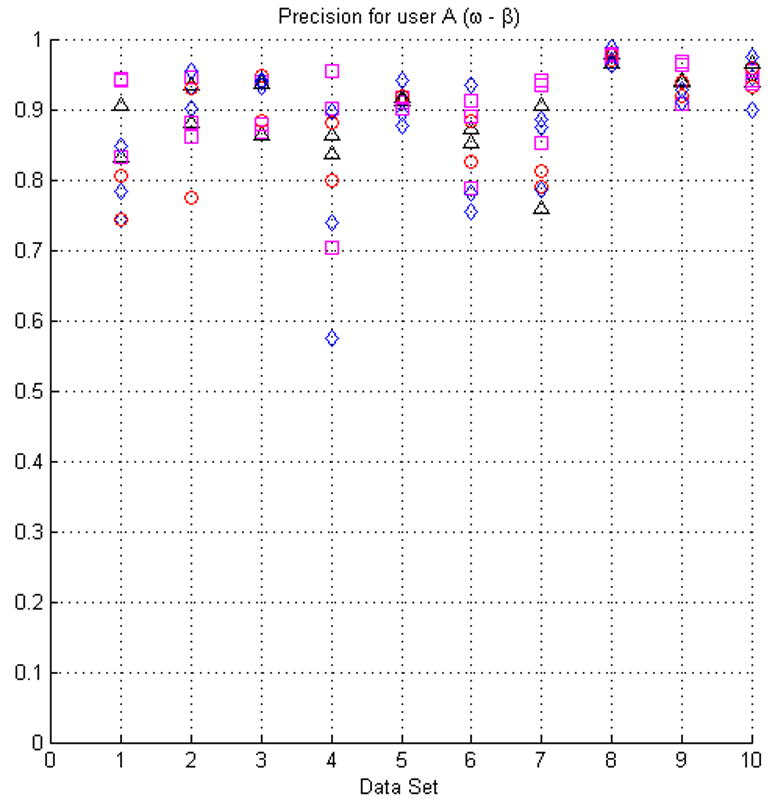
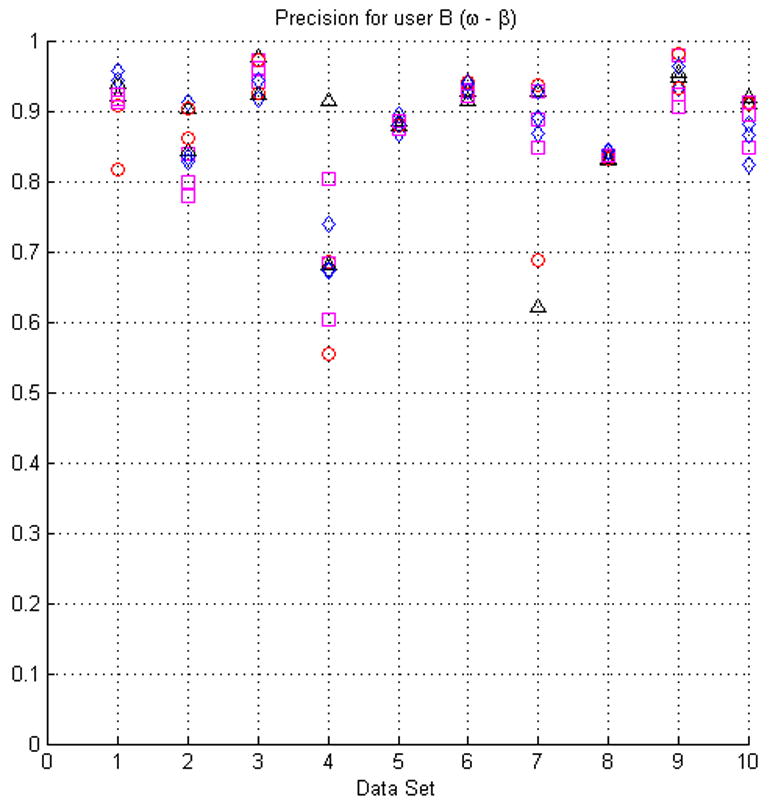
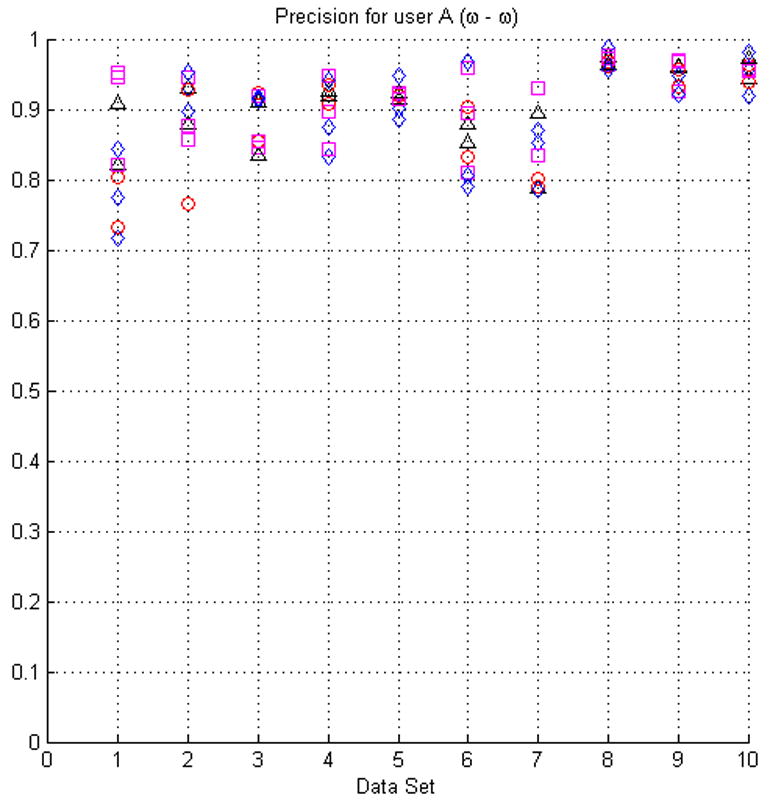
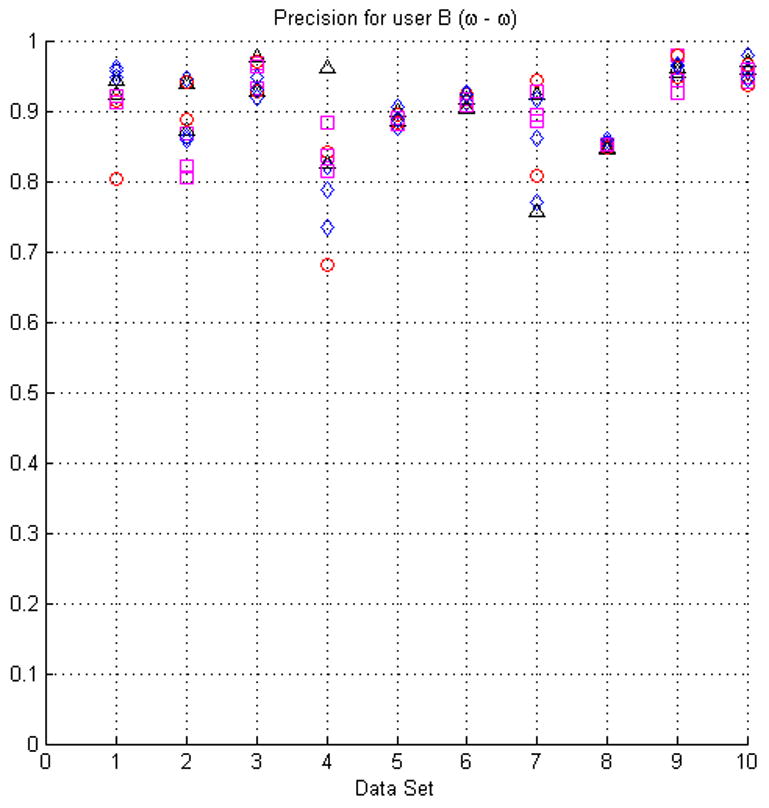
The plots in this figure represent the precision, produced by equation (4), for all the original seed points with respect to randomly modified seed points (see the text for details of how the seed points were modified). The upper row represents the results for face (ω) and face-edge (β) adjacencies for foreground and background classes, respectively. The bottom row represents the results for foreground and background classes using face (ω) adjacency.

In most cases the modification of the seed points did not produce low precision values. However, in some instances (e.g., dataset 4) the precision appears to be relatively low for some sets of seeds. This situation is the result of the datasets having poor SNR and consequently being difficult to segment, see Fig. 3(a). It should also be kept in mind that the average precision for manual segmentation is ∼84%.

The second approach to calculate the precision was to measure how similar the results among operators were, the so-called interoperator precision. For each dataset, we calculated the segmentations produced by the operators using Eq. (4), see Fig. 8. In general, the lower values were the result of one of the operators, not always the same, selecting seeds that produced a larger false positive fraction. In many cases, the portion of false positives has a lower connectivity and it can be reduced by thresholding the result of the fuzzy segmentation. As mentioned before, we evaluated all the results without processing the data any further. Generally, the precision of the software is in the range of the precision determined for manual segmentation.

Fig. 8.

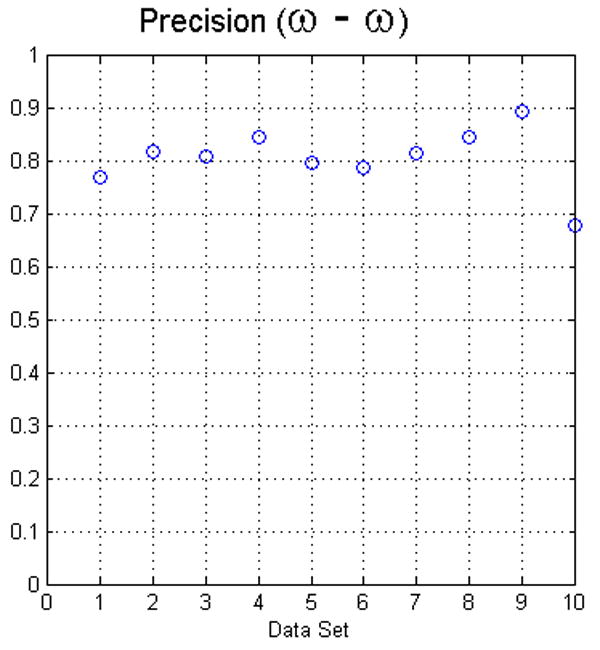
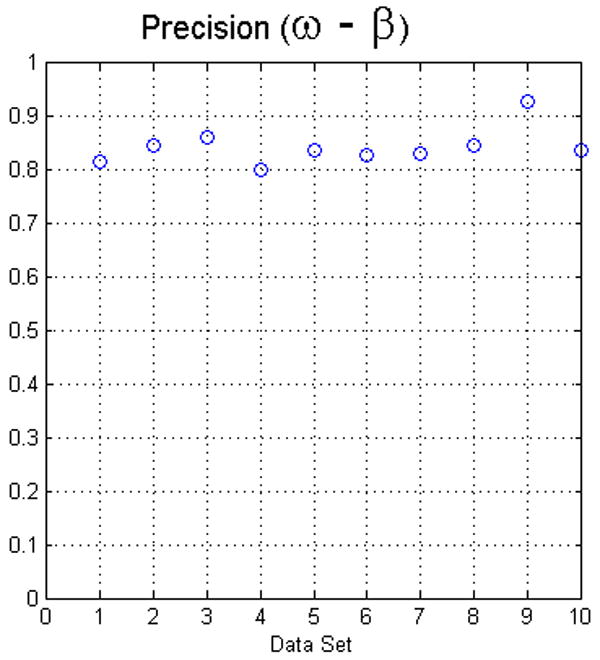
The plots in this figure represent the precision, produced by equation (4), for all data sets. The left image represents the results for foreground and background classes using face (ω) adjacency. The right image represents the results for face (ω) and face-edge (β) adjacencies for foreground and background classes, respectively.

4 Conclusions

Manual segmentations of data sets is a rather time consuming task as well as prone to variations and subjectivity. There has been an immense effort by the computer science and engineering communities to produce semi-automatic and automatic segmentation algorithms. Unfortunately, most of these algorithms were never rigorously tested because they require a well established protocol and because it is difficult to carry out a large number of experiments to evaluate the algorithms. So far, none of the segmentation algorithms appear to be capable of producing satisfying results under a large set of conditions. Hence, algorithms should be evaluated within the limits of a given task or protocol. For example we followed the protocol suggested by (Udupa et al., 2002a) since it takes into account a group of measures that evaluate an algorithm in the context of a given specimen.

The degree of success of image processing applications usually depends strongly on the specimen characteristics. This is particularly true for segmentation tools; however, the results produced by the fuzzy segmentation algorithm within the framework presented are encouraging. Furthermore, the fact that the results of the fuzzy segmentation are very encouraging for the specimen used in this study indicates that the method is likely to be useful for other types of electron tomograms as well. We believe the algorithm can already reduce the burden that manual delineation places on operators in certain situations. Since segmentation algorithms are not perfect for all tasks, it is important to develop a set of tools that complement each other.

The encouraging results of the segmentation algorithm allows us to contemplate further research and tackle other issues such as creating a better way to select the seeds, a better way to compute the statistics for the affinity function that could include some learning process and testing other affinity functions.