Attenuated T₂ relaxation by mutual cancellation of dipole–dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution

Abstract

Fast transverse relaxation of ¹H, ¹⁵N, and ¹³C by dipole-dipole coupling (DD) and chemical shift anisotropy (CSA) modulated by rotational molecular motions has a dominant impact on the size limit for biomacromolecular structures that can be studied by NMR spectroscopy in solution. Transverse relaxation-optimized spectroscopy (TROSY) is an approach for suppression of transverse relaxation in multidimensional NMR experiments, which is based on constructive use of interference between DD coupling and CSA. For example, a TROSY-type two-dimensional ¹H,¹⁵N-correlation experiment with a uniformly ¹⁵N-labeled protein in a DNA complex of molecular mass 17 kDa at a ¹H frequency of 750 MHz showed that ¹⁵N relaxation during ¹⁵N chemical shift evolution and ¹H^N relaxation during signal acquisition both are significantly reduced by mutual compensation of the DD and CSA interactions. The reduction of the linewidths when compared with a conventional two-dimensional ¹H,¹⁵N-correlation experiment was 60% and 40%, respectively, and the residual linewidths were 5 Hz for ¹⁵N and 15 Hz for ¹H^N at 4°C. Because the ratio of the DD and CSA relaxation rates is nearly independent of the molecular size, a similar percentagewise reduction of the overall transverse relaxation rates is expected for larger proteins. For a ¹⁵N-labeled protein of 150 kDa at 750 MHz and 20°C one predicts residual linewidths of 10 Hz for ¹⁵N and 45 Hz for ¹H^N, and for the corresponding uniformly ¹⁵N,²H-labeled protein the residual linewidths are predicted to be smaller than 5 Hz and 15 Hz, respectively. The TROSY principle should benefit a variety of multidimensional solution NMR experiments, especially with future use of yet somewhat higher polarizing magnetic fields than are presently available, and thus largely eliminate one of the key factors that limit work with larger molecules.

NMR spectroscopy with proteins based on observation of a small number of spins with outstanding spectral properties, which either may be present naturally or introduced by techniques such as site-specific isotope labeling, yielded biologically relevant information on human hemoglobin (M = 65,000) as early as 1969 (1), and subsequently also for significantly larger systems such as Igs (2). In contrast, the use of NMR for de novo structure determination (3, 4) so far has been limited to relatively small molecular sizes, with the largest NMR structure below molecular weight 30,000. Although NMR in structural biology may, for practical reasons of coordinated use with x-ray crystallography (5), focus on smaller molecular sizes also in the future, considerable effort goes into attempts to extend the size limit to bigger molecules (for example, see refs. 6–8). Here we introduce transverse relaxation-optimized spectroscopy (TROSY) and present experimental data and theoretical considerations showing that this approach is capable of significantly reducing transverse relaxation rates and thus overcomes a key obstacle opposing solution NMR of larger molecules (7).

At the high magnetic fields typically used for studies of proteins and nucleic acids, chemical shift anisotropy interaction (CSA) of ¹H, ¹⁵N, and ¹³C nuclei forms a significant source of relaxation in proteins and nucleic acids, in addition to dipole–dipole (DD) relaxation. This leads to increase of the overall transverse relaxation rates with increasing polarizing magnetic field, B₀. Nonetheless, transverse relaxation of amide protons in larger proteins at high fields has been reduced successfully by complete or partial replacement of the nonlabile hydrogen atoms with deuterons and, for example, more than 90% of the ¹⁵N, ¹³C^α, and ¹H^N chemical shifts thus were assigned in the polypeptide chains of a protein-DNA complex of size 64,000 (6). TROSY uses spectroscopic means to further reduce T₂ relaxation based on the fact that cross-correlated relaxation caused by DD and CSA interference gives rise to different relaxation rates of the individual multiplet components in a system of two coupled spins ½, I and S, such as the ¹⁵N–¹H fragment of a peptide bond (9, 10). Theory shows that at ¹H frequencies near 1 GHz nearly complete cancellation of all transverse relaxation effects within a ¹⁵N–¹H moiety can be achieved for one of the four multiplet components. TROSY observes exclusively this narrow component, for which the residual linewidth is then almost entirely because of DD interactions with remote hydrogen atoms in the protein. These can be efficiently suppressed by ²H-labeling, so that in TROSY-type experiments the accessible molecular size for solution NMR studies no longer is primarily limited by T₂ relaxation.

Theory

We consider a system of two scalar coupled spins ½, I and S, with a scalar coupling constant J_IS, which is located in a protein molecule. T₂ relaxation of this spin system is dominated by the DD coupling of I and S and by CSA of each individual spin, because the stereochemistry of the polypeptide chain restricts additional interactions of I and S to weak scalar and DD couplings with a small number of remote protons, I_k. The relaxation rates of the individual multiplet components of spin S in a single quantum spectrum then may be widely different (9, 11, 12). They can be described by using the single-transition basis operators S₃₄^± and S₁₂^± (13), which refer to the transitions 1→2 and 3→4 in the standard energy-level diagram for a system of two spins ½, and are associated with the corresponding resonance frequencies, ω_S¹² = ω_S + πJ_IS and ω_S³⁴ = ω_S − πJ_IS (13–16):

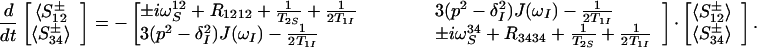1

ω_S and ω_I are the Larmor frequencies of the spins S and I, T_2S and T_1I account for the transverse relaxation of spin S and the longitudinal relaxation time of spin I, respectively, by all mechanisms of relaxation except DD coupling between the spins S and I and CSA of the spins S and I.

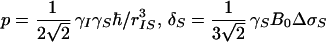and

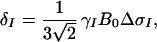where γ_I and γ_S are the gyromagnetic ratios of I and S, ℏ is the Planck constant divided by 2π, r_IS the distance between S and I, B₀ the polarizing magnetic field, and Δσ_S and Δσ_I are the differences between the axial and the perpendicular principal components of the axially symmetric chemical shift tensors of spins S and I, respectively. R₁₂₁₂ and R₃₄₃₄ are the transverse relaxation rates of the individual components of the S doublet (11) given by Eqs. 2 and 3,

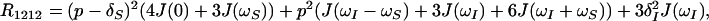2

3

where J(ω) represents the spectral density functions at the frequencies indicated:

4

In deriving Eqs. 2 and 3, parallel orientation of the principal symmetry axis of the chemical shift tensor and the vector r_IS was assumed. These equations show that whenever CSA and DD coupling are comparable, i.e. p ≈ δ_S, the resonance at frequency ω_S¹² may exhibit slow transverse relaxation even for very large molecules.

For a treatment of the relaxation of spin I by Eq. 1 the symbols I and S simply can be interchanged. The single-transition operators I₁₃^± and I₂₄^± then refer to the transitions between the energy levels 1→3 and 2→4, respectively, which are associated with the frequencies ω_I¹³ = ω_I + πJ_IS and ω_I²⁴ = ω_I − πJ_IS, and the relaxation rates R₁₃₁₃ and R₂₄₂₄ are determined by equations obtained by permutation of the S and I indices in Eqs. 2 and 3, respectively.

To evaluate the contributions from other mechanisms of relaxation we identify I and S as the ¹H^N and ¹⁵N spins in a ¹⁵N–¹H moiety. The relaxation of ¹⁵N then is mainly determined by the CSA of ¹⁵N and the DD interactions with the directly attached proton (17), so that the contributions from other interactions, 1/T_1S and 1/T_2S, to a good approximation can be neglected. For ¹H^N, 1/T_1I and 1/T_2I are dominated by DD interactions with other protons I_k at distance r_k. These can be accounted for by spectral density functions J_k(ω), which describe the motions of the vectors joining the individual ¹H^N–¹H_k spin pairs (17):

5

6

Here, Eqs. 1-6 were used to calculate theoretical lineshapes of spin multiplets for given sets of the relaxation parameters, which subsequently were compared with the experimental NMR data. In particular, the in-phase absorptive spectrum was calculated using Eq. 7 (14),

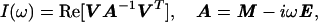7

where V = (1,1), and the relaxation matrix A is the (2×2) matrix on the right side of Eq. 1, and E is the unity matrix.

Experimental Procedures

NMR spectra were recorded on Bruker DRX 750 and Varian Unityplus 400 spectrometers with a 2 mM solution of the specific 1:1 complex formed between a uniformly ¹⁵N-labeled 70-residue fushi tarazu (ftz) homeodomain polypeptide and an unlabeled 14-bp DNA duplex (18, 19) in 95% ¹H₂O/5% ²H₂O at pH 6.0 and 4°C.

The isotropic rotational correlation time, τ_c, of the complex was estimated from the T₁/T₂ ratio of the relaxation times of the backbone ¹⁵N nuclei (20). The experimental schemes of Farrow et al. (21) were used for measurements of T₁ (¹⁵N) and T₂ (¹⁵N) for backbone nitrogen atoms.

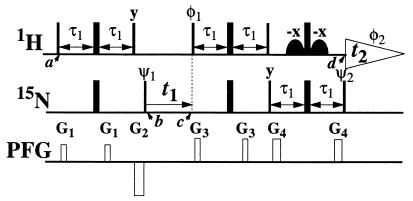
The TROSY approach (Fig. 1) and conventional [¹⁵N,¹H]correlation spectroscopy (COSY) (22, 23) experiments were used to correlate ¹H and ¹⁵N resonances. For all spectra t_1max = 90 ms and t_2max = 171 ms were used. In TROSY the evolution of the I,S spin system due to the ¹J_IS scalar coupling was not refocused during t₁ and t₂, thus avoiding suppression of cross-correlated relaxation during these periods. To obtain the pure absorptive spectrum containing only the most slowly relaxing component of the two-dimensional multiplets, the scheme of Fig. 1 was used (see also Appendix: Quantitative Analysis of TROSY).

Figure 1.

Experimental scheme for TROSY-type two-dimensional ¹H,¹⁵N correlation spectroscopy. In the rows marked ¹H and ¹⁵N, narrow and wide bars stand for nonselective 90° and 180° rf-pulses, respectively. Water suppression is achieved by watergate (34), using the two off-resonance rf-pulses indicated by curved shapes. The ¹H and ¹⁵N carrier frequencies are placed at 9 and 127 ppm, respectively. The delay τ₁ corresponds to 1/(4¹J(¹H,¹⁵N)) = 2.7 ms. Phases used are ψ₁ = {y,−y,−x,x,y,−y,−x,x}; ψ₂ = {4(x),4(-x)}; φ₁ = {4(y),4(-y)}; φ₂ (receiver) = {x,−x,−y,y,x,−x,y,−y}; x on all other pulses. The row marked PFG (pulsed field gradient) indicates the applied magnetic field gradients along the z-axis: G₁, amplitude = 30 G/cm, duration = 0.4 ms; G₂, −60 G/cm, 1 ms; G₃, 50 G/cm, 0.4 ms; G₄, 48 G/cm, 0.6 ms. Two free induction decays are recorded per t₁ delay, with ψ₁ incremented by 90° in between and stored as the real and imaginary parts of the interferogram in t₁. The Fourier transformation results in a two-dimensional ¹H,¹⁵N correlation spectrum that contains only the component of the four-line ¹⁵N–¹H multiplet that has the slowest T₂ relaxation rates for both nuclei. With this scheme, DD/CSA relaxation interference, which has been known for many years (35, 36), can be used to extend the limits of protein NMR.

Results

The NMR experiments with the uniformly ¹⁵N-labeled ftz homeodomain complexed with a 14-bp DNA duplex were performed at 4°C. The T₁/T₂ ratio of ¹⁵N was used to estimate the effective global correlation time, τ_c, of the complex (20). For the backbone amide groups, average T₁ (¹⁵N) and T₂ (¹⁵N) values of 0.720 ± 0.03 and 0.042 ± 0.005 s, respectively, were measured at 400 MHz, resulting in a global rotational correlation time of τ_c = 20 ± 2 ns. This τ_c value corresponds to that expected for a spherical protein of size 40 kDa in H₂O solution at 35°C.

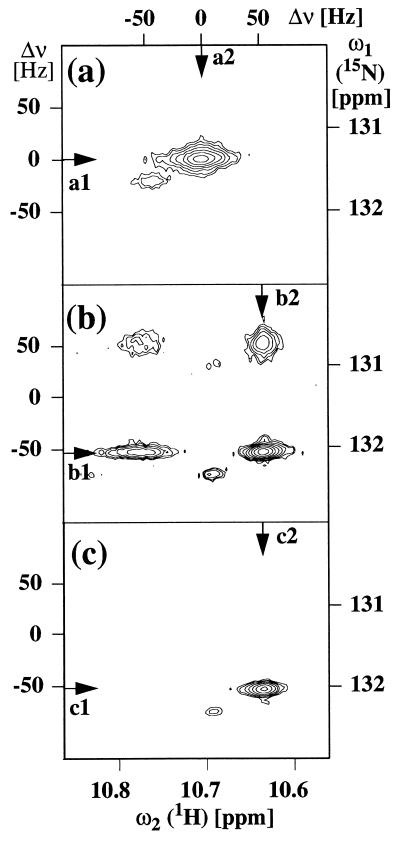
Fig. 2 shows a small region from ¹⁵N–¹H correlation spectra of the ftz homeodomain-DNA complex that contains the resonance of the indole ¹⁵N–¹H moiety of Trp-48, which is buried in the core of the protein (19). In the conventional [¹⁵N,¹H]COSY experiment (22, 23), decoupling of ¹H and ¹⁵N during the time periods t₁ and t₂, respectively, leads to detection of a single correlation peak per ¹⁵N–¹H moiety (Fig. 2a). If the same [¹⁵N,¹H]COSY spectrum is recorded without decoupling, four cross-peaks are observed per ¹⁵N–¹H moiety, which show largely different linewidths (Fig. 2b). The cross-peak at (ω₁ = 130.7 ppm, ω₂ = 10.78 ppm) exhibits the broadest linewidths in both dimensions, which shows that it originates from the rapidly relaxing components of both ¹H^N and ¹⁵N. One-dimensional cross-sections taken along ω₂ and ω₁ at the positions indicated by arrows in the spectra presented in Fig. 2 show that the two cross-peaks at (ω₁ = 132.1 ppm, ω₂ = 10.78 ppm) and (ω₁ = 130.7 ppm, ω₂ = 10.65 ppm) are broadened either along ω₁ or along ω₂ (Fig. 3). The cross-peak at (ω₁ = 132.1 ppm, ω₂ = 10.65 ppm) displays narrow linewidths in both dimensions, showing that it originates from the two slowly relaxing components of the ¹⁵N–¹H doublets. The TROSY-type correlation experiment, which does not use decoupling either during t₁ or t₂, contains only this narrowest correlation peak (Fig. 2c), which shows about 60% and 40% decrease in the linewidths of the ¹⁵N and ¹H resonances, respectively, when compared with the collapsed cross-peak in the conventional, broadband-decoupled spectrum (Fig. 2).

Figure 2.

Contour plots of ¹⁵N,¹H correlation spectra showing the indole ¹⁵N–¹H spin system of Trp-48 recorded in a 2 mM solution of uniformly ¹⁵N-labeled ftz homeodomain complexed with an unlabeled 14-bp DNA duplex in 95% H₂O/5% ²H₂O at 4°C, pH = 6.0, measured at the ¹H frequency of 750 MHz. (a) Conventional broad-band decoupled [¹⁵N,¹H]COSY spectrum (22, 23). The evolution caused by the ¹J(¹H,¹⁵N) scalar coupling was refocused in the ω₁ and ω₂ dimensions by a 180° proton pulse in the middle of the ¹⁵N evolution time t₁, and by waltz composite pulse decoupling of ¹⁵N during data acquisition, respectively. (b) Conventional [¹⁵N,¹H]COSY spectrum recorded without decoupling during t₁ and t₂. (c) TROSY-type ¹⁵N,¹H correlation spectrum recorded with the pulse scheme of Fig. 1. Chemical shifts relative to DSS in ppm and shifts in Hz relative to the center of the multiplet are indicated in both dimensions. The arrows identify the locations of the cross-sections shown in Fig. 3.

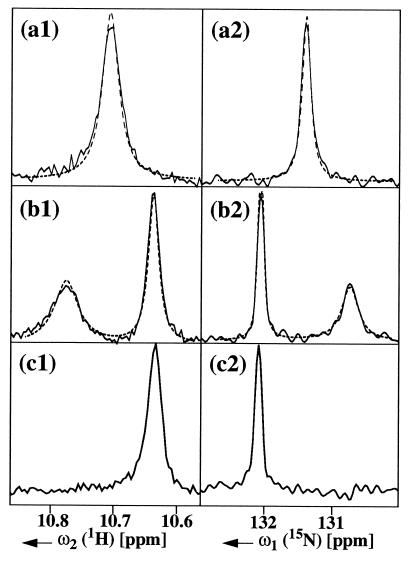
Figure 3.

Cross-sections through the spectra of Fig. 2 (solid lines). To facilitate a comparison of the linewidths in the different spectra the cross-sections were normalized to the same maximal signal amplitude. (a1), (a2), etc. refer to the arrows in Fig. 2. Simulated line shapes (dashed lines in a and b) were calculated using ¹J(¹H,¹⁵N) = −105 Hz, a rotational correlation time of τ_c = 20 ns, and chemical shift anisotropies of Δσ_H = −16 ppm and Δσ_N = −160 ppm. A long-range scalar coupling ²J(¹H^δ1,¹⁵N^ɛ1) = −5 Hz was included in the simulation of the ¹⁵N lineshapes (24), but possible effects of the small scalar couplings ³J(¹H^δ1,¹H^ɛ1) and ³J(¹H^ζ2,¹⁵N^ɛ1) were neglected. For ¹H^N the relaxation due to DD coupling with other protons in the nondeuterated complex was approximated by three protons placed at a distance of 0.24 nm from ¹H^N.

The fits of the experimental line shapes shown in Fig. 3 were obtained with line-shape calculations using the parameters τ_c = 20 ns and ¹J(¹H,¹⁵N) = 105 Hz, where the chemical shift anisotropies, Δσ_H and Δσ_N, were adjusted for the best fit. Because there was an otherwise unaccountable deviation from the Lorentzian lineshape we included a long-range scalar coupling ²J(¹H^δ1,¹⁵N^ɛ1) = −5 Hz (24) in the calculations, and T₁ and T₂ relaxation of ¹H^N because of DD coupling with other protons was modeled by placing three protons at a distance of 0.24 nm from ¹H^N. Application of one or a series of 180° pulses on spin I during the evolution of spin S interchanges the slowly and rapidly relaxing components of the S multiplet, which results in averaging of the slow and fast relaxation rates and elimination of the CSA/DD interference (25, 26). Indeed, the line shapes of the ¹H^N and ¹⁵N resonances measured with conventional [¹⁵N,¹H]COSY are well reproduced if the average of the two relaxation rates is used in the simulation (Fig. 3 a1 and b1). The best-fit values of Δσ_H = −16 ppm and Δσ_N = −160 ppm correspond closely to the experimentally measured chemical shift anisotropies of ¹H and ¹⁵N in ¹⁵N–¹H moieties. With solid-state NMR studies of ¹⁵N–²D moieties, values for Δσ_D near −14 ppm (27) and for Δσ_N of −160 ppm (28) were determined. Independently, solution NMR experiments yielded values for Δσ_H of backbone amide protons in the range 3 to 15 ppm (37) and Δσ_N near −170 ppm (10).

Discussion

In the experiments with the ftz homeodomain-DNA complex the overall transverse relaxation rates of ¹⁵N and ¹H^N in the indole ¹⁵N–¹H moiety of a buried tryptophan were reduced by 60% and 40%, respectively, when using a TROSY-type [¹⁵N,¹H]correlation experiment instead of the conventional [¹⁵N,¹H]COSY scheme. At a first glance this may appear to be a modest improvement, but a closer look reveals that DD coupling with remote protons, which could be nearly completely suppressed by replacement of the nonlabile hydrogen atoms with ²H (e.g., refs. 6 and 8), accounts for 95% of the residual T₂(¹H^N) relaxation and 75% of the residual T₂(¹⁵N) relaxation. In a corresponding DNA complex with the perdeuterated ftz homeodomain the reduction of the T₂ relaxation rates of the ¹⁵N–¹H moieties by the use of TROSY at 750 MHz would be about 40-fold for ¹H^N and about 10-fold for ¹⁵N.

Using Eqs. 1–6 with Δσ_H = −16 ppm, Δσ_N = −160 ppm, r_HN = 0.101 nm and parallel orientation of the principal axis of the CSA tensor with the vector r_HN, we evaluated the dependence of the residual T₂ relaxation rates of ¹⁵N and ¹H in TROSY-type experiments on the polarizing magnetic field B₀ and the molecular size. These calculations showed that nearly complete compensation of T₂ relaxation because of DD and CSA within the ¹⁵N–¹H moieties is obtained at a B₀ strength corresponding to a ¹H frequency near 1,100 MHz, i.e., at this field strength (p − δ_S) ≅ 0 and (p − δ_I) ≅ 0 in Eq. 2. Theory further predicts that the residual TROSY T₂ relaxation rates because of DD and CSA interactions within the ¹⁵N–¹H fragment are practically independent of the molecular size. For perdeuterated proteins the size limit for TROSY-type [¹⁵N,¹H]correlation experiments thus is not critically determined by T₂ relaxation, but one needs nonetheless to consider that the effect of deuteration of the nonlabile proton sites in the protein is dependent on conformation. For the ¹⁵N–¹H moieties in β-sheet secondary structure, DD and CSA interactions within the ¹⁵N–¹H^N fragment are the only sources of transverse relaxation that need to be considered, whereas in α-helices the two sequentially adjacent ¹H^N protons (3) contribute significantly to the transverse relaxation of the ¹⁵N and ¹H^N spins.

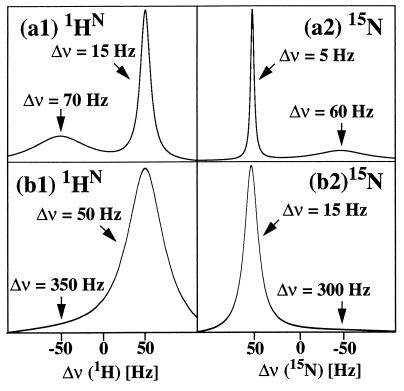
To provide a tangible illustration (Fig. 4) we calculated the ¹H^N and ¹⁵N line shapes for two perdeuterated spherical proteins in ¹H₂O solution with rotational correlation times τ_c of 60 and 320 ns, which corresponds to molecular masses of 150 and 800 kDa, respectively. A magnetic field B₀ corresponding to a resonance frequency 750 MHz for protons was assumed. To account for the worst possible situation for DD interaction with remote protons, two protons were placed at 0.29 nm from ¹H^N. The linewidth of the narrow component of the ¹⁵N doublet increases only slightly with molecular mass and is about 5 Hz at 150 kDa and 15 Hz for a 800-kDa protein (Fig. 4). The ¹H^N linewidth depends more strongly on the residual DD interactions with remote protons and is about 15 Hz at 150 kDa and 50 Hz for a 800-kDa protein. For the 150-kDa protein these numbers correspond to 10- and 4-fold reduction of the ¹⁵N and ¹H^N TROSY linewidths, respectively, when compared with a conventional [¹⁵N,¹H]COSY experiment with broad-band decoupling of ¹⁵N and ¹H. For large molecular sizes the experimental scheme of Fig. 1 may, in principle, be further improved by elimination of the 180° refocusing radio frequency (rf)-pulses during the insensitive nuclei enhanced by polarization transfers (INEPTs), because during the INEPT mixing times these pulses mix the multiplet components with slow and fast T₂ relaxation in a similar way as during the entire experiment in conventional [¹⁵N,¹H]COSY. The elimination of decoupling sequences and 180° pulses from TROSY-type NMR pulse sequences also may have implications for future probe designs, because the constraints by the requirements for minimal radio frequency heating and maximal B₁ homogeneity then may be relaxed, permitting a better optimization of other parameters such as sensitivity or sample diameter.

Figure 4.

1H and ¹⁵N lineshapes predicted for the broad and narrow multiplet components of ¹H^N and ¹⁵N of the ¹⁵N–¹H moiety in a [¹⁵N,¹H]COSY experiment of the type of Fig. 3 b1 and b2 for large proteins in H₂O solution at 20°C and a ¹H frequency of 750 MHz. (a1 and a2) Spherical protein of size 150 kDa. For the calculation a rotational correlation time of 60 ns, Δσ_H = −16 ppm and Δσ_N = −160 ppm were used, and all nonlabile protons were replaced with deuterons. Relaxation due to DD coupling with other labile protons was modeled by placing two protons at a distance of 0.29 nm from ¹H^N. The full linewidths at half height are indicated. (b1 and b2) Spherical protein of size 800 kDa. The calculation used τ_c = 320 ns and otherwise the same parameters as in a.

The TROSY principle drastically reduces all major sources of relaxation throughout the entire NMR experiment, including signal acquisition, and is clearly distinct from the use of heteronuclear multiple-quantum coherence to reduce dipolar relaxation between heteronuclei (29), which previously was used for measurements of ³J_HαHβ scalar coupling constants in proteins (30). Heteronuclear multiple-quantum coherences are subject to dipolar relaxation with remote spins as well as to CSA relaxation, which limits the use of these coherences at high polarizing magnetic fields. Moreover, the slow relaxation of the multiple-quantum coherences cannot be used during signal acquisition (14), which is critical for large molecules.

The following are some initial considerations on practical applications of the TROSY principle: (i) Because only one of the four multiplet components of ¹⁵N–¹H moiety is retained in TROSY-type experiments, the conventional [¹⁵N,¹H]COSY is intrinsically more sensitive. However, for measurements with proteins at ¹H frequencies higher than 500 MHz, TROSY will provide a much better ratio of signal height to noise. (ii) TROSY-type [¹³C,¹H]correlation experiments with the ¹³C–¹H moieties of the aromatic rings of Tyr, Phe, and Trp yield comparable results to those for ¹⁵N–¹H moieties (unpublished results). (iii) Two-dimensional nuclear Overhauser effect spectroscopy (NOESY) experiments correlating amide protons and aromatic protons can be relayed by TROSY-type heteronuclear correlation experiments. In favorable cases this might result in low resolution structures for several-fold larger proteins than have been accessible so far. (iv) We anticipate that a wide variety of NMR experiments currently used for resonance assignments and collection of conformational constraints can be optimized for larger molecular sizes by use of the TROSY approach in one or several dimensions.

ABBREVIATIONS

rf

radio frequency

DD

dipole–dipole

CSA

chemical shift anisotropy

COSY

correlation spectroscopy

TROSY

transverse relaxation-optimized spectroscopy

ftz homeodomain

fushi tarazu homeodomain polypeptide of 70 amino acid residues, with the homeodomain in positions 3–62

Quantitative Analysis of TROSY

The coherence transfer during the pulse sequence of Fig. 1 was evaluated using the product operator formalism (31) as implemented in the program poma (32), and the resulting phases of the rf-pulses and the receiver were transferred into the experimental pulse program according to (33). The transverse proton magnetization after the first 90° pulse on protons (a in Fig. 1) then is given by Eq. 8:

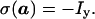8

During the delay 2τ₁ the scalar coupling ¹J(¹H,¹⁵N) evolves, so that the first 90°(¹⁵N) pulse generates two-spin coherence. With τ₁ = 1/(4¹J(¹H,¹⁵N)) we have at time b for the first step of the phase cycle (Fig. 1):

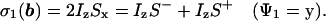9

The evolution of these terms during t₁, including relaxation, was evaluated using the single-transition basis operators S₁₂^± and S₃₄^±:

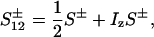10

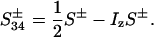11

The time evolution of the expectation values of these operators can be obtained by integration of Eq. 1 with initial conditions derived from Eq. 9 and the assumption that 1/T_1I ≪ ¹J(¹H,¹⁵N), which results in the following density matrix at time c:

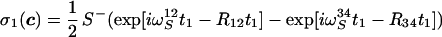12

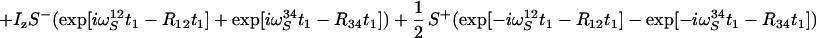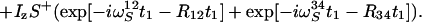The relaxation factors R_ij are related to the individual relaxation rates of the multiplet components by Eqs. 13 and 14:

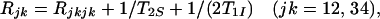13

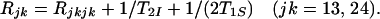14

The subsequent polarization transfer step (time period c to d in Fig. 1) links the evolution period t₁ with the acquisition period t₂. The density matrix at time point c is represented by Eq. 15, where only those I⁻ and I⁻S_z coherences are retained that result in detectable signals during data acquisition:

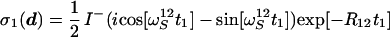15

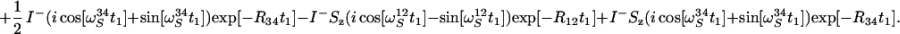The other steps in the phase cycle of Fig. 1 can be analyzed in an analogous fashion. Accumulation of the eight transients of the pulse sequence results in the following density matrix for the real part of the interferogram:

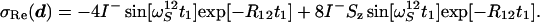16

Incrementation of the phase ψ₁ by 90° at each discrete value of t₁ leads to the corresponding imaginary part:

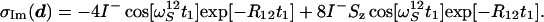17

Eqs. 16 and 17 are combined to the hypercomplex interferogram that represents pure phase correlation in the ω₁ dimension.

The treatment of the relaxation of the ¹H^N coherences during the acquisition period t₂ is similar to the treatment of ¹⁵N during t₁ (see Theory). The signals generated by I⁻ and I⁻S_z coherences that are received during t₂ are described by Eqs. 18 and 19, respectively:

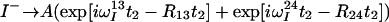18

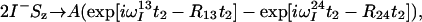19

where A is a proportionality coefficient. Substitution of Eqs. 18 and 19 into Eqs. 16 and 17 results in the hypercomplex interferogram corresponding to the 1→2 and 2→4 transitions of the ¹H,¹⁵N spin system:

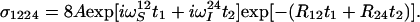20

Finally, the Fourier transformation of the hypercomplex interferogram represented by Eq. 20 results in the pure absorptive correlation spectrum, with resonance frequencies in ω₁ and ω₂ corresponding to the desired individual component of the ¹⁵N–¹H multiplet.