Design of fast enzymes by optimizing interaction potential in active site

Abstract

The diffusional encounter between substrate and enzyme, and hence catalytic efficiency, can be enhanced by mutating charged residues on the surface of the enzyme. In this paper we present a simple method for screening such mutations. This is based on our earlier result that electrostatic enhancement of the enzyme-substrate binding rate constant can be accounted for just by the interaction potential within the active site. Assuming that catalytic and structural integrity is maintained, the catalytic efficiency can be optimized by surface charge mutations which lead to stronger interaction potential within the active site. Application of the screening method on superoxide dismutase shows that only charge mutations close to the active site will have practical effect on the catalytic efficiency. This rationalizes a large number of findings obtained in previous simulation and experimental studies.

It is well known that a number of important enzymes exploit electrostatic interactions with their substrates to enhance the diffusional encounter with the substrates and hence the overall catalytic efficiency. Over the past decade, McCammon and coworkers (1–10) have developed more and more sophisticated Brownian dynamics simulation methodologies to study the effects of electrostatic interactions on enzyme–substrate binding rate. A significant achievement is that these methodologies led to the identification of charge mutations on the surface of superoxide dismutase (SOD) that were later confirmed experimentally by Getzoff et al. (11) to enhance the catalytic efficiency of the enzyme. Recently, we (12–14) discovered that a qualitative and perhaps even a semi-quantitative account of the electrostatic rate enhancement can be obtained just from the interaction potential within the active site. This opens the possibility of a different approach for designing enzymes with enhanced catalytic efficiency. In this paper we test this approach and examine other implications of our earlier work.

Explicitly, what we discovered is that, to a good approximation, the rate enhancement is given by the average Boltzmann factor:

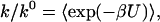1

where k and k⁰ are the binding rate constant in the presence and absence of an interaction potential U, and the averaging of the Boltzmann factor is over the region in space where substrate can bind with the enzyme. The approximation is good when the binding region is small (i.e., binding is specific). For a given binding region, the accuracy of Eq. 1 will deteriorate when the spatial variation of the interaction potential around the binding region is increased.

The focus of the present study is the use of Eq. 1 to screen charge mutations that may result in maximal rate enhancement. In principle, one can build a series of charge mutations and use Brownian dynamics simulations to find their effects on the substrate binding rate constant (5). Eq. 1 suggests that one can simply look at the effects of the charge mutations on the average Boltzmann factor in the binding region and dispense with Brownian dynamics simulations. Furthermore, one should focus on charge mutations near the binding region, as these will have maximal effect on the average Boltzmann factor. The main aim of this study is to find out how successful this approach is. We choose the well studied enzyme SOD (1, 2, 5, 10, 11, 15–17) as a test case. Success of the approach is judged by checking whether the predicted rate enhancement agrees with that from Brownian dynamics simulations.

We also address two related issues. Eq. 1 appears to imply that the electrostatic rate enhancement is primarily determined by the potential within the substrate binding region. How is it possible that the potential outside this small region seems to be unimportant in rate control? The conventional view of electrostatic rate enhancement is that the electric field “steers” or “guides” the substrate toward the active site. In light of Eq. 1, is this an accurate or useful description?

METHODS

When the binding region is small, a Brownian dynamics simulation procedure that we previously developed (18, 19) is particularly suitable for calculating the enzyme–substrate binding rate constant. According to this procedure, substrates are started in the binding region with a Boltzmann distribution exp(−βU)/〈exp(−βU)〉V_br, where V_br is the volume of the binding region. If a substrate is inside the binding region, it will bind with the enzyme with a first-order rate constant k_b. When this happens, its trajectory is terminated. Trajectories are otherwise terminated when they reach a cutoff time. The fraction of trajectories that are not terminated due to binding, S(t), at time t gives the time-dependent rate coefficient k(t) through

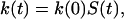2

where

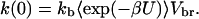3

The enzyme–substrate binding rate constant k is the long-time limit of k(t) (20).

Definition of Binding Region and Average Boltzmann Factor.

In line with previous studies of SOD (10, 11, 17), the substrate binding region was modeled by a spherical shell centered at each of the two active-site Cu atoms, with inner and outer radii set to 7 and 7.5 Å, respectively. Only the portion of the spherical shells accessible to the substrate, modeled as a 2.05-Å sphere, was used as the binding region. To calculate the volume of and the average Boltzmann factor in the binding region, 400,000 points were randomly distributed within the two spherical shells. Because of exclusion by atoms of the enzyme (human SOD; Brookhaven Protein Data Bank entry 1sos), only ≈3,600 points allowed for the positioning of a substrate. The volume of the binding region is thus

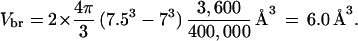4

The interaction potential was obtained by treating the superoxide substrate as a test charge influenced by the electrostatic potential of SOD. The latter was calculated by the program uhbd (21) using a 140 × 140 × 140 grid with a 1-Å spacing. The ionic strength was set to 0.01 M to match with experimental conditions (11). By linear interpolation, the electrostatic potential at each of the 3,600 allowable substrate positions was calculated. The Boltzmann factor was then averaged over these 3,600 positions.

Boltzmann Distribution of Initial Positions.

A Boltzmann distribution of initial positions in the binding region was generated by repeating each of the randomly chosen 3,600 positions according to its Boltzmann weight. Specifically, these positions were passed through several rounds. In each round, the normalized Boltzmann factor at every position was compared with a random number uniformly distributed between 0 and 1. If the random number was smaller, the particular position was selected. The process was stopped until a desired number of initial positions was accumulated. For each simulation of the binding rate constant, 12,000 initial positions were used.

Propagation of Brownian Dynamics Trajectories.

The substrate trajectories were propagated according to the Ermak–McCammon algorithm (22). As in previous Brownian dynamics simulations of SOD (10), the relative diffusion constant of SOD and the substrate was D = 129 Ų/ns. The force on the substrate was calculated by linear interpolation from the forces at the eight corners of the cubic grid that contained the substrate, which in turn were calculated from the potential by central difference.

The inner boundary of each of the two spherical shells defining the binding region and the rest of the enzyme surface were reflecting to the substrate. A large amount of simulation time was spent in treating this boundary condition. To make this as efficient as possible, first the outermost atom from the geometric center of the enzyme was identified. The distance encompassed plus the radius of the substrate, denoted by r_surf, is the distance beyond which there is no chance of enzyme-substrate collision. For human SOD, r_surf = 38.9 Å. This distance was also used to set the time step. For distance r from the geometric center < r_surf, the time step was 4 × 10⁻⁵ ns; beyond r_surf, the time step was 4 × 10⁻⁵ ns + (r − r_surf)²/200D.

For each move inside r_surf, one has to test whether the new position is excluded by the enzyme. Before the simulations started, we put a Cartesian coordinate system at the center of geometry of the enzyme and collected into one group all the atoms that were either wholly or partially in a particular octant. Atoms that intersected the planes or axes of the coordinate system were found in more than one group. In this way we needed to check the substrate for collision only against the group of enzyme atoms that shared the same octant, or, when the substrate intersected a plane or an axis of the coordinate system, against two or four groups in the neighboring octants. The practical effect of grouping the enzyme atoms is dramatic: the Brownian dynamics simulations usually run three times faster compared with the case where every atom of the enzyme is tested for collision every step.

Enzyme–Substrate Binding Rate Constant.

Trajectories were propagated up to 20 or 40 ns. The enzyme substrate binding rate constant k was obtained by fitting the long-time tail of k(t) to its general asymptotic behavior (19)

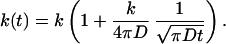5

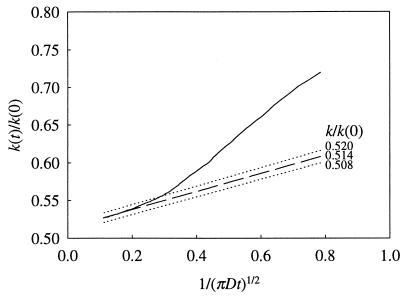
This is easily accomplished by using 1/(πDt)½ as the independent variable. The fact that the intercept and the slope of k(t) vs. 1/(πDt)½ are related makes the fitting very sensitive. This is illustrated in Fig. 1 by the fitting for native human SOD.

Figure 1.

Fitting of the time-dependent rate coefficient k(t) to its asymptotic behavior for obtaining the binding rate constant k. The independent variable is 1/(πDt)½. The dependent variable k(t) is scaled by its initial value k(0). A slight change in k results in noticeable deviation of the fitting function from the actual curve.

RESULTS

Strategy for Charge Mutation.

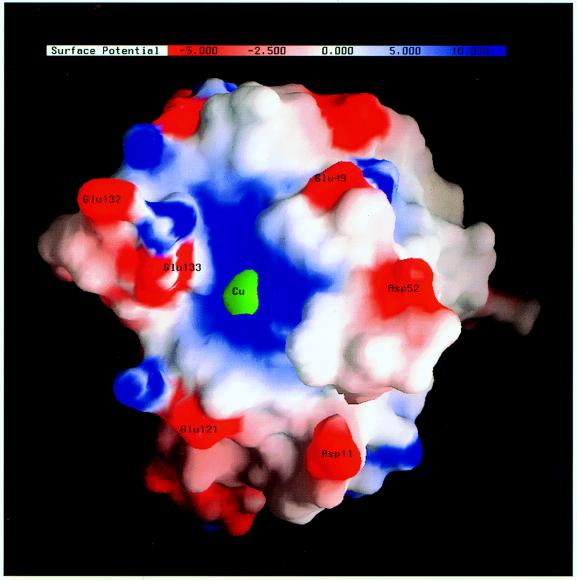
The electrostatic potential on the surface of native human SOD, rendered by the program grasp (23), is shown in Fig. 2. The active-site Cu atom is engulfed by a patch of positive potential. On moving away from the Cu atom, one encounters several small patches of negative potential around residues Glu-133, Glu-132, Glu-49, Asp-52, Glu-121, and Asp-11. These residues make unfavorable contributions to the average Boltzmann factor in the binding region and thus are expected to suppress the substrate binding rate. Based on consideration of the average Boltzmann factor, one also expects that the effects of the six residues on the binding rate are more significant than residues farther away from the active site. We have therefore studied the effects of replacing these residues by their amide forms. With these relatively mild mutations, the disruption of the structural integrity of the native protein would be minimized.

Figure 2.

The electrostatic potential (in units of k_BT/e = 0.59 kcal/mol/e) on the surface of human Cu/Zn superoxide dismutase. Only one subunit of the homodimer is shown. The active-site Cu atom is represented by a 3-Å green sphere.

Average Boltzmann Factor.

The values of the average Boltzmann factor in the binding regions of the native enzyme and 12 single and double mutants are listed in Table 1. As expected, all the charge neutralizations increase the average Boltzmann factor. Moreover, as the site of mutation moves farther away from the active-site Cu atom, the increase in the average Boltzmann factor over that of the native enzyme becomes less.

Table 1.

Average Boltzmann factors for native SOD and 12 mutants

Enzyme	Distance between Cu and CG/CD, Å	Average Boltzmann factor
Native		95.2
Gln-133	10	464.0
Gln-49	12	156.2
Gln-121	12	151.1
Asn-52	15	151.5
Asn-11	16	151.1
Gln-132	17	148.2
Gln-133/Gln-49		759.3
Gln-133/Asn-52		736.9
Gln-133/Gln-132		726.4
Gln-49/Asn-52		249.1
Gln-49/Gln-132		244.2
Asn-52/Gln-132		236.3

Test Against Brownian Dynamics Simulations.

The critical question is whether such increase in average Boltzmann factor is predictive of increase in substrate binding rate constant. To address this question, we used Brownian dynamics simulations to calculate the binding rate constant for the native enzyme and 10 single and double mutants. The first-order rate constant k_b (see Eq. 3) was chosen to be 12.8 ns⁻¹ so the simulated binding rate constant for the native enzyme was the same as the experimental value, 2.3 × 10⁹ M⁻¹⋅s⁻¹ (11). Mechanistically, k_b might describe the bond formation between superoxide and the active-site Cu atom or the subsequent reduction of Cu (24, 25). The molecular model and the chosen parameters were judged to be reasonable as the experimental values of the substrate binding rate constant for the Gln-132 and Gln-133 single mutants and the Gln-132/Gln-133 double mutant, 4.3 × 10⁹, 6.7 × 10⁹, and 7.2 × 10⁹ M⁻¹⋅s⁻¹, respectively, were all quite accurately reproduced. The simulated results were 3.4 × 10⁹, 6.3 × 10⁹, and 8.6 × 10⁹ M⁻¹⋅s⁻¹, respectively.

In Table 2 the ratios of the simulated binding rate constants of 10 single and double mutants over that of the native enzyme are compared with the corresponding quantities for the average Boltzmann factors. For the six mutants not containing Gln-133, the increases in binding rate constant are close to the increases in average Boltzmann factor. For the four mutants containing Gln-133, the average Boltzmann factor correctly ranks the Gln-133 single mutant above the three double mutants without Gln-133 and below the three double mutants with Gln-133. The magnitudes of the effects of the mutations are overestimated by a factor of ≈2 by the average Boltzmann factor. Overall, the average Boltzmann factor is very predictive of the effects of the mutations studied.

Table 2.

Correlation of increases in average Boltzmann factor and in substrate binding rate for 10 SOD mutants

Mutant	Average Boltzmann factor	Binding rate constant
Gln-133	4.9	2.8
Gln-49	1.6	1.5
Asn-52	1.6	1.5
Gln-132	1.6	1.5
Gln-133/Gln-49	8.0	3.8
Gln-133/Asn-52	7.7	3.7
Gln-133/Gln-132	7.6	3.8
Gln-49/Asn-52	2.6	2.2
Gln-49/Gln-132	2.6	2.2
Asn-52/Gln-132	2.5	2.2

DISCUSSION

We have tested the value of the average Boltzmann factor in the binding region as a screening tool for maximal rate enhancement by surface charge mutations on superoxide dismutase and found that the it is a good predictor of the effects of charge mutations on the binding rate constant. It may be suggested that for this particular purpose one can rely on the average Boltzmann factor and dispense with Brownian dynamics simulations. Let us now examine the physical basis of the apparent local control of the electrostatic rate enhancement.

Local and Nonlocal Effects in Rate Enhancement.

Enzyme–substrate binding occurs in two steps: a substrate in the bulk solvent first diffuses to a region around the active site and there it binds to the enzyme with a first-order rate constant k_b (modeling, for example, covalent bond formation). If the two steps are described by a kinetic scheme

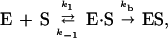6

then the rate constant for forming the enzyme–substrate complex ES from separated enzyme and substrate is

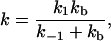7

provided that the transient complex E⋅S, with the substrate in the binding region but not yet bound to the enzyme, is in steady state. The two rate constants k₁ and k₋₁ for the transitions between separated enzyme and substrate and the transient complex E⋅S are related by an equilibrium constant. This is given by the integration of the Boltzmann factor exp(−βU) over the binding region (26), thus

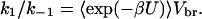8

The last equation allows us to write

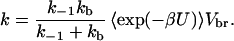9

Scaling of the binding rate constant k with the average Boltzmann factor 〈exp(−βU)〉 is trivially obtained when the binding process is reaction-controlled (i.e., k_b ≪ k₋₁). For the scaling to hold in general, k₋₁ must be insensitive to the interaction potential. We now check this by tracing the diffusive trajectories of substrates that are started from an equilibrium distribution in the binding region and are not allowed to bind with the enzyme. Gradually more and more of the substrates will diffuse out, and according to an earlier work (27) k₋₁ is just the decay constant of the substrate population in the binding region. Obviously, the smaller the binding region, the faster the substrate population in it will decay (and hence the higher the value of k₋₁ will be). If the substrate population in the binding region decays really fast, then the substrates that have diffused out will not move very far. Moreover, if the interaction potential does not vary significantly in the binding region and its vicinity, then the substrates would have moved in an essentially uniform potential. Consequently k₋₁ would be almost the same even if the potential is absent.

The above “derivation” of Eq. 1 by a physical analysis of k₋₁ allows us to see clearly the relationship between local and nonlocal effects in the control of the binding rate constant by the interaction potential. It is misleading to interpret Eq. 1 as that only the local potential in the binding region is implicated in rate enhancement and that the potential outside is unimportant. The apparent insensitivity of k₋₁ to the potential relies on the condition that the potential does not change significantly on going from the binding region to its vicinity (the “near” region). The importance of this condition can be illustrated by the binding of a point-like substrate to a spherical enzyme (radius, R) with a disk-shaped absorbing patch (radius, a) under the influence of a centrosymmetric step-function potential U(r) = −U₀ for R < r < R₁ and 0 for r > R₁. When a/r = 0.09, R₁/r = 1.5, and βU₀ = 2, the prediction of Eq. 1, approximately equal to 4Daexp(βU₀), is accurate to within 18% (13, 19). However, if the change in potential at r = R₁ approaches infinity (i.e., βU₀ → ∞), then k will be given by 4πDR₁, which does not scale with the average Boltzmann factor exp(βU₀).

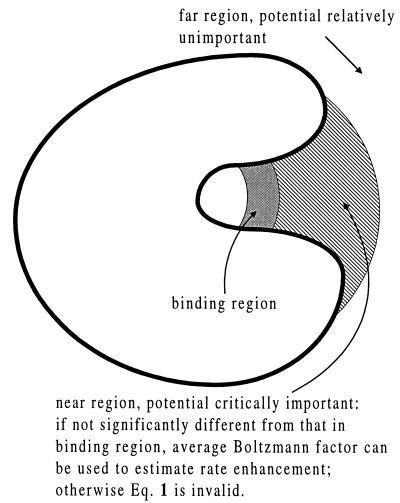
It should be noted that the physical analysis of k₋₁ has not implicated the potential in the region far away from the binding site (the “far” region). In other words, as long as the potential does not change significantly on going from the binding region to the near region, Eq. 1 will be a good approximation and the potential in the far region will be relatively unimportant in the determination of rate enhancement. The roles of the interaction potential in the three different regions are schematically shown in Fig. 3.

Figure 3.

Schematic illustration of the roles of the interaction potential in three regions around the active site of an enzyme. The binding region is where the substrate can get bound (e.g., via a covalent bond) to the enzyme. The near region is right outside the binding region. This is where a substrate tends to stay for a relatively long time after diffusing out of the binding region. The far region is the rest of space. The potential in the near region is critical for rate control. If it does not differ significantly from the potential in the binding region, then the average Boltzmann factor in the binding region can predict the rate enhancement via Eq. 1 and at the same time the potential in the far region is unimportant. Otherwise Eq. 1 will not be valid.

When the binding process is diffusion-controlled, the near region may be called the “capture region,” in the sense that once a substrate is in it, it has a high (i.e., close to unit) probability of diffusing to the binding region and being absorbed there. If the binding region is small, the substrate has to spend a long time in the capture region before absorption. Then the binding rate constant k = k₁ can be approximated by the product of the equilibrium constant for being in the capture region and the first-order rate constant k_c→b for reaching the binding site. The former is proportional to the average Boltzmann factor in the capture region (in analogy to Eq. 8), which will be nearly the same as 〈exp(−βU)〉 if the potential is smooth in and around the binding site. Under the last condition, k_c→b will be insensitive to the potential because on diffusing to the binding site the substrate is influenced by a nearly uniform potential. Taken together, one obtains the result k ∝ 〈exp(−βU)〉, or equivalently Eq. 1. This analysis of k₁, complementary to the earlier analysis of k₋₁, provides a physical interpretation of Eq. 1 in the diffusion-controlled limit. That the substrates first diffuse to the capture region and then explore the space there to reach the binding site is a form of reduction in dimensionality (28).

Because of their relatively weak distance dependence, one can reasonably expect that the potential due to electrostatic interactions will not change significantly on going from the binding region to its immediate vicinity. This is rather fortunate. We can thus conclude that, even though physically the potential outside the binding region is important in the control of rate enhancement, the relatively weak distance dependence of electrostatic interactions allows us to only worry about the potential in the binding region for the sake of estimating the magnitude of the rate enhancement.

Analysis of the “Steering” Mechanism.

The rate enhancement by electrostatic interactions is generally viewed to be due to the steering or guidance of the substrate toward the active site by the electric field of the enzyme. We now analyze this view carefully. Again we look at the potential in the near and far regions separately. If a steering mechanism were at play, a repulsive potential in the near region may have a positive role in rate enhancement, as this would help the approaching of the substrate toward the binding region. Such a role was suggested in the initial work of Getzoff et al. (15) on bovine SOD for the negative potential around Glu-131 (analogue of Glu-133 in human SOD), which is near the mouth of the active site. If this were correct, neutralizing the negative charge on Glu-131 would decrease the substrate binding rate. Through extensive Brownian dynamics simulations, Sharp et al. (18) and Sines et al. (5) found just the opposite effect. A later experimental study by Getzoff et al. (11) confirmed the rate enhancing effect of neutralizing Glu-133 in human SOD.

Our results in Table 2 show that the rate increase due to neutralizing Glu-133 is actually predicted by the average Boltzmann factor in the binding region. Let us now consider a hypothetical situation where the potential in the binding region and hence the average Boltzmann factor are the same as in the native enzyme but the potential around Glu-133 is less repulsive or even slightly attractive to superoxide. Relative to the native enzyme, a substrate in the binding region now will be more likely to diffuse out as the resistance from the potential around Glu-133 becomes less. Accordingly k₋₁ will be increased. Because by design the average Boltzmann factor is unchanged, we see from Eq. 9 that the substrate binding rate constant k will also be increased. A rate increase is also predicted by the reduction-in-dimensionality argument (28). In the hypothetical situation, the substrate will be more likely to diffuse from outer space to the neighborhood of Glu-133. This in turn will make finding the binding region easier by a two dimensional search over the protein surface. In contrast, one may expect a rate decrease based on the steering mechanism, because now the guiding electric field toward the active site is weakened.

Let us turn to the far region. Our earlier analysis of Eq. 1 shows that the potential in this region is unimportant in the rate enhancement. This is entirely consistent with the simulation results of Sharp et al. (16) and Sines et al. (5). In one simulation of Sharp et al. (16), the potential on the backside of bovine SOD was turned off and the binding rate constant was found to be unaffected at all. Sines et al. (5) studied a large number of charge mutations far away from the active site of bovine SOD and found these to have minimal effects on the substrate binding rate. These results are incompatible with an electrostatic steering mechanism in the far region. Perhaps the strongest evidence against the steering mechanism comes from the simulation result of Sines et al. (5) that neither negative charges were ever found to enhance nor positive charges were ever found to suppress the superoxide binding rate. It is also interesting to note that negatively charged bovine, neutral porcine, and positively charged ovine SODs have nearly identical catalytic behaviors (29). This observation would be difficult to comprehend if the steering mechanism is naively interpreted.

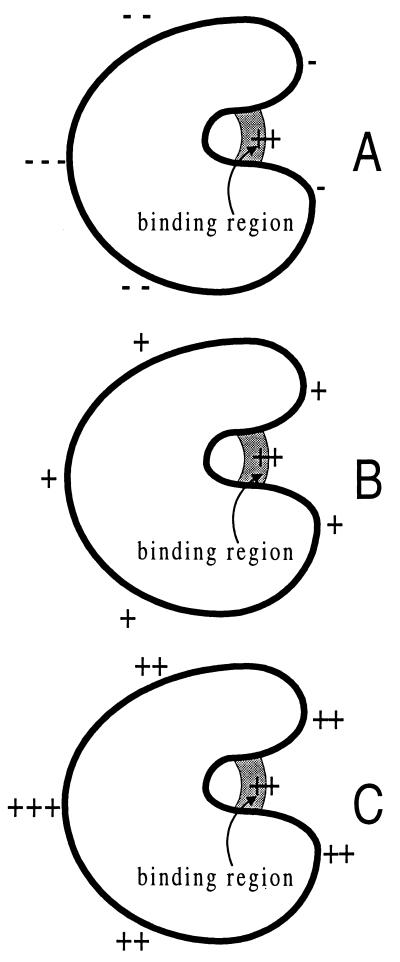
The pitfall of the steering mechanism may be highlighted by the substrate binding rate constants in the three situations shown in Fig. 4. According to this mechanism, the binding rate constants are expected to decrease on going from A to B and from B to C. However, based on Eq. 9, we predict that the rate constants will increase. This trend is also predicted by the reduction-in-dimensionality argument.

Figure 4.

Three potentials around an enzyme that binds a negatively charged substrate. The sign of a potential at a particular location is indicated by “+” or “−” whereas the magnitude is indicated by the number of “+” or “−”.

Possible Electrostatic Suppression of Product Release Rate.

By enhancing the substrate binding rate through charge mutations, a question naturally arises: will such mutations adversely reduce catalytic efficiency by simultaneously suppressing the product release rate? Indeed the concern had led Gilson at al. (30) to propose a “back door” mechanism for product release. We have already addressed this question in an earlier work (20). The answer is that the suppression of the product release rate is insignificant. This is simply because the rate constant for dissociating from the binding region, k₋₁ in Eq. 6 for the substrate or its analogue for the product, is insensitive to the interaction potential. Enzymes thus enjoy all the benefits of electrostatic interactions but suffer very little from their side effects.

In conclusion, both by noting that substrates which temporarily leave the binding site tend to stay near the binding site and by noting that substrates have to spend a long time in a capture region around the binding site before getting bound to the enzyme, we have made it clear that the apparent local control of the rate enhancement by electrostatic interactions occurs because of their relatively weak distance dependence. We also carefully analyzed the generally held view that electrostatic rate enhancement comes because the electric field of the enzyme steers or guides the substrate toward the active site. A number of results obtained in previous simulation and experimental studies as well as results obtained in the present study were used to argue that the steering mechanism may result in misleading predictions on electrostatic rate enhancement. A capture region around the binding site, which results in reduction in dimensionality and leads to the scaling of the binding rate constant with the average Boltzmann factor, should provide a much better physical picture for enzyme–substrate binding. The average Boltzmann factor is not only computationally inexpensive but also conceptually simple. It is easy to understand that the effects of charge mutations on the average Boltzmann factor will diminish as the sites of mutations move away from the binding region. Now we see that this rationalizes the parallel effects on the substrate binding rate constant found in simulations and experiments.