Abstract
We have developed and tested a complete set of nonbonded parameters for a continuum polarizable force field. Our analysis shows that the new continuum polarizable model is consistent with B3LYP/cc-pVTZ in modeling electronic response upon variation of dielectric environment. Comparison with experiment also shows that the new continuum polarizable model is reasonable, with similar accuracy as B3LYP/cc-pVTZ in reproduction of dipole moments of selected organic molecules in the gas phase. We have further tested the validity to interchange the Amber van der Waals parameters between the explicit and continuum polarizable force fields with a series of dimers. It can be found that the continuum polarizable model agrees well with MP2/cc-pVTZ, with deviations in dimer binding energies less than 0.9 kcal/mol in the aqueous dielectric environment. Finally we have optimized atomic cavity radii with respect to experimental solvation free energies of 177 training molecules. To validate the optimized cavity radii, we have tested these parameters against 176 test molecules. It is found that the optimized PB atomic cavity radii transfer well from the training set to the test set, with an overall root-mean-squared deviation of 1.30 kcal/mol, unsigned average error of 1.07 kacl/mol, and correlation coefficient of 92% for all 353 molecules in both the training and test sets. Given the development documented here, the next natural step is the construction of a full protein/nucleic acid force field within the new continuum polarization framework.
Introduction
Most commonly used force fields are additive or nonpolarizable in computational simulations of structures, dynamics, and functions of biomolecules. They incorporate a relatively simple potential energy function:
| (1) |
The first three summations are over bonds (1-2 interactions), angles (1-3 interactions), and proper/improper torsions (1-4 interactions). The final summation (over pairs of atoms i and j) excludes 1-2 and 1-3 interactions and often uses different parameters for atoms separated by three covalent bonds (i.e. the 1-4 interactions) from those for atoms separated by more than three covalent bonds. It describes electrostatics interactions that are represented by a Coulombic potential, and dispersion and exchange repulsion interactions that are represented by a Lennard-Jones 6-12 potential. Many such force fields have been developed for biomolecular simulations, such as Amber,1-6 CHARMM,7,8 GROMOS,9 and OPLS.10-12
In force field applications, the covalent bonding terms are not that critical in biomolecular simulations, as long as bond and angle parameters are taken from small molecule structures and vibrational frequencies, and torsion terms are fitted to high level quantum mechanical potential energy surfaces. The van der Waals parameters are not very different among various force fields either, mostly derived from Jorgensen’s OPLS parameter set.10 The most important differences among various force fields are the treatments of electrostatics.
To develop parameters for electrostatics, all force fields face the problem of how to effectively wrap polarization into the total potential energy as physically and cleanly as possible. Amber based its parameter development on a set of HF/6-31G* calculations to effectively increase molecular dipole moments,3 to a similar amount observed in the TIP3P and SPC water models.13,14 In CHARMM charges were derived primarily from fits to solute-water dimer energetics. In addition to fitting the dimer interaction energies, charges for model compounds were adjusted to obtain dipole moments somewhat larger than experimental or gas-phase ab initio values. OPLS placed a strong emphasis on deriving nonbonded interactions by comparison to liquid-phase thermodynamics.11,12 Although the OPLS parameters were principally derived with reference to condensed phase simulations, comparisons to gas-phase peptide energetics also show good results.15
A cornerstone for accurate biomolecular simulations is the molecular mechanical force field. Accuracy of the force field parameters ultimately determines that of the simulations. Arguably, polarizable force fields of various forms offer more consistent and balanced treatment of solute-solute and solute-solvent interactions for biomolecular simulations, at least for the environment-sensitive electrostatic components. Indeed, it is widely recognized that the use of an electrostatic model based on fixed charges as in nonpolarizable force fields has a significant shortcoming: the model is unable to respond directly to the molecular environment. Nevertheless, it should be pointed out that the need for explicit inclusion of polarization effects in force fields is still a matter of current discussion in the literature.16,17
Three basic methods for including polarization have been studied: fluctuating charge, Drude oscillator, and induced dipole models. Fluctuating charge models use the principle of electronegativity equalization to produce a set of point charges that optimize the total electrostatic energy. In theory, intermolecular charge transfer is then handled by requiring conservation of charge for the whole system. In applications, charge conservation is often enforced for each individual molecule.18-21 Drude oscillator methods, also referred to as shell models, use a harmonic restraint potential to tether a mobile point charge to an interaction site. In a general Drude oscillator model, an atom carries a charge fixed at the nucleus and a second restrained charge of variable position. The charge magnitudes and harmonic force constants are fit to atomic and molecular polarizability data and experimental energies. As with fluctuating charge model, the Drude oscillator model is most often used with an extended Lagrangian treatment of the variable charges during a molecular dynamics simulation.22 Probably the best-studied method for handling polarization is use of induced multipole moments. While higher-order multipole polarization and hyperpolarization can be included in force fields,23 only induced dipoles are usually considered.
To date, most polarizable force fields are still under developments with a few published applications limited to those from the development groups. The Amber ff02 potential represents an initial polarizable member in the Amber force fields with most of its components retained from nonpolarizable force fields.24,25 The Amoeba force field is a fully polarizable force field with its own polarizable water potential.26,27 The CHARMM fluctuating charge force field is another fully polarizable force field.28,29 This force field has been tested with 7 representative globular proteins in explicit polarizable solvent represented by the TIP4P-FQ potential.28,29 Drude polarizable CHARMM force field incorporates induced polarization into the potential function on the basis of the classical Drude oscillator model.30-34 The early versions of PROSA force fields were first based on a fluctuating charge formalism.35 This model was later extended via the addition of induced dipoles on some sites.36 The SIBFA force field has been applied to a series of protein structure and molecular recognition problems.37-39 The energy function is based on a rather direct decomposition of ab initio SCF computations, including multipole electrostatics, repulsion, and dispersion-like terms.37-39 Notably, separate terms are used for polarization and charge transfer.37-39 Very recently, the NEMO potential for a capped glycine residue has been reported.40 This study devoted considerable attention to the intramolecular potential.40 The SDFF force field is unique among current polarizable protein force-field efforts in its extensive use of cross-terms and emphasis on valence potential functions.41
With ever improving accuracy in implicit solvents,42-45 an interesting question in the development of polarizable force fields is how to incorporate electronic polarization in implicit solvents. Maple et al directly incorporated an explicit polarizable force field in their generalized Born implicit solvent.46 Schneiders et al combined a Poisson-Boltzmann solvent and the explicit polarizable Amoeba force field successfully.47 Alternatively, it is also reasonable to treat electronic polarization in a continuum manner since implicit solvents have treated solvent polarization in a continuum manner. However, adoption of such a strategy does not argue for its capability to handle atomic-detailed polarization effects within a molecular environment. Instead, it is intended to offer an efficient and self-consistent approach in treating polar interactions in biomolecular simulations more satisfactory than existing additive force fields with implicit solvents. Continuum treatment of electronic polarization was often used in many calculations related to solvation free energies.48,49 Typical implicit solvents, such as numerical Poisson-Boltzmann approaches50,51 and generalized Born approaches52,53 were developed to deal with non-vacuum solute interior. However, a molecular mechanics force field that is designed to be consistent with such a treatment of electronic polarization just began to emerge.54 In a previous study we explored the feasibility to treat electronic polarization in a continuum manner.54 We found that an electrostatic model with a single set of parameters can be used in different environments and conformations with such a continuum treatment of electrostatic polarization.54 In this work we want to investigate the highly important nonbonded components for such a force field.
Method
Continuum Polarizable Force Field
In our proposed continuum polarizable model a continuum dipole moment density within the solute interior is used to represent electronic polarization. The dipole moment density, termed polarization (P) in classical electrostatics, is related to electric filed (E) as
| (2) |
whereε is the solute dielectric constant, a value of 4 was found to be optimal for tested molecules.54
Note that this is different from the commonly used high protein dielectric constants > 20 or the widely accepted low protein dielectric constant of 2. This discrepancy can be better understood after a brief review of protein dielectric constants as discussed by Warshel and co-workers.55 Warshel and co-workers have pointed out that the protein dielectric constant is 1 when all electrostatic details, such as permanent dipoles and induced dipoles, are represented and sampled explicitly. This is the case for explicit polarizable force fields. Incidentally, this also argues for why existing additive force fields that are designed with a protein dielectric constant of 1 are already fundamentally flawed. They have also pointed out that the protein dielectric constant is 2 or higher when all except induced dipoles are represented and sampled. This is the case for continuum polarizable force fields. In other words, the solute dielectric in the continuum polarizable force fields should be similar to its dielectric at high frequency limit, ε∞, as in the Debye equation for frequency dependent complex dielectric constant: ε=ε’+ε”, with and . Here εs is static dielectric value at zero frequency and ω is angular frequency, τ is the relaxation time for molecular orientation. It should be pointed out that ε∞ are different for different molecules, ranging from about 2.0 for cyclohexane, to 4.0 for N-methyl acetamide (NMA) and 5.2 for liquid water at room temperature. Thus, this value is very different from measured or simulated protein macroscopic dielectric constant, which can be as high as 20 and above. The much higher value is to account for rotational polarization, exchange of protein and water in the solvent-exposed region of protein, and also average over ionization states of acids and bases. This in part explains why a value as high as 20 has to be used in many previous applications of implicit solvents in protein stability and pK a predictions where no explicit representation or sampling of any polarization details presents.55-57 The current model adopts an empirically optimized “average” solute dielectric constant of 4 in all molecular mechanics calculations. This value was shown to give the best agreement in included dipole moments between the continuum electronic polarizable model and the B3LYP/cc-pVTZ theory for tested model compounds in tested continuum solvents.54
Once polarization is known from Eqn (2), the polarization energy (Vpol) can then be calculated from induced charges (ρind) due to polarization and potential generated by solute point charges (ϕperm):
| (3) |
| (4) |
Note that the use of Eqns (2) - (4) requires electrostatic field, E. In the proposed continuum polarizable force field, E (= -∇ϕ) can be obtained by solving the Poisson’s equation with a given set of solute point charges (ρperm, permanent charges):54
| (5) |
In the continuum polarizable force field, atomic charges of each molecule are fitted with respect to the quantum mechanical electrostatic potential (ESP) simultaneously in vacuo, a low dielectric environment (ε = 4), and a high-dielectric aqueous environment (ε = 78.39) with a modified RESP methodology that was developed to accommodate the proposed continuum electronic polarization treatment.54 The modified RESP was based on a least square fit between the molecular mechanical (MM) electrostatic potential and the quantum mechanical (QM) electrostatic potential as in the original RESP.58,59 The procedure can be summarized in the following steps:
Atomic charges Q are initialized by fitting EQM, i.e. the electrostatic potential from QM, without considering electronic polarization.
Induced electronic dipole moment density (P) is calculated by Eqn. (2) and Poisson’s equation (∇·εE = 4πρperm) with given ρperm, i.e. atomic charges Q.
Eind, electrostatic potential from induced electronic dipole moment density (P), is computed.
New atomic charges Q are refitted to the difference between electrostatic potential from QM and that from induced electronic dipole moment density (EQM-Eind).
Go to Step 2) until convergence is achieved.
As discussed in our previous study, when the environment is not in vacuo, there are two contributions to polarization, the first is electronic and the second is solvent. What complicates the picture is that there is, in general, a coupling between the two polarization effects. Thus it is not straight forward to separate the final polarization effect into two isolated components: solvent and electronic polarization effects. The MM electrostatic field from solving Poisson’s equation includes all the effects. However, the QM electrostatic field does not include the contribution of solvent polarization due to the way that ESP is computed in the Gaussian program.60 Therefore the contribution of solvent polarization has to be subtracted from the included electrostatic field to achieve a consistency between QM and MM as discussed in our previous study.54
In this study, the quantum mechanical electrostatic potential was obtained in B3LYP/cc-pVTZ with the Gaussian03 program.60 The PCM solvent61,62 was used to model polarization responses to different dielectric environments. The charge fitting calculations were performed with a revised Amber9 package.63 The electrostatic field was calculated with a numerical Poisson-Boltzmann (PB) solver64,65 (igb=10) in the SANDER module. Atomic radii were set to be consistent with those in the PCM solvent61,62 in Gaussian03.60 The probe radius was set to be 0.6 Å.44 Solvent excluded surface was used to assign dielectric constant in the solute interior. Dielectric constant for the solute region was set to be 4 as discussed above, and that for the solvent region was set to be 1 for vacuum, 4 for a low dielectric environment, and 78.39 for a high-dielectric aqueous environment to be consistent with the PCM solvent in Gaussian03.60 The ionic strength was set to 0 mM. A grid spacing of 0.2 Å was used in the finite-difference PB solver. To ensure accurate boundary potential on the finite-difference grid, the longest dimension of the finite-difference grid was set to be 4 times that of solute. The relative convergence criterion was 0.0001 for the finite-difference solver. No cutoff for electrostatic interactions was used.
Parameter Development Strategy
Since covalent components vary little upon treatments of non-covalent components, it is safe to retain these parameters from previous generations of force fields, at least at this stage of the development. However, the two non-covalent components, namely, electrostatics and van der Waals interactions need careful refinement. Accurate treatment of non-covalent interactions were pioneered by OPLS developers in their efforts to pursuing accurate reproduction of the thermodynamic properties of pure organic liquids.11,66 Indeed, the OPLS non-covalent parameters have become the basis for all other modern force fields.
The accuracy of non-covalent parameters is also crucial for the development of any polarizable force fields. In this study we assumed that there is an overall consistency between implicit and explicit polarizable models, at least for intramolecular electrostatic interactions, because both models are designed to be consistent with the same benchmark ab initio training data, the B3LYP/cc-pVTZ electrostatics.54 Due to the consistency in electrostatics, intramolecular non-covalent parameters can be made interchangeable, at least approximately, between implicit and explicit polarizable models in Amber. Any future update of van der Waals parameters for the explicit polarizable model can be plugged into the continuum polarizable force field without further changes. This strategy apparently simplifies future refinements of all force fields based on the same benchmark ab initio quantum mechanical theory.
The only issue left in the development of non-covalent terms in the continuum polarizable force field is reproduction of solvation free energies of model compounds in a given solvent. In this study, we adopted the widely used thermodynamic cycle shown in Fig. 1 to compute solvation free energies of small organic compounds.49 In the thermodynamic cycle, electrostatic free energy, , is evaluated by discharging the solute in the first solvent (here in vacuum). The solute, now completely nonpolar, is transferred between the two solvents. This step gives the nonpolar, or repulsive/attractive contributions to the solvation energy, . The solute is then recharged in the second solvent (here in water), and the associated electrostatic interaction energy, , is calculated. The total solvation free energy, , is obtained from the sum of the free energies of the three separate steps:
Fig. 1.
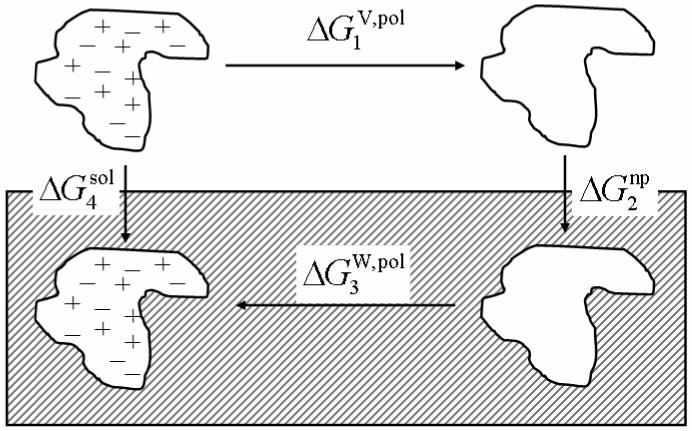
Thermodynamic cycle for solvation free energy calculation.
The total electrostatic solvation free energy at steps 1 and 3 is usually termed polar solvation free energy and the nonelectrostatic solvation free energy at step 2 is usually termed nonpolar solvation free energy. Thus, the total solvation free energy of a molecule can be expressed as a sum of polar (electrostatic) and nonpolar (van der Waals) solvation free energies. Both polar and nonpolar components need to be optimized for the continuum polarizable force field. Our previous study of nonpolar solvation free energy, however, shows that the nonpolar solvation free energy model does not contain any compound specific parameters that can be adjusted for optimal accuracy.45 Thus only polar solvation free energy needs to be optimized. In doing so the accuracy of the nonpolar solvation free energy model is on the order of ∼1.0 kcal/mol when it is compared with the TIP3P solvent even if an exhaustive optimization was utilized.45 Thus the lack of compound specific parameters does limit the overall accuracy of the calculated total solvation free energy.
Since only atomic cavity radii are the freely adjustable parameters in the polar component, the optimization of the polar component becomes rather straightforward. Here we have used a large and diversified set of generic organic molecules to optimize the atomic cavity radii. Following our previous effort in the calibration of atomic cavity radii for the nonpolarizable Amber force field,44 the atomic cavity radii can first be grouped by Amber atom types and the net charges of functional groups to increase the ratio between parameters and fitting data constraints. To further increase the ratio between parameters and fitting data constraints, we have removed a few rare atom types that cover less than 10 training molecules. Finally, a total of 20 parameters are used for the 39 Amber atom types against 353 experimental data constraints.
Computational Details
Polar solvation free energy is calculated by the PB solvent with the continuum polarizable solute force field. The boundary between solute and solvent is the solvent excluded surface with a probe radius of 0.6 Å44 and atomic cavity radii to be optimized. The solute and solvent, with associated charges and dielectric boundaries, are mapped onto a finite-difference grid. Electrostatic potentials are calculated by solving the PB equation with the finite-difference solver.64,65 The total polar solvation energy is the sum of steps 1 and 3 of Fig. 1,
where qi and ϕi are the charge and calculated potential at the ith gridpoint, for the case of transfer from vacuum (V) to water (W).
Nonpolar solvation free energy is decomposed into two terms: ΔGrep, repulsive (cavity) free energy, and ΔGatt, attractive (dispersion) free energy.45 Free energy simulations of spherical cavities have shown that for small cavities, ΔGrep correlates with the cavity volume, while for large cavities, ΔGrep correlates with the cavity surface.67-69 The crossover occurs around the cavity radius of 10 Å.70,71 Interestingly, a surprising conclusion from our previous analysis is that both molecular surfaces and volumes can be used as estimators of repulsive solvation free energies with very similar high accuracies even if the tested monomer molecules are all within the previously reported switching region (spherical radii around 10 Å) from volume-dependence to surface-dependence.45 A probable reason for the apparent discrepancy between our previous conclusion45 and the literature is that our simulations were on “realistic” molecules,45 while the literature simulations were performed on ideal spherical cavities. Our additional tests of both molecular surfaces and volumes on larger biomolecules show that molecular volumes transfer better from small molecules to large biomolecules (Tan and Luo, in preparation). Thus the molecular volumes were used to estimate ΔGrep. Specifically, the solvent accessible volume (SAV, i.e. the molecular volume enclosed by the solvent accessible surface) was used:45
| (6) |
where p = 0.0378 kcal/mol-Å3 is a solvent pressure parameter and c = -0.5692 kcal/mol.45 These parameters were optimized with respect to the TIP3P solvent, and the SAV was computed with the atomic van der Waals rmin radius definition and an optimized solvent probe of 1.30 Å.45
ΔGatt is approximated by the van der Waals attractive interaction potential energy between solute (u) and solvent (v) as72-74
| (7) |
In general, the solute-solvent van der Waals interaction energy can be analytically expressed as the following volume integral
| (8) |
Here the sum is over all solute atoms (Ns) and the integration is over the solvent occupied volume. ρaw(raw) is a solvent distribution function around solute atom a at a given solute-solvent distance raw. Vatt(raw) is the attractive van der Waals potential in the σ decomposition scheme: 45
| (9) |
| (10) |
where is the Lennard-Jones 6-12 potential. Here, A = 4εσ12 and B = 4εσ6, ε and σ are the well-depth and radius parameters of the Lennard-Jones potential, respectively. The Amber ff02 nonbonded parameters were used in this study for all molecules.
As a first approximation, a uniform distribution (i.e. constant density) can be used in Eqn (8). Under the constant water density approximation the volume integral in Eqn (8) can be transformed into an integral over the solute accessible surface (SAS) with a simple application of the divergence theorem:75
| (11) |
where indexes a and b run over all solute atoms. The surface integration is over the SAS of atom b (Sb). Θatt(ras) is a function defined on the SAS of atom b , and τ is the outward normal vector associated with the SAS element, dσs. In the σ decomposition scheme, the corresponding Θatt in Eqn (11) can be shown to be
| (12) |
| (13) |
Here Aaw, Baw are the van der Waal coefficients for interactions between solute atom a and water oxygen atoms (w).45
Empirical parameter optimization was conducted with a genetic algorithm (GA) based optimizer.76 GA is an efficient stochastic optimization method that has been widely applied to minimization problems because it is ideally suited for multiple-dimensional global search problems where the search space contains multiple local minima and the search variables may or may not be correlated. The GA begins with the generation of an initial population of a given number of solutions. The fitness of each solution, here the root mean squared deviations between the computed and experimental solvation free energies, is first evaluated. Then a new population is generated via selection, crossover, and mutation based on their fitness. This process is repeated until a desired fitness is reached or the maximum number of generations exceeded.
Molecular Systems
A set of 353 organic molecules77 was used in the parameterization of the polar component of the continuum polarizable force field. The complete 353-molecule set is further divided into two sets for the optimization and validation of PB cavity radii: 1) training set, which consists of odd sequence-numbered molecules; and 2) test set, which consist of even sequence-numbered molecules. Only the solvation free energies in water were used in the parameterization.78-81 All molecules were built with the SYBYL software package of Tripos Inc.82 and optimized using the MMFF94 force field.83-87 For each molecule, only the global minimum conformation was used. Simple conformational searches were performed for some molecules in cases where the global minimum conformations were not apparent. The geometry of each molecule was further optimized in HF/6-31G* using the Gaussian03 program.60
Results and Discussion
Quality of Atomic Charges
The agreement between theoretical and experimental solvation free energies strongly depends on the quality of atomic charges for tested molecules. As shown in our previous study, in principle it is possible to use one set of atomic charges to describe different solvent dielectric environments with the continuum polarizable model.54 However, it is impossible to do so when a traditional nonpolarizable model is used.54 This turns out to be the case in the current study with a much larger set of test molecules. Figure 2 shows the correlations of total molecular dipole moments between the continuum polarizable model and B3LYP/cc-pVTZ for the three dielectric environments used, in vacuo, ε=4, and ε=78.39. It should be pointed out that the total molecular dipole moment from the continuum polarizable model is the sum of the permanent dipole moment from the atomic point charges and the induced dipole moment computed from Eqn (4) after solving the PB equation. It can be found that the continuum polarizable model is consistent with B3LYP/cc-pVTZ as far as molecular dipole moments are concerned with correlation coefficients higher than 99% for all three different dielectric environments. It should also be emphasized again that it is impossible to use a single set of charges in the nonpolarizable model to achieve the same agreement with B3LYP/cc-pVTZ in all three environments simultaneously, as pointed out in our previous study for a smaller set of molecules.54
Fig. 2.
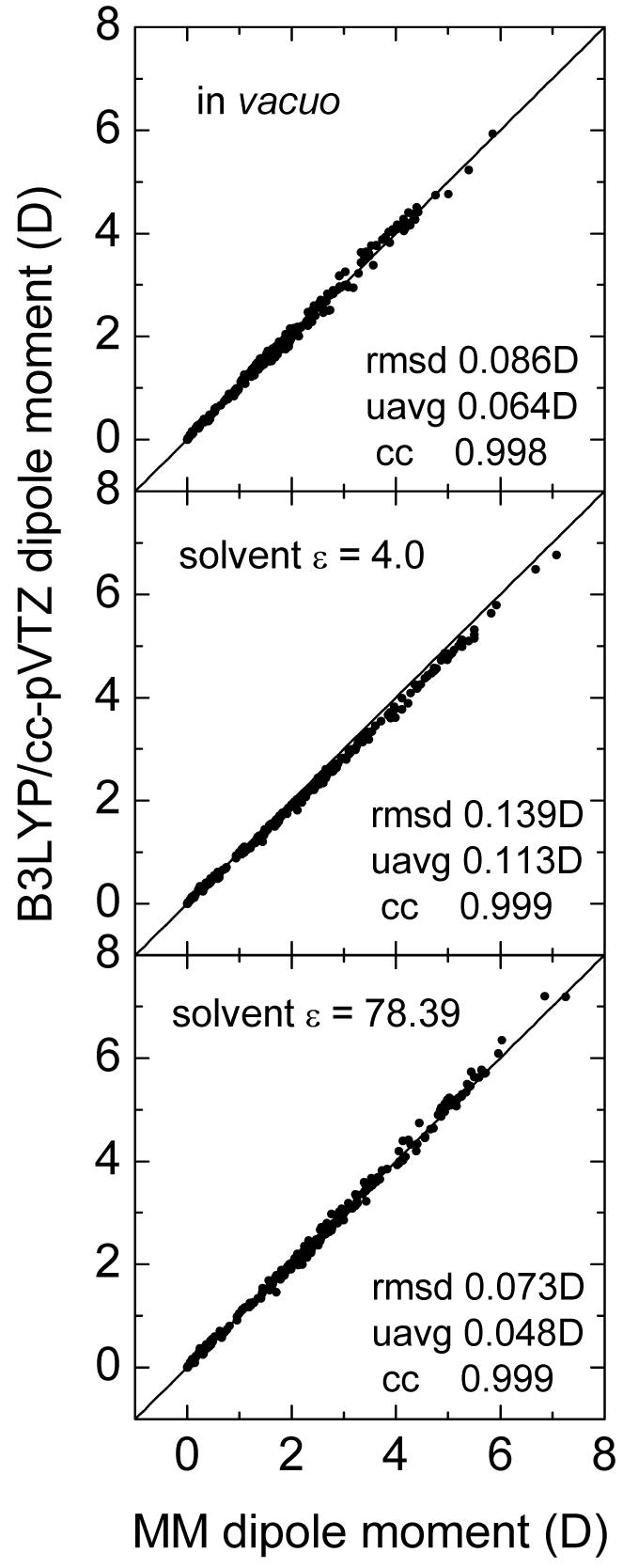
Dipole moments in vacuo, ε = 4, and ε = 78.39 for the 353-molecule set.
Comparison with experimental dipole moments also shows that the continuum polarizable model is reasonable as shown in Table 1. The root mean square deviation (RMSD), unsigned average error (UAVG), correlation coefficient is 0.50 Debye, 0.22 Debye, 90%, respectively, between the continuum polarizable model and experiment. This agreement should be viewed in the context that the same set of charges has to be used for all three different dielectric environments. Thus, the agreement with experiment in the gas phase alone is not trivial. The dipole moments with B3LYP/cc-pVTZ are also given. Given that B3LYP/cc-pVTZ and the continuum polarizable model are highly correlated, its agreement with experiment should be similar to that of the continuum polarizable model with RMSD of 0.52 Debye, UAVG of 0.20 Debye, and correlation coefficient of 90%. It should be pointed out that noticeable deviations exist between the continuum polarizable model and experiment for formates. However, similar deviations also exist for the same compounds with B3LYP/cc-pVTZ. This is not a surprise because the continuum polarizable model is trained to be consistent with B3LYP/cc-pVTZ. Finally the atomic charges for all molecules are given in the Amber prepin format in the Supplementary Material.
Table 1.
Gas-phase dipole moments (D) of selected organic compounds in the 353 molecule set. About two per functional groups are chosen. MM: continuum polarizable model. QM:B3LYP/cc-pVTZ. EXPT: Experimental values from the CRC Handbook of Chemistry and Physics, 87th.
| Compound | MM | QM | EXPT |
|---|---|---|---|
| propane | 0.06 | 0.09 | 0.08 |
| 2-methyl-1,3-butadiene | 0.23 | 0.26 | 0.25 |
| propyne | 0.76 | 0.8 | 0.78 |
| 1-butyne | 0.77 | 0.77 | 0.78 |
| 1-hexyne | 0.93 | 0.93 | 0.83 |
| toluene | 0.32 | 0.36 | 0.38 |
| ethylbenzene | 0.30 | 0.35 | 0.59 |
| fluoromethane | 1.54 | 1.71 | 1.86 |
| chlorofluoromethane | 1.72 | 1.72 | 1.82 |
| chloromethane | 1.87 | 1.94 | 1.9 |
| dichloromethane | 1.66 | 1.67 | 1.6 |
| bromomethane | 1.89 | 1.92 | 1.82 |
| dibromomethane | 1.58 | 1.52 | 1.43 |
| methanol | 1.39 | 1.57 | 1.7 |
| ethanol | 1.35 | 1.49 | 1.69 |
| phenol | 1.24 | 1.28 | 1.22 |
| diethyl ether | 0.95 | 0.99 | 1.15 |
| diisopropyl ether | 1.04 | 1.11 | 1.13 |
| acetaldehyde | 2.44 | 2.55 | 2.75 |
| propanal | 2.63 | 2.69 | 2.72 |
| acetone | 2.68 | 2.82 | 2.88 |
| acetic acid | 1.67 | 1.7 | 1.7 |
| methyl formate | 3.94 | 4.08 | 1.77 |
| ethyl formate | 4.03 | 4.16 | 1.93 |
| ethyl acetate | 1.95 | 2.04 | 1.78 |
| methylamine | 1.1 | 1.26 | 1.31 |
| ethylamine | 1.1 | 1.22 | 1.22 |
| propylamine | 1.06 | 1.16 | 1.17 |
| diethylamine | 0.78 | 0.81 | 0.92 |
| pyridine | 2.14 | 2.15 | 2.21 |
| 2-methylpyridine | 1.88 | 1.86 | 1.85 |
| 4-methylpyridine | 2.61 | 2.63 | 2.7 |
| acetonitrile | 3.81 | 3.92 | 3.92 |
| nitroethane | 3.38 | 3.59 | 3.23 |
| 1-nitropropane | 3.62 | 3.76 | 3.66 |
| 2-nitropropane | 3.44 | 3.64 | 3.73 |
| N-methylformamide | 4.04 | 4.08 | 3.83 |
| acetamide | 3.63 | 3.77 | 3.68 |
| dimethyl sulfide | 1.51 | 1.57 | 1.55 |
| diethyl sulfide | 1.49 | 1.59 | 1.54 |
Quality of van der Waals Parameters
The second important component in the continuum polarizable model that has to be properly calibrated is the van der Waals interaction. As discussed in Methods, the van der Waals parameters are assumed to be interchangeable between explicit and implicit polarizable force fields if an overall consistent electrostatic treatment can be maintained as the case between the ff02 explicit polarizable force field and the newly proposed continuum polarizable force field in Amber.
We have used dimer binding energies at the MP2/cc-pVTZ level of theory in the PCM solvent to test the compatibility between the continuum polarizable model and the existing van der Waals treatment in the Amber force fields. Table 2 lists the binding energies of four tested dimers in water, the intended environment to use the continuum polarizable model. It can be found that overall the continuum polarizable model agrees with MP2/cc-pVTZ very well, with deviations less than 0.9 kcal/mol. This can be compared with the agreement between the ff02 explicit polarizable force field and MP2/cc-pVTZ, which is also shown in Table 2. Note that the deviations between ff02 and MP2/cc-pVTZ are much larger in the gas phase, as high as 3.0 kcal/mol. However, it should be pointed that all binding energies are also uniformly larger in the gas phase. The electrostatic screening in water in general brings down the deviation in the aqueous phase as in the case for the continuum polarizable model. Thus, whether implicit or explicit polarizable treatment is used, reasonable agreement with MP2/cc-pVTZ can be achieved in the molecular mechanics approaches.
Table 2.
Dimer binding potential energies (kcal/mol). NMA: n-methylamine. ASH: acetate. SER: methanol. A: adenine. T: thymine. C: cytosine. G: guanine. ff02: explicit polarizable ff02 model. MP2: MP2/cc-pVTZ. MM: continuum polarizable model. Note that ff02 and associated MP2 calculations were performed in gas phase.
| Dimers | MM | MP2 | ff02 | MP2 |
|---|---|---|---|---|
| NMA/NMA | -3.85 | -3.01 | -7.16 | -7.47 |
| ASH/SER | -3.24 | -2.64 | -8.93 | -11.95 |
| AT | -6.41 | -6.50 | -13.25 | -15.29 |
| CG | -12.53 | -11.71 | -28.65 | -28.04 |
Calibration of PB Cavity Radii
The third important issue in the development of the continuum polarizable force field is the accuracy of solvation treatment. Note that this is very different from any polarizable or nonpolarizable force field that is intended for explicit solvent simulations, where the solvent interactions have been incorporated within the calibration of the van der Waals parameters of both solute and solvent molecules. As discussed in Methods, a total of 20 parameters are used for the 39 Amber atom types in the optimization against 353 experimental data constraints.
The new PB atomic cavity radii are optimized by reproducing the solvation free energies of 177 molecules in the training set, and are tested against the test set of 176 molecules. Genetic algorithm (GA) was used to optimize the cavity radii. The optimized cavity radii along with the corresponding Amber atom types in the continuum polarizable model are given in Table 3. The statistics for the training set, the test set, and the complete 353-molecule set are shown in Table 4. It can be found that the optimized PB atomic cavity radii transfer well from the training set to the test set. RMSD, UAVG, correlation coefficient are 1.27 kcal/mol, 1.06 kcal/mol, 93% for the training set, and 1.34 kcal/mol, 1.08 kcal/mol, 91% for the test set, respectively. Overall an RMSD of 1.30kcal/mol, UAVG of 1.07 kcal/mol, and correlation coefficient of 92% are achieved for the 353-molecule set. Correlation between theoretical and experimental solvation free energies for the 353-molecule set is also given in Fig. 3. Table 5 lists the solvation free energies for all molecules by both theory and experiment. The polar components, the nonpolar cavity components, and the nonpolar attractive components of solvation free energies are also given for all 353 molecules.
Table 3.
PB atomic cavity radii (Å) and atom types.
| Atom type | PB radius | Description |
|---|---|---|
| h1 | 0.421 | H bonded to aliphatic carbon with 1 electrwd. group |
| h2 | 0.327 | H bonded to aliphatic carbon with 2 electrwd. group |
| h4 | 0.577 | H bonded to non-sp3 carbon with 1 electrwd. group |
| h5 | 2.021 | H bonded to non-sp3 carbon with 2 electrwd. group |
| ha | 0.735 | H bonded to aromatic carbon |
| hc | 0.753 | H bonded to aliphatic carbon without electrwd. group |
| hn | 0.681 | H bonded to nitrogen atoms |
| ho | 0.000 | Hydroxyl group |
| o | 1.117 | Oxygen with one connected atom |
| oh | 1.293 | Oxygen in hydroxyl group |
| os | 1.094 | Ether and ester oxygen |
| c | 1.200 | Sp2 C carbonyl group |
| c1 | 1.139 | Sp C |
| c2 | 1.200 | Sp2 C |
| c3 | 1.181 | Sp3 C |
| ca | 1.139 | Sp2 C in pure aromatic systems |
| cc | 1.139 | Sp2 carbons in non-pure aromatic systems |
| cd | 1.139 | Sp2 carbons in non-pure aromatic systems, identical to cc |
| ce | 1.139 | Inner Sp2 carbons in conjugated systems |
| cf | 1.139 | Inner Sp2 carbons in conjugated systems, identical to ce |
| cp | 1.139 | Head Sp2 C that connect two rings in biphenyl sys. |
| n | 1.114 | Sp2 nitrogen in amide groups |
| n1 | 1.114 | Sp N |
| n2 | 1.114 | Aliphatic Sp2 N with two connected atoms |
| n3 | 1.114 | Sp3 N with three connected atoms |
| na | 1.114 | Sp2 N with three connected atoms |
| nb | 1.114 | Sp2 N in pure aromatic systems |
| nc | 1.114 | Sp2 N in non-pure aromatic systems |
| nd | 1.114 | Sp2 N in non-pure aromatic systems, identical to nc |
| nh | 1.114 | Amine N connected one or more aromatic rings |
| no | 1.114 | Nitro N |
| s | 2.210 | S with one connected atom |
| sh | 2.210 | Sp3 S connected with hydrogen |
| ss | 2.210 | S with one connected atom |
| p5 | 1.514 | Phosphate with four connected atoms, such as O P(OH)3 |
| py | 1.514 | Special p5 in conjugated system |
| f | 1.612 | Fluorine |
| cl | 2.488 | Chlorine |
| br | 2.616 | Bromine |
Table 4.
Statistics for the training set (177), the test set (176), and the 353-molecule set. RMSD: root-mean-squared deviation (in kcal/mol). UAVG: unsigned average error (in kcal/mol). CC: correlation coefficient.
| training | test | all | |
|---|---|---|---|
| RMSD | 1.27 | 1.34 | 1.30 |
| UAVG | 1.06 | 1.08 | 1.07 |
| CC | 93% | 91% | 92% |
Fig. 3.
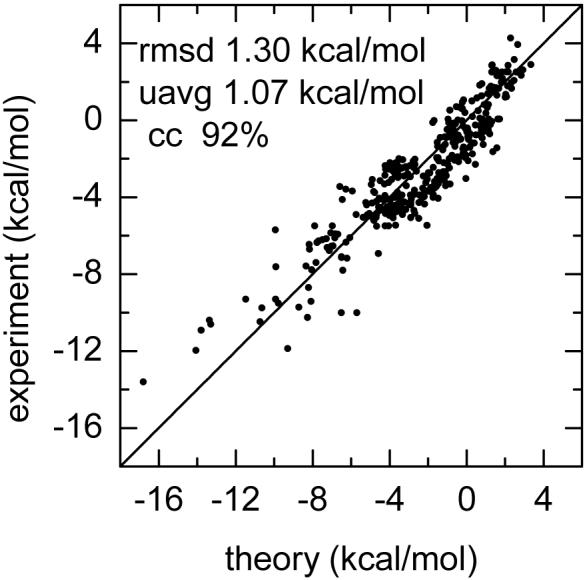
Calculated and experimental solvation free energies for the 353-molecule set.
Table 5.
Solvation free energies (in kcal/mol) of all 353 organic compounds. POL: the polar/electrostatic component; NPrep: the repulsive nonpolar component; NPatt: the attractive nonpolar component; TOT: total theoretical values; EXP: experimental values.
| No. | Compound | POL | NPrep | NPatt | TOT | EXP |
|---|---|---|---|---|---|---|
| 1 | methane | -0.75 | 6.35 | -3.78 | 1.82 | 1.98 |
| 2 | propane | -0.39 | 11.18 | -8.46 | 2.33 | 1.96 |
| 3 | 2-methyl propane | -1.19 | 13.17 | -10.40 | 1.58 | 2.32 |
| 4 | 2,2-dimethyl propane | -1.44 | 14.97 | -12.23 | 1.31 | 2.50 |
| 5 | n-butane | -0.61 | 13.44 | -10.36 | 2.47 | 2.08 |
| 6 | 2,2-dimethylbutane | -1.48 | 16.82 | -13.80 | 1.54 | 2.59 |
| 7 | cyclopentane | -0.05 | 13.83 | -11.77 | 2.01 | 1.20 |
| 8 | n-pentane | -0.33 | 15.68 | -12.50 | 2.85 | 2.33 |
| 9 | 2-methylpentane | -1.08 | 17.48 | -14.23 | 2.17 | 2.52 |
| 10 | 3-methyl pentane | -0.53 | 17.26 | -14.14 | 2.58 | 2.51 |
| 11 | 2,4-dimethyl pentane | -1.89 | 19.22 | -15.99 | 1.34 | 2.88 |
| 12 | 2,2,4-trimethyl pentane | -2.09 | 20.75 | -17.35 | 1.31 | 2.85 |
| 13 | methylcyclopentane | -0.90 | 15.93 | -13.52 | 1.52 | 1.60 |
| 14 | n-hexane | -0.57 | 17.94 | -14.66 | 2.71 | 2.49 |
| 15 | cyclohexane | -0.02 | 15.62 | -13.52 | 2.08 | 1.23 |
| 16 | methylcyclohexane | -0.76 | 17.63 | -15.46 | 1.41 | 1.71 |
| 17 | cis-1,2-dimethylcyclohexane | -1.24 | 19.36 | -16.80 | 1.32 | 1.58 |
| 18 | n-heptane | -0.72 | 20.20 | -16.56 | 2.92 | 2.62 |
| 19 | n-octane | -0.58 | 22.49 | -18.57 | 3.34 | 2.89 |
| 20 | ethylene | -1.99 | 7.72 | -4.95 | 0.77 | 1.27 |
| 21 | propylene | -2.03 | 10.20 | -7.38 | 0.79 | 1.27 |
| 22 | 2-methyl propene | -2.37 | 12.44 | -9.54 | 0.53 | 1.16 |
| 23 | 1-butene | -1.92 | 12.54 | -9.52 | 1.10 | 1.38 |
| 24 | 2-methyl-2-butene | -1.35 | 14.56 | -11.63 | 1.58 | 1.31 |
| 25 | 3-methyl-1-butene | -2.66 | 14.61 | -11.26 | 0.69 | 1.83 |
| 26 | 1-pentene | -1.99 | 14.79 | -11.61 | 1.18 | 1.66 |
| 27 | trans-2-pentene | -1.27 | 15.02 | -11.70 | 2.05 | 1.34 |
| 28 | 4-methyl-1-pentene | -2.54 | 16.62 | -13.27 | 0.80 | 1.91 |
| 29 | 1-hexene | -1.92 | 17.07 | -13.47 | 1.68 | 1.66 |
| 30 | cyclohexene | -1.07 | 14.86 | -12.78 | 1.01 | 0.37 |
| 31 | trans-2-heptene | -1.44 | 19.54 | -15.77 | 2.33 | 1.66 |
| 32 | 1-methylcyclohexene | -1.41 | 17.05 | -14.57 | 1.07 | 0.67 |
| 33 | 1-octene | -2.13 | 21.59 | -17.58 | 1.87 | 2.17 |
| 34 | 1,3-butadiene | -3.29 | 11.44 | -8.37 | -0.22 | 0.61 |
| 35 | 2-methyl-1,3-butadiene | -3.23 | 13.44 | -10.58 | -0.37 | 0.68 |
| 36 | 2,3-dimethyl-1,3-butadiene | -2.93 | 15.35 | -12.50 | -0.09 | 0.40 |
| 37 | 1,4-pentadiene | -3.56 | 13.84 | -10.49 | -0.21 | 0.94 |
| 38 | 1,5-hexadiene | -3.38 | 16.18 | -12.51 | 0.29 | 1.01 |
| 39 | acetylene | -4.28 | 6.80 | -4.20 | -1.68 | -0.01 |
| 40 | propyne | -3.75 | 9.40 | -6.66 | -1.01 | -0.48 |
| 41 | 1-butyne | -3.71 | 11.85 | -8.78 | -0.65 | -0.15 |
| 42 | 1-pentyne | -3.94 | 14.08 | -11.00 | -0.86 | -0.16 |
| 43 | 1-hexyne | -3.85 | 16.37 | -12.98 | -0.45 | 0.01 |
| 44 | 1-heptyne | -3.89 | 18.62 | -14.97 | -0.25 | 0.60 |
| 45 | 1-octyne | -4.07 | 20.87 | -17.32 | -0.52 | 0.71 |
| 46 | 1-nonyne | -3.98 | 23.14 | -19.30 | -0.15 | 1.05 |
| 47 | benzene | -2.56 | 12.95 | -10.93 | -0.54 | -0.89 |
| 48 | toluene | -3.10 | 15.25 | -12.97 | -0.82 | -0.76 |
| 49 | 1,2,4-trimethylbenzene | -3.50 | 19.40 | -16.81 | -0.91 | -0.86 |
| 50 | ethylbenzene | -2.57 | 17.49 | -14.91 | 0.01 | -0.61 |
| 51 | m-xylene | -3.49 | 17.51 | -14.92 | -0.90 | -0.80 |
| 52 | o-xylene | -3.45 | 17.11 | -15.03 | -1.36 | -0.90 |
| 53 | p-xylene | -3.37 | 17.55 | -14.96 | -0.78 | -0.80 |
| 54 | propylbenzene | -2.99 | 19.75 | -16.70 | 0.07 | -0.53 |
| 55 | 2-propylbenzene | -3.28 | 19.37 | -16.27 | -0.18 | -0.30 |
| 56 | butylbenzene | -3.36 | 21.99 | -18.59 | 0.04 | -0.40 |
| 57 | 2-butylbenzene | -3.09 | 21.46 | -18.41 | -0.04 | -0.45 |
| 58 | tert-butylbenzene | -3.60 | 20.85 | -17.95 | -0.69 | -0.44 |
| 59 | tert-amylbenzene | -3.59 | 22.73 | -19.72 | -0.58 | -0.18 |
| 60 | naphthalene | -4.55 | 17.89 | -16.48 | -3.14 | -2.41 |
| 61 | anthracene | -5.85 | 22.82 | -21.67 | -4.69 | -4.23 |
| 62 | phenanthrene | -5.48 | 22.55 | -21.61 | -4.54 | -4.06 |
| 63 | acenaphthene | -4.43 | 20.71 | -19.41 | -3.13 | -3.4 |
| 64 | p-chlorotoluene | -2.40 | 16.85 | -14.82 | -0.37 | -1.92 |
| 65 | fluoromethane | -1.16 | 6.73 | -4.32 | 1.25 | -0.22 |
| 66 | 1,1-difluoroethane | -1.54 | 9.94 | -7.38 | 1.02 | -0.11 |
| 67 | tetrafluoromethane | -0.10 | 8.94 | -6.36 | 2.48 | 3.16 |
| 68 | hexafluoroethane | -0.08 | 12.27 | -9.53 | 2.67 | 3.94 |
| 69 | octafluoropropane | -0.27 | 15.19 | -12.63 | 2.29 | 4.28 |
| 70 | fluorobenzene | -2.83 | 13.61 | -11.44 | -0.66 | -0.78 |
| 71 | 2-chloro-1,1,1-trifluoroethane | -2.97 | 11.98 | -9.98 | -0.96 | 0.05 |
| 72 | chlorofluoromethane | -2.19 | 8.35 | -6.60 | -0.44 | -0.77 |
| 73 | chlorotrifluoromethane | -0.01 | 9.90 | -7.84 | 2.05 | 2.52 |
| 74 | dichlorodifluoromethane | 0.00 | 10.89 | -9.36 | 1.53 | 1.69 |
| 75 | fluorotrichloromethane | -0.01 | 11.85 | -10.70 | 1.14 | 0.82 |
| 76 | 1,1,2-trichloro-1,2,2-trifluoroethane | -0.02 | 14.89 | -13.59 | 1.28 | 1.77 |
| 77 | 1,1,2,2-tetrachlorodifluoroethane | -0.03 | 15.76 | -14.80 | 0.92 | 0.82 |
| 78 | chloropentafluoroethane | -0.04 | 13.17 | -10.99 | 2.15 | 2.86 |
| 79 | 1,1-dichorotetrafluoroethane | -0.04 | 14.04 | -12.16 | 1.84 | 2.50 |
| 80 | 1,2-dichlorotetrafluoroethane | -0.02 | 14.06 | -12.34 | 1.70 | 2.31 |
| 81 | 1-bromo-1-chloro-2,2,2-trifluoroethane | -2.67 | 14.37 | -12.61 | -0.91 | -0.13 |
| 82 | bromotrifluoromethane | -0.01 | 10.98 | -8.85 | 2.13 | 1.79 |
| 83 | 1-bromo-1,2,2,2-tetrafluoroethane | -3.08 | 13.50 | -11.28 | -0.86 | 0.52 |
| 84 | chloromethane | -1.77 | 7.74 | -5.96 | 0.02 | -0.56 |
| 85 | dichloromethane | -2.41 | 9.37 | -8.14 | -1.19 | -1.36 |
| 86 | tetrachloromethane | -0.03 | 12.78 | -12.05 | 0.70 | 0.10 |
| 87 | chloroethane | -0.85 | 10.29 | -8.29 | 1.15 | -0.63 |
| 88 | 1,1-dichloroethane | -1.41 | 11.82 | -10.28 | 0.14 | -0.85 |
| 89 | e-1,2-dichloroethane | -1.68 | 11.72 | -10.21 | -0.18 | -1.73 |
| 90 | 1,1,1-trichloroethane | -0.79 | 13.39 | -12.15 | 0.46 | -0.25 |
| 91 | 1,1,2-trichloroethane | -2.57 | 13.19 | -12.16 | -1.54 | -1.95 |
| 92 | 1,1,1,2-tetrachloroethane | -2.43 | 14.69 | -13.79 | -1.52 | -1.15 |
| 93 | 1,1,2,2-tetrachloroethane | -3.65 | 14.60 | -13.89 | -2.93 | -2.36 |
| 94 | pentachloroethane | -2.04 | 16.04 | -15.50 | -1.50 | -1.36 |
| 95 | hexachloroethane | -0.05 | 17.40 | -17.17 | 0.17 | -1.40 |
| 96 | 1-chloropropane | -1.33 | 12.61 | -10.38 | 0.90 | -0.35 |
| 97 | 2-chloropropane | -1.13 | 12.54 | -10.36 | 1.05 | -0.24 |
| 98 | 1,2-dichloropropane | -2.87 | 13.91 | -12.15 | -1.10 | -1.25 |
| 99 | 1,3-dichloropropane | -2.18 | 14.00 | -12.29 | -0.47 | -1.90 |
| 100 | 1-chlorobutane | -1.51 | 14.86 | -12.55 | 0.80 | -0.14 |
| 101 | 2-chlorobutane | -1.25 | 14.69 | -12.28 | 1.16 | 0.07 |
| 102 | 1,1-dichlorobutane | -1.84 | 16.26 | -14.24 | 0.19 | -0.70 |
| 103 | 1-chloropentane | -1.31 | 17.11 | -14.49 | 1.31 | -0.07 |
| 104 | 2-chloropentane | -1.10 | 16.95 | -14.14 | 1.71 | 0.07 |
| 105 | 3-chloropentane | -1.00 | 16.80 | -14.16 | 1.64 | 0.07 |
| 106 | chloroethylene | -1.60 | 9.36 | -7.17 | 0.60 | 0.49 |
| 107 | cis-1,2-dichloroethylene | -1.44 | 10.91 | -9.21 | 0.26 | -1.17 |
| 108 | trans-1,2-dichloroethylene | -1.16 | 10.99 | -9.33 | 0.49 | -0.76 |
| 109 | trichloroethylene | -0.50 | 12.53 | -11.23 | 0.81 | -0.44 |
| 110 | tetrachloroethylene | 0.00 | 14.06 | -13.25 | 0.82 | 0.05 |
| 111 | 3-chloropropane | -1.30 | 12.61 | -10.40 | 0.91 | -0.57 |
| 112 | chlorobenzene | -2.02 | 14.55 | -12.87 | -0.35 | -1.01 |
| 113 | o-chlorotoluene | -2.47 | 16.60 | -14.71 | -0.59 | -1.15 |
| 114 | 1,2-dichlorobenzene | -1.73 | 16.02 | -14.90 | -0.61 | -1.36 |
| 115 | 1,3-dichlorobenzene | -1.40 | 16.14 | -15.03 | -0.29 | -0.98 |
| 116 | 1,4-dichlorobenzene | -1.29 | 16.17 | -14.77 | 0.11 | -1.01 |
| 117 | 2,2′-dichlorobiphenyl | -3.97 | 24.52 | -21.99 | -1.45 | -2.73 |
| 118 | 2,3-dichlorobiphenyl | -3.64 | 24.48 | -22.57 | -1.72 | -2.45 |
| 119 | 2,2,3′-trichlorobiphenyl | -3.56 | 25.93 | -23.88 | -1.52 | -1.99 |
| 120 | bromotrichloromethane | -0.03 | 13.75 | -12.91 | 0.81 | -0.93 |
| 121 | 1-chloro-2-bromoethane | -1.79 | 12.78 | -11.06 | -0.06 | -1.95 |
| 122 | bromomethane | -2.32 | 8.90 | -6.98 | -0.41 | -0.82 |
| 123 | dibromomethane | -3.08 | 11.57 | -9.93 | -1.44 | -2.11 |
| 124 | bromoethane | -0.96 | 11.34 | -9.17 | 1.21 | -0.70 |
| 125 | 1,2-dibromoethane | -1.85 | 13.85 | -11.92 | 0.09 | -2.10 |
| 126 | 1-bromopropane | -1.61 | 13.66 | -11.27 | 0.78 | -0.56 |
| 127 | 2-bromopropane | -1.13 | 13.50 | -11.25 | 1.13 | -0.48 |
| 128 | 1,2-dibromopropane | -3.48 | 15.82 | -13.82 | -1.48 | -1.94 |
| 129 | 1,3-dibromopropane | -2.68 | 16.13 | -14.14 | -0.70 | -1.96 |
| 130 | 1-bromo-2-methylpropane | -2.65 | 15.46 | -13.04 | -0.23 | -0.03 |
| 131 | 1-bromobutane | -1.85 | 15.94 | -13.33 | 0.76 | -0.41 |
| 132 | 1-bromo-3-methylbutane | -2.47 | 17.73 | -14.96 | 0.30 | 0.20 |
| 133 | 1-bromopentane | -1.57 | 18.19 | -15.41 | 1.21 | -0.08 |
| 134 | 3-bromopropene | -3.48 | 12.70 | -10.34 | -1.12 | -0.86 |
| 135 | bromobenzene | -1.97 | 15.60 | -13.68 | -0.04 | -1.46 |
| 136 | 1,4-dibromobenzne | -1.14 | 18.24 | -16.64 | 0.46 | -2.30 |
| 137 | p-bromotoluene | -2.40 | 17.89 | -15.63 | -0.14 | -1.39 |
| 138 | 1-bromo-2-ethylbenzene | -1.97 | 19.57 | -17.20 | 0.40 | -1.19 |
| 139 | o-bromocumene | -2.49 | 21.42 | -18.85 | 0.07 | -0.85 |
| 140 | methanol | -5.21 | 6.71 | -5.32 | -3.81 | -5.07 |
| 141 | ethanol | -4.98 | 9.30 | -7.64 | -3.33 | -4.90 |
| 142 | 2,2,2-trifluoroethanol | -6.56 | 11.02 | -9.36 | -4.90 | -4.30 |
| 143 | ethylene glycol | -10.63 | 9.72 | -9.01 | -9.92 | -9.30 |
| 144 | 1-propanol | -5.93 | 11.60 | -9.88 | -4.21 | -4.85 |
| 145 | 2-propanol | -5.52 | 11.63 | -9.72 | -3.61 | -4.75 |
| 146 | 1,1,1-trifluoro-2-propanol | -6.18 | 13.19 | -11.28 | -4.27 | -4.16 |
| 147 | 2,2,3,3-tetrafluoropropanol | -7.53 | 13.53 | -11.74 | -5.74 | -4.90 |
| 148 | 2,2,3,3,3-pentafluoropropanol | -5.84 | 14.15 | -12.27 | -3.96 | -4.15 |
| 149 | hexafluoro-2-propanol | -6.68 | 14.66 | -12.75 | -4.77 | -3.76 |
| 150 | 2-methyl-1-propanol | -6.44 | 13.54 | -11.67 | -4.57 | -4.51 |
| 151 | 1-butanol | -5.53 | 13.86 | -11.89 | -3.56 | -4.72 |
| 152 | 2-butanol | -5.49 | 13.82 | -11.81 | -3.48 | -4.61 |
| 153 | tert-butyl alcohol | -6.07 | 13.67 | -11.70 | -4.09 | -4.51 |
| 154 | 2-methyl-1-butanol | -5.78 | 15.59 | -13.49 | -3.67 | -4.42 |
| 155 | 3-methyl butanol | -6.02 | 15.70 | -13.67 | -3.98 | -4.42 |
| 156 | 2-methyl-2-butanol | -5.99 | 15.64 | -13.39 | -3.74 | -4.43 |
| 157 | 2,3-dimethylbutanol | -6.34 | 17.30 | -15.20 | -4.25 | -3.91 |
| 158 | 1-pentanol | -5.58 | 16.12 | -13.94 | -3.39 | -4.49 |
| 159 | 2-pentanol | -5.36 | 16.09 | -13.63 | -2.90 | -4.39 |
| 160 | 3-pentanol | -4.56 | 16.04 | -13.67 | -2.18 | -4.35 |
| 161 | 2-methyl-1-pentanol | -6.02 | 17.86 | -15.42 | -3.58 | -3.93 |
| 162 | 2-methyl-2-pentanol | -6.17 | 17.89 | -15.38 | -3.66 | -3.93 |
| 163 | 2-methyl-3-pentanol | -5.82 | 17.79 | -15.33 | -3.36 | -3.89 |
| 164 | 4-methyl-2-pentanol | -6.07 | 17.85 | -15.37 | -3.59 | -3.74 |
| 165 | cyclopentanol | -5.44 | 14.32 | -13.11 | -4.23 | -5.49 |
| 166 | 1-hexanol | -6.03 | 18.40 | -15.93 | -3.56 | -4.36 |
| 167 | 3-hexanol | -4.73 | 18.32 | -15.68 | -2.10 | -3.68 |
| 168 | cyclohexanol | -5.22 | 16.10 | -14.89 | -4.01 | -4.95 |
| 169 | 4-heptanol | -4.64 | 20.56 | -17.66 | -1.74 | -4.01 |
| 170 | cycloheptanol | -5.39 | 17.86 | -16.52 | -4.05 | -5.49 |
| 171 | 1-heptanol | -5.91 | 20.66 | -17.97 | -3.22 | -4.25 |
| 172 | 1-octanol | -5.81 | 22.92 | -19.98 | -2.87 | -4.10 |
| 173 | allyl alcohol | -6.83 | 10.63 | -8.70 | -4.90 | -5.03 |
| 174 | cyclopentanol | -5.44 | 14.32 | -13.11 | -4.23 | -5.49 |
| 175 | phenol | -8.16 | 13.61 | -12.39 | -6.94 | -6.53 |
| 176 | 4-bromophenol | -7.69 | 16.25 | -15.06 | -6.50 | -7.10 |
| 177 | 4-nitrophenol | -12.28 | 15.95 | -16.97 | -13.29 | -10.6 |
| 178 | 4-tert-butylphenol | -8.95 | 21.52 | -19.26 | -6.69 | -5.92 |
| 179 | 2-creol | -8.57 | 15.75 | -14.24 | -7.06 | -5.86 |
| 180 | 3-creol | -8.52 | 15.88 | -14.33 | -6.97 | -5.49 |
| 181 | 4-creol | -8.38 | 15.91 | -14.38 | -6.85 | -6.12 |
| 182 | 2,2,2-trifluoroethanol | -6.56 | 11.02 | -9.36 | -4.90 | -4.31 |
| 183 | p-bromophenol | -7.69 | 16.25 | -15.06 | -6.50 | -7.13 |
| 184 | 2-methoxyethanol | -8.09 | 12.26 | -11.30 | -7.13 | -6.77 |
| 185 | dimethoxymethane | -4.02 | 12.45 | -11.35 | -2.92 | -2.93 |
| 186 | methyl propyl ether | -2.39 | 14.15 | -11.91 | -0.15 | -1.66 |
| 187 | methyl iopropyl ether | -3.11 | 13.90 | -11.69 | -0.90 | -2.00 |
| 188 | methyl tert-butyl ether | -3.51 | 15.68 | -13.35 | -1.18 | -2.21 |
| 189 | diethyl ether | -2.08 | 14.45 | -12.07 | 0.30 | -1.75 |
| 190 | ethyl propyl ether | -2.66 | 16.73 | -14.10 | -0.03 | -1.81 |
| 191 | dipropyl ether | -3.51 | 19.04 | -16.22 | -0.69 | -1.16 |
| 192 | diiopropyl ether | -4.12 | 18.53 | -15.24 | -0.84 | -0.53 |
| 193 | di-n-butyl ether | -2.42 | 23.56 | -20.38 | 0.77 | -0.83 |
| 194 | tetrahydrofuran | -2.23 | 12.28 | -11.21 | -1.17 | -3.12 |
| 195 | 2-methyltetrahydrofuran | -3.04 | 14.64 | -13.06 | -1.46 | -3.3 |
| 196 | aniole | -4.45 | 15.87 | -14.53 | -3.11 | -2.45 |
| 197 | ethyl phenyl ether | -4.68 | 18.45 | -16.24 | -2.46 | -4.28 |
| 198 | 1,1-diethoxyethane | -4.17 | 19.83 | -16.73 | -1.07 | -3.27 |
| 199 | 1,2-dimethoxyethane | -4.19 | 14.80 | -13.30 | -2.70 | -4.84 |
| 200 | 1,2-diethoxyethane | -4.60 | 19.98 | -17.65 | -2.28 | -3.53 |
| 201 | 1,3-dioxolane | -3.96 | 10.69 | -10.70 | -3.97 | -4.09 |
| 202 | 1,4-dioxane | -4.67 | 12.65 | -12.68 | -4.70 | -5.05 |
| 203 | 2,2,2-trifluoroethyl vinyl ether | -4.47 | 15.28 | -12.56 | -1.75 | -0.12 |
| 204 | acetaldehyde | -3.67 | 8.77 | -6.95 | -1.85 | -3.50 |
| 205 | propanal | -3.69 | 11.13 | -9.19 | -1.74 | -3.44 |
| 206 | butanal | -3.82 | 13.41 | -11.24 | -1.66 | -3.18 |
| 207 | pentanal | -3.90 | 15.67 | -13.29 | -1.53 | -3.03 |
| 208 | hexanal | -3.83 | 17.93 | -15.36 | -1.26 | -2.81 |
| 209 | heptanal | -4.00 | 20.17 | -17.27 | -1.10 | -2.67 |
| 210 | octanal | -4.04 | 22.44 | -19.37 | -0.97 | -2.29 |
| 211 | nonanal | -3.96 | 24.71 | -21.37 | -0.62 | -2.07 |
| 212 | trans-2-butenal | -4.42 | 12.51 | -10.47 | -2.38 | -4.23 |
| 213 | trans-2-hexenal | -4.61 | 17.11 | -14.54 | -2.05 | -3.68 |
| 214 | trans-2-octenal | -4.48 | 21.61 | -18.70 | -1.57 | -3.44 |
| 215 | trans,trans-2,4-hexadienal | -5.65 | 16.23 | -13.74 | -3.16 | -4.64 |
| 216 | benzaldehyde | -5.06 | 15.05 | -13.73 | -3.74 | -4.02 |
| 217 | m-hydroxybenzaldehyde | -10.33 | 15.69 | -15.14 | -9.78 | -9.51 |
| 218 | p-hydroxybenzaldehyde | -11.26 | 15.70 | -15.17 | -10.73 | -10.47 |
| 219 | acetone | -4.10 | 11.15 | -9.25 | -2.19 | -3.80 |
| 220 | 2-butanone | -4.04 | 13.41 | -11.26 | -1.89 | -3.71 |
| 221 | 3-methyl-2-butanone | -4.45 | 15.37 | -13.03 | -2.12 | -3.24 |
| 222 | 3,3-dimethylbutanone | -4.68 | 16.88 | -14.44 | -2.25 | -2.89 |
| 223 | 2-pentanone | -4.18 | 15.69 | -13.16 | -1.66 | -3.52 |
| 224 | 3-pentanone | -3.61 | 15.67 | -13.15 | -1.09 | -3.41 |
| 225 | 4-methyl-2-pentanone | -4.61 | 17.53 | -14.96 | -2.04 | -3.06 |
| 226 | 2,4-dimethyl-3-pentanone | -5.02 | 19.49 | -16.39 | -1.92 | -2.74 |
| 227 | cyclopentanone | -3.99 | 13.90 | -12.63 | -2.73 | -4.68 |
| 228 | 2-hexanone | -4.35 | 17.96 | -15.15 | -1.55 | -3.41 |
| 229 | 2-heptanone | -4.23 | 20.21 | -17.32 | -1.34 | -3.04 |
| 230 | 4-heptanone | -4.24 | 20.23 | -17.10 | -1.12 | -2.93 |
| 231 | 2-octanone | -4.31 | 22.46 | -19.20 | -1.05 | -2.88 |
| 232 | 2-nonanone | -4.45 | 24.75 | -21.20 | -0.89 | -2.48 |
| 233 | 5-nonanone | -4.86 | 24.76 | -21.11 | -1.21 | -2.67 |
| 234 | 2-undecanone | -4.46 | 29.27 | -25.22 | -0.41 | -2.15 |
| 235 | acetophenone | -5.23 | 17.23 | -15.94 | -3.95 | -4.58 |
| 236 | acetic acid | -9.05 | 9.44 | -8.56 | -8.17 | -6.70 |
| 237 | propionic acid | -9.33 | 11.72 | -10.57 | -8.18 | -6.46 |
| 238 | butyric acid | -9.27 | 13.99 | -12.5 | -7.77 | -6.35 |
| 239 | pentanoic acid | -8.94 | 16.26 | -14.61 | -7.29 | -6.16 |
| 240 | hexanoic acid | -9.40 | 18.52 | -16.60 | -7.48 | -6.21 |
| 241 | 4-amino-3,5,6-trichloropyridine-2-carboxylic acid |
-12.64 | 20.39 | -21.81 | -14.07 | -11.96 |
| 242 | methyl formate | -4.01 | 9.43 | -8.48 | -3.06 | -2.78 |
| 243 | ethyl formate | -3.95 | 12.04 | -10.68 | -2.60 | -2.65 |
| 244 | propyl formate | -4.23 | 14.32 | -12.82 | -2.73 | -2.48 |
| 245 | methyl acetate | -5.64 | 11.96 | -10.59 | -4.27 | -3.31 |
| 246 | iopropyl formate | -4.28 | 14.21 | -12.60 | -2.67 | -2.02 |
| 247 | iobutyl formate | -4.46 | 16.29 | -14.61 | -2.78 | -2.22 |
| 248 | ioamyl formate | -4.62 | 18.44 | -16.59 | -2.76 | -2.13 |
| 249 | ethyl acetate | -5.77 | 14.56 | -12.69 | -3.89 | -3.08 |
| 250 | propyl acetate | -6.30 | 16.87 | -14.82 | -4.24 | -2.85 |
| 251 | iopropyl acetate | -5.99 | 16.66 | -14.48 | -3.81 | -2.65 |
| 252 | butyl acetate | -5.84 | 19.13 | -16.90 | -3.61 | -2.55 |
| 253 | iobutyl acetate | -6.45 | 18.77 | -16.55 | -4.23 | -2.36 |
| 254 | amyl acetate | -6.11 | 21.40 | -18.80 | -3.50 | -2.45 |
| 255 | ioamyl acetate | -6.47 | 20.96 | -18.47 | -3.98 | -2.21 |
| 256 | hexyl acetate | -6.35 | 23.64 | -20.90 | -3.61 | -2.26 |
| 257 | methyl propionae | -5.25 | 14.25 | -12.55 | -3.56 | -2.97 |
| 258 | ethyl propionate | -5.82 | 16.85 | -14.60 | -3.56 | -2.80 |
| 259 | propyl propionate | -6.63 | 19.16 | -16.73 | -4.20 | -2.54 |
| 260 | iopropyl propionate | -6.16 | 18.95 | -16.48 | -3.69 | -2.22 |
| 261 | amyl propionate | -6.38 | 23.69 | -20.81 | -3.51 | -1.99 |
| 262 | methyl butyrate | -5.70 | 16.52 | -14.54 | -3.71 | -2.84 |
| 263 | ethyl butyrate | -5.80 | 19.11 | -16.73 | -3.43 | -2.50 |
| 264 | propyl butyrate | -6.47 | 21.44 | -18.75 | -3.78 | -2.28 |
| 265 | methyl pentanoate | -6.15 | 18.78 | -16.64 | -4.01 | -2.54 |
| 266 | ethyl pentanoate | -6.02 | 21.40 | -18.82 | -3.45 | -2.52 |
| 267 | methyl hexanonate | -5.68 | 21.05 | -18.70 | -3.32 | -2.48 |
| 268 | ethyl heptanoate | -5.90 | 25.89 | -22.67 | -2.68 | -2.30 |
| 269 | methyl octanoate | -6.23 | 25.57 | -22.65 | -3.31 | -2.05 |
| 270 | methyl benzoate | -6.54 | 18.15 | -16.84 | -5.23 | -4.28 |
| 271 | methylamine | -5.24 | 7.03 | -5.50 | -3.70 | -4.60 |
| 272 | ethylamine | -5.34 | 9.60 | -7.90 | -3.64 | -4.61 |
| 273 | propylamine | -6.04 | 11.89 | -9.98 | -4.12 | -4.50 |
| 274 | butylamine | -5.61 | 14.16 | -11.99 | -3.44 | -4.38 |
| 275 | pentylamine | -5.81 | 16.43 | -14.06 | -3.44 | -4.09 |
| 276 | hexylamine | -6.18 | 18.68 | -16.00 | -3.49 | -4.04 |
| 277 | dimethylamine | -4.32 | 9.52 | -8.10 | -2.90 | -4.28 |
| 278 | diethylamine | -3.89 | 14.64 | -12.23 | -1.48 | -4.06 |
| 279 | dipropylamine | -5.08 | 19.26 | -16.36 | -2.18 | -3.65 |
| 280 | dibutylamine | -4.01 | 23.79 | -20.64 | -0.86 | -3.31 |
| 281 | trimethylamine | -5.73 | 11.68 | -10.00 | -4.05 | -3.23 |
| 282 | triethylamine | -2.87 | 18.58 | -15.74 | -0.04 | -3.03 |
| 283 | piperazine | -7.80 | 13.10 | -13.13 | -7.83 | -7.40 |
| 284 | N,N’-dimethylpiperazine | -8.69 | 17.43 | -17.09 | -8.35 | -7.58 |
| 285 | N-methylpiperazine | -8.19 | 15.25 | -15.11 | -8.05 | -7.77 |
| 286 | aniline | -9.22 | 13.86 | -12.53 | -7.89 | -5.49 |
| 287 | 1,1-dimethyl-3-phenyl urea | -10.22 | 21.83 | -20.90 | -9.30 | -11.87 |
| 288 | N,N-dimethyl aniline | -4.470 | 18.00 | -16.78 | -3.25 | -2.90 |
| 289 | ethylenediamine | -11.57 | 10.34 | -9.41 | -10.64 | -9.75 |
| 290 | hydrazinehydrazine | -12.42 | 5.90 | -4.96 | -11.47 | -9.30 |
| 291 | 2-methoxyethanamine | -8.15 | 12.57 | -11.45 | -7.03 | -6.55 |
| 292 | morpholine | -6.14 | 12.86 | -12.93 | -6.20 | -7.17 |
| 293 | N-methylmorpholine | -6.47 | 15.03 | -14.83 | -6.26 | -6.34 |
| 294 | N-methylpyrrolidine | -3.44 | 14.74 | -13.49 | -2.20 | -3.97 |
| 295 | N-methylpiperidine | -3.80 | 16.54 | -15.18 | -2.45 | -3.89 |
| 296 | pyrrolidine | -3.12 | 12.49 | -11.42 | -2.05 | -5.47 |
| 297 | piperidine | -3.67 | 14.36 | -13.17 | -2.49 | -5.10 |
| 298 | pyridine | -5.70 | 12.29 | -11.11 | -4.52 | -4.69 |
| 299 | 2-methylpyridine | -6.06 | 14.70 | -13.03 | -4.39 | -4.62 |
| 300 | 3-methylpyridine | -5.73 | 14.56 | -13.07 | -4.24 | -4.77 |
| 301 | 4-methylpyridine | -6.68 | 14.57 | -13.04 | -5.16 | -4.92 |
| 302 | 2-ethylpyridine | -5.09 | 16.95 | -14.88 | -3.03 | -4.32 |
| 303 | 3-ethylpyridine | -5.67 | 16.83 | -14.96 | -3.80 | -4.60 |
| 304 | 4-ethylpyridine | -6.04 | 16.83 | -14.98 | -4.20 | -4.72 |
| 305 | 2,3-dimethylpyridine | -5.64 | 16.61 | -14.95 | -3.98 | -4.81 |
| 306 | 2,4-dimethylpyridine | -7.00 | 16.97 | -15.02 | -5.05 | -4.85 |
| 307 | 2,5-dimethylpyridine | -5.91 | 17.03 | -15.09 | -3.97 | -4.70 |
| 308 | 2,6-dimethylpyridine | -6.31 | 17.11 | -15.00 | -4.20 | -4.60 |
| 309 | 3,4-dimethylpyridine | -6.47 | 16.49 | -14.83 | -4.81 | -5.21 |
| 310 | 3,5-dimethylpyridine | -5.63 | 16.87 | -15.03 | -3.79 | -4.84 |
| 311 | 2-methylpyrazine | -5.46 | 14.03 | -13.23 | -4.67 | -5.51 |
| 312 | 2-ethylpyrazine | -4.93 | 16.29 | -15.04 | -3.68 | -5.45 |
| 313 | 2-iobutylpyrazine | -6.95 | 20.31 | -18.73 | -5.37 | -5.05 |
| 314 | 2-ethyl-3-methoxypyrazine | -6.38 | 19.22 | -18.03 | -5.19 | -4.39 |
| 315 | 2-iobutyl-3-methoxypyrazine | -7.82 | 23.25 | -21.36 | -5.93 | -3.68 |
| 316 | 9-methyladenine | -15.43 | 17.37 | -18.74 | -16.80 | -13.60 |
| 317 | 1-methylthymine | -12.83 | 17.31 | -17.84 | -13.36 | -10.40 |
| 318 | methylindole | -8.17 | 18.48 | -17.13 | -6.83 | -5.91 |
| 319 | methylimidazole | -9.11 | 12.68 | -11.84 | -8.26 | -10.25 |
| 320 | N-propyl guanidine | -14.84 | 15.92 | -14.86 | -13.79 | -10.92 |
| 321 | acetonitrile | -4.95 | 8.75 | -6.70 | -2.91 | -3.89 |
| 322 | propionitrile | -4.94 | 11.18 | -8.95 | -2.71 | -3.85 |
| 323 | butyronitrile | -5.06 | 13.44 | -11.09 | -2.71 | -3.64 |
| 324 | nitroethane | -5.09 | 11.24 | -10.98 | -4.83 | -3.71 |
| 325 | 1-nitropropane | -5.57 | 13.55 | -12.91 | -4.94 | -3.34 |
| 326 | 2-nitropropane | -5.10 | 13.40 | -12.79 | -4.48 | -3.14 |
| 327 | 1-nitrobutane | -5.70 | 15.80 | -15.00 | -4.90 | -3.08 |
| 328 | nitrobenzene | -6.13 | 15.31 | -15.63 | -6.45 | -4.12 |
| 329 | 2-nitrotoluene | -6.45 | 17.30 | -17.12 | -6.27 | -3.59 |
| 330 | 3-nitrotoluene | -6.66 | 17.60 | -17.53 | -6.59 | -3.45 |
| 331 | N,N’-dimethyl formamide | -5.58 | 11.92 | -11.02 | -4.68 | -4.90 |
| 332 | N-methylformamide | -6.55 | 9.72 | -8.87 | -5.70 | -10.00 |
| 333 | acetamide | -9.72 | 9.72 | -8.71 | -8.70 | -9.72 |
| 334 | z-N-methylacetamide | -7.78 | 12.22 | -10.95 | -6.51 | -10.00 |
| 335 | propionamide | -9.29 | 12.00 | -10.79 | -8.08 | -9.42 |
| 336 | thioanisole | -3.73 | 16.97 | -15.22 | -1.98 | -2.73 |
| 337 | dimethyl sulfide | -3.09 | 10.50 | -8.64 | -1.23 | -1.54 |
| 338 | diethyl sulfide | -1.02 | 15.53 | -12.92 | 1.58 | -1.43 |
| 339 | methyl ethyl sulfide | -2.43 | 13.04 | -10.80 | -0.19 | -1.49 |
| 340 | dipropyl sulfide | -2.12 | 20.15 | -17.15 | 0.87 | -1.27 |
| 341 | dimethyl disulfide | -2.66 | 12.80 | -10.89 | -0.75 | -1.83 |
| 342 | diethyl disulfide | -1.29 | 17.82 | -15.16 | 1.38 | -1.63 |
| 343 | trimethyl phosphate | -8.96 | 17.05 | -16.31 | -8.22 | -8.70 |
| 344 | triethyl phosphate | -8.83 | 24.77 | -22.38 | -6.43 | -7.80 |
| 345 | tripropyl phosphate | -9.60 | 31.69 | -28.16 | -6.06 | -6.10 |
| 346 | 2,2-dichloroethenyl dimethyl phosphate | -7.96 | 22.01 | -21.29 | -7.24 | -6.61 |
| 347 | dimethyl 4-bromo-2,5-dichlorophenyl thiophosphate |
-10.51 | 28.50 | -27.93 | -9.94 | -5.70 |
| 348 | dimethyl 2,4,5-trichlorophenyl thiophosphate |
-4.37 | 28.97 | -27.50 | -2.89 | -5.06 |
| 349 | dimethyl 4-nitrophenyl thiophosphate | -9.79 | 27.12 | -27.24 | -9.91 | -7.62 |
| 350 | diethyl 2,4-dichlorophenyl thiophosphate | -4.91 | 32.47 | -29.28 | -1.72 | -3.86 |
| 351 | dimethyl 3-methyl-4-thiomethoxyphenyl thiophosphate |
-6.88 | 31.24 | -28.94 | -4.58 | -6.92 |
| 352 | diethyl 4-nitrophenyl thiophophosnate | -9.16 | 30.51 | -29.04 | -7.68 | -6.27 |
| 353 |
O-ethyl O’-4-bromo-2-chlorophenyl S-propyl phosphorothioate |
-7.77 | 35.75 | -32.49 | -4.50 | -4.09 |
A detailed analysis of agreement between theory and experiment for each functional group is shown in Table 6. It can be found that the agreements for the first five classes of compounds (alkanes, alkenes, alkynes, aromatic hydrocarbons, and fluorides) are very well, with RMSD’s less than 1.0 kcal/mol. The performance for aromatic groups is particularly excellent with RMSD of 0.54 kcal/mol only. However, agreements for nitro compounds and compounds with nitrogen on hetero rings are much worse with RMSD higher than 2.0 kcal/mol. Note that we have use a uniform PB cavity radius value for all nitrogen atom types. This may be an over-simplification of highly diversified chemical environments of different nitrogen atoms. A similar discrepancy between theoretical and experimental solvation free energies for amines and amides was also reported before for free energy simulations in explicit solvent in both the Amber and OPLS force fields.88-90 As shown in Table 1, theoretical dipole moments for nitrogen containing compounds generally agree well with experiment. Therefore the poor agreement for solvation free energies are mostly likely related to either the continuum solvation approximation or the classical electrostatic approximation of solute solvent interactions.
Table 6.
Performance by solute functional group. No. of solute: number of solute molecules. The ranges of compound sequence numbers as in Table 5 are also shown for the listed solute groups. RMSD and UAVG are in kcal/mol.
| Solute group | No. of solute | RMSD | UAVG |
|---|---|---|---|
| alkanes | 19(1 - 19) | 0.74 | 0.59 |
| alkenes | 20(20 - 39) | 0.78 | 0.68 |
| alkynes | 7(40 - 46) | 0.84 | 0.78 |
| aromatic hydrocarbons | 18(47 - 64) | 0.54 | 0.41 |
| fluorides | 19(65 - 83) | 0.89 | 0.74 |
| chlorides | 38(84 - 121) | 1.10 | 0.98 |
| bromides | 18(122 - 139) | 1.35 | 1.16 |
| alcohols | 45(140 - 184) | 1.07 | 0.90 |
| ethers | 19(185 - 203) | 1.44 | 1.25 |
| aldehydes | 15(204 - 218) | 1.44 | 1.33 |
| ketones | 17(219 - 235) | 1.59 | 1.52 |
| acids | 6(236 - 241) | 1.55 | 1.52 |
| esters | 29(242 - 270) | 1.10 | 1.00 |
| amines | 27(271 - 297) | 1.65 | 1.36 |
| amides | 23(298 - 320) | 1.43 | 1.10 |
| nitriles | 4(321 - 324) | 1.05 | 1.05 |
| nitro compounds | 6(325 - 330) | 2.24 | 2.15 |
| compounds with N in heterorings | 5(331 - 335) | 2.59 | 2.07 |
| compounds with S | 7(336 - 342) | 1.94 | 1.66 |
| compounds with P | 11(343 - 353) | 1.97 | 1.59 |
Conclusions
In this work we have developed and tested a complete set of nonbonded parameters for a continuum polarizable force field. Our analysis shows that the new continuum polarizable model is consistent with B3LYP/cc-pVTZ in modeling electronic response upon variation of dielectric environment. Comparison with experiment also shows that the new continuum polarizable model is reasonable, with similar accuracy as B3LYP/cc-pVTZ in reproduction of dipole moments of selected organic molecules in the gas phase. However, it should be pointed out that the proposed continuum polarization scheme is not intended to describe the atomic-detailed polarization within molecular environment. For example, the response of the continuum polarizable model under an external electric field is left unstudied. Incidentally, such studies have never been conducted for published explicit polarizable models either. It is likely that none of the existing classical polarizable models can properly reproduce experiment in such studies. Instead we intend to offer an efficient and self-consistent approach in treating polar interactions in biomolecular simulations more satisfactory than existing additive force fields with implicit solvents.
The modest goal is justified because implicit solvents have been developed for their efficiency. Apparently there are limitations in these simplified solvation treatments, for example the limitations of atom-centered dielectric models91 and the related issue in the use of solvent excluded surface in molecular dynamics simulations.65 Further improvements in the nonpolar components are also needed.45 Interestingly, efforts to address these limitations have emerged, such as in the treatment of coupling between polar and nonpolar components.92,93
We have further tested the validity to interchange the Amber van der Waals parameters between the explicit and continuum polarizable force fields with a series of dimers. It can be found that the continuum polarizable model agrees well with MP2/cc-pVTZ, with deviations in dimer binding energies less than 0.9 kcal/mol in the aqueous dielectric environment.
Finally we have optimized atomic cavity radii with respect to experimental solvation free energies of 177 training molecules. To validate the optimized cavity radii, we have tested these parameters against 176 test molecules. It is interesting to note that the optimized PB atomic cavity radii transfer well from the training set to the test set. Overall an RMSD of 1.30 kcal/mol, UAVG of 1.07 kacl/mol, and correlation coefficient of 92% are achieved for all 353 molecules in both sets. In addition, a detailed analysis of the agreement between theoretical and experimental solvation free energies for each functional group shows that the new polarizable model works excellently for alkanes, alkenes, alkynes, aromatic hydrocarbons, and fluorides. However, agreements for nitro compounds and compounds with nitrogen on hetero rings are much worse. Because theoretical dipole moments for nitrogen containing compounds agree very well with experimental values, a likely reason for the discrepancy between theory and experiment may be the over-simplification in using a single PB cavity radius value for all nitrogen atom types in the highly diversified chemical environments. The poor agreement in solvation free energies may also be related to the lack of modeling electron transfer between the solute and solvent molecules in the continuum solvation treatments, which has been argued for the particular difficult modeling of solvation free energies of amines by classical force fields.88-90
Based on the development documented here, our next natural step is the construction of a full protein/nucleic acid force field within the new continuum polarization framework. Given implicit solvents that are based on the Poisson-Boltzmann theory, for example either numerical Poisson-Boltzmann approaches50,51 and generalized Born approaches52,53 that were developed to deal with non-vacuum solute interiors, the dielectric forces can be computed on-the-fly in molecular dynamics simulations. Therefore, such a polarizable force field can be applied in implicit-solvent molecular dynamics simulations with virtually no additional cost over a nonpolarizable force field. Nevertheless, more detailed refinement efforts in both the covalent terms and the van der Waals terms in the Amber polarizable force fields, which have left untouched, should also be addressed in future publications.
Supplementary Material
Acknowledgements
We thank the Amber developer team for exciting discussion in the development of the new continuum polarizable force field. This work is supported by NIH (GM069620 and GM079383).
References
- (1).Weiner PK, Kollman PA. Journal of Computational Chemistry. 1981;2:287–303. [Google Scholar]
- (2).Weiner SJ, Kollman PA, Case DA, Singh UC, Ghio C, Alagona G, Profeta S, Weiner P. Journal of the American Chemical Society. 1984;106:765–84. [Google Scholar]
- (3).Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. Journal of the American Chemical Society. 1995;117:5179–97. [Google Scholar]
- (4).Wang JM, Cieplak P, Kollman PA. Journal of Computational Chemistry. 2000;21:1049–74. [Google Scholar]
- (5).Duan Y, Wu C, Chowdhury S, Lee MC, Xiong GM, Zhang W, Yang R, Cieplak P, Luo R, Lee T, Caldwell J, Wang JM, Kollman P. Journal of Computational Chemistry. 2003;24:1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- (6).Yang LJ, Tan CH, Hsieh MJ, Wang JM, Duan Y, Cieplak P, Caldwell J, Kollman PA, Luo R. Journal of Physical Chemistry B. 2006;110:13166–76. doi: 10.1021/jp060163v. [DOI] [PubMed] [Google Scholar]
- (7).Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. Journal of Computational Chemistry. 1983;4:187–217. [Google Scholar]
- (8).Mackerell AD, Bashford D, Bellott M, Dunbrack RL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-Mccarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. Journal of Physical Chemistry B. 1998;102:3586–616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- (9).Oostenbrink C. Journal Of Computational Chemistry. 2004;25:1656–76. doi: 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- (10).Jorgensen WL, Tiradorives J. Journal of the American Chemical Society. 1988;110:1657–66. doi: 10.1021/ja00214a001. [DOI] [PubMed] [Google Scholar]
- (11).Jorgensen WL, Maxwell DS, Tiradorives J. Journal of the American Chemical Society. 1996;118:11225–36. [Google Scholar]
- (12).Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Journal of Physical Chemistry B. 2001;105:6474–87. [Google Scholar]
- (13).Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Journal of Chemical Physics. 1983;79:926–35. [Google Scholar]
- (14).Hermans J, Berendsen HJC, Vangunsteren WF, Postma JPM. Biopolymers. 1984;23:1513–8. [Google Scholar]
- (15).Beachy MD, Chasman D, Murphy RB, Halgren TA, Friesner RA. Journal of the American Chemical Society. 1997;119:5908–20. [Google Scholar]
- (16).Van Der Vaart A, Bursulaya BD, Brooks CL, Merz KM. Journal of Physical Chemistry B. 2000;104:9554–63. [Google Scholar]
- (17).Roux B, Berneche S. Biophysical Journal. 2002;82:1681–4. doi: 10.1016/S0006-3495(02)75520-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Rappe AK, Goddard WA. Journal of Physical Chemistry. 1991;95:3358–63. [Google Scholar]
- (19).Rick SW, Stuart SJ, Berne BJ. Journal of Chemical Physics. 1994;101:6141–56. [Google Scholar]
- (20).Liu YP, Kim K, Berne BJ, Friesner RA, Rick SW. Journal of Chemical Physics. 1998;108:4739–55. [Google Scholar]
- (21).Kitao O, Ogawa T. Molecular Physics. 2003;101:3–17. [Google Scholar]
- (22).Mitchell PJ, Fincham D. Journal of Physics-Condensed Matter. 1993;5:1031–8. [Google Scholar]
- (23).Dykstra CE. Journal of the American Chemical Society. 1989;111:6168–74. [Google Scholar]
- (24).Cieplak P, Caldwell J, Kollman P. Journal of Computational Chemistry. 2001;22:1048–57. [Google Scholar]
- (25).Lybrand TP, Kollman PA. Journal of Chemical Physics. 1985;83:2923–33. [Google Scholar]
- (26).Ren PY, Ponder JW. Journal of Computational Chemistry. 2002;23:1497–506. doi: 10.1002/jcc.10127. [DOI] [PubMed] [Google Scholar]
- (27).Ren PY, Ponder JW. Journal of Physical Chemistry B. 2003;107:5933–47. [Google Scholar]
- (28).Patel S, Brooks CL. Journal of Computational Chemistry. 2004;25:1–15. doi: 10.1002/jcc.10355. [DOI] [PubMed] [Google Scholar]
- (29).Patel S, Mackerell AD, Brooks CL. Journal of Computational Chemistry. 2004;25:1504–14. doi: 10.1002/jcc.20077. [DOI] [PubMed] [Google Scholar]
- (30).Lamoureux G, Mackerell AD, Roux B. Journal of Chemical Physics. 2003;119:5185–97. [Google Scholar]
- (31).Lamoureux G, Harder E, Vorobyov IV, Roux B, Mackerell AD. Chemical Physics Letters. 2006;418:245–9. [Google Scholar]
- (32).Noskov SY, Lamoureux G, Roux B. Journal of Physical Chemistry B. 2005;109:6705–13. doi: 10.1021/jp045438q. [DOI] [PubMed] [Google Scholar]
- (33).Vorobyov IV, Anisimov VM, Mackerell AD. Journal of Physical Chemistry B. 2005;109:18988–99. doi: 10.1021/jp053182y. [DOI] [PubMed] [Google Scholar]
- (34).Lopes PEM, Lamoureux G, Roux B, Mackerell AD. Journal of Physical Chemistry B. 2007;111:2873–85. doi: 10.1021/jp0663614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Banks JL, Kaminski GA, Zhou RH, Mainz DT, Berne BJ, Friesner RA. Journal of Chemical Physics. 1999;110:741–54. [Google Scholar]
- (36).Stern HA, Kaminski GA, Banks JL, Zhou RH, Berne BJ, Friesner RA. Journal of Physical Chemistry B. 1999;103:4730–7. [Google Scholar]
- (37).Gresh N. Journal De Chimie Physique Et De Physico-Chimie Biologique. 1997;94:1365–416. [Google Scholar]
- (38).Gresh N. Journal of Physical Chemistry A. 1997;101:8680–94. [Google Scholar]
- (39).Masella M, Gresh N, Flament JP. Journal of the Chemical Society-Faraday Transactions. 1998;94:2745–53. [Google Scholar]
- (40).Hermida-Ramon JM, Brdarski S, Karlstrom G, Berg U. Journal of Computational Chemistry. 2003;24:161–76. doi: 10.1002/jcc.10159. [DOI] [PubMed] [Google Scholar]
- (41).Palmo K, Mannfors B, Mirkin NG, Krimm S. Biopolymers. 2003;68:383–94. doi: 10.1002/bip.10254. [DOI] [PubMed] [Google Scholar]
- (42).Nina M, Beglov D, Roux B. Journal of Physical Chemistry B. 1997;101:5239–48. [Google Scholar]
- (43).Swanson JMJ, Adcock SA, Mccammon JA. Journal of Chemical Theory and Computation. 2005;1:484–93. doi: 10.1021/ct049834o. [DOI] [PubMed] [Google Scholar]
- (44).Tan CH, Yang LJ, Luo R. Journal of Physical Chemistry B. 2006;110:18680–7. doi: 10.1021/jp063479b. [DOI] [PubMed] [Google Scholar]
- (45).Tan CH, Tan YH, Luo R. Journal of Physical Chemistry B. 2007;111:12263–74. doi: 10.1021/jp073399n. [DOI] [PubMed] [Google Scholar]
- (46).Maple JR, Cao YX, Damm WG, Halgren TA, Kaminski GA, Zhang LY, Friesner RA. Journal of Chemical Theory and Computation. 2005;1:694–715. doi: 10.1021/ct049855i. [DOI] [PubMed] [Google Scholar]
- (47).Schnieders MJ, Baker NA, Ren PY, Ponder JW. J Chem Phys. 2007;126:124114. doi: 10.1063/1.2714528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (48).Sharp K, Jeancharles A, Honig B. Journal of Physical Chemistry. 1992;96:3822–8. [Google Scholar]
- (49).Sitkoff D, Sharp KA, Honig B. Journal of Physical Chemistry. 1994;98:1978–88. [Google Scholar]
- (50).Gilson MK, Honig B. Proteins-Structure Function and Genetics. 1988;4:7–18. doi: 10.1002/prot.340040104. [DOI] [PubMed] [Google Scholar]
- (51).Honig B, Nicholls A. Science. 1995;268:1144–9. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- (52).Sigalov G, Scheffel P, Onufriev A. Journal of Chemical Physics. 2005;122 doi: 10.1063/1.1857811. [DOI] [PubMed] [Google Scholar]
- (53).Feig M, Im W, Brooks CL. Journal of Chemical Physics. 2004;120:903–11. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- (54).Tan YH, Luo R. Journal of Chemical Physics. 2007;126:094103. doi: 10.1063/1.2436871. [DOI] [PubMed] [Google Scholar]
- (55).Schutz C, Warshel A. PROTEINS-STRUCTURE FUNCTION AND GENETICS . 2001;44:400–17. doi: 10.1002/prot.1106. [DOI] [PubMed] [Google Scholar]
- (56).Honig B, Sharp K, Yang AS. Journal of Physical Chemistry. 1993;97:1101–9. [Google Scholar]
- (57).Gilson MK. Current Opinion in Structural Biology. 1995;5:216–23. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- (58).Woods RJ, Khalil M, Pell W, Moffat SH, Smith VH. Journal of Computational Chemistry. 1990;11:297–310. [Google Scholar]
- (59).Dupradeau FY, Pigache A, Zaffran T, Cieplak P.
- (60).Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery J,JA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Al-Laham MA, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. Gaussian, Inc., Wallingford CT. 2004 [Google Scholar]
- (61).Tomasi J, Persico M. Chemical Reviews. 1994;94:2027–94. [Google Scholar]
- (62).Tomasi J, Mennucci B, Cammi R. Chemical Reviews. 2005;105:2999–3093. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- (63).Case DA, Darden TA, Cheatham I,TE, Simmerling CL, Wang CL, Duke RE, Luo R, Merz KM, Pearlman DA, Crowley M, Walker RC, Zhang W, Wang B, Hayik S, Roitberg A, Seabra G, Wong KF, Paesani F, Wu X, Brozell S, Tsui V, Gohlke H, Yang L, Tan C, Mongan J, Hornak V, Cui G, Beroza P, Mathews DH, Schafmeister C, Ross WS, K. PA.2006. Amber 9 University of California, San Francisco
- (64).Luo R, David L, Gilson MK. Journal of Computational Chemistry. 2002;23:1244–53. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- (65).Lu Q, Luo R. Journal of Chemical Physics. 2003;119:11035–47. [Google Scholar]
- (66).Kaminski G, Duffy EM, Matsui T, Jorgensen WL. Journal of Physical Chemistry. 1994;98:13077–82. [Google Scholar]
- (67).Pierotti RA. Chemical Reviews. 1976;76:717–26. [Google Scholar]
- (68).Irisa M, Nagayama K, Hirata F. Chemical Physics Letters. 1993;207:430–5. [Google Scholar]
- (69).Chandler D. Nature. 2005;437:640–7. doi: 10.1038/nature04162. [DOI] [PubMed] [Google Scholar]
- (70).Lum K, Chandler D, Weeks JD. Journal of Physical Chemistry B. 1999;103:4570–7. [Google Scholar]
- (71).Huang DM, Chandler D. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:8324–7. doi: 10.1073/pnas.120176397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (72).Pratt LR, Chandler D. Journal of Chemical Physics. 1980;73:3434–41. [Google Scholar]
- (73).Gallicchio E, Kubo MM, Levy RM. Journal of Physical Chemistry B. 2000;104:6271–85. [Google Scholar]
- (74).Huang DM, Chandler D. Journal of Physical Chemistry B. 2002;106:2047–53. [Google Scholar]
- (75).Floris F, Tomasi J. Journal of Computational Chemistry. 1989;10:616–27. [Google Scholar]
- (76).Holland JH. SIAM journal on computing. 1973 [Google Scholar]
- (77).Wang JM, Wang W, Huo SH, Lee M, Kollman PA. Journal of Physical Chemistry B. 2001;105:5055–67. [Google Scholar]
- (78).Hine J, Mookerjee PK. Journal of Organic Chemistry. 1975;40:292–8. [Google Scholar]
- (79).Pearson RG. Journal of the American Chemical Society. 1986;108:6109–14. [Google Scholar]
- (80).Hawkins GD, Cramer CJ, Truhlar DG. Journal of Physical Chemistry B. 1997;101:7147–57. [Google Scholar]
- (81).Li JB, Zhu TH, Hawkins GD, Winget P, Liotard DA, Cramer CJ, Truhlar DG. Theoretical Chemistry Accounts. 1999;103:9–63. [Google Scholar]
- (82).1998.
- (83).Halgren TA. Journal of Computational Chemistry. 1996;17:490–519. [Google Scholar]
- (84).Halgren TA. Journal of Computational Chemistry. 1996;17:20–52. [Google Scholar]
- (85).Halgren TA. Journal of Computational Chemistry. 1996;17:553–86. [Google Scholar]
- (86).Halgren TA, Nachbar RB. Journal of Computational Chemistry. 1996;17:587–615. [Google Scholar]
- (87).Halgren TA. Journal of Computational Chemistry. 1996;17:616–41. [Google Scholar]
- (88).Rizzo RC, Jorgensen WL. Journal of the American Chemical Society. 1999;121:4827–36. [Google Scholar]
- (89).Morgantini PY, Kollman PA. Journal of the American Chemical Society. 1995;117:6057–63. [Google Scholar]
- (90).Ding YB, Bernardo DN, Kroghjespersen K, Levy RM. Journal of Physical Chemistry. 1995;99:11575–83. [Google Scholar]
- (91).Swanson JMJ, Mongan J, Mccammon JA. Journal Of Physical Chemistry B . 2005;109:14769–72. doi: 10.1021/jp052883s. [DOI] [PubMed] [Google Scholar]
- (92).Dzubiella J, Swanson JMJ, Mccammon JA. Journal of Chemical Physics . 2006;124 doi: 10.1063/1.2171192. [DOI] [PubMed] [Google Scholar]
- (93).Dzubiella J, Swanson JMJ, Mccammon JA. Physical Review Letters. 2006;96 doi: 10.1103/PhysRevLett.96.087802. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


