Bifunctional Binding of Cisplatin to DNA: Why Does Cisplatin Form 1,2-Intrastrand Cross-links with AG, But Not with GA?

Abstract

The bifunctional binding of the anticancer drug cisplatin to two adjacent nucleobases in DNA is modeled using density functional theory. Previous experimental studies revealed that cisplatin binding to adjacent guanine and adenine is sensitive to nucleobase sequence. Whereas AG 1,2-intrastrand cross-links are commonly observed, the analogous GA adducts are not known. This study focuses on understanding this directional preference by constructing a full reaction profile using quantum chemical simulation methods. Monofunctional and bifunctional cisplatin adducts were generated and the transition states that connect them were located for the dinucleotides d(pApG) and d(pGpA), assuming that initial platination takes place at the guanine site. Our computer simulations reveal a significant kinetic preference for formation of the AG over the GA adduct. The activation free energies of ~23 kcal/mol for AG and ~32 kcal/mol for GA suggest that bifunctional closure is ~6 orders of magnitude faster for AG than for GA. Responsible for the stabilization of the transition state that affords the AG adduct is a strong hydrogen bond between one of the ammine ligands of cisplatin and the 5′ phosphate group of the DNA backbone. This interaction is absent in the transition state that leads to the GA adduct, because the right-handed helix of the DNA backbone places the phosphate out of reach for the ammine ligand. We found only an insignificant thermodynamic difference between AG and GA adducts and conclude that the preference of AG over GA binding is largely under kinetic control. The puckering of the deoxyribose ring plays an important role in determining the energetics of the bifunctional platination products. Whereas the 3′-nucleoside remains in the native C2′-endo/C3′-exo form of B-DNA, the deoxyribose of the 5′-nucleoside always adopts the C2′-exo/C3′-endo puckering in our simulations. A detailed analysis of the energies and structures of the bifunctional adducts revealed that the observed sugar puckering patterns are necessary for platinum to bind in a relaxed coordination geometry.

Introduction

cis-Diamminedichloroplatinum(II), cisplatin, is a potent anti-cancer drug^1–4 that is widely used to treat testicular, ovarian, head, neck and small cell lung tumors.^5,6 Although cisplatin was FDA-approved in 1978⁷ and is one of the most successful anti-cancer drugs, side-effects, natural and acquired resistance of patients towards the drug^8,9 and the limited scope have motivated searches for structurally and/or functionally analogous alternatives.^10,11 These efforts included functionalization of ligands,¹¹ bimetallic platinum systems,¹² and different metal centers, most notably Rh^13,14 and Ru.^15–7 Unfortunately, finding analogous compounds that outperform cisplatin has proved to be difficult. To date, only two cisplatin-derived drugs have been FDA-approved, namely carboplatin¹⁸ and oxaliplatin.^19,20 Despite its widespread therapeutic utility, many aspects of the mode of action of cisplatin remain poorly understood, although the general reaction patterns are largely agreed upon.^6,7,21–25 Cisplatin contains two labile chlorido ligands in a cis disposition to each other that function as leaving groups.²⁶ These ligands remain bound to platinum in the plasma due to its high chloride concentration of around 100 mM. Once inside a cell, however, the sharply decreased intracellular chloride concentration of around 4 – 12 mM causes cisplatin to undergo aquation,²¹ whereby the chlorido ligands are replaced by aqua ligands to form the activated complexes [Pt(NH₃)₂Cl(H₂O)]⁺ (Eqs. 1) and [Pt(NH₃)₂(H₂O)₂]²⁺. These complexes bind to various cellular components like DNA, RNA, proteins, and membrane phospholipids.^27–31 major target leading to cell death, however, is genomic DNA.^6,32,33 Specifically, the N7 atom of purine bases is the main binding site, with guanine being preferred over adenine.³⁴ The possible binding modes include monofunctional binding to a single purine base (eq 2, 4), intra and interstrand bifunctional binding (eq 3, 5), and DNA-protein cross-linking.⁷ Due to the cis orientation of the leaving groups, intrastrand cross-links between two adjacent nucleobases are most preferred, with GpG adducts³⁵ being the major and ApG cross-links^36,37 being the next most abundant products.^38–40 Surprisingly, GpA adducts have not been observed in full-length DNA.^41,42 The details of how these adducts are formed and what distinguishes them are important for a number of reasons. Most importantly, a deep understanding of the thermodynamics and kinetics of the reactions leading to bifunctional cross-link formation may provide guidance in future efforts towards rational design of cisplatin analogues^43,44 by exposing electronic and structural features of cisplatin chemistry that dictate recognition and binding to DNA. Previous experimental studies on DNA oligonucleotides showed a preference for bifunctional closure towards the 5′ direction.⁴⁵ For example, in DNA containing the ApGpA sequence, after initial platination of the central guanine, closure to form the bifunctional adduct progresses exclusively to the 5′ direction to afford the ApG adducts (Scheme 1),⁴⁶ whereas alternative closure to the 3′ direction was not observed. Similar conclusions can be drawn from studies using GpApG fragments.⁴⁰ Previously, this preference was rationalized by contending that the N7 atom of the adenine at the 5′ end is structurally closer (3 Å) than the N7 position of adenine to the 3′ end (5 Å).⁴⁶ Although plausible, this rationalization is not satisfactory, because it did not take into account local distortions upon monofunctional binding that may occur in solution.⁷ In addition, 1,3-intrastrand^47–49 cross-links are relatively common binding motifs, suggesting that a reasoning based on Pt–N distance alone is not sufficient. Another explanation was proposed based on molecular mechanics simulations⁵⁰ identifying sterically unfavorable interactions between the monofunctionally bound cisplatin moiety and the neighboring adenine to be responsible for the preference of closure to the 5′-direction. In the present study, we have examined the thermodynamic and kinetic properties of bifunctional adduct formation using density functional simulations and draw a very different conclusion.

Scheme 1.

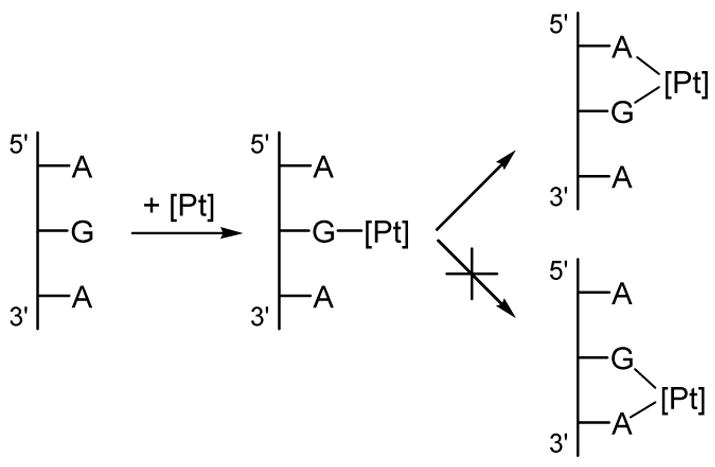
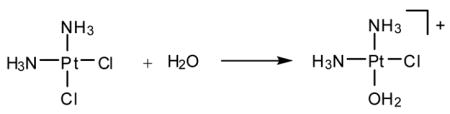(1)

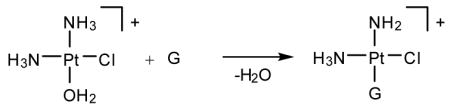(2)

(3)

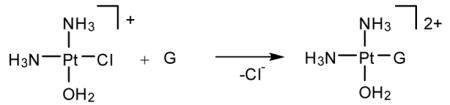(4)

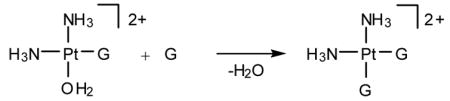(5)

Computational details

All monofunctional, bifunctional and transition state structures were modeled as dinucleotides with 5′-hydrogen phosphate and 3′-hydroxyl terminations. Sodium ions were added as counterions for each phosphate group to avoid artificial electrostatic effects that may interfere with the platinum binding. In reality, solvent screening and/or ion pair formation will minimize such interactions. Thus, our model carries a molecular charge of 2+ (Figure 1). Water was used as the fourth platinum ligand for monofunctional structures and as the leaving group in the transition states. The starting structures for geometry optimizations were obtained by modifying cisplatin-bound structures published previously⁵¹ (PDB: 5BNA,⁵² 1SKB⁵³). Attempts were made to explore different structural motifs, and the ones adopted generated lowest energy structures that displayed no obvious structural strains or other unreasonable distortions.

Figure 1.

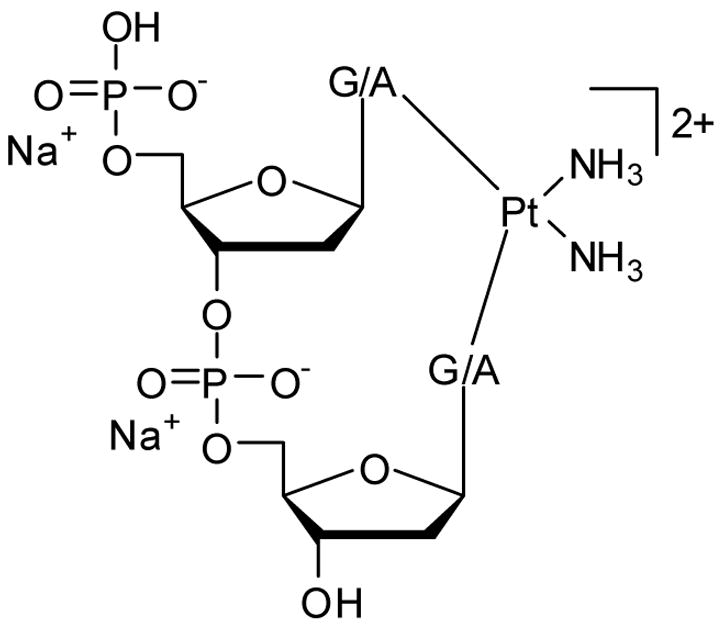
Computational model utilized in this work.

All calculations were carried out using Density Functional Theory^54,55 as implemented in the Jaguar 5.5⁵⁶ suite of ab initio quantum chemistry programs. Geometries were optimized by using the B3LYP^57,58 functional with the 6-31G** basis set. Platinum was represented by the LosAlamos LACVP basis,^59,60 which includes relativistic effective core potentials. The energies were reevaluated by additional single point calculations at each optimized geometry using Dunning’s correlation consistent triple-ζ basis set cc-pVTZ(-f)⁶¹ with the standard double set of polarization functions. In these single-point calculations, Pt was described by a modified version of LACVP, designated as LACV3P, where the exponents were decontracted to match the effective core potential with the triple-ζ quality basis. Single-point energies of all stationary points on the potential energy surface for bifunctional closure were also evaluated using the PBE⁶² functional with the cc-pVTZ(-f) basis set; practically identical relative energies were obtained. The PBE results are summarized in Supporting Information and not further discussed. Vibrational frequency calculation results based on analytical second derivatives at the B3LYP/6-31G**/LACVP level of theory were used to confirm proper convergence to local minima and first-order saddle points for equilibrium and transition state geometries, respectively, and to derive the zero-point-energy (ZPE) and vibrational entropy corrections at room temperature. Unscaled vibrational frequencies are used for these corrections. Vibrational frequency calculations are computationally very demanding. We performed these calculations for the dinucleotide models (~80 atoms), but the trinucleotide models (~110 atoms) are beyond reach for currently available computational resources. Solvation energies were evaluated by a self-consistent reaction field (SCRF)^63–65 approach with a solvent-excluding surface cavity, based on accurate numerical solutions of the Poisson-Boltzmann equation.^63,66 In the results reported below, solvation calculations were carried out at the gas-phase geometry using the 6-31G**/LACVP basis and employing a dielectric constant of ε = 80.37 for water. Whereas the accurate computation of absolute solvation energies remains a challenge and potentially requires careful inspection of the empirical parameters, the differential solvation energy is expected to be less sensitive owing to a significant error cancellation when the same empirical parameters are used. Thus, the differential solvation corrections are most likely more reliable than the absolute energies of solvation. Because all continuum solvation models only give free energies of solvation G(Solv), simply adding the electronic energy E(SCF) and the free energy of solvation gives a fictitious energy E(Sol) that is in principle physically not meaningful. In cases where the full vibrational analysis could not be done, this energy serves as a substitute.

It is prudent to recognize the limitations of the modeling approach we have taken in this work. In addition to the necessarily small size of the quantum chemical model mimicking full length DNA, there are other more fundamental concerns. For example, we only sampled the electronic energy landscape and take a simplistic approach by adding gas phase entropies at the computed geometries to approximate free energies. We thus assume that the free energy and the electronic surfaces are sufficiently similar, which may not necessarily be true. Solvent effects are treated in a similarly crude fashion with a continuum model. More sophisticated reaction dynamics models that incorporate, for example, transition path ensembles⁶⁷ and require Monte Carlo sampling are currently out of reach for reactivity studies of transition metal complexes of realistic sizes. Given these limitations, it is important to interpret the results with caution. We refer to reaction barriers and energy differences between reactants and products as “kinetic” and “thermodynamic” properties of the reaction, respectively, throughout the study with the explicit realization that our computed values are approximations. The main goal of this work is not to construct a quantitative model of the chemistry that will allow for calculation of reliable reaction rates, but to recognize qualitatively plausible concepts of cisplatin binding.

Results and Discussion

One rationalization for why cisplatin prefers to close to the 5′ over the 3′ direction in an AGA sequence is that the adenine neighbor at the 5′ position is geometrically closer to the platinum center bound to G than the adenine neighbor at the 3′ position.⁴⁶ This purely geometric rationalization was based on the X-ray crystal structure determination of B-DNA containing the AGA sequence⁴⁶ and assumed that there is no structural distortion upon initial monofunctional platination. This approximate treatment revealed that the distance between the presumed position of Pt and the N7 of adenine to the 5′ side of AGA is ~3 Å, whereas the Pt···N7 distance for the adenine in the 3′ direction is ~5 Å. Although plausible, neglecting structural distortions upon initial, monofunctional binding of cisplatin to G is difficult to accept. In addition, intrastrand 1,3-cross-links are well known to be one of the platination products, indicating that cisplatin can overcome notably longer Pt···N distances. Computer models offer a unique opportunity to address these questions in greater detail and with higher precision.

Monofunctional Adducts

Our unrestricted geometry optimizations of the monofunctionally platinated d(pApGpA) fragment identified two reasonable isomers. The basic platinum coordination geometry is consistent with structures found previously^34,68,69 and displays a strong hydrogen-bond between the ammine N–H and the C6=O group of guanine. In the lower energy isomer 1a (Figure 2a), the dihedral angle between the molecular planes of guanine and the cisplatin fragments is 45.1° and the aqua ligand points to the 5′ direction. Because of the right-handedness of the DNA helix, this coordination geometry places the aqua ligand close enough to the backbone phosphate groups to form strong hydrogen bonds with the phosphate-oxygen atoms. In the alternative structure 1b, where the cisplatin fragment is coordinated such that the aqua ligand points to the 3′ direction, however, the phosphate groups are too far away to serve as hydrogen-bond acceptors. Instead, the aqua ligand forms hydrogen-bonds with the N7 and C6-amino fragments (Figure 2b). As a result, isomer 1b is ~15 kcal/mol higher in energy than 1a. Adding solvation free energy decreases the energy difference slightly to give a preference of 1a over 1b by ~11 kcal/mol (Figure 2). It is important that we consider differential solvation energies in this case, because interactions with solvent water may disproportionately stabilize 1b, where fragments that are involved in less than ideal hydrogen-bonding networks may interact more strongly with solvents to give a lower overall energy. Using a continuum solvation model, we capture some of these effects. But, we must not overinterpret this approximate approach to including solvation effects. In addition to general reservations about how accurately continuum models reproduce solvation effects, our solvation energies are most likely exaggerated. In reality many atoms of the purine bases are not solvent accessible because they are buried in the DNA-duplex, but our model places the entire trinucleotide fragment in a continuum solvation field. It is reasonable, however, to draw the conclusion that there is significant preference for the monofunctional adduct adopting a geometry that places the aqua ligand closer to the 5′-adenine, i.e., structure 1a is preferred over structure 1b by at least 11 kcal/mol.

Figure 2.

Optimized geometries of the two isomers of the monofunctionally platinated d(pApGpA).

The hydrogen bonding network in 1a requires a change of sugar-puckering in the adenosine fragment at the 5′ position. The deoxyribose transforms from the standard C2′-endo/C3′-exo puckering of B-DNA to a C2′-exo/C3′-endo puckering. This feature is of general importance for bifunctional adduct formation, as discussed below. In 1b, all nucleosides maintain C2′-endo/C3′-exo puckering. The distances between Pt and the N7 positions of the neighboring adenine bases are 4.98 and 5.17 Å for the 5′ and 3′ adenine bases, respectively, in 1a. In 1b, on the other hand, the N7 positions of the 5′ and 3′ adenines are 4.16 and 4.33 Å away from the platinum center, respectively. Whereas the previous speculation that the N7 of adenine at the 5′ position is geometrically closer to the platinum is correct based on our calculations, the magnitude of the difference (0.19 and 0.17 Å in 1a and 1b, respectively) is smaller than estimated before.

In principle, the most obvious approach to modeling the 1,2-cross-linking process is to utilize the monofunctionally platinated ApGpA fragment. After much exploration, however, we found that the flanking adenine moieties are structurally too flexible, giving rise to a number of undesirable and physically meaningless artifacts. Most importantly, the structural changes that occur when the reaction progresses towards the product cause the adenine moiety that is not involved in the reaction to move away from its initial geometry and to converge to one of many possible local minima. It is practically impossible to construct comparable models for the 5′ and 3′ closure reactions where the energy penalties introduced by the dangling adenine groups cancel in a consistent fashion. In addition, the size of the model (110 atoms) renders impossible the vibrational frequency calculations that are needed to check the convergence to stationary points and to derive vibrational entropy corrections. Therefore, it was necessary to simplify our computer model even further. Starting from 1a, the 3′-adenosine was removed to afford a dinucleotide AG model 2a; removal of the 5′-adenosine gave a GA model, labeled as 2b (Figure 3).

Figure 3.

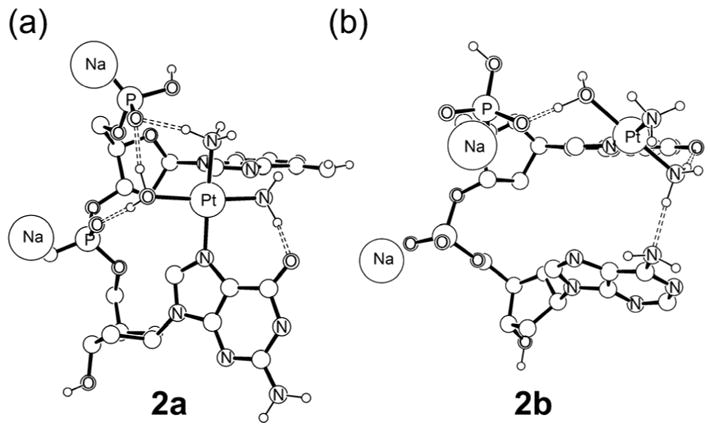
Monofunctional adducts (a) ApG (b) GpA

In general, the dinucleotide models display more distorted structures than the trinucleotide models discussed above, which is expected because the lack of constraints by the flanking adenosine allows for more significant structural reorganization to take place. Specifically, removal of the 3′-adenosine leads to a more pronounced tilting of the platinated guanine group, as illustrated in Figure 2a, decreasing the distance between Pt and the N7 position of adenine to 3.80 Å. Similarly, the removal of 5′-adenosine leads to a Pt···N7 distance of 4.95 Å. The energy difference between these two models is small, with 2a being 2.56 kcal/mol lower in gas phase free energy than 2b. Inspecting the structures shown in Figure 2, the origin of this small energetic difference becomes obvious. In 2a, the strong hydrogen bonding between the phosphate and the aqua ligand of the cisplatin fragment is maintained, whereas only one such hydrogen-bond occurs in 2b, due to truncation of the model. Moreover, the ammine ligand of cisplatin in 2a is also positioned to form a hydrogen-bond with the terminal 5′-phosphate, while in 2b the ammine ligand points away from the nucleobases and cannot participate in a similar hydrogen-bonding network. It should be noted, however, that the ammine-phosphate hydrogen-bond in 2a is a result of the greater structural distortion of the 3′-guanine, which may be exaggerated in our smaller model. Because these structural differences leave the water and ammine ligands and the terminal phosphate available for interacting with solvent, we can expect model 2b to experience high stabilization by solvation. The continuum solvation treatment should be able to capture this difference and we found such to be the case, as enumerated in Table 1. Our calculations indicate that the solvation energy for 2b is greater by 7.26 kcal/mol. As a result, structure 2b is preferred by 4.70 kcal/mol on the solution phase free energy surface. Although it is important to consider solvation energy corrections, we must interpret them with caution, as discussed above. Fortunately, we found that this intrinsic deficiency of our model makes no physically meaningful difference to the overall conclusions (vide infra).

Table 1.

Computed energy components of all species shown in Figure 3 in kcal/mol.

	ΔE(SCF)	ΔH	ΔG(gas)	ΔG(Sol)
2a	0.00	0.00	0.00	0.00
2b	6.20	5.24	2.56	−4.70
2a-TS	23.31	22.42	23.35	27.92
2b-TS	35.88	34.80	34.51	33.17
3	9.25	5.22	−8.72	−15.18
4	11.58	8.06	−5.13	−10.74

A subtle but important observation relates to the sugar puckering in our dinucleotide models. As observed in the trinucleotide model 1a, the 5′-adenosine in 2a displays a C2′-exo/C3′-endo puckering, whereas the platinated guanosine shows the C2′-endo/C3′-exo puckering expected for standard nucleotides in B-DNA. In 2b, on the other hand, the platinated guanine, now at the 5′-position of the GA model, switches sugar puckering to C2′-exo/C3′-endo, while the 3′-adenosine remains in the C2′-endo/C3′-exo configuration. Thus, given a higher degree of structural freedom the nucleoside at the 5′-side always prefers to adopt the unusual C2′-exo/C3′-endo puckering. Sugar puckering of the 5′-nucleoside in bifunctional 1,2-cross-links are commonly observed to display the C2′-exo/C3′-endo puckering.^7,51,70–72 A simple rationale for this behavior is that the change in sugar puckering at the 5′-nucleoside allows for the N7-binding sites of neighboring nucleoside to be closer by pushing the 5′-base to the 3′ direction. The driving force for this structural change is already present at the monofunctionally platinated stage where stronger hydrogen-bonds can be formed and become more pronounced upon bifunctional closure.

Reaction energy profiles

Figure 4 shows the reaction energy profiles for bifunctional adduct formation, where the closure to the 5′-direction is modeled starting from 2a and the closure to the 3′-direction is probed using model 2b. Gas phase free energies are plotted in Figure 3 and the corresponding solution phase free energies are given in parentheses. Although the absolute numbers are somewhat different due to differential solvation energies, as discussed above, the most important features of the reaction energy profiles are maintained in both gas and solution phase free energy curves. The electronic (E(SCF)) energies were also re-evaluated using the PBE functional and the results are in very good agreement with those from B3LYP (See Supporting Information). Our calculations indicate that closure to the 5′-direction is associated with a barrier of 23.35 kcal/mol. Addition of solvation energies increases this barrier by 4.57 kcal/mol to give 27.92 kcal/mol (Table 1). Bifunctional closure to the 3′-direction, on the other hand, is computed to require a free energy of activation of 31.95 and 37.87 kcal/mol in gas phase and solution phase, respectively. Thus, after initial platination of guanine in an AGA sequence the closure to the 5′-adenine is preferred by ~9–10 kcal/mol at the transition state over closure to the 3′-adenine, which translates to a faster reaction by ~6 orders of magnitude.

Figure 4.

Computed reaction energy profile for the bifunctional adduct formation reaction. Gas phase and solution phase free energies are given in round and square brackets, respectively. The labels “ex” and “en” refer to C2′-exo/C3′-endo and C2′-endo/C3′-exo, respectively.

Figure 5 shows the transition states 2a-TS and 2b-TS. The platinum center displays trigonal-bipyramidal coordination geometry expected for a ligand substitution reaction via an interchange mechanism with associative character, in good agreement with previous work.⁷³ In both cases, we found that the phosphate groups of the DNA-backbone play a crucial role in stabilizing and directing the water ligand, which is the leaving group of the substitution reactions. At the transition state 2a-TS the Pt–OH₂ bond is nearly broken at a distance of 2.38 Å and the Pt–N7 bond with adenine is almost formed at a distance of 2.62 Å. Similar bond distances were found for 2b-TS. These structural features are consistent with previous studies and are not further discussed here.

Figure 5.

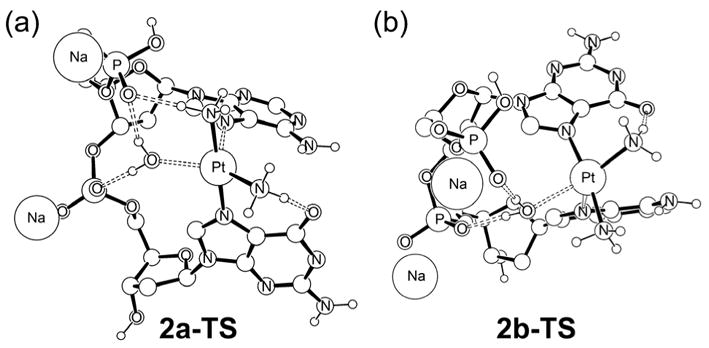
Optimized structures of the transition states 2a-TS and 2b-TS.

Why is 2a-TS so much lower in energy than 2b-TS?

Examining the structures of the transition states more carefully, one prominent difference is the presence of a strong hydrogen-bond between the axial ammine ligand and the phosphate group in 2a-TS. In 2b-TS, the axial ammine necessarily points away from the phosphate group and therefore cannot participate in hydrogen-bonding. As conceptualized in Figure 6, this feature is a general structural property of right-handed double-helical DNA. Here the hydrogen-bond accepting phosphate groups of the DNA-backbone are directly to lie closer to the axial ammine when it points to the 5′-direction compared to the analogous attack from the 3′-direction.

Figure 6.

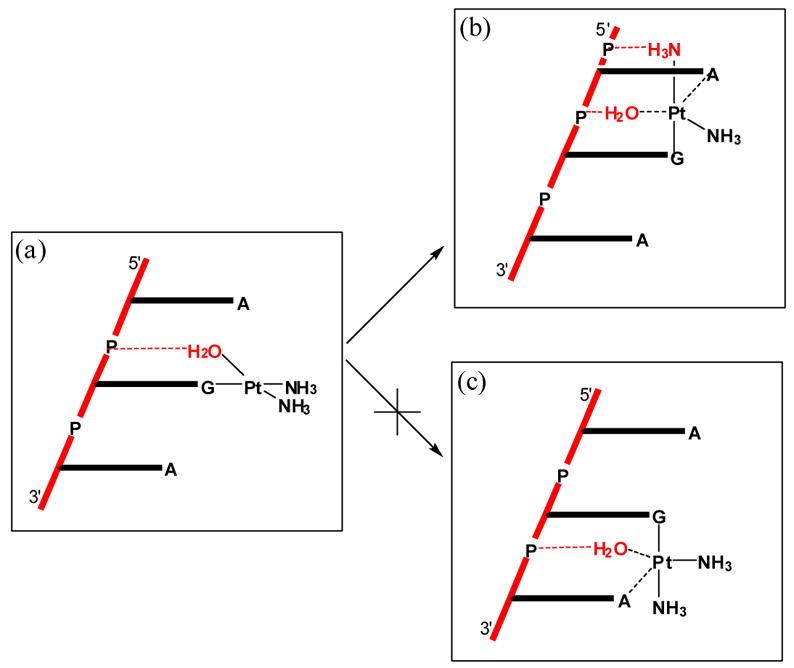
Conceptual cartoon illustrating the hydrogen-bonding network in the transition states. Water and ammine ligands that form strong hydrogen-bonds are shown in red.

To test further the hypothesis that the additional hydrogen-bond between the ammine-hydrogen and the phosphate group determines the observed transition state energy difference, we conducted a “computational experiment”. The phosphate group at the 5′-position was replaced by a methyl group in both 2a-TS and 2b-TS, thus removing all hydrogen-bonding interactions. We found that the electronic energy difference (ΔE(SCF)) decreases by 9.73 to give 2.84 kcal/mol confirming that the ammine-phosphate hydrogen-bonding is the dominating term of the energy difference. Adding solvation energy corrections changes this energy difference only slightly to 2.18 kcal/mol.

Given the prominent role of the 5′-phosphate group described above, it is prudent to assess critically whether or not the model that we utilize is appropriate. Could the additional hydrogen-bonding between the axial-NH₃ and the 5′-phosphate group possibly be a computational artifact resulting from an unrealistically flexible phosphate group in our model?⁷⁴ In other words, is a structural distortion that would place the 5′-phosphate group in hydrogen-bonding distance to the Pt-ammine ligand realistic in full-length DNA? To address this question, we overlaid our calculated transition state structure 2a-TS (red in Figure 7) and the high-resolution crystal structure of a full-length DNA containing a Pt-d(pGpG) adduct (grey in Figure 7).⁷⁵ The two structures were centered at the platinum positions and the C1′ positions of the two nucleosides were used as alignment points. These alignment anchors are shown as red and grey balls in Figure 7. The experimental bifunctional adduct structure is of course more compact than the transition state and, accordingly, the C1′ atoms are notably closer to each other in the experimental structure than in 2a-TS. The ammine and 5′-phosphate groups that form the key hydrogen bond in 2a-TS are highlighted in green and the corresponding phosphate group in the experimental crystal structure is shown in blue. The phosphate groups are structurally very close to each other in the overlaid positions. This comparison suggests that the structural change required for the proposed hydrogen bond is reasonable and lends support to the validity of our small model for the structural features present in full-length DNA.

Figure 7.

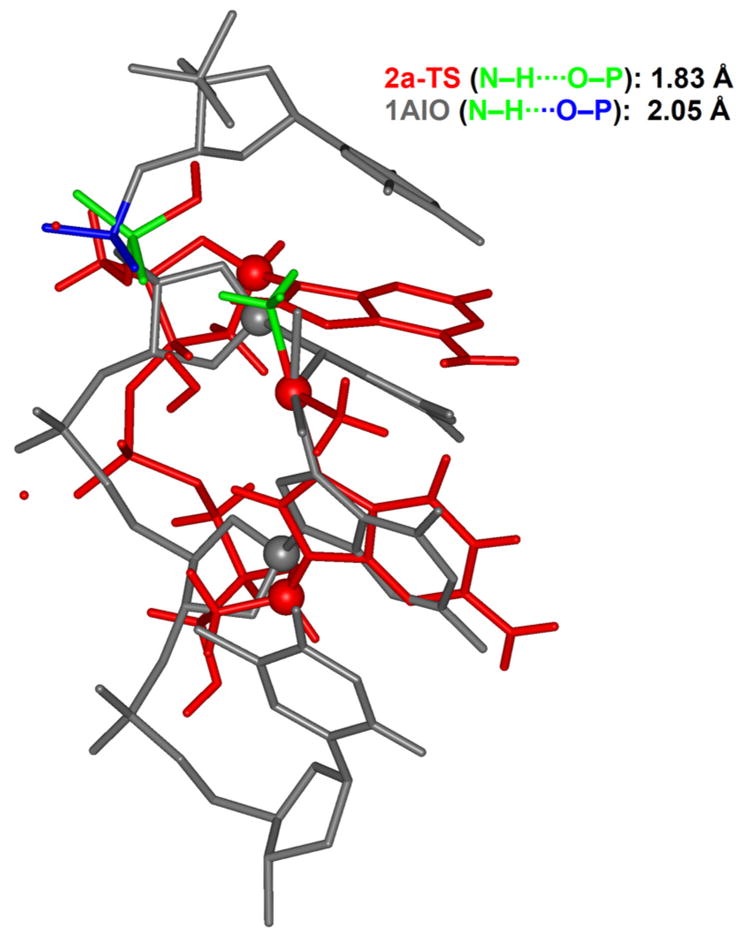
Structural comparison between the computed transition state 2a-TS (red line) and the bifunctional cisplatin adduct to a full-length DNA (grey line) containing a d(pGpG) motive (1AIO).⁷⁵ The most important ammine and phosphate ligands are highlighted in green and blue.

Bifunctional Adducts

Having established the kinetic preference for closing to the 5′-direction, another remaining question is whether or not there is also a thermodynamic preference for forming AG over GA cross-links. Figure 8 shows fully optimized geometries of both possible bifunctional adducts 3 and 4. Comparing these structures to previously reported results that utilized smaller models,^34,76 we note that the presence of the sugar-phosphate backbone introduces a directional distortion resulting from the structural confinement of the DNA-backbone (Figure 8).

Figure 8.

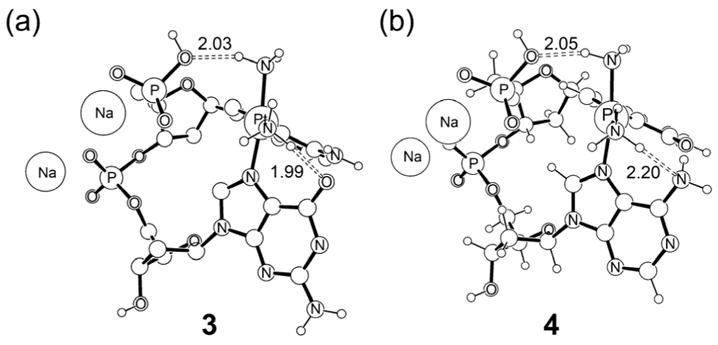
Optimized structures of the two possible bifunctional adducts.

Energetically, our calculations indicate that there is a slight electronic preference of 3 over 4 by 2.33 kcal/mol. Addition of entropy and solvation corrections gives a free energy preference of 4.44 kcal/mol (Table 1). Thus, our calculations indicate that there is a slight thermodynamic preference of the AG over the GA adduct. But the energy difference of ~2–4 kcal/mol is too small to justify the exclusive observation of AG over GA on thermodynamic arguments alone. Moreover, these results are in disagreement with those reported by Burda and co-workers⁷⁶ who report a slight thermodynamic preference for the GA adduct over the AG adduct. Instead, it is more plausible that the barrier of bifunctional closure to the 3′-direction of ~32–38 kcal/mol for the GA sequence is too high to play a physiologically meaningful role, whereas the barrier for AG closure is low enough to be overcome under physiological conditions.

Another previously proposed explanation for the exclusive preference of the AG vs. GA platination is that there is an unfavorable steric clash between the NH₂ group of the 3′-adenine and one of the ammine ligands of cisplatin in the case of GA, whereas in AG this repulsive interaction is replaced by a highly favorable hydrogen bond between the O6 of the 3′ guanine and the corresponding ammine ligand of cisplatin.⁵⁰ In the light of the structural features examined in this study, those previous conclusions must be reevaluated. Our computed structures are in good agreement with the previous study in the sense that the ammine ligand of the cisplatin moiety is close to the amine group of the neighboring adenine. However, in the molecular mechanics framework that was used in the previous study, the amine group of the adenine cannot serve as a hydrogen-bond acceptor. In contrast, our quantum mechanical treatment allows for a rehybridization of the amine moiety exposing the lone-pair in a pseudo-tetrahedral geometry to hydrogen-bond donors. As a result, this interaction that was previously recognized as unfavorable on steric grounds becomes weakly favorable. Moreover, this study reasoned that the same steric interaction may persist at the transition state, increasing the kinetic barrier for GA compared to AG. Again, due to the limitations of the computational method used in that study, this feature could not be addressed explicitly. Our calculations suggest that there is neither a steric nor any other interaction between the amine group of the adenosine and cisplatin in the transition state.

Sugar puckering

In agreement with common experimental observations,^70–72 our calculations consistently show that the 5′-nucleoside adopts a C2′-exo/C3′-endo sugar puckering, whereas the 3′-nucleoside maintains the more natural C2′-endo/C3′-exo puckering of standard B-DNA. We found this effect to be present both in AG and GA adducts. To delineate the energetic and structural impact of the sugar puckering on bifunctional cisplatin binding, we recomputed the bifunctional structures enforcing the C2′-endo/C3′-exo puckering for both nucleosides to afford the hypothetical AG and GA complexes 5 and 6, respectively. To our surprise, we found that the AG complex 5 is 12.52 kcal/mol higher in energy electronically than its analogue 3. Addition of solvation energies gives an energy difference of 7.92 kcal/mol (Table 2).

Table 2.

Relative energies (kcal/mol) of hypothetical bifunctional adduct complexes with enforced C2′-endo/C3′-exo sugar puckering.

	ΔE(SCF)	ΔE(Sol)
3	0	0
4	2.33	3.18
5	12.52	7.92
6	--	--

For the GA-adduct, we were unable to find a stable structure, because the guanosine moiety spontaneously adopted the C2′-exo/C3′-endo sugar puckering. Figure 9 compares the most salient structural features of the complexes 3 and 5. Overall, enforcing the C2′-endo/C3′-exo puckering for both nucleosides pushes the platinum moiety farther away from the sugar-phosphate backbone. In 3, the distance between the platinum center and the central phosphate moiety of the dinucleotide is 7.59 Å, whereas in 5 the distance is 8.35 Å. The C1′···C1′ distances are 6.92 Å and 5.48 Å in 3 and 5, respectively, reflecting on the vertical contraction that is coupled to the horizontal elongation. Figure 10 illustrates the impact of this structural distortion on the coordination geometry at cisplatin. The structural arrangement of the nucleobases in 3 allows for a greater tilt angle of the two purine bases, which leads to a less constrained N7–Pt interaction. The G-Pt-A binding angle is 90.7° and adenine moiety can adopt a nearly planar binding mode with a Pt-N7-purine angle of 172.5°. The glycosidic linkage is also fairly relaxed and we found the C1′-N9-purine angle to be 175.8°. In contrast, the distance between the purines is decreased and they adopt a more parallel arrangement in 5, enforcing a smaller “bite-angle” between the two purine bases. As a consequence, the G-Pt-A binding angle is slightly strained at 88.7° and the Pt-N7-purine dihedral angle is significantly distorted at 156.4° from the ideal planar arrangement. The glycosidic linkage is similarly distorted with a C1′-N9-purine angle of 161.4°, as illustrated in Figure 10. In summary, our calculations suggest that the C2′-exo/C3′-endo sugar puckering of the 5′-nucleoside is crucial for the formation of a structurally relaxed and properly hydrogen-bonded bifunctional adduct. Because the underlying considerations relate to simple and basic structural necessities of the oligonucleotides in general, we expect our findings to be generally valid for all bifunctional adducts of platinum-complexes, and probably for other 1,2-cross-links of similar complexes.

Figure 9.

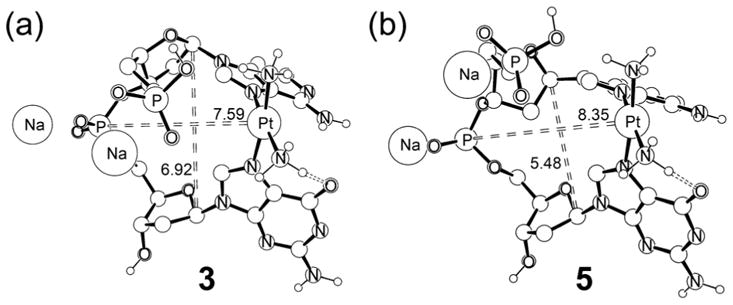
Computed structures of 3 and 5. Distances are shown in Å.

Figure 10.

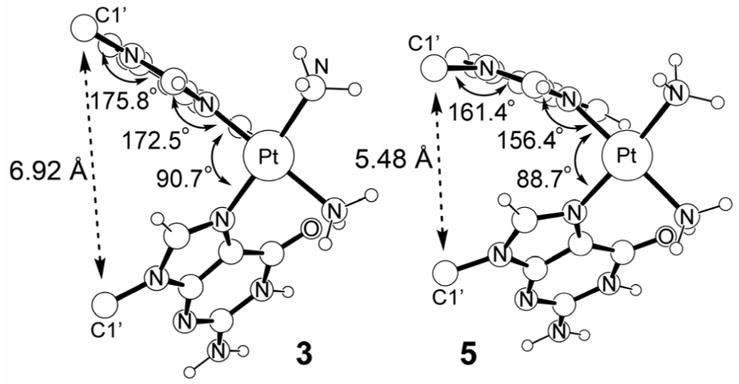
Coordination geometry of Pt in 3 and 5.

Conclusions

We determined how cisplatin binds to DNA containing an AGA sequence to give the physiologically important bifunctional adduct using quantum chemical molecular simulations. In good agreement with experimental observations, we found that cisplatin prefers to react with the 5′-adenine after initial platination at the central guanine site. Thermodynamically, both AG and GA adducts are similar in energy with AG being slightly preferred by 2–4 kcal/mol. The preference of AG over GA binding of cisplatin is attributed to a significantly higher reaction barrier for the GA closure over the alternative AG binding motif. Our calculations estimate the energy difference at the transition states to be in the range of 9–10 kcal/mol. With a reaction barrier of at least 31.95 kcal/mol, the formation of the GA adduct starting from the monofunctional G-Pt complex is predicted to be prohibitively slow. The main difference between the two transition states lies in the presence of a strong hydrogen bond between the axial ammine ligand and the phosphate backbone in the transition state that leads to the AG adduct. Due to the right-handedness of the DNA α-helix, this interaction cannot be formed in the GA-transition state. Examining the structures of the bifunctional adducts, we found that the deoxyribose of the nucleoside at the 5′ position must undergo a sugar puckering change to adopt the C2′-exo/C3′-endo configuration, which allows for a greater tilt angle of the two purine bases and gives rise to a more relaxed coordination geometry at the platinum center.

Supplementary Material

1

Supporting Information Available: Computed Cartesian coordinates of all calculated structures and all energy components. This material is available free of charge via the internet at http://pubs.acs.org.