Abstract
Recent studies have extensively examined the large-scale genetic variants in the human genome known as copy-number variations (CNVs), and the universality of CNVs in normal individuals, along with their functional importance, has been increasingly recognized. However, the absence of a method to accurately infer alleles or haplotypes within a CNV region from high-throughput experimental data hampers the finer analyses of CNV properties and applications to disease-association studies. Here we developed an algorithm to infer complex haplotypes within a CNV region by using data obtained from high-throughput experimental platforms. We applied this algorithm to experimental data and estimated the population frequencies of haplotypes that can yield information on both sequences and numbers of DNA copies. These results suggested that the analysis of such complex haplotypes is essential for accurately detecting genetic differences within a CNV region between population groups.
Introduction
Humans vary greatly in phenotypic traits such as susceptibility to disease, and the inherited components of phenotypic variation are often derived from differences in genomic DNA sequences among individuals.1 Extensive studies are currently being performed to associate disease susceptibility with a form of genetic variation called single nucleotide polymorphism (SNP). Meanwhile, another type of genetic variation known as structural variation, which includes copy-number variation (CNV) of DNA segments, has recently been characterized at the genome level.2 A recent study has reported that CNV regions of intermediate and large sizes cover as many as 360 megabases in the human genome,3 clearly greater than the 10 megabases covered by common SNP sites. Because CNV regions of these sizes often include entire genes and their regulatory regions, they are likely to influence human diversity and disease susceptibility as a result of changes in gene dosage, disruption of coding sequences, or perturbation of long-range gene regulation.4
Usually, alleles or genotypes must be determined in order to associate phenotypic traits such as disease susceptibility with genetic variation. Identification of alleles or genotypes is also necessary for basic genetic analyses, such as those of allele frequencies, Mendelian inheritance, Hardy-Weinberg equilibrium, and linkage disequilibrium, as well as for further applied analyses. In the case of SNP, alleles and genotypes at single SNP sites for each individual can be experimentally determined even in high-throughput platforms, and haplotypes and diplotypes at multiple sites and their frequencies can be inferred from such experimental data by many computational algorithms.5 For the trisomic case, such SNP haplotype-inference algorithms are extended into an algorithm6 that processes data on three alleles at each SNP site to infer three haplotypes on three chromosomes, as observed in Down syndrome (MIM 190685). Also, SNP phasing algorithms are extended for pooled DNA samples so that the extended algorithms can process the data with >2 DNA copies to infer the frequencies of SNP haplotypes.5 However, for CNV, the methods in use are insufficient to rigorously determine alleles or haplotypes in high-throughput platforms. Currently, deletion can be handled,7 because the deletion allele together with the normal one-copy allele constitutes only three easily detectable genotypes, though this determination method is not applicable to combinations with duplication alleles. A recent study3 that used microarrays employed a basically similar procedure, which detects three clusters of experimental signal-intensity measurements that correlate with copy numbers of individuals. Those three clusters are treated as genotypes composed of the alleles of lower and higher copy numbers, though it is unclear how to handle patterns other than three clusters and how many copies the lower and higher alleles have. The fosmid pair-end method8 can detect genotypes in principle, but it is unclear how it could be used to genotype many individuals at high speed.
Here we developed an algorithm to infer alleles and haplotypes within a CNV region from data in high-throughput experimental platforms. Our algorithm processes data on the total numbers of polymorphic bases over two homologous chromosomes within a CNV region for individuals or, in a special case, just the total numbers of allelic copies over two homologous chromosomes within a CNV region for individuals. The former data set is represented by, for example, three counts of polymorphic base A and zero counts of polymorphic base G within a CNV region for an individual. Here, the sum of the counts over bases A and G is not two but three because of copy-number variation. This kind of data is actually obtained from a high-throughput experimental platform, the Invader assay combined with quantitative PCR on multiwell plates.9 In this combined platform, the Invader assay determines the ratio of polymorphic bases whereas quantitative PCR on 384-well plates determines the total copy number; from these two data sets, the number of each polymorphic base is determined. Other high-throughput techniques such as pyrosequencing10 and the Illumina bead array11 would produce the same or similar data. Our algorithm processes such data to estimate the frequencies of haplotypes that can yield information on both sequences and numbers of DNA copies. We applied this algorithm to CNV data9 of the CYP2D6 (MIM 124030) and MRGPRX1 (MIM 607227) genes in two populations of the HapMap project12 and found considerable differences in the haplotype frequencies between the two populations. This suggests that our algorithm is applicable to disease-association studies that detect differences in the frequencies of CNV haplotypes between case and control groups.
Material and Methods
Definitions
Let us consider haplotypes within one CNV region. Let us call a copy unit the unit of DNA sequence that is duplicated within a CNV region (Figure 1). Here, we also consider a case where no copy unit exists within a CNV region on a chromosome; this case corresponds to the deletion of the DNA sequence within the region on the chromosome (Figure 1). In addition to simple copy-unit situations such as shown in Figure 1, in principle, very complex situations could also be conceived. However, to make the calculations practical, we do not consider very complex situations, as described below. Let us use the term single-nucleotide variation in a copy unit (SNVC), which represents the variation of a single nucleotide in a copy unit when the DNA sequences of copy units are aligned (Figure 1). Let us call a variant base a different base at an SNVC site in a copy unit (Figure 1). When we need to distinguish variant bases that are classified by different kinds of bases, we refer to them as variant base types (e.g., A and G at the SNVC1 site in Figure 1).
Figure 1.
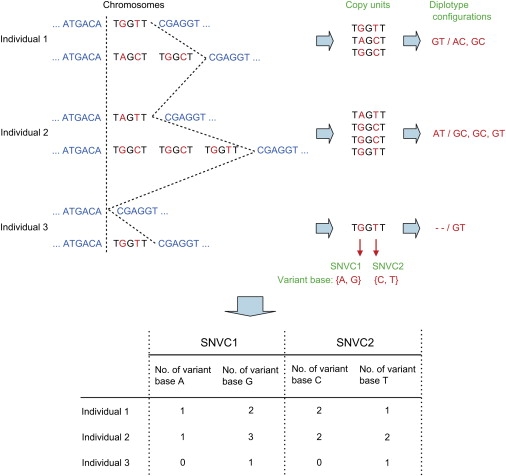
An Illustration of the Definitions Used in This Study
The chromosomal region sectioned by broken lines for individuals indicates a CNV region that includes copy units, the units of DNA sequence that are duplicated within a CNV region. Here, the copy units have two SNVC sites, which represent the sites of single nucleotide variation in copy units when their DNA sequences are aligned. The red characters in the copy units indicate variant bases, which are different bases at SNVC sites. For the sake of simplicity, most invariant bases in the copy units have been deleted. Copy units can be denoted only by variant bases. We call different kinds of variant bases variant base types; for example, A and G are two variant base types at the SNVC1 site. Haplotypes are denoted by combinations of copy units, such as [GT] and [AC, GC], and diplotype configurations are denoted by a pair of such haplotypes separated by a slash. The symbol “-” indicates a deletion. The numbers of variant bases for an individual in an experimental data set are derived from the numbers of variant bases included in real chromosomes from that individual.
Let us denote a copy unit by a variant base or bases at one or more SNVC sites. For example, suppose three copy units, TAGCT, TGGCT, and TGGTT, where the plain characters represent invariant bases and underlined characters represent variant bases at two SNVC sites. (In reality, there may be many more invariant bases in the copy units; for the purpose of explanation, we have simplified this example by deleting most of the invariant bases in the copy units.) We denote these copy units simply by their variant bases AC, GC, and GT, respectively. In these copy units, the former SNVC site has two variant base types, A and G, and the latter site also has two variant base types, C and T. Let us denote a haplotype within a CNV region on a chromosome by a combination of copy units denoted as above. For example, the combination AC, GC (or simply [AC, GC]) represents a haplotype containing the two copy units within a CNV region on a chromosome. We do not distinguish the order of copy units in a haplotype. Let us denote a diplotype configuration by a pair of haplotypes denoted as above (Figure 1). For example, the pair of [GT] and [AC, GC] (or simply, [GT/AC, GC]) represents a diplotype configuration containing haplotypes [GT] and [AC, GC], and this diplotype contains a total of three copy units. We do not distinguish the order of haplotypes in a diplotype configuration. A variant base or bases, or a whole copy unit, might be deleted from a chromosome. In such a case, let us denote a deletion at an SNVC site by a hyphen (-). For example, [--/GT] represents a diplotype configuration that consists of a haplotype without any copy unit within a CNV region and a haplotype with a copy unit [GT].
Suppose that we have a data set listing the numbers of variant bases for variant base types at SNVC sites within a CNV region (lower part of Figure 1). The number of variant bases for each individual in the data set is derived from the total number of variant bases over two homologous chromosomes in the individual (Figure 1). Such individuals are sampled from unrelated individuals. In the case of SNP data, the sum of observed base counts over two alleles is always 2 because one allelic base exists in each homologous chromosome. However, in the case of SNVC data, the sum of observed base counts over two variant base types is not always 2; it may be 0, 1, 3, or some other number, because copy units with variant bases are deleted or duplicated in each homologous chromosome.
The EM Algorithm
By using this SNVC data set, we estimate haplotype frequencies. Several algorithms can be suggested to estimate haplotype frequencies, such as Gibbs sampling, coalescent-based sampling, or the parsimony (Clark's) algorithm.5 Here, we employ the expectation-maximization (EM) algorithm powered by the partition-ligation (PL) algorithm.13 The EM algorithm can be decomposed into two procedures: a procedure to list all possible diplotype configurations that are consistent with an observed data set, and a procedure to iteratively calculate and update the frequencies of haplotypes that are present in those diplotype configurations.
In the first procedure, there might be diplotype configurations whose copy units are involved in very complicated situations. For example, copy units might be distributed over different nonhomologous chromosomes (e.g., over chromosomes 1 and 4), or variant bases in multiple copy units within a CNV region might be complexly deleted, such as in the cases of A-G---C and -TG-A--. However, consideration of these complicated situations makes computation much harder. Hence, as a simple, practical model, we consider that copy units exist only on the same (i.e., two homologous) chromosomes and that variant bases are not complexly deleted in copy units within a CNV region (more specifically, we consider that a whole copy unit is deleted; and, although the following consideration depends on the data sets, we enumerate as many copy units without any deleted variant base as the data sets permit in the enumeration step described below).
Under this simple model, we list for each individual all possible diplotype configurations in which the total number of variant bases over the two haplotypes for each variant base type at each SNVC site is the same as the observed number of variant bases in an SNVC data set. We enumerate such diplotype configurations as follows: (1) list all possible sets of copy units whose variant base number for each variant base type at each SNVC site is the same as the observed base number in a data set; and (2) make up all possible diplotype configurations by separating the copy units in each listed set into two subsets. For example, suppose that a data set includes two counts of variant base A and one count of variant base G at an SNVC site for an individual. In this case, the set of copy units {A, A, G} is possible. Cases at more than one SNVC site are more complicated, but the principle is the same. In the second step, in this example, the following diplotype configurations are possible: [A/A, G], [A, A/G], and [-/A, A, G] (the last is a special case: the entire copy-unit deletion in one haplotype). All these configurations can explain the variant base counts in the above example data set, and we have to consider all of them. See Appendix A for more details on the enumeration procedure.
To better understand this procedure, we compare a case of one SNVC site with a case of one SNP site. In the case of one SNP site, the SNP genotype data set uniquely specifies the diplotype configuration. For example, one count of allele A and one count of allele G at one SNP site for an individual in a data set unambiguously indicate only one possible diplotype configuration: [A/G]. Meanwhile, a data set at even one SNVC site does not uniquely specify the diplotype configuration. For example, one count of variant base A and one count of variant base G at one SNVC site for an individual in a data set indicate two possibilities: [A/G] or [-/A, G], in which the latter case considers a possibility of deletion on a chromosome and two-copied duplication on another chromosome. Therefore, frequency estimation is necessary at even one SNVC site.
After enumerating all diplotype configurations, we go to the second procedure, which iteratively calculates and updates the frequencies of haplotypes contained in the diplotype configurations. This procedure is essentially the same as in the EM algorithm of SNP haplotype-frequency estimation.14 At the expectation (E) step, the proportion of the frequency of a diplotype configuration to the sum of the frequencies of all diplotype configurations in a count pattern is calculated. Here, we refer to a count pattern as a unique series of counts across all variant base types and all SNVC sites. For example, in the table in the lower part of Figure 1, the count pattern for individual 1 is 1 2 2 1. If multiple individuals have the same series of counts, because such series have the same information for haplotype phasing, we arrange those redundant series of counts into a unique series and store the number of those individuals. The equation at this E step is:
| (1) |
where wjk denotes the diplotype proportion, P denotes the population frequency, and djk denotes the diplotype configuration indexed by k for a count pattern j. P(djk) is calculated from Hardy-Weinberg equilibrium:
| (2) |
where the diplotype configuration djk consists of (denoted by “⊕”) the haplotypes hl and hm. At the maximization (M) step, the frequency of a haplotype is calculated from the number of individuals with the haplotype in consideration of the diplotype proportion calculated at the E step. The equation at the M step is:
| (3) |
| (4) |
where Nj denotes the number of individuals that have the count pattern j, and n denotes the number of all individuals in a data set. After this M step, the iteration goes back to the E step to update the diplotype proportion, and in turn goes to the M step to update the haplotype frequency, until the log-likelihood is converged. The log-likelihood ln L is:
| (5) |
The PL Algorithm
As is widely known in the SNP haplotype inference, the simple EM algorithm cannot handle haplotypes with many SNP sites, because as the number of SNP sites increases, the number of possible haplotypes drastically increases. This is the case for SNVC sites, too. Therefore, we reinforce the EM algorithm with the PL algorithm13 to handle haplotypes composed of copy units with many SNVC sites. We use the hierarchal PL strategy15 with the backup buffering of haplotypes.13
In brief, the PL method first breaks down a data set with many SNVC sites into small data sets with a few SNVC sites. Second, for each of the small data sets, the method independently executes the EM algorithm and stores haplotypes with greater-than-threshold frequencies into a buffer prepared for haplotypes. The method also stores other haplotypes as long as the haplotype buffer is not filled up. The criterion for choosing such a haplotype is the rank of its average estimated frequency over all EM iterations. Third, for haplotypes in the buffers of two small data sets that neighbor each other, the haplotypes are ligated to make larger haplotypes with more SNVC sites. This ligation step is executed for all neighboring small data sets. Fourth, with only ligated haplotypes with a larger number of SNVC sites, the second step described above is performed again; that is, the EM algorithm is executed for the data sets with the larger number of SNVC sites and the selected haplotypes are stored in the buffer. The second to fourth steps are repeated until the number of SNVC sites of ligated haplotypes reaches the number of SNVC sites in the original data set.
At the ligation step, whereas the SNP PL method ligates SNP sites between haplotypes, our method ligates SNVC sites between copy units (Figure 2). Specifically, in our method, we count the number of copy units of each haplotype for each partitioned data set and then ligate SNVC sites between the copy units of neighboring haplotypes that have the same number of copy units. For example, in the third table of Figure 2, we count one copy unit for the haplotype h5, two for h6, and two for h7, and count zero for the neighboring haplotype h8, one for h9, and two for h10. Then, because h5 and h9 have the same number of copy units, we ligate SNVC sites between the copy units of h5 and h9. Also, because h6 and h10, and h7 and h10 have the same number of copy units, we ligate SNVC sites between the copy units of h6 and h10, and of h7 and h10. Because h8 does not have any neighboring haplotype that has the same number of copy units, we do not ligate it. The reason for ligating SNVC sites between copy units is that a partition of SNVC sites in an original data set at the partition step corresponds to a partition of the SNVC sites located in copy units. In addition, the reason for using only haplotypes with the same number of copy units is that, if we ligated SNVC sites between the copy units of haplotypes with different numbers of copy units, we would generate ligated copy units with complex deletion structures, which would go against the simple model concept described in the The EM Algorithm subsection.
Figure 2.
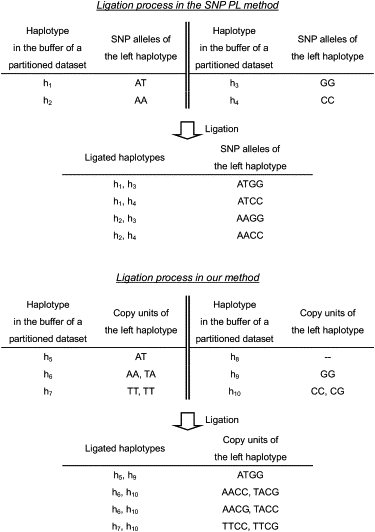
Illustration of the PL Algorithm's Ligation Process Used in SNP Haplotype Inference and Our Inference
The symbols “h” and “-” represent the haplotype and the deletion character, respectively.
Only Copy Number Inference
Here, as a special case, we will focus on only the number of copy units and will not look at variant bases in copy units. Let us refer to the number of copy units in one of two homologous chromosomes as the allelic copy number. Our algorithm, in its simplest but still important application, can infer the allelic copy number in each homologous chromosome and its frequency from the total of allelic copy numbers over two chromosomes within a CNV region in unrelated individuals. In this case, the copy units do not necessarily have SNVC sites in reality. High-throughput platforms such as quantitative PCR on multiple-well plates can measure such total copy numbers but not allelic copy numbers. When allelic copy numbers are required, there is a problem in that the measured total copy numbers do not uniquely specify the allelic state of copy numbers.16 For example, a total copy number of 2 suggest two possible genotypes: [0 copy/2 copies] or [1 copy/1 copy].16 Our algorithm can offer a solution by providing each state with an estimated population frequency (e.g., if a diplotype frequency is quite low, that diplotype is unlikely to exist). To perform this estimation, users only have to temporarily treat the total copy number as the number of one temporal variant base type at one temporal SNVC site in the algorithm. For example, when the total copy number is experimentally obtained as two, users merely have to temporarily treat the data as two counts of one temporal variant base type A at an SNVC site. From these counts, the algorithm enumerates the following possibilities: [-/A, A] and [A/A]. It then estimates the haplotype and diplotype frequencies. Just by counting the copy units in each haplotype, users can obtain the frequencies of diplotype configurations composed of allelic copy numbers, [0 copy/2 copies] and [1 copy/1 copy], respectively.
CNVphaser
We implemented our algorithm in a computational tool called CNVphaser. This tool has many helpful features to analyze CNV data sets, including the following. (1) The core algorithm is based on PL-EM. (2) Users can select three types of initial values in the EM algorithm, including a type that can use any (user-specified) number of sets of random initial values (and compare the resultant log-likelihoods to output the best solution, because the EM algorithm might be trapped into suboptimals depending on initial values). (3) The tool can handle missing calls (failures to count variant bases) at several SNVC sites by considering all possibilities17 under the assumption that the total base number over all variant base types at a missing call site is equal to the mode (the most frequent value) of the total base numbers (over all variant base types) among successfully called sites in a data set. (4) The tool can handle any number of variant base types, though in the text we mostly demonstrate the case of two types of variant base. As described above, the case of one type of variant base (and one SNVC site) is also important because this setting allows the tool to infer allelic copy numbers in each homologous chromosome and their frequencies. (5) The tool can seed already known copy units in the enumeration procedure of the EM algorithm, by limiting possible haplotypes in the enumeration procedure to haplotypes that consist only of such copy units listed in an additional file. The CNVphaser software package is available online (see the Web Resources).
Simulation
We tested the algorithm with simulated data sets. These data sets were generated as follows. First, haplotypes with or without copy units carrying variant bases and the haplotype frequencies were predefined and treated as true haplotypes and frequencies. Second, diplotype frequencies were calculated from the true haplotype frequencies under Hardy-Weinberg equilibrium, and individuals with diplotypes were randomly sampled based on the multinomial distribution of the diplotype frequencies. Finally, variant bases in copy units in the diplotype for each individual were counted, and the numbers were arranged with respect to variant base types at each SNVC site to make a simulated observed data set. The test was whether or not the algorithm could correctly restore the true haplotypes and frequencies just from the observed data set.
We will next explain the details on settings in the simulated data sets and those in our tool. To generate simulated data sets, we first prepared sets of haplotypes to be treated as true haplotypes. We used haplotypes with copy units in which the number of SNVC sites was 1, 2, 3, or 8 and the number of variant base types was 2. In the case that only allelic copy numbers were inferred, we used haplotypes with temporal copy units in which the number of SNVC sites was one and the number of variant base types was one.
We made sets of such haplotypes as follows. In the case of one SNVC site, we took all possible combinations of haplotypes with up to three copy units. More specifically, for two variant base types, we listed such haplotypes as [-], [1], [2], [1, 1], [1, 2], [2, 2], [1, 1, 1], [1, 1, 2], [1, 2, 2], and [2, 2, 2], where “-,” “1,” and “2” represent a deletion, a variant base type, and another variant base type, respectively. Then we took all combinations of these 10 haplotypes to obtain 210 − 1 combinations (= 1023, excluding a set without any haplotype), or sets, of haplotypes. Also for one variant base type (the inference of allelic copy numbers), we listed [-], [1], [1, 1], and [1, 1, 1] to obtain 24 − 1 (= 15) haplotype sets.
For more than one SNVC site, because the enumeration of all combinations was practically impossible, we instead randomly generated sets of haplotypes. For each set, we determined in advance the number of haplotypes to be contained in the set. The number we used was 3, 8, 13, or 18. Then we randomly chose the number of copy units to be contained in each haplotype from the range of 0 to 3, and we randomly picked out the variant base character of “1” or “2” at each SNVC site in each copy unit, unless the number of copy units was set at zero. If this number was set at zero, we assigned “-” to the haplotype. We then removed redundant haplotypes, if any, and obtained a set of unique haplotypes. In the case that the number of SNVC sites was set at 2 or 3, we made 250 sets of random haplotypes for either SNVC number and for each setting of the number of haplotypes (3, 8, 13, or 18). When the number of SNVC sites was set at 8, in order to finish all tests within an acceptable time, we made 25 sets of random haplotypes for this SNVC number and for each setting of the number of haplotypes. As a result, we obtained 250 × 2 × 4 (= 2000) + 25 × 1 × 4 (= 100) haplotype sets, in addition to 1023 + 15 (= 1038) sets for one SNVC site.
In each haplotype set, we assigned a random (standardized) value as a haplotype frequency to each haplotype. Then, we used the haplotypes and frequencies in each set to make simulated observed data sets of variant base counts as described in the first paragraph of this subsection. In this process, the sample size (the number of sampled individuals) was set at 50, 100, or 500. The number of replications, which was the number of simulated data sets generated from one haplotype and frequency set, was set at 30 when the number of SNVC sites was 1, 2, or 3. When this SNVC number was 8, the number of replications was set at 3 for acceptable computation time (we noticed that this replication number did not make much difference in the results). In total, we obtained (2000 + 1038) × 3 × 30 + 100 × 3 × 3 (= 274,320) observed data sets.
For each simulated data set, we executed CNVphaser. We used five sets of values as the initial values for the EM algorithm in CNVphaser. The values in one of the five sets were the uniform values of the diplotype proportions (wjk, see above) in each count pattern, and those in the other four were random values. The tool compared the resultant five log-likelihoods to obtain the best solution. We set at <0.001 the difference in the log-likelihoods between two successive EM iterations to determine the convergence for the EM algorithm.17 For the PL algorithm, we set the number of SNVC sites in each partition to 1, (maximally) 2, or 4 for the 2, 3, or 8 SNVC sites, respectively. For the EM algorithm in each partition, we used the same settings as above. These and the other main parameters used in CNVphaser were as follows: max_em_iteration, 100000; ll_diff_for_convergence, 0.001; initvalue_type, 1; random_initvalue_set_num, 5; partition_markernum, 1, 2, or 4, as described above; partition_initvalue_type, 1; partition_random_initvalue_set_num, 5; partition_hapfreq_cutoff, 10−2; partition_hapbuffer_size, 50. Details on these options are given in the CNVphaser manual.
Performance Evaluation
We quantified the performance of our algorithm by measuring the deviation of estimated haplotype frequencies from the true haplotype frequencies. For this measure, we used the total variation distance in probability theory, which is essentially the same as the index used for the evaluation of SNP haplotype inference.14 This metric is defined as:
| (6) |
where and are the true and estimated frequencies of the haplotype i, which is present in either or both of the estimated and true sets. When the haplotype i is present only in either the estimated set or the true set, the value zero is assigned to the frequency in the other set. The value of this index ranges from zero to one; the larger the value, the worse the performance.
This metric can be decomposed into two parts:
| (7) |
| (8) |
| (9) |
where is the estimated frequency of the false-positive haplotype j, which is not present in the true set but in the estimated set, and and are the true and estimated frequencies of the true haplotype k, which is present in the true set. When this haplotype k is not present in the estimated set, the value zero is assigned to the estimated frequency. The first part, TVfp, represents the deviation due to the false-positive haplotypes, and twice the value is equal to the sum of the frequencies of the false-positive haplotypes. The second part, TVt, represents the deviation only from the true haplotype frequencies. We used these indices, too.
After the computations, we examined the relationships between parameters in the simulation settings and the performance of CNVphaser. Among the simulation parameters, the number of all possible haplotypes consistent with the observed data sets was obtained from the output of CNVphaser. The unevenness of haplotype frequencies was measured with the entropy, standardized by the maximum value:
| (10) |
where pi denotes the frequency of the haplotype i, and n denotes the number of haplotypes in a true set. The range is 0 ≤ UE ≤ 1. This value is 0 when the haplotype frequencies are uniform, and it is 1 when the frequencies are 1 for only one haplotype and 0 for the other haplotypes.
Settings in Real Data Application
In the application to real data, we used the plain EM and the same parameters for CNVphaser as described for the settings in the simulation. We used 60 unrelated individuals (only parents) of CEU and YRI as input individuals.
Results
Simulation Studies
We used simulated data sets to test the algorithm (see Material and Methods for the settings). We checked whether or not predefined, true haplotypes and their frequencies in the simulated data sets were close to those estimated by CNVphaser. Figure 3A shows a result for when the numbers of variant base types, SNVC sites, and sampled individuals were set at 2, 2, and 500, respectively. Because all true haplotypes were included in the estimated set and the true frequencies were close to the estimated frequencies, and because haplotypes that existed in the estimated set but did not exist in the true set were all of low frequency, we concluded that the algorithm successfully estimated the frequencies of haplotypes with the structures including deletion and duplication. We also tested the algorithm in the case that only the total numbers of allelic copies over two haplotypes were known. The algorithm succeeded in this inference as well (Figure 3B).
Figure 3.
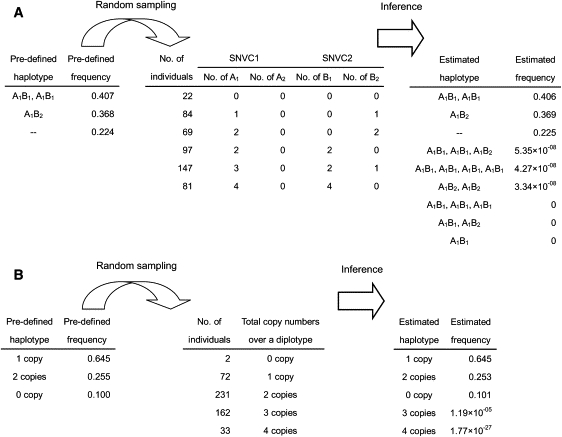
Examples of Simulation Tests
(A) An example of simulation tests when the number of SNVC sites was two and the number of variant base types was two.
(B) An example of simulation tests when only the total copy numbers over a diplotype are known.
Next, we systematically examined the performance (i.e., the accuracy) of the algorithm, by using a variety of simulated data sets. The detailed settings in this examination are described in the Material and Methods section. To quantify the performance, we used the deviation of estimated frequencies from true frequencies (see Material and Methods). We plotted in Figure 4 the median deviation in each category that was composed of simulated data sets classified by the sample size, the SNVC site, the algorithm type (either EM or PL-EM), and the inference type (either copy unit combinations with variant bases or only allelic copy numbers). We found that as the sample size increased, the deviation decreased; that is, the performance improved. Interestingly, the deviation resulting solely from false-positive haplotypes (those estimated by the algorithm but not present in true sets) was mostly unchanged even as the sample size increased. Because the total amount of the deviation is decomposed into this partial deviation and the deviation only from true haplotypes (see Material and Methods), this result means that the larger sample size lessened the deviation only from true haplotypes.
Figure 4.
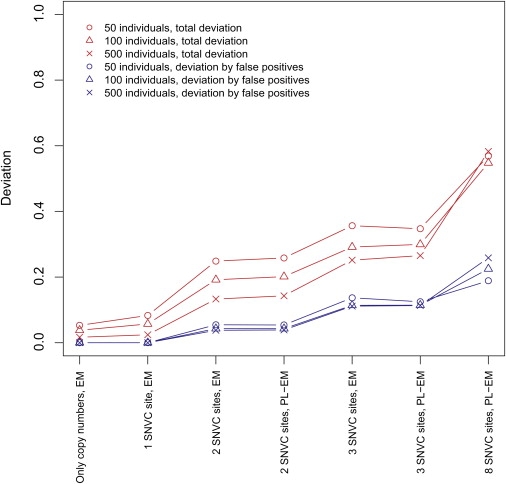
The Performance of the Algorithm
The performance was measured by the deviations of estimated frequencies from true frequencies for all haplotypes (red lines) and only false-positive haplotypes (blue lines). This figure shows the median of the deviations in each category that was composed of (at least 10) simulated data sets classified by the criteria indicated in the labels on the x axis and in the key.
In accordance with the increase in the number of SNVC sites, the deviation increased (Figure 4). Unexpectedly, the deviation in the PL-EM algorithm, which is an approximate method to the plain EM algorithm for fast computing, was not worse than that in the EM up to at least three sites (for more than three sites, the EM mostly required too much computation time). The inference of allelic copy numbers from only the total copy numbers, which was the simplest inference, showed the best performance. The inference at eight sites was the worst.
Figure 5 shows that as the number of true haplotypes and the number of unique copy units (excluding redundant copy units) increased, the deviation increased. Because larger numbers of these parameters generally indicate greater haplotype diversity, which is often related to low levels of linkage disequilibrium (LD), these results suggest that greater haplotype diversity or low LD levels have the effect of decreasing the performance. In accordance with the number of all possible haplotypes consistent with the count data sets, the deviation increased. As the unevenness of haplotype frequencies increased, the deviation generally tended to decrease, which suggests that the performance is better when a few haplotypes have high frequencies and many other haplotypes have low frequencies than when all haplotypes have equal frequencies. The increased sample size generally lessened the deviation increase related to these parameters.
Figure 5.
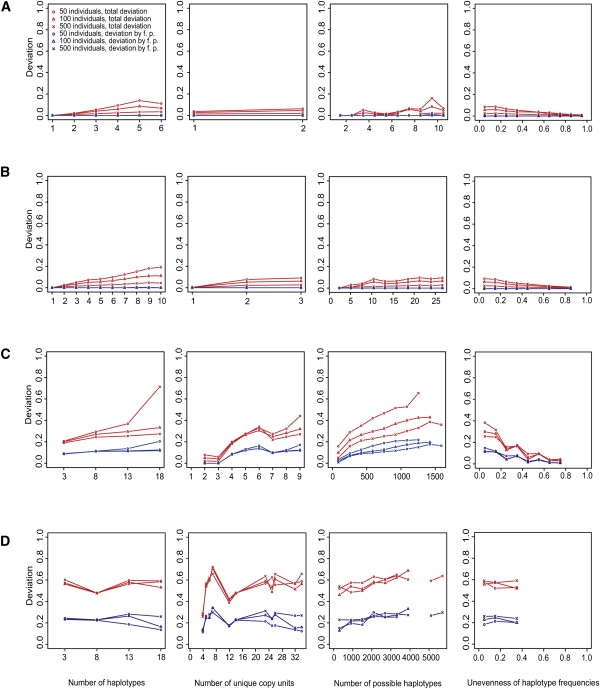
The Deviation versus the Number of True Haplotypes; the Number of Unique Copy Units in the True Haplotypes; the Number of All Possible Haplotypes Consistent with the Count Data Sets; and the Unevenness of the True Haplotype Frequencies
The numbers of all possible haplotypes and the unevenness were arranged by the bin and plotted at the median point on the x axis. On the y axis, we plotted the median of the deviations (red for all haplotypes, blue for false-positive haplotypes) in each category that was composed of (at least 10) simulated data sets classified by the criteria indicated in the labels on the x axis and in the key.
(A) Results of the inference of only copy numbers.
(B–D) Results of the inference of copy unit combinations with variant bases.
(B) For the one SNVC site and the plain EM.
(C) For the three sites and the plain EM.
(D) For the eight sites and the PL-EM.
Application to Real Data Sets
We used CNVphaser to estimate haplotype frequencies from real data sets9 in CYP2D6 and MRGPRX1 genes for individuals of European descent from Utah, USA (CEU) and for individuals of the Yoruba from Nigeria (YRI) in the HapMap populations12 (see Material and Methods for the tool's settings in this calculation). These data sets have complex count patterns of variant bases and would be difficult to use in the analysis of haplotype frequencies without this algorithm. For each data set, the computation took 7.5 s on average and 22.0 s at the maximum with an Opteron 2.8 GHz CPU (1 MB cache, 32 GB RAM). The results in both genes and both populations showed that the major haplotypes were those with the standard one copy (Figure 6A and 6B). Also, the results showed substantial frequencies of non-one-copy haplotypes; for example, for CYP2D6 in YRI, non-one-copy haplotypes [---] and [GCT, GCT] had frequencies of 8% and 3%, respectively.
Figure 6.
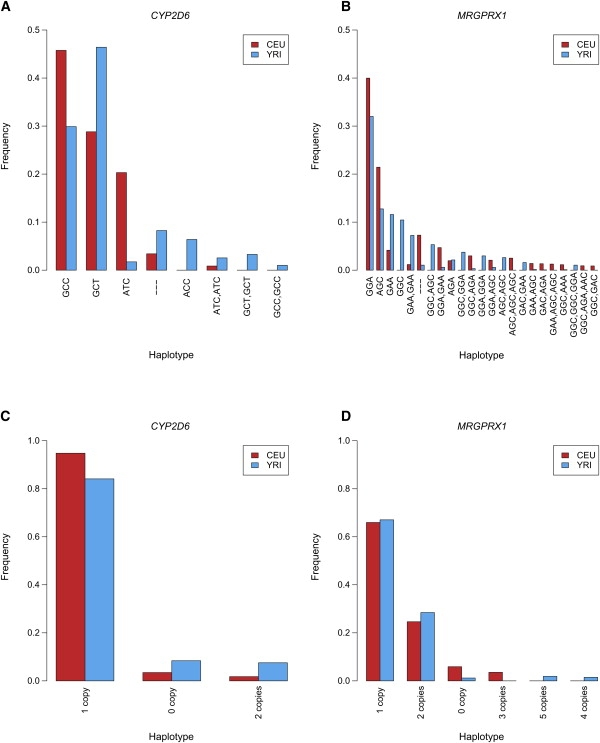
Applications of our Algorithm to Real Data Sets of the CYP2D6 and MRGPRX1 Genes in the CEU and YRI Populations
(A and B) Inference from the data on the numbers of variant bases.
(C and D) Inference from the data on the copy numbers. We showed bases on the backward strand in the direction from the 5′ end to the 3′ end because those genes are coded on this strand (A and B).
Interestingly, we found considerable differences in haplotype frequencies between the two populations for both genes. For example, in CYP2D6, the most common haplotype [GCC] in CEU had a 46% frequency, whereas this haplotype was the second most common in YRI, with a 30% frequency. Among non-one-copy haplotypes, the frequency of the deletion haplotype [---] was 3% in CEU but 8% in YRI. Moreover, the frequency of a two-copy haplotype, [GCT, GCT], was almost zero in CEU but 3% in YRI. For MRGPRX1, a one-copy haplotype, [GGA], was the most common in both CEU and YRI but its frequency differed by 8% between them. Regarding non-one-copy haplotypes, the frequency of a two-copy haplotype, [GAA, GAA], was 1% in CEU but 7% in YRI. Moreover, that of another two-copy haplotype, [GGC, AGC], was almost zero in CEU but 5% in YRI. These results demonstrated that our algorithm enabled us to analyze the differences in haplotype frequencies between the two groups. Similar analyses would be applicable to disease-association studies, in which the frequencies of haplotypes including non-one-copy haplotypes would be compared between case and control groups.
We also inferred the frequencies of only copy number haplotypes without variant bases, by using the data9 on the total copy numbers over two homologous chromosomes and intentionally not using the data on the variant base counts (Figures 6C and 6D). The computation time per data set was 0.10 s on average and 0.18 s at the maximum. Most importantly, we found smaller differences in haplotype frequencies between the two populations, compared with the above results from the data on the variant base counts. For MRGPRX1, the frequencies of the one-copy haplotype differed by 1% between the two populations (Figure 6D). Meanwhile, in the above results, even when we looked at a few one-copy haplotypes with variant bases such as [GGA] and [AGC], we found that the frequencies differed by 8% and 9% (Figure 6B). This was also the case for the two-copy haplotype. The frequencies of this haplotype differed by 4% (Figure 6D), whereas only for three two-copy haplotypes with variant bases, [GAA, GAA], [GGC, AGC], and [GGA, GAA], the frequencies differed by 6%, 5%, and 4%, respectively (Figure 6B). This is probably because the frequency differences in copy-number haplotypes that were subclassified by variant bases were balanced out in the original copy-number haplotypes. This indicates that it is important for finer association studies to use haplotypes that are subclassified by variant bases, if copy units have variant bases in reality.
Discussion
Information on genotypes and haplotypes is essential for genetic analyses and disease-association studies. However, because there is no method to practically determine genotypes or haplotypes composed of deleted and multiple-copied sequences from data in high-throughput experiments, CNV data analyses are currently insufficient. For example, previous studies handle only deletions1,7 or only genotypes related to three clusters of signal intensities correlating with copy numbers.3 Another study2 directly uses signal intensities, in which the allelic state is unidentified. Recent reviews18,19 describe that it is urgent for precise analyses to develop techniques that accurately determine the allelic state of individuals in a CNV region, just as SNP genotyping techniques determine the allelic state at each SNP site.
In this research, we made a conceptual framework that differs from that of SNP haplotype inference, and based on this framework, we developed an algorithm to infer genotypes and haplotypes within a CNV region from high-throughput experimental data. Unlike previously proposed concepts such as paralogous sequence variant (PSV), duplicon SNP, and multisite variation (MSV),20 our framework is organized to mathematically formalize CNV haplotype inference so that our notations can express all those phenomena and can easily be extended to multiple SNVC sites. For example, when the population frequencies of [T, T], [T, C], and [C, C] are all non-zero, they would represent MSV, and when only the frequency of [T, T] is zero, they would represent duplicon SNP.20
By using simulated data sets, we demonstrated the high accuracy of our algorithm and then systematically examined the changes in accuracy according to simulation parameters. Because not much is known about complex haplotypes with variations of both copy numbers and nucleotide sequences, in this study, as a first trial, we set the parameter ranges as wide as possible in consideration of the calculation time and investigated the general tendencies of the computational performance. To evaluate the performance when the algorithm is applied to real data, more realistic settings and detailed analyses will be needed. In our simulation studies, we assumed that the populations were under Hardy-Weinberg equilibrium (HWE). HWE is appropriate for large populations stably existing for a long time period but may be violated for some CNVs, such as those under selection pressure. The performance of our method may be worse when HWE is violated than when it is held. It is known that departures from HWE do not drastically impact the performance of SNP haplotype inference methods and have the least impact on methods using the EM (and PL-EM) algorithm, which is an unexpected conclusion because the EM algorithm explicitly uses the HWE assumption.15 However, detailed studies are needed to clarify whether this conclusion holds true for the CNV haplotype-inference method with the EM algorithm.
In the EM algorithm for SNP haplotypes, sample size has a great impact on the estimation accuracy.21 This is because in larger sample sizes, not only are Hardy-Weinberg proportions more closely attained, but also the number of new haplotypes does not increase linearly with sample size, and the multiple appearances of the same haplotype in a data set allow the EM algorithm to distinguish correct haplotypes from among many possible haplotypes.14 In our CNV case, the number of possible haplotypes derived from observed data more drastically increases with the number of copy units or SNVC sites than with the number of SNP loci in the SNP case; hence, sample size is clearly important also for the CNV case. In our simulation experiments, the estimation accuracy was almost always better for larger sample sizes. A specific sample size value that is required for accurate estimate would depend on the number and pattern of haplotypes in respective CNV regions, so that the specific value is not easy to predict unless true haplotype frequencies are known beforehand. However, if sample size is not overly small, one can at least check whether the sample size reaches a level for the EM algorithm to work well. One approach is to check whether the number of new haplotypes (or count patterns) is saturated or at least decelerated with increasing sample size. A simple and practical way for checking this is to randomly subtract a certain number of samples from a set of given samples and then to plot the number of subtracted samples versus the possible haplotypes. Alternatively, the standard error of an estimated haplotype frequency, which is the standard deviation of the estimator for different sample sets of the same size, could be used as a simplified index. In our software package, we included a program that calculates the standard error by the jackknife method.22
By using real data, we estimated population frequencies of complex CNV haplotypes in two populations. This demonstration showed that the algorithm, in conjunction with the data on the total numbers of variant bases or allelic copies over two homologous chromosomes, enabled rigorous analysis of CNV data on the basis of alleles or haplotypes. In these results, we found considerable differences in the frequencies between the two populations. Because similar analyses are applicable to case and control groups, this demonstration could be a prototype for disease-association studies based on CNV haplotypes. Currently, it is possible to practically measure hundreds of such base or copy numbers in one experiment via quantitative PCR with 384-well plates.9 Other high-throughput techniques such as the Illumina bead array11 and pyrosequencing,10 the latter of which is used in trisomic haplotype inference,6 may also be useful for providing such data. Because the Invader assay combined with quantitative PCR currently focuses on at most several CNV loci, the measurements are precise (for example, the coefficient of determination R2 between prepared samples and observed variant-base ratios was almost one9), and it is assumed that the experiments will be repeated if experimental errors are found in the data. However, this case would not apply to genome-wide platforms. It is more likely that genome-wide platforms such as the Illumina bead array provide a probability distribution for the numbers of copy units or variant bases.23 For such cases, we would have to extend our algorithm by incorporating such a probability distribution. In SNP haplotype phasing, there is a model of such an extension, which incorporates a probability distribution for multilocus SNP genotypes (“GenoSpectrum”) into the EM algorithm.24 In our EM algorithm, a probability distribution for the numbers of copy units or variant bases could be included in a similar way.
Currently, many CNV studies are interested in characterizing the phenotypic states of copy-number differences (often classified as “gain” for duplication or “loss” for deletion).18,19 Here we showed the inference of the allelic states of not only copy-number differences but also nucleotide-sequence differences in copy units. These qualitative (nucleotide sequence) and quantitative (copy number) differences within CNV regions will be ultimately useful for accurately understanding the relationship between genotypes and phenotypes in CNV regions.9 For example, it is known that both kinds of differences in the CYP2D6 gene are important for the metabolism of plant toxins such as alkaloids in food and of many drugs in clinical use, leading to different drug reactions.25 In conclusion, our algorithm will infer complex haplotypes and their frequencies within a CNV region and support rigorous population genetics analyses concerning CNV as well as association studies that detect copy-number and nucleotide differences related to phenotypic traits such as disease susceptibilities.
Appendix A
Details on the Enumeration Procedure
Consider a data set that lists counts for variant base types at SNVC sites within a CNV region (Figure A1). For each count pattern in an observed data set, we enumerate all possible diplotype configurations that are consistent with that pattern. In practice, there could be several ways to enumerate such diplotype configurations by computer. We used the following approach: (1) list all possible sets of copy units in which the number of variant bases for each variant base type at each SNVC site is the same as the number of variant bases in the count pattern; and (2) make up all possible diplotype configurations by separating copy units in each listed set into two subsets of copy units.
Figure A1.
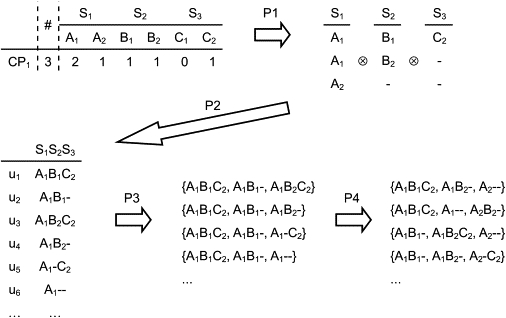
Illustration of the First Step in the Enumeration Procedure
The symbols “A,” “B,” and “C” represent the variant bases. The symbols “S,” “CP,” “#,” “u,” “-,” and “P” represent the SNVC site, the count pattern, the number of individuals with the count pattern, the copy unit, the deletion character, and the subprocedure, respectively. The symbol “⊗” denotes taking all combinations of the variant base characters along all SNVC sites.
In the first step, we first enumerate the characters of variant bases up to the number of the variant base counts in a data set (the subprocedure P1 in Figure A1). In the example of Figure A1, because we have two counts of A1 and one count of A2 for site S1, we enumerate the characters A1, A1, A2 for this site. If there are SNVC sites for which the total copy number over variant base types is smaller than the largest total copy number (over variant base types) among all SNVC sites, we add the deletion character “-” to the SNVC sites up to the number of this difference. In Figure A1, because the total copy number over variant base types of 1 (= 0 + 1) for site S3 is smaller than the largest total copy number among all sites of 3 for site S1, we list 2 (= 3 − 1) deletion characters (as well as the character C2) for site S3.
We then make strings that correspond to copy units by taking all combinations of the enumerated characters along all SNVC sites (P2 in Figure A1). Next, we make sets of copy units (sets of strings) by taking all combinations of the generated copy units under the condition that the number of copy units in a set is equal to the largest total copy number (3 in Figure A1) among all SNVC sites (P3 in Figure A1). Finally, we check to see whether each of the generated copy unit sets has the same number of variant bases as in the original count pattern, for all variant base types and all SNVC sites (P4 in Figure A1). We keep only the copy unit sets that satisfy this consistency.
In the second step, we make all possible diplotype configurations for each of the copy unit sets. To this end, we simply separate copy units in each set into two subsets of copy units. For the example of {A1B1C2, A1B2-, A2--} in Figure A1, we generated three diplotype configurations: [A1B1C2/A1B2-, A2--], [A1B1C2, A1B2-/A2--], and [A1B1C2, A2--/A1B2-], where two haplotypes (two subsets of copy units) are separated by a slash. As a special case, we also make a diplotype configuration that consists of a haplotype with all copy units in a given set and a haplotype without any copy units. For that example, we generated [A1B1C2, A1B2-, A2--/---]. Ultimately, we obtain all possible diplotype configurations for each count pattern.
Web Resources
The URLs for data presented herein are as follows:
The CNVphaser software package, http://emu.src.riken.jp/CNVphaser
Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/
Acknowledgments
Author contributions are as follows: M.K. developed the algorithms, performed the analyses, and wrote the paper; T.T. checked the algorithms and the analyses and reviewed the paper; and Y.N. reviewed the paper. We thank Takahisa Kawaguchi for implementing the phasing algorithm into CNVphaser. We thank Takashi Morizono for coding the simulation and evaluation algorithms. We acknowledge Naoya Hosono and Michiaki Kubo for providing information on the mPCR-RETINA (multiplex PCR-based real-time Invader assay) combined with quantitative PCR and the experimental data. We acknowledge Naoyuki Kamatani for his useful suggestions about the definitions. We thank Todd A. Johnson for his help with the English. This work was partly supported by JSPS.KAKENHI (20790269).
References
- 1.Hinds D.A., Kloek A.P., Jen M., Chen X., Frazer K.A. Common deletions and SNPs are in linkage disequilibrium in the human genome. Nat. Genet. 2006;38:82–85. doi: 10.1038/ng1695. [DOI] [PubMed] [Google Scholar]
- 2.Stranger B.E., Forrest M.S., Dunning M., Ingle C.E., Beazley C., Thorne N., Redon R., Bird C.P., de Grassi A., Lee C. Relative impact of nucleotide and copy number variation on gene expression phenotypes. Science. 2007;315:848–853. doi: 10.1126/science.1136678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Redon R., Ishikawa S., Fitch K.R., Feuk L., Perry G.H., Andrews T.D., Fiegler H., Shapero M.H., Carson A.R., Chen W. Global variation in copy number in the human genome. Nature. 2006;444:444–454. doi: 10.1038/nature05329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Feuk L., Marshall C.R., Wintle R.F., Scherer S.W. Structural variants: changing the landscape of chromosomes and design of disease studies. Hum. Mol. Genet. 2006;15:R57–R66. doi: 10.1093/hmg/ddl057. [DOI] [PubMed] [Google Scholar]
- 5.Niu T. Algorithms for inferring haplotypes. Genet. Epidemiol. 2004;27:334–347. doi: 10.1002/gepi.20024. [DOI] [PubMed] [Google Scholar]
- 6.Clark A.G., Dermitzakis E.T., Antonarakis S.E. Trisomic phase inference. In: Istrail S., Waterman M., Clark A.G., editors. Computational Methods for SNPs and Haplotype Inference, Lecture Notes in Bioinformatics 2983. Springer-Verlag; Heidelberg: 2004. pp. 1–8. [Google Scholar]
- 7.McCarroll S.A., Hadnott T.N., Perry G.H., Sabeti P.C., Zody M.C., Barrett J.C., Dallaire S., Gabriel S.B., Lee C., Daly M.J. Common deletion polymorphisms in the human genome. Nat. Genet. 2006;38:86–92. doi: 10.1038/ng1696. [DOI] [PubMed] [Google Scholar]
- 8.Tuzun E., Sharp A.J., Bailey J.A., Kaul R., Morrison V.A., Pertz L.M., Haugen E., Hayden H., Albertson D., Pinkel D. Fine-scale structural variation of the human genome. Nat. Genet. 2005;37:727–732. doi: 10.1038/ng1562. [DOI] [PubMed] [Google Scholar]
- 9.Hosono N., Kubo M., Tsuchiya Y., Sato H., Kitamoto T., Saito S., Ohnishi Y., Nakamura Y. Multiplex PCR-based real-time invader assay (mPCR-RETINA): a novel SNP-based method for detecting allelic asymmetries within copy number variation regions. Hum. Mutat. 2008;29:182–189. doi: 10.1002/humu.20609. [DOI] [PubMed] [Google Scholar]
- 10.Ahmadian A., Gharizadeh B., Gustafsson A.C., Sterky F., Nyren P., Uhlen M., Lundeberg J. Single-nucleotide polymorphism analysis by pyrosequencing. Anal. Biochem. 2000;280:103–110. doi: 10.1006/abio.2000.4493. [DOI] [PubMed] [Google Scholar]
- 11.Peiffer D.A., Le J.M., Steemers F.J., Chang W., Jenniges T., Garcia F., Haden K., Li J., Shaw C.A., Belmont J. High-resolution genomic profiling of chromosomal aberrations using Infinium whole-genome genotyping. Genome Res. 2006;16:1136–1148. doi: 10.1101/gr.5402306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.The International HapMap Consortium A haplotype map of the human genome. Nature. 2005;437:1299–1320. doi: 10.1038/nature04226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Qin Z.S., Niu T., Liu J.S. Partition-ligation-expectation-maximization algorithm for haplotype inference with single-nucleotide polymorphisms. Am. J. Hum. Genet. 2002;71:1242–1247. doi: 10.1086/344207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Excoffier L., Slatkin M. Maximum-likelihood estimation of molecular haplotype frequencies in a diploid population. Mol. Biol. Evol. 1995;12:921–927. doi: 10.1093/oxfordjournals.molbev.a040269. [DOI] [PubMed] [Google Scholar]
- 15.Niu T., Qin Z.S., Xu X., Liu J.S. Bayesian haplotype inference for multiple linked single-nucleotide polymorphisms. Am. J. Hum. Genet. 2002;70:157–169. doi: 10.1086/338446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Conrad D.F., Hurles M.E. The population genetics of structural variation. Nat. Genet. 2007;39:S30–S36. doi: 10.1038/ng2042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hawley M.E., Kidd K.K. HAPLO: a program using the EM algorithm to estimate the frequencies of multi-site haplotypes. J. Hered. 1995;86:409–411. doi: 10.1093/oxfordjournals.jhered.a111613. [DOI] [PubMed] [Google Scholar]
- 18.Freeman J.L., Perry G.H., Feuk L., Redon R., McCarroll S.A., Altshuler D.M., Aburatani H., Jones K.W., Tyler-Smith C., Hurles M.E. Copy number variation: new insights in genome diversity. Genome Res. 2006;16:949–961. doi: 10.1101/gr.3677206. [DOI] [PubMed] [Google Scholar]
- 19.McCarroll S.A., Altshuler D.M. Copy-number variation and association studies of human disease. Nat. Genet. 2007;39:S37–S42. doi: 10.1038/ng2080. [DOI] [PubMed] [Google Scholar]
- 20.Fredman D., White S.J., Potter S., Eichler E.E., Den Dunnen J.T., Brookes A.J. Complex SNP-related sequence variation in segmental genome duplications. Nat. Genet. 2004;36:861–866. doi: 10.1038/ng1401. [DOI] [PubMed] [Google Scholar]
- 21.Fallin D., Schork N.J. Accuracy of haplotype frequency estimation for biallelic loci, via the expectation-maximization algorithm for unphased diploid genotype data. Am. J. Hum. Genet. 2000;67:947–959. doi: 10.1086/303069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Efron B., Tibshirani R.J. Chapman & Hall; New York: 1993. An Introduction to the Bootstrap. [Google Scholar]
- 23.Wang K., Li M., Hadley D., Liu R., Glessner J., Grant S.F., Hakonarson H., Bucan M. PennCNV: an integrated hidden Markov model designed for high-resolution copy number variation detection in whole-genome SNP genotyping data. Genome Res. 2007;17:1665–1674. doi: 10.1101/gr.6861907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kang H., Qin Z.S., Niu T., Liu J.S. Incorporating genotyping uncertainty in haplotype inference for single-nucleotide polymorphisms. Am. J. Hum. Genet. 2004;74:495–510. doi: 10.1086/382284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ingelman-Sundberg M. Genetic polymorphisms of cytochrome P450 2D6 (CYP2D6): clinical consequences, evolutionary aspects and functional diversity. Pharmacogenomics J. 2005;5:6–13. doi: 10.1038/sj.tpj.6500285. [DOI] [PubMed] [Google Scholar]


