A BIOLOGIC BASIS FOR INTEGRATED MALARIA CONTROL

Abstract

In a series of models of Plasmodium falciparum dynamics, spontaneous local extinctions of the parasite sometimes occurred under steady, perennial-transmission conditions. These extinctions occurred only with extremely low mosquito densities or when the parameter describing the duration of human infection-blocking immunity was at its maximum value, and, simultaneously, those describing vector survivorship and the duration of human infectivity were at their minimum values. The range and frequency of extinctions increased with seasonal transmission, and decreased with the emergence of recombinant genotypes. Here we extend the immunity parameter up to levels that would describe a successful vaccine, and examine the combined influences of seasonality, genotype cross-reactivity, meiotic recombination, and human population turnover on parasite persistence. As Ross did 90 years ago, we conclude that malaria control programs that encompass several methods and targets of intervention are the most likely to succeed. Success is more likely if programs are cognizant of local circumstances of transmission, and, within that context, aim to reduce vector survivorship and human infectivity as well as augment human immunity.

INTRODUCTION

In 1911, Ross evaluated the cost, feasibility, and epidemiologic effects of vector reduction (anti-larvae measures), drug treatment (quinine), and personal protection (bed nets), and concluded that while any one of these might eliminate malaria at a particular site, combinations of them were far more likely to prove effective.¹ In theory, of course, it may be possible to ensure that mosquitoes do not live long enough to transmit infection, or that human immune responses block infection on a lifelong basis, or that a given insecticide or vaccine, respectively, comes close enough to those goals to break the chain of transmission. Experience has seemed to support Ross, however, arguing that malaria is best attacked at several points at once; analytical tools can help to identify those points and develop practical intervention strategies.^2–5

Discrete-event models of malaria transmission adapt the population-compartment scheme of classic models to the level of individuals within host and vector populations (Figure 1). They embed simple, explicit models of Plasmodium falciparum life-cycle dynamics within individual humans and mosquitoes in thousands of interacting representations of individual humans and mosquitoes, and use a single timeline variable to track each parasite life cycle within and between these individuals. This approach intrinsically incorporates multiple interactions among P. falciparum variants, their partitioning across individual human characteristics and infection histories, and their sampling through mosquito transmission. We have previously described the assumptions, implementation, and behaviors of these models in detail, and compared them to those of classic malaria-transmission models.^6–9

Figure 1.

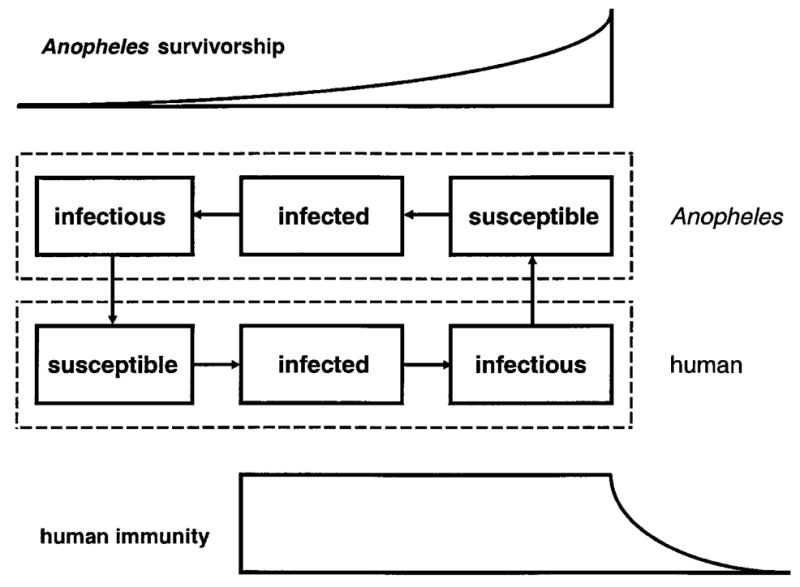
A schematic of the basic discrete-event model, representing the status of a female Anopheles mosquito (top) and a human (bottom) with respect to appropriate stages of the Plasmodium falciparum life cycle. Vector blood meals allow parasite transmission, linking the two phases.²,³

Under steady, perennial-transmission conditions, spontaneous local extinctions of the parasite sometimes occurred. These extinctions occurred only with extremely low mosquito densities or when the parameter describing the duration of human infection-blocking immunity was at its maximum value, and, simultaneously, those describing vector survivorship and the duration of human infectivity were at their minimum values.^8,9

Here we model seasonal fluctuation in Anopheles populations (Figure 2) and meiotic recombination among P. falciparum genotypes (Figure 3), and in that context examine how rates of human population turnover and the frequency with which new parasite genotypes are introduced might affect the local persistence of malaria. We approximate the introduction of a vaccine by setting infection-blocking immunity at levels that would eliminate the parasite, and examine the influence of vector survivorship, duration of human infectivity, seasonality of transmission, and parasite cross-reactivity on its success. The results of this exercise bear upon the planning of malaria control programs.

Figure 2.

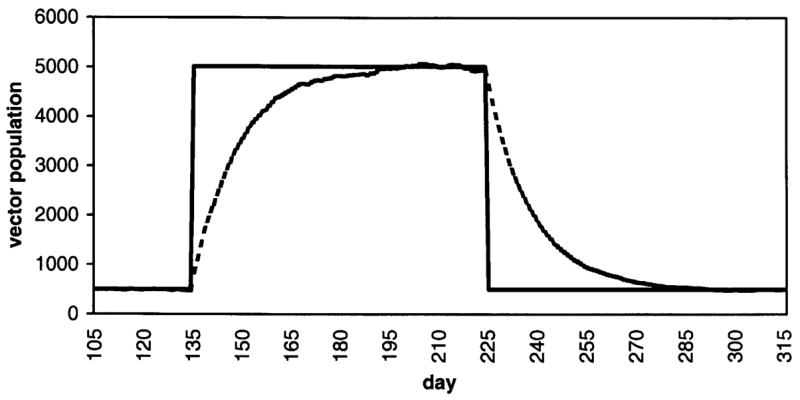
A sample time course of Anopheles population density, with daily vector mortality set at 0.069 and a target 10-fold increase in density for a 90-day high season.⁵

Figure 3.

The cross-reactivity structures m0, m1, m4, and m5 with the four distinct Plasmodium falciparum genotypes in each given as a two-locus, two-allele system Ab, aB, AB, and ab. With meiotic recombination, Ab and aB are the initial and introduced genotypes, respectively; ab and AB are recombinant forms.⁴

MATERIALS AND METHODS

Our discrete-event models typically set the human population at 500, fix the intervals required to progress from an infected to an infectious state at 10 and 20 days for a mosquito and human, respectively, and allow the duration of human infectivity to range from 10 to 30 days.^6–9 A given number of humans and mosquitoes are drawn at random each day, with replacement, for interaction through the taking of blood meals; we generally fix the number of such bites per day at half the number of vectors, thereby assuming that humans are the sole source of blood meals and that there are no density-dependent changes in host access.

The mosquito-dynamics component of the model assumes a constant daily probability of death (parameter range = 0.046–0.139, half-life = 5–15 days). The relationship of this and other parameter ranges in the model to available data is described in detail elsewhere.^6–9 Each dead mosquito is replaced by a number of newly emerged adults that is a Poisson random variable with parameter K/N, where N is the current vector population size; the length of each of two seasons each year and its corresponding value of K are parameters in the model. Here we set K at a high-season value (5,000, a 10:1 ratio with the human population) for 0, 30, 60, 90, 180, 270, 300, 330, or 360 days, and at a low-season value (500, a 1:1 ratio) for the remainder of each 360-day year.⁹ Note that a high-season length of 0 days implies a mosquito population size perennially 10% of that at a 360-day (i.e., perennial) high season. For perennial-transmission conditions, we have derived an epidemiologic power-law relationship over a wide range of mosquito:human ratios.⁶

We represent meiotic recombination between P. falciparum genotypes within a two-locus, two-allele-per-locus system.⁸ A parameter r describes a recombination rate between the loci, 0 ≤ r ≤ 1. For each mosquito blood meal taken, the probability distribution of oocyst genotypes that might result is calculated using the given value of r and the distribution of gametocyte genotypes in the blood meal. The number of oocysts resulting from the blood meal is a Poisson random variable with parameter 0.8 (in accord with data on naturally-infected Anopheles gambiae); a sample of that size is drawn from the probability distribution of genotypes calculated above. With this representation, on average roughly 55% of mosquito feeds on gametocyte carriers produce oocysts (again in line with field data). Within the malaria research community, assumptions differ about whether at most one, two, or four genotypes might be represented within a single P. falciparum oocyst; here we assume four, but we have also carried out parallel studies with models that incorporate the two alternative hypotheses.⁸ One of the anonymous reviewers feels that we “are being over-generous in [our] consideration of other views” on this point. We hope that empirical evidence will soon resolve the question to the satisfaction of all parties.

The model defines immunity in terms of an individual human’s susceptibility to re-infection with a given parasite entity, determined by a daily increase in the probability of infection in response to challenge following clearance. Although susceptibility to homologous re-infection can persist through many challenges, the absence of definitive empirical data makes it difficult to determine a relevant parameter range under this operational (or any other) definition of human immunity in malaria.^10,11 Our initial work focused on 100 days as a standard time until the probability of infection increases to 0.5 (i.e., the half-life of immunity), and systematically explored the effects of values ranging from 50 to 150 days; we later expanded the overall range by setting 2,000 days as the standard half-life and exploring the range from 1,000 to 3,000 days.^6–9 Here we set 40,000 days as the standard half-life, thereby shifting this parameter into a range in which it may lead to extinction of the parasite. We caution that such numbers in individual-based models bear, at best, highly complex relationships to seemingly comparable quantities in classic compartment models.⁶ For purposes of illustration, however, we calculate that, all else being equal, a 40,000-day half-life implies that, on average, an individual clearing an infection would be re-infected after 340 days of daily homologous challenge, or after 1,077 days of homologous challenge every tenth day (5.3 times the intervals with the previous 2,000-day standard). Keeping in mind that we model immunity only in this strictly operational sense, i.e., response to homologous challenge, any particular value of the half-life parameter per se is best interpreted in relative terms. With this one change, with perennial transmission and r = 0, we repeated all previous runs and systematically explored the effects of half-lives ranging from 20,000 to 60,000 days. The numerator used to calculate prevalence in either hosts or vectors is the total number of individuals infected and/or infectious; all prevalence figures represent averages over 100 replicates for each parameter set (standard deviations < 0.01).

As before, we used the best-fit planes for the full series of prevalence-response surfaces to compare the average effects of parameters. Each such surface proved to be lower than that with shorter immunity half-lives, but remained well within the bounds of field data and fully in accord with the qualitative conclusions of our previous work on perennial-transmission conditions.^6–8 Here, with two fully independent phenotypes, the mean overall prevalence in humans was 0.00–0.21, and, with two fully cross-reactive phenotypes, 0.00–0.12. The relative influence of variation in vector mortality was, on average, greater than that of the duration of host infectivity, and that of the duration of human infectivity was greater than that of the duration of host immunity. With parameter sets that included the maximum daily vector mortality (0.139), spontaneous extinctions of the parasite occurred within three years in all runs, except a small fraction (1–5%) of those runs that included both the maximum duration of infectivity (30 days) and the minimum half-life of immunity (20,000 days).

The model defines cross-reactivity between parasite entities as complete and reciprocal, i.e., entities that are cross-reactive share every aspect of a host’s immune-response dynamics except, in general, the phenotype-specific value of the immune-decay parameter. Obviously, the dynamic repertoire of the system could be increased by incorporating fractional or asymmetric values, but there is as yet no clear empirical basis for doing so. Here we set the values of the immune-decay parameter for the four genotypes equal, then consider various cross-reactivity structures among them. Note that as with the parameter values describing duration of human infectivity or immunity, the different structures of cross-reactivity refer to parasite phenotypes, which may have no direct relationship to the parasite genotypes considered subject to recombination.⁸ In particular, structure m0 implies a complete lack of cross-reactivity, while m4 is the most plausible for two immunogenic loci.

Within this framework we initiated each replicate run with no vectors infected, and examined one set of circumstances that included and one that excluded potential meiotic recombination between parasite genotypes. 1) For r > 0, each replicate run began with 15% of the human population infected with a single genotype. After two years, this initial genotype had reached its equilibrium prevalence, and a second genotype was introduced in the form of a single infectious human; each run continued for three more years. Here the initial Ab and introduced aB may or may not be cross-reactive with each other, or with the recombinants ab and AB, as indicated in Figure 3. 2) For r = 0, each replicate run began with 15% of the human population infected with each of the four genotypes (through random selection, with replacement), and continued for five years. In this case the genotypes Ab, aB, ab, and AB may or may not be cross-reactive with each other, again as indicated in Figure 3.

In each case, we recorded the average prevalence of each genotype over the final (fifth) year, and defined genotype persistence in the human population as a run in which that prevalence was > 0.0005 (equivalent to 3–4 completed infections over the course of the year). We calculated the fraction of total runs in which the genotype persisted, and aggregated results over the genotypes as appropriate. Resetting the initially infected fraction of the human population at 2% or 40% did not alter the results reported here.

For the range of human immunity half-lives between 3,000 and 20,000 days, we then extended the model to examine the effects of variation in the timing of the introduction of a new parasite genotype (i.e., in the second set of circumstances above), and of turnover in the human population (in the first set). 1) Rather than introduce the new genotype aB only after 720 days of genotype Ab transmission, we introduce aB at 180, 360, 540, 720, 900, 1,080, 1,260, 1,440, or 1,620 days. The characteristic persistence of the initial and introduced forms is already familiar, so here we focus on that of the recombinant forms ab and AB. 2) Rather than consider the composition of the local human population static, we represent its turnover as a process in which, at a given rate, a randomly selected human is removed from the population and immediately replaced by a malaria-naive human. The number of individuals replaced each day is described by a Poisson random variable with parameter K, the average number of individuals replaced each day, here with values between 0 and 1.

RESULTS

Figure 4 shows the relationship of consistent spontaneous local extinctions of P. falciparum, i.e., extinction in 100% of runs, over all four cross-reactivity structures, to the duration of human infection-blocking immunity, duration of human infectivity, vector survivorship, and high-season length, in the absence of potential meiotic recombination. With parameter sets that included the minimum level of vector survivorship (daily vector mortality = 0.139), the parasite occasionally persisted, but only when the parameter sets also included the minimum duration of immunity, maximum duration of infectivity, and high seasons ≥ 300 days; the average final-year prevalence in these runs was 0.001–0.003. The parasite never persisted when parameter sets included the maximum level of vector survivorship, the minimum duration of immunity and infectivity, and high seasons ≤ 60 days.

Figure 4.

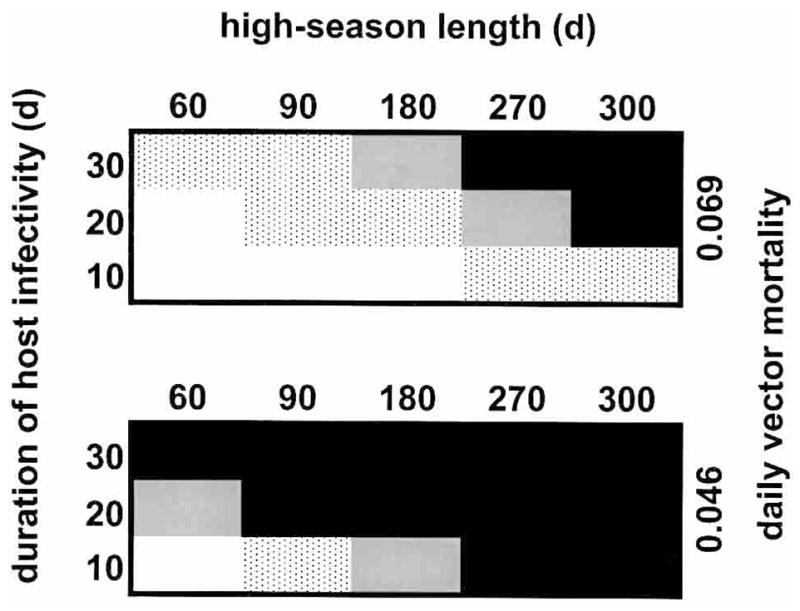
Consistent spontaneous local extinctions of Plasmodium falciparum, i.e., extinction in 100% of runs, over all four cross-reactivity structures, in relation to other variables, with the half-life of human infection-blocking immunity increased to the 20,000–60,000-day range. The white areas indicate that the parasite does not persist if the immunity half-life is 20,000 days, the gray dots indicate that it may persist (depending on cross-reactivity structure) if the half-life is 20,000–40,000 days, the gray area indicates that it may persist if the half-life is 40,000–60,000 days, and the black areas indicate that it may persist even if the half-life is greater than 60,000 days. The upper block represents a daily vector mortality of 0.069 (half-life = 10 days) and the lower block represents a value of 0.046 (half-life = 15 days). In each block the x-axis represents the length of the annual high season, in days, and the y-axis represents the length of time an infected human is infectious to a mosquito.

Thus, vector survivorship exerts a strong influence on the outcome. Furthermore, even with the duration of immunity set at these high levels, parasite persistence may depend on the duration of infectivity: strong restrictions on the influx of parasites to individual humans do not overwhelm the influence of the outflow of parasites from individual infections. An enduring influence of high-season length is also evident, and also greatest at intermediate levels of vector survivorship. As one would expect, regions of parasite persistence typically expand when the model incorporates meiotic recombination, but to an extent that depends on the particular recombination rate, seasonality, cross-reactivity structure, and parameter set. In presenting the results that follow, we focus on frequencies of P. falciparum persistence with durations of immunity between 3,000 and 20,000 days, high-season lengths of 0, 180, or 360 days, and cross-reactivity structures m0 or m4, but the same general principles apply to results with other conditions.

Figure 5 illustrates the effects of variation in the timing of the introduction of a new parasite genotype (aB), when the model incorporates meiotic recombination, on the persistence of recombinant forms (ab and AB). With a high-season length of 0 days (i.e., a perennially small vector population), recombinant forms can persist only with cross-reactivity structure m0, and then only with a half-life of immunity ≤ 5,000 days and a new-genotype introduction at day 1,440, i.e., at the start of the final year of each run. With seasonal-transmission conditions, differences in frequencies of recombinant persistence may depend in part on whether the new genotype is introduced at the start of a high season or an adjacent low season, e.g., in the lower left panel of Figure 5, with the half-life of immunity = 9,000 days. Overall, however, in this context the duration of immunity is a stronger influence than the timing of the new-genotype introduction. While the in-migration of a new genotype is modeled here as a one-time event, for these few genotypes interacting within these simple cross-immunity structures, this conclusion can be extended to probabilities of recombinant persistence under repeated challenge to the human population.

Figure 5.

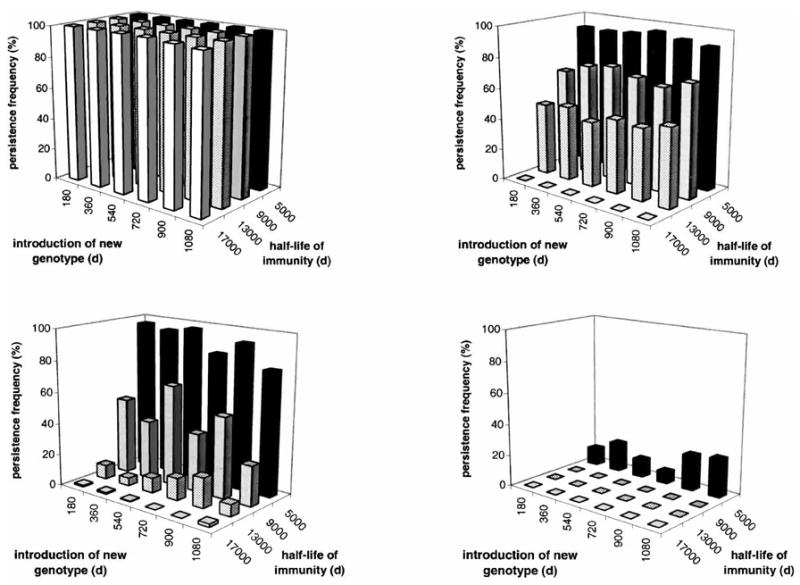
Effects of variation in the timing of the introduction of a new Plasmodium falciparum genotype on the persistence of recombinant forms, with the recombination rate = 0.05, daily vector mortality = 0.069, duration of human infectivity = 20 days, cross-reactivity structures m0 (left panels) or m4 (right panels), and high-season length = 360 days (top panels) or 180 days (bottom panels). With a high-season length = 0 days (i.e., a perennially small vector population), recombinant forms can persist only with the most favorable combination of circumstances (see Results). Note the broad similarity between the influence of cross-reactivity structure (upper right panel) and that of seasonality (lower left panel).

Figure 6 illustrates the effects of turnover in the human population, in the absence of potential meiotic recombination, on the overall persistence of the parasite. With a high-season length of 360 days (i.e., a perennially large vector population), persistence is generally at very high levels, and population turnover has little (m4) or no (m0) effect. With seasonal-transmission conditions or perennially small vector populations, however, the effects can be striking, e.g., in the left panels of Figure 6, with the half-life of immunity = 17,000 days. The simple process in this model does not fully represent the complexities of birth, death, and migration in a human population, but its results reflect a similarly potent interplay between local immunologic and transmission dynamics: in terms of overall prevalence and persistence, a continual introduction of naive hosts may be even more influential than a continual introduction of hosts harboring new parasite genotypes.

Figure 6.

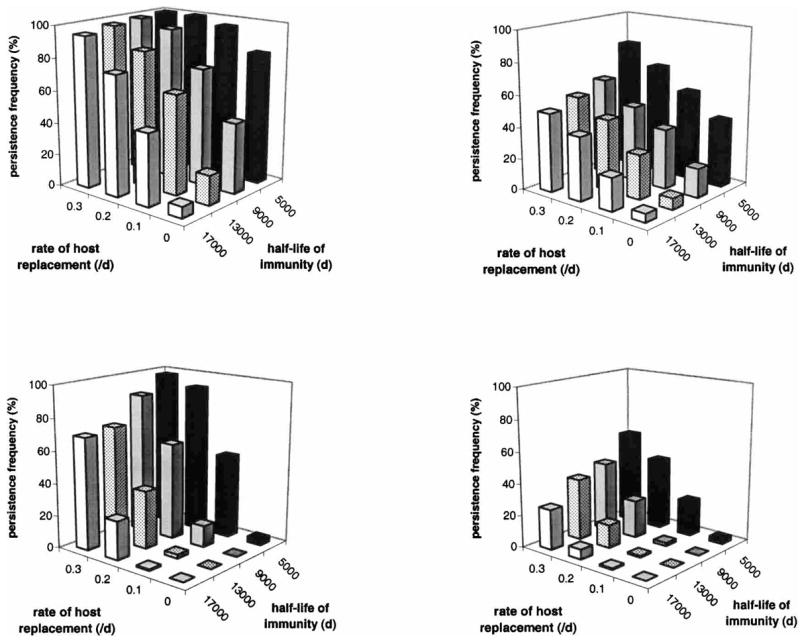
Effects of turnover in the human population on the overall persistence of Plasmodium falciparum, with the recombination rate = 0, daily vector mortality = 0.069, duration of human infectivity = 20 days, cross-reactivity structures m0 (left panels) or m4 (right panels), and high-season length = 180 days (top panels) or 0 days (bottom panels). With a high-season length = 360 days (i.e., a perennially large vector population), turnover in the human population has little or no effect on parasite persistence (see Results). Note the broad similarity between the influence of cross-reactivity structure (upper right panel) and that of seasonality (lower left panel).

DISCUSSION

Malaria is more likely to persist, at a higher prevalence, if the vector lifespan and duration of host infectivity are longer, transmission is more consistent, cross-reactivity is lower, duration of host immunity is shorter, and frequency of host turnover and new-parasite-genotype introduction are greater. This conclusion is not surprising, but the particular manner in which these factors combine to influence an outcome may be. Any of these seven factors may critically affect local persistence, as the findings in Figures 4–6 suggest. Our results indicate how these factors interact, and how the last three, through their influence on overall anti-parasite immunity in a human population, may be phenomenologically interchangeable with respect to parasite persistence.

In mathematical models, vector lifespan can be set so as to render the duration of human immunity irrelevant, or vice versa, but intervention programs are more likely to operate between such extremes. They must operate within the context of local patterns of seasonality, migration, births, and deaths, which strongly influence the factors targeted by intervention, and may change from year to year. Our results indicate that, in any such context, vector control would greatly improve the success rate of a vaccine, and vice versa; both would benefit from abbreviated human infectivity.

Of course intervention programs operate amid more complexity than we address here. Parasite populations are more diverse. Immune responses differ between human individuals, due to genetic factors and age as well as particular histories of exposure, and may encompass transmission-blocking effects; aggregates of immune responses differ between human populations, and change with time.^12,13 Interactions between parasites and vectors are highly heterogeneous and dynamic. Complexity suggests that we allow ample margins for error, and so reinforces the argument for an integrated approach.

Malaria is resilient to interference in part because relatively rare, individual-level events can affect large populations. The prevalence and persistence of P. falciparum in a human population is affected by the persistence of a P. falciparum infection in a human individual, for instance. We describe the latter in terms of a discrete, relatively brief interval, though in fact a single infection may consist of multiple waves of recrudescent parasitemia over long periods; one classic study reported several primary infections that lasted more than a year,¹⁴ and recently published records include several that were intermittently infectious for more than 10 months.¹⁵ Thus, P. falciparum persists through intervals in which there is no detectable transmission, and the apparent success of an intervention may prove transient.^16,17

Current knowledge of malaria does not allow precision or great confidence in predicting long-term outcomes of an intervention, but it does signal that intervention programs that are too narrowly-focused are likely to fail.^18,19 Seasoned malariologists have long implored public health officials to apply integrated approaches to intervention. Our model examines the interplay of seven critical interacting factors known to profoundly impact malaria control efforts, and, in a broad sense, its results communicate this message of experience: attack malaria at several points at once. Choosing the particular array of measures that uses available resources to maximum effect constitutes the primary challenge to those designing and managing an intervention. Local conditions vary, and so does the constellation of measures that makes for locally-effective malaria control. Intervention effects may change with time, and with intervention itself. Beyond what may be gleaned from individual or institutional experience, responsible officials rarely can predict the impact of a given set of prescribed interventions. However, recognizing relationships among dominant variables that may define integrated control, as in our model, constitutes a step toward addressing the problem. As Ross wrote, in 1911, “To say that a disease depends upon certain factors is not to say much, until we can also form an estimate as to how largely each factor influences the whole result. And the mathematical method of treatment is really nothing but the application of careful reasoning to the problems at issue.”