Evaluation of individual particle capillary electrophoresis experiments via quantile analysis

Abstract

The number of particles in a sample heavily influences the shape of the distribution describing the corresponding individual particle measurements. Selecting an adequate number of particles that prevents biases due to sample size is particularly difficult for complex biological systems in which statistical distributions are not normal. Quantile analysis is a powerful statistical technique that can rapidly compare differences between multiple distributions of individual particles. This report utilizes quantile analysis to show that the number of events detected affects the mobility distributions for rat liver and mouse liver mitochondria, sample individual particles, when analyzed via capillary electrophoresis with laser-induced fluorescence. When the mitochondrial sample is small (e.g. <78), there are not enough events to obtain statistically relevant mobility data. Adsorption to the capillary surface also significantly affects the mobility distribution at a small number of events in uncoated and dynamically coated capillaries. These adsorption effects can be overcome when the mitochondrial load on the capillary is sufficiently large (i.e. >609 and >1426 events for mouse liver on uncoated capillaries and rat liver on dynamically coated capillaries, respectively). It is anticipated that quantile analysis can be used to study other distributions of individual particles, such as nanoparticles, organelles, and biomolecules, and that distributions of these particles will also be dependant on sample size.

Introduction

Capillary electrophoresis (CE) has a long history of advancing the separation of complex particles, such as whole cells [1], viruses [2,3], bacteria [2,4,5], and DNA [6] with Kremser et al providing an excellent review on the recent advances in this field [7]. The capability of CE systems, equipped with laser-induced fluorescence (LIF) detectors, to separate individual organelles has also been demonstrated [8]. Although flow cytometry was historically used first to detect individual organelles [9,10], CE has the additional analytical advantage of being able to separate organelles based on their electrophoretic mobilities [11-14]. In general, the electrophoretic mobility of a particle stems from its size [12,14,19] and surface characteristics [13,19], which makes CE useful for comparing the size or surface characteristics of individually detected biological species, such as proteins [15], mitochondria [8,16], nuclei [17], and acidic organelles [18]. The size and surface characteristics of these particles may be highly heterogeneous, making it extremely important to analyze samples with a sufficient number of individual species so that an accurate statistical description is observed.

To date, there have been no studies comparing the number of detected events to the properties measured in the separation of individual particles. Previous reports on the CE-LIF analysis of mitochondrial samples, showed that for samples containing ∼50 events, the electrophoretic mobility histograms are flat and broadly distributed [8], while for samples containing ∼2000, the corresponding histograms appear more Gaussian in nature [21]. This suggests that sample size is important when analyzing individual particles and statistical descriptions are needed to help identify how the number of events affects a distribution.

The quantiles (i.e. the value at a given fraction of a distribution; the median is the 0.5 quantile) provide an evaluation of a distribution’s location, spread, and skew, which are the three main parameters in defining a distribution. A quantile-quantile plot (q-q plot) is a graphical representation of the quantiles that allows differences between the location and shape of multiple distributions to be easily observed.

This report shows how the q-q plot, which is not in common use within the field of separation science, can be used as a powerful tool to compare the distributions of electrophoretic mobilities obtained from electropherograms of individual biological particles. A series of q-q plots are used to investigate the effects of mitochondrial adsorption to the capillary surface on the mobility distribution. Though only mitochondria were studied, the q-q plot is just as valid for the analysis of electrophoretic mobility distributions of other particles (e.g. nanoparticles) or individually detected species (e.g. post-translationally modified proteins in single molecule experiments). It is also envisioned that q-q plots may be used to analyze any other measured parameter that has a distribution of values. A few examples include chromatographic peaks, mitochondrial membrane potentials analyzed in flow cytometry [22], and fluorescence intensity distributions measured in confocal microscopy [23].

Mitochondria were chosen as the sample because of their biological relevance, in house expertise, mobilities independent of size [8,21], and their slightly larger representation in the literature of individual organelle analysis via CE. To carry out this investigation, mouse and rat mitochondria were separated via CE-LIF with varying number of mitochondrial events per sample on uncoated, PVA dynamically coated, and poly-acryloylaminopropanol coated capillaries.

Experimental

Reagents

Poly(vinyl alcohol) (99% hydrolyzed; MW: 31-50 kDa) and HEPES in the free acid form were purchased from Aldrich (Milwaukee, WI). Sucrose was purchased from Sigma (St. Louis, MO). d-Manitol was purchased from Fisher Scientific (Hampton, NH). Fluorescein and 10-N-nonyl acridine orange (NAO) were purchased from Invitrogen (Eugene, OR). Potassium hydroxide, EDTA, and hydrochloric acid were purchased from Mallinkrodt (Paris, KT). DMSO was purchased from Burdick&Jackson (Muskegon, MI). Ethanol (95%) was purchased from Pharmco (Brookfield, CT). CE buffer is 10 mM HEPES, 250 mM Sucrose, and adjusted to pH 7.4 with potassium hydroxide. PVA buffer is made by dissolving 0.2% (w/w) PVA in CE buffer at 60 °C (to speed dissolution). Mitochondria isolation buffer was 210 mM d-Manitol, 70 mM Sucrose, 5 mM EDTA, 5 mM HEPES, and pH 7.4 adjusted with potassium hydroxide. All buffers were made with deionized water and filtered through a 0.2 μm filter prior to use. Stock solutions of 10^-3 M Fluorescein and NAO were made in ethanol and DMSO, respectively, and stored at -20 °C. Samples from these stocks were serially diluted in CE buffer immediately prior to use.

Mitochondrial preparation

Mouse and rat liver cells were obtained from surgically removed and homogenized livers of BALB/c mice and Fischer 344 rats and suspended in mitochondria isolation buffer. A differential centrifugation protocol based on procedures from Howell et al [24]. and Bogenhagen et al [25]. was followed to extract mitochondria. Briefly, cells were washed three times with cold mitochondria isolation buffer and counted using a Fuchs-Rosenthal hemacytometer (Hausser Scientific, Horsham, PA). Cell disruption was 100 % by using 30 strokes in a Potter-Elvehjem homogenizer with a clearance of 0.004-0.006 inches (Kontes, Dusseldorf, Germany). Nuclei and large cell debris were pelleted and removed from the suspension by centrifugation at 1400g for 5 min. The supernatant containing mitochondria was centrifuged two more times to remove any remaining cellular debris. The remaining mitochondrial fraction was then frozen and stored in liquid nitrogen as described previously [21].

All mitochondrial samples were obtained by removing an aliquot from liquid nitrogen and placing it in a -20 °C freezer for 5 min before being thawed out at room temperature and then stored on ice. The aliquots were then prepared for CE analysis by removing debris caused by the freeze-thaw process by pelleting at 600g for 6 min. The supernatant was removed, stored on ice, and treated for 10 min with 10 μM NAO, a fluorescent mitochondrion-selective probe [26]. The mitochondrial suspension was then washed with CE buffer by pelleting the mitochondria twice at 16100g for 10 min and resuspending in CE buffer. All samples were stored on ice and were mixed immediately prior to analysis by CE to prevent settling effects.

Capillary electrophoresis

The homebuilt CE instrument with a post column, sheath-flow laser-induced fluorescence detector used in these studies has been described previously [27]. The 488 nm line from an air-cooled Ar-ion laser was used for excitation (Melles Griot, Irvine, CA). Emission in the range 520 ± 17 nm was selected with a bandpass filter (Omega Optical, Brattleboro, VT) and laser line scattering was reduced using a 490 nm long wave pass sharp edge filter (Semrock, Rochester, NY) and monitored with a photomultiplier tube (R1477, Hamamatsu City, Japan) biased at 1000V.

Separations were carried out using 50-μm i.d., 150-μm o.d. fused silica capillaries (Polymicro, Pheonix, AZ). The uncoated and dynamically coated capillaries were preconditioned before analysis by rinsing the capillary with the following solutions at 20 psi: 0.5 M potassium hydroxide for 60 min, 0.5 M hydrochloric acid for 30 min, water for 30 min, and CE (uncoated) or PVA (dynamic) buffer for 30 min. If an uncoated or dynamically coated capillary became fouled, or otherwise needed to be cleaned, the following wash procedure was performed at 20 psi: 0.5 M potassium hydroxide for 10 min, 0.5 M hydrochloric acid for 5 min, water for 5 min, and CE (uncoated) or PVA (dynamic) buffer for 5 min. AAP coated capillaries were prepared as described previously [28]. The instrument was aligned using a continuous flow of 10^-9 M fluorescein in CE buffer. Electroosmotic flow (EOF) rates were determined by the current change method [21] immediately prior to the analysis of mitochondria on the capillary. All mitochondrial samples were injected using a 2 second hydrodynamic injection at 11.7 kPa. All separations were performed at 400 v/cm on uncoated capillaries and -400 V/cm on AAP coated capillaries.

Data analysis

Output from the photomultiplier tube was electronically filtered (RC = 0.01 s) and digitized at 200 Hz using a PCI-MIO-16E-50 I/O data acquisition card operated by Labview 5.1 software (National Instruments, Austin, TX). The data was stored in a binary format and analyzed via Igor Pro software (Wavemetrics, Lake Oswego, OR). Analysis of all electropherograms was performed using in-house written procedures. A threshold of 5 times the standard deviation of the background noise was used to identify peaks. All electrophoretic mobilities reported are corrected for EOF. Kolmogorov-Smirnov tests were performed using the Igor Pro procedure NeuroMatic available publicly on the internet [24].

Results and Discussion

Statistical analysis of samples

The goal of this report is to determine the minimum number of events required to obtain a consistent mobility distribution, and consequently, improve the ability to predict mitochondrial mobility in a given sample. Quantile-Quantile plots were generated by plotting the data at a specific percentage of the distribution versus the data at the same quantile from a different distribution [29]. If the two distributions match, then the q-q plot should fall along a 45° reference line that bisects the graph. Deviations from the reference line indicate differences between the distributions.

Figure 1 combines several q-q plots by plotting the sample with the largest number of events (x-axis) against several other samples (y-axis). The mouse liver samples (Figure 1 A and B for uncoated and AAP coated capillaries, respectively) tend to have very similar quantiles close to the reference line. In Figure 1 B, the q-q plots have the best correlation between the data and the reference line, suggesting that mouse liver mitochondria separated on an AAP coated capillary yield the most reproducible mobility distributions. The most significant deviation in this figure appears at the extremes of the distribution where the density of events is the thinnest and more susceptible to a small number of randomly distributed events, such as events carried over from a previous run. It is not surprising to then observe that even larger deviations appear at the extreme of the distributions obtained with uncoated capillaries (Figure 1 A). It has been shown that some carryover occurs when mouse liver mitochondria are separated with uncoated capillaries while practically no carryover is observed on AAP coated capillaries [21].

Figure 1.

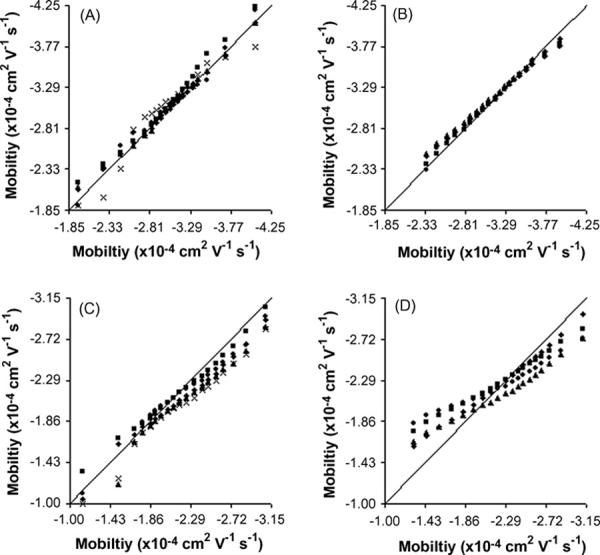
Quantile-Quantile plots of mitochondrial populations. Every 0.05 quantile from 0.05 to 0.95 (left to right) for each sample population (y-axis data) is plotted versus the quantiles of the population with the largest number of events (x-axis data). The solid line is a reference that represents a perfect match between the two data sets. A) mouse liver on uncoated capillaries, B) mouse liver on AAP capillaries, C) rat Liver on AAP capillaries, and D) rat liver with PVA coated capillaries. Legends for the symbols are presented in supporting information (Table S-1).

On the other hand, there is a large degree of variability in the q-q plots described in Figure 1 C and D, representing rat liver mitochondria separated on AAP and PVA coated capillaries, respectively. Though these plots diverge from the reference line, they all appear to have a similar shape. While similar shapes in a q-q plot suggest that the skew and spread of the data are similar, deviations from the reference line suggests that the location of the electrophoretic mobilities is variable (in this instance, for samples with different number of particles).

While it is common to see distributions statistically compared for similarity using the Kolmogorov-Smirnov test (KS-test), the data presented here does not meet the requirements for use of this test. The KS-test assumes that the two distributions being compared are exactly similar with only a small degree of random variation in the location, scale, and shape of the two distributions [29]. Since the location of the distributions appears to be variable, the KS-test will likely generate several false negatives (i.e. similar distributions will be determined to be statistically different).

Based on these observations, the three quartiles of the distributions (i.e. the 0.25, 0.50, and 0.75 quantiles) were chosen to provide an easily tabulated means for describing and comparing electrophoretic mobility distributions.

Effects of undersampling on the electrophoretic mobility quartiles of mitochondria

The three quartiles from electrophoretic mobility distributions with varying numbers of mitochondrial events were compared to determine if there is a correlation between the shape of a distribution and the number of detected events. Figure 2 plots these mobility quartiles versus the number of detected mitochondrial events for mouse liver mitochondria on uncoated capillaries (A), mouse liver mitochondria on AAP capillaries (B), rat liver mitochondria on PVA capillaries (C), and rat liver on AAP capillaries (D). When the number of detected events is high, the three quartiles resemble each other in each of the samples; similarly, the inter quartile distance (IQD = the distance between the first and third quartile) is fairly consistent. This observation is particularly accurate for the mouse liver mitochondria data (Figures 2A and 2B).

Figure 2.

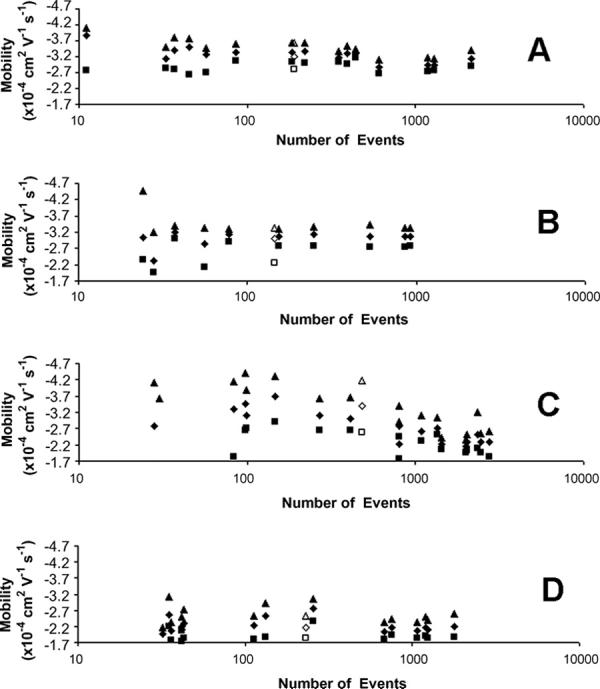
Electrophoretic mobility quartiles from distributions of individual mitochondrial events. (A) mouse liver mitochondria on uncoated capillaries, (B) mouse liver mitochondria on AAP capillaries, (C) rat liver mitochondria on PVA capillaries, and (D) rat liver mitochondria on AAP capillaries. Open symbols represent data pooled from undersampled populations (<269 for rat liver mitochondria on PVA capillaries, <78 for all other samples). Graphs are presented in log scale along the x-axis to more easily perceive all the data. Legend: ■ first quartile, ◆ median, and ▲ third quartile.

On the other hand, when the number of detected events is low, the quartiles are inconsistent and the IQDs appear larger than the quartiles for samples with a large number of events. From these observations, it is possible to define a threshold below which the quartile locations and IQDs are inconsistent. This threshold will be called the undersampling threshold (N_UT), and will be defined as the smallest observed sample with visually consistent quartile locations and IQDs. Distributions whose number of detected events are below this threshold will be called undersampled. The N_UT values for all of the separations in this study are summarized in Table 1.

Table 1.

Undersampling and adsorption thresholds for mitochondria separated by CE.

	NUTa	Adsorption Thresholdb
Mouse - AAP	78
Rat - AAP	113
Mouse - Uncoated	86	609
Rat - PVA	269	1426

^aThe minimum number of events required to obtain a statistically stable distribution

^bThe minimum number of events required for mobility distributions to statistically overcome adsorption effects

The average standard deviations (SD) of the quartiles corroborate the N_UT findings. Table 2 compares the SDs of the quartiles above and below the N_UT. As expected, the SDs are significantly larger for undersampled distributions than for non-undersampled distributions. Similarly, plots of the variances of the electrophoretic mobility distributions versus the number of detected events show that a distribution’s spread becomes small and consistent when it is above the N_UT (supporting information Figure S-1).

Table 2.

Standard deviations of mitochondrial mobility quartiles and variances.

		Mouse Uncoateda	Mouse AAP	Rat Dynamica	Rat AAP
First Quartileb	Non-undersampled	0.05	0.07	0.12	0.05
	Undersampled	0.08	0.46	2.38	0.21
Medianb	Non-undersampled	0.02	0.03	0.17	0.07
	Undersampled	0.31	0.38	0.89	0.21
Third Quartileb	Non-undersampled	0.01	0.05	0.14	0.10
	Undersampled	0.36	0.58	0.29	0.33
Variancec	Non-undersampled	0.29	0.14	0.05	0.38
	Undersampled	1.66	1.49	4.57	1.15

^aOnly first three non-undersampled populations were used

^bQuartile data is ×10^-4 cm² V^-1 s^-1

^cVariance data is ×10^-9

The N_UT is expected to be independent of sample type if it is statistical in origin. The smallest N_UT value is 78 for mouse liver mitochondria on an AAP capillary. Since there are no data points between 86 and 78 for mouse liver mitochondria on uncoated capillaries, or between 113 and 78 for rat liver mitochondria on AAP capillaries, all of these values likely represent the same minimum. This suggests that the N_UT should be the same for both rat and mouse liver mitochondria. Rat liver mitochondria on PVA capillaries, however, have three data points between their N_UT of 269 and 78 (146, 99, and 86). This higher N_UT value suggests that other factors, such as interactions of mitochondria with the capillary surface, can affect the N_UT.

Although two different mitochondrial types is not enough to make a general conclusion regarding the N_UT for all mitochondria, or any other particles analyzed via CE, previous reports on different kinds of mitochondria show relatively small standard deviations in the quartiles when the samples contain at least 150 events [8,20,30]. Therefore, as practical advice, if a sample of mitochondria is to be analyzed by CE without first identifying the N_UT, the number of detected events should exceed 150.

Undersampling alters the shape of mitochondrial mobility distributions

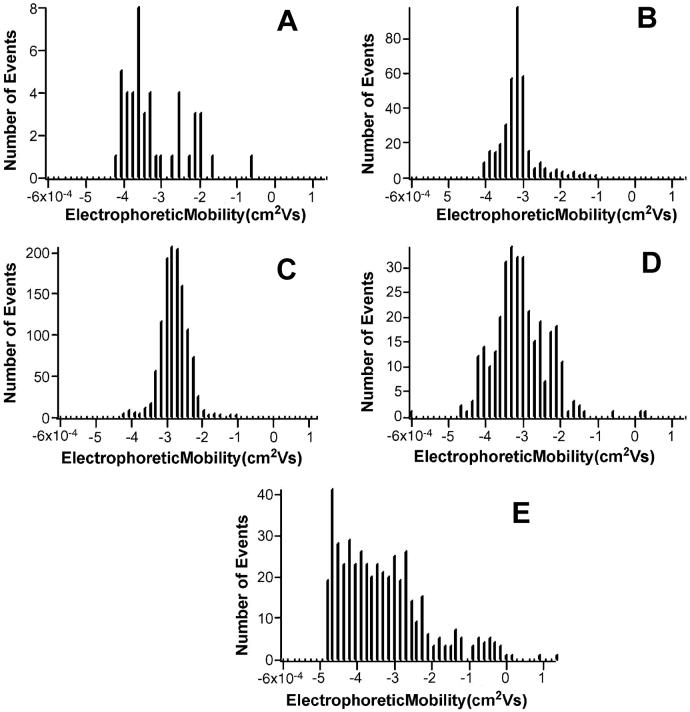
As suggested by the electrophoretic mobility quartiles, the number of detected events affects the shape of their distributions. Figures 3 A, B, and C show representative electrophoretic mobility histograms for mouse liver mitochondria on an uncoated capillary with low (45), medium (351), and high (1196) numbers of detected events, respectively. As the number of events increases, the histograms begin to appear more Gaussian. When the number of mitochondria is low, the distribution appears somewhat flat and the relative number of mitochondria with extreme mobilities (e.g. -3.7 to -4.2 × 10^-4 cm² V^-1 s^-1) is larger.

Figure 3.

Mobility histograms of mouse liver mitochondria separated on an uncoated capillary with varying number of events. A) 45 events, B) 351 events, and C) 1196 events, D) compiled from undersampled distributions, and E) compiled from undersampled distributions of rat liver mitochondria data on PVA dynamically coated capillaries.

If undersampling is primarily statistical in origin, pooling the data from several samples below the N_UT should eliminate this effect if the total population size is > N_UT. This should produce: (i) reliable statistical information comparable to samples above the N_UT and (ii) a more Gaussian histogram. Figure 3 D is a histogram of the pooled undersampled data obtained from mouse liver mitochondria on uncoated capillaries, and it shows significantly more Gaussian character than the undersampled data in Figure 3 A. It is interesting to note the broad nature of the histogram observed in the pooled undersampled data (Figure 3 D) compared to a sample with a large number of events (Figure 3 C). This is likely broadening of the distribution due to non-specific adsorption of mitochondria to the capillary surface, which is discussed in more detail below.

The undersampled data from each sample type were pooled together and the quartiles from the pooled distribution were plotted against the new total number of events in Figure 2 as open symbols. Visual inspection shows that the open symbols appear more similar to non-undersampled distributions than the individual components of the pooled data for mouse liver mitochondria (Figure 2 A and B) and rat liver mitochondria on AAP capillaries (Figure 2D). Interestingly, rat liver mitochondria separated on uncoated capillaries (Figure 2 C) do not appear to fit this trend. This data probably fails to overcome undersampling via pooling undersampled data because other factors, such as adsorption to the capillary surface, are occurring. Together, this data further supports the hypothesis that undersampling is statistical in origin, when adsorption of mitochondria to the capillary is absent.

Adsorption of mitochondria to the capillary surface

Rat liver mitochondria are known to strongly adsorb to uncoated fused silica [21], have apparent mobilities that are significantly reduced compared to separations on AAP capillaries, and have broad, flat electrophoretic mobility distributions. This explains why the pooled undersampled data obtained for rat liver mitochondria on PVA capillaries (Figure 3 E) produces broad, flat distributions with no apparent Gaussian character. Additionally, the open symbols in Figure 2 C show that the median and third quartiles from the pooled data are quite different than the quartiles from any non-undersampled data.

Consequently, to obtain reliable electrophoretic mobility distributions for strongly adsorbing mitochondria, the number of detected events must overcome both statistical undersampling and adsorption effects. Overcoming adsorption should be possible by injecting enough mitochondria to saturate the adsorption sites on the capillary, which is similar to the process of overloading a column in HPLC [31]. As the number of injected mitochondria increases, the effects of adsorption on the observed electrophoretic mobility distributions become less significant. Thus, the N_UT for rat liver mitochondria on PVA capillaries is defined by a combination of statistical undersampling and strong adsorption to the capillary surface.

The quartile distributions also show that there is a shift in the quartiles as the number of detected events increases for mitochondria on non-AAP coated capillaries (Figure 2 A and C). This shift is easier to see in Figure 4, which is a q-q plot of the average of the quantiles from three largest distributions versus the quantiles of all the non-undersampled distributions that are affected by this shift. The quantiles for these distributions undergoing the shift are similar in shape but above the reference line, which corresponds to a larger electrophoretic mobility and a slower migration time. This means that mitochondrial mobilities are being slowed down without changing the distribution’s spread or skew, which suggests that the shift in mobility is the result of a chromatographic type of adsorption to the capillary surface.

Figure 4.

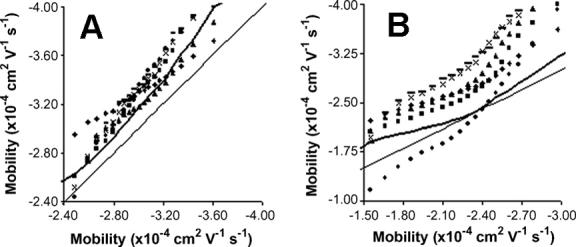
Quantile-Quantile plots of the distributions of mitochondria undergoing adsorption to the capillary surface. The x-axis is the average of the quantiles from the three largest distributions and the y-axis is the quantiles from individual distributions. The thin line represents the reference line and the heavy line represents 1.5 SD from the reference line. A) Mouse liver mitochondria separated on uncoated capillaries. B) Rat liver mitochondria separated on PVA coated capillaries.

This adsorption effect seems to disappear as the number of detected events becomes very large, which is likely due to a limited number of adsorption sites, as described previously. It is important to define a threshold where the locations of the electrophoretic mobility distributions are no longer affected by this weaker adsorption. The adsorption threshold was defined by the first sample that had a majority of its quantiles falling within 1.5 SD of the reference line in Figure 4, which is defined as the average quantiles of the three largest distributions in a data set. By this definition, the adsorption threshold is 609 for mouse liver mitochondria on uncoated capillaries and 1426 for rat liver on PVA capillaries (Table 3). The 1.5 SD thresholds are presented in Figure 4 as a heavy solid line, and they clearly show that a majority of the quantiles from distributions below the adsorption threshold fall above the dashed line.

Table 3.

Comparison of mitochondrial mobilities at low and high numbers of detected events.

Mitochondria Type	Capillary Type	Low Number of Eventsa	Median Mobilityb	High Number of Eventsc	Median Mobilityb	Differenced
Mouse	Uncoated	87	-3.26	1292	-2.87	-0.39
Mouse	Uncoated	184	-3.32	2133	-3.16	-0.16
Mouse	Uncoated	260	-3.40	1091	-2.86	-0.56
Mouse	AAP	78	-3.13	917	-3.06	-0.07
Rat	Dynamic	269	-3.09	2756	-2.28	-0.81
Rat	AAP	113	-2.24	1775	-2.18	-0.06

^aThis value represents the lowest number of detected events that was ≥ N_UT.

^bMobility units are ×10^-4 cm² V^-1 s^-1

^cThe largest population of mitochondria that came from a sample

^dThe increase in mobility between low and high numbers of detected events

One distribution in Figure 4 B (represented by ●) shows a significant number of quantiles below the dashed line. However, it also shows that the spread and skew of this distribution is nothing like the other distributions. Thus, it is possible to conclude that this piece of data is an outlier, which further shows the power and utility of the q-q plot.

As expected, no shift was observed by this definition on AAP coated capillaries, confirming that the observed shift is most likely the result of interactions between mitochondria and the capillary surface.

An estimation of the bias to the electrophoretic mobility of mitochondria due to adsorption to the capillary surface can be determined by adding an adsorption factor (μ_a) to the true electrophoretic mobility of the mitochondria (μ_p), to get the observed electrophoretic mobility (μ_T), as given by equation 1:

$${\mu }_T={\mu }_p+{\mu }_a$$ (1)

Since not all mitochondria necessarily undergo adsorption at the capillary surface, the apparent mobility of the sample’s quartiles will be governed by a slightly different equation:

$${\mu }_T={\mu }_p+\rho {\mu }_a$$ (2)

where ρ represents the statistical weight of the adsorption term. When the number of events in a sample is sufficiently small, ρ = 1, suggesting that all mitochondria undergo adsorption to the capillary wall. When the number of events in a sample is significantly larger than the number of adsorption sites, the number of mitochondria that undergo adsorption will become statistically insignificant, and ρ will approach 0. Large samples therefore have apparent mobility quartiles dependant solely on their actual electrophoretic mobility. Characterizing the effect of ρ when not in either of the two described regimes is beyond the scope of this work.

By comparing the median mobility terms from Table 3 for data operating under ρ = 1 and ρ = 0 the value of μ_a can be calculated using equation 2. The ρ = 1 data can be estimated by using the mobility data from the smallest sample ≥ N_UT. It is possible that the adsorption effect will continue to get stronger below the N_UT, but because of the difficulty with obtaining statistical information below the N_UT, this is the best estimate available. The ρ = 0 data is taken from the largest available sample. Three experiments with mouse liver mitochondria produced an μ_a of -0.37 ± 0.20 × 10^-4 cm² V^-1 s^-1. Only a single experiment with rat liver was analyzed to estimate the μ_a as -0.81 × 10^-4 cm² V^-1 s^-1, which is significantly different than the average μ_a for mouse liver (P < 0.05). This is in line with previous results that claim rat liver mitochondria observe significantly more adsorption to the capillary surface [21].

Conclusions

This is the first report that empirically determines the minimum number of events required to obtain statistically stable results for a sub-cellular particle. The N_UT for rat and mouse liver mitochondria when analyzing electrophoretic mobilities is 78, but a minimum of 150 events is recommended when they type of mitochondria has not been fully characterized. Mobility distributions operating below the N_UT become erratic and broad, as described by their quartile distributions and variances, and their histograms appear flat and without any Gaussian character. Pooling the data below the N_UT provides distributions and histograms that are significantly improved, unless the mitochondria undergo strong adsorption with the capillary. Strong adsorption characteristics were observed in rat liver mitochondria on PVA dynamically coated capillaries at low injection numbers, which agrees with previous results. The adsorption of mitochondria to the capillary surface more drastically affects mobility distributions when the number of mitochondrial events is small, but this can be statistically overcome by injecting sample with a large number of mitochondria. The effect of adsorption on a mitochondrial sample is used to compare the adsorption behavior between rat and mouse liver mitochondria. While AAP capillaries are better at preventing adsorption, it is possible to operate uncoated and dynamically coated capillaries in a regime where adsorption is statistically insignificant. It is anticipated that the methods described here can be used to determine the N_UT for other particles with heterogeneous characteristics, such as other sub-cellular organelles.