Hierarchical coding for sequential task events in the monkey prefrontal cortex

Abstract

The frontal lobes play a key role in sequential organization of behavior. Little is known, however, of the way frontal neurons code successive phases of a structured task plan. Using correlational analysis, we asked how a population of frontal cells represents the multiple events of a complex sequential task. Monkeys performed a conventional cue–target association task, with distinct cue, delay, and target phases. Across the population of recorded cells, we examined patterns of activity for different task phases, and in the same phase, for different stimulus objects. The results show hierarchical representation of task events. For different task phases, there were different, approximately orthogonal patterns of activity across the population of neurons. Modulations of each basic pattern encoded stimulus information within each phase. By orthogonal coding, the frontal lobe may control transitions between the discrete steps of a mental program; by correlated coding within each step, similar operations may be applied to different stimulus content.

Many complex functions are computed in the brain by parallel pattern recognition (1). Like the program of a conventional serial computer, however, much of our behavior achieves its ends through a structured sequence of operations, each moving one step on the path to solution (2). Since the pioneering work of Bianchi (3), Luria (4), and Fuster (5), it has been recognized that prefrontal cortex (PFC) plays a key role in construction of mental programs for sequential behavior (6–8).

Prefrontal neurons are known to code many kinds of task-relevant information (9, 10). They can show selective responses during the different phases of complex tasks, including stimulus presentations, delay periods, responses, and feedback intervals (11–16). Within each task phase, there can be selective coding of stimulus and response identity, working memory contents, task rules, and rewards (16–20). Even when neurons are randomly sampled, a large proportion code some form of task-relevant information (21). Together, these results suggest a dense, broadly distributed code of information that bears on the animal's current activity (9, 10).

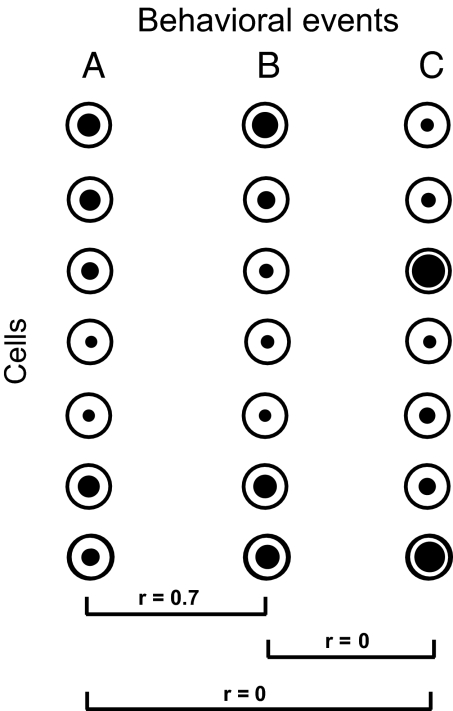
A key question for any representation is its similarity structure. The problem is illustrated in Fig. 1, showing distributed patterns of activity across a population of cells for three different behavioral events. At one extreme, uncorrelated or orthogonal neural representations (e.g., Fig. 1, events A and C) minimize interference (22). Orthogonal codes provide efficient representation of many independent events in a fixed population of units. At the other extreme, strongly correlated codes (Fig. 1, events A and B) imply similarity of meaning and consequences. In distributed representations, correlated coding underlies the ability of neural networks to generalize from one instance to another (22). Here we examined the structure of prefrontal coding in successive phases of a complex task. We asked how task phase is coded in a prefrontal cell population, how stimulus information is coded within each phase, and how stimulus coding changes from one phase to the next.

Fig. 1.

Distributed population codes for different behavioral events. Activity levels (black dots) are shown for a fixed cell population, coding three different behavioral events. For events A and B, patterns of activity across the population are strongly correlated (r: correlation coefficient). For A–C and B–C, activity patterns are orthogonal.

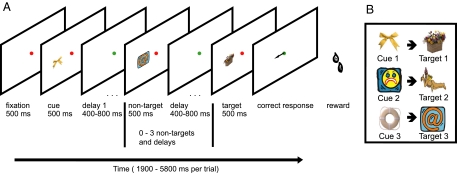
We trained two monkeys to perform a conventional cue–target association task (Fig. 2A), similar to tasks previously used in studies of temporal lobe function (23). Each trial began with a cue picture, presented to the left or right of a central fixation point. This cue simultaneously instructed the animal where a following series of pictures would be presented, and which target picture to search for. The experiment involved three well learned cue–target pairs (Fig. 2B), which were different for different animals. On each trial, zero to three nontargets preceded the target, each picture shown for 500 ms and separated from the next by an interval randomly varying between 400 and 800 ms. The majority (two thirds) of nontarget objects were targets associated with other cues, but they could also be neutral stimuli not associated with any cue and never serving as targets. Monkeys were required to maintain central fixation until the target appeared, and then at target offset, to make an immediate saccade (response window 500 ms) to the target location for a juice reward. As an additional timing cue, the fixation point was red during stimulus presentations, but green during interstimulus delays. Gray dots, marking left and right stimulus positions, were present throughout the trial.

Fig. 2.

Task, stimuli and recording locations. (A) Task. At the beginning of each trial, one of three possible cue stimuli (here, a ribbon) was presented 6° to the left or right of the fixation point. The cue indicated the relevant hemifield for that trial and the target picture to be detected (flower basket). A sequence of stimuli followed in the cued location, consisting of 0–3 nontargets followed by the associated target. Monkeys were required to maintain central fixation until the target appeared, and then at target offset, to make an immediate saccade to its location for juice reward (black arrow; not present on actual display). (B) Cue–target pairs for one animal.

For each neuron, we analyzed activity for the different cues, delay periods, and targets in each visual hemifield. For each task phase (cue, delay, or target), and for different stimulus information (e.g., different cue identities) within each phase, we accordingly obtained a pattern or vector of activity across the population of all recorded cells. The results show that successive task phases are coded by successive, approximately orthogonal activity vectors. Within each phase, activity patterns are strongly correlated for different stimuli, suggesting that stimulus information is coded by modulation of the basic task phase vector. This scheme would allow independent control of the different operations required in successive task events, whereas within each task phase, similar operations are applied to different stimulus identities. Such hierarchical coding may provide a fundamental structure for prefrontal control of sequential activity.

Results

Behavior and Cell Sample.

Across all recording sessions, monkey A made 74% correct responses to targets (saccade at offset), 79% correct responses (no saccade) to nontargets that were targets on other trials, and 98% correct responses (no saccade) to nontargets that were never targets. For monkey B, the respective values were 91%, 84%, and 95%. When errors were made to targets, 95% (monkey A) and 71% (monkey B) were premature saccades (before target offset), suggesting incorrect response timing rather than failed target identification. Neural data were analyzed only for correctly completed trials.

Across the two animals, responses were recorded from a total of 383 neurons, widely distributed across dorsolateral and ventrolateral PFC [supporting information (SI) Fig. S1]. Data were recorded from all isolated neurons, irrespective of task-related activity. For present purposes, data were analyzed from three task phases: presentation of cue (window 50–500 ms from cue onset), interstimulus delay (final 200 ms of each delay between cue and target), and presentation of target (50–500 ms from target onset). For each cell, we accordingly calculated a mean firing rate for 18 distinct task events: 3 (task phases: cue, delay, target) × 3 (trial types, labeled 1, 2, 3 for the different cue–target pairs) × 2 (visual hemifields). As each cue could be followed by several possible nontargets, some physically identical to targets on other trials, nontargets were excluded to simplify the data structure. According to ANOVA, 324/383 cells (85%) showed some significant difference between the 18 task events (one-factor ANOVA with 18 levels, P < 0.05). Only these 324 cells were retained for subsequent analysis (156 cells from monkey A and 168 from monkey B).

In this cell population we found many different patterns of activity, including activity during one or several task phases, and selective coding of stimulus/trial type at each phase (12, 15, 16). Three examples are shown in Fig. S2. As anticipated, these results show dense prefrontal coding of this task's events.

Similarity Structure of the Prefrontal Representation.

To move beyond the activity of individual neurons we used correlation analysis. In a first normalization step, mean firing rates for each cell during each task event were divided by that cell's mean firing rate across all 18 events. For each task event, we thus obtained a vector of normalized mean activity levels across the sample of 324 cells (cf. Fig. 1). By correlating these vectors we assessed the similarity of frontal activity during different task events.

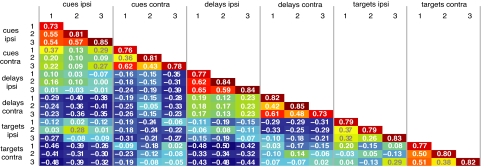
The complete correlation matrix is shown in Fig. 3. For correlation analysis, the first question concerns reliability of individual activity vectors. Reliability assesses the stability of each activity pattern; formally it is the proportion of variance due to true between-cell differences, removing the effect of trial-by-trial variability within cells. Because correlations can be based only on true between-cell differences, they are scaled by reliability; the maximum possible correlation between two variables is the square root of the product of their reliabilities (24). In our data, reliabilities of ≈0.80 (Fig. 3, diagonal; see Materials and Methods, Data Analysis) show a highly repeatable pattern of mean neural activities for each task event. These high reliabilities indicate suitable data for correlational analysis.

Fig. 3.

Correlation analysis of the prefrontal representation. Off-diagonal entries show correlations between each pair of task events; entries on diagonal show reliabilities for each event. Color scale reflects correlation magnitude. ipsi, ipsilateral to recording location; contra, contralateral.

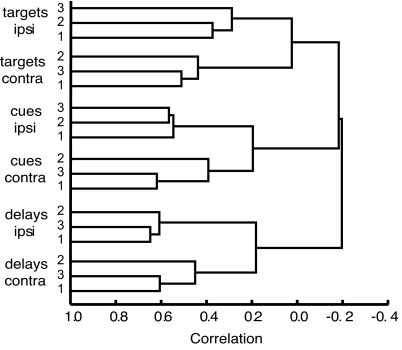
Off-diagonal entries in Fig. 3 show the complete matrix of correlations between activity vectors for different events. To summarize the results, we took each correlation coefficient (r) as a measure of distance between two events (distance = 1 − r) and input the resulting distances into cluster analysis (conventional average link method). The results (Fig. 4) show six clear clusters, each corresponding to a single task phase and hemifield. For events within a cluster (e.g., cues 1, 2, and 3 in the hemifield ipsilateral to the recording location), the median correlation of firing rates across the cell population was 0.50. These six clusters further organize into three pairs, corresponding to events from the same phase in opposite hemifields. For event pairs of this sort, the median correlation was 0.17. For events from different task phases, correlations were somewhat negative (median = −0.08 for same-hemifield events, −0.31 for different-hemifield).

Fig. 4.

Cluster analysis of between-event correlations. Six clusters, at a higher level organized into three pairs, show strong positive correlations for events of the same type (cue, delay, target) in the same hemifield, weak positive correlations for events of the same type in opposite hemifields, and weak negative correlations for events of different types. ipsi, ipsilateral to recording location; contra, contralateral.

To assess the significance of these differences, we organized correlations into the three sets suggested by the cluster analysis: all those for events from the same phase and hemifield, those for events from the same phase but different hemifields, and those for events from different phases. Each set was significantly different from the other two (Mann–Whitney test, P < 0.001 for each comparison).

Orthogonality of Different Task Phases.

As described above, the results in Fig. 3 are based on mean normalized data. Normalization is necessary to avoid strong positive correlations between all events, reflecting large differences between cells in overall activity. For each cell, an ideal normalizer would be a true mean firing rate across many different behavioral conditions. Then normalized firing rates for each event under analysis would reflect deviations from the true mean. In practice, the mean must be estimated from the data. Although the pattern of correlations is stable across normalization methods (i.e., methods for estimating the true mean), the absolute value is not. We can, however, bracket true values by methods with opposite biases.

In the analysis described above, the mean was estimated from the same data under analysis (mean firing rate across the 18 different task events). With this procedure, correlations are negatively biased (25). For each cell, necessarily, values above the obtained mean must be balanced by others below. For a set of truly orthogonal variables, this type of mean normalization imposes obtained correlations of −1/(k − 1), where k is the number of variables entering into each mean (here, 18). When some of the variables are positively correlated, as here, the negative bias among remaining correlations is increased. This negative bias will contribute to the negative values obtained, in our data, for different task phases.

An alternative is to estimate the mean from independent data. This will be increasingly accurate as the number of conditions contributing to the estimate increases, but in general will produce positive correlation bias, as errors in the mean estimate affect all normalized values in the same way (26). When the estimated mean is below a neuron's true mean, using this estimate for normalization increases the normalized activity rate for all task events; similarly, an estimated mean that is above the true value decreases normalized activity for all events. Because the independent-data method has a bias opposite to the same-data method, by using the two methods together we can bracket true correlation values that would be obtained under optimal conditions.

For 153 cells in our analysis, data were available from a second target detection task, providing data for eight separate task events (see Materials and Methods, Task Details). For these cells, the two possible normalizers—mean firing rate across the 18 events of the main task, and mean rate across the 8 events of the independent task—were correlated at 0.97, showing highly similar estimates of mean activity for each cell. As expected, however, when the analysis of Fig. 3 was repeated, but this time by using the independent-data normalizer, correlations were all shifted positively: median 0.57 for same task phase, same hemifield; 0.40 for same phase, different hemifield; 0.24 for different phase, same hemifield; and 0.11 for different phase, different hemifield. Although each method of normalization has its own bias, taken together they show a clear picture. Across the analyzed cell population, each task phase was associated with its own distinct pattern of prefrontal activity. These patterns were similar for different trial types/stimuli in the same hemifield, and weakly similar for trials in different hemifields. For different task phases, true correlations may have been weakly negative or weakly positive, but in any case were likely close to zero. For different task phases, these data show approximately independent or orthogonal prefrontal representation (12, 15).

Stimulus Selectivity.

Although Fig. 3 shows strong correlations for events from the same task phase and hemifield, these correlations were still beneath the single-event reliabilities. This result reflects significant prefrontal coding of stimulus information, i.e., activity vectors that were at least somewhat stimulus specific even within one phase and hemifield. In our next analyses we addressed trial type or stimulus selectivity.

In a first analysis, we used ANOVA (P < 0.05) to test for trial type selectivity in each cell, separately at each task phase. Data from the two hemifields were tested separately, for a total of 648 tests (324 cells × 2 hemifields) at each task phase. At the cue phase, significant selectivity was seen in 22% (140/648) of tests; at the delay phase, in 22% (140/648) of tests; and at the target phase, in 29% (191/648) of tests. Confirming stimulus/trial type selectivity, all these values are substantially in excess of the 5% expected by chance at this statistical threshold. Significant selectivity occurred rather independently across task phases. When the cue test was significant for a given cell and hemifield, delay and target tests were also significant in 24% and 44% of cases, respectively; when the delay test was significant, cue and target tests were also significant in 24% and 36% of cases; when the target test was significant, cue and delay tests were also significant in 32% and 26% of cases.

Having established the basic frequency of stimulus preferences at different task phases, we went on to ask about the direction of these preferences. Specifically we searched for associated cue and target preferences (e.g., joint preferences for cue 1 and target 1).

For our first examination of this question, we used the whole population of 324 cells. Again, data were separated by hemifield, giving 648 data sets. For each set, we calculated 3 selectivity indices for cue stimuli, one comparing cues 1 and 2, another cues 1 and 3, the third cues 2 and 3. If mean activity during cue x is cx, and mean activity during cue y is cy, selectivity index was calculated as (cx − cy) ÷ (cx + cy). Similarly, we calculated selectivity indices for targets, defining target activity as tx, ty and the selectivity index as (tx − ty) ÷ (tx + ty). For each pair of trial types (12, 13, and 23), we correlated selectivity index for cues against selectivity index for targets, across the full 648 data sets.

Again, possible correlations are scaled by reliabilities for each single selectivity index. For cue data, reliabilities (see Materials and Methods, Data Analysis) ranged from 0.45 to 0.48, whereas for targets they ranged from 0.59 to 0.64. For each score, accordingly, ≈50% of variance was due to true differences in stimulus preference between cells. Relations between cue and target selectivities are shown in Fig. S3. Although correlations were positive and significant (P < 0.001) for each pair of trial types, they were extremely modest, with only 1.8% to 3.4% shared variance (r²). Thus, within each task phase, the cell population showed a fairly reliable pattern of stimulus/trial type selectivities. There was only a minor tendency, however, for these selectivities to be matched across cue and target phases.

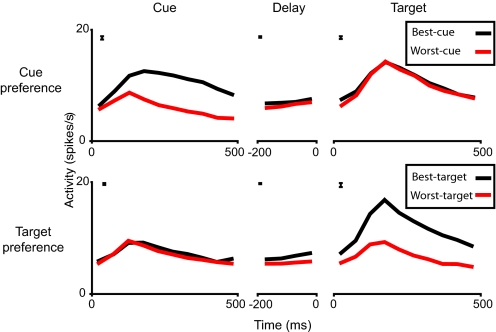
To amplify this point we selected just those cases of significant cue or target selectivity. Across the 648 data sets, there were 140 cases of significant cue selectivity, defined by ANOVA as described above. For each case, the trial type (1, 2, or 3) giving the strongest cue activity was called “best-cue,” and the trial type giving the weakest cue activity was called “worst-cue.” Having determined best-cue and worst-cue trial types for the particular cell and hemifield, we then compared their associated delay and target activities. Mean (non-normalized) firing rates across all 140 cases of significant cue preference are shown in Fig. 5Upper. By definition, response to the best cue stimulus was always greater than response to the worst cue stimulus. Classifying trials by cue responses, however, was only weakly predictive of activity during delays, and not at all predictive of responses to targets. Across cells, ANOVA showed a significant difference in mean delay activity for best-cue and worst-cue trials (P < 0.01), but no such difference for target activity (P > 0.5). In an equivalent analysis, we defined best-target and worst-target trials for all 191 cases of significant target preference, and examined the associated cue and delay activity. The results (Fig. 5, Lower) were essentially similar. Target preference was somewhat predictive of delay preference (ANOVA across cells, P < 0.001), but not at all predictive of cue preference (P > 0.1). Activity of an example cell with mismatched cue and target preferences is shown in Fig. S4.

Fig. 5.

Mean activity for cue- and target-selective cells. Upper shows mean activity at each task phase for best-cue and worst-cue trials, across all cases (n = 140, see text) of significant cue preference within one hemifield. Lower shows equivalent data for best-target and worst-target trials, across all cases (n = 191) of significant target preference. For cues and targets, time 0 corresponds to stimulus onset; for delays, time 0 corresponds to onset of the following stimulus. Bar at upper left of each panel shows average standard error of difference of means between best-cue/target and worst-cue/target trials.

The findings show that in each task phase, there was reliable coding of stimulus information. Like overall activity vectors, however, stimulus preferences were rather independent in different task phases. Cue and target preferences, in particular, were almost entirely unrelated, although both were somewhat predictive of delay preference.

Comparison of Stimulus and Phase Selectivities.

Analysis of correlations between activity patterns is complementary to analysis of single cell selectivities. Low correlations between two patterns mean that many cells respond differently to these task events, and vice versa for high correlations (Fig. 1). As we should expect, accordingly, many more cells in our sample were selective for task phase than for stimulus. As described in the previous section, separate ANOVAs for each cell tested stimulus/trial type selectivity at each phase and hemifield; on average, the main effect of stimulus was significant in 24% of cases. Equivalently, separate tests of hemifield selectivity for each combination of trial type and phase were significant in 29% of cases, whereas separate tests of phase selectivity for each combination of trial type and hemifield were significant in 45% of cases. Separately evaluated by pairwise comparisons, the frequency of significant phase discrimination was similar for cues versus delays (31% of comparisons), cues versus targets (37%), and delays versus targets (33%).

Sequential Position of Events Within a Trial.

In a final analysis, we asked whether activity vectors might be more similar for events closer together in time. Specifically we asked whether cue activity might be more related to the immediately following delay than to the fourth delay in those trials with three nontargets preceding the target. Similarly we asked whether target activity might be more related to fourth delays than to first delays. The results (see SI Results) showed no such tendency.

Discussion

Many previous experiments show dense coding of task-relevant information across populations of PFC neurons. Neural activity may be selective for particular phases of a complex task, and for stimulus or other information within one phase. Here we examined the similarity structure of this neural representation in a cue–target association task.

For different task phases, we found approximately orthogonal patterns of PFC activity. Although many cells discriminated different task phases, this was not achieved by separate cell populations uniquely responsive to a particular phase. Instead, many cells were active in each phase, and a cell's activity in one phase was not predictive of its activity in others (cf. Fig. S2). Within one task phase, in contrast, we found correlated activity patterns for different stimuli/trial types. Together, these results show a hierarchical representation, with one basic activity pattern associated with each task phase, and stimulus information coded by modulations of the phase pattern. Both within and between task phases, PFC representations were also modulated by hemifield, with generally lower correlations between hemifields.

Selective neural activity associated with different task phases has been described in different species, and in lateral prefrontal, orbital prefrontal, and anterior cingulate cortex (12, 15, 27–30). In maze tasks, for example, cells in the rat frontal cortex may fire at trial onset, or while approaching or leaving a goal, often rather independently of current maze location (28). As in our data, previous studies show activity of single PFC cells at one or multiple task phases (12, 15, 29). Our finding of distributed, orthogonal coding for discrete task phases gives quantitative form to such results. The benefits of orthogonal coding are well known, providing efficient representation and discrimination of many independent events in a fixed population of cells (22). Sequential activity can contain an arbitrary number of successive steps, each requiring different information and operations. Successive steps may be seen as different contexts (10) determining what information is relevant and what must be done. Orthogonal coding may allow PFC to support a large number of these somewhat independent steps or task contexts.

In contrast, similarity between two distributed representations allows for similarity of their functional effects. In our task, phase information is presumably important in controlling the separate operations appropriate for each phase: for cues, to retrieve the associated target; for delays, to wait while maintaining a target description; for targets, to await stimulus offset before releasing a saccade. Correlated coding for different stimuli at the same task phase—strongly within hemifield, and weakly between hemifields—may reflect similar operations applied to different information content.

The distributed codes of neural networks are sometimes contrasted with the symbolic codes of conventional digital computers (7). In symbolic codes, the different symbols are independent: the meaning of one does not depend on its similarity to others. In this respect, prefrontal coding of task phase resembles conventional symbolic codes, with separate, unrelated descriptions for each of the phases to be distinguished. Hierarchical coding for successive task phases also resembles the function and argument structure of some symbolic systems, with a series of functions (cognitive operations) each applied across a domain of possible arguments (stimulus alternatives).

A further question is the relationship of stimulus preferences at different task phases. In the monkey temporal lobe, many cells respond to both members of a learned cue–target pair (31, 32). Similar results have also been reported in dorsal PFC in a cross-modal matching task (33). For our task, however, learned associations were not strongly reflected in correlated PFC activity. Instead stimulus preferences were close to independent in cue and target phases: stimulus information was coded by rather independent modulations of the basic activity patterns describing each task phase. Across tasks, there can be many relations between relevant stimulus information in different task stages. Potentially independent stimulus coding across task stages may be important in addressing such complexity. Both cue and target preferences weakly predicted delay preferences, suggesting some element of both retrospective (memory for cue) and prospective (anticipation of target) coding in delay intervals (23, 34).

Beyond the present task, the similarity structure of prefrontal coding will likely depend on the similarity structure of task operations and events. Although we found orthogonal coding for discrete task phases, more similar codes might be expected for task segments with more similar cognitive operations. Correspondingly, there might be less correlated activity patterns for very different stimuli (e.g., auditory and visual) at the same task phase, as we already found for events in opposite visual hemifields. In this sense, hierarchical prefrontal coding may be a special case, with somewhat different structures for tasks with different operations and events.

Like the sequential steps of standard computer programs, structured behavior proceeds through a complex series of operations to the desired goal. At each step, the program must know which step it is in and what information from previous steps must be maintained. In PFC, our data suggest a series of activity patterns marking the separate steps of a serial mental program (35). For successive steps there are largely orthogonal codes and, at least for cues and targets, largely orthogonal stimulus preferences. Orthogonal codes may underlie the construction of complex behavioral sequences, each consisting of many, dissimilar cognitive segments. Within each step, in contrast, correlated codes describe different stimulus alternatives. Correlated codes are useful for similar operations, in this case, when fixed cognitive processes are applied to varying stimulus content.

Materials and Methods

Task Details.

Eye movements were monitored and stored by using an infrared eye tracking system (Iscan). The fixation window was from 2.5° × 2.5° to 3.5° × 3.5° visual angle for 280 of the analyzed cells (86.4%), 5° × 5° for the remaining 44. Excluding cells with the larger window left results essentially unchanged. Trials ended without reward if fixation was broken before target offset. Data were analyzed only from successfully completed trials, with typically more than 30 repetitions of each cue, delay, and target in each hemifield (minimum 15). For approximately half of the cells (153/324), trials of the present task were randomly interleaved with those of another task, using no cue, a fixed target (fish), and two fixed nontargets (burger, teddy-bear) (36).

Recording Methods.

We performed extracellular single-unit microelectrode recordings in the lateral PFC of two awake, behaving macaque monkeys (Macaca mulatta). We placed a custom-designed titanium chamber (Max Planck Institute, Tuebingen, Germany) over the right hemisphere of monkey A (male, 12.8 kg) at AP = 32, ML = 22.2 (AP, anterior-posterior; ML, medio-lateral), and over the left hemisphere of monkey B (male, 12.7 kg) at AP = 25.8, ML = 21.2, over the principal sulcus and anterior to the arcuate sulcus. Recording locations were confirmed with histology and correspond to areas 8, 9/46, and 45 (37) (Fig. S1). Data were combined from dorsal and ventral sites (divided by the principal sulcus), as we found no differences between them. We used arrays of tungsten microelectrodes (FHC) mounted on a Delrin grid (Crist Instrument Co.) with 1-mm spacing between adjacent locations inside the recording chamber. We used custom-made screw mini-microdrives to advance the microelectrodes (38) or a hydraulic, digitally controlled microdrive (Multidrive 8 Channel System; FHC). Neural activity was amplified, filtered, and stored for off-line cluster separation and analysis with the Plexon MAP system. We did not preselect neurons for task-related responses, and we advanced the microelectrodes until we could isolate neuronal activity before starting data collection. All procedures were approved by the U.K. Home Office and were in compliance with European Union guidelines of the for the care and use of laboratory animals (EUVD, European Union directive 86/609/EEC).

Data Analysis.

Reliabilities of the mean normalized response to each task event (Fig. 3, diagonal) were calculated by the standard ANOVA method (39). Error variance was estimated from replications, i.e., trial-to-trial variability in response rates. For selectivity indices, reliability was calculated by using the split-half method. For each pair of stimuli, e.g., cues 1 and 2, the selectivity index was calculated twice, once by using one random half of the trials for each stimulus, and a second time by using the other half. Correction of the correlation between these two values to reliability for the full data set was approximated by the Spearman–Brown formula (24). ANOVA and split-half methods give equivalent estimates, one estimating error variance from replication across individual trials, the other from replication across two halves of the data. The ANOVA method, however, cannot be used for a score based on combination of variables. Note that to reflect actual data, correlations reported here are raw, i.e., not adjusted for unreliability.

For activity normalization based on independent data (153 cells only; see Results, Orthogonality of Different Task Phases), the normalizer was derived from activity in the interleaved trials of the fixed-target task (see Materials and Methods, Task Details). In this task there were eight different task events: delays, two nontargets, and targets, each in two hemifields. Using the same analysis windows as for the main data, we obtained each cell's mean activity rate for these eight events, then averaged these to give the independent-data normalizer.