Orientation of Human Semicircular Canals Measured by Three-Dimensional Multiplanar CT Reconstruction

Abstract

Analysis of vestibulo-ocular reflex experiments requires knowledge of the absolute orientations (with respect to skull landmarks) of semicircular canals (SCC). Data relating SCC orientations to accessible skull landmarks in humans are sparse, apart from a classic study of 10 skulls, which concluded that the horizontal and anterior SCC are not mutually orthogonal (111 ± 7.6°). Multiple studies of isolated labyrinths have shown the inter-SCC angles are close to 90°. We hypothesized that a larger sample would yield mean absolute SCC orientations closer to the mutual orthogonality demonstrated for isolated labyrinths. We measured canal orientations with respect to accessible skull landmarks using 3-D multiplanar reconstructions of computerized tomography scans of the temporal bones of 22 human subjects. Images were acquired with 0.5-mm thickness and reconstructed with in-plane resolution of 234 μm. There was no significant difference between the left and a mirror image of the right (p > 0.57 on multiway ANOVA of orientation vector coefficients), so data were pooled for the 44 labyrinths. The angle between the anterior and posterior SCC was 94.0 ± 4.0° (mean ± SD). The angle between the anterior and horizontal SCC was 90.6 ± 6.2°. The angle between the horizontal and posterior SCC was 90.4 ± 4.9°. The direction angles between a vector normal to the left horizontal SCC and the positive Reid's stereotaxic X (+nasal), Y (+left), and Z (+superior) axes were 108.7 ± 7.5°, 92.2 ± 5.7°, and 19.9 ± 7.0°, respectively. The angles between a vector normal to the left anterior SCC and the positive Reid's stereotaxic X, Y, and Z axes were 125.9 ± 5.2°, 38.4 ± 5.1°, and 100.1 ± 6.2°, respectively. The angles between a vector normal to the left posterior SCC and the positive Reid's stereotaxic X, Y, and Z axes were 133.6 ± 5.3°, 131.5 ± 5.1°, and 105.6 ± 6.6°, respectively. The mean anterior SCC–contralateral posterior SCC angle was 15.3 ± 7.2°. The absolute orientations of human SCC are more nearly orthogonal than previously reported.

Introduction

The semicircular canals (SCC) of the vestibular labyrinth encode head rotational velocity and provide input to the vestibulo-ocular reflex (VOR), vestibulo-collic reflex, vestibulo-spinal system, vestibulo-reticular system, cerebellum, and cortex (Ewald 1892; Cohen et al. 1964; Suzuki and Cohen 1964; Wilson et al. 1995; Maeda et al. 1975; Shinoda et al. 1994, 1997; Peterson and Abzug 1975; Wilson et al. 1976; Ebata et al. 2004). Accurate knowledge of the absolute orientation (with respect to skull landmarks) and position of SCC is essential for design of experiments studying the vestibular system and for understanding exam findings during clinical evaluation of patients with vestibular disorders. Apart from a widely cited classic study of 10 human skulls by Blanks et al. (Blanks et al. 1975; Curthoys et al. 1977), few of the many studies of human labyrinth morphology have related SCC orientations to accessible skull landmarks that can guide an investigator in orienting a subject's head for canal-plane-specific vestibular stimulation. Blanks et al. reported that the angles between ipsilateral SCC of one labyrinth depart significantly from mutual orthogonality, with the angle between the anterior SCC and horizontal SCC equal to 111.8 ± 7.6° (mean ± SD). Multiple studies of the inter-SCC angles of isolated human labyrinths using high-resolution histologic or radiographic reconstructions suggest that SCC orientations are much more nearly orthogonal to one another (Archer et al. 1988; Harada et al. 1990; Hashimoto 2003; Ifediba et al. 2004; Takagi et al. 1989; Spoor and Zonneveld 1995, 1998). This disparity suggests that one or more of the absolute SCC orientations reported by Blanks et al. may have been up to ∼20° off of the true population mean, a deviation that would be significant for many experimental designs.

We hypothesized that the departure from canal orthogonality observed by Blanks et al. does not represent the true population mean, and that a larger sample would yield mean canal orientations that are closer to mutual orthogonality. To test our hypothesis, we measured SCC orientations with respect to accessible skull landmarks using three-dimensional multiplanar reconstructions of high-resolution computed tomography (CT) scans of 44 labyrinths in 22 human subjects.

Methods

Subjects

Computed tomography scans were acquired for both ears of 7 male and 15 female subjects aged 48 ± 15 years. CT scans were performed for accepted clinical indications in all patients. The indication for CT imaging was headache with disequilibrium in nine subjects; motion sickness, fatigue, lightheadedness, or anxiety associated with dizziness in six subjects; evaluation of middle ear or mastoid inflammatory disease in three subjects; conductive hearing loss in two subjects; benign paroxysmal positional vertigo (BPPV) in one subject; and sensorineural hearing loss in one subject. Diagnosis after 1.5 years of follow-up was migraine in 10 subjects; middle ear or mastoid inflammatory disease in three subjects; otosclerosis in two subjects; depression or anxiety in two subjects; and obstructive sleep apnea, enlarged vestibular aqueduct, orthostatic hypotension, BPPV, and Eustachian tube dysfunction in one subject each. No subject had a history of temporal bone fracture. Except for the one subject whose CT scan revealed mildly enlarged vestibular aqueducts without abnormal SCC configuration or significant deviation in SCC orientation from the rest of the dataset, no patient had cochlear or labyrinthine dysmorphism (abnormal location, patency, caliber, shape, size, or orientation) as judged by the neuroradiologists reading the CT for purposes of routine clinical care and by two of the authors (C.C.D.S., J.P.C.). This study was a review of existing clinical data with patient identifiers removed. The Joint Committee on Clinical Investigation of the Johns Hopkins University School of Medicine determined that the study was exempt from a protocol requirement and that it qualified for exemption from an institutional review board protocol based on Department of Health and Human Services criteria 45 CFR 46.101(b)(4).

Data acquisition

The CT scans were acquired on a 16-detector Toshiba Aquilion CT scanner, using a bone algorithm. To avoid loss of in-plane resolution that can occur in helical scanning modes, scans were performed in step-scan mode. Each axial slice was scanned with the subject stationary, and the table was axially stepped 0.5 mm before each subsequent acquisition. The x-ray beam was generated with a 300 mA/100 kVP source and collimated to 0.5-mm slice thickness at full-width half-maximum. Each temporal bone was separately encompassed by 120-mm diameter region of interest using a 512 × 512 voxel matrix, creating voxels of 0.234 × 0.234 × 0.5 mm. Axial scans of the whole head were acquired using a 240-mm region of interest, yielding 0.468 × 0.468 × 0.5 mm voxels. The 3-D datasets were exported to a workstation for multiplanar analysis using Vitrea® 2.3.3.1 software (Vital Images, Inc., Plymouth, MN) and Matlab (Mathworks, Cambridge, MA). The higher-resolution temporal bone reconstructions were used to measure distances and angles reported for the semicircular canals, and whole-head reconstructions were used to define Reid's planes with respect to skull landmarks (as defined below).

Measurement of head and SCC orientation using multiplanar slice reconstructions

The Vitrea® software system allows one to view a CT dataset simultaneously using a 3-D rendered image and a set of three 2-D images that represent mutually orthogonal “slices” through the dataset. We measured a SCC's orientation by optimally aligning one slice plane with the SCC, then extracting the coordinate transformation matrix Vitrea® used to reach that alignment from a space-fixed coordinate frame defined by the CT dataset volume's boundaries (Kuipers 1999). Measurements were made with 1-voxel resolution (∼0.22° angular, 0.234 mm in-plane translational).

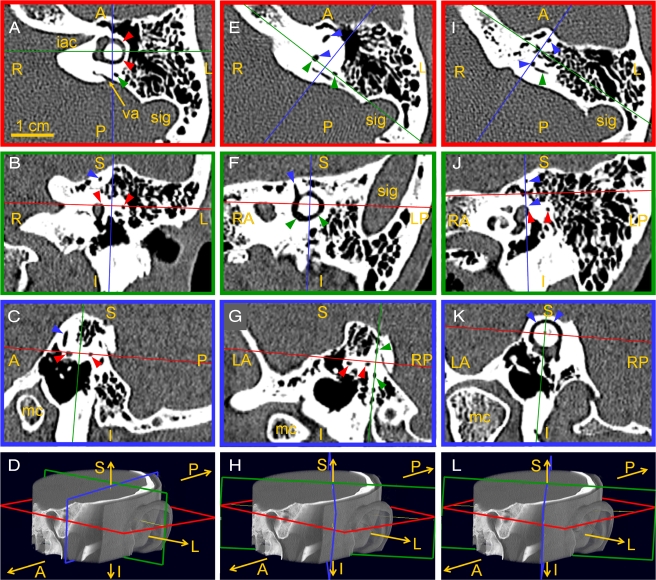
Figure 1 shows how this was performed for the left temporal bone CT of one subject. Each column illustrates the measurement of one SCC's orientation, and the four images in a column show a set of simultaneous 3-D and 2-D views for a single orientation/position of the measurement coordinate frame. For example, panels A–D show measurement of the left horizontal SCC (red arrowheads point to the horizontal SCC lumen). Panels A–C show in-plane views for each of the three color-coded slice planes illustrated in the 3-D temporal bone rendering in panel D. In panel A, the red plane slice shows the full circle of the SCC lumen (like the cut face of a sliced bagel), while the same red plane viewed on edge in panels B and C appears to be just a line that passes through the vestibule and bisects the horizontal SCC lumen. In panels A–D, the orientations of the green and blue planes are arbitrary. Similarly, panels E–H show simultaneous views when the green plane is “bagel-slicing” the posterior SCC (seen best in panel F), with the red and blue planes arbitrary. Panels I–L show views when the blue plane is “bagel-slicing” the anterior SCC (seen best in panel K), with the red and green planes arbitrary.

Fig. 1.

Measuring semicircular canal (SCC) orientations and centroid positions using 3D multiplanar reconstructions of left temporal bone CT of a 56-year-old woman. Within each column, images show three mutually orthogonal slices through the volume data in the orientations shown by the color-coded planes in the 3D rendering at bottom. All three planes are shown in each image, but two planes appear as lines in each slice image (ABC, EFG, IJK), because they are viewed on edge. In all images, red arrows = horizontal SCC (HSCC); green arrows = posterior SCC (PSCC); blue arrows = anterior SCC (ASCC); iac = internal auditory canal; sig = sigmoid sinus; va = vestibular aqueduct; mc = mandibular condyle; A/P/R/L/S/I = anterior/posterior/right/left/superior/inferior. In the first set (A–D), the red plane is aligned with the HSCC; the blue and green planes are arbitrary. In the second set (E–H), the green plane is aligned with the PSCC; the red and blue planes are arbitrary. In the third set (I–L), the blue plane is aligned with the ASCC; the red and green planes are arbitrary.

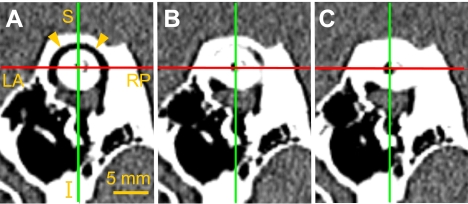
After initially rotating the 3-D reconstruction to bring one image plane approximately coplanar with a semicircular canal, we employed two techniques to optimize placement of the image plane through a canal. First, a candidate image plane was translated along its normal vector. Orientation was adjusted until this maneuver caused the entire SCC lumen to leave the image simultaneously to the greatest extent possible. Figure 2 shows how this procedure was applied to the anterior SCC of Figure 1K. As the slice plane is stepped away from the aligned position shown in panel A, the SCC lumen leaves the image plane almost uniformly (panel B, then C), although evidence of slight SCC nonplanarity is evident in panel B. Second, the orientation was adjusted to maximize the in-plane cross-sectional area of the SCC without counting the contribution from the vestibule. SCC planes were initially measured by one investigator (V.P.), then independently reviewed by two others (C.C.D.S., J.P.C.).

Fig. 2.

Confirming optimal alignment of image plane with a semicircular canal plane. (A) Image plane tentatively aligned with canal lumen of the anterior SCC of Figure 1K. Stepping one (B) then two (C) voxel lengths (∼234 μm each) along the image plane normal causes uniform disappearance of canal lumen.

We pooled SCC orientation and position data across subjects by translating each into a common coordinate system defined by Reid's planes (Stedman 1976). Reid's horizontal plane (Z_REID) was defined as a plane passing through the center of each bony external auditory canal (at the lateral entrance of the tympanic bone) and the cephalic edge of the inferiormost aspect of each infraorbital rim. Although only three points are required to define a plane, we found in practice that all four of these points lie within 0.5 mm of a common plane. We defined the interaural axis as a line passing through the bony external auditory canal centers (and thus in Z_REID). Reid's sagittal plane (Y_REID) was defined as the plane that bisects and is perpendicular to the interaural axis. Reid's coronal plane (X_REID) was defined as the plane containing the interaural axis and perpendicular to Z_REID. We defined a coordinate system using unit normal vectors (X_REID, Y_REID, Z_REID) perpendicular to each Reid plane, with the +X_REID axis pointing anterior (perpendicular to X_REID), +Y_REID pointing left (along the interaural axis, perpendicular to Y_REID), and +Z_REID pointing superior (perpendicular to Z_REID). Throughout this report, planes are denoted with bold characters, while the unit vector normal (perpendicular) to a plane is denoted by the same letters in italic characters.

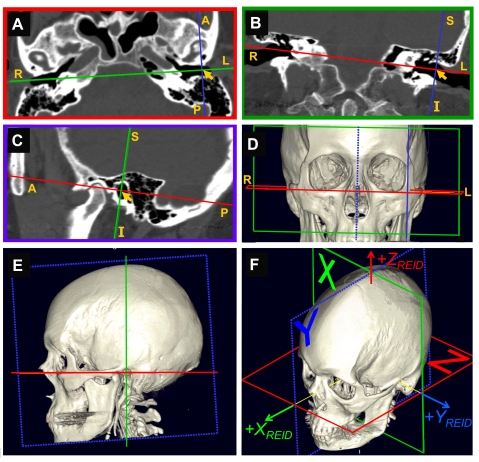
Figure 3 demonstrates how Reid's planes were measured. In all panels of this figure, the red plane is Z_REID, the green plane is X_REID, and the dotted blue plane is Y_REID. As had been carried out with SCC measurements, a coordinate system was adjusted using 2-D slice views and 3-D renderings until its origin was at the center of the left external auditory canal entrance (arrow in panels A–C), the interaural axis (Y_REID) passed through both ear canal entrances (green line in panel A, red line in panel B), and the red plane passed through the lowest point of each orbital rim (panels D and E). The coordinate system was then moved along Y_REID to the midsagittal plane halfway between the ear canal entrances, to yield the final Reid coordinate system (panel F).

Fig. 3.

Measuring orientations of Reid's planes. (A–C) Mutually orthogonal slices through the head CT of one subject, with relative orientations, as illustrated in the color-coded three-dimensional rendering in panels D–F. In all images, red = Reid's horizontal plane Z_REID; green = Reid's coronal plane X_REID; dotted blue = Reid's midsagittal plane Y_REID. Solid blue = a plane parallel to Y_REID and passing through the left external auditory canal entrance center (LEAC, arrowheads in ABC) used as the starting point for measuring Reid's planes. All three planes are shown in each image, but two planes appear as lines in each slice image (ABC), because they are viewed on edge. A/P/R/L/S/I = anterior/posterior/right/left/superior/inferior. (A) Reid's horizontal plane (Z_REID), with X_REID plane viewed “on edge” overlying the interaural axis (which is also the Y_REID axis). (B) X_REID coronal plane as viewed from anterior; here, the Z_REID plane viewed “on edge” overlies the interaural axis. (C) A parasagittal slice through the LEAC center point parallel to Reid's midsagittal plane, viewed from the left. (Y_REID itself is later defined to lie midway between the center points of the left and right EAC entrances, perpendicular to the interaural axis connecting these points.) (D–F) Three-dimensional renderings showing relative orientation of planes within skull.

To account for variations in head orientation within the CT scanner, CT datasets were mathematically rotated to align the (X_REID, Y_REID, Z_REID ) coordinate frames for all subjects with an Earth-fixed coordinate frame of reference (X_Earth, Y_Earth, Z_Earth). We defined +Z_Earth (the “yaw” or “horizontal rotation” axis) as an Earth-vertical axis that points up; +X_Earth (the “roll” axis) is perpendicular to +Y_Earth and +Z_Earth and points anteriorly, and +Y_Earth (the “pitch” axis) is perpendicular to +X_Earth and +Z_Earth and points out the left ear.

Head and eye rotations in this report are described from the subject's perspective (not the examiner's), using the right-hand rule and the coordinate systems described above. Thus, a leftward horizontal (positive yaw) rotation is a rotation about the +Z_REID axis, moving the nose toward the left ear. A clockwise rotation (positive roll) is a clockwise (from the patient's perspective) rotation about the +X_REID axis, moving the top of the head toward the right ear. A nose-down rotation (positive pitch) is a nose-downward rotation about the +Y_REID axis, moving the top of the head toward the nose.

For each SCC plane and Reid plane measured by multiplanar reconstruction, a unit vector normal to that plane was extracted and used for computation of angles between planes and distances between points in space using Matlab® software. In addition to rotational orientations, the (X_REID, Y_REID, Z_REID) Cartesian coordinate position of the center of each SCC was measured by placing a crosshair at the visually estimated centroid of the canal (as in Fig. 2).

The angle between two planes is equal to the direction angle between normal vectors perpendicular to the two planes. The angle θ between planes was computed as the inverse cosine of the dot product (scalar product) of the two planes' unit length normal vectors, u and v

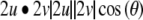1

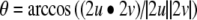2

As a check on precision of our measurements, Reid's planes were separately computed using the left (default) and right external auditory canal (EAC) entrance center as a starting reference point for defining the Z_REID plane. The angle between the Z_REID plane measured from the left EAC center and the same plane measured from the right EAC center (denoted Z_REID-R) was negligible (0.6 ± 0.4°), as was the difference in all measurements of SCC center distance from the plane (0.3 ± 0.5 mm).

To correct for potential quantization error of vector coefficients extracted from Vitrea® (resolution to 0.0001), we renormalized unit vector lengths to exactly 1 at 64-bit resolution in Matlab® before angle calculations using Eq. 2. Similarly, we renormalized the mean unit vectors in Table 1A and B, because averaging the coefficients of multiple unit vectors does not generally result in a vector of exact unit length. This correction only became significant for calculating the angle between a vector and itself, because of the strong nonlinearity of the arccosine function around 1.0 (arcos(0.9999) ∼0.8°, rather than 0°). It had a negligible effect on other calculations.

Table 1A.

Left and right canal plane unit normal vector coefficients (mean ± SD)

	XREID	YREID	ZREID	LA	LH	LP	RA	RH	RP	ZREID-R
XREID	1	0	1	−0.58954	−0.31645	−0.69611	−0.58905	−0.32891	−0.69248	0.00302
				± 0.06787	± 0.12805	± 0.06961	± 0.07930	± 0.11925	± 0.06477	± 0.00996
YREID	0	1	0	0.78750	−0.04108	−0.66820	−0.78928	0.03566	0.66561	0.00256
				± 0.04598	± 0.09289	± 0.06523	± 0.06425	± 0.10795	± 0.06852	± 0.00473
ZREID	0	0	1	−0.17971	0.94772	−0.26257	−0.17334	0.94369	−0.27826	0.99999
				± 0.09830	± 0.04707	± 0.10917	± 0.11482	± 0.04393	± 0.11218	± 0.00007

Each column lists the mean X_REID, Y_REID, Z_REID coefficients of unit length vectors perpendicular to each semicircular canal (mean ± SD, renormalized after averaging over N = 22 subjects so that the mean coefficients define a vector with unit length to within <10⁻⁵). As illustrated in Figure 4, the X_REID, Y_REID, and Z_REID coordinate system axes are the naso-occipital, left–right, and superior–inferior axes (+X_REID anterior, +Y_REID leftward, and +Z_REID superior) perpendicular to X_REID, Y_REID, and Z_REID, respectively, which are the coronal, midsagittal, and horizontal Reid's planes as defined in the text. Z_REID-R is ideally identical to Z_REID, but was measured using a CT image plane passing through the right external auditory canal (EAC) center point, rather than the left EAC as used for Z_REID.

L = left, R = right; A, H, P = anterior, horizontal, and posterior semicircular canals, respectively. Of the two antiparallel vectors normal to each plane, the vector pointing posterior of the Y_REID plane is listed (corresponding to those displayed in Figure 4B), so that right-hand rule (RHR) head rotations about LA, LH, and LP normal vectors would excite the LA, LH, and LP canals, respectively, while RHR rotations about the RA, RH, and RP normal vectors would inhibit the RA, RH, and RP canals.

Table 1B.

Pooled (left and mirrored right) canal plane unit normal vector coefficients (mean ± SD)

	XREID	YREID	ZREID	LA	LH	LP	RA	RH	RP
XREID	1	0	0	−0.58930	−0.32269	−0.69432	−0.58930	−0.32269	−0.69432
				± 0.07296	± 0.12244	± 0.06647	± 0.07296	± 0.12244	± 0.06647
YREID	0	1	0	0.78839	−0.03837	−0.66693	−0.78839	0.03837	0.66693
				± 0.05522	± 0.09956	± 0.06612	± 0.05522	± 0.09956	± 0.06612
ZREID	0	0	1	−0.17655	0.94573	−0.27042	−0.17655	0.94573	−0.27042
				± 0.10568	± 0.04505	± 0.10967	± 0.10568	± 0.04505	± 0.10967

Mean unit normal vector coefficients (mean ± SD) derived by pooling left data with a mirror image of the right side, then constraining both sides to be symmetric about the midline.

L = left, R = right; A, H, P = anterior, horizontal, and posterior semicircular canals, respectively.

Direction angles versus Euler angles

It is important to note the distinction between direction angles and rotational Euler angles (which are commonly used in oculomotor research) as the two are related but different (Kuipers 1999). Direction angles are convenient for describing the angle between two vectors (and thus between the two planes to which they are perpendicular), and they are therefore useful for describing the orientation of a vector with respect to cardinal axes of a coordinate system. The direction angle θ between two unit length vectors u and v is the angle subtended by u and v when they are placed tail to tail. Direction angles are always positive and range from 0 to 180°. To describe the direction of u with respect to three mutually orthogonal unit vectors (x, y, z) defining a coordinate system, one can use Eqs. 1 and 2 to compute direction angles α, β, and γ between u and x, y, z, respectively. If u is a unit length vector with its tail at the origin, then cos(α), cos(β), cos(γ) (called the “direction cosines” of u) are the x, y, z coordinates of the position of its tip. The three direction angles α, β and γ are not rotations applied in any particular sequence, and directional angles are not meant to describe rigid body rotations (although they are related to rotation vectors and quaternions, and θ can be interpreted as the minimum angle by which one can rotate u to make it parallel to v while staying in the plane in which u and v reside). Data in Table 2 and Figure 5 are direction angles.

Table 2.

Angles (mean ± SD, in degrees) between Reid's planes X_REID, Y_REID, and Z_REID and semicircular canal planes

	XREID	YREID	ZREID	LA	LH	LP	RA	RH	RP
XREID	0	90	90	125.9 ±5.2	108.7 ±7.5	133.6 ±5.3	125.9 ±5.2	108.7 ±7.5	133.6 ±5.3
YREID	90	0	90	38.4 ±5.1	92.2 ±5.7	131.5 ±5.1	141.6 ±5.1	87.8 ±5.7	48.5 ±5.1
ZREID	90	90	0	100.1 ±6.2	19.9 ±7.0	105.6 ±6.6	100.1 ±6.2	19.9 ±7.0	105.6 ±6.6
LA	125.9 ± 4.8	38.4 ± 4.2	100.3 ± 5.7	0	90.6 ±	94.0 ±	103.4 ±9.5	87.1 ±10.0	15.3 ±7.2
LH	108.4 ± 7.8	92.3 ± 5.3	19.5 ± 7.4	91.1 ±6.3	0	90.4 ±	87.1 ±10.0	11.3 ±6.9	93.1 ±9.0
LP	133.8 ± 5.6	131.6 ± 5.0	105.2 ± 6.5	93.9 ±3.7	90.1 ±4.6	0	15.3 ±7.2	93.1 ±9.0	83.2 ±9.7
RA	125.8 ± 5.7	141.7 ± 5.9	99.9 ± 6.8	103.4 ± 9.5	87.0 ± 10.5	15.5 ± 7.4	0	90.6 ±	94.0 ±
RH	109.1 ± 7.3	88.0 ± 6.2	20.4 ± 6.9	87.2 ± 9.7	11.3 ± 6.9	92.2 ± 9.2	90.2 ±6.3	0	90.4 ±
RP	133.5 ± 5.2	48.6 ± 5.3	106.1 ± 6.8	15.0 ± 7.1	94.0 ± 9.0	83.2 ± 9.7	94.2 ±4.3	90.7 ±5.2	0
ZREID-R	89.8 ± 0.6	89.9 ± 0.3	0.6 ± 0.4	100.3 ± 5.6	19.6 ± 7.4	105.4 ± 6.4	100.2 ± 6.5	20.5 ± 6.8	106.1 ± 6.9

Angles listed are the direction angles (not Fick/Euler angles) between positive Reid's axes, +X_REID (anterior), +Y_REID (left), +Z_REID (superior), and positive tips of normal vectors perpendicular to semicircular canals as defined in the text and illustrated in Table 1A and Figure 4. Z_REID-R is as defined in Table 1A and B. Below the diagonal, left, and right values are separately averaged pooled over the N = 22 subjects; italicized values above the diagonal are for all N = 44 labyrinths, after mirror-imaging each labyrinth across the Y_REID (midsagittal) plane, and thus represent the best symmetric estimate of the overall dataset. Note that inter-SCC angles within a single labyrinth (bold values) are close to 90°.

L = left, R = right; A, H, P = anterior, horizontal, and posterior semicircular canals, respectively.

Fig. 5.

Orientations of mean planes for the horizontal (red), posterior (blue), and anterior (green) SCC of the left labyrinth, with respect to Reid's cardinal axes (+X_REID, +Y_REID, +Z_REID). (A–D) Views from the +X_REID (anterior), +Y_REID (left), +Z_REID (superior), and −X_REID (posterior) axes, respectively. (E, F) High/left/anterior and high/left/posterior views, respectively. To simplify visual interpretation, the intersection of the SCC planes shown was translated to the intersection of the interaural axis and midsagittal plane [the center of the Reid coordinate system (X_REID, Y_REID, Z_REID) = (0, 0, 0)].

In contrast to the three direction angles that define a vector's direction, a triplet of Euler angles describes a reorientation of a three-dimensional rigid body (such as the eye or head) as a sequence of rotations about the cardinal axes x, y, and z. The order of Euler angle rotations must be predetermined by some convention, because rotations of rigid bodies in 3-space are not commutative. (Turning the nose 90° toward the left ear then 90° toward the top of the head results in a head orientation different from that reached by switching the order of the rotations.) By convention, the sense of each rotation about a cardinal axis is determined by the right-hand rule, so that positive rotation about an axis +n is a rotation in the direction the fingers of one's right hand would curl when one's thumb is pointing along the direction of +n. Euler angles are therefore signed (or described qualitatively, e.g., “pitch nose up” and “pitch nose down”). The most commonly used Euler sequence in vestibular and oculomotor research is the Fick sequence, in which an object is first rotated about its H (horizontal) axis, then rotated about its newly reoriented V (pitch) axis, then finally rotated about its newly oriented T (torsion) axis (Haslwanter 1995); however, any convention can be chosen as long as it is consistently applied (Kuipers 1999). The sequential rotations in Table 4 are Euler rotations, with the sequences and axes chosen to simplify the process of positioning a subject for vestibular tests involving rotation about Earth-vertical or Earth-horizontal axes.

Table 4A.

Orienting angles for optimal alignment of a human subject's head for (A) rotary chair testing about an Earth-vertical axis, (B) caloric stimulation, and (C) head-on-body “head impulses” with the subject seated upright, for each SCC separately and for functional canal pairs

Rotary chair testing	Explanation of orienting rotations	Semicircular canal to align		First orienting rotation			Second orienting rotation
				Angle	Axis	Direction	Angle	Axis	Direction
Orient head to align axis of SCC being tested with chair rotation axis parallel to ZEarth axis.	Starting in Reid-Earth Aligned Starting Orientation (REASO, in which +XREID, +YREID, +ZREID axes align with +XEarth, +YEarth, +ZEarth, respectively), first rotation is a nose-up (NU) or nose-down (ND) pitch about YEarth axis. Second rotation is a left-ear-down (LED) or right-ear-down (RED) roll about XEarth	Left	Horizontal	18.8°	YEarth	ND	2.2°	XEarth	LED
			Anterior	73.3°	YEarth	NU	52.0°	XEarth	LED
			Posterior	68.7°	YEarth	NU	41.8°	XEarth	RED
		Right	Horizontal	18.8°	YEarth	ND	2.2°	XEarth	RED
			Anterior	73.3°	YEarth	NU	52.0°	XEarth	RED
			Posterior	68.7°	YEarth	NU	41.8°	XEarth	LED
		Best Fit Canal Pair	LH RH	18.8°	YEarth	ND	n/a	n/a	n/a
			LA RP	70.8°	YEarth	NU	47.0°	XEarth	LED
			RA LP	70.8°	YEarth	NU	47.0°	XEarth	RED

Measurement of SCC Position

A plane is uniquely defined by a vector u_o = [x_o, y_o, z_o] pointing from the origin to a point in the plane and the plane's unit normal vector n. The shortest distance to the plane from another point at the tip of v = [x, y, z] is

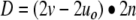3

with D > 0 implying that (x, y, z) and the origin are on the same side of the plane and D < 0 implying that they are not. We used Eq. 3 to compute the (X_REID, Y_REID, Z_REID) position coordinates of the center of each SCC.

Statistical analysis

Statistical analysis was performed using Matlab® and PASS 2002® (NCSS, Inc., Kaysville, UT). Interplane angles, plane normal vector coefficients, and distances for each canal center point to the Reid planes were aggregated separately for the left and right labyrinths of all 22 subjects. A multiway analysis of variance with interaction was used to compare orientation vectors for left and right SCC, after reflecting the right side data through the Y_REID plane. The same procedure was used to perform left–right comparison of SCC positions. Coefficients of unit normal vectors were renormalized after computation of their mean values, so as to yield a mean normal vector of unit length. Student's t-test with Bonferroni correction (two-tailed, α = 0.05) was used to compare inter-SCC angles to the hypothesized mean inter-SCC angle of 90°.

Results

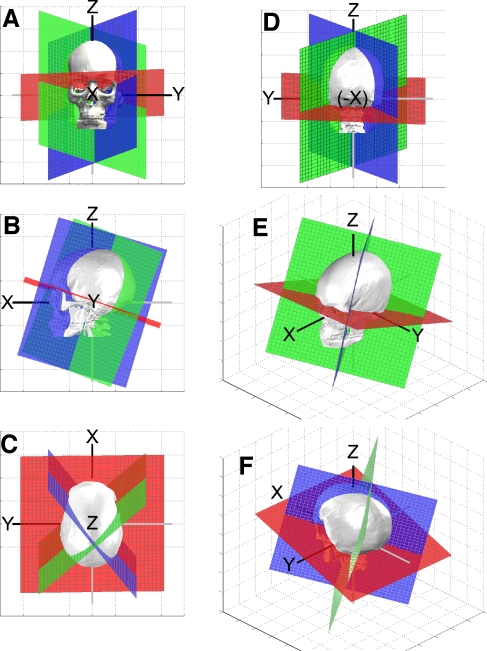
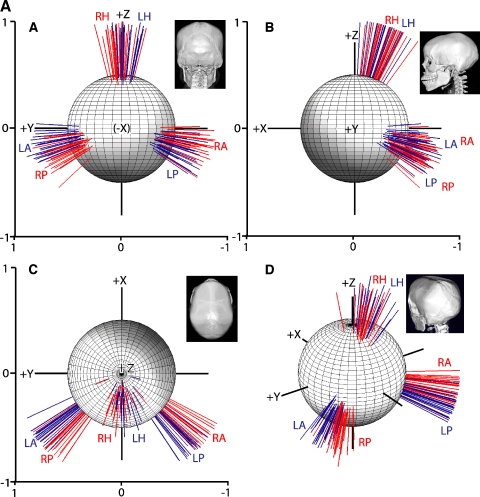
The individual and mean unit normal vectors for each SCC plane are displayed in Figure 4 and summarized in Table 1A. Figure 4A shows all measured unit SCC normal vectors for each of the 22 subjects, tail-aligned at the Reid coordinate system origin and viewed along each cardinal axis (panels A–C) and from a high/left/posterior viewpoint (panel D). The skull insets may be compared to Figure 3 for orientation. The sphere shown in each image is of radius 0.5, centered on the Reid origin. In Figure 4A, each unit length vector represents the orientation of the axis of one SCC in one subject; the corresponding SCC plane would be perpendicular to the vector shown. Figure 4B shows the same data, reduced to mean vectors for each SCC and a circle of radius equivalent to 1 standard deviation of the direction angles measured for each SCC axis. Left SCC (blue) vectors represent the axis about which a right-hand rule head rotation would be excitatory for that SCC, whereas right-hand rule head rotations about the right SCC (red) vectors axes would inhibit the corresponding right SCC.

Fig. 4.

(A) Unit length vectors normal to semicircular canals of left (blue, L) and right (red, R) horizontal (H), anterior (A), and posterior (P) semicircular canals of 22 human subjects, shown as viewed from each cardinal axis (A, B, C views from −X_REID, +Y_REID, +Z_REID axes, respectively) and left-high-posterior view (D), after vectors were rotated so as to align Reid's planes for all subjects. +X = anterior along +X_REID, perpendicular to the Reid coronal plane. +Y = left along +Y_REID, the interaural axis perpendicular to the Reid sagittal plane. +Z = superior along +Z_REID, perpendicular to Reid horizontal plane. (B) Mean normal vectors, same views as in A. Radius of each circle = geometric mean of standard deviations of direction angles between the mean vector and each of the three positive axes (+X_REID, +Y_REID, +Z_REID).

There was no significant difference in any canal plane orientation vector coefficient between the left side and a mirror image of the right (MANOVA, p > 0.57, power 80% to detect a 1 standard deviation difference), so data were pooled for the 44 labyrinths after reflecting right-side data through the Y_REID plane (Table 1B).

The planes corresponding to the pooled mean left labyrinth SCC planes are illustrated from several different angles in Figure 5, along with a 3-D skull rendering of one subject's skull. The mean left labyrinth SCC planes (red = LH, blue = LA, green = LP) are shown from a different viewpoint in each panel, as are the Reid coordinate axes. Panels A, B, C, D show views from the +X_REID (anterior), +Y_REID (left), +Z_REID (superior), and −X_REID (posterior) axes, respectively. Panels E and F show high/left/anterior and high/left/posterior views, respectively. To simplify visual interpretation, the intersection of the SCC planes shown was translated to the center of the head [(X_REID, Y_REID, Z_REID ) = (0, 0, 0)] for these images. The approximate mutually orthogonality of the SCC planes is clearly apparent.

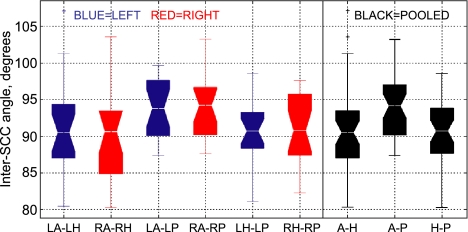
Inter-SCC angles are summarized in Figure 6 and Table 2. When inter-SCC angles were computed separately for each individual and then left labyrinth and mirror-imaged right labyrinth data were pooled, the angle between the anterior and horizontal SCC was 90.6 ± 6.2° (mean ± SD), not significantly different from 90° (p > 0.4, power 80% for true difference of 2.7°). The angle between the horizontal and posterior SCC was 90.4 ± 4.9°, not significantly different from 90° (p > 0.4, power 80% for true difference of 2.1°). The angle between the anterior and posterior SCC was 94.0 ± 4.0°. This mean anterior–posterior inter-SCC angle was close to, but significantly different from, 90° (p < 0.0001, 95% confidence interval 92.8–95.3). Computing inter-SCC angles using the population mean SCC normal vectors yielded similar inter-SCC angles of 90.4°, 90.4°, and 94.0° for ipsilateral anterior–horizontal, horizontal–posterior, and anterior–posterior SCC combinations, respectively.

Fig. 6.

Inter-SCC angles for left (red), right (blue), and pooled (black) canal pairs. Box plots show median (waist), estimated range of median (notch), first and third quartiles (box ends), expected data range (whiskers) and outliers (+). All are close to 90°, and there is no significant difference between sides.

The direction angles between a vector defining the axis of the left horizontal (LH) SCC and the +X_REID (nasal), +Y_REID (left), and +Z_REID (superior) Reid's axes were 108.7 ±7.5°, 92.2 ± 5.7°, and 19.9 ± 7.0°, respectively. The direction angles between a vector defining the axis of the left anterior (LA) SCC and +X_REID, +Y_REID, and +Z_REID were 125.9 ± 5.2°, 38.4 ± 5.1°, and 100.1 ± 6.2°, respectively. The direction angles between a vector defining the axis of the left posterior (LP) SCC and +X_REID, +Y_REID, and +Z_REID were 133.6 ± 5.3°, 131.5 ± 5.1°, and 105.6 ± 6.6°, respectively.

When measured separately for each individual, then pooled for left and mirrored-right, and then averaged, the angle between the two horizontal SCC was 11.3 ± 6.9°. In contrast, the angle between the mean LH and right horizontal (RH) SCC axes was 4.5°. This occurs because the LH and RH SCC vectors have overlapping distributions. Thus, the angle between the mean horizontal SCC axes in Table 1B underestimates the expected angle between the horizontal SCCs in any single subject.

In contrast with the findings by Blanks et al., the horizontal SCC was within 2.2 ± 5.8° of being coplanar with the interaural axis and did not, on average, “droop” downward laterally. In fact, the mean horizontal SCC plane tilted slightly up laterally 2.2° above the interaural axis (and 18.8° up-anteriorly above the +X_REID axis).

When measured separately for each individual, pooled for left and mirrored-right, and then averaged, the angle between an anterior SCC and the contralateral posterior SCC was 15.3 ± 7.2°. The angle between the mean anterior and contralateral posterior SCC axes was 10.7°, with the mean posterior SCC unit normal vector being posterior and inferior of that for the mean anterior canal.

The mean distances from each of Reid's stereotaxic planes to the center of each canal and the center points of the tympanic bone entrances are summarized in Table 3. There was no significant difference in any SCC center position between the left side and a mirror image of the right (MANOVA, p > 0.44, power 80% to detect a 1.5 standard deviation difference). The right external auditory canal entrance center point was within 0.3 ± 0.5 mm of the Z_REID plane defined using the left external auditory canal entrance. The center points of the three SCC in a labyrinth lie approximately 38–41 mm off the midline. Variance in SCC center position along the interaural axis (distance from Y_REID) was largely a result of the difference in head size. Normalizing these distances to the distance from midline to left external auditory canal entrance markedly reduced this variance between subjects (Table 3).

Table 3.

Cartesian coordinates (mean ± SD, in mm) of the centroid of each semicircular canal (SCC) and external auditory canal (EAC) center point with respect to Reid's planes X_REID (coronal through interaural axis), Y_REID (midsagittal), and Z_REID (horizontal through interaural axis)

Center of...	Distance anterior to XREID plane (mm)	Distance left of YREID plane (mm)	Distance left of YREID plane, normalized to mean LEAC–REAC length (mm)	Distance superior to ZREID plane (mm)
Left EAC entrance	0.0 ± 0.0	49.8 ± 3.6	49.8 ± 0.0	0.0 ± 0.0
LA SCC	−4.9 ± 1.9	38.5 ± 3.2	38.4 ± 1.4	11.2 ± 1.5
LH SCC	−5.1 ± 1.8	40.9 ± 3.2	40.9 ± 1.4	7.4 ± 1.4
LP SCC	−8.5 ± 1.9	38.9 ± 3.2	38.9 ± 1.4	6.5 ± 1.6
Right EAC entrance	0.2 ± 0.3	−50.5 ± 3.6	−50.6 ± 1.1	0.3 ± 0.5
RA SCC	−4.9 ± 1.7	−38.4 ± 3.3	−38.4 ± 1.4	11.6 ± 2.0
RH SCC	−5.0 ± 1.5	−40.9 ± 3.2	−40.9 ± 1.4	8.0 ± 1.9
RP SCC	−8.3 ± 1.7	−38.7 ± 3.2	−38.7 ± 1.3	7.2 ± 2.1
Pooled left EAC entrance	0.1 ± 0.2	50.2 ± 3.6	50.2 ± 0.8	0.1 ± 0.4
Pooled LA SCC	−4.9 ± 1.8	38.4 ± 3.2	38.4 ± 1.4	11.4 ± 1.8
Pooled LH SCC	−5.1 ± 1.7	40.9 ± 3.2	40.9 ± 1.4	7.7 ± 1.6
Pooled LP SCC	−8.4 ± 1.8	38.8 ± 3.2	38.8 ± 1.4	6.8 ± 1.9

Data represent pooling of left and right labyrinth data. Much of the variation in lateral position is due to head width; normalizing lateral dimensions to the distance between left and right EAC (third column) reduces variance.

Discussion

The absolute orientations (with respect to accessible skull landmarks) of semicircular canals of the normal human labyrinth are more nearly orthogonal to each other than previously reported. Neither the mean anterior–horizontal nor the mean horizontal–posterior inter-SCC angle was significantly different from 90°. Although the mean anterior–posterior inter-SCC angle is different from 90° (94.0 ± 4.0°), all mean inter-SCC angles in the present data set are much closer to 90° than the 111° angle between the anterior and horizontal SCC found by Blanks et al. (1975).

For conceptual and computational simplicity, the six labyrinthine canals are commonly grouped into three approximately coplanar pairs—the left and right horizontal canals (LHRH); the right anterior and left posterior (RALP) canals; and the left anterior and right posterior (LARP) canals. Our data support the use of this approximation, because the intercanal angles for these pairs are small. Although the two SCC of each pair are not exactly coplanar, the difference in orientation is negligible, because head rotation stimulates canals to a degree dictated by the cosine of the angle between the axis of head rotation and the SCC axis. Rotation of the head about an axis midway between the mean LH and RH SCC axes (which are 5.7° from a compromise axis) would approximate maximally aligned rotation about each individual SCC's axis to within (1 − cos(11.3°/2)) < 0.5%. Rotation of the head about an axis midway between the mean LA and mean RP SCC axes (which are 7.7° from a compromise axis) would simulate rotation about each individual SCC's axis to within (1−cos(15.3°/2)) < 0.9%.

Tables 1A–3 permit calculation of the equivalent in-plane stimulation of each SCC during head rotations about arbitrary axes. A nose-leftward horizontal rotation of velocity 100°/s about Z_REID is equivalent to an in-SCC-plane stimulus of 94, −18, and −26°/s, respectively for the LH, LA, and LP SCC. (Here, a negative sign denotes rotation in the direction inhibitory for a given canal.) A nose-downward 100°/s pitch about Y_REID is equivalent to an in-SCC-plane stimulus of −4, 78, and −66°/s, respectively for the LH, LA, and LP SCC. A left-ear-upward roll of 100°/s about X_REID is equivalent to an in-SCC-plane stimulus of −32, −58, and −69°/s for the LH, LA, and LP SCC, respectively. One can improve the specificity of canal stimulation by pitching the head 20° nose down to bring both horizontal SCC planes approximately into the Earth-horizontal plane Z_Earth. A 100°/s nose-leftward rotation about Z_REID is then equivalent to an in-SCC-plane stimulus of 99.5, −1.0, and 0.2°/s, respectively, for the LH, LA, and LP SCC. A 100°/s LA excitatory rotation about the mean LARP axis yields an in-SCC-plane stimulus of −4.3, 97.4, and 2.0°/s for the LH, LA, and LP SCC, respectively, and −2.0, +15.3, and −97.2°/s, for the RH, RA, and RP SCC, respectively. A 100°/s LP excitatory rotation about the mean RALP axis yields an in-SCC-plane stimulus of 2.6, −15.3, and 97.1°/s for the LH, LA, and LP SCC, respectively, and 2.0, −97.0, and −2.0°/s for the RH, RA, and RP SCC, respectively.

Ideal head orientations for vestibular stimulation

Table 4 presents instructions for alignment of a subject's head with mean canal orientations for maximal SCC stimulation with rotation about an Earth-vertical axis Z_Earth (typical of most rotary chairs), caloric stimulation in the presence of an Earth-vertical gravitational field, or head-on-body rotations (Aw et al. 1996; Della Santina et al. 2002). Instructions are presented both for side-specific SCC alignment and for the best compromise plane between a functional pair of SCC. Each instance in Table 4 presumes the subject is initially in the “Reid-Earth aligned starting orientation” (REASO) aligning the (+X_REID, +Y_REID, +Z_REID) axes with an Earth-fixed, right-hand-rule Cartesian coordinate frame of reference (+X_Earth, +Y_Earth, +Z_Earth), in which +Z_Earth is an Earth-vertical axis pointing up. The REASO is not necessarily the natural resting orientation of a seated or standing human; however, our data could be easily combined with skull landmarks measured fluoroscopically (Vidal et al. 1986; de Beer 1947) or via Optotrak® (e.g., Moore et al. 1999), in seated, standing or walking humans to determine SCC orientations with respect to Earth-fixed coordinates under those conditions.

In rotary chair testing, the subject is typically seated in a chair that rotates about an Earth-vertical axis, Z_Earth. Although one could align a given SCC axis with +Z_Earth using a single reorientation from the REASO, in practice it is easier to employ two rotations in sequence such as shown in Table 4A. For example, starting from the REASO, one may bring the mean LH SCC into alignment with +Z_Earth by first rotating the head 18.8° pitch-nose-down about the interaural axis +Y_REID, then rolling the head 2.2° counterclockwise about the +X_Earth axis (bringing the top of the head toward the left ear). This slight roll yields only a 0.07% change in the effective stimulus experienced by the mean LH SCC, so in practice it can be omitted, and a compromise axis midway between the two horizontal SCC can be used by simply rotating the head 18.8° pitch-nose-down from the REASO. Table 4A describes similar sequences of reorienting rotations for all other SCC. Note that these sequential rotations are not the same as the direction angles listed in Table 2, because they represent a sequence of nested rotations about cardinal axes, rather than the single most direct rotation that would bring the SCC axis in line with +Z_Earth.

For caloric testing, the head is oriented to maximize the thermal convection current generated in a SCC's endolymph by warm or cool water irrigation of the ipsilateral ear canal. This can be achieved by orienting the SCC in an Earth-vertical plane while keeping the interaural axis (which approximates the thermal gradient vector during irrigation of the ear canal) Earth-horizontal (Minor and Goldberg 1990). Starting from the REASO, this can be achieved for either horizontal SCC with a 71.2° pitch nose-up rotation about the interaural axis, or by lying supine semirecumbent on a table inclined 18.8° open-posteriorly (Table 4B). Caloric stimulation of the anterior and posterior SCC of the test ear is minimal in this position, because the thermal gradient, gravitational vector, and the axes of these SCCs are all approximately coplanar.

Table 4B.

Orienting angles for optimal alignment of a human subject's head for calorie stimulation

Caloric testing	Explanation of orienting rotations	Semicircular canal to align		First orienting rotation			Second orienting rotation
				Angle	Axis	Direction	Angle	Axis	Direction
Make both the axis of SCC being tested and the interaural axis (YREID) Earth-horizontal to maximize thermal convection in SCC	Starting in REASO, pitch head about the YEarth axis.	Both sides	Horizontal	71.2°	YEarth	NU (or start supine on table then incline head end of table 18.8° up from floor)
			Anterior	16.7°	YEarth	ND	n/a
			Posterior	21.3°	YEarth	ND	n/a

Caloric stimulation is less effective for the anterior and posterior SCC's, because neither has an axis that is nearly perpendicular to the thermal gradient (Bohmer et al. 1996). However, the head may be oriented to maximize the caloric effect on the anterior and posterior SCCs. To maximize caloric stimulation of an anterior SCC, the head should be pitched 16.7° nose-down from the REASO. For a posterior SCC, the head should be pitched 21.3° nose-down from the REASO. In each case, the horizontal SCC plane is nearly Earth-horizontal, so its contribution to the caloric response nystagmus should be minimized, allowing a semiselective probing of “vertical SCC” (combined anterior and posterior SCC) function.

In performing the “head thrust test” (Halmagyi and Curthoys 1988; Aw et al. 1996; Della Santina et al. 2002), an examiner typically delivers head-on-body impulsive rotation stimuli with the subject sitting erect and fixating a target directly anterior of the nose (i.e., along +X_REID). As listed in Table 4C, optimal orientation of the head for stimulation of the horizontal SCCs with head rotation about Z_Earth is the same as for chair rotations about Z_Earth. Selective stimulation for the other SCCs can be achieved by orienting the head to bring the axis of the SCC into the Earth-horizontal plane, then delivering impulsive head rotations about that SCC axis. Given the lack of precision of manual positioning for head rotation, a reasonable approximation is to place the head 19° pitch nose down from the REASO and then deliver horizontal rotations (for the LH RH SCC pair) about +Z_Earth and left anterior–right posterior (LARP) and right anterior–left posterior (RALP) head rotations about Earth-horizontal axes 45° off the midline. The resulting departure from the maximal effective stimulus for each SCC would only be 0.09%, 0.76%, and 0.24% for the horizontal, anterior, and posterior SCC, respectively.

Table 4C.

Orienting angles for optimal alignment of a human subject's head for head-on-body “head impulses” with the subject seated upright, for each SSS separately and for functional canal pairs

	Semicircular canal to stimulate		Orienting rotations starting from REASO	Stimulus Rotation should be about an axis that is...	Excite SCC by turning head
Head-on-body rotational head acceleration impulses (“head thrusts”) with subject sitting erect	Left	Horizontal	18.8° ND about YEarth then 2.2° LED about XEarth	YEarth	Leftward
Subject sitting upright and visually fixating a target directly anterior of nose (along +XREID).		Anterior	16.7° ND about YEarth	In Earth-horizontal plane, 38.0° posterior to +YEarth 38.0° anterior to −YEarth	CCW/ND
For horizontal SCC, it is convenient to deliver head impulses about the ZEarth axis, just as for rotary chair test.		Posterior	21.3° ND about YEarth	In Earth-horizontal plane, 48.2° anterior to +YEarth 48.2° posterior to −YEarth	CCW/NU
For anterior and posterior SCC, limited neck range of motion prevents delivery of head thrust rotation stimuli when SCC axis is aligned with ZEarth and body is sitting upright. Instead, reorient head pitch-nose-down to bring anterior or posterior SCC axis of interest into Earth-horizontal plane, then deliver rotational stimuli about that SCC axis.	Right	Horizontal	18.8° ND about YEarth then 2.2° RED about XEarth	ZEarth	Rightward
		Anterior	16.7° ND about YEarth	In Earth-horizontal plane, 38.0° posterior to +YEarth 38.0° anterior to −YEarth	CCW/ND
		Posterior	21.3° ND about YEarth	In Earth-horizontal plane, 48.2° posterior to +YEarth 48.2° anterior to −YEarth	CW/NU
Rotation directions are from subject's point of view, so counterclockwise (CCW) and leftward (L) rotations move the forehead toward the left ear. ND = nose down. NU = nose up. LED = left-ear-down. RED = right-ear-down. REASO defined in Table 4A. Axes illustrated in Figures 3 and 4.	Canal Pair	LH RH	18.8° ND about YEarth	ZEarth	See side-specific directions above
		LA RP	19.2° ND about YEarth	In Earth-horizontal plane, 43.0° posterior to +YEarth 43.0° anterior to −YEarth
		RA LP	19.2° ND about YEarth	In Earth-horizontal plane, 43.0° anterior to +YEarth 43.0° posterior to −YEarth

Distinction between anatomic and physiologic canal planes

In using these data to design and analyze rotational tests of SCC function, one should note that anatomic SCC planes approximate but do not exactly equal the planes of maximum and minimum directional sensitivity for each SCC. Morphologically precise fluid dynamic models suggest that coupling of endolymph flow between SCCs alters each SCC's directional sensitivity. For example, head rotation purely about the mean axis of the anterior SCC causes some movement of posterior SCC endolymph via their communication in the common crus. The extent of this effect varies depending on labyrinthine morphology. In toadfish (Opsanus tau), the difference between anatomic and maximal sensitivity directions is ∼8.8°, ∼16.8°, and ∼3.8° for the horizontal, anterior, and posterior SCC, respectively (Rabbitt 1999). Similarly, in rhesus monkeys (Macaca mulatta), the difference between anatomic and maximal sensitivity directions is ∼3.1°, ∼9.9°, and ∼5.3° for the horizontal, anterior, and posterior SCC, respectively (Reisine et al. 1988). In humans, the difference between anatomic and maximal response planes is smaller, estimated to be 0.7°, 1.1°, and 5.7° for the horizontal, anterior, and posterior canals, respectively (Rajguru et al. 2004). These angles are equal to or less than the intersubject variation of anatomic SCC orientation angles we observed. Because of the cosine dependence of maximal response on misalignment angle, using anatomic SCC planes to approximate maximal response directions would lead to errors of ≤0.5%. Anatomic SCC planes are therefore a useful proxy for maximum directional sensitivity orientations.

In contrast to the case of maximum sensitivity directions, even small angle errors in estimates of SCC null-response directions or prime directions (rotations for which only one SCC of a labyrinth is stimulated, while others have no response (Rabbitt 1999)) can cause significant differences between expected and actual ampullary nerve activity. Prime directions align poorly with anatomic planes (Rajguru et al. 2004), and cosine dependence magnifies effects of misalignment in this case. Intersubject variability alone can also cause significant error. For example, during a head rotation expected to elicit no response for the mean LH SCC, an individual with that SCC misaligned 1 standard deviation (∼7.5° in Table 2) from the population mean would experience an LH SCC stimulus 13% of maximal. A 15° error would result in 26% of maximal response. Thus, one should exercise caution in relying upon mean anatomic planes to estimate SCC null directions and prime directions.