Simultaneous Measurements of Ossicular Velocity and Intracochlear Pressure Leading to the Cochlear Input Impedance in Gerbil

Abstract

Recent measurements of three-dimensional stapes motion in gerbil indicated that the piston component of stapes motion was the primary contributor to intracochlear pressure. In order to make a detailed correlation between stapes piston motion and intracochlear pressure behind the stapes, simultaneous pressure and motion measurements were undertaken. We found that the scala vestibuli pressure followed the piston component of the stapes velocity with high fidelity, reinforcing our previous finding that the piston motion of the stapes was the main stimulus to the cochlea. The present data allowed us to calculate cochlear input impedance and power flow into the cochlea. Both the amplitude and phase of the impedance were quite flat with frequency from 3 kHz to at least 30 kHz, with a phase that was primarily resistive. With constant stimulus pressure in the ear canal the intracochlear pressure at the stapes has been previously shown to be approximately flat with frequency through a wide range, and coupling that result with the present findings indicates that the power that flows into the cochlea is quite flat from about 3 to 30 kHz. The observed wide-band intracochlear pressure and power flow are consistent with the wide-band audiogram of the gerbil.

List of Symbols:

U_s

stapes volume velocity (mm³/s)

V_s

stapes velocity (mm/s)

A_fp

effective footplate area (mm²)

Z_c

cochlear input impedance

Z_E

radiation impedance looking out the external ear from the TM

Z_T

middle ear input impedance (Pa s/m³ = N s/m⁵)

P

Power

P_ME

middle ear power (W)

P_sv

SV pressure

P_EC

EC pressure (Pa)

Introduction

The motion of the stapes footplate upon the fluid in the scala vestibuli (SV) produces intracochlear pressure. The stapes exhibits both tilting and piston motions. In a recent study (Decraemer et al. 2007a), we conducted measurements of SV pressure close to the stapes, directly followed by measurements of the three-dimensional (3D) stapes velocity in the same experimental animal (gerbil). We found that the tilting motion of the stapes was not small compared to the piston motion—it was usually within a factor of 10, and could be of equal size. We correlated the pressure and velocity to explore whether the tilting motion appeared to produce pressure behind the footplate. If it did, the tilting motion would contribute to the input to the cochlea and help in realizing the remarkably smooth and flat pressure gain as a function of frequency (Olson 1998, 2001; Dong and Olson 2006). We did not find evidence for this hypothesis: dips in the piston component of the velocity were not systematically filled by peaks in tilt and peaks in tilt were not apparent in the SV pressure. We found that the SV pressure had the best correlation with the stapes piston velocity but differences in these curves were also present. However, the experimental method necessitated changing the experimental set-up, reorienting the animal and moving the sound source between pressure and motion measurements. We concluded that truly simultaneous measurements were likely required for a detailed comparison between SV pressure and stapes velocity.

To undertake simultaneous measurements of pressure and velocity, we designed a new experimental protocol based on the following rationale: assuming that the stapes piston motion is the only determinant of the input pressure to the cochlea, we should only measure this component and correlate it to the simultaneously measured intracochlear SV pressure. If the outcome of the experiment shows that the SV pressure frequency response is a good reflection of the piston-motion frequency response we will confirm the hypothesis that stapes piston motion alone leads to cochlear input pressure. If not, we can ask whether the correlation is improved compared to our study based on the non-simultaneous measurements. If an improvement is apparent, we can argue that the SV pressure is mainly determined by the piston motion but we still remain with the question of what other factors influence the cochlear input pressure. If the correlation between the two is not good at all, then factors other than stapes piston motion must be substantial.

A single component motion measurement simplifies the experimental procedure considerably and reduces animal manipulation and duration of the experiment. With some extra precautions to secure the pressure probe, we could do both pressure and motion measurements in the same experimental environment. For the single component measurement of stapes piston motion, it was mandatory to have the interferometer observation direction aligned along the piston direction. In gerbil, the pars flaccida is remarkably large (diameter ∼ 1.5 mm; Dirckx et al. (1997)) and one has only to remove it partly to get a view of the stapes that is almost perfectly in-line with the stapes piston axis and wide enough to allow for velocity measurements. The present paper reports on measurements following this new strategy.

We found that the SV pressure close to the stapes followed the piston component of the stapes velocity with high fidelity. We used the measured velocity and pressure to calculate cochlear input impedance and power flow into the cochlea.

Materials and methods

Animal preparation

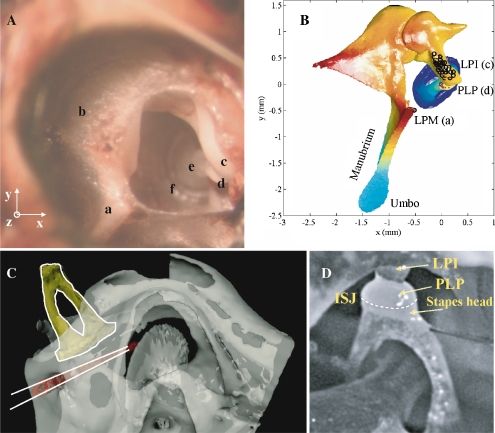
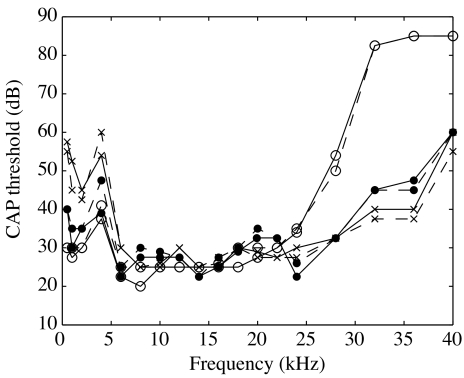
Data from five gerbils, 50–70 g in mass, are presented here. The care and use of animals were approved by the Institutional Animal Care and Use Committee of Columbia University. The animal was first sedated with ketamine (40 mg/kg) and then deeply anesthetized with sodium pentobarbital (initial dose 60 mg/kg; supplemental dose 10 mg/kg). Buprenex was used as an analgesic; the initial dose (0.2 mg/kg) was renewed every 6 h. The animal was lying on a heated blanket to keep its body temperature at 37°C. A head holder was cemented to the top surface of the skull to secure the animal’s position during surgery and measurement. A tracheotomy was performed to maintain a clear airway. The external ear canal (EC) was cut short to its bony end to expose the entire pars flaccida (PF). The posterior half of the pars flaccida was removed to give visual access to the long process (LPI) and plate of the lenticular process (PLP) of the incus (Fig. 1A). In gerbil, the present approach allows observation in a direction almost perfectly in-line with the stapes piston axis. In some experiments, pars flaccida was resealed with saran wrap or a glass cover. A hole, a few millimeters wide, was made in the bulla to have access to SV to insert a pressure sensor and to put an electrode at the edge of the round window niche for measurement of the compound action potential (CAP). The CAP threshold was measured with tone pips that ranged from 0.5 to 40 kHz (Johnstone et al. 1979). The CAP measurement was performed at different steps of the surgery to gauge the consequences of the surgery on the hearing. All animals had normal hearing. Figure 2 assembles the open-field CAP thresholds measured before (solid line) and after (dashed line) opening the pars flaccida. These were measured for the first three experiments: 26m5 (curves with circles), 30m5 (crosses), and 1j5 (dots). The thresholds were ∼25 dB SPL over the most sensitive frequency region (5–25 kHz). The CAP thresholds barely changed due to the opening (±5 dB). Therefore, the pars flaccida opening did not affect the hearing capability substantially. With this experimental set-up, experiments were shorter, allowing the data acquisition from animals in a living condition. Four animals were overdosed with anesthetic at the end of the experiment, the other animal died during the course of measurements (1j5).

FIG. 1.

A Photograph of the gerbil middle ear: view through the open pars flaccida. a Lateral process of the malleus (LPM), b pars flaccida (PF), c long process of the incus (LPI), d plate of the lenticular process of the incus (PLP), e anterior crus, and f annular ligament. The experimental reference system (x, y, z) is indicated in the left corner. B Model of the gerbil middle ear in the experimental reference system. The origin is at the PLP. The observation direction was, on average, only 6.8° from alignment with the stapes piston axis. Dots illustrate measurement positions. a, c, and d correspond to locations labeled in A. C CT scan illustrates the position of the pressure sensor in the scala vestibuli behind the footplate. The typical insertion depth was only 0.2 mm, but was larger in the scan to illustrate the path clearly. D View of the stapes showing the incus/stapes joint (ISJ) and the relative position of the PLP compared to the stapes head.

FIG. 2.

CAP thresholds measured using open-field stimulation before (solid line) and after (dashed line) opening the pars flaccida. Results are from three experiments: 26m5 (curves with circles), 30m5 (crosses), and 1j5 (dots).

Stimulus and data acquisition

Stimulus delivery and data acquisition were performed with a Tucker–Davis Technologies (TDT) System 3, using the RX6 and RP2.1 DA/AD components, the HB7 headphone buffer and PA5 attenuator. This system can record data from three channels simultaneously. The first two channels are synchronized while the third (which resides in a separate component) has a short relative delay that was measured at the beginning of each experiment and corrected for off-line. The stimulus and acquisition programs were written in Matlab and the TDT visual design studio.

A Sony “walkman” earphone (diameter ∼ 10 mm) was used to stimulate the ear in an open-field configuration. The earphone was positioned about 15 mm from and posterior to the entrance of the remaining part of the ear canal and oriented toward its opening. A 1/2″ Bruel & Kjaer microphone with probe tube was placed at the edge of the ear canal, ∼5 mm from the speaker, at the central part of the sound field. The microphone and sound driver were affixed either to the animal mounting post or to a free-standing post on the laboratory table, uncoupled from the animal holder and interferometer.

The input to the sound driver was adjusted to keep the sound level at the probe tip (i.e. at ∼10 mm outside the EC entrance) at a level of 80, 90, or 95 dB SPL (sound pressure level = dB re 20 μPa peak). (Note that in our previous paper, Decraemer et al. (2007a), SPL was expressed re 20 Pa rms.) For the first three experiments (26m5, 30m5, and 1j5), the frequency was stepped between 200 and 1 kHz with a step of 200 Hz, between 1 and 10 kHz with 250 Hz, between 10 and 20 kHz with 500 Hz, and between 20 and 50 kHz with 1 kHz. For the last two experiments (8d6 and 13d6), more frequencies were tested below 10 kHz (step of 100 Hz from 200 Hz to 3.4 kHz and step of 200 Hz from 3.5 to 10 kHz), with the same step size as in the early experiments above 10 kHz.

For each stimulus frequency 25 averages were performed, which corresponded to 0.5 s signal duration. The sampling period was ∼5 μs. The data were analyzed off-line via FFT to find the amplitude and phase of the component at the stimulus frequency.

The sound driver pressure was very repeatable in amplitude and phase for a given configuration of the animal, sound driver, and probe tip. Changing this configuration resulted in a slight change in the measured stimulus pressure. The relationship between the speaker, microphone probe tube, and EC entrance was not specifically maintained from experiment to experiment. Therefore, in this open-field stimulus condition the stimulus was not tightly controlled. This was acceptable because we were primarily interested in the relationship between stapes velocity and SV pressure.

Stapes velocity measurement

The plate of the lenticular process of the incus forms a tight-fitting cap on the head of the stapes (Figs. 1D, see also Fig. 2 in Funnell et al. (2005)). Because the PLP covers most of the top surface of the stapes head, “stapes measurements” were actually made on the edge of the PLP. This will be discussed further in the “Results” section. The temporal bones of the first three animals were harvested so that micro-CT (computed tomography) scans could be made. Using the scans a 3D representation of the ossicular anatomy was made and was registered in the position of the experiment (Decraemer et al. 2007a) as shown in Figure 1B. We can see that the observation direction (z-axis, out of the page) was almost perfectly along the piston axis, defined as the perpendicular to the stapes footplate annulus. The angle between the z-axis and piston axis was measured using the registered 3D representations; the offset of the observation direction from the piston axis was between 6° and 10°, confirming that the difference between the piston component and the measured component was small.

Two different interferometers were used to gather the data presented here. The first three experiments (26m5, 30m5, and 1j5) were performed with the confocal microscope/heterodyne laser interferometer designed and built in the laboratory (Khanna et al. 1996). The animal’s body was resting on a support with the head immobilized by firmly clamping the head holder to the positioning system of the interferometer set-up (for details see Decraemer et al. (2007a)). In this configuration, the SV pressure sensor was fixed as described in the next section. The animal could be moved and rotated allowing velocity measurements at different positions. We focused precisely on a chosen reference point at the PLP and reset our coordinate read-out system. We made measurements at slightly different points on a small moon-shaped protruding part of the PLP and also on the top surface of the LPI directly above the stapes footplate center (black circles, Fig. 1B). Coordinates of observation points were recorded for precise documentation of the anatomical geometry during the experiment. The last two experiments (8d6 and 13d6) were performed with a commercially available interferometer (Polytec, sensor head OFV-534 with controller OFV-5000—VD01). A small goniometer was used to orient the animal head to aim along a single axis (the piston axis) at one location on the PLP. In this configuration, the measurement location of the stapes velocity was fixed and the pressure sensor mounted on a micromanipulator could be moved to measure the SV pressure at different positions behind the footplate, simultaneous with the piston-like stapes velocity. With both set-ups, the data were acquired without reflecting beads or foils.

The noise floor of the velocity measurements varies inversely with the “carrier level,” which is largely determined by the amount of reflected light and thus varies between measurements. With the interferometer developed by Khanna and colleagues, reporting from two typical cases, the noise level was ∼2 × 10⁻⁴ mm/s (2 Hz bandwidth) over a wide range of frequencies in one case and 10⁻³ mm/s in another case. With the Polytec interferometer, the noise floor was slightly higher, roughly 1 and 4 ×  10⁻³ mm/s in representative cases. Vibrations of the EC bony rim defined the background vibrations of the experiment. The background vibration was 30–40 dB less than the motion of the stapes from 5 to 35 kHz, and this gap was smaller (15–20 dB) but still reasonable at the highest frequencies of measurement.

Pressure measurements in the scala vestibuli

The pressure in the SV was measured with a fiber-optic based micro-pressure sensor (diameter 170 μm) with a gold coated plastic membrane of ∼1 μm thickness as its sensing component. The sensor was inserted into the cochlea just adjacent to the stapes (Olson 1998; Dong and Olson 2006). The hole to the cochlea was just slightly bigger than the sensor diameter, and the insertion was performed using a micromanipulator (MM33, Fine Science Tools). Figure 1C, based on a CT scan, shows the position of the hole with respect to the stapes. Usually the pressure was measured at an insertion depth of ∼0.2 mm. (The figure shows an extreme insertion depth in order to illustrate the path clearly.)

The sensors have a sensitivity that is flat to within a few dB up to at least 40 kHz. The uncertainty in the pressure sensor sensitivity is ∼±10 dB (Dong and Olson 2006; Decraemer et al. 2007a). The sensors are calibrated by immersing the tip under the surface of a vial of water that is secured to a shaker containing a monitor accelerometer (Bruel and Kjaer, model 4290). When a sensor’s sensitivity changes (comparing pre- to post-experimental calibrations, or calibrations on subsequent days) the entire flat sensitivity curve shifts down or up without introducing frequency structure. Therefore, the uncertainty in sensitivity does not influence the reliability of the frequency response measurement. Sensor sensitivity changes seem to occur due to a mechanical perturbation of the membrane upon insertion. Stability post-insertion is checked with repeat measurements, as reported below. The sensor output is typically in phase with shaker acceleration, and with the phase of a condenser microphone when calibrations are performed in air (the latter illustrated in Ravicz et al. (2007)). However, in rare cases (approximately 1–2%), the phase flips 180°. The sensor works optically, and the amount of light returning to the fiber after reflecting from the membrane is the optical read-out. The amount of returning light typically increases with negative pressure acting on the membrane. When sensors with the opposite behavior appear in the calibration step they are not used, in order to avoid phase ambiguity. However, if the sensor membrane is mechanically perturbed when being inserted, the condition can develop in situ. This apparently did happen in the experiment of December 8, 2006 (8d6). We present these data with the phase adjusted by 180°. Based on our experience with the sensors, this action, along with the explanation provided here, is the most appropriate course.

As originally designed, approximately 1 cm of the sensor’s delicate tip component emerges from a glass capillary that is secured to a metal rod which in turn is held in a micromanipulator throughout the experiment. In the present experiments, this design was modified. For experiments 26m5, 30m5, and 1j5, the pressure sensor tip emerged a few millimeters from a glass capillary a few centimeters long. At its other end, the capillary was inserted into flexible tubing (∼2 mm in diameter and ∼10 cm in length). The sensor’s optic fiber protruded from the back of the tubing. This assembly was secured fairly lightly to a stainless steel rod, using double-sided tape. The rod was held in a micromanipulator. Following insertion, the glass capillary was cemented to the bulla with dental cement, and then the assembly was released from the manipulator rod and sutured and taped to the animal body so that the animal and sensor could be safely moved to the interferometer set-up.

For the last two experiments (8d6 and 13d6), using the Polytec interferometer, the surgery and the data acquisition were performed in the same room. The sensor did not need to be fixed onto the bulla as the animal’s head was not repositioned during the experiment. Therefore, the original sensor design, with firm attachment to the manipulator, was used. At the end of the experiment, the sensor could be removed and recalibrated. The average of the sensitivities before and after the experiment was taken as the sensitivity of the sensor during the experiment. Because the sensor remained on the manipulator, its position inside SV could be adjusted and the pressure could be measured at different depths inside the scala, as in experiment 8d6.

The noise level in the pressure sensor is set by shot noise in the opto-electronics and is flat with frequency. It corresponds to a pressure level that depends on the sensitivity of individual sensors: for these five experiments, it was ∼55–70 dB SPL (2 Hz bandwidth).

Synchronization of the pressure and velocity measurement systems

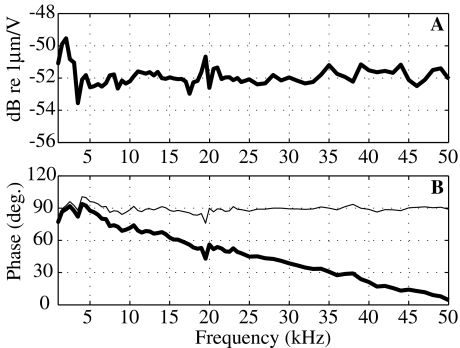
To couple the measured SV pressure and stapes velocity, we need to account for filtering and relative delays in the opto-electronic processing of the pressure sensor and interferometer. Therefore, as a preparatory experiment, we drove the membrane of a pressure sensor with acoustic tones from an open-field sound source. The membrane motion was measured simultaneously using the interferometer focused at the center of the membrane and with the sensor’s fiber optic system on the other side. The voltage output of the sensor is proportional to the displacement of the membrane; the voltage output of either of the interferometers is proportional to velocity. The displacement measured with the interferometers (reported velocity divided by ω) had very similar shapes in amplitude compared to the pressure sensor output, confirming that the sensor’s fiber optic system operated as a displacement sensor. Figure 3 assembles results comparing the Polytec interferometer output to the output of a sensor from 1 to 50 kHz. In Figure 3A, we present the ratio of the displacement based on the interferometer’s factory-calibrated sensitivity to the voltage from the sensor. The response is flat to within 1 to 2 dB, and the variations are random; therefore, no amplitude correction is needed. The relative phase between the interferometer and the sensor is approximately a straight line (thick line in Fig. 3B), indicative of a delay of 4.7 μs. The interferometer demodulation electronics are expected to produce a delay of approximately this size, so it is a reasonable result. After subtracting this delay, the relative phase is almost exactly 90° (thin line), as expected since the interferometer measures velocity and the sensor measures displacement. The variations from exactly 90° are small and random, generally less than 7°. The lowest two frequency points, at 250 and 500 Hz, showed larger variations, likely because of low frequency vibration (not shown). (Because the sensor’s optic fiber is glued to the membrane housing and the interferometer is only mechanically coupled to the membrane via the experimental table, background vibrations within the chamber would influence the sensor and interferometer measurements differently, which would lead to discrepancies.) Overall, the result assures our ability to make a detailed comparison between pressure and motion.

FIG. 3.

Comparison of the displacement of a pressure-sensor’s sensitive membrane measured by the Polytec interferometer on one side (reported velocity divided by ω) and the sensor’s optic fiber system on the other side. A Interferometer measured displacement divided by sensor output voltage (amplitude in dB re 1 μm/V). The ratio is constant as a function of frequency, and therefore no amplitude correction is needed when comparing velocity and pressure with the two systems. B Phase difference (in degrees) between the interferometer and the pressure sensor illustrates a pure delay (thick line). When corrected for a delay of 4.7 μs (thin line), the phase response is equal to 90° (as expected since the interferometer measures velocity and the pressure sensor optics measure displacement).

The same measurement was performed with the interferometer developed by S. Khanna. Curves similar to those in Figure 3 were obtained, which confirmed and extended results obtained in a different manner in Willemin et al. (1988). For this interferometer, a delay of 14 μs and a small amplitude correction to account for low-pass filtering in the interferometer’s electronics were applied (Decraemer et al. 2007a).

The relationship between SV pressure and EC pressure in gerbil has been explored under closed-field conditions (Olson 1998; Olson and Cooper 2000; Dong and Olson 2006; Decraemer et al. 2007a) with the main finding that the SV pressure was quite flat with frequency from 1 through 40 kHz or above, with a delay-like phase. The relationship between stapes velocity and EC pressure has also been studied in closed-field, with roughly similar but more variable results Rosowski et al. 1999; Olson and Cooper 2000. In the present study, the sound stimulus was set to a constant level just outside the EC in open-field conditions and stapes piston motion and SV pressure were measured. Their relative value is the study’s main result.

Results

Relative motion across the incudostapedial joint

As is apparent in Figure 1D, the lenticular plate of the incus (PLP) is closely coupled to the stapes head, whereas the connection between the LPI and the PLP is formed by a strip of cartilaginous bone about 0.03 mm thick and with overall dimensions of 0.07 × 0.14 mm (Elkhouri et al. 2006). In the present study, motion was measured on the PLP rather than the stapes head because the PLP covers the stapes head when viewed along the axis corresponding to stapes piston motion. Based on these anatomical features, one would expect the PLP to move with the stapes, even though it is truly part of the incus. Therefore, for clarity and economy, we prefer to report that we measure “stapes piston velocity”, as opposed to “incus PLP velocity in the direction of stapes piston motion”, and we use this nomenclature when reporting our findings.

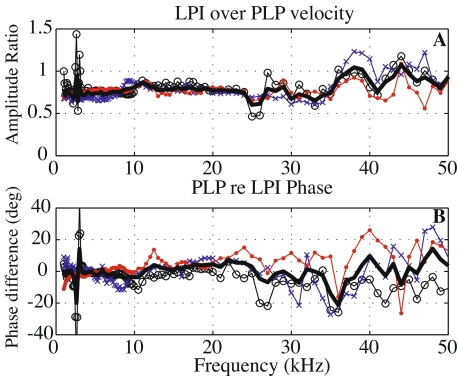
It is notable on this topic (and just a small digression from the main topic of the paper) that although the anatomy might suggest that the PLP and LPI could possess substantial relative motion, our measurements across the pedicle that connects them did not bear this out. Instead, we observed that the piston motion of the LPI was very much like that of the PLP. Figure 4 compares velocities measured in direct succession above and below the junction, on the LPI and PLP. Amplitude and phase results from three experiments are shown: 26m5 (curve with circles), 30m5 (crosses), and 1j5 (dots). The thick curve is the mean of the three data sets. The amplitude ratio (LPI over PLP velocity) is flat with a constant ratio of ∼0.8 from 1 to 35 kHz. The PLP re LPI phase was close to zero (0.5 ± 5°) in the same frequency range. In brief, the velocity amplitude at the PLP was just slightly higher than at the LPI and they moved nearly in phase. Above 35 kHz, the PLP and LPI moved with very nearly identical amplitudes. Random dips and peaks grew a little bit in this frequency range. Thus, in gerbil, the velocity did not show a significant amplitude boost or phase lag across the pedicle as has been described in chinchilla (Robles et al. 2005; Robles et al. 2006; Decraemer et al. 2007b). A species difference might account for this difference, but it is also possible that the different results arose from viewing angle or some other methodological difference, and further work is required to sort it out.

FIG. 4.

Comparison of the velocity at the LPI and at the PLP. A Magnitude ratio of the velocity measured at the LPI just above the stapes footplate to the PLP velocity. From 1 to 35 kHz, the LPI velocity was slightly lower than the PLP velocity (mean of ∼0.8). B PLP phase relative to the LPI phase (degrees). Differences were small (mean of −0.5° ± 5°). Results are from three experiments 26m5 (black curves with circles), 30m5 (blue crosses), and 1j5 (red dots). The thick curve is the mean of the three curves.

Stapes piston velocity and scala vestibuli pressure

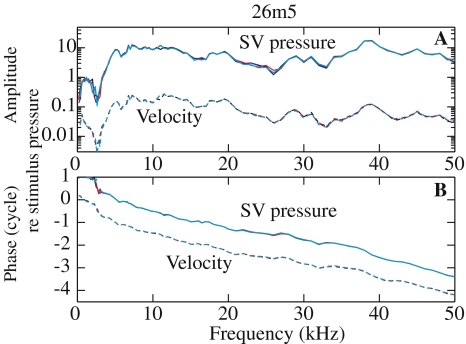
The stapes piston component determines the scala vestibuli pressure Figure 5 illustrates the repeatability of the measurements. It assembles the simultaneously measured SV pressure and stapes velocity: amplitude (A) and phase (B) relative to the stimulus pressure. Measurements are from the same animal, 26m5, at the same location, under the same experimental conditions, and at different times. R#5 was at t = 0, R#9 at t = 32 min, R#11 at t = 48 min, and R#14 at t = 68 min. The stimulus pressure outside the EC was set to 80 dB SPL and the bulla and pars flaccida were open. The curves overlapped nearly perfectly, illustrating the stability of the preparation and of the pressure sensor. The velocity phase has been offset by a cycle to separate the curves. The SV pressure phase relative to the stimulus pressure phase presents a delay of ∼70 μs: 30 μs can be accounted for by the middle ear delay from within the EC opening to the cochlea (Dong and Olson 2006) and the other 40 μs by the travel time from the microphone to the EC (∼1.4 cm at 340 m/s).

FIG. 5.

Demonstration of measurement stability over time (26m5). SV pressure (unitless—solid line) and stapes velocity amplitude relative to stimulus pressure (mm/s/Pa—dashed line) (A) and phase relative to the stimulus pressure phase (B) measured at the same position and under the same experimental condition (bulla and PF open, 80 dB outside the EC) at different times: At t = 0 R#5 (black), t = 32 min R#9 (blue), t = 48 min R#11 (red), and t = 68 min R#14 (cyan). Thin lines are used to help discern the small differences.

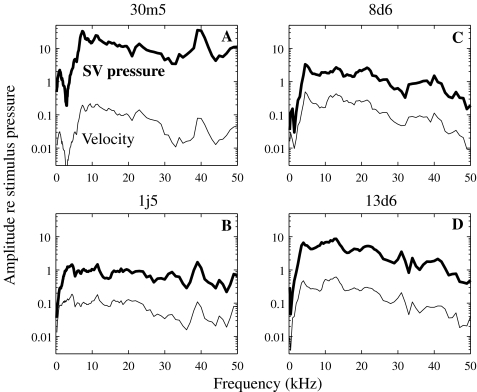
Figure 6 assembles the amplitude of the piston-like stapes velocity (thin line) and the SV pressure (thick line) measured in four animals (30m5, 1j5, 8d6, and 13d6). All data were obtained in a living anesthetized condition except 1j5, which were collected 1 h after the animal died. Middle ear measurements are known to be quite linear (Guinan and Peake 1967), as are SV pressure measurements near the stapes (Olson 1998, 2001). Therefore, the post mortem condition is only relevant in that it might lead to drying but this develops over hours and is not a factor in the results. Each of the plots was obtained under slightly different experimental conditions: for the 30m5 curves (A), the stimulus level was set at 90 dB, the bulla was sealed with clay and PF open. For the 1j5 curves (B), the bulla was sealed with clay and PF was covered with saran wrap, and the stimulus level was 90 dB. The 8d6 curves (C) were obtained using the Polytec interferometer, a stimulus level of 95 dB, the bulla sealed, and PF open. The 13d6 curves (D) were obtained with the Polytec at a 95 dB stimulus level, with both the bulla and PF openings sealed (PF with a glass cover). To compare the data measured with different open-field sound pressure levels, the amplitude of the response is normalized to the open-field stimulus pressure amplitude.

FIG. 6.

Simultaneously measured scala vestibuli pressure relative to the stimulus pressure (unitless—thick line) and stapes velocity relative to the stimulus pressure (mm/s/Pa—thin line). The stimulus pressure was measured outside the ear canal. Results from four animals with slightly different experimental conditions are presented: A 30m5—90 dB SPL, bulla sealed with clay and PF open; B 1j5—90 dB SPL, bulla sealed with clay and PF covered with saran wrap; C 8d6—using the Polytec interferometer, 95 dB SPL, bulla sealed and PF open; D 13d6—using the Polytec interferometer, 95 dB SPL, bulla sealed and PF covered with a glass cover.

For each of the five cases presented here (Figs. 5 and 6), plotting the pressure and velocity in the same frame illustrates the similarity between the two when they are measured simultaneously in the same animal: pressure and velocity follow each other closely with almost every small detail in the velocity repeated in the pressure. This argues strongly that the piston component of the stapes motion determined the pressure in the SV. In other words, our hypothesis is supported: the piston component of the stapes seems to be the main stimulus that causes the SV pressure.

Below, we explore the inter-animal variability in the velocity and pressure with respect to different anatomical conditions (open or closed experimental openings) and discuss other likely sources of variability. This will inform our understanding of the variability in their ratio, the input impedance of the cochlea.

Velocity and pressure: inter-animal variability In Figure 6 the velocity amplitude varied between animals by ±5 dB. The velocity amplitude had the following general features: below 5 kHz, it was sensitive to the anatomical conditions (bulla open or closed; PF open or closed). In this open-field condition, having the middle ear cavity open caused a large decrease in response at frequencies below 5 kHz. Figure 6B and D show data in which the bulla and PF were closed, and the low frequency response dropped off much less precipitously in these cases. (We will explore the anatomical manipulations further in Fig. 8.) From ∼5–50 kHz, the response did not depend on whether the holes were closed; it was flat to 20–25 kHz, and then showed a slight decrease with frequency, accumulating about 10 dB at 50 kHz. The shape of the SV pressure curves was similar to that of the velocity curves. The amplitude level varied more (±10 dB) between experiments than the velocity did, likely due to sensor calibration uncertainty.

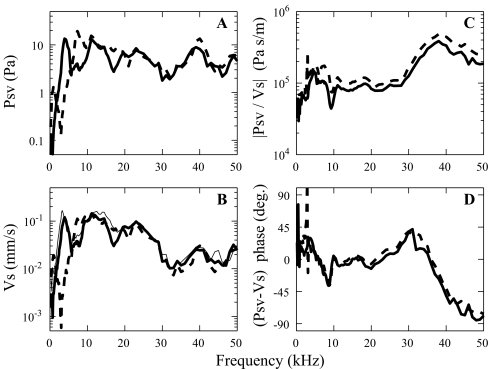
FIG. 8.

Pressure in scala vestibuli (A) and stapes velocity (B) measured with the stimulus pressure set at 90 dB at the EC entrance (30m5) measured for different conditions of opening and closing of the bulla and PF: dashed thick line with the bulla and PF open (R#18), solid thick line with the bulla closed and PF open (R#26). The solid thin line in B is the velocity with both PF and bulla closed (R#28)—no pressure data for this condition. The resulting pressure to velocity amplitude ratios (C) and relative phases (D) are in the right panels.

Some factors change velocity and pressure the same way and therefore their ratio (the input impedance) is not affected. For one, the distance between the speaker and the EC entrance was not strictly maintained between experiments and did change the effective sound stimulation. It was found to affect both stapes velocity and SV pressure but in the same way. This was also true for the open or closed character of experimental openings.

Other factors might affect either the velocity or the pressure but not both. Stapes velocity was always measured with the laser beam focused on the PLP but not exactly the same position with all animals. During preparatory experiments, the motion was recorded at several positions on the PLP of the same animal (as illustrated Fig. 1B) and compared, with the result that the position did not influence the measured response. This point was rechecked during experiment 26m5.

Another factor that might affect velocity or pressure in a different way is the insertion depth of the pressure sensor in SV, typically about 0.2 mm. To determine if the sensor position in the SV could account for some of the variability in the pressure, we measured the pressure at different depths inside SV: 1.5, 1, 0.5 mm and at the entrance (animal 8d6). The long axis of the stapes footplate measures about 1 mm (Elkhouri et al. 2006). An insertion depth of 0.5 mm correlates to ∼ the posterior end of the footplate and an insertion depth of 1.5 mm to the anterior end. The sensor position was adjusted using a micromanipulator. As illustrated in Figure 1C, the sensor was inserted in SV nearly parallel to the stapes footplate (at a distance of roughly 0.2–0.3 mm from it) and was not angled to approach the basilar membrane (BM). Amplitude responses at the different positions are in Figure 7A and relative phase responses (compared to the deepest response measured at ∼1.5 mm) are in Figure 7B. Differences were small (less than ±3 dB in amplitude and less than 10–15° in phase) except when the sensor was right at the cochlear wall opening. This confirms previous results (Fig. 8 in Olson (1998); Fig. 11 in Nedzelnitsky (1980)). The velocity responses measured simultaneous with these pressures overlapped each other ∼ exactly (not shown). Therefore, the pressure was uniform in the region of SV behind the footplate and the insertion depth of the sensor in SV did not affect the measured stapes velocity.

FIG. 7.

A Pressure (dB) measured at different depths within scala vestibuli: ∼1.5 mm deep (thick line), 1 mm (dashed line), 0.5 mm deep (line with dots), and just at the opening in the cochlear wall at a depth of ∼0 mm (thin line). Amplitudes were very similar except when pressure was measured at the opening. B Pressure phase relative to the phase measured the deepest in SV (in degrees). Same symbols as for Figure 7A (animal 8d6).

FIG. 11.

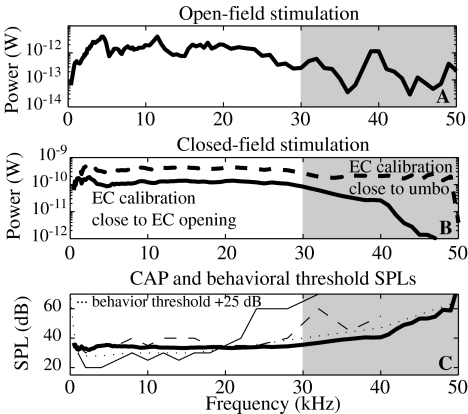
A Experimental open-field power inside the inner ear normalized to a stimulus of 80 dB outside the EC. The bulla and PF were open (experiment 1j5). B Power delivered to the cochlea in closed-field condition, with a stimulus level of 80 dB inside the ear canal, found with the average cochlear input impedance of Figure 9 and the closed-field SV pressure from Dong and Olson (2006)—thick solid line and from Olson (1998)—dashed thick line. See text for explanation for difference. C Constant power threshold compared to CAP threshold and behavioral threshold. The solid line power curve from B is used to show the stimulus pressure necessary to deliver a constant power of 3 × 10⁻¹⁵ W to the cochlea in the closed-field configuration of Dong and Olson (2006). The thin solid and dashed lines are experimental CAP resulting from two experiments (wg68 and wg70 from Figure 2 of Dong and Olson (2006)). The dotted line is the behavior threshold from Ryan (1976) displaced upward by 25 dB to aid the comparison of curve shapes. Above 30 Hz, our experiments cannot be interpreted as measuring a point impedance (as discussed in the first section of the “Discussion” section); therefore we colored this region in grey.

Usually, the SV pressure read-out was stable in time (as illustrated in Fig. 5), but sometimes it was not. In one case (13d6), instability seemed tied to sensor instability in situ. In this experiment, there was a slow creep up in pressure over 2 h. The change was the same at all frequencies (the curves were simply shifted up +15 dB). The sensor was recalibrated at the end of the experiment and only a change of 4 dB was noticed, which was less than the in situ changes, so if the source of the in situ changes was due to the sensor, they were caused by some aspect of the in situ environment—likely a mechanical distortion of the sensor membrane. A different sensor was inserted at the same position and the same frequency response was measured as had been measured with the first sensor, which confirmed the stability of the preparation and the good reliability of the sensors in terms of frequency response, although their absolute sensitivity is a weakness. In another experiment (8d6), time-dependent changes in the pressure of ∼10 dB were measured. In this case, they happened only over a certain range of frequencies (below 20 kHz) and they were not seen in the velocity.

To summarize, and leaving discussion of anatomical manipulations to the next paragraph, variations in the velocity in different animals are likely due to (1) true inter-animal variation and (2) variations in the stimulus pressure, which was in an open-field configuration. The position of the laser on the PLP had no significant influence on the response. For the SV pressure, variability is likely due to (1) true inter-animal variation and (2) variations in the stimulus pressure, just as for stapes velocity. In addition, variability was caused by (3) uncertainty in sensor sensitivity (so that in situ sensitivity was different than calibrated sensitivity) and perhaps (4) changes of the fluid level inside the cochlea. Variations in the stimulus pressure will affect SV pressure and stapes velocity similarly so will not affect their ratio, the cochlear input impedance. In general, sensor calibration uncertainty will produce vertical shifts in the ratio of SV pressure to stapes velocity, without altering the shape of the frequency response of the impedance.

Reclosing the openings In some of the measurements, the experimental holes in the bulla and pars flaccida were reclosed and it is informative to see the effect of holes on the pressure, the velocity, and their ratio. During experiment 30m5, pressure (Fig. 8A) and velocity (Fig. 8B) were measured with a 90 dB SPL open-field stimulus. The dashed line was obtained with the PF and bulla open. For the thick solid line, the PF was open and the bulla was closed with plasticine. The thin solid line corresponded to both bulla and PF closed (the PF with saran wrap), but at that time the sensor broke and only the velocity could be measured. Differences appear mainly at frequencies below 10 kHz and appear in both the SV pressure and the stapes velocity. As a minor exception to this statement, at 8–9 kHz, the pressure was bigger in the open bulla condition and the stapes velocity was also bigger, but less so. Above 12 kHz, all curves were almost the same. Most significantly, the prominent dip in pressure and velocity at about 3 kHz disappeared when we closed the bulla. When both the bulla and PF were closed (resulting in a closed middle ear cavity, thin solid line in Fig. 8B) the velocity response only changed at frequencies below 1 kHz. There, the velocity amplitude increased by ∼5 dB compared to the case with only the bulla hole closed. This result is consistent with observations in previous studies (Ravicz et al. 1992; Teoh et al. 1997; Rosowski et al. 1999).

Most important to this study is that both pressure and velocity changed in almost identical ways with anatomical manipulation, confirming our expectation that we could make valid measurements of the pressure to velocity ratio with the PF open. The ratio of pressure to velocity is defined as the specific cochlear input impedance. The conditions of open and sealed bulla did not change the magnitude (Fig. 8C) or phase (Fig. 8D) of the impedance significantly. The sharp changes at 3 kHz are due to the very sharp notch in pressure and velocity in the open bulla condition which is not perfectly cancelled out when taking the pressure to velocity ratio. The anatomical manipulations required moving the animal to have surgical access and the general 2 dB decrease in impedance magnitude observed in Figure 8C might have its source in a small change in observation angle upon replacing the animal into the experimental chamber.

Input impedance of the gerbil cochlea

The cochlear input impedance is closely related to the specific impedance above, except that pressure is divided by the stapes volume velocity, which is the piston velocity multiplied by stapes footplate area: U_s = A_fpV_s. A_fp, the effective footplate area equals 0.62 mm² (Lay 1972; Decraemer et al. 2007a). The cochlear input impedance represents the load that the cochlea presents to the middle ear. The amount of sound energy that is absorbed by the cochlea depends on the amplitude and phase of the impedance (Rosowski et al. 1986). The simultaneous measurement of stapes piston velocity and intracochlear pressure gives a direct measurement of the specific cochlear input impedance and including the stapes footplate area allows us to also calculate the cochlear input impedance.

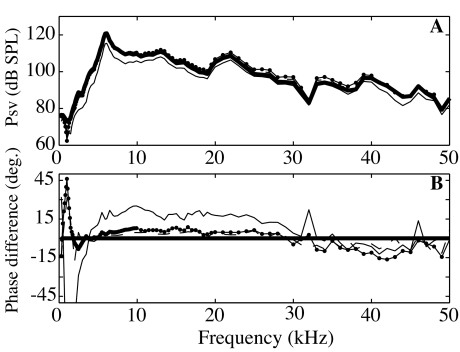
The cochlear impedances of the five animals whose SV pressure and stapes velocity were shown in Figures 5 and 6 are assembled in Figure 9, with specific impedance indicated on the right axis, and input impedance on the left. The smaller panels to the right give an expanded view of the lower frequency results. The bold curve represents the mean value of the five experimental curves. The mean magnitude of the input impedance is 10¹¹ Pa s/m³ = 10¹¹ N s/m⁵. The five impedance magnitude responses contain the same general features. The level variation can for the greater part be attributed to the sensor uncertainty reported above. In terms of frequency response, from 0.5 to 3 kHz, the impedance magnitude increased by about 6 dB, then the curves stayed flat up to 25–30 kHz where we see the onset of a broad maximum with peak at about 37 kHz for two of the curves and at 33 kHz for a third (1j5). The data gathered using the Polytec interferometer (8d6 and 13d6) while similar to the other three curves up to ∼37 kHz, show a monotonic gradual increase rather than a broad peak. The animal’s head was held with the dorsal surface of the head up when using the original (horizontal) interferometer and with the dorsal surface of the head to the side when using the (vertical) Polytec interferometer, so this curve shape difference might reflect something like position-dependent fluid level in the region of the cochlear windows. The idea that fluid-level might cause changes is bolstered by the observation that in one experiment (26m5) the impedance response 1 day post-mortem lost its broad peak and became more like the latter experiments. In post-mortem cochleae, the fluid level within the cochlea decreases, as can be observed at the round window. Pre-mortem, the fluid typically swells the round window membrane outward; post-mortem, the membrane is typically sucked inward.

FIG. 9.

A Magnitude of the cochlear input impedance (pressure/volume velocity) in Pa s/m³ (=N s/m⁵). The right scale corresponds to the specific input impedance (pressure/velocity) in Pa s/m. C Expanded view of low frequency results from A. B Phase difference between the SV pressure and the velocity (in degrees). D Expanded view of low frequency results from B. The experimental conditions and stimulus levels were slightly different for the different animals, as for Figures 5 and 6: 26m5 (black circles): 80 dB SPL, bulla and PF open; 30m5 (blue crosses): 90 dB SPL, bulla sealed with clay and PF open; 1j5 (red dots): 90 dB SPL, bulla sealed with clay and PF covered with saran wrap; 8d6 (cyan plus symbols): using the Polytec interferometer, 95 dB SPL, bulla sealed and PF open; 13d6 (magenta squares): using the Polytec interferometer, 95 dB SPL, bulla sealed and PF covered with a glass cover. The thick lines are the average magnitude and phase.

The phase curves start at a small angle (0 to 35°) and stay in a small ∼30° band around zero up to 20 kHz. At this point, the phase curves of the original three experiments and the later two experiments diverge somewhat, as in the magnitude results. The early curves undergo a small increase with frequency and then decrease steadily, ending at ∼−80° at 50 kHz. The phase responses from the later experiments decrease steadily from 20 kHz but end up at the same ∼−80° point as the early experiments at 50 kHz. A possible reason for the increasing magnitude with decreasing phase above 30 kHz is presented in the “Discussion” section.

In spite of the variety of experimental details, the shape of the magnitude and phase of the input impedance of the cochlea is conserved, and can best be described as quite flat within the 3–30 kHz range. (It is reassuring to see the technical variations such as sensor assembly type, attachment or lack thereof of the sensor to the bulla, and interferometer type did not make a difference; in addition the impedance was not sensitive to the anatomical manipulations to the PF and bulla). If we pick out a single curve, experiment 1j5, small dots, and restrict the discussion to the wide range between 3 and 30 kHz, the amplitude varies by only 6 dB, and the phase is always within ±15° of zero. This observation of wide-band resistive impedance is the main result of the paper. The strength and accuracy of this statement is a consequence of the close correlation found between stapes piston velocity and SV pressure at the stapes.

Discussion

How to explain the experimental cochlear input impedance above 30 kHz

The resistive nature of the impedance (flat magnitude and phase close to 0°) apparent in the results of Figure 9 is expected due to the cochlear traveling wave, which transports energy down the cochlear spiral (Zwislocki 1965). This energy-absorbing characteristic is central to models of cochlear input impedance (Zwislocki 1965; Dallos 1973; Lynch et al. 1982; Puria and Allen 1991; Shera and Zweig 1991). In our results, the resistive behavior of the impedance was a good approximation from 3 kHz up to ∼30 kHz at which point the impedance magnitude increased (and in some cases peaked broadly) and the phase decreased. A plausible explanation for the high frequency behavior is that the SV pressure was influenced by the local cochlear traveling wave. The location of the SV sensor in the cochlear base corresponds to best frequencies (BF) ∼40–50 kHz (Müller 1996). In the frequency region approaching the BF, the magnitude of the response increases due to cochlear tuning and the phase decreases (Békésy 1960), and our observed SV pressure is in keeping with these basic characteristics. Arguing against this idea is the insensitivity of SV pressure to the insertion depth of the sensor into the scala shown in Figure 7, since at frequencies around the BF and close to the basilar membrane the traveling wave pressure shows substantial spatial variation (Steele and Taber 1979; Olson 1999; Yoon et al. 2007). On the other hand, the depth measurement we performed in the present study was not angled to approach the BM. Therefore, it remains plausible that traces of basal-turn tuning and traveling wave were evident in our SV pressure, and responsible for the broadly tuned response and mild phase delay that was observed in the impedance calculation. Independent support for this idea is in a model of cochlear input impedance that predicted a delay in phase when pressure was measured a short distance apical of the stapes (Puria and Allen 1991). It is also notable that human temporal bone measurements of Merchant et al. (1996) and Aibara et al. (2001) showed a magnitude peak and phase delay at frequencies close to 10 kHz, so the mechanics producing the effect in gerbil might also be at work in human. (10 kHz might seem too low for the peak frequency in the very basal region of the human cochlea given the 20 kHz range of human hearing; however, passive frequency peaks are known to shift downward significantly several hours post-mortem (Cooper 2000).) In this interpretation, the measured pressure and stapes velocity cannot be considered as a point impedance at frequencies above 30 kHz. It is worth noting that regardless of the explanation for the behavior, the increasing magnitude combined with decreasing phase above 30 kHz are incompatible with a point impedance, which must on theoretical grounds be a minimum phase function (Bode 1945; Papoulis 1962).

Cochlear input impedance: simultaneous vs nonsimultaneous measurements

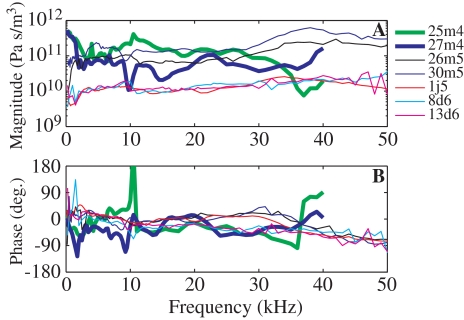
In Figure 10, our experimental results are compared to the previous set of measurements from our own laboratory (Decraemer et al. 2007a). In that set, velocity and pressure measurements were performed in the same animal but in two different experimental chambers and with more than 1 h between pressure and velocity measurements. A set of velocity measurements from different viewing angles was analyzed for the 3D motion of the stapes. Pars flaccida was not opened and therefore none of the viewing angles was even approximately aligned with the piston axis. The five thin lines in Figure 10 are from Figure 9 and the two thick lines correspond to 25m4 and 27m4 (Fig. 17 in Decraemer et al. (2007a)). Experiment 27m4 showed the most similarity with the present results: the magnitude was approximately constant from 2 to 35 kHz, with a small increase observed above 35 kHz. The phase response was within ±50° up to 40 kHz. The 25m4 phase response presented a jump at 10.5 kHz and has been forced down a full cycle at that point so that curves could be compared. The impedance measured from animal 20m4 has not been included: the magnitude was quite flat with a small increase at high frequencies but the phase showed a smooth increase through two cycles from 5 to 20 kHz. The source of the large phase excursion was the velocity, and such large phase excursions were never measured in the present experimental sets, in which piston velocity was measured directly. Large phase excursions were typical in the off-piston-axis velocity components measured in Decraemer et al. (2007a). It is likely that the large phase excursion in the impedance of animal 20m4 is due to the off-piston-axis nature of the velocity measurements. The 3D analysis of that paper requires rigid body motion, and while the stapes appears to not flex, even small flexing might affect the analytical ability to correctly balance away the large phase excursions when calculating piston velocity.

FIG. 10.

A Magnitude of the cochlear input impedance in Pa s/m³. B Phase difference between the SV pressure and the velocity (in degrees). The experimental results from this study (five thin lines—same as in Fig. 9) are compared to two (thick lines) of the three experimental results obtained in our laboratory nonsimultaneously (Fig. 17 in Decraemer et al. (2007a)).

All the curves in Figure 10 span about an order of magnitude in amplitude and are roughly similar in phase. However, the simultaneous measurements resulted in smoother impedance curves, with phases within the ±90° range that is valid for an input impedance. Therefore, the simultaneous measurements were required for a detailed comparison of pressure and motion.

Cochlear input impedance in the literature

Cochlear input impedance has been measured or approximated in a number of species and those results and their frequency ranges are summarized in Table 1. A variety of experimental techniques were employed to find the impedance: Overstreet and Ruggero (2002) combined their stapes velocity (oriented less than 30° with the piston axis) with SV pressure (Olson 1998) to determine the gerbil cochlear input impedance. The magnitude was in good agreement with the one obtained in this study. The phase response differed as it was flat up to 6 kHz and then increased with frequency. In cat (Lynch et al. 1982), the cochlear input impedance was found by directly driving the stapes with pressure and measuring the resulting stapes velocity and intracochlear pressure. The impedance, primarily resistive, was quite similar to our result in gerbil. The impedance was found using nonsimultaneous pressure and velocity measurements in chinchilla (Ruggero et al. 1990) and guinea pig (Dancer and Franke 1980). Merchant et al. (1996) and Aibara et al. (2001) reported human cochlear input impedance measured in fresh temporal bone. The method of Merchant et al. did not include an intracochlear pressure measurement; instead, the stapes was driven with a known pressure and the stapes velocity was measured. This gives the impedance of the cochlea plus stapes. A second measurement was made with the inner ear drained in order to separate out the impedance of the stapes (due to stiffness and resistance of the annular ligament and stapes mass). Aibara et al.’s experiments measured stapes velocity and SV pressure simultaneously. The stapes velocity was measured at an angle with the piston axis and then compensated with a “cosine correction” by dividing by the cosine of the measurement angle. In a more recent paper, Puria measured stapes velocity and SV pressure in the same human temporal bone and presented the resulting cochlear input impedance (Fig. 4G and H in Puria (2003)). Differences between those and the earlier (Aibara et al. 2001) results (lower magnitude and higher angles) might be explained by the large angle with the piston axis (∼55°) of the velocity measurement, with a cosine correction applied afterward. It is known that below ∼2 kHz a slight angle to the piston axis can be accurately accounted for with a cosine correction. However, due to complexity in stapes motion, above 2 kHz a cosine correction is not justified (Chien et al. 2006; Decraemer et al. 2006). Another explanation for the divergence in results, suggested by the authors, was that the tubing used to drive the middle ear in reverse had altered the cochlear input impedance.

TABLE 1.

Cochlear input impedance in the literature

Species	Reference	Freq. (kHz)	|Zc| (N s/m5)	Zc phase (°)
Gerbil	Fig. 6 in Overstreet and Ruggero 2002	1–40	1–2 × 1011	∼45° up to 6 kHz then increased with frequency
Cat	Fig. 20 in Lynch et al. 1982	0.5–8	∼2 × 1011	Flat, ∼0°
Chinchilla	Figs. 15 and 17 in Ruggero et al. 1990	0.4–16	∼0.65 × 1011	Flat, ∼30° up to 6 kHz then increased with frequency
Guinea pig	Fig. 2 in Dancer and Franke 1980	up to 20	∼0.45 × 1011	Not available
Human	Fig. 8 in Merchant et al. 1996	0.1–3	∼0.6 × 1011	Flat, ∼0°
		3–10	Broad peak	Decrease in phase from 3 to 10 kHz
	Fig. 9 in Aibara et al. 2001	0.02–5	∼0.28 × 1011	Flat, ∼ 0°
		5–10	Broad peak	Decrease in phase from 5 to 10 kHz
	Fig. 4 in Puria 2003	0.2–10	Increase from 0.06 × 1011 to 0.2 × 1011	∼30–35°

The results in Table 1 are similar in showing a region in which the magnitude is fairly flat with frequency and a phase close to zero, corresponding to a resistive impedance. The average values of the impedance magnitude between species in the flat region varied by about a factor of five, from 0.2–1 × 10¹¹ N s/m⁵. (Note that the impedance magnitude from Aibara et al. is multiplied by √2 as a correction (O’Connor and Puria 2006)).

Power input to the cochlea

Sound in the environment is collected by the external ear and transmitted through the EC, the tympanic membrane (TM), and ossicles to the inner ear. The amount of power that reaches the inner ear depends on the efficiency of the auditory periphery in collecting sound power from the external environment and transmitting it to the middle ear and the efficiency of the middle ear to transmit this power to the inner ear. The better the matching of the impedances along the acoustic path, the more sound energy will be absorbed, and the less reflected. Rosowski et al. (1986) formulated this quantitatively. The relevant impedances are the radiation impedance looking out the external ear from the TM (Z_E), the impedance looking into the middle ear at the TM (Z_T—the middle ear input impedance), and the impedance of the cochlea at the stapes (Z_c). The radiation and middle ear impedances can be combined to calculate the power utilization ratio (PUR), the fraction of the power available at the TM that is absorbed by the middle ear. In gerbil studies, above 2 kHz, the PUR was generally about 0.3 (30% of the power available at the TM entered the middle ear) and was as high as 0.9 at some frequencies (Ravicz et al. 1996).

The middle ear efficiency is defined as the fraction of the power available at the middle ear (P_ME) that is absorbed by the inner ear (MEE = P/P_ME). The power input to the cochlea is a function of the SV pressure and the stapes velocity:

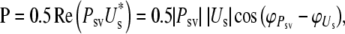1

and can also be expressed as a function of Z_c, the cochlear input impedance:

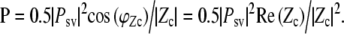2

Similarly, the power into the middle ear is: 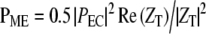, with P_EC the ear canal pressure. From Figure 8 in Ravicz et al. (1992), over the range 3–20 kHz, for gerbil, |Z_T| is roughly constant and equal to ∼10⁸ N s/m⁵ with a phase close to 0 (±30°). Therefore, 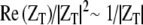. From our experimental results, the mean value of |Z_c| is ∼10¹¹ N s/m⁵ and the phase is close to 0 over the same frequency range. The gerbil middle ear forward gain, |P_sv|/|P_EC|, is ∼25 dB (Dong and Olson 2006). Therefore, the ratio of the power entering the inner ear over the power entering the middle ear is MEE ∼ 0.3.

Concatenating this result to the PUR from Ravicz et al. (1996), we find the efficiency of the system: 30% of the power available at the TM enters the middle ear and, again, 30% of the power available at the middle ear enters the inner ear. Therefore, over a wide frequency range, approximately 9% of the power available at the TM enters the cochlea.

The power curve in Figure 11A was determined using Eq. 1 and the experimental data for which the bulla and PF were closed (1j5). The power was calculated for an open-field stimulus pressure of 80 dB. As the stimulus level was set outside the EC, we emphasize the shape of the curve more than the absolute level. We only consider frequencies up to 30 kHz, as at higher frequencies, the experiments cannot be interpreted as measuring a point impedance (as discussed previously). For open-field stimulation, the power at the cochlea was quite flat from ∼4 to 24 kHz. The cochlear input impedance measured in this study was independent of experimental manipulations and also will apply under closed-field stimulation. Therefore, we can determine the power input to the cochlea that would obtain in closed-field stimulation using P_sv from previous closed-field measurements, and Z_c, the average input impedance from this study (thick lines in Fig. 9). Closed-field stimulation is better controlled than open-field stimulation, but at frequencies above 30 kHz, standing wave pressure variations within the gerbil EC cause even the closed-field condition to be subject to systematic variations that are greater than 15 dB (Khanna and Stinson 1985; Olson 1998; Dong and Olson 2006; Ravicz et al. 2007). In Figure 11B, we show the power calculated using P_sv from Dong and Olson (2006), for which EC pressure was calibrated close to the EC opening with a Bruel and Kjaer microphone and probe tube (thick solid line), and using P_sv from Olson (1998), for which EC pressure was calibrated closer to the umbo with a fiber optic pressure sensor (thick dashed line). The 2006 measurements are more reliable in terms of absolute level, while the 1998 measurements are better in terms of proximity of the calibration spot to the TM. (See also discussion in Dong and Olson (2006).) The differences in the two curves in Figure 11B show that the shape of the frequency–power curve at high frequencies depends on the location where the stimulus level is set within the EC. The ambiguity is caused by the basic difficulty of specifying acoustic stimulus pressure to the ear: at high frequencies the pressure field in (and also outside) the EC is not uniform and single point pressure measurements depend on the location of measurement.

It has been proposed that the cochlea’s detection threshold is determined by power (Khanna and Tonndorf 1969), and in Figure 11C, we use the solid power curve from Figure 11B to find the power threshold curve (the SPL necessary to attain a constant power level in the cochlea), and compare the shape of that curve to CAP threshold curves found with the same stimulus and EC calibration conditions (thin solid line corresponds to wg68 and dashed line to wg70 in Dong and Olson (2006)). The threshold power level was set at 3 × 10⁻¹⁵ W, as this yielded threshold SPLs that corresponded best with the CAP threshold SPLs. The behavioral threshold curve for gerbil (Ryan 1976) is also shown (thin dotted line). This curve is elevated by 25 dB to facilitate comparison with the shapes of the other curves. Through 30 kHz, the shapes of the behavioral and power threshold curves are similarly flat. At the lowest frequencies, the behavioral curve climbs rapidly but our data do not probe this region thoroughly. The experimental CAP from wg70 is also quite flat through ∼30 kHz, whereas that from wg68 begins a steep ascent slightly above 20 kHz. In general, the CAP threshold at frequencies above 20 kHz is quite variable, likely due to the vulnerability of the basal cochlea to surgery and cooling. While the figure is based on the idea that the cochlea operates as a power detector, previous studies (Dallos 1973; Puria et al. 1997) considered it as a pressure detector. Because both the power and the SV pressure are quite flat through at least 30 kHz, our results are consistent with either of these possibilities.

Note on a practical matter

In the present paper, we emphasized the component of stapes velocity that lies along the piston axis, and developed a technique for simultaneous measurements of pressure and stapes piston velocity by opening the pars flaccida and using open-field stimulation. Based on our previous work (Decraemer et al. 2007a), nonpiston stapes velocity components are also substantial and can be of similar size to the piston components. The piston motion was the most highly correlated to the SV pressure, and the tilting motions did not appear to augment the piston motion in useful ways (i.e., they did not exhibit peaks at frequencies where the piston motion had dips, which was the possibility we explored in that work.) However, in many physiological recordings, it is not practical to measure stapes piston motion directly, and an off-axis measurement is necessary. A question arises: are off-axis measurements similar enough to on-axis measurements that they are still a useful reference? As already stated, off-axis velocity components are of similar size to the on-axis component. The bigger problem is in the phase, where, as described above, off-axis components sometimes go through much larger phase excursions than the on-axis component. In the present set of experiments, the piston component and SV pressure were always similar in terms of phase accumulation. Therefore, an off-axis stapes velocity measurement might present difficulties as a phase reference for the physiological measure under study (SV pressure, BM motion, etc...). A practical response to this cautionary information would be to make several off-axis stapes measurements, and assume that the one with the shallowest phase accumulation is most like what an on-axis measurement would have shown.

Conclusion

We simultaneously measured the pressure in scala vestibuli close to the stapes and the piston component of the stapes velocity. The SV pressure followed the piston velocity in detail even when conditions of opening and closing bulla holes were changed, strongly supporting the idea that the piston motion of the stapes is responsible for the pressure in the cochlear fluid. The simultaneously measured SV pressure and piston motion could therefore be used to find the input impedance of the gerbil cochlea, and it was mainly resistive over a wide frequency range, from 3 to 30 kHz. Combining the impedance result with closed-field SV pressure measurements, we found that the acoustic power that flows into the cochlea is close to constant from 3 kHz to at least 30 kHz. Above ∼30 kHz, at frequencies approaching the BFs of the cochlear base, the present method for measuring point impedance appears to break down since pressure is measured near but not at the stapes.

Abbreviations

SV

scala vestibuli

EC

ear canal

PF

pars flaccida

LPI

long process of the incus

PLP

plate of the lenticular process of the incus

CAP

compound action potential

SPL

sound pressure level

CT

computed tomography

BM

basilar membrane

BF

best frequency

TM

tympanic membrane

PUR

power utilization ratio

MEE

middle ear efficiency