Quasi-static Transfer Function of the Rabbit Middle Ear‚ Measured with a Heterodyne Interferometer with High-Resolution Position Decoder

Abstract

Due to changes in ambient pressure and to the gas-exchange processes in the middle ear (ME) cavity, the ear is subject to ultra-low-frequency pressure variations, which are many orders of magnitude larger than the loudest acoustic pressures. Little quantitative data exist on how ME mechanics deals with these large quasi-static pressure changes and because of this lack of data, only few efforts could be made to incorporate quasi-static behavior into computer models. When designing and modeling ossicle prostheses and implantable ME hearing aids, the effects of large ossicle movements caused by quasi-static pressures should be taken into account. We investigated the response of the ME to slowly varying pressures by measuring the displacement of the umbo and the stapes in rabbit with a heterodyne interferometer with position decoder. Displacement versus pressure curves were obtained at linear pressure change rates between 200 Pa/s and 1.5 kPa/s, with amplitude ±2.5 kPa. The change in stapes position associated with a pressure change is independent of pressure change rate (34 μm peak-to-peak at ±2.5 kPa). The stapes displacement versus pressure curves are highly nonlinear and level off for pressures beyond ±1 kPa. Stapes motion shows no measurable hysteresis at 1.5 kPa/s, which demonstrates that the annular ligament has little viscoelasticity. Hysteresis increases strongly at the lowest pressure change rates. The stapes moves in phase with the umbo and with pressure, but the sense of rotation of the hysteresis loop of stapes is phase inversed. Stapes motion is not a simple lever ratio mimic of umbo motion, but is the consequence of complex changes in ossicle joints and ossicle position. The change in umbo position produced by a ±2.5 kPa pressure change decreases with increasing rate from 165 μm at 200 Pa/s to 118 μm at 1.5 kPa/s. Umbo motion already shows significant hysteresis at 1.5 kPa/s, but hysteresis increases further as pressure change rate decreases. We conclude that in the quasi-static regime, ossicle movement is not only governed by viscoelasticity, but that other effects become dominant as pressure change rate decreases below 1 kPa/s. The increasing hysteresis can be caused by increasing friction as speed of movement decreases, and incorporating speed-dependent friction coefficients will be essential to generate realistic models of ossicle movements at slow pressure change rates.

Introduction

Apart from acoustic pressures, the middle ear (ME) is also subject to very slow pressure variations caused by changes in ambient pressure and by the gas exchange processes through the ME mucosa. These quasi-static pressure variations are orders of magnitude larger than the highest sound pressures, and have been measured both indirectly and directly by many authors (e.g., Flisberg et al. 1961; Hergils and Magnuson 1985; Tideholm et al. 1996). Recently, we reported results of ME pressure monitoring in intact human MEs (Dirckx et al. 2000) and found pressure changes up to 1 kPa over intervals of hours and minutes (e.g., when rising from recumbent to upright position). When caused by mechanisms of gas exchange, pressure varies very slowly. When caused by changes in ambient pressures, e.g., when taking an elevator or an airplane, or when submerging the head under water, pressure changes can be much faster and can have amplitudes of the order of several thousands of pascals. Large quasi-static pressure variations are therefore an important aspect in the mechanics of the ME. As to practical implications, the large ossicle movements caused by changing ME pressure should be taken into account when designing ossicle prosthesis and implantable ME hearing aids.

It is well known that static pressure changes the stiffness of the ME mechanical system, and hence its acoustic transfer function. This property of the ME is the basis of tympanometry, which has been used as a diagnostic tool for many years now. More recently, the effect of static pressure on eardrum and ossicle vibration has also been investigated (Lee and Rosowski 2001; Teoh et al. 1997). From the early days of tympanometry, the effect of “pumping speed” has been a subject of investigation (e.g., reviewed by Therkildsen and Gaihede 2005) and, more recently, the effects of preconditioning in repeated tympanometric cycles were investigated (Therkildsen and Gaihede 2005). From these results, it is clear that the response of the ME chain at a given static pressure value can be quite different depending on the pressure change rate (pumping speed) and the direction (pumping direction) of the change that lead to the given pressure value.

Although insight has been gained in how static pressure influences acoustic vibration of the umbo (Rosowski and Lee 2002) and of the pars tensa (PT) and pars flaccida (PF) of the tympanic membrane (TM; Lee and Rosowski 2001; Teoh et al. 1997), it was never investigated experimentally how much of the large quasi-static movements of the eardrum is transferred to the cochlea. The large quasi-static motions of the eardrum and ME ossicles are strongly nonlinear, and hence they are not integrated in current finite-element models that use an infinitesimal linearizing approach. The nonlinear behavior of the ossicular chain can be attributed to nonlinear viscoelastic behavior of the eardrum and the ligaments (e.g., Price and Kalb 1991), but other factors, e.g., static friction within the joints or between the ossicles and the cavity walls, may be involved as well. To expand existing models into the quasi-static, high-amplitude pressure range, the motion of the ossicles under these conditions needs to be known.

The deformation of the eardrum and the displacement of the umbo as function of pressure have been measured in intact MEs of gerbil (Dirckx and Decraemer 2001), cat (Ladak et al. 2004), and human (Dirckx and Decraemer 1991) using moiré interferometry. This technique allows full field deformation measurement, but it takes several seconds to measure the deformed TM shape at a single pressure. Hence, the technique does not allow measurements of the deformation at different rates of pressure change. Hüttenbrink (1989) presented a detailed study of the displacements of malleus, incus, and stapes in human cadaver temporal bones under static pressure. Here, also, pressure was maintained at the same value over a longer period of time, so dynamic changes were not studied and the effect of pressure change rate could not be measured.

The object of the present work is to investigate the pressure transfer function of the ME in the quasi-static regime by measuring the motion of umbo and stapes at different pressure change rates, and to see how different pressure change rates influences this transfer function.

Materials and methods

Animals and specimen preparation

Conventional New Zealand White rabbits (2.8 ± 0.3 kg) were used for the study. In total, nine animals were used for the study. When giving mean values of measurement results, we will add the standard deviation as a measure of variability. We chose the rabbit as animal model because their ME is rather large, and these animals are easy to keep and are readily available. Animals were sacrificed using intravenous injection of sodium pentobarbital 60 mg/kg. Injection was performed in the vein of the pinna after local surface anesthesia with lidocain spray. The study was performed according to the regulations of the local ethical committee (application number 02/063).

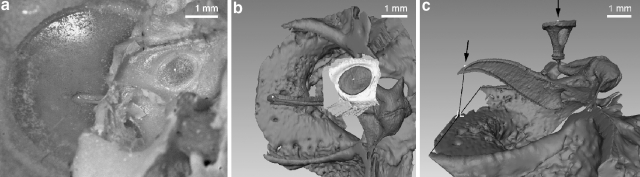
The temporal bone was removed from the skull and the ME cavity was opened so that a free view on the malleus is obtained from the medial side. The cochlea was carefully removed in such a way that the bone around the oval window and the attachment of the tensor tympani muscle was kept perfectly intact. By removing the cochlea, we obtain a free view on the stapes footplate and we can measure the pure mechanical response of the ME ossicles without fluid pressure effects of the cochlea. Figure 1a shows a photograph of the prepared specimen. To perform the measurement, the specimen was turned and tilted so that either the plane of the stapes footplate or the plane of the annulus of the TM was at right angles with the measuring direction.

Fig. 1.

(a) Prepared specimen as seen under the operation microscope. The specular reflection from the glass beads saturates the camera. (b) View on a 3-D partial reconstruction from an x-ray CT scan of the same specimen. Glass beads absorb x-rays well, so they are clearly seen in CT slices and their position can be exactly reconstructed in the model. Petrous bone has been partly reconstructed (shown in white) so the location of the stapes footplate in the bone is seen. (c) Side view on the same model. Arrows indicate the direction in which ossicle displacements were measured: for the umbo, at right angles with the annulus of the TM; for the stapes, at right angels with the plane of the footplate.

In previous work on eardrum elasticity in gerbils (von Unge et al. 1993), we found that drying out of the specimen can cause artifacts: When the walls of the bulla and the medial side of the TM start to dry, eardrum and malleus mobility drop dramatically. Therefore, precautions were taken to prevent dehydration: During the whole surgical procedure, the specimen is kept under a stream of water-saturated air from an ultrasonic humidifier, and during the measurement the temporal bone is wrapped in moist paper, with only a small opening for viewing the ossicles open to the air. The surgical procedure took <20 min, and installation of the specimen in the setup and measuring both ossicles at all frequencies took <15 min; thus, all measurements were finished within about half an hour postmortem.

A plastic tube was glued to the bony part of the ear canal, and through this tube air pressure was applied to the eardrum. In all of the following, we will refer to pressure as the pressure difference between the ME side of the TM to the ear canal side. Therefore, pressure values are positive when the pressure at the ME side of the eardrum is higher than the pressure at the ear canal side (when negative pressures were applied to the tube).

Glass microbeads with a diameter of ∼25 μm were put on the tip of the malleus and on the footplate. In Figure 1a, the specular reflection of the beads is seen on the specimen. The beads adhere to the moist structures by natural adhesion and serve to obtain enough light reflectivity and to keep track of the exact measuring location. Figure 1b shows a partial reconstruction of a computed tomography (CT) scan we made of the same specimen. The petrous bone is partly reconstructed (shown in white in Fig. 1b) so that the location of the stapes foot plate in the bone can be seen as in the photograph of Figure 1a. In the model, we left out some bony structures so the position of the ossicles can be well seen. The glass beads absorb x-rays strongly so we can easily pinpoint their position in the CT slices and reconstruct them in the model. Figure 1b shows a view on the model from approximately the same angle as the direct photograph of Figure 1a. Figure 1c shows a side view of the model, where we have indicated with arrows the directions in which stapes and umbo motion was measured.

Displacement measurement

The motions of the beads are measured using a Polytec laser interferometer vibrometer (OFV353 sensor head and OFV 5000 controller), equipped with a digital high-resolution position decoder (Polytec DD-100). The Polytec vibrometer uses a 1 mW HeNe laser beam that is focused on the reflecting beads, and delivers a calibrated analog output signal that is proportional to the object position. The output signal is linear with position to a precision better than 0.25%; in the range of amplitudes we measured, the apparatus has a resolution of 160 nm. In all of the following, displacements are defined as positive when the bead moves away from the interferometer, thus when the malleus moves in lateral direction out of the ME and when the footplate moves in lateral direction out of the cochlea. The motion of the umbo was measured in the direction perpendicular to the TM annulus plane, the motion of the stapes was measured in the direction perpendicular to the plane of the footplate, as indicated by the arrows in Figure 1c. The position signal is relative to a chosen reference position, which is set by pushing the system reset button. As reference position, we chose the position the ossicle returns to at 0 Pa, after pressure has been increased to 2.5 kPa (−2.5 kPa in the tube at the ear canal side) with the pressure change rate used to perform the measurement. In Results, we will see that large hysteresis is observed, so the origin point of the curves is not uniquely defined. Therefore, the choice of a reference position is rather arbitrary, and we will describe the measurements without referring to a (0,0) reference point on the displacement versus pressure curves. To report on the magnitude of ossicle motion, we will give peak-to-peak values. The position of the ossicle and the pressure were simultaneously sampled at a rate of 1000 samples per second, and were stored in computer. We thus obtain input/output curves of ossicle displacement versus pressure at given pressure change rates. It is important to note that this is very different from classical acoustic input/output curves, where amplitude is given as function of frequency, at a given sound pressure.

Pressure generation

To apply pressure to the eardrum, we use a custom-made pressure generator. Two buffer vessels are respectively kept at constant positive and negative pressure. A solid-state pressure transducer measures the pressure in the ear canal tube, and an electronic feedback system controls two proportional valves to constantly adjust ear canal pressure to the value set by an analog input signal. After calibration, the system keeps pressure at the desired value to a precision better than 20 Pa. For pressure changes up to frequencies of 150 mHz, the system is nearly perfectly linear. It should be noted that we did not vary pressure in a sinusoidal way, but that we are using a triangular-shaped input signal. In that way, we measure the response as a function of pressure to a constant pressure change rate. Using linear pressure changes corresponds to the constant pumping speed used in tympanometry, but test experiments showed us that a sinusoidal pressure change delivers nearly identical results.

Preliminary experiments showed that the important part of the motions occurred in a pressure range between −2.5 and +2.5 kPa. In all of the following, we will denote pressure variation in a range from −2.5 to +2.5 kPa as ±2.5 kPa. For the final experiments, we decided to use ±2.5 kPa (5 kPa peak to peak) and pressure change rates from 200 Pa/s to 1.5 kPa/s. A 200 Pa/s pressure change rate corresponds to a frequency of 20 mHz of the triangular pressure control signal because in a full period of 50 s, pressure decreases from 2.5 to −2.5 kPa and back again; thus, in a half period of 25 s, pressure changes between −2.5 and +2.5 kPa, or 5 kPa/25 s. We performed measurements at 200 Pa/s (corresponding to 20 mHz and ±2.5 kPa for the triangular wave), 300 Pa/s (30 mHz, ±2.5 kPa), 500 Pa/s (50 mHz, ±2.5 kPa), 1 kPa/s (100 mHz, ±2.5 kPa), and 1.5 kPa/s (150 mHz, ±2.5 kPa).

Ten rabbits were used in preliminary experiments (which are not part of this report) to determine the most relevant pressure and frequency ranges. The linearity of our pressure generation system is limited to about 150 mHz; at frequencies lower than 20 mHz, specimen stability becomes a problem.

Results

Repeatability over time and postmortem changes

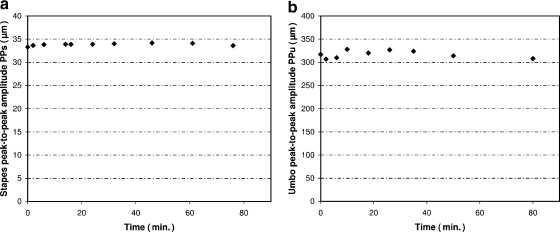
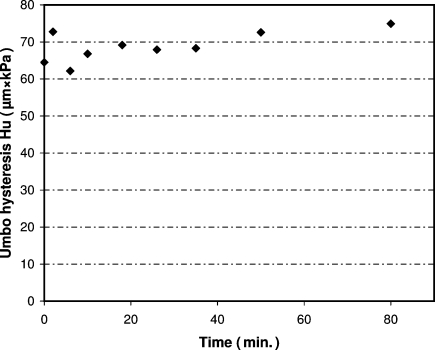
As explained before, all measurements on each specimen were obtained within half an hour postmortem. To control for repeatability, we measured the motion of the stapes and of the umbo at 1 kPa/s over an extended period of time. Figure 2a shows stapes peak-to-peak amplitude (PPs) as a function of time over a period of >1 h. We see that stapes amplitude stays perfectly constant. Figure 2b shows the same measurement for umbo peak-to-peak motion: Here, also, no significant changes are seen. At 1 kPa/s, stapes motion showed no measurable hysteresis, and this remained so for >1 h. Figure 3 shows umbo hysteresis (calculated as the surface area enclosed by the position versus pressure curve) as a function of measuring time. Small variations in the curve cause a little variability on calculated hysteresis values, but once again there are no significant systematic changes with measuring time. These measurements show that repeatability is very good and that postmortem artifacts are minimal in the 15-min time span needed for the entire measurement protocol.

Fig. 2.

(a) Stapes peak-to-peak amplitude (PPs) at pressure change rate of 1 kPa/s and ±2.5 kPa pressure amplitude as a function of measuring time: Even after >1 hour, no changes occur. (b) Umbo peak-to-peak amplitude (PPu) at 1 kPa/s and ±2.5 kPa as a function of measuring time: Over >1 hour, no systematic changes are seen.

Fig. 3.

Umbo motion hysteresis (Hu) at 1 kPa/s over a pressure range of ±2.5 kPa as a function of measuring time: Over a period of >1 hour, no significant changes are seen.

Displacement versus pressure curves

As we may be dealing with viscoelastic material, repeated measurements of the same displacement versus pressure curves may differ. To obtain stable results, we cycled through each given frequency three times before performing the actual measurement to obtain stable preconditioning. The changes during the preconditioning were, however, minimal, and repeated curves nearly coincided. Only at the lowest frequencies, there were sometimes limited differences between subsequent cycles.

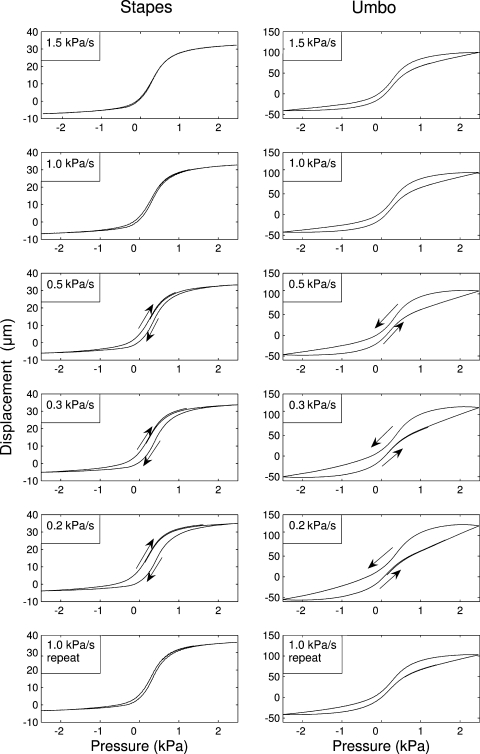
Figure 4 shows typical measurement results of displacement as a function of pressure for the stapes and for the umbo, respectively. All data presented in this figure were obtained in a single ear. Note that the scale used for umbo displacement (right column in Fig. 4) is four times larger than the scale used for the stapes. The curves are not averages, but raw data obtained in single pressure cycles. The only processing used was a 50-point median filter to remove electronic noise from the vibrometer and pressure transducer (as mentioned, recordings were made at a sampling rate of 1000/s). Comparable results were obtained in six animals. In all animals, we inspected the motion of the PF and PT before measurements by looking with the operation microscope into the space between the malleus head and the overhanging bone. In two animals in the group of nine, the PF was so soft that it ballooned inward so much during underpressures that it touched the malleus head and even the stapes. We did not quantify the possible effect of this touching, but this counterpressure on the malleus head may impede its normal motion so we decided to discard these ears from the start. These ears were not used for this study. In one animal, a strange jump occurred in the displacement curves. We were not able to trace the cause of this anomaly and did not use the ear for further measurements.

Fig. 4.

Stapes displacement (left column) and umbo displacement (right column) as a function of pressure at different ultra-low frequencies obtained in one ear. Displacement is given in micrometer, and the scale for umbo displacement is four times larger than the scale of stapes displacement. Stapes motion is extremely nonlinear and shows no hysteresis at 1.5 kPa/s. Hysteresis increases with decreasing pressure change rate, and the sense of rotation of the hysteresis loop is inversed, as indicated by the arrows. Umbo motion is also nonlinear and shows hysteresis at 1.5 kPa/s. Hysteresis increases as pressure change rate decreases. The bottom row shows repeat measurement at 1 kPa/s, after completion of all other measurements: Curves are identical to those obtained in the first measurement (second row).

From Figure 4, we see that stapes motion is extremely nonlinear and nearly looks like a step function: The peak-to-peak amplitude at ±2.5 kPa is 39.46 μm, and 90% of that maximal value is already reached at a pressure of 1 kPa; for pressures beyond 1 kPa, the stapes only moves a few more micrometers. The curves also demonstrate the extremely high precision of these measurements: The use of a very sturdy specimen mount and a well-stabilized pressure generator allows us to measure the ossicle motion with a precision better than 1 μm. At 1.5 kPa/s, the stapes motion shows extremely little hysteresis. As pressure change rate decreases, peak-to-peak amplitude remains practically unchanged, but hysteresis increases. In the right column of Figure 4, we see that the umbo motion is also strongly nonlinear, but not as much as the stapes: At 1 kPa, about 80% of the maximal amplitude at 2.5 kPa is reached. The umbo peak-to-peak amplitude (PPu) is 141.25 μm at 2.5 kPa, which is 3.57 times larger than the stapes amplitude. The curve shows large hysteresis already at 1.5 kPa/s, and hysteresis strongly increases with decreasing pressure change rate: At 200 Pa/s, hysteresis, seen as the surface area enclosed by the curve, is more than doubled compared with the 1.5 kPa/s curve. In six animals, curves with the same main features were obtained. Finally, we remark a peculiarity in the umbo position curves: For pressures beyond ±2 kPa, the position of the umbo decreases a little bit. Observation through the stereomicroscope showed that at these high pressures, a wrinkle appears in the membrane around the umbo. Once this wrinkle is present, the manubrium moves back a little bit, whereas the membrane itself is pushed further outward or inward. The effect is, however, very small.

Repeatability

In all ears, we repeated the 1 kPa/s cycle after making the recordings at the other pressure change rates. Within the standard deviation, all measured parameters remained the same between the first and the repeated measurement when averaged over the six animals.

The frames at the bottom of Figure 4 show the result for the stapes and the umbo. If we compare these to the first recording at 1 kPa/s (second row in Fig. 4), we see that the curves are practically identical. For the stapes as well as for the umbo, peak-to-peak amplitude is the same as in the first recording (second frame in Fig. 4) and the hysteresis is also practically unchanged. This very good repeatability emphasizes once again that the changes we find with decreasing pressure change rate are only a result of different change rate and are not caused by measuring time or increasing postmortem artifact.

Interanimal variation: peak-to-peak amplitude

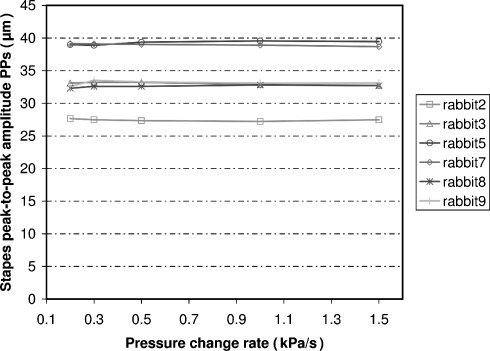
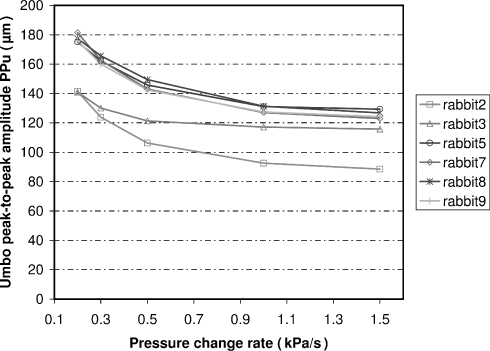
Figure 5 shows PPs as a function of pressure change rate in six animals, Figure 6 shows the result for the umbo (PPu). In all animals, PPs remains constant at all pressure change rates, with a value of 34 ± 5 μm (mean ± S.D., n = 6). PPu is nearly the same at 1.5 and 1 kPa/s (118 ± 15 μm at 1.5 kPa/s; 121 ± 15 μm at 1 kPa/s, n = 6). At lower pressure change rates, PPu increases a bit (165 ± 19 μm at 200 Pa/s, n = 6). In animal number 2, PPu at 1 and 1.5 kPa/s is a bit lower than in the other animals, but it increases relatively more with decreasing pressure change rate than the others. At 1.5 Pa/s, the average ratio of PPs/PPu is (0.29 ± 0.02, n = 6); at 200 Pa/s, this ratio decreases to (0.21 ± 0.02, n = 6).

Fig. 5.

Stapes peak-to-peak displacement amplitude PPs as a function of pressure change rate, measured in six animals. For each animal, amplitude remains constant for all pressure change rates.

Fig. 6.

Umbo peak-to-peak amplitude PPu as a function of pressure change rate, measured in six animals: Amplitude increases slightly from 1.5 to 1 kPa/s, and increases more strongly at lower pressure change rates.

Interanimal variation: hysteresis

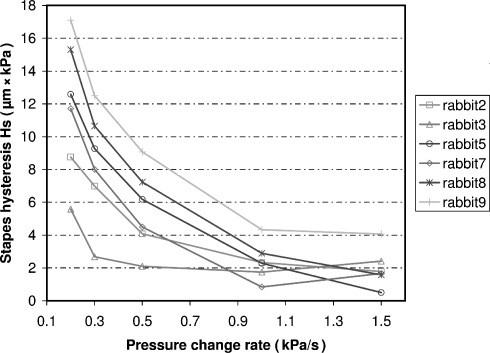
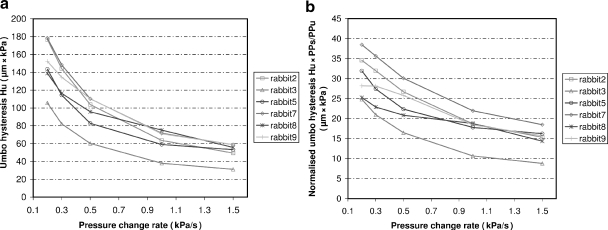
Figure 7 shows hysteresis in the stapes motion (Hs) as a function of pressure change rate. Hs was calculated as the area enclosed by the position–pressure curve, and hence is given in μm kPa. Between pressure change rates 1.5 and 1 kPa/s, hysteresis is extremely small and changes little. At lower pressure change rates, hysteresis rises strongly from 2.0 ± 1.2 μm kPa (n = 6) at 1.5 kPa/s to 12 ± 4 μm kPa (n = 6) at 200 Pa/s. As PPs remains the same at all frequencies, changes in Hs are only caused by increasing energy loss, not by amplitude changes. Because umbo motions are much larger than stapes motions, the area enclosed in the position versus pressure curves will scale accordingly, and it will also grow when umbo amplitude increases. Hysteresis of umbo motion (Hu) is shown in Figure 8a. Between the first 1 kPa/s run and the repeated run, which was recorded after all the other pressure change rates, no significant difference was found for the stapes hysteresis: 2.4 ± 1.2 μm kPa (n = 6) and 2.5 ± 1.8 μm kPa (n = 6). For the umbo, there was a slight decrease and a bit more variability in the repeated run compared with the first run, 63 ± 14 μm kPa (n = 6) and 51 ± 20 μm kPa (n = 6), respectively. Still, this small change is within the standard deviation and far smaller than the differences induced by different pressure change rates.

Fig. 7.

Stapes hysteresis Hs as a function of pressure change rate measured in six animals. Hysteresis is practically absent between 1.5 and 1 kPa/s, but increases strongly at the lower pressure change rates.

Fig. 8.

(a) Umbo hysteresis Hu as a function of pressure change rate, measured in six animals. Hysteresis increases constantly as pressure change rate decreases. (b) Normalized umbo hysteresis, measured in six animals: Umbo hysteresis Hu is multiplied by the ratio of stapes peak-to-peak amplitude over umbo peak-to-peak amplitude PPs/PPu at each pressure change rate to make values independent of changing amplitude and to compare umbo to stapes at the same value of displacement. Also, normalized hysteresis increases constantly as pressure change rate decreases.

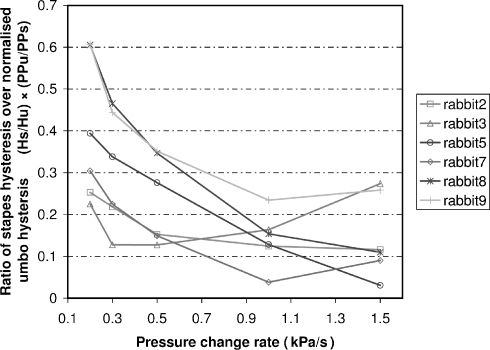
To be able to compare hysteresis of umbo and stapes, and to scale Hu for changing amplitude, we normalize umbo hysteresis by multiplying Hu with PPs/PPu: Figure 8b shows Hu.PPs/PPu as a function of pressure change rate. At 1.5 kPa/s, nonnormalized umbo hysteresis (Fig. 8a) is 51 ± 10 μm kPa (n = 6) and it gradually increases, as pressure change rate decreases, to obtain a value of 149 ± 27 μm kPa (n = 6) at 200 Pa/s. Normalized umbo hysteresis (Fig. 8b) increases from 15 ± 3 μm kPa (n = 6) at 1.5 kPa/s to 30 ± 5 μm kPa (n = 6) at 200 Pa/s. To compare stapes hysteresis to normalized umbo hysteresis, we have plotted their ratio, Hs/(Hu.PPs/PPu), as a function of pressure change rate in Figure 9. Because of the combination of measurement errors in the computed ratios, the inter-ear variability increases, but, nevertheless, we can see that stapes hysteresis grows faster than normalized umbo hysteresis as pressure change rate decreases, especially at the lowest frequencies of 300 and 200 Pa/s. At 1.5 kPa/s, Hs is 13.5% of normalized umbo hysteresis, whereas at 20 mPa/s, Hs is 38.8% of Hu.PPs/PPu.

Fig. 9.

Ratio of stapes hysteresis Hs over normalized umbo hysteresis Hu.PPs/PPu, measured in six animals: As errors accumulate due to calculations, measuring points show more variability, but it is clear that stapes hysteresis increases more rapidly than umbo hysteresis for pressure change rates <1 kPa/s.

To be more explicit, hysteresis is directly related to the energy dissipated per cycle and we can rewrite m Pa as J/m². If the TM were a uniformly moving plate, one could multiply with the hysteresis observed at the umbo with the area of the TM to obtain the energy dissipated in Joules. For the stapes, the relationship between pressure applied to the TM and the force present on the stapes is less straightforward. On our specimens, we measured the projected PT surface area and found 25.7 mm², which is comparable with the value of 28.2 given in literature Hemilä et al. (1995). In the approximation that the PT moves as a uniform plate, multiplication with umbo movement gives a value of 1.3 μJ of dissipated energy per movement cycle at a pressure change rate of 1.5 kPa/s and 3.8 μJ at 200 Pa/s.

Sense of rotation of the hysteresis loop

From the motion curves like the ones presented in Figure 4, we see that both for increasing and decreasing pressures, ossicle motion is of course in phase with pressure change. At first glance, we also expected that during decreasing ME pressure, ossicle position will be a bit more lateral than at the same pressure value during increasing pressure: In normal hysteresis curves for viscoelastic materials, the motion lags behind the applied force, so the up-going curve lies below the down-going curve. For the motion of the umbo, this is indeed the case, but closer inspection of the exact ordering of the measurement points drew our attention to a very peculiar aspect of stapes hysteresis: In all of the rabbits, we found that stapes motion runs ahead of pressure instead of lagging behind. In Figure 4, we indicated with arrows the course of the curves: When pressure decreases, umbo position is more lateral than at corresponding pressures in the increasing part of the curve, but stapes position is more medial during pressure decrease than during pressure increase. This phenomenon was found at all frequencies in all ears.

Discussion

Umbo displacement

The measurement of quasi-static displacements with high resolution poses stringent long-term stability requirements. By careful design of the measurement setup, combined with automated continuous pressure cycling, we managed to measure displacements with submicrometer accuracy down to pressure change rates of 200 Pa/s (2.5 kPa amplitude at 20 mHz).

Quantitative data on eardrum and ossicle displacements caused by static pressure are sparse. Using moiré topography in four gerbils, we measured eardrum displacements near the umbo as a function of pressure (Dirckx and Decraemer 2001). Because these measurements were made on the medial side of the TM, the sharp ridge running underneath the manubrium did not allow to obtain moiré data on the umbo itself. At best, we can compare the present data to measurements obtained on the eardrum in a zone near the umbo. In our 2001 article, we showed for the first time full pressure cycle curves of eardrum displacement at different stages of dissection and found that eardrum displacement remained the same before and after removing the cochlea, so we can compare our measurements of umbo displacements to results obtained with intact MEs. Our moiré technique was also used by Ladak et al. (2004) in cats. The cat TM movement was measured from the lateral side, and umbo displacements of 156, 181, and 226 μm at +2.2 kPa were reported. Because negative pressures cause somewhat smaller displacements, peak-to-peak amplitude will be a bit less than twice these values. In both articles, hysteresis was observed, but it was not quantified. From the graphs (Ladak et al. 2004, Fig. 6; Dirckx and Decraemer 2001, Figs. 8–11), one can, however, see that the eardrum hysteresis was considerably smaller than the hysteresis we observed now (Fig. 4). The moiré technique offers a resolution of, at the best, 10 μm. In all of these measurements, several seconds elapsed between each subsequent pressure step, and the moiré measurement itself also takes several seconds, so pressure variation from 0 to 2 kPa took at least several minutes. In our 2001 article, we reported a duration of 7 min to obtain measurements in one pressure cycle (Dirckx and Decraemer 2001, p. 128), Ladak et al. (2004, p. 3010) reported 1.25 h to perform measurements in three subsequent cycles. For pressures varying between 2.5 and −2.5 kPa, we found PPu of 118 ± 15 μm at 1.5 kPa/s, increasing slightly to 165 ± 19 μm at 200 Pa/s. Compared with the peak-to-peak values found by Ladak et al. in cat, which are of the order of 300 to 600 μm, these values are much smaller. Of course, both results were obtained in different animal models, but eardrum sizes are comparable, although the cat eardrum is narrower than in rabbit: The annulus of the rabbit eardrum resembles the shape in humans more. A possible major reason for the difference may be that we increase pressure gradually from 0 to 2.5 kPa in seconds, whereas in the moiré measurements the pressure increase was stepwise, with several minutes of time interval between steps.

Hüttenbrink (1989) reported a mean value (n = 6) of umbo peak-to-peak amplitude in human temporal bones: 475 μm when pressure is changed from +2 to −2 kPa, and 610 μm when pressure varied between +3 and −3 kPa. These measurements were made on temporal bones using a surgical microscope, which, according to the author, offers a resolution of 2 μm. Each pressure value was maintained over several minutes while the measurement was performed. In his work, no closed pressure cycles were used, and, therefore, no hysteresis data are available. Using moiré interferometry in a human temporal bone study, we found an umbo peak-to-peak displacement of 375 μm in a pressure range of ±0.8 kPa. The human eardrum is larger than rabbit eardrum, and once again both Hüttenbrink's and our moiré measurements were obtained in the fully static regime. If we interpolate between values obtained at 2 and 3 kPa, Hüttenbrink found about 540 μm peak-to-peak umbo amplitude at 2.5 kPa for human ears, whereas for the rabbit we found 165 μm, which is a factor of 3.2 less. Once again, the TM is a bit larger in human than in rabbit, and the pressure sequence used in both experiments is different, but also the motion mechanism of the ossicles may be different as we will discuss below. For acoustic frequencies below 1 kHz, Rosowski (1995) calculated values of acoustic stiffness of the eardrum and ossicles on the basis of acoustic stiffness measurements of total ME and ME air space, and found 500 Pa/mm³ in rabbit and 170 Pa/mm³ in human. Thus, in the low-frequency acoustic range, the rabbit ear is a factor of 2.9 stiffer than the human, which approximately corresponds to the factor of 3.2 now observed in the static regime.

Stapes displacement and the incudomallear lever ratio

As far as we know, the only available quantitative data on stapes static pressure–induced motion were measured by Huttenbrink in his human temporal bone study, again at given static pressure values and with the cochlea attached. From his tables, we can read that in the direction perpendicular to the footplate, he found a mean (n = 6) stapes peak-to-peak amplitude of 34 μm when pressure varies between −2 and +2 kPa, and 30 μm for pressure variation between −3 and +3 kPa, a difference that is close to the measuring accuracy. We found a value of 34 ± 4 μm (n = 6) for PPs in the ±2.5 kPa pressure range, and the value is independent of pressure change rate. Using the values given by Hüttenbrink for 2 kPa, the ratio of stapes to umbo motion in human is 0.07. At 1.5 kPa/s, we found a ratio of 0.29 ± 0.02 (n = 6) at 200 Pa/s; this ratio decreases to 0.21 ± 0.02 (n = 6), which is still the threefold of the value reported in human.

To interpret this difference, it is of course important to note that significant differences exist between morphology of the human and rabbit ME. On the basis of data from literature (Hemilä et al. 1995), the ratio of the incus lever length and the manubrium lever length is 0.71 in human and 0.4 in rabbit. Between mammal species, the lever ratio varies only moderately, between 0.28 and 0.83 (Henson 1974). The lever length is defined as the distance from the tip of manubrium and of the tip of the long process of the incus to the so-called axis of rotation of the incudomallear (I–M) complex. In rabbit, we found a ratio of stapes over umbo motion in the order of 0.2–0.3, which is a bit smaller than the lever ratio of 0.4. As will be explained below (section Sense of rotation of the hysteresis loop), a gap develops within the incudo–stapedial (I–S) joint at overpressures, which at least can partly account for the difference between lever ratio and amplitude ration in rabbit. In human, however, the lever ratio of 0.7 is a factor of 10 larger than the displacement ratio of 0.07 measured by Hüttenbrink. In our moiré study, we found that, at least in the static regime, the concept of a single fixed rotation axis is not valid in human: From full-field displacement measurements on the manubrium, we found that 125 μm of the total umbo displacement can be accounted by malleus rotation around an axis located within the I–M joint, but superimposed on this motion there is a pure translation of the malleus of 232 μm; thus, only about one third of umbo motion is involved in a lever action. On the other hand, this still does not account for a factor of 10. A possible other mechanism involved in human could be attributed to slippage in the I–M joint. Besides, our present measurements were obtained in extremely fresh material, whereas human measurements were performed many hours postmortem.

Another prominent morphologic difference between the human and rabbit ossicle structure is the anterior process of the malleus. In human, it is only a small nub of bone to which the anterior ligament of the malleus is attached, whereas in the rabbit it is a bony structure closely connected to the tympanic bone (Rosowski 1995). This much more rigid connection can be a cause of the higher stiffness of the ossicular chain in rabbit. As to the I–S joint, Funnell et al. (2005) reported that, in cat, the ossicles are closely coupled together by a fibrous capsule around the joint. Also, in human, this thick fibrous capsule is seen around the I–S joint, whereas in rabbit we observed that the ossicles are very loosely coupled and may even separate at ME overpressures. Whether there is slippage in the I–M joint, we cannot decide from the present measurements. We have performed a few full 3-D measurements of ossicle motion using x-ray CT, and from these measurements it seems that slippage in the I–M joint is minimal in the rabbit; however, results are on the edge of the resolution of the technique. More high-resolution interferometric measurements will be necessary to determine the 3-D motions of the separate ossicles. The absence of slippage could explain the existence of an additional protective mechanism formed by the separation of the I–S joint in the rabbit.

Finally, we should note that we performed measurements without the fluid load of the cochlea on the stapes footplate. In the present work, we wanted to measure simultaneously umbo and stapes movement caused by pressure in the ear canal and we decided to investigate first the transfer function of the ossicles only, so the cochlea was removed. It can be expected, however, that for quasi-static displacements, the presence of the cochlear fluid will not considerably impede the motion of the stapes due to the high static compliance of the round window. The impedance of the cochlea becomes important at acoustic frequencies; however, for quasi-static pressure variations, little effect is to be expected. Clearly, more measurements will be useful here, and it would be interesting to remeasure the ratios of umbo and stapes movement in humans on fresh material or living subjects to verify if the small stapes motions that were previously reported are indeed correct.

Motion asymmetry

As explained before, the choice of a reference position for positive and negative motions is somewhat arbitrary because of the presence of hysteresis. As zero position, we choose the position the ossicles take at 0 Pa after the application of −2 kPa. Relative to this reference position, one can calculate the amplitude at overpressure and underpressure separately. From Figure 4, we can already see that amplitudes at ME overpressures are always significantly larger than amplitudes at equal ME underpressures. When choosing the position after application of negative pressure as a reference, the effect is a little bit overestimated for the umbo and a bit underestimated for the stapes (as for the stapes, the increasing pressure curve lies above the decreasing curve). The position difference between the two points of pressure–zero crossing is, however, small compared with the maximal amplitudes, so the effect of overestimation and underestimation due to hysteresis is rather moderate when calculating the ratio of maximal overpressure and underpressure amplitudes. We calculated the ratio of maximal amplitudes at +2.5 and −2.5 kPa at all pressure change rates and found no systematic changes in function of pressure change rate. Averaged over all ears and all pressure change rates, the ratio is 2.6 ± 0.8 for the stapes motion and 1.6 ± 0.2 for the umbo motion.

Lee and Rosowski (2001) measured sound-induced umbo velocity in live gerbils at different levels of static pressure in the ±3 kPa range. When pressure deviated from zero, the umbo velocity was reduced, and at all measured acoustic frequencies the reduction of velocity magnitude at large ME underpressure was always greater than at large overpressure. The authors also observed dependence on the direction of pressure change. From our data, we see that ME overpressures make the umbo move more than equal underpressures. Earlier, we observed the same effect in human (Dirckx and Decraemer 1991) and gerbil (Dirckx and Decraemer 2001), and we attribute it at least partially to the conical shape of the TM: Due to this shape, the TM can easily balloon at overpressure but is stretched at underpressure. In gerbil, Lee and Rosowski (2001) observed a factor of 10 difference between acoustic velocities measured with large static underpressures and overpressures. In combination with the present results of quasi-static umbo displacement, one tends to conclude that the smaller inward motion at negative pressure is indeed accompanied by a greater stiffening of the system than the larger outward motion.

Hysteresis

We found that hysteresis in umbo displacement is much more pronounced than in stapes displacement. Even at the slowest pressure change rates, stapes hysteresis is still <40% of normalized umbo hysteresis (Fig. 8b). At faster pressure changes (2.5 kPa amplitude at 150 mHz, or 1.5 kPa/s), stapes hysteresis nearly disappears. From this result, we draw two conclusions. On the one hand, the absence of hysteresis at higher pressure change rates indicates that damping and viscous effects in the stapedial annular ligament is negligible. On the other hand, this result indicates that stapes hysteresis is not a simple mimic of malleus hysteresis, but that a complex mechanical transfer of motion is involved.

In previous work on effects of otitis media on ME mechanics, it was shown that diseased ears in which the TM becomes more compliant show increasing hysteresis (Gaihede et al. 1997). As a function of pressure change rate, our data show the opposite relationship: As rate decreases, both umbo motion and hysteresis increase. Apparently, different mechanisms are involved. In the diseased ear, the viscoelastic parameters of the TM may be changing, whereas, in our work, we are looking at the transition between moving and nearly static ossicles.

Umbo hysteresis increases as pressure change rate or frequency of the triangular wave decreases. This is in clear contradiction with the notion that the main cause of such hysteresis would be the viscoelastic properties of the eardrum and the mallear ligaments: In a pure viscoelastic system, hysteresis should increase with increasing frequency and disappear as the static regime is approached. Our measurements show that a very different process is governing the system at the lowest pressure change rates. A possible explanation is friction between the ossicles and the ME walls and within the ossicle joints. As the coefficient of static friction will be higher than the coefficient of dynamic friction, static friction effects take over as pressure change rate decreases. This effect will not be seen when pressure is increased in steps to reach a certain value.

From volume displacement measurements of human TMs in living subjects, Gaihede (1999) measured a hysteresis of about 20 μJ. The volume displacements he applied corresponded to a peak-to-peak pressure change of approximately 3.5 kPa over a 3.5-s time period, so to a pressure change rate of 1 kPa/s. As the value was determined from overall volume displacements, it includes the contribution to hysteresis of the PT as well as of the PF. From our results, we found an umbo hysteresis of 63 mJ/m². The projected surface area of the PT in our rabbit specimens was 25.7 mm², which leads to a PT hysteresis of 1.6 μJ if the membrane would move like a uniform plate. This is of course only a very crude approximation, because, at the edges, the membrane does not move at all. To calculate actual hysteresis, full field displacement data would be needed, but if we regard the deformation as a cone being formed, the mean surface displacement would be about one third of the displacement at the center, which results in a PT hysteresis of 0.53 μJ. The projected surface area of the human TM is about 60 mm², which is a factor of 2.3 larger than the rabbit, but the hysteresis values determined by Gaihede are a factor of 37 larger than the ones we found. When we scale for the 2.3 difference in surface area, the human global TM hysteresis is 16 times larger than the rabbit umbo hysteresis. An important part of this difference may be attributed to the inclusion of the PF contribution in the human measurements. In any case, the present measurements show that PT hysteresis in rabbit is much smaller than the one previously reported in human, and only little of the energy due to static pressure–induced motion is dissipated within the TM and the joints.

We found that hysteresis decreases as pressure change rate increases, but the curves do not go to zero but rather tend to flatten and seem to converge to a certain nonzero value at higher pressure change rates. This can be a consequence of the viscoelastic properties of the membrane and the joints: We therefore think that in the quasi-static regime, friction effects are important, but that for acoustic frequencies viscoelasticity may be the remaining factor. ME models that describe both dynamic and static ME behavior will need to incorporate both effects. We are currently undertaking experiments to bridge the gap between quasi-static and acoustic measurements.

Sense of rotation of the hysteresis loop

The sense inversion of the stapes hysteresis loop came as a surprise and is a rather puzzling phenomenon. Observation of the I–S joint with the operation microscope showed that as the umbo moves laterally, the I–S joint remains closed at first and the stapes head follows the movement of the lenticular process. For pressures beyond +1 kPa, a gap develops in the I–S joint. Stapes and incus do not separate, they keep connected together at a small distance by fibers and the gap between the stapes head and the capsule is filled with fluid. When the pressure is released, the stapes immediately starts to move inward into the cochlea, the gap in the I–S joint remains and only in the negative part of the pressure cycle the gap between both ossicles closes again. At the start of the next pressure increase, the ossicles are again closely coupled. This way, the stapes is pulled to a more lateral position during pressure increase than during pressure decrease at the same pressure value, and motion seems to lead pressure rather than lag behind like in normal hysteresis behavior. As the magnitude of stapes hysteresis increases with slower pressure changes and has inversed phase on top of that, viscoelasticity can certainly not be its major cause. Adhesion between the ossicles appears to play an essential role in this process. It should be noted that this behavior may be specific for rabbit and maybe other animals such as the gerbil, but that it may not be representative for humans where the I–S joint is constructed in a much different way, with a much thicker cuff of strong fibers closely connecting both ossicles all around the I–S joint.

Relation to results from tympanometry

In older work on tympanometry, there was much debate on the effect of pumping speed, which causes a separation between the peaks obtained during the increasing and decreasing part of the pressure cycle. Much of the difference could be attributed to phase lag in the instruments. In a recent article using a modern high-speed tympanometer (Therkildsen and Gaihede 2005), no significant effect of pumping speed was found. In previous work, pressure differences of 500 Pa (Shanks and Wilson 1986) and 350 Pa (Kobayashi et al. 1987) were seen between the tympanographic peaks recorded for increasing and decreasing pressure, using pumping speeds of 700 Pa/s (Shanks and Wilson 1986) and 500 Pa/s (Kobayashi et al. 1987). Gaihede used pumping speeds going from 500 to 4000 Pa/s, and found no significant changes: Pressure difference between peaks remained constant at about 120 Pa. This finding concurs largely with our results in rabbit: For pressure change rates of 1 and 1.5 kPa/s, stapes hysteresis remains unchanged and umbo hysteresis changes little. At 500 Pa/s, we find some increase in both stapes and umbo hysteresis. At the lowest rates (300 and 200 Pa/s), stapes hysteresis increases dramatically. This may mean that tympanography with low pumping speeds could reveal information about static friction effects in the ossicles, and that increasing distance between positive and negative tympanographic peaks with decreasing pumping speed could contain clinically relevant information.

Conclusions

We performed high-resolution measurements of stapes and umbo displacements caused by increasing and decreasing pressure at different pressure change rates, and determined the quasi-static pressure transfer function of the ME. PPs is independent of pressure change rate and does not show hysteresis for pressure change rates faster than 1 kPa/s. We conclude that the annular ligament possesses little viscoelastic properties. Stapes motion is limited to pressures of about ±1 kPa; for pressures beyond ±1 kPa, stapes position remains practically constant. Stapes motion and hysteresis are not just a lever ratio transformed mimic of umbo behavior, but are caused by very complex changes in ossicle joints and ossicle position.

Umbo displacement amplitude increases with decreasing pressure change rate. Umbo hysteresis is present at 1.5 kPa/s, which may result from the viscoelastic properties of the eardrum and the ossicle joints. Umbo hysteresis, however, increases strongly as pressure change rate decreases, also after normalizing for increasing umbo displacement amplitude. This finding is in direct contradiction with the notion that umbo and eardrum motion under static pressure is mainly governed by viscoelastic properties, in which case hysteresis should diminish at slower pressure change rates. We conclude that viscoelasticity is not the main source of the hysteresis at the lowest pressure change rates, and we put forward the hypothesis that static and dynamic friction in the joints play an important role as the static pressure situation is being approached. It will be essential to take this result into account and to incorporate speed-dependent friction coefficients to obtain realistic models of large quasi-static ossicle motions.

The changes in ossicle motion with decreasing pressure change rate may be related to the changes of difference between peak location during increasing and decreasing pressure cycles, observed in tympanometry at different pressure change rates. If the observed behavior is indeed caused by increasing friction, tympanometric measurements and measurements of ossicle motion at different pumping speeds could contain clinically relevant information.

In future work, we will investigate the effect of the cochlea on these quasi-static ossicle motions, and we are currently improving our pressure generation system so we can bridge the gap from the quasi-static regime to (ultra)low-frequency sound.