Like Buridan's Ass—and somewhat ironically—we often feel frustrated if given more choice than expected. Yet, the converse appears to be true as well. Frustration that results from the impossibility of satisfying all competing interests simultaneously itself implies a greater diversity of distinct behaviors for the overall system. Nature seems to use just this unsettling device of built-in conflict to ensure adaptability and functionality at many levels of organization, ranging from the molecular scale, as in protein-conformational dynamics, to the macroscopic scale, as in socioeconomic processes. Identification and quantitative characterization of the precise sources of frustration is key to understanding the workings of existing systems and the ability to design new, useful systems. This task, however, is difficult for two reasons: (i) direct computational studies of systems with many states are almost always costly and often are simply out of reach for today's computer technology, and (ii) once the calculation is done, even bookkeeping and grouping states are usually unobvious, again because the states are so many. In this issue of PNAS, Materese et al. (1) accomplish both tasks for the native state dynamics of a small protein, eglin c, which inhibits serine protease. By identifying the key conflicts between different physical interactions, they move us toward the goal of designing proteins that are not just sculptures but can also function.
The effectiveness of eglin c literally hinges on the flexibility of its extended loop portion, which must conform to the variability of the target. What are the precise sources of frustration that ensure the loop will always have enough configurations to choose from? How can we ensure that no essential states have been overlooked, in the first place? We learn from the free-energy landscape methodology (2, 3) that a controlled classification of protein conformations, whose number is vast even in the native state, is possible because the states are organized into a multitier hierarchy, much like the hierarchy of employees in a large corporation. The hierarchy is temporal (4). Suppose the duration of our experiment is τ; in this time a system will have a chance to overcome a barrier at most kBT ln(τ/τ0), where τ0 is the Arrhenius prefactor of the order a picosecond. Conversely, this means that the protein was confined to a free-energy basin surrounded by a ridge of height kBT ln(τ/τ0). The total collection of these basins, for all possible time resolutions, comprises “the free energy landscape” of the protein. Such basins would correspond to subunits, at different levels of a large corporation, taking ever longer times to communicate, in the social analogy. The concept of the free-energy landscape is useful because it is simple: We only need a few, statistically defined parameters to characterize the landscape, rather than listing individually the astronomically large number of diverse protein conformations.
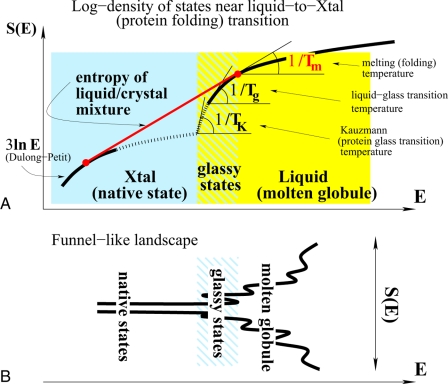
To illustrate the landscape idea, we may turn to a macroscopic system, namely a bulk liquid. A liquid will crystallize if cooled slowly, but will freeze into a glass if cooled sufficiently rapidly. The entirety of configurations of this macrosystem comprise two large blocks corresponding to fluid states, at high energies, and to a mechanically stable crystal, at low energies (see Fig. 1A). At the temperature Tm, equal to the inverse slope of the common tangent of the entropy of the two blocks, the system will be a mixture of liquid and crystal, if the experiment is done slowly. The liquid and crystalline component have energies εliq and εXtal per unit volume, respectively, whereas the total energy is related to the composition by the standard lever rule: E = εliqVliq + εXtalVXtal, where the total volume, V = Vliq + VXtal, generally changes somewhat during the transition. As crystallization proceeds, the total energy takes on all intermediate values between εliqV and εXtalV, yet the system actually never explores the states whose energy density is intermediate between εliq and εXtal, except perhaps in the interface regions, whose volume fraction is negligibly small for regular first-order transitions in macroscopic systems. Nonetheless, these intermediate states, of macroscopically uniform density, do indeed exist, as we can learn by cooling the liquid faster than the nucleation rate of the crystal phase; hereby, the system remains in the liquid set of states as if the crystal set did not even exist. It turns out the barriers for molecular motions in the fluid grow rapidly on supercooling below Tm—approximately inversely proportionally to the liquid entropy (5). When the typical relaxation time reaches a certain magnitude, at some temperature Tg < Tm (say, ≈100 sec for a typical experiment), we no longer have the time to wait for the liquid to equilibrate and say that the system is a “glass” at all temperatures below Tg, which is called the (laboratory) glass transition temperature. Clearly, Tg depends on the time scale of the experiment, as did the depth of the typical basin on the landscape; indeed, the glass transition is inherent in hierarchical free-energy surfaces. Now, because the viscosity is the greater the closer we are to Tg, we immediately conclude that systems whose Tm and Tg are close should be good glass formers, because crystalline nuclei have less chance to grow beyond the critical size the slower the transport at Tm. Conversely, when Tm is significantly higher than Tg, crystals easily form.
Fig. 1.
Illustration of the analogy between the free-energy landscapes for liquid and protein-conformational dynamics. (A) The log-number of states (i.e., entropy), as a function of energy, for two systems with similar free-energy landscapes. At liquid-to-crystal transition, the system increases its entropy by phase separation and follows the red line, while bypassing the structural states intermediate between the liquid and crystal states. Analogously, to fold, the protein must bypass glassy, trap states that are intermediate between the numerous, highly mobile molten globule states, and the native states. (B) A funnel-like landscape that reflects a scarcity of configurations between a set of numerous high-energy states, where transport is facile, and a unique low-energy, stable structure. It is essentially the entropy plot from A turned on its side.
If, however, equilibration of the supercooled liquid were not an issue, we could in principle continue to cool the system until it reached the lowest energy configuration that could be called amorphous. The corresponding temperature TK is dubbed the Kauzmann temperature. Whether such a well defined ideal state actually exists and what its precise molecular arrangement is are presently unknown, except that it must be aperiodic. Even if it is an unattainable extrapolation, like the absolute zero, TK is a useful concept because it is truly thermodynamic, that is, time-independent. In any case, Tg and TK are straightforwardly related through the measurable heat capacity jump at the laboratory glass transition and are usually close to each other.
Supercooled liquids exemplify a true frustration-induced landscape. Clearly, the system is frustrated. It does not satisfy all of its attractive interactions and remains a much higher energy state than the crystal. At the same time, the number of actually reachable liquid states, at the laboratory glass transition, is enormous relative to the crystal. Although the conformational dynamics of a protein is measured in ways quite distinct from transport in liquids, the thermodynamic, static aspects of the corresponding free-energy landscapes are quite similar (compare Fig. 1A). There are two blocks, the higher energy one corresponding to the molten globule states, resembling a liquid crystal, and the much smaller block of native states, where the atoms' positions are stationary and can be extracted by x-ray diffraction. The role of the melting temperature is now played by the folding temperature Tf, and the protein glass transition temperature Tgpr is the surrogate of the Kauzmann temperature. (The folding transition is not sharp, of course, because of finite-size effects.) In direct analogy with liquids, the greater the Tf/Tgpr ratio is, the more readily the protein will bypass its glassy states, implying more robust folding. These glassy states correspond to various “traps” or misfolded conformations. Numerically, the Tf/Tgpr ratio is ≈1.6 for good folders (2). Interestingly, the typical Tm/Tg ratio for good glass formers (which are analogs of bad folders) is only a bit lower—1.5—underscoring the rather different barriers manifest in the extended and finite, nanoscale systems. The combination of a relatively small set of low-energy conformations well separated from the liquid-like, molten globule states has been vividly described as a “funnel” landscape (2) (see Fig. 1B).
Note that the diagrams in Fig. 1 give the thermodynamic, long-time characteristics of the landscape, but do not actually depict it completely accurately because they cannot show the multidimensional barriers between states/basins. To map out the landscape, we must agree on an appropriate set of coordinates and graph the free energy of the protein as a function of these coordinates. Materese et al. (1) obtain the set of relevant coordinates for native state dynamics of eglin c via principle component analysis of an all-atom MD simulation. Only 11 lowest-frequency modes appear to show nontrivial dynamics between distinct free-energy minima by the time adequate statistics are gathered. Essentially, 211 states appear to be probed thermally. The rest of the modes exhibit a nearly Gaussian distribution indicating motion within featureless, that is, single minimum, free-energy basins. The presence of nontrivial native state dynamics represents a pleasant, and still quite rare, variation on the simplest theme from Fig. 1A, which oversimplifies by drawing a unique native state, for the lack of better knowledge. Now that we have a measure for the phase–space size, it will be interesting to test this estimate of the entropy of the native state of eglin c. Perhaps this could be done experimentally, similarly to studies of solvent-induced relaxation of myoglobin (6).
Materese et al. (1) identify the specific interactions whose competition causes the frustration by analyzing contacts formed/broken during transitions between distinct basins. They discover that several chemically distinct interactions participate in the competition, including hydrogen bonding, salt bridging, hydrophobic collapse, and also, interestingly, water-mediated interaction between hydrophilic residues. As in Frauenfelder's slaved glass transition (7), the solvent is a key source of conformational diversity. Clearly, the protein/solvent free-energy landscape exhibits much more texture than the generic hierarchy of states of a neat liquid.
Proteins have evolved to employ frustration caused by competing interactions to perfect functionality, while avoiding frustration-induced traps on the way to the native state. Similarly, societies have finessed antimonopoly laws to improve long-term economic performance. The analogs of human-designed antimonopoly laws in the world of protein dynamics now, too, appear to be in sight.
Acknowledgments.
This work is supported in part by the Petroleum Research Fund of the American Chemical Society and the Arnold and Mabel Beckman Foundation Beckman Young Investigator Award.
Footnotes
The author declares no conflict of interest.
See companion article on page 10659.
References
- 1.Materese CK, Goldmon CC, Papoian GA. Hierarchical organization of eglin c native state dynamics is shaped by competing direct and water-mediated interactions. Proc Natl Acad Sci USA. 2008;105:10659–10663. doi: 10.1073/pnas.0801850105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Onuchic JN, Luthey Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 3.Wales D. Energy Landscapes. Cambridge, UK: University of Cambridge; 2004. [Google Scholar]
- 4.Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science. 1991;254(5038):1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 5.Lubchenko V, Wolynes PG. Theory of structural glasses and supercooled liquids. Annu Rev Phys Chem. 2007;58:235–266. doi: 10.1146/annurev.physchem.58.032806.104653. [DOI] [PubMed] [Google Scholar]
- 6.Lubchenko V, Wolynes PG, Frauenfelder H. Mosaic energy landscapes of liquids and the control of protein conformational dynamics by glass-forming solvents. J Phys Chem B. 2005;109(15):7488–7499. doi: 10.1021/jp045205z. [DOI] [PubMed] [Google Scholar]
- 7.Fenimore PW, Frauenfelder H, McMahon BH, Parak FG. Slaving: Solvent fluctuations dominate protein dynamics and functions. Proc Natl Acad Sci USA. 2002;99:16047–16051. doi: 10.1073/pnas.212637899. [DOI] [PMC free article] [PubMed] [Google Scholar]