A test-bed for optimizing high-resolution single particle reconstructions

Abstract

It is becoming routine for cryoEM single particle reconstructions to result in 3D electron density maps with resolutions of ∼10Å, but maps with resolutions of 5Å or better are still celebrated events. The electron microscope has a resolving power to better than 2Å, and thus should not be a limiting factor; instead the practical limitations in resolution most likely arise from a combination of specimen preparation methods, data collection parameters, and data analysis procedures. With the aid of a highly automated system for acquiring images, coupled to a relational database to keep track of all processing parameters, we have taken a systematic approach to optimizing parameters affecting the resolution of single particle reconstructions. Using GroEL as a test-bed, we performed a series of 3D reconstructions where we systematically varied the number of particles used in computing the map, the accelerating voltage of the microscope, and the electron dose used to acquire the images. We also investigated methods for excluding unacceptable or “bad” particles from contributing to the final 3D map. Using relatively standard instrumentation (Tecnai F20, 4K×4K CCD, side entry cold stage) and a completely automated approach, these approaches resulted in a map with a nominal resolution of 5.4Å (FSC_0.5) in which secondary structure is clearly discernable and the handedness of some of the α-helices in the GroEL structure can be determined.

Introduction

Why is high-resolution important?

Cryo-electron microscopy (cryoEM) and single particle reconstruction (SPR) are very powerful techniques for determining the structures of large, biologically important complexes. However, in the absence of supporting high-resolution information for a structure, interpretations of the EM density map may be subjective, and 3D EM has sometimes been criticized as “blobology”. One of the consequences of higher-resolution, therefore is that interpretations become less subjective. When α-helices are resolved as tubes and β-sheets become plates of density, atomic resolution components of the molecule can be docked very accurately into the EM density map, and under some favorable circumstances the backbone of the structure can be traced with a reasonable degree of confidence (Baker et al., 2007; Zhang et al., 2008). Higher resolution maps in which secondary structure can be clearly discerned also provide much higher confidence in reconstructions and can resolve concerns over initial model bias and also unequivocally determine the handedness of the structure.

What are the limits to resolution in single-particle-reconstruction?

Factors that degrade resolution in single particle reconstructions of cryoEM data arise from three independent sources: as a result of the specimen and its preparation, as a result of the microscope and imaging conditions during data collection, or because of errors during data processing. The factor over which we currently have the least control is the specimen itself. The resolution could be fundamentally limited by the purity, stability or heterogeneity of the specimen, and we do not directly address these issues in this paper. We have some control over factors affecting the quality of the preparation of the specimen for EM such as the quality of vitreous ice and the thickness of the layer of ice in which the particles are embedded. Though we have the most control of the data collection and processing parameters, the number of parameters makes it difficult to optimize them for high-resolution. During data collection, the images that are acquired of the specimen can be affected by the microscope alignment, choice of accelerating voltage, electron dose, defocus range, astigmatism correction, acceptable drift rate, and beam induced specimen motion. Finally, errors may be introduced during processing from numerous sources, including incorrect particle picking, CTF estimation, and alignment and classification.

Automated and systematic data collection and analysis protocols afford us the opportunity to quantify the results of varying the factors that influence resolution. Here we have focused specifically on the results of varying magnification, electron dose, acceleration voltage, and numbers of particles on the final resolution of 3D electron density maps of GroEL. GroEL makes an excellent test bed for this investigation as its molecular weight and stability make it ideally suited to structural analysis using single particle methods, and it has been extensively studied both structurally and functionally (Ludtke et al., 2004; Ranson et al., 2001; Sigler et al., 1998).

How do we measure resolution in single particle reconstruction?

The question of how to measure resolution is still somewhat controversial in cryoEM and SPR, and there are a number of methods that are used in practice. Most methods depend on randomly splitting the dataset into halves, typically one half corresponds to the even images of particles and the other half corresponds to the odd images. Resolution is estimated by calculating a Fourier shell correlation (FSC) (Harauz and Van Heel, 1986) curve between two volumes generated from the even and odd particles, respectively. The resolution that is quoted in the literature for a given SPR is measured from an arbitrary cutoff on the FSC curve. The most common convention is to use a cutoff of 0.5 (Bottcher et al., 1997; Conway et al., 1997), as this has been in practice for the longest time, but several other cutoff criteria have also been proposed (Orlova et al., 1997; Rosenthal and Henderson, 2003; Saxon and Baumeister, 1982). Most recently a sliding scale for determining the optimal cutoff value based on the noise and symmetry of the reconstruction (van Heel and Schatz, 2005) has been described but it remains to be seen whether this method will be widely adopted by the EM community.

All of these methods suffer from the same problem; they depend on splitting the particles into even and odd sets after they have been iteratively aligned and classified. Thus, iterative model and noise bias can potentially artificially inflate the reported resolution (Stagg et al., 2006; Stewart and Grigorieff, 2004). A solution to this problem is to split the data into even and odd sets that are refined independently, but given that resolution is dependent on the number of particles, this method does not allow for the highest resolution reconstructions possible. A different method has recently been proposed to estimate the resolution directly from the final reconstructed density map (Sousa and Grigorieff, 2007). This method, which is referred to here as rmeasure, does not rely on a comparison of separately computed structures but instead calculates the correlation between neighboring Fourier pixels of the final 3D electron density map computed from all images. Not only does this give a good estimation of the resolution, but the algorithm is resistant to model bias (Sousa and Grigorieff, 2007)

The ultimate standard for determining the approximate resolution of a reconstructed density map is the extent to which details in the 3D model can be usefully interpreted. Thus, when secondary structure becomes discernable we know the resolution is on the order of 10Å or better (Ludtke et al., 2004; Ranson et al., 2006; Stagg et al., 2006), when the handedness of alpha helices can be determined we are in a resolution range of ∼5Å, being able to trace the atomic backbone would indicate a resolution in the range of 3-4Å (Zhang et al., 2008), and finally, being able to distinguish side chains would correspond to a resolution of better than 3Å (Gonen et al., 2005). For the results described in this paper, we report both the FSC_0.5 and rmeasure criteria and provide a quantitative assessment of the reported numbers based on a visual inspection of interpretable details and comparisons between our highest-resolution structure and an electron density map computer from a crystal structure of GroEL (Braig et al., 1995).

Materials and Methods

Data collection

The GroEL specimen was kindly provided by Art Horwich and Eli Chapman. Grids were prepared as previously described (Stagg et al., 2006). Data were acquired using a Tecnai F20 Twin transmission electron microscope equipped with a Tietz F415 4k × 4k pixel CCD camera (15μm pixel) and a Gatan side entry cryostage. Images were acquired using 8 different sets of data collection parameters (datasets 1-8) in separate sessions using 8 cryoEM grids prepared under identical conditions. Parameters that were varied across the 8 experiments include magnification, accelerating voltage, and dose; the conditions that were used are summarized in Table 1. The Leginon automated data acquisition system (Suloway et al., 2005) was used to control the microscope and acquire images to the CCD camera. This helped to provide consistency in performance across the different data acquisition sessions. For data analysis, particles were randomly selected from images across a defocus range from -1μm to -3μm. Data were processed with the aid of a new software package, called Appion, under development in our lab, that tracks all processing parameters and results using an extension of the Leginon database infrastructure (Fellmann et al., 2002). The Appion package provides utilities for particle picking (Roseman, 2003) and CTF estimation (Mallick et al., 2005), and provides wrappers for a variety of EMAN utilities (Ludtke et al., 1999), including single particle refinement.

Table 1. Data collection parameters.

Dataset	Accelerating voltage (keV)	Magnification (X)	Dose (e-/Å2)	Binning	Pixel Size (Å/pixel)	Total particles
1	120	50,000	13	none	1.63	41289
2	120	100,000	13	2	1.63	55351
3	200	100,000	13	2	1.63	28021
4	80	100,000	13	2	1.63	31659
5	120	100,000	13	2	1.63	43720
6	120	100,000	19	2	1.63	60547
7	200	100,000	13	2	1.63	11298
8	200	100,000	19	2	1.63	26892

Single particle reconstructions

Individual stacks were created for all datasets by boxing particles out of the micrographs and flipping the phases using the CTF parameters estimated by ACE. For each dataset, the particles were split into logarithmically smaller stacks by randomly choosing particles from the original full stack to generate a stack of a given size. Thus, two different stacks from the same dataset might contain completely different particles. For instance, 41,289 particles were collected in dataset #1 and these were split into 14 separate stacks where the number of particles in the stacks were 100, 159, 253, 401, 638, 1014, 1612, 2562, 4071, 6471, 10,284, 16,346, 25,979, and 41,289, respectively, with the particles for each of the substacks drawn randomly from the full 41,289 particle stack.

Single particle reconstructions were carried out using the EMAN reconstruction package (Ludtke et al., 1999). The initial model for all refinements was a GroEL reconstruction (Stagg et al., 2006) (EMDB accession # 1200) that had been low-pass filtered to 30Å. Each stack was subjected to one of two refinement schemes. Scheme 1 was used for stacks that contained less than 1000 particles. In this scheme, particles were refined with an angular increment that started at 8° and decreased by 1° every four iterations for a total of twenty iterations. Thus, the final angular increment was 4°. Whenever the angular increment changed, the particles were subjected to two iterations of refinement including 8 rounds of iterative class averaging, followed by two iterations of refinement with 3 rounds of iterative class averaging. Scheme 2 was used for stacks that contained greater than 1000 particles. This scheme was similar to scheme 1 with the exception being that the angular increment started at 5° and went to 1°. These methods allowed us to determine the lowest angular increment where the refinement converged. Thus, our reconstruction scheme is adapted to the number of particles, and we have confidence that the reported resolution constitutes a fair comparison between datasets. The distribution of euler angle orientations was similar for all datasets and was typical for GroEL in vitreous ice with all Euler angles well represented but with some preferred orientations in top and side views.

The refinements were typically run on 48 processors on our in-house Linux cluster. The total processing time in CPU hours was approximately one year for a given dataset, including processing of the full particle stack and all the substacks. Thus, ∼8 years of processing time was used for these studies.

Resolution assessment

Resolution was assessed for each reconstruction in three ways: 1) By calculating the Fourier Shell Correlation at a cutoff of 0.5 (FSC_0.5) between the even and odd particles. 2) By using rmeasure (Sousa and Grigorieff, 2007) on the final reconstructed volume of a refinement. No masking or filtering was performed before the rmeasure resolution calculation and the conservative 0.5 cutoff was used. 3) By visually inspecting the final amplitude corrected and filtered volume of a refinement.

Amplitude correction

If the final volumes for a given refinement had a calculated resolution better than 10Å then the volume was also amplitude corrected by multiplying the map by the square root of the ratio of the one-dimensional power spectrum of the EM map and the X-ray scattering curve for GroEL¹ followed by low-pass filtering the volumes to the resolution reported by the FSC_0.5 criterion (Gabashvili et al., 2000). This procedure was used only to enhance the details of the map for the purposed of visual assessment and no amplitude correction was performed during the refinement or prior to resolution estimation.

DQE estimation

The detective quantum efficiency (DQE) of the scintillator and CCD camera combination was measured using the methods outlined in Mooney 2007 (Mooney, 2007). Supplemental figure S1 shows the DQE curves at the magnification of the specimen for 50kX, 100kX, and 143kX at 120keV and 200keV.

Calculating Euler jumps

The Euler angles calculated for the orientation of every particle at each iteration of a refinement are stored in the Appion database and were used to determine the relative change in orientation of each particle at each iteration of the refinement. We refer to the change in the orientation of the particles from iteration to iteration as an Euler jump.

We used a standard metric on the space of rotations to measure the size of the Euler jumps. For a particle with Euler angles (a, b, c) in iteration i and Euler angles (a′, b′, c′) in iteration i+1, the Euler jump, d, was computed as follows. Denote the rotation matrices corresponding to the Euler angles (a,b,c) and (a′,b′,c′) by

$$\text{V}=\left(\begin{array}{ccc}{v}_{00}& v_{01}& v_{02}\\ v_{10}& v_{11}& v_{12}\\ v_{20}& v_{21}& v_{22}\end{array}\right)\text{and}\text{V}\prime =\left(\begin{array}{ccc}{v}_{00}^{\prime }& v_{01}^{\prime }& v_{02}^{\prime }\\ v_{10}^{\prime }& v_{11}^{\prime }& v_{12}^{\prime }\\ v_{20}^{\prime }& v_{21}^{\prime }& v_{22}^{\prime }\end{array}\right)$$

Because of the invariant properties of the metric, the distance between V and V′ is the same as the distance between the identity, I, and V^tV′ (where V^t denotes the transpose of V). We thus computed the new matrix

$$\text{R}=\left(\begin{array}{ccc}{r}_{00}& r_{01}& r_{02}\\ r_{10}& r_{11}& r_{12}\\ r_{20}& r_{21}& r_{22}\end{array}\right)=\left(\begin{array}{ccc}{v}_{00}^t& v_{01}^t& v_{02}^t\\ v_{10}^t& v_{11}^t& v_{12}^t\\ v_{20}^t& v_{21}^t& v_{22}^t\end{array}\right)\left(\begin{array}{ccc}{v}_{00}^{\prime }& v_{01}^{\prime }& v_{02}^{\prime }\\ v_{10}^{\prime }& v_{11}^{\prime }& v_{12}^{\prime }\\ v_{20}^{\prime }& v_{21}^{\prime }& v_{22}^{\prime }\end{array}\right)$$

and measured the distance from I to R. The formula for this distance and hence for the Euler jump is

$$d=\left|\frac{s}{2sin\left(s\right)}\right|\sqrt{{\left(r_{01}+r_{10}\right)}^2+{\left(r_{02}+r_{20}\right)}^2+{\left(r_{12}+r_{21}\right)}^2}$$

where

$s={cos}^{-1}\left(\frac{r_{00}+r_{11}+r_{22}-1}{2}\right)$ with the understanding that d=0 if s=0

Visualization and fitting

All of the 3D reconstructions were visualized using UCSF Chimera (Pettersen et al., 2004). Chimera was also used to manually fit a GroEL crystal structure (PDB ID 1OEL) (Braig et al., 1995) into the cryoEM maps. The fits were automatically refined using the Fit Model in Map function in Chimera.

Results

What is the effect of number of particles on resolution?

Because of the damaging effects of the electron beam, cryoEM micrographs must be taken with very low dose (typically 10-20e^-/Ų). Thus, the data has a very low signal-to-noise ratio (SNR). To improve the SNR, particles must be averaged, and thus resolution is dependent on the number of particles contributing to the reconstructed density map. It is estimated that for particles with no symmetry, more than 1,000,000 particles would be required to achieve maps with atomic resolution (Glaeser, 1999; Glaeser, 2004; Henderson, 1995). To test the practical effect of the number of particles on the final resolution, we used a dataset of GroEL acquired using fairly typical data collection parameters. Approximately 41,000 particles were collected at an accelerating voltage of 120keV, 50,000X nominal magnification (1.63Å/pix), and a dose of 13e^-/Ų (dataset 1 in Table 1). These particles were randomly split into sets containing logarithmically fewer particles and each set was reconstructed using one of the two refinement schemes described above. When the FSC_0.5 measure of resolution is plotted against the number of particles (Fig. 1A, blue), the resolution is observed to increase roughly linearly with the log of the number of particles. Note: this graph and subsequent graphs are plotted on the log scale on the x-axis and the reciprocal scale on the y-axis. However, when the resolution is calculated using the rmeasure method (Fig. 1A, red), the shape of the curve is quite different. As with the FSC_0.5 method, resolution increases linearly with relatively small sets of particles, but the curve appears to flatten out asymptotically at around 6,500 particles. Furthermore, the resolution reported by the rmeasure method for more than 6,500 particles is considerably worse than that of the FSC_0.5 method; the resolution for the complete stack containing the full dataset is reported as 6.5Å by the FSC_0.5 method and 8.8Å by the rmeasure method. As expected for a subnanometer reconstruction, α helices are clearly visible in the GroEL volume (Fig. 1B) as distinct tubes of density, but it is not clear which reported value for resolution is more reflective of the apparent details in the structure.

Fig. 1.

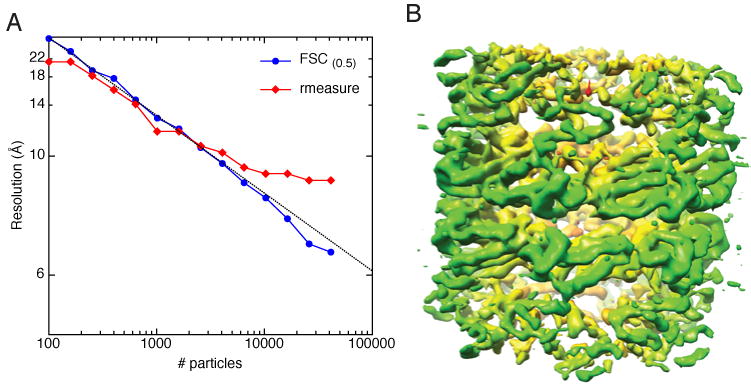
Reconstruction of GroEL at 120keV and 50,000X (dataset 1 in Table1). A) Plot of resolution as a function of number of particles. The data are plotted with reciprocal spacing on the y axis and log spacing on the x axis. The GroEL particles were split into logarithmically decreasing sets and reconstructed. The blue curve corresponds to the resolution as determined by the FSC_0.5 criterion while the red curve corresponds to resolution as determined by rmeasure. A line corresponding to the equation $f\left(x\right)=\frac{1}{Alog\left(x\right)+B}$ (grey) was fit to the FSC_0.5 data. B) 3D reconstruction of the highest resolution stack in A. The volume has been amplitude corrected and low-pass filtered to 6.5Å. The volume is colored from red to yellow to green according to the radius from the center of a cylinder aligned along the Z-axis.

What is the effect of magnification on resolution?

The data in Fig. 1A suggest that we could obtain higher-resolution reconstructions by collecting more particles, and that we could approach atomic resolution by collecting hundreds of millions of particles. Collecting this number of particles is unfeasible in practice, so instead the most logical next step to improving the resolution was to collect data at higher magnification in order to offset the high-frequency dampening effects of the CCD camera (Sander et al., 2005). We thus collected a dataset of ∼55,000 particles of GroEL at a magnification of 100,000X using the same keV and dose as before (dataset #2, Table 1). The particles were again split into stacks containing logarithmically fewer particles and reconstructed. As predicted, the resolution of the higher magnification data is improved considerably over the lower magnification data, and this was true regardless of the number of particles used for the reconstruction (Fig. 2A,B). The reported improvement in resolution was supported by an observation of increased detail in the reconstructions (Fig 2C,D). More helices are visible in the 100kX reconstruction and the helices have progressed from being smooth tubes to having the appearance of grooves and crevices. According to the plots of resolution calculated by the FSC_0.5 criterion versus number of particles (Fig. 2A), the curves suggest that data collected at both 50kX and 100kX could ultimately achieve atomic resolution if sufficient numbers of particles were collected (Fig. 2A). When resolution was estimated by the rmeasure criterion, on the other hand, the resolution vs. particles curves again indicate asymptotic flattening with increasing numbers of particles (Fig. 2B). When compared to the 50kX data, the 100kX data are clearly shifted toward higher resolution and seem to have less flattening with increasing particles. This likely reflects better performance of the CCD camera with higher magnification (Sander et al., 2005)

Fig. 2.

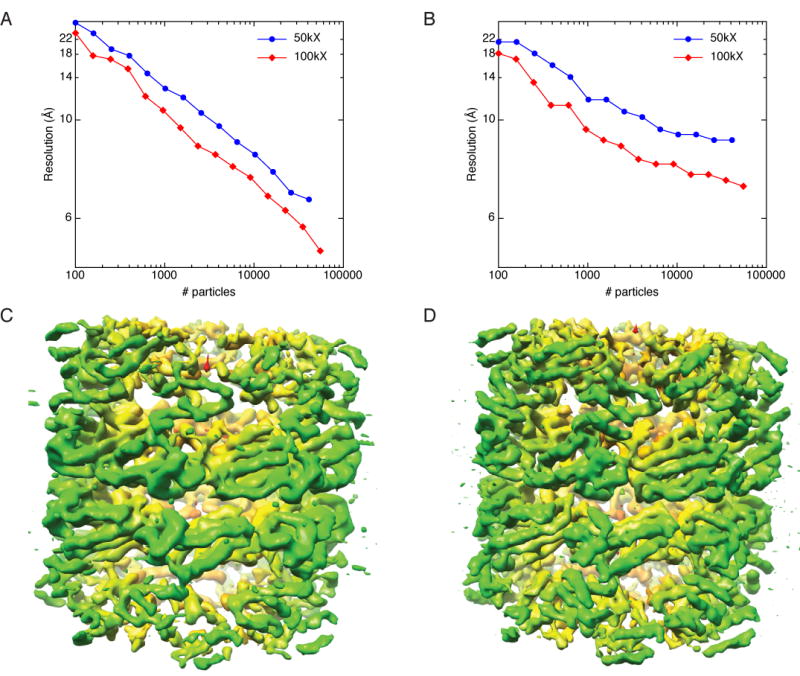
Comparison of GroEL data collected at 50,000X (dataset 1) vs. 100,000X (dataset 2). A) Plot of resolution as a function of number of particles for data collected at 50,000X (blue) and 100,000X (red). Resolution was estimated by the FSC_0.5 criterion. B) Same as A, but resolution was estimated by rmeasure. C) The highest-resolution volume from the 50,000X data. D) The highest-resolution volume from the 100,000X data. The resolution for the volume reconstructed from the 100,000X data is better than the 50,000X data as judged by FSC_0.5, rmeasure, and visual inspection. Coloring for the volumes is the same as in Fig. 1.

What is the effect of accelerating voltage on resolution?

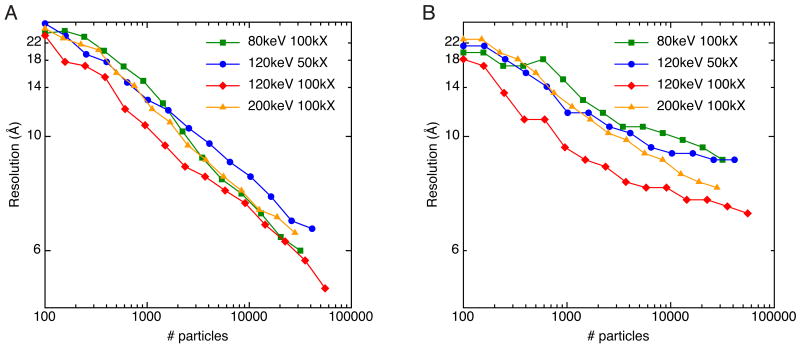
The choice of the TEM accelerating voltage to use for data collection depends on a number of factors. Higher voltage allows for visualization of thicker specimens and reduces radiation damage. The performance of the digital CCD, on the other hand, decreases with increasing voltage (Fig. S1). In addition, image contrast decreases with increasing voltage and SPR depends on this contrast for accurate alignment and classification. Thus, there may be an optimal voltage for SPR that balances increased image contrast and CCD performance against the benefits of high voltage. To test this, we collected GroEL datasets at 80keV, 120keV, and 200keV (datasets 1-4 in Table 1). The particles were logarithmically split and reconstructed as described previously. If judged by the FSC_0.5 criterion, these results indicate that for data collected at a given magnification, the accelerating voltage has very little effect on the resolution of reconstructions (Fig. 3A, 100kX curves). The rmeasure criterion, however, indicates a substantial difference in resolutions among datasets collected at different voltages (Fig. 3B).

Fig. 3.

Comparison of GroEL data collected at different accelerating voltages. A) Plot of resolution as a function of number of particles for data collected at 80keV (green, dataset 4), 120keV (blue and red, datasets 1 and 2), and 200keV (orange, dataset 3). Resolution was estimated by the FSC_0.5 criterion. B) Same as A, but resolution was estimated by rmeasure.

In order to better understand what are the interpretable differences between the datasets collected at different voltages, we took the following approach. We started with the highest resolution reconstructed map from the 50kX, 120keV dataset and compared it to the maps that had approximately the same resolution according to the FSC_0.5 criterion in the 100kX, 80keV, 120keV, and 200keV datasets. It should be noted that the reported resolution by the FSC method would be the same for all the reconstructions regardless of which cutoff criterion we were to use for the FSC curve; the curves for all four of the reconstructions are quite similar (Fig. 4, right column).

Fig. 4.

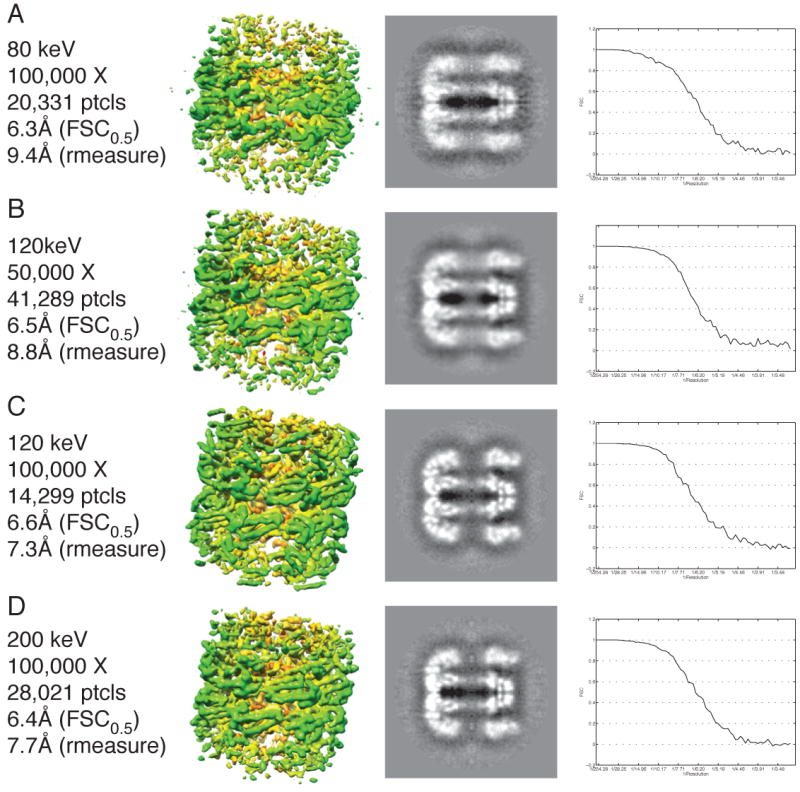
Comparison of the 3D reconstructions of GroEL collected at different accelerating voltages and the same resolution by the FSC_0.5 criterion. The figure is organized in four columns from left to right where the first column is the metadata about a particular reconstruction, the second column is a picture of the volume, the third column is a slice along the 7-fold symmetry axis, and the fourth column is the FSC curve for the particular reconstruction. A) Data collected at 80keV and 100,000X. B) Data collected at 120keV and 50,000X. C) Data collected at 120keV and 100,000X. D) Data collected at 200keV and 100,000X. The FSC curves are very similar for all datasets, but the observable details are very different.

Though all of the maps were nominally supposed to be at the same resolution, there were dramatic differences in the level of detail among them (Fig 4). The 80keV reconstruction had a resolution of 6.3Å but it was difficult to distinguish the tubes corresponding to α-helices that are a hallmark of reconstructions better than 10Å. From highest to lowest observable detail as judged by visualization of the 3D reconstructions and slices through the z-axis of the volumes, the reconstructions are ranked 100kX, 120keV; 100kX, 200keV; 50kX, 120keV; and 100kX, 80keV. This is more reflective of the resolution reported by the rmeasure criterion (7.3Å, 7.7Å, 8.8Å, and 9.4Å, respectively). According to this analysis, the FSC_0.5 criterion seems a poor reporter of resolution. Furthermore, for a particle like GroEL, it seems that 120keV is the optimal voltage for SPR data collection, at least when using data acquisition parameters like the ones used in this investigation (i.e. field emission gun, automated data collection, CCD camera, etc.).

The same analysis was repeated for the rmeasure criterion where we started with the highest resolution reconstructed map from the 50kX, 120keV dataset and compared it to the maps that had approximately the same resolution in the other datasets (Supplemental Fig. S2). While this showed that the reconstructions were more similar than in the analysis using the FSC_0.5 criterion, there were still some noticeable differences in the maps. Thus, neither method is a perfect indicator of resolution, though rmeasure seems to more accurately report differences in detail between different volumes.

What is the influence of dose on resolution?

The SNR of cryo-micrographs increases with increasing dose, but there is also an increased occurrence of radiation damage. Furthermore, the amount of damage is dependent on the accelerating voltage at which the microscope is operated with higher voltages causing theoretically less damage. We carried out some preliminary experiments to determine the influence of increasing the dose of the data collection for both 120keV and 200keV accelerating voltages.

To establish a baseline for variations between datasets collected with the same imaging and processing parameters, we first collected two independent GroEL datasets at accelerating voltages of 120keV (datasets 2 and 5 in Table 1) and 200keV (datasets 3 and 7 in Table 1). The datasets were collected with different grids on different days, which further established their independence. When the particles were logarithmically split and reconstructed, this showed that the datasets collected at 120keV and 13e^-/Ų were fairly similar in resolution (Fig. 5A,B blue) and observable details (Fig. 5C,D) though one dataset was consistently slightly better than the other. The 200keV datasets were essentially identical (Fig. 5F-I). These data show that although there are some variations between datasets, collecting data with a given set of parameters is relatively repeatable.

Fig. 5.

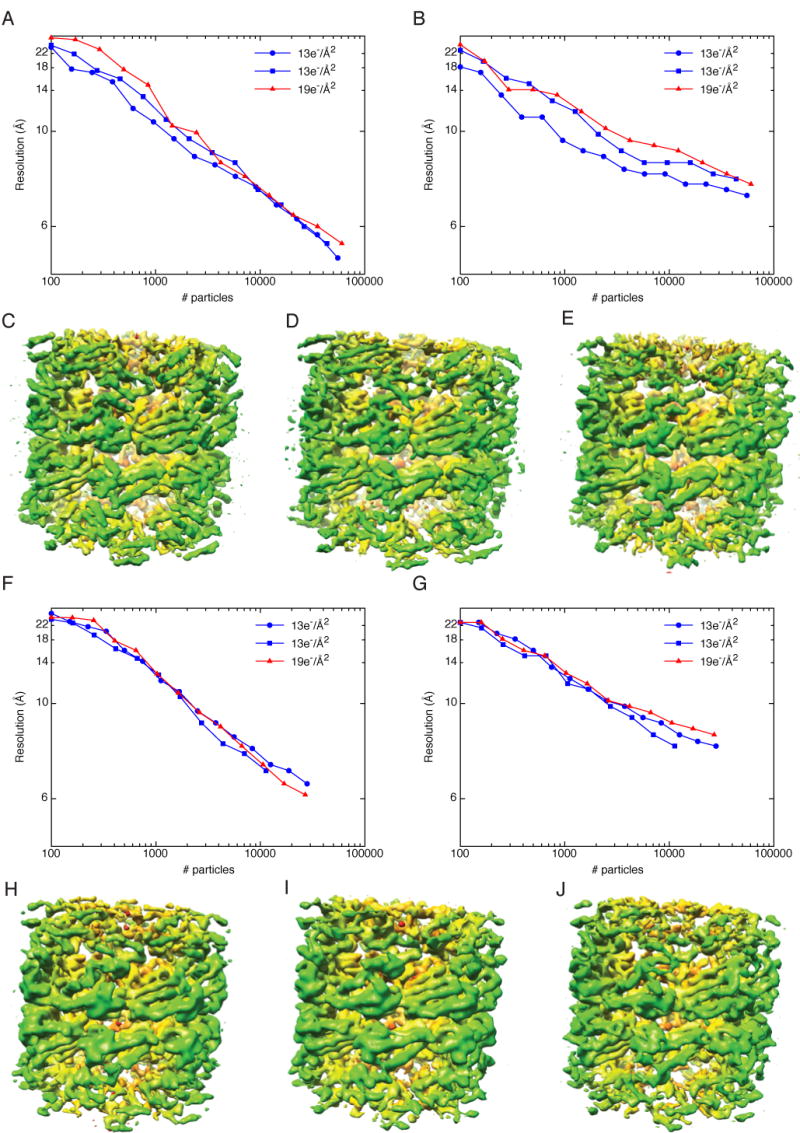
Variations between datasets and the influence of dose on resolution. Panels A-E are for data collected at 120keV and F-J are for data collected at 200keV. A) Plot of resolution as a function of number of particles for data collected at 120keV and 100,000X. Two datasets were acquired with a dose of 13e^-/Ų (blue curves) while the third was acquired with a dose of 19e^-/Ų (red curve). Resolution was estimated by the FSC_0.5 criterion. B) Same as A, but resolution was estimated by rmeasure. C,D) The highest-resolution 3D reconstructions for the data collected with a dose of 13e^-/Ų. E) The highest-resolution 3D reconstructions for the data collected with a dose of 19e^-/Ų. F) Plot of resolution as a function of number of particles for data collected at 200keV and 100,000X. Two datasets were acquired with a dose of 13e^-/Ų (blue curves) while the third was acquired with a dose of 19e^-/Ų (red curve). Resolution was estimated by the FSC_0.5 criterion. G) Same as A, but resolution was estimated by rmeasure. H,I) The highest-resolution 3D reconstructions for the data collected with a dose of 13e^-/Ų. J) The highest-resolution 3D reconstructions for the data collected with a dose of 19e^-/Ų.

We typically collect data with a dose of 12-13e^-/Ų. To determine the effects of increasing the dose, we collected GroEL datasets at 120keV (dataset 6 in Table 1) and 200keV (dataset 8 in Table 1) with a dose of 19e^-/Ų. The resulting reconstructions had slightly worse resolutions than the lower-dose reconstructions for the 120keV dataset, though the degree to which they were worse was not much greater than the variations between datasets with identical dose (Fig. 5A,B). Some differences could be observed in the structural details of the reconstructions; secondary structure was clearly visible (Fig. 5E), but fewer α-helices could be identified, particularly in the apical domain (Fig. 5C-E). The resolutions for the higher-dose 200keV data set were essentially the same as the lower-dose data (Fig. 5F,G), however, there appears to be slightly more detail visible in the higher-dose dataset (Fig. 5J). As addressed further in the discussion below, we believe that we will need tighter controls over the experimental parameters of data collection in order to determine the optimal dose for SPR.

What is the relationship between Euler jumps and resolution?

The above data suggest that a reasonable way to increase the resolution of a reconstruction is to increase the number of particles. Another way of increasing the resolution is to focus only on the “good” particles, (i.e. identifying and eliminating particles that do not contribute to an increase in the SNR). Several methods have been proposed (Borgnia et al., 2004; Liu et al., 2007), and here we have explored the possibility that the best particles would be ones whose orientation, as indicated by their Euler angles, was relatively stable between iterations of the SPR refinement.

To test this idea, we took our dataset that refined to the highest resolution (dataset 2) and removed particles that were not classified to a single Euler angle for the majority of the iterations. In other words, for a given particle, we calculated the distance its Euler angle jumped from one iteration to the next and only allowed it to contribute to the final reconstruction if it had a median Euler jump of 0° from iteration to iteration throughout the refinement. We chose to use the median Euler jump as the criteria for elimination because many particles had typical jumps of 0° from iteration to iteration but would occasionally have a large jump. We reasoned that the large jumps could be considered outliers, thus the median would be a more sensitive measure than the mean for the likelihood of a particle to jump. Analyzing the data in this way eliminated 42% of the particles. The resolution of the reconstruction calculated from the reduced set of particles as measured by the FSC_0.5 or rmeasure criteria was the same as that obtained with the full set of particles. Thus, the volume calculated with particles eliminated in this way was considerably better than would be predicted from this number of particles based on the particle vs. resolution curves in Fig 2. In addition, the level of detail observed in the final 3D maps of the reduced data set was an improvement over the full dataset, in that the handedness of several of the GroEL helices could now be discerned (Fig. 6).

Fig. 6.

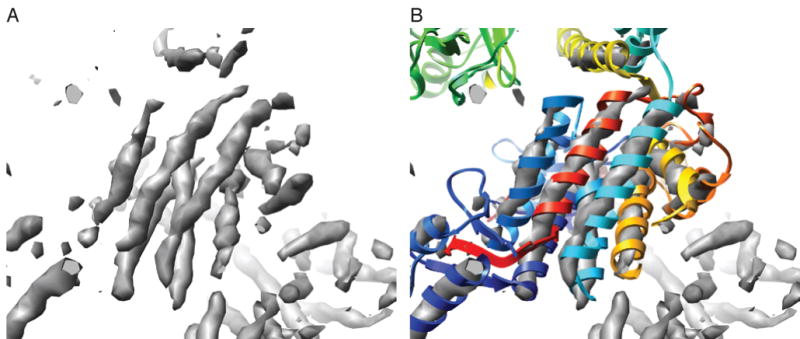
GroEL with some evidence of helices with handedness. A) The GroEL map with the highest level of detail displayed at a high contour level. Grooves that are typical of a right-handed α-helix can be seen in the tubes of EM density (grey). B) A fit of a GroEL crystal structure (colored ribbons) to the EM density shows the correspondence of the helices in the crystal structure to the helical tubes seen in the EM density map.

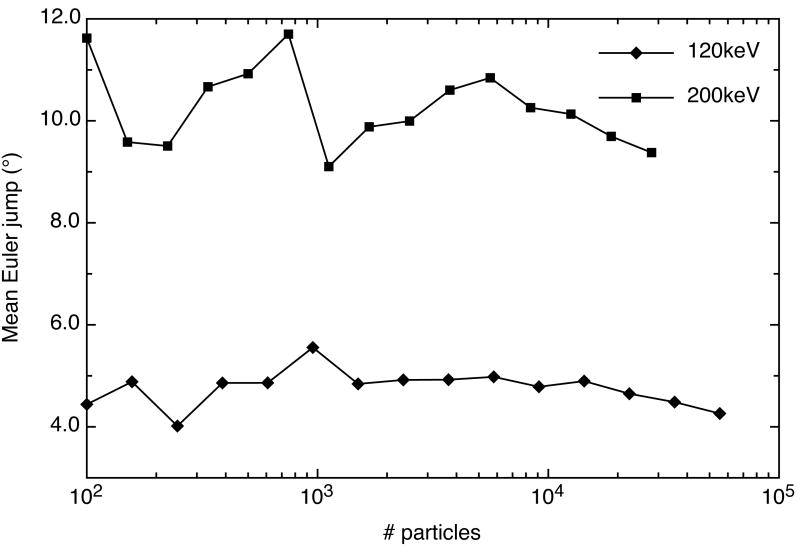
We were interested to see if the mean Euler jumps were dependent on the number of particles in a dataset. Thus, we determined the mean Euler jumps for logarithmically split particles from our best data set collected at 120keV (Table 1, dataset 2) and a data set collected at 200keV (Table 1,dataset 3). Surprisingly, the mean Euler jumps were not dependent on the number of particles for either the 120keV or 200keV data (Fig. 7). However, the average Euler jump for the 200keV data (∼10.4°) was much greater than the average for the 120keV data (∼4.8°). This indicates that there is less confidence in the classification of the particles collected at 200keV for these particular data sets.

Fig. 7.

Average Euler jumps in a 3D reconstruction refinement versus number of particles. Diamonds represent the average Euler jump from one iteration to the next in a 3D reconstruction refinement of GroEL data collected at 120keV and 100,000X. Squares represent data collected at 200keV and 100,000X. The average Euler jumps do not seem to be dependent on the number of particles, however, on average, the jumps for data collected at 120keV are much less than data collected at 200keV.

Our highest-resolution volume reconstructed after eliminating the jumping particles was compared to a map of GroEL generated from an X-ray crystal structure (Braig et al., 1995) in order to compare the levels of detail apparent in each. First, we used the crystal structure to estimate the resolution of the EM map by generating an FSC curve between the EM map and the X-ray map (Supplemental Fig. S3). This curve indicates that at a cutoff of FSC_0.5 the resolution is 8.1Å. For this single reconstructed density map, we thus have three different estimates of resolution: 5.4Å (FSC_0.5), 6.9Å (rmeasure) and 8.1Å (FSC_0.5 comparison to X-ray map). In order to determine which value more accurately represents the levels of detail apparent in the EM map, we low-pass filtered the atomic resolution X-ray map to a resolution of 5.4Å (Fig. 8B), 6.9Å (Fig. 8C), and 8.1Å (Fig. 8D), respectively. From a visual inspection, we believe our EM map (Fig. 8A) lies somewhere between the 5.4Å and 6.9Å X-ray maps in terms of interpretable detail. In the 5.4Å X-ray map, individual strands of β-sheets can be distinguished, while we were unable to make such distinctions in our EM map. On the other hand, the grooves in the α-helices of our map appear to be better defined than in the α-helices of the 6.9Å X-ray map. Finally, the apical domain of GroEL is more ordered in the X-ray maps than in our EM map, but that is likely due to conformational heterogeneity in the EM data.

Fig. 8.

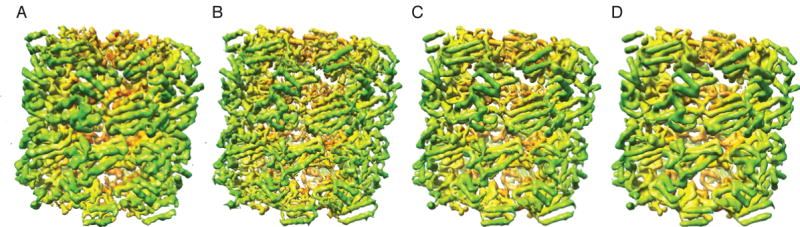
Comparison of the details of the highest-resolution EM map and maps generated from an X-ray crystal structure. A) Surface representation of our GroEL reconstruction with the highest-resolution. B) X-ray map filtered to 5.4Å resolution. C) X-ray map filtered to 6.9Å resolution. D) X-ray map filtered to 8.1Å resolution.

Discussion

We have used GroEL as a test bed to show that it is possible to achieve maps with a resolution on the order of 5-6Å, sufficient to discern the handedness of some α-helices, using relatively standard instrumentation (Tecnai F20, 4K×4K CCD, side entry cold stage) and a completely automated approach.

Our data illustrate one of the major issues in cryoEM and SPR: how to accurately assess resolution. We show that we get different values for resolution from the FSC_0.5 and rmeasure methods. The resolution reported by rmeasure, however, tended to be more consistent with the observable details of the reconstructions than the FSC_0.5. This was particularly evident in the comparison of reconstructions from data collected at different accelerating voltages (Figs. 3,4). Reconstructions that had the same resolution as reported by the FSC_0.5 method had dramatically different levels of detail as observed by visual inspection. The resolution reported by rmeasure, on the other hand, was more consistent with the details observed in the reconstructions. It is unclear why rmeasure was a better reporter of resolution, but the most likely interpretation is that it is less sensitive to noise bias.

Our data also demonstrate the importance of collecting large numbers of images. For all of our datasets, the resolution increases dramatically from 100 particles to about 2000 particles (equivalent to about 28,000 asymmetric subunits of GroEL), after which it requires exponentially more particles for relatively modest increases in resolution (Supplemental Fig. S4). Nevertheless, while these later improvements in resolution are small, they are worth fighting for as they increase the confidence of interpretations based on secondary structure and other model building. We thus argue that it is always worth acquiring on the order of several tens of thousands of particles (corresponding to several hundreds of thousands of asymmetric units) for every dataset that will be subjected to single particle reconstruction. Achieving data throughput on this order has been the goal of the development of automated data acquisition methods in our lab (Suloway et al., 2005).

Our highest resolution reconstruction of GroEL resulted from data collected at 120keV. This is likely the result of improved performance of the digital CCD cameras at the lower keV ranges. However, the influence of contrast on the alignment of particles and the effect of dose are complicating factors and it is clear that it will require additional experiments undertaken under more careful and exacting conditions before we can draw any conclusions on this issue.

At an accelerating voltage of 120keV, a dose of 19e^-/Ų appears to degrade the high-resolution features of the reconstruction; indicted by the fact that helices are not as clearly defined. We anticipated that when the number of particles were limiting (less than 10,000) the higher-dose data would have higher resolution because the images have higher signal-to-noise ratios, however in this case, the opposite is true. It is possible that the individual particles are starting to be degraded and they are losing features by which to classify them. In contrast, at an accelerating voltage of 200keV, a dose of 19e^-/Ų does not appear to make much difference. The resolution is very close to the lower-dose datasets, and similar features can be observed in the reconstructions, although it is possible that more features can be observed in the higher-dose dataset. The more likely conclusion is that we need to control the data acquisition parameters far more carefully to fully understand this issue.

We also showed that keeping track of particle orientation, as measured by the jump in Euler angle between iterations, was useful in eliminating bad particles from the reconstruction and improving the resolution. This method might be most useful in reducing the numbers of particles in the dataset at an early stage of the iterations and thus save considerable amounts of CPU time, particularly for very large data sets. The mean Euler jump measured across all particles also appears to be a good indicator of the quality of the data that is independent of number of particles and thus may be used to quickly identify problems in incoming data while the grid is still in the microscope. We intend to explore these issues further.

What will it take to achieve even higher resolution? One of the strongest resolution-limiting factors for our data is the high-frequency falloff characteristic of the CCD camera. We were able to considerably improve the resolutions of our reconstructions by increasing the magnification at which the data were collected. The results agree well with predictions from a detective quantum efficiency (DQE) (Mooney, 2007) plot measured for our CCD camera (Supplemental Fig. S1). The DQE plots also predict that we could further improve resolution by collecting data at higher magnifications such as 143,000X or 200,000X, though the improved DQE at higher magnification would need to be balanced against the fewer particles one could feasibly collect in any given session.

We have made a modest start at beginning to quantify some of the factors that affect the resolution of single particle reconstructions. We are well aware however that there is much more work to be done. Even for a relatively simple investigation like the dependence of resolution on image dose, factors like beam coherence and exposure time must be carefully measured and controlled (Chen et al., 2008), and the performance of the particle alignment algorithms as a function of image contrast must be factored in and considered in the context of the magnification and defocus range of the images. Finding an optimal solution in this multi-parameter space requires careful experimental design built on a solid mathematical and statistical foundation. This will be the focus of future work in our lab.

Maps of the unfiltered volume and amplitude corrected volume of the highest-resolution 120keV, 100kX dataset have been deposited in the EM databank under the accession numbers 1457 and 1458, respectively.

Supplementary Material

01

Supplemental Fig. S1. Detective quantum efficiency curves at different magnifications at 120keV and 200keV. 120keV data is indicated by broken lines and 200keV data by solid lines. Data collected at 50kX is indicated as red, 100kX as blue, and 143kX as green.

02

Supplemental Fig. S2. Comparison of the 3D reconstructions of GroEL collected at different accelerating voltages and the same resolution by the rmeasure criterion. The figure is organized in two columns where the first column is the metadata and the second column is the volume for a particular reconstruction. All volumes shown have a resolution of 8.8Å by the rmeasure criterion.

03

Supplemental Fig. S3. FSC curve between our highest-resolution EM map and a map generated from an X-ray crystal structure of GroEL.

04

Supplemental Fig. S4. Observable details for GroEL reconstructions from data collected at 120keV and 100,000X with A) 100 particles, B) 1,400 particles, and C) 55,000 particles.