Skip to main content
PMC home page
Clinical Orthopaedics and Related Research logoLink to Clinical Orthopaedics and Related Research
. 2008 Feb 10;466(3):670–676. doi: 10.1007/s11999-007-0096-0

Hierarchy of Stability Factors in Reverse Shoulder Arthroplasty

Sergio Gutiérrez 1,2, Tony S Keller 2, Jonathan C Levy 3, William E Lee 1, Zong-Ping Luo 2,✉
PMCID: PMC2505225  PMID: 18264855

Abstract

Reverse shoulder arthroplasty is being used more frequently to treat irreparable rotator cuff tears in the presence of glenohumeral arthritis and instability. To date, however, design features and functions of reverse shoulder arthroplasty, which may be associated with subluxation and dislocation of these implants, have been poorly understood. We asked: (1) what is the hierarchy of importance of joint compressive force, prosthetic socket depth, and glenosphere size in relation to stability, and (2) is this hierarchy defined by underlying and theoretically predictable joint contact characteristics? We examined the intrinsic stability in terms of the force required to dislocate the humerosocket from the glenosphere of eight commercially available reverse shoulder arthroplasty devices. The hierarchy of factors was led by compressive force followed by socket depth; glenosphere size played a much lesser role in stability of the reverse shoulder arthroplasty device. Similar results were predicted by a mathematical model, suggesting the stability was determined primarily by compressive forces generated by muscles.

Introduction

Management of patients who have an irreparable rotator cuff tear in the presence of glenohumeral arthritis and instability historically has been a challenge. Treatment options continue to evolve, and one of the newest is reverse shoulder arthroplasty (RSA) [3, 13]. The uniqueness of RSA is its conversion of the humerus into a socket (humerosocket) and the glenoid into a ball (glenosphere) with more stable congruent articulation for compensation of the dysfunctional rotator cuff. Clinical studies have provided evidence of pain relief and functional improvements after RSA [3, 5, 9, 12, 13, 28, 32, 36].

Although improving glenohumeral stability is the ultimate aim of RSA, subluxation and dislocation of RSA devices still occur. Studies have shown various dislocation rates: 2.4%, 6.3%, 8.6%, 16.7%, and 31% [7, 8, 10, 34, 36]. In one study, in which the dislocation rate was 7.5%, dislocation was the most common complication [35]. Joint stability, extensively studied in total shoulder arthroplasty (TSA) [2, 31], has been associated with joint contact characteristics, such as prosthetic surface geometry and the coefficient of friction present at the interface. Preservation of the joint compressive force is also a key factor in stability. Based on this biomechanical information in TSA and clinical observations, we believe these factors also may be critical to joint stability in RSA. However, their importance in relation to the stability of the implant has not been defined. As a result, selection by the surgeon of current prosthetic designs is largely empirical, which inevitably increases the probability of undesirable outcomes in RSA.

To elucidate the concept of stability in reverse shoulder implants, we addressed two questions: (1) What is the hierarchy of importance of joint compressive force, prosthetic socket depth, and glenosphere size in relation to stability?; and (2) Is this hierarchy defined by underlying joint contact characteristics, including surface geometry and coefficient of friction, theoretically predictable?

Materials and Methods

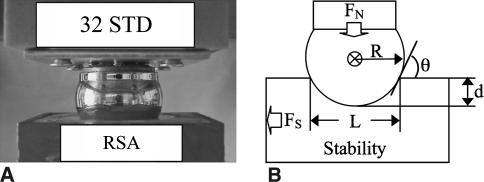
We examined RSA stability in experimental and theoretical models. In the experimental model, the dependent variable, dislocation force FS, was examined through three independent variables: the compressive force FN, the humerosocket depth d, and the glenosphere radius R (Fig. 1). The results were analyzed statistically by either two-sample or multisample inference. A theoretical simulation was performed using a rigid body joint contact model.

Fig. 1A–B.

Fig. 1A–B

Open in a new tab

(A) A photograph shows how the glenosphere (32 mm) lays on top of the standard humerosocket liner. (B) The diagram illustrates the stability model and its variables. FN = compressive force applied to glenosphere; FS = force required to dislocate glenosphere; R = radius of glenosphere; d = depth of humerosocket; L = chord length of humerosocket; θ = incident angle between the glenosphere and the humerosocket edge.

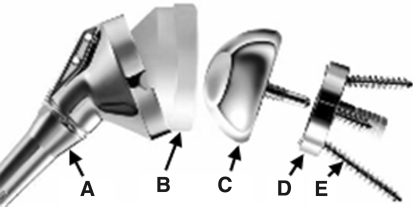
We used eight currently available RSA devices, six Encore Reverse® Shoulder Prostheses (Encore Medical Corp, Austin, TX) and two Delta III® prostheses (DePuy Orthopaedics, Warsaw, IN), in the study. The devices consisted of congruent ball and socket components with cobalt-chrome glenospheres and ultrahigh-molecular-weight polyethylene (UHMWPE) sockets (Fig. 2). We used three component sizes defined by the diameter of the glenosphere as 32 mm, 36 mm, and 40 mm. Each humerosocket had a known depth and socket radius (Fig. 2). For a given component size, socket depth was evaluated in terms of the ratio of socket depth d to socket radius R (d/R). The RSA UHMWPE socket inserts were either of standard (STD) depth or of a semiconstrained (SC) depth, in which the SC socket is deeper than the STD socket. The typical 36 Encore SC, 36 Encore STD, 36 Delta SC, and 36 Delta STD had d/R ratios of 0.56, 0.48, 0.68, and 0.46, respectively.

Fig. 2.

Fig. 2

Open in a new tab

A representation of a typical reverse shoulder implant and all of its parts is shown: A = humerosocket; B = UHMWPE humerosocket liner; C = glenosphere; D = baseplate; E = peripheral screws (Delta III® 36-mm glenosphere and standard polyethylene humerosocket).

Three additional congruent glenospheres and humerosockets were machined from Delrin® (DuPont, Wilmington, DE) for evaluation of the mathematical model. In these specimens, the glenosphere radius varied, and the d/R ratio (chosen to be in the midrange of the studied RSA devices) was held constant at 0.56.

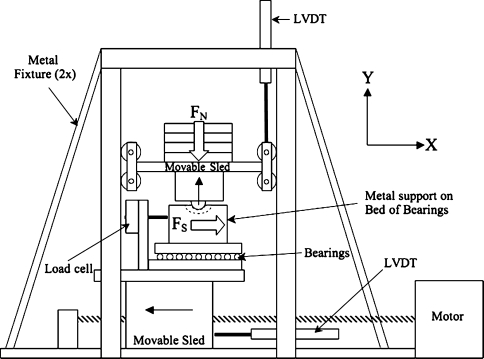
We performed mechanical testing of RSA stability on a custom biaxial loading fixture (Fig. 3) that was based on TSA stability studies [2, 31]. The humerosocket was attached to a horizontal sled that could translate freely only in the x-axis, whereas the glenosphere was attached to a vertical sled that could translate freely only in the y-axis. We used weights, placed on the vertical sled, to apply compressive forces FN (up to 200 N) to each RSA device. The FN corresponded to the range of unresisted physiologic shoulder forces [20, 27, 31]. A motor translated the horizontal sled at a constant speed of 5 cm/minute [1, 2], and a 2200-N load cell (Omega Engineering Inc, Stamford, CT) was used to measure the dislocation force FS. We performed five conditioning runs and then five recorded runs for each RSA configuration at each force level. Custom LabVIEW software (National Instruments Corp, Austin, TX) and a 12-bit data acquisition system (National Instruments Corp) were used to collect data (100 samples/second). We used silicone spray lubricant to simulate synovial fluid [14, 23, 29, 30].

Fig. 3.

Fig. 3

Open in a new tab

A schematic illustration shows the custom, biaxial testing apparatus used to measure RSA stability. A compressive force (FN: 66 N, 110 N, 155 N, or 200 N) is applied in the Y direction to the glenosphere, which is attached to the bottom of a movable sled. The amount of force it takes to dislocate the glenosphere from the humerosocket FS is measured by a load cell attached to a metal fixture resting on a bed of bearings. The load cell, metal fixture, and bearings all rest on a movable sled that moves in the X direction at a constant 5 cm/minute. LVDT = linear voltage displacement transducer used to measure movement of the sleds.

The mathematical model of RSA stability was modified from a previous model for studying conventional TSA [2]. For dislocation to occur in a ball and socket joint (Fig. 1), the resultant force must be directed outside the socket surface [26]. If both ball and socket components are assumed to be rigid bodies, the dislocation force FS is determined by the ball-socket incident angle (constraint angle) and friction and is given by

graphic file with name M1.gif 1

with

graphic file with name M2.gif 2

where μ is the coefficient of friction between the glenosphere and humerosocket, L is the chord length of the humerosocket, and θ is the incident angle between the glenosphere and the humerosocket edge.

For RSA, the congruency of ball and socket components determines the chord length and is given as L = 2[d(2R − d)]1/2; the expression for θ then can be rewritten as

graphic file with name M3.gif 3

In the experiment, we examined three factors and implants were grouped into three subsets accordingly: (1) The compressive force FN: We applied four compressive forces (66 N, 110 N, 155 N, and 200 N) corresponding to the range of unresisted physiologic shoulder forces [20, 27] to the implants with the 36 ball and socket size: 36 Encore SC, 36 Encore STD, 36 Delta SC, and 36 Delta STD. (2) The socket depth (quantified by d/R ratios): We used four pairs of implants of the same size but with different socket depths: 32 Encore SC and 32 Encore STD, 36 Encore SC and 36 Encore STD, 40 Encore SC and 40 Encore STD, and 36 Delta SC and 36 Delta STD. The test was performed under 155 N compressive force. This force corresponded to a typical value of unresisted physiologic shoulder force [20, 27]. (3) The RSA size: We grouped implants of different sizes defined by the radius R with the same d/R ratio into two groups, Group I (32 Encore SC, 36 Encore SC, and 40 Encore SC) and Group II (32 Encore STD, 36 Encore STD, and 40 Encore STD). The test also was performed under 155 N compressive force.

In the model computation, we calculated analytical values of FS from Equation 1. Friction coefficients were chosen to be 0.07 for the DePuy and Encore cobalt-chrome glenospheres and UHMWPE humerosockets based on that reported in the literature [6]. For the additional Delrin® component, μ was 0.27. This was estimated from Equations 1 and 3 using the Delrin®-Delrin® ball and socket d/R ratio and the experimentally measured FN and FS.

We used a t test in detection of differences in each pair (32 Encore SC and 32 Encore STD, 36 Encore SC and 36 Encore STD, 40 Encore SC and 40 Encore STD, and 36 Delta SC and 36 Delta STD) to examine d/R ratio effect on RSA stability. A one-way analysis of variance was used to detect differences in dislocation force among multiple groups of prostheses for determination of ball and socket size factor and compressive force factor. When we found significant differences, Tukey’s honestly significant difference test was applied for post hoc comparison [19].

Results

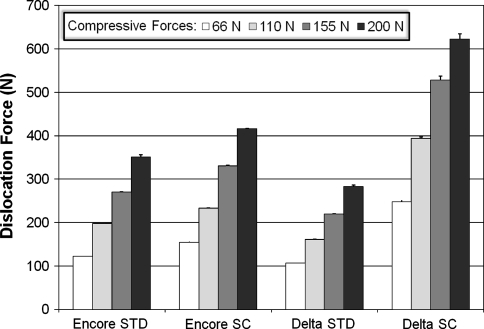
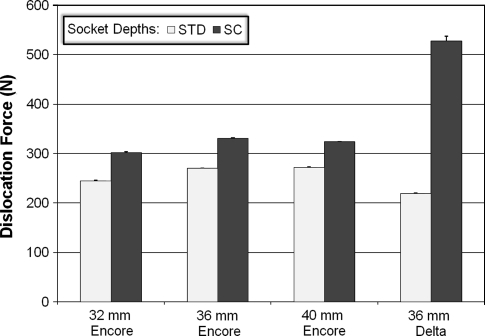
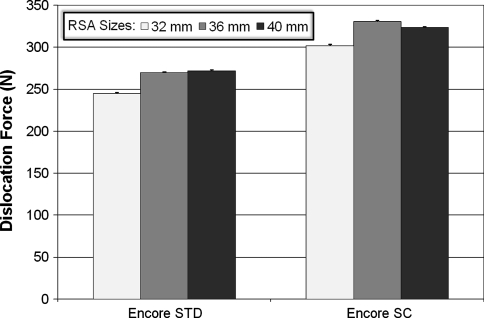
Implant stability was most affected by the compressive force with differences among the four compressive force conditions (Fig. 4). In the 36 Encore STD, the dislocation force increased 186.1% (p = 4.2 × 10−34) and the difference was seen between every force level. In the 36 Encore SC, the same force increased 168.3% (p = 4.4 × 10−25), with the difference seen between every level. Similarly, the dislocation force increased 165.4% in 36 Delta STD (p = 4.9 × 10−21) and 150.8% in 36 Delta SC (p = 2.2 × 10−27), respectively. The differences also were seen between every force level in each case. The d/R ratio had an effect on the stability of RSAs but to a lesser extent than the compressive force (Fig. 5). The force FS required to dislocate the ball and socket components was higher in SC devices (those with a deeper socket) than in STD devices for each pair compared. We observed an increase of 23.3% (p = 4.3 × 10−23) from 32 Encore STD to 32 Encore SC; 22.6% (p = 5.3 × 10−24) from 36 Encore STD to 36 Encore SC; 19.1% (p = 7.4 × 10−22) from 40 Encore STD to 40 Encore SC; and 140.6% (p = 3.0 × 10−46) from 36 Delta STD to 36 Delta SC. Overall, the 36 Delta SC with the highest d/R ratio of 0.68 showed the highest stability, with a dislocation force of 527.7 N. The ball and socket size had much less of an effect on RSA stability (Fig. 6). Only the smallest glenosphere (32) had smaller dislocation force than the other two sizes (36 and 40) in STD (p = 9.3 × 10−14) and SC (p = 6.3 × 10−13) (the difference ranging from 22.2 N to 29.2 N), which was approximately 10% of the dislocation force. The dislocation force had no difference between sizes 36 Encore STD and 40 Encore STD. The dislocation force also decreased from 36 Encore SC to 40 Encore SC (p = 6.3 × 10−13), but the decrease was only 7 N or approximately 2% of the dislocation force.

Fig. 4.

Fig. 4

Open in a new tab

The graph shows how successively larger forces are required to dislocate the 36 mm glenospheres from the humerosocket when larger and larger compressive forces are applied to the glenosphere. It can also be seen how increasing the depth of the humerosocket (going from a STD depth to a SC depth) increases the force required to dislocate the glenosphere.

Fig. 5.

Fig. 5

Open in a new tab

The graph shows how increasing the depth of the humerosocket (going from a STD depth to a SC depth) increases the force required to dislocate the glenosphere. The 36-mm Delta SC humerosocket has 2.4 times the stability when compared with the 36-mm Delta STD humerosocket.

Fig. 6.

Fig. 6

Open in a new tab

The graph shows minimum differences in dislocation forces for different implant sizes (32 mm, 36 mm, and 40 mm).

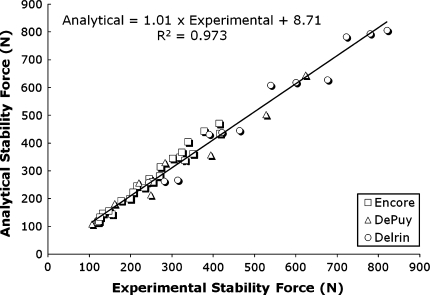
The theoretical rigid body model accurately predicted the hierarchy of these factors associated with RSA stability (Fig. 7). Considering all of the RSA and Delrin® devices tested, a considerable positive linear correlation (R2 = 0.973, absolute average error [4] of 7.98%) between the analytical and experimentally measured FS was obtained: Analytical FS = 1.01 · Experimental FS + 8.71.

Fig. 7.

Fig. 7

Open in a new tab

The graph shows a linear correlation between analytical and experimental data of stability force FS with all RSA components studied.

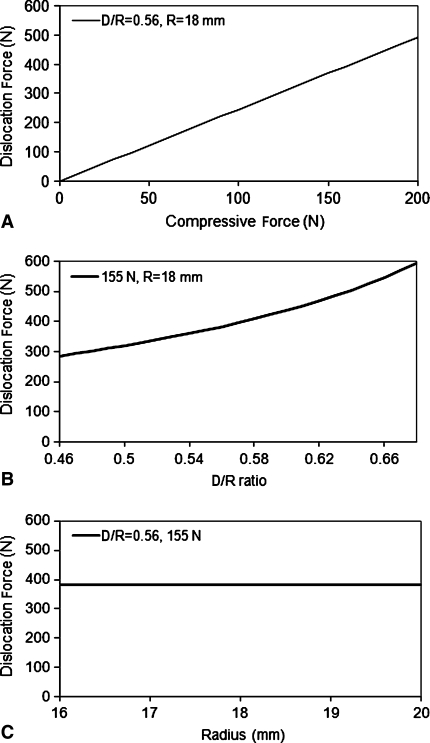
When simulating the compressive force from 0 N to 200 N, the dislocation force changed from 0 N to 492.5 N. The relationship was linear as defined in Equation 1 (Fig. 8A). The d/R ratio affected the dislocation force in a less dramatic fashion. For the d/R ratio from 0.46 to 0.68, the dislocation force increased from 283.4 N to 592.6 N (Fig. 8B). The rigid body model also predicted, for a given d/R ratio, the change of ball and socket size would not cause any alteration in the dislocation force (Fig. 8C).

Fig. 8A–C.

Fig. 8A–C

Open in a new tab

The graphs show the trends present when the analytical model for RSA stability is used to calculate dislocation force. (A) This graph shows how the force it takes to dislocate the glenosphere from the humerosocket increases linearly as a function of increasing the compressive force applied. (B) This graph shows how the force it takes to dislocate the glenosphere from the humerosocket increases exponentially as a function of increasing the depth of the humerosocket, represented by the d/R ratio. (C) This graph shows how the force it takes to dislocate the glenosphere from the humerosocket remains constant as a function of increasing the radius of the glenosphere.

Discussion

As the use of RSA increases, efforts to maximize functional outcomes and limit complications become more important. Understanding how to prevent and manage prosthetic instability therefore is of paramount importance. Our intent was to clarify two critical concerns associated with RSA stability: the hierarchy of factors associated with the inherent stability of RSA devices and the predictability of the hierarchy by a simple theoretical rigid body model.

There are inherent assumptions and limitations associated with the study design. The glenosphere was limited to one joint motion component: translation relative to the humerosocket. This constraint was used to verify mathematical model predictions. Additional studies are needed to examine the validity of the hierarchy by including a rotational component and a full six-degree motion configuration. The second limitation was on the loading applied to the implant. A static compressive force was applied to simulate joint compression followed by a quasistatic transverse force to dislocate the ball-socket joint. We carefully selected the loading range corresponding to the range of unresisted physiologic shoulder forces [20, 27]. Such a loading condition had been used in mechanical studies for shoulder arthroplasty [24, 31]. Compared with this idealized experiment, the manner in which RSA components are loaded in vivo may differ appreciably, namely the normal and surgically repaired shoulder experience complex forces that vary in magnitude, direction, and loading rate. Currently, however, the magnitudes and the directions of resultant forces that cause dislocation of the ball-socket articulation are not well understood. Also, resistance afforded by ligaments, joint capsule, and muscles was represented as a net compressive load, and the effects of asymmetric loading were not considered. Additional work may be needed to determine the role, if any, of active and passive tissue in RSA stability, and studies using cadavers are warranted. Finally, stability is not the only factor that should be considered in selecting a RSA design and selection; several others also are critical. The effect of prosthetic design on range of motion (ROM) of the device, impingement, scapular notching, glenosphere-baseplate fixation, muscular weakness or deficiency, and ability to manage bone deficiencies also should be considered [11, 13, 22].

Measurement of joint resistance to dislocation provides quantitative support to the general concept that RSA devices are much more stable than the normal glenohumeral joint and TSA devices. The normal glenohumeral joint has a stability force ratio (maximum allowable subluxation force/joint compression force) of approximately 0.5 [16], whereas TSA has less than 1.0 [2, 18]. In contrast, RSA has a stability force ratio greater than 2. Additionally, stability was altered only slightly by glenosphere size in the laboratory experiment, but this was not seen in the theoretical simulation, indicating the size effect was associated with the nonrigidity of the actual system. The possible explanation was temporary distortion of the local congruency at the surface contact because of nonrigidity, leading to reduced stability as in the case of incongruent ball-socket systems [2]. This size effect could be observed more clearly in the smaller implants because of the increase in surface stress concentration.

The data suggest the most effective approach to increase RSA stability is through the joint compressive force. Clinically, the compressive force is generated largely by active and passive structures of soft tissue together with the negative pressure in the glenohumeral joint. To date, techniques described to enhance RSA stability through soft tissue tension have focused on tensioning of the deltoid. This may be accomplished by lowering the humerus relative to the glenoid [9], lengthening the humerus by inserting a thicker polyethylene humeral component and retaining as much proximal humerus as possible, or by lateralizing the humerus [13]. In the case of lateralizing the humerus, the center of rotation (COR) of the glenosphere-humerosocket joint becomes closer to that of the anatomic COR of the humerus. The normal tension range of the soft tissues, including the deltoid and the residual rotator cuff muscles, may be preserved after surgery, prohibiting long-term adverse adaptability of soft tissues attributable to either undertensioning or overtensioning. The anatomically preserved soft tissues, in turn, may provide sufficient compressive force similar to that present in the normal glenohumeral joint and in anatomic TSA [17, 21] (eg, 200 N compressive force at 50° abduction [33]) to keep the glenosphere-humerosocket joint stable.

Another approach to improve RSA stability is with the use of a deeper socket. In this case, a potential tradeoff is a decrease in ROM. Clinically, however, this tradeoff may be diminished by placing the glenosphere more inferiorly relative to the glenoid or by increasing the glenosphere COR offset relative to the glenoid (selecting a glenosphere with a more lateral COR). Inferior placement of the glenosphere has been shown to provide glenohumeral abduction ROM of 81° compared with 68° for a glenosphere placed flush with the glenoid rim [25], and a glenosphere with a 10-mm COR offset lateral to the glenoid surface has been shown to provide glenohumeral abduction of 97° compared with 54° for a glenosphere with a COR at the glenoid [15].

Glenosphere-humerosocket stability is an important variable in selecting an appropriate RSA and is closely correlated to compressive force, socket depth, and, to a lesser extent, implant size. Theoretical simulation further suggests this hierarchy of mechanical factors is defined primarily by rigid body contact characteristics. Greater understanding of the key components to stability of the RSA will help the surgeon prevent and manage complications related to prosthetic instability. Additional research is needed to more fully understand the interrelationship between factors that affect stability and long-term clinical outcomes.

Acknowledgments

We thank Allen Smith and Karmen Anderson for technical support.

Footnotes

Deceased.

SG, TSK, and ZPL received funding from the Florida Orthopaedic Institute Research Foundation.

References

  • 1.American Society for Testing and Materials (ASTM). Standard specification for ultra-high-molecular-weight polyethylene powder and fabricated form for surgical implants. Designation F648–696.
  • 2.Anglin C, Wyss UP, Pichora DR. Shoulder prosthesis subluxation: theory and experiment. J Shoulder Elbow Surg. 2000;9:104–114. [DOI] [PubMed]
  • 3.Boileau P, Watkinson DJ, Hatzidakis AM, Balg F. Grammont reverse prosthesis: design, rationale, and biomechanics. J Shoulder Elbow Surg. 2005;14(1 suppl S):147S–161S. [DOI] [PubMed]
  • 4.Bonnet DG, Seier E. Confidence intervals for mean absolute deviations. Am Stat. Nov. 2003;57:233–236.
  • 5.Boulahia A, Edwards TB, Walch G, Baratta RV. Early results of a reverse design prosthesis in the treatment of arthritis of the shoulder in elderly patients with a large rotator cuff tear. Orthopedics. 2002;25:129–133. [DOI] [PubMed]
  • 6.Brockett C, Williams S, Jin Z, Isaac G, Fisher J. Friction of total hip replacements with different bearings and loading conditions. J Biomed Mater Res B Appl Biomater. 2007;81:508–515. [DOI] [PubMed]
  • 7.Bufquin T, Hersan A, Hubert L, Massin P. Reverse shoulder arthroplasty for the treatment of three- and four-part fractures of the proximal humerus in the elderly: a prospective review of 43 cases with a short-term follow-up. J Bone Joint Surg Br. 2007;89:516–520. [DOI] [PubMed]
  • 8.Cazeneuve JF, Cristofari DJ. [Grammont reversed prosthesis for acute complex fracture of the proximal humerus in an elderly population with 5 to 12 years follow-up] [in French]. Rev Chir Orthop Reparatrice Appar Mot. 2006;92:543–548. [DOI] [PubMed]
  • 9.De Wilde L, Mombert M, Van Petegem P, Verdonk R. Revision of shoulder replacement with a reversed shoulder prosthesis (Delta III): report of five cases. Acta Orthop Belg. 2001;67:348–353. [PubMed]
  • 10.De Wilde L, Sys G, Julien Y, Van Ovost E, Poffyn B, Trouilloud P. The reversed Delta shoulder prosthesis in reconstruction of the proximal humerus after tumour resection. Acta Orthop Belg. 2003;69:495–500. [PubMed]
  • 11.Endo K, Ikata T, Katoh S, Takeda Y. Radiographic assessment of scapular rotational tilt in chronic shoulder impingement syndrome. J Orthop Sci. 2001;6:3–10. [DOI] [PubMed]
  • 12.Favard L, Lautmann S, Sirveaux F, Oudet D, Kerjean Y, Huguet D. Hemi-arthroplasty versus reverse arthroplasty in treatment of osteoarthritis with massive rotator cuff tear. In: Walch G, Boileau P, Molé D, eds. 2000 Prothéses d’épaule: recul de 2 à 10 ans. Paris, France: Sauramps Médical; 2001:261–268.
  • 13.Frankle M, Siegal S, Pupello D, Saleem A, Mighell M, Vasey M. The Reverse Shoulder Prosthesis for glenohumeral arthritis associated with severe rotator cuff deficiency: a minimum two-year follow-up study of sixty patients. J Bone Joint Surg Am. 2005;87:1697–1705. [DOI] [PubMed]
  • 14.Friction Center Coefficient Database. Center for Advanced Friction Studies, Southern Illinois University Carbondale, 2005. Available at: http://frictioncenter.siu.edu/databaseSearch.html. Accessed 22 October 2007.
  • 15.Gutiérrez S, Levy JC, Lee WE 3rd, Keller TS, Maitland ME. Center of rotation affects abduction range of motion of reverse shoulder arthroplasty. Clin Orthop Relat Res. 2007;458:78–82. [DOI] [PubMed]
  • 16.Halder AM, Kuhl SG, Zobitz ME, Larson D, An KN. Effects of the glenoid labrum and glenohumeral abduction on stability of the shoulder joint through concavity-compression: an in vitro study. J Bone Joint Surg Am. 2001;83:1062–1069. [DOI] [PubMed]
  • 17.Halder AM, Zhao KD, Odriscoll SW, Morrey BF, An KN. Dynamic contributions to superior shoulder stability. J Orthop Res. 2001;19:206–212. [DOI] [PubMed]
  • 18.Karduna AR, Williams GR, Williams JL, Iannotti JP. Joint stability after total shoulder arthroplasty in a cadaver model. J Shoulder Elbow Surg. 1997;6:506–511. [DOI] [PubMed]
  • 19.Kirk RE. Experimental Design: Procedures for the Behavioral Sciences. 3rd ed. Pacific Grove, CA: Brooks/Cole; 1995.
  • 20.Labriola JE, Lee TQ, Debski RE, McMahon PJ. Stability and instability of the glenohumeral joint: the role of shoulder muscles. J Shoulder Elbow Surg. 2005;14(1 suppl S):32S–38S. [DOI] [PubMed]
  • 21.Lee SB, Kim KJ, O’Driscoll SW, Morrey BF, An KN. Dynamic glenohumeral stability provided by the rotator cuff muscles in the mid-range and end-range of motion: a study in cadavera. J Bone Joint Surg Am. 2000;82:849–857. [DOI] [PubMed]
  • 22.Lin JJ, Lim HK, Yang JL. Effect of shoulder tightness on glenohumeral translation, scapular kinematics, and scapulohumeral rhythm in subjects with stiff shoulders. J Orthop Res. 2006;24:1044–1051. [DOI] [PubMed]
  • 23.Linn FC. Lubrication of animal joints. I. The arthrotripsometer. J Bone Joint Surg Am. 1967;49:1079–1098. [PubMed]
  • 24.Matsen FA 3rd, Chebli C, Lippitt S; American Academy of Orthopaedic Surgeons. Principles for the evaluation and management of shoulder instability. J Bone Joint Surg Am. 2006;88:648–659. [DOI] [PubMed]
  • 25.Nyffeler RW, Werner CM, Gerber C. Biomechanical relevance of glenoid component positioning in the reverse Delta III total shoulder prosthesis. J Shoulder Elbow Surg. 2005;14:524–528. [DOI] [PubMed]
  • 26.Oosterom R, Herder JL, van der Helm FC, Swieszkowski W, Bersee HE. Translational stiffness of the replaced shoulder joint. J Biomech. 2003;36:1897–1907. [DOI] [PubMed]
  • 27.Parsons IM, Apreleva M, Fu FH, Woo SL. The effect of rotator cuff tears on reaction forces at the glenohumeral joint. J Orthop Res. 2002;20:439–446. [DOI] [PubMed]
  • 28.Rittmeister M, Kerschbaumer F. Grammont reverse total shoulder arthroplasty in patients with rheumatoid arthritis and nonreconstructible rotator cuff lesions. J Shoulder Elbow Surg. 2001;10:17–22. [DOI] [PubMed]
  • 29.Roberts BJ, Unsworth A, Mian N. Modes of lubrication in human hip joints. Ann Rheum Dis. 1982;41:217–224. [DOI] [PMC free article] [PubMed]
  • 30.Scholes SC, Unsworth A. Comparison of friction and lubrication of different hip prostheses. Proc Inst Mech Eng H. 2000;214:49–57. [DOI] [PubMed]
  • 31.Tammachote N, Sperling JW, Berglund LJ, Steinmann SP, Cofield RH, An KN. The effect of glenoid component size on the stability of total shoulder arthroplasty. J Shoulder Elbow Surg. 2007;16(3 suppl):S102–S106. [DOI] [PubMed]
  • 32.Valenti PH, Boutens D, Nerot C. Delta 3 reversed prosthesis for osteoarthritis with massive rotator cuff tear: long term results. In: Walch G, Boileau P, Molé D, eds. 2000 Prothéses d’épaule: recul de 2 à 10 ans. Paris, France: Sauramps Médical; 2001:253–259.
  • 33.van der Helm FC. Analysis of the kinematic and dynamic behavior of the shoulder mechanism. J Biomech. 1994;27:527–550. [DOI] [PubMed]
  • 34.Van Seymortier P, Stoffelen D, Fortems Y, Reynders P. The reverse shoulder prosthesis (Delta III) in acute shoulder fractures: technical considerations with respect to stability. Acta Orthop Belg. 2006;72:474–477. [PubMed]
  • 35.Wall B, Nové -Josserand L, O’Connor DP, Edwards TB, Walch G. Reverse total shoulder arthroplasty: a review of results according to etiology. J Bone Joint Surg Am. 2007;89:1476–1485. [DOI] [PubMed]
  • 36.Werner CM, Steinmann PA, Gilbart M, Gerber C. Treatment of painful pseudoparesis due to irreparable rotator cuff dysfunction with the Delta III reverse-ball-and-socket total shoulder prosthesis. J Bone Joint Surg Am. 2005;87:1476–1486. [DOI] [PubMed]

Articles from Clinical Orthopaedics and Related Research are provided here courtesy of The Association of Bone and Joint Surgeons

RESOURCES