Does the Release of Potassium from Astrocyte Endfeet Regulate Cerebral Blood Flow?

Abstract

Local increases in neuronal activity within the brain lead to dilation of blood vessels and to increased regional cerebral blood flow. Increases in extracellular potassium concentration are known to dilate cerebral arterioles. Recent studies have suggested that the potassium released by active neurons is transported through astrocytic glial cells and released from their endfeet onto blood vessels. The results of computer simulations of potassium dynamics in the brain indicate that the release of potassium from astrocyte endfeet raises perivascular potassium concentration much more rapidly and to higher levels than does diffusion of potassium through extracellular space, particularly when the site of a potassium increase is some distance from the vessel wall. On the basis of this finding, it is proposed that the release of potassium from astrocyte endfeet plays an important role in regulating regional cerebral blood flow in response to changes in neuronal activity.

Roy and Sherrington, in 1890, suggested that “the brain possesses an intrinsic mechanism by which its vascular supply can be varied locally in correspondence with local variations of functional activity” (1, p. 105). Such an intrinsic homeostatic mechanism would help to maintain an adequate supply of oxygen and nutrients to the brain despite widely varying levels of neuronal activity. Although the existence of such a regulatory process has been established (2–5), the mechanism that links neuronal activity and regional cerebral blood flow (rCBF) remains unknown. Interstitial concentrations of potassium and hydrogen ions, adenosine, and several neuro-transmitters vary with neuronal activity. These substances all cause changes in arteriole diameter (6, 7) and have been implicated in the regulation of rCBF. However, the relative importance of each of these factors is not known.

Extracellular K⁺ concentration ([K⁺]_o) varies widely during periods of neuronal activity and can rise from a quiescent level of approximately 3 mM to a maximum level of more than 10 mM (8). Cerebral arteries and arterioles (but not capillaries) are extremely sensitive to changes in K⁺ concentration, increasing in diameter as much as 50% in response to a change in [K⁺]_o from 3 to 10 mM (9, 10). This sensitivity to K⁺ could be an important factor in regulating rCBF. Potassium released by active neurons could diffuse through extracellular space to the ablumenal wall of arterioles and cause arteriole dilation. The resulting decrease in vascular resistance (11) would increase rCBF, thus bringing a greater supply of oxygen to precisely the region where it is needed, to the activated portion of the brain. However, arterioles are widely spaced within the brain [they are often separated by more than 500 μim (12)] and may not necessarily be near regions of activated tissue. Thus, the K⁺ released by active neurons would have to diffuse tens or hundreds of micrometers before reaching arterioles and effecting dilation.

The fate of the K⁺ released by neurons into the interstitial fluid is determined, in part, by astrocytes. The K⁺ released by neurons increases [K⁺]_o, which in turn generates a passive influx of K⁺ current into astrocytes. The K⁺ influx depolarizes these cells and causes a passive efflux of current from other cell regions or from astrocytes electrically coupled to them. Because astrocytes are almost exclusively permeable to K⁺ (13), this outward current is carried by K⁺.

The endfeet of astrocytes, which terminate on blood vessels and on the pial surface of the brain, have a much greater K⁺ conductance than other regions of the cell (14). Thus, a large fraction of the outward K⁺ current generated by [K⁺]_o increases would flow out from astrocyte endfeet. The efflux of K⁺ current from the endfeet of astrocytes is termed “K⁺ siphoning” (15).

Cerebral arterioles are completely surrounded by the endfeet of astrocytes. Thus, during periods of neuronal activity, K⁺ siphoned from astrocyte endfeet would be deposited directly onto arteriole walls. This process could be important in the regulation of rCBF. Potassium siphoning could raise the K⁺ concentration ([K⁺]) at the arteriole wall more rapidly and to a higher level than would diffusion of K⁺ through extracellular space. The resulting dilation of the arteriole would augment rCBF to a greater extent than otherwise possible.

We have evaluated the effectiveness of K⁺ siphoning in increasing [K⁺] at the arteriole wall with computer simulations. We have incorporated the following processes into our model: (i) an imposed, instantaneous rise in [K⁺]_o from 3.0 to 10.0 mM in the interstitial space of the brain (simulating the release of K⁺ from neurons), (ii) diffusion of K⁺ through extracellular space, (iii) the transfer of K⁺ by current flow through astrocytes (K⁺ siphoning), and (iv) passive uptake of K⁺ into a cellular distribution space (16). Details of the model are given in (17).

The K⁺ concentration at the arteriole wall was calculated as a function of time after the imposed increase in [K⁺]_o. When the [K⁺]_o increase was distributed uniformly throughout the brain, K⁺ siphoning enhanced the rise in |K⁺] at the arteriole wall to a small but significant extent (Fig. 1A). When driven solely by diffusion (Fig. 1A, diffusion), [K⁺] rose with a slight delay, peaking with a latency of 324 msec. When both diffusion and siphoning were included in the calculations (Fig. 1A, diffusion and siphoning), the [K⁺] rise was more rapid (peaking at 60 msec) and was 6% larger in peak magnitude.

Fig. 1.

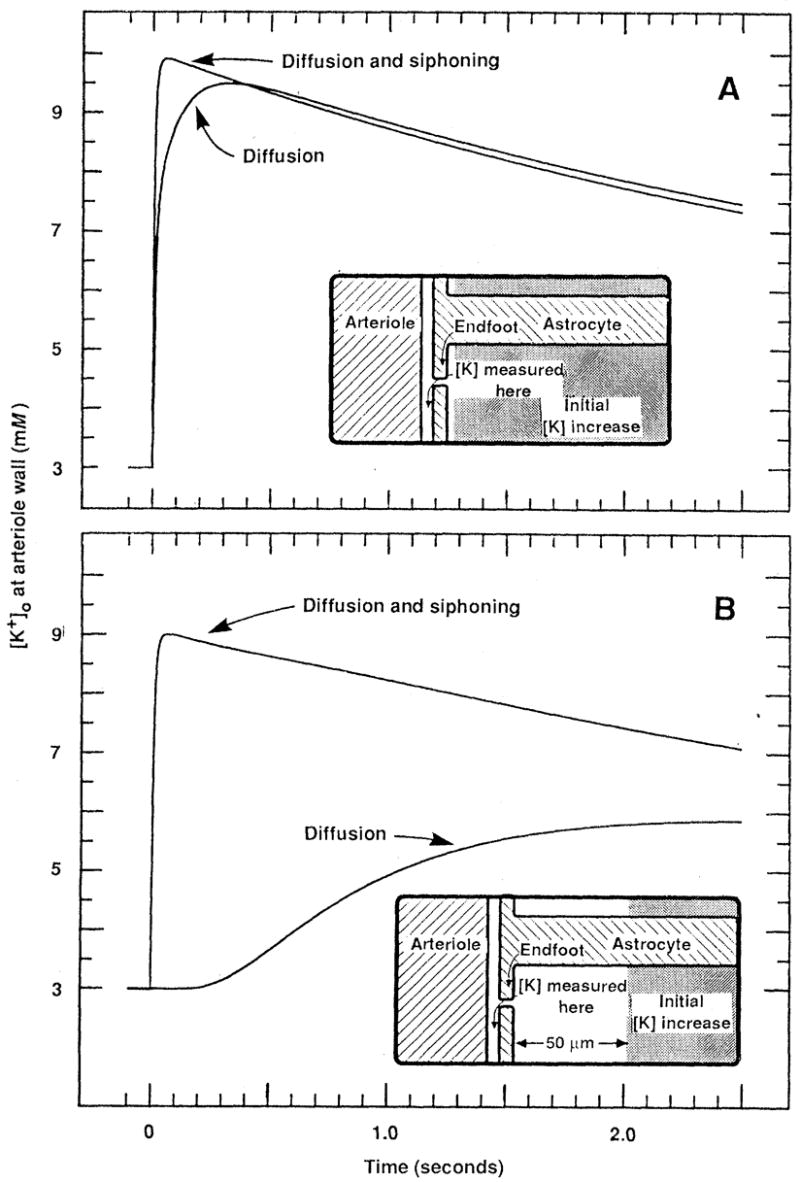
Simulation of the [K⁺] buildup at the external wall of an arteriole after an imposed, instantaneous rise in [K⁺]_o from 3 to 10 mM within the brain. Transport of K⁺ from the region of [K⁺]_o increase to the arteriole occurred either by diffusion through extracellular space (diffusion curves) or by both K⁺ siphoning through astrocytes and diffusion (diffusion and siphoning curves). (A) The imposed [K⁺]_o increase was distributed uniformly throughout the brain (beginning 2.5 μm from the arteriole). (B) The imposed [K⁺]_o increase began a distance of 50 μm from the arteriole. Insets illustrate the geometry of the model system and the initial distribution of the imposed [K⁺]_o increase (shaded region). In both (A) and (B) [K⁺] at the arteriole increased more rapidly and to a higher level when diffusion was augmented by K⁺ siphoning.

The effect of K⁺ siphoning was far greater when the imposed increase in [K⁺]_o occurred at some distance from the arteriole. When the imposed [K⁺]_o increase began just 50 μm from the arteriole wall, the increase in [K⁺] at the arteriole due to diffusion alone was delayed severely, peaking at 2520 msec (Fig. 1B, diffusion). This delay was almost completely eliminated when siphoning currents were included in the calculations; [K⁺] at the arteriole peaked at 66 msec (Fig. 1B, diffusion and siphoning). In addition, the maximal [K⁺] attained was more than double (109% larger) in die latter case.

Simulation results were insensitive to variations in many system parameters including changes in the magnitude of the imposed K⁺ increase, the volume of the K⁺ distribution space, the absolute value of astrocyte membrane conductance, and the percentage of astrocyte membrane conductance localized to the endfoot. Large changes in these parameters had little effect on the comparative effectiveness of K⁺ siphoning and diffusion in transferring K⁺ to the arteriole wall.

The simulations indicate that K⁺ siphoning significantly augments diffusion in increasing |K⁺] at arterioles. Potassium siphoning is effective for two reasons, (i) The transfer of K⁺ by the siphoning process, unlike that by diffusion, occurs almost instantaneously (15). (It is mediated by current flow and is slowed down only by the time constant of astrocytes.) (ii) The space between astrocyte endfeet and arterioles is extremely narrow [the width of the basal lamina, approximately 20 nm (18)]. Thus, even a small efflux of K⁺ from the endfoot will increase [K⁺] rapidly within this narrow space.

On the basis of our simulations, we conclude that K⁺ release from astrocyte endfeet could be an important mechanism for raising [K⁺] at the arteriole wall, particularly when the site of the initial [K⁺]_o increase is some distance from the arteriole. Undoubtedly, many mechanisms play an important role in the regulation of cerebral blood flow under various physiological conditions. We propose that K⁺ siphoning onto arteriole walls is an important mechanism for modulating rCBF in response to local variations in neuronal activity.