INTRODUCTION
Passive stiffness is often cited as a contributing factor to various gait impairments. For example, hip flexor tightness may limit step length, and hence gait speed, in elderly populations [1]. In addition, excessive ankle plantarflexor stiffness arising from muscle spasticity can limit dorsiflexion and thereby contribute to equinus gait patterns [2]. While the detrimental effects are recognized, the potential functional role that passive stiffness plays in normal gait is not well established. A quantitative assessment of passive elastic mechanisms present in normal walking could therefore provide an improved basis for investigating factors underlying pathological gait.
A number of previous investigators have identified mathematical models of the passive joint moment-angle relationship [3-8]. These models suggest that substantial passive joint moments could be present in normal gait [5, 8], and may also be influenced by the stretch of biarticular muscles [3, 5]. To the extent that the passive joint moments arise from elastic deformation, passive mechanisms may also provide for energy storage and return during gait [8]. For example, stretch of the hip flexors during late stance may store energy that is subsequently returned in pre- and initial swing [9].
The purpose of this study was to quantitatively estimate the contribution of passive mechanisms to lower extremity joint kinetics in normal walking at varied speeds. Based on previous implications regarding pathologitcal gait patterns, we tested the hypotheses that the passive-elastic moments at the hip and ankle contribute substantially to the hip flexor and ankle plantarflexor power bursts seen during walking. We also hypothesized that these passive mechanisms would include contributions from biarticular muscles.
METHODS
Subject Selection
Twenty healthy young adults participated in the study including 9 males (age 24±4, height 182±10 cm, weight 79±8 kg) and 11 females (age 24±3, height 166±10 cm, weight 58±13 kg). Subjects had no history of major orthopedic diagnosis or pain in the lower back, pelvis, or lower extremity. Each subject gave informed consent in accordance with a protocol approved by the University of Wisconsin’s Health Sciences Institutional Review Board.
Experimental Testing
The experimental testing included two components: a passive testing protocol [10] and gait analysis. During all testing, body segment kinematics (100Hz) were measured with a passive motion capture system (Motion Analysis Corporation, Santa Rosa, CA) and processed using motion capture software (EVaRT v. 4.7.1). The kinematic marker set consisted of 23 anatomical markers placed on identifiable landmarks and 19 additional tracking markers placed on limb segments to aid in segment tracking [11]. A subset of the marker set, consisting of the markers on the dominant lower extremity, was used in tracking limb motion during passive testing (Fig. 1a).
Figure 1.
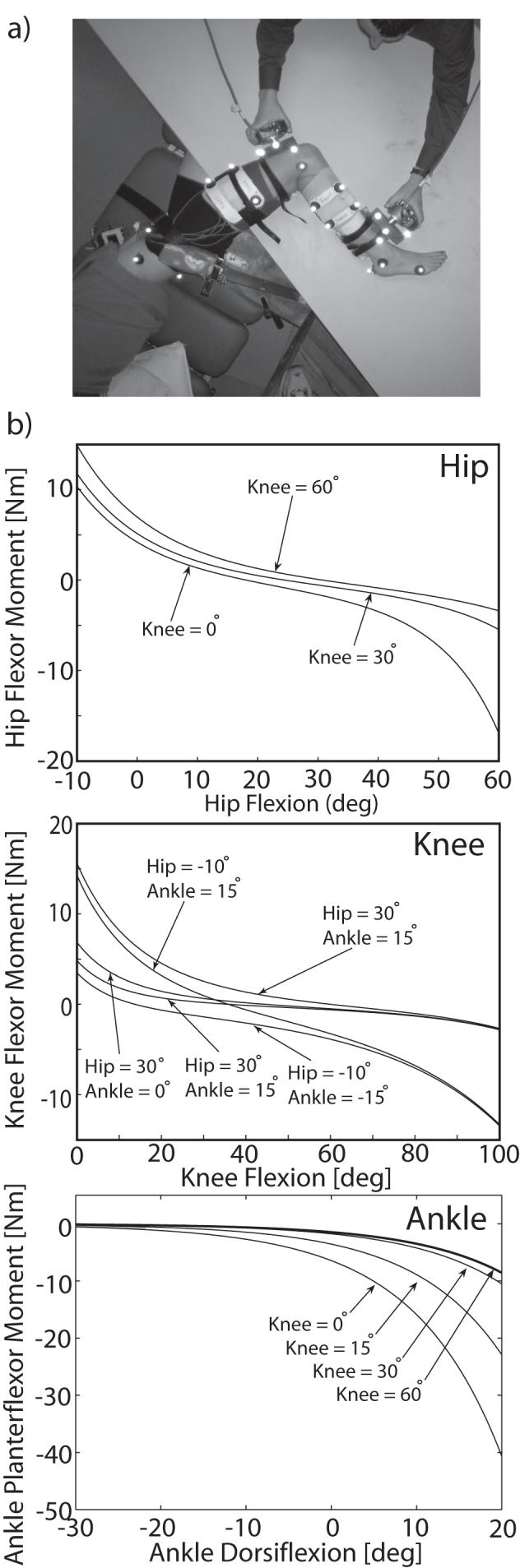
(a) During passive testing, the subject was in a side lying position with the pelvis restrained while the dominant limb was manipulated using two 3D handheld load cells. The set-up is viewed here from a top view with the table angled posterior to the subject to allow for full hip extension and knee flexion. Retroreflective markers were placed on bony landmarks and limb segments to track joint angles. (b) A set of exponential functions were used to describe the relationship between joint angles and passive joint moments. These functions accounted for the contribution of passive stretch of biarticular muscles to the passive moments observed.
A passive testing protocol was designed to obtain continuous joint angle and passive joint moment measurements while the subject’s dominant limb was manipulated through full sagittal ranges of motion about the hip, knee and ankle. The subject was positioned side lying such that sagittal plane motion would occur in a non-gravitational plane. A padded brace was used to secure the pelvis. The subject’s limb was supported on a smooth table by two carts each comprising a plate supported by ball bearings to allow for motion with negligible resistance. The limb was manipulated by a physical therapist using two three-dimensional handheld load cells (Model 45E15A, JR3 Inc., Woodland, CA). Manipulations were conducted at a slow speed (< 10 deg/sec) in order to minimize inertial contributions to the observed joint moments. Fifteen unique trials were performed to elicit passive contributions from the uniarticular soft tissues as well as major biarticular muscles acting about the hip, knee and ankle joints [10]. Four markers, rigidly attached to each load cell, were used to continuously track the position and orientation of the load cell relative to the lower extremity.
Load cell forces, moments and electromyographic (EMG) activities were recorded (2000 Hz) simultaneously with the kinematics using a 12 bit A/D converter interfaced with the collection computer. EMG activities were recorded using seven pre-amplified single differential surface electrodes (DE-2.1, DelSys, Inc, Boston, MA) placed over the rectus femoris, vastus lateralis, medial hamstrings, lateral hamstrings, tibialis anterior, soleus and gastrocnemius muscles. The electrodes had a fixed 10mm inter-electrode distance, were interfaced with an amplifier/processor unit (CMRR >84 dB at 60 Hz; input impedance > 100 MΩ), and were coated with conducting gel prior to application. Electrode locations, determined by the same investigator for each subject, were prepared by shaving the skin and cleaning with alcohol. EMG signals were visually monitored during passive testing and any trial with detectable muscle activity was repeated.
Each subject also performed a series of five walking trials at three speeds (80%, 100%, and 120% of a self-selected speed) along a 10m walkway. Preferred speed was first established by measuring the subjects average normal gait speed in the laboratory. Subjects were then asked to walk at the same speed, slower or faster, with the order randomized for each subject. Trials were repeated if the subject was not within ±5% of the desired speed. Ground reaction forces for two successive foot strikes were recorded at 2000 Hz using three imbedded force plates (Model BP400600, AMTI, Watertown, MA).
Biomechanical Modeling and Analysis
A seven segment, 18 degree-of-freedom (dof) model of the pelvis and lower extremity [12] was used to characterize joint kinematics and kinetics. Six degrees of freedom (dof) were used to define the position and orientation of the pelvis. The hip was represented by a 3 dof spherical joint. The knee was represented as a one dof joint in which non-sagittal rotations, and both tibiofemoral and patellofemoral translations were computed as a function of the sagittal knee angle [13]. The ankle and subtalar joints were represented as pin joints aligned with the anatomical axes [14].
Scaled models were developed for each subject. Body segment coordinate systems, tracking marker locations, and segment lengths were first established using the marker positions collected during an upright calibration trial. Hip joint locations were then determined by applying a functional spherical joint center identification algorithm to trials in which the subjects circumducted their legs [15]. Segment lengths and joint centers were then used to scale the segments of the generic 18 dof model.
The pelvis position, pelvis orientation, and lower extremity joint angles were computed at each time step in both the passive and gait trials using an inverse kinematics routine that minimized the sum of squared differences between measured marker positions and corresponding positions on the model [16]. Joint angles were low-pass filtered at 3 Hz (passive testing) or 6 Hz (gait testing). Joint angles were subsequently numerically differentiated to obtain the angular velocities and accelerations. Inverse dynamics analysis was used to compute the hip, knee, and ankle joint moments from the joint kinematics and measured load cell forces (passive testing) or ground reactions (gait testing). SIMM Pipeline (Musculographics Inc., Motion Analysis Corpl, Santa Rosa, CA) was used in conjunction with SD/FAST (Parametric Technology Corporation, Waltham, MA) and custom code to perform the inverse kinematics and inverse dynamics analyses.
The relationship between sagittal joint angles and passive joint moments was modeled by exponential functions that accounted for the stretch of uniarticular structures and biarticular muscles about the hip, knee, and ankle. Uniarticular functions representing the hip extensors, hip flexors, knee extensors, knee flexors, and ankle plantarflexors were each described by:
| (1) |
where is the passive joint moment associated with a joint angle θ, β is a gain parameter, and α is an offset angle. Biarticular functions representing the hamstrings, rectus femoris, and gastrocnemius were each described by:
| (2) |
| (3) |
where prox and distare the proximal and distal passive joint moments associated with proximal joint angle θprox and distal joint angle θ dist. The biarticular function was formulated with a proximal gain parameter β prox, a distal gain parameter β dist and an offset angle α in such a way that conservation of energy storage and release across the joints was ensured. Model parameters were estimated for each subject using a least squares fitting method that minimized the sum of squared differences between the measured and predicted passive moments (lsqcurvefit, MATLAB®, The Mathworks Inc.). A full description of the passive moment-angle model is available elsewhere [10].
Passive joint moments during walking were estimated using the joint angles measured during gait as inputs to the passive models (eqn’s. 1-3). These passive moments, along with net moments measured during gait testing, were multiplied by their respective joint angular velocities to determine passive and net joint powers. Passive and net power curves were then integrated over the gait cycle and over specific power bursts to provide estimates of the work attributable to passive mechanisms. To understand the relative timing and role of the individual passive structures included in the passive model, we also separately computed the passive power attributable to each uniarticular structure and biarticular muscle.
At each speed condition, a t-test was used to determine if a joint’s net passive work across the gait cycle was significantly different from zero. A significant result would suggest that biarticular components transferred energy either to or from that joint. The effect of speed on passive joint work measures was evaluated using a one-way ANOVA. All statistical analyses were conducted using MATLAB ® with a significance level of p<0.05.
RESULTS
The exponential models identified for each subject were able to accurately reproduce the passive joint moments from the measured joint angles. Average root mean square errors were 2.5 (±0.5) Nm in hip flexion-extension, 1.4 (±0.3) Nm in knee flexion-extension, and 0.7 (±0.2) Nm in ankle plantar-dorsiflexion. The influence of the biarticular muscles on the passive moments was found to be substantial at joint angles representative of normal gait (Fig. 1b).
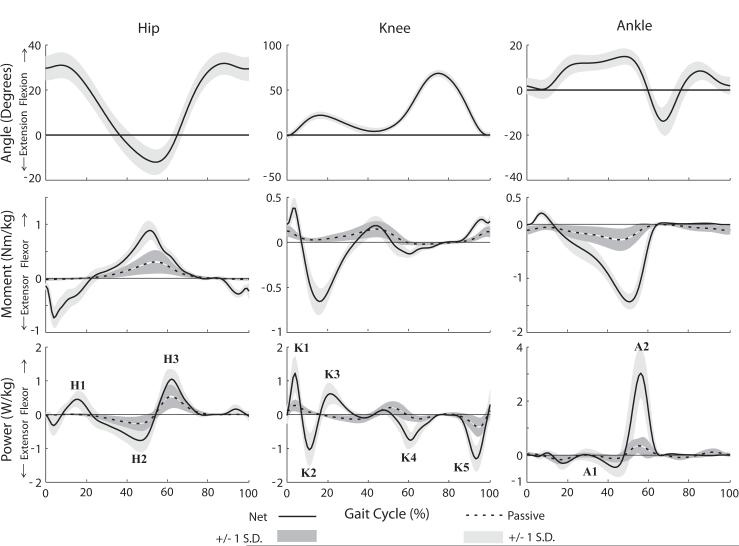
The estimated passive moments during gait were largest from mid-stance through initial swing phase (Fig. 2). The passive hip moments coincided temporally with the net hip flexor moment, producing on average ∼35% of the peak net moment. The passive ankle moments coincided temporally with the net ankle plantarflexor moment, producing on average ∼21% of the peak net moment.
Figure 2.
Ensemble-averaged joint angle, net joint moment, and net joint power curves from gait analysis for 20 subjects. Overlaid are the average (±1 SD) estimated passive joint moment and joint power curves. The largest passive moments arise in hip flexion between 30% and 60% of the gait cycle, contributing substantially to both the H2 and H3 power bursts.
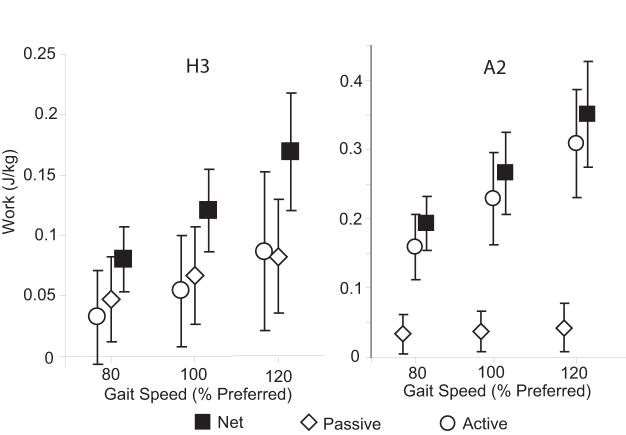
The most substantial contribution of passive moments to joint power occurred during the H2, H3 and A2 power bursts (Fig. 2). A negative passive hip flexor power during H2 resulted in 38% of the negative H2 work being elastically absorbed. This energy was released during H3, thereby contributing an average of 58% of the positive work done during H3. Passive ankle plantarflexor power contributed an average of 15% of the net work done during A2. The work attributed to passive elements increased significantly with speed for all the hip and ankle power bursts considered (p<0.05, Fig. 3). The work done by passive elements across the gait cycle was non-zero (p<0.05) at each joint except at the knee at the slow walking speek. with positive work being done at the hip and ankle and negative work being done at the knee (p<0.05) (Fig. 4). This was a direct result of the passive exchange of energy between the knee and hip via the rectus femoris, and between the knee and ankle via the gastrocnemius (Fig. 5).
Figure 3.
Speed effects on passive, active, and net works during hip flexor (H3) and ankle plantarflexor (A2) power bursts. Passive work, attributed to stretch of soft tissues, increased significantly (p<0.05) with speed for both the hip and ankle.
Figure 4.
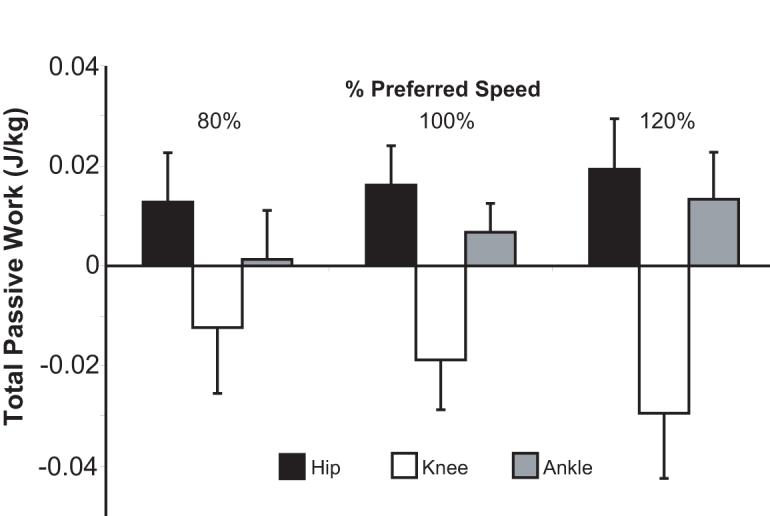
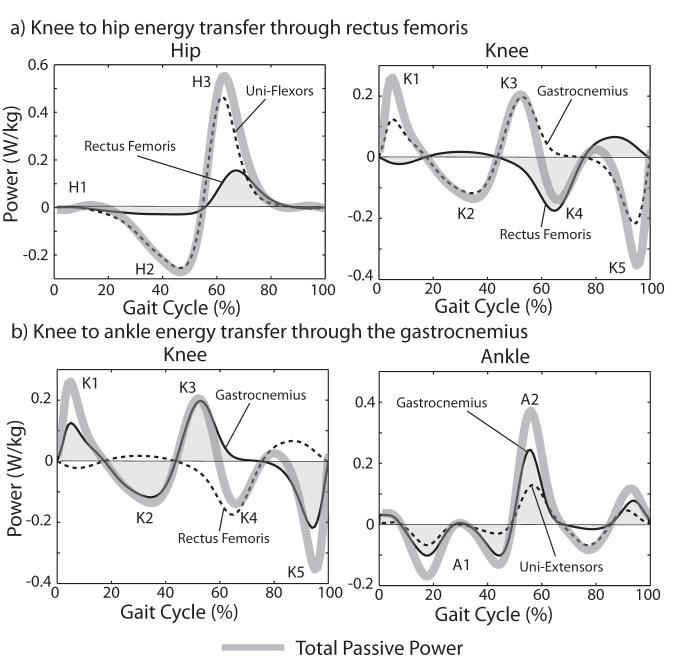
The total passive work at an individual joint across a gait cycle can be non-zero due to biarticular muscle stretch transferring energy across joints. At all speeds, a significant amount of energy was absorbed at the knee (p<0.05). This energy was returned at the hip (all speeds) and ankle (100%, 120%) via rectus femoris and gastrocnemius stretch, respectively.
Figure 5.
Shaded regions of the power curves represent the energy absorbed and released at the specific joints via the biarticular rectus femoris and gastrocnemius. (a) Energy absorption at the knee in the rectus femoris occurs coincidentally with energy release at the hip, suggesting that the muscle is facilitating simultaneous energy transfer across joints. (b) In contrast, energy transfer between the knee and ankle displays more of a stretch-recoil effect in which the gastrocnemius stores energy as the knee extends (K3) and releases that energy later when the ankle plantarflexes (A2).
DISCUSSION
In this study, we quantitatively investigated the role of passive-elastic mechanisms during normal gait in a subject-specific manner. Our results suggest that uni- and biarticular soft tissue stretch about the hip and ankle contribute substantially to the power bursts generated from mid stance through initial swing. The largest passive moments arose as a result of hip flexor stretch during pre- and initial swing, reaching ∼0.88 Nm/kg or ∼35% of the net hip flexor moment. Others have estimated the passive hip flexor moments near toe-off as between 10-50% [7, 8] of the net moment. The passive hip flexor moment enabled the absorption of energy during terminal stance and subsequent return of energy during pre- and initial swing. This mechanism may therefore reduce the active energy required to initiate swing and generate propulsion [9]. Passive mechanisms also contributed to the ankle plantarflexor power burst which may further reduce active energetic requirements. However, the relative magnitude of net plantarflexor work (15%) was not as impressive as that seen at the hip.
Passive stretch of the biarticular muscles, particularly the gastrocnemius and rectus femoris, contributed to the net moments and powers seen in normal gait. A decomposition of the net passive power curve into the constitutive components reveals the important role these muscles can play (Fig. 5). Our analysis suggests that the rectus femoris can be passively stretched during pre- and initial-swing, contributing to a net negative power at the knee and simultaneously to a net positive power at the hip. Thus the stretched rectus femoris may act to transfer energy proximally. The gastrocnemius, on the other hand, utilized a stretch-recoil mechanism to transfer energy distally by absorbing energy at the knee during mid- to terminal stance, and then returning that energy at the ankle during pre- and initial swing. It is interesting to note that our analysis did not reveal a significant role of the hamstrings in normal walking. However, others[17] have shown a significant correlation between hamstring tightness and available knee extension in patients with cerebral palsy, suggesting that the contributions of passive hamstring stretch may be important to consider in pathological gait.
Passive contributions to the net hip flexor work increased significantly with gait speed. This result was a direct consequence of the larger peak hip extension (from ∼10 to ∼14°) that occurred when increasing from a slow to fast gait speed. Similar changes in peak hip extension have been observed in other studies [1].
The methods and results presented may be relevant for identifying the role that range-of-motion impairments at the hip may play in gait impairments afflicting elderly adults. For example, it has been suggested that passive forces generated by tight hip flexors may be used to compensate for reduced ankle plantarflexor power during gait in individuals with knee osteoarthritis [9]. Mild hip flexion contractures may also restrict hip extension in healthy elderly populations [1], and thereby contribute to the reduction in ankle plantarflexor power that is commonly observed in elderly gait [1, 18, 19]. This study clearly shows that normal hip flexor tightness can be efficiently utilized to reduce the need for active hip flexor power generation. One could thus presume that an increase in hip flexor tightness due to contracture would necessitate a change in kinematics (less hip extension, e.g. [1]) to achieve the same passive contributions. Alternatively, walking with the same kinematic pattern could potentially result in an increase in hip flexor power, which has been observed in the gait of older adults [18]. Further investigation of the utilization of passive mechanisms in elderly gait seems warranted to better understand the role that range-of-motion limitations may play.
Various assumptions are important to consider when interpreting the quantitative results of this study. First, our methodology, and that of others [5, 6], inherently assumes that passive properties are additive with the active components present. This is likely a reasonable assumption for fully passive structures such as the joint capsule, ligaments, and skin. However, the interaction of passive and active components in muscle remains an area of active research [20], making it more challenging to quantify precisely how passive components are utilized in movement. Secondly, our passive moment-angle model does not account for some hysteresis present in the passive data [10]. Our parameter estimation includes both the increasing and decreasing parts of the moment-angle curve, thereby splitting the difference in the fit. This compromise likely resulted in a slight under-estimation of the peak passive moment and an over-estimation of the passive energy returned. Thirdly, our passive model did not account for viscoelastic effects due to the complexity of distinguishing and identifying the velocity-dependent forces arising from stretch of each uni- and bi-articular muscle. It is noted however that a prior study found that passive moments seemed to be independent of velocity for passive hip manipulations [8]. Finally, our passive testing and identification procedure only considered the influence of limb motion in the sagittal plane. This may be a reasonable approximation for normal gait, but not necessarily when applying the techniques to pathological gait, where the influence of non-sagittal motion (e.g. hip muscle stretch due to adduction) may be important to consider.
In conclusion, this study clearly shows that during normal walking passive mechanisms have the potential to contribute substantially to joint kinetics. Thus, it seems important to consider passive elements in the modeling and analysis of normal gait, and could also be relevant to understand pathological gait where impairments may disrupt normal passive mechanisms.
ACKNOWLEDGEMENTS
This research was supported by NIH (AG24276) and a NSF pre-doctoral fellowship (AS).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- [1].Kerrigan D, Todd M, Della Croce U, Lipsitz L, Collins J. Biomechanical gait alterations independent of speed in the healthy elderly: evidence for specific limiting impairments. Archives of Physical Medicine and Rehabilitation. 1998;79(3):317–322. doi: 10.1016/s0003-9993(98)90013-2. [DOI] [PubMed] [Google Scholar]
- [2].Koman LA, Brashear A, Rosenfeld S, Chambers H, Russman B, Rang M, Root L, Ferrari E, Garcia de Yebenes Prous J, Smith BP, Turkel C, Walcott JM, Molloy PT. Botulinum toxin type a neuromuscular blockade in the treatment of equinus foot deformity in cerebral palsy: a multicenter, open-label clinical trial. Pediatrics. 2001;108(5):1062–71. doi: 10.1542/peds.108.5.1062. [DOI] [PubMed] [Google Scholar]
- [3].Edrich T, Riener R, Quintern J. Analysis of passive elastic joint moments in paraplegics. IEEE Trans Biomed Eng. 2000;47(8):1058–65. doi: 10.1109/10.855933. [DOI] [PubMed] [Google Scholar]
- [4].Hoang PD, Gorman RB, Todd G, Gandevia SC, Herbert RD. A new method for measuring passive length-tension properties of human gastrocnemius muscle in vivo. J Biomech. 2005;38(6):1333–41. doi: 10.1016/j.jbiomech.2004.05.046. [DOI] [PubMed] [Google Scholar]
- [5].Mansour JM, Audu ML. The passive elastic moment at the knee and its influence on human gait. J Biomech. 1986;19(5):369–73. doi: 10.1016/0021-9290(86)90013-8. [DOI] [PubMed] [Google Scholar]
- [6].Riener R, Edrich T. Identification of passive elastic joint moments in the lower extremities. J Biomech. 1999;32(5):539–44. doi: 10.1016/s0021-9290(99)00009-3. [DOI] [PubMed] [Google Scholar]
- [7].Vrahas MS, Brand RA, Brown TD, Andrews JG. Contribution of passive tissues to the intersegmental moments at the hip. J Biomech. 1990;23(4):357–62. doi: 10.1016/0021-9290(90)90065-b. [DOI] [PubMed] [Google Scholar]
- [8].Yoon YS, Mansour JM. The passive elastic moment at the hip. J Biomech. 1982;15(12):905–10. doi: 10.1016/0021-9290(82)90008-2. [DOI] [PubMed] [Google Scholar]
- [9].McGibbon CA. Toward a better understanding of gait changes with age and disablement: neuromuscular adaptation. Exerc Sport Sci Rev. 2003;31(2):102–8. doi: 10.1097/00003677-200304000-00009. [DOI] [PubMed] [Google Scholar]
- [10].Silder A, Whittington B, Heiderscheit BC, Thelen DG. Identification of passive elastic joint moment-angle relationships in the lower extremity. Journal of Biomechanics. 2007 doi: 10.1016/j.jbiomech.2006.12.017. In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Cappozzo A, Catani F, Croce UD, Leardini A. Position and orientation in space of bones during movement: anatomical frame definition and determination. Clin Biomech (Bristol, Avon) 1995;10(4):171–178. doi: 10.1016/0268-0033(95)91394-t. [DOI] [PubMed] [Google Scholar]
- [12].Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Transactions on Biomedical-Engineering. 1990;37(8):757–67. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- [13].Walker PS, Rovick JS, Robertson DD. The effects of knee brace hinge design and placement on joint mechanics. J Biomech. 1988;21(11):965–74. doi: 10.1016/0021-9290(88)90135-2. [DOI] [PubMed] [Google Scholar]
- [14].Delp SL, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Comput Biol Med. 1995;25(1):21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
- [15].Piazza SJ, Erdemir A, Okita N, Cavanagh PR. Assessment of the functional method of hip joint center location subject to reduced range of hip motion. J Biomech. 2004;37(3):349–56. doi: 10.1016/s0021-9290(03)00288-4. [DOI] [PubMed] [Google Scholar]
- [16].Lu TW, O’Connor JJ. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J Biomech. 1999;32(2):129–34. doi: 10.1016/s0021-9290(98)00158-4. [DOI] [PubMed] [Google Scholar]
- [17].Cooney KM, Sanders JO, Concha MC, Buczek FL. Novel biomechanics demonstrate gait dysfunction due to hamstring tightness. Clin Biomech (Bristol, Avon) 2006;21(1):59–66. doi: 10.1016/j.clinbiomech.2005.08.014. [DOI] [PubMed] [Google Scholar]
- [18].Judge JO, Davis R, Ounpuu S. Step length reductions in advanced age: the role of ankle and hip kinetics. Journal of Gerontology: Medical Sciences. 1996;51(6):M303–M312. doi: 10.1093/gerona/51a.6.m303. [DOI] [PubMed] [Google Scholar]
- [19].DeVita P, Hortobagyi T. Age causes a redistribution of joint torques and powers during gait. Journal of Applied Physiology. 2000;88(5):1804–1811. doi: 10.1152/jappl.2000.88.5.1804. [DOI] [PubMed] [Google Scholar]
- [20].Epstein M, Herzog W. Aspects of skeletal muscle modelling. Philos Trans R Soc Lond B Biol Sci. 2003;358(1437):1445–52. doi: 10.1098/rstb.2003.1344. [DOI] [PMC free article] [PubMed] [Google Scholar]