Using idealized known RNA secondary-structural fragments, it is demonstrated that it is possible to solve novel complex RNA structures without resort to heavy-atom phasing methods.
Keywords: RNA, phase problem, molecular replacement
Abstract
The crystallographic phase problem [Muirhead & Perutz (1963 ▶), Nature (London), 199, 633–638] remains the single major impediment to obtaining a three-dimensional structure of a macromolecule once suitable crystals have been obtained. Recently, it was found that it was possible to solve the structure of a 142-nucleotide L1 ligase ribozyme heterodimer that possesses no noncrystallographic symmetry without heavy-atom derivatives, anomalous scattering atoms or other modifications and without a model of the tertiary structure of the ribozyme [Robertson & Scott (2007 ▶), Science, 315, 1549–1553]. Using idealized known RNA secondary-structural fragments such as A-form helices and GNRA tetraloops in an iterative molecular-replacement procedure, it was possible to obtain an estimated phase set that, when subjected to solvent flattening, yielded an interpretable electron-density map with minimized model bias, allowing the tertiary structure of the ribozyme to be solved. This approach has also proven successful with other ribozymes, structured RNAs and RNA–protein complexes.
1. Introduction
The macromolecular X-ray crystallographic phase problem must be solved in order to compute an electron-density map (the image of the molecule) from the observed X-ray diffraction pattern (Taylor, 2003 ▶). This requires an estimation of the phase angle associated with each of many thousands of experimentally measured diffraction amplitudes and is thus an intractable computational problem. Instead, phase estimates must be obtained experimentally by using isomorphous replacement of heavy atoms or covalent incorporation of anomalous scattering atoms such as Br or by using molecular replacement, in which a highly homologous three-dimensional structure, typically better than 1.5 Å r.m.s.d., is used as a search model (Chen et al., 2000 ▶; Qian et al., 2007 ▶). In the case of complex RNAs with tertiary structures, such as tRNA, ribozymes and other structural RNAs, experimental estimation of phases requires successful soaking and binding of heavy-metal ions to the RNA structure or synthetic incorporation of modified nucleotides such as 5-bromouracil (5BrU), procedures that may be laborious and unsuccessful. Successful molecular replacement requires a homologous prior high-resolution three-dimensional structure and has thus been of limited utility for solving novel RNA structures. Hence, if neither isomorphous modifications nor homologous three-dimensional structures are readily available, the macromolecular phase problem becomes a major impediment to solving RNA crystal structures (Keel et al., 2007 ▶).
Faced with just such a predicament in the case of the 71-nucleotide L1 ligase ribozyme (Fig. 1 ▶ a), we developed an approach for solving RNA structures having novel folds. The crystallographic asymmetric unit contains two copies of the ligase ribozyme (142 nucleotides) in radically different conformations, so despite the dimeric asymmetric unit no apparent noncrystallographic symmetry was available to exploit. The ribozyme crystallized as a covalently closed 71-nucleotide circular adduct, making synthetic incorporation of 5BrU impossible, and transcripts incorporating 11 5BrU yielded crystals that diffracted quite poorly, making the identification and use of 22 Br sites in the asymmetric unit to estimate phases in an isomorphous difference or MAD experiment impossible.
Figure 1.
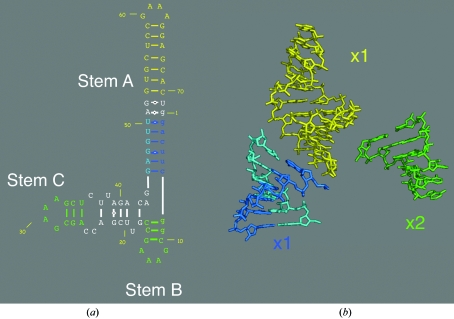
The predicted secondary structure of the 71-nucleotide L1 ligase ribozyme. Sequences thought to be involved in canonical Watson–Crick (or wobble) base pairing or corresponding to the known GNRA tetraloop structure are colored in blue, green and yellow (a). Idealized models of these sequences were generated within Coot (b). The GAAA tetraloop was modeled using the previously determined minimal hammerhead RNA GUAA structure obtained from the PDB (299d).
Unlike the tertiary structures of RNAs, many RNA secondary-structural elements are fairly easy to predict based upon sequence complementarity and phylogenetic conservation patterns (Eddy, 2004 ▶). For example, most of the RNA secondary-structural elements in the ribosome were predicted correctly long before the crystal structures became available (Noller et al., 1981 ▶; Noller & Woese, 1981 ▶; Woese et al., 1980 ▶). In addition, these structural elements typically conform fairly closely to idealized structural motifs, such as ideal A-form Watson–Crick helices, stable tetraloops (Antao & Tinoco, 1992 ▶) and the like. High-resolution three-dimensional structures of these individual motifs are available in the Protein Data Bank and can also be constructed de novo in molecular-modeling software packages such as Coot (Emsley & Cowtan, 2004 ▶). Modeling the RNA stem-loop regions in the L1 ligase was therefore very straightforward. The GNRA tetraloop is a canonical nonhelical RNA secondary structure that is very common and thermodynamically favorable (Varani, 1995 ▶). RNA tetraloops that have a G at position 1, any residue (N) at position 2, a purine (R) at position 3 and an A at position 4 all adopt the same thermodynamically stable structure. Many canonical GNRA tetraloop structures are available in the PDB; we chose a GUAA tetraloop and flanking residues from a minimal hammerhead ribozyme (Scott et al., 1996 ▶) as a template and generated canonical A-form helices within Coot.
Our original intent was to obtain a very approximate phase estimate based on a partial molecular-replacement solution and to then use these phases to discover the positions of the 22 Br sites using a conventional difference Fourier. The quality of the Br-derivative data set, however, proved to be insufficient for phasing, but the phases obtained from the iterative phasing procedure described here nonetheless enabled us to solve the structure. (The weakly diffracting Br-derivative data set was, however, of sufficient quality to enable us to check the final structure for consistency; the Br sites all appeared proximal to the 5-carbon position on each of the uracil bases.)
2. Experimental procedures
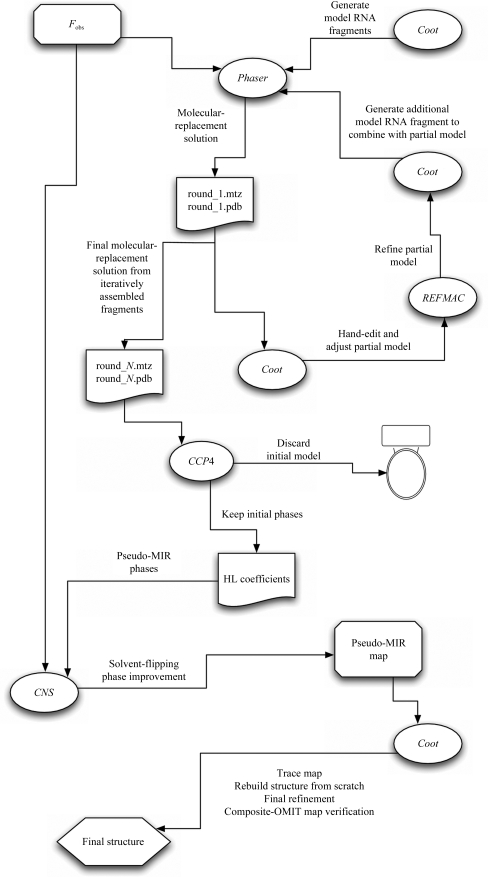
The main steps of the procedure employed to solve the L1 ligase ribozyme structure are outlined in Fig. 2 ▶ and are described in the accompanying caption. Briefly, a set of model fragments is generated for simultaneous piecewise molecular replacement in Phaser (McCoy et al., 2005 ▶) using a native RNA data set (Table 1 ▶). The best solution from Phaser is then edited in Coot to remove steric clashes and obvious positional errors (atoms placed in weak or no density). The remaining model consisting of several disjointed fragments is then refined and used as a fixed partial model for a subsequent round of molecular replacement in which a single additional structural fragment is positioned. This solution is then edited as before and is combined with the previous model. The procedure is repeated iteratively until no additional single fragments can be added successfully. The model consisting of an accumulated set of fragments is completely discarded, but the phases are retained and are subsequently solvent-flattened within CNS (Brünger et al., 1998 ▶) to generate a ‘pseudo-MIR map’ that is then used as a starting point for tracing, modeling and refining the genuine structure.
Figure 2.
Flowchart of the procedure used to solve the L1 ligase structure. An initial assembly of modeled RNA fragments (helices, loops) is used in combination with a native data set (F obs) to obtain a starting molecular-replacement solution in Phaser (round_1.mtz and round_1.pdb). This solution is examined in Coot; all steric clashes are removed by manual editing and any nucleotide that does not reside in strong electron density in the σA-weighted 2F o − F c map is manually excised. The remaining model is then positionally refined using REFMAC (which can be performed within Coot) and any unoccupied density is modeled and refined in Coot. In addition, a new helical fragment (typically five base pairs of A-form helix) for a subsequent iteration of molecular replacement is generated. Using the edited and refined model as a fixed partial model, the next (ith) round of molecular replacement in Phaser and subsequent editing and refinement is carried out with the new helical fragment. This cycle is repeated until no more helical fragments can be added. At this point, at the Nth cycle, the best molecular-replacement solution (round_N.mtz and round_N.pdb) is used to generate a solvent-flattened electron-density map. The model itself (round_N.pdb) in the case of the L1 ligase was clearly flawed in that the positioning of the secondary-structural elements was not consistent with the primary sequence and it was clear that the ‘solution’ was one in which the secondary-structural fragments were generically positioned by Phaser without regard to the detailed sequence-based structure. For this reason, the model (round_N.pdb) was discarded and the calculated phase probability distributions were converted to Hendrickson–Lattmann coefficients within CCP4 and were then imported into CNS along with the native data set (F obs) and treated as if they were experimentally determined MIR phases to be solvent-flattened. We employed solvent-flipping, using a solvent content of 50% predicted by the xtriage module of PHENIX, which simultaneously improved the quality of the electron-density map and helped to minimize model bias. The resulting map, pictured in Fig. 3 ▶, was then used to build the final model from scratch (i.e. without reference to the discarded molecular-replacement solution round_N.pdb), as if the map had been derived from experimental MIR phases. The resulting structure was then checked against a composite-OMIT map generated within CNS in which 10% of the model was omitted from each element of the composite and phases were regenerated from a standard simulated-annealing procedure with a starting temperature of 4000 K.
Table 1. Data collection and processing.
Values in parentheses are for the outer shell.
| Space group | P21 |
| Unit-cell parameters (Å, °) | a = 45.3, b = 100.0, c = 71.9, α = γ = 90, β = 104.4 |
| X-ray data wavelength (Å) | 0.9840 |
| Low-resolution limit (Å) | 100.00 (2.74) |
| High-resolution limit (Å) | 2.60 (2.60) |
| Rmerge | 0.044 (0.467) |
| Rmeas (within I+/I−) | 0.060 (0.626) |
| Rmeas (all I+ and I−) | 0.056 (0.615) |
| Rp.i.m. (within I+/I−) | 0.040 (0.413) |
| Rp.i.m. (all I+ and I−) | 0.028 (0.299) |
| Fractional partial bias | −0.022 (−0.116) |
| Total No. of observations | 77375 (11410) |
| Total unique observations | 19071 (2767) |
| Mean I/σ(I) | 20.2 (2.5) |
| Completeness (%) | 99.5 (99.9) |
| Multiplicity | 4.1 (4.1) |
2.1. Modeling structural fragments
The secondary structure of the L1 ligase was established well before the crystal structure was solved (Robertson & Ellington, 1999 ▶). The predicted secondary structure for the sequence used in crystallization is shown in Fig. 1 ▶(a) and consists of three GNRA tetraloops, several regions of predicted canonical A-form Watson–Crick paired helices, ‘internal bulge’ regions of unpredicted structure and regions of non-Watson–Crick pairing (Robertson & Scott, 2007 ▶).
We constructed four model fragments corresponding to the color-coded secondary-structural elements, as shown in Fig. 1 ▶(b). The yellow and green segments were modeled using a GNRA tetraloop structure (PDB code 299d) as a template, extended with canonical A-form model helices within Coot. The blue region was modeled as a canonical A-form helix within Coot. No attempt was made to model the sequences shown in white and no attempt was made to orient the four fragments with respect to one another in three dimensions. Instead, the four fragments were together used simultaneously but as independent rigid bodies to comprise a single starting model having 24 degrees of freedom (three rotational and three translational degrees of freedom for each of four rigid bodies) for molecular replacement.
2.2. Molecular replacment
The unit-cell contents of the L1 ligase ribozyme were estimated using the xtriage module of PHENIX (Adams et al., 2002 ▶, 2004 ▶) and were found to be consistent with either one, two or three 71-nucleotide ribozyme molecules in the asymmetric unit. No noncrystallographic symmetry was detected, consistent with either one molecule in the asymmetric unit or multiple molecules in the asymmetric unit adopting different conformations.
Molecular replacement was carried out using the program Phaser distributed with the CCP4 (Collaborative Computational Project, Number 4, 1994 ▶; Winn, 2003 ▶) and PHENIX (Adams et al., 2002 ▶, 2004 ▶) packages. Three initial searches were carried out in separate but parallel Phaser runs.
The first molecular-replacement attempt assumed that there was only one ribozyme molecule per crystallographic asymmetric unit and thus used the four RNA fragments described above together simultaneously, a single starting model having 24 degrees of freedom.
The second independent molecular-replacement attempt instead assumed that there were two molecules per asymmetric unit and thus used two copies of each set of four fragments, or eight rigid-body fragments, comprising a single starting model having 48 degrees of freedom in total.
The third molecular-replacement attempt used three copies of each fragment or 12 rigid-body fragments, comprising a single starting model having 72 degrees of freedom in total.
In each independent trial, Phaser produced a best estimate phased reflection and PDB file and these were visually inspected within Coot. Using the molecular-replacement phase set and PDB file, σA-weighted 2F o − F c and difference Fouriers were calculated and displayed in Coot.
The initial solution obtained from the first molecular-replacement trial consisting of four rigid-body fragments appeared to yield the most promising estimated phases, although several nucleotides were observed to have very poor electron density and several others involved steric clashes between fragments. The offending nucleotides were deleted from the initial solution within Coot, so that the manually edited model contained no major steric clashes and every remaining nucleotide was contained in well defined electron density in the initial 2F o − F c map. A subsequent round of minimization carried out in REFMAC (Murshudov et al., 1997 ▶) within Coot produced a refined model structure and an αA-weighted 2F o − F c map in which additional recognizable features, such as nucleotide base pairs, began to emerge. Based on this criterion, we judged that the initial model possessed at least some legitimate predictive phasing power.
2.3. Iterative model building
Using the edited solution from the first molecular-replacement trial, corresponding to one 71-nucleotide ribozyme molecule in the crystallographic asymmetric unit, as a starting point, we carried out subsequent rounds of molecular replacement and refinement by iteratively supplying individual helical or stem-loop fragments to Phaser, along with the edited starting model, allowing Phaser to position the additional RNA structural fragment. Although solutions often involved considerable steric clashes, it was noteworthy that helical fragments were often positioned in such a way as to bridge gaps in the initial disjoined model. After each iteration, the new combined solution was visually inspected; residues involved in steric clashes or inhabiting weak or nonexistent electron density were deleted and the edited model was then further refined. Using this procedure, about 75% of the RNA, corresponding to a dimeric asymmetric unit of 142 nucleotides, was eventually accounted for within the iteratively assembled model. The actual sequence bore no sensible correspondence to Fig. 1 ▶(a), but it was clear that the generic positions of the tetraloops and helical regions had been successfully identified by Phaser.
2.4. Calculating phases
After further positional refinement in REFMAC or PHENIX’s refine module and editing of the model to remove residues involved in steric clashes or in weak density, the phase estimates calculated from the model consisting of the remaining assembled helical fragments were converted using the CCP4 program HLTOFOM (Collaborative Computational Project, Number 4, 1994 ▶) to Hendrickson–Lattmann coefficients and these phase probability distributions, together with the experimentally measured amplitudes, were treated as if they were an initial MIR phase set and were subjected to solvent-flattening (in solvent-flipping mode; Abrahams & Leslie, 1996 ▶) within CNS to minimize the model bias and to improve the quality of the estimated phases. A solvent content of 50% was employed, consistent with 142 nucleotides of RNA per asymmetric unit.
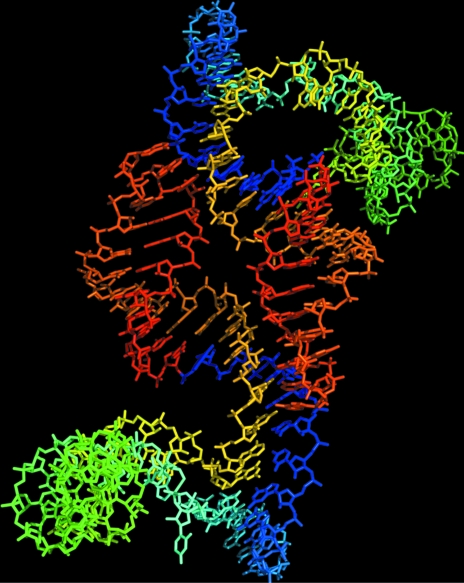
The resulting solvent-flattened electron-density map (Fig. 3 ▶) was then treated as if it was an experimentally phased map and was skeletonized and then traced with polyC within Coot, with no reference to the discarded prior model structure. The quality of this map was such that purines were readily distinguishable from pyrimidines and in many cases an adenine could be distinguished from a guanosine. These features, as well as the distinctive GNRA tetraloop density, enabled the construction and refinement of two 71-nucleotide ribozyme monomers without any sequence ambiguities (Fig. 4 ▶). The final refined structure and accompanying structure-factor amplitudes are available from the PDB (PDB code 2oiu).
Figure 3.
The solvent-flattened ‘pseudo-MIR’ electron-density map. The electron-density map was generated in CNS using an initial phase probability distribution obtained from the iterative RNA-fragment molecular-replacement procedure outlined in Fig. 2 ▶ and described in the accompanying caption and in the main text.
Figure 4.
The final refined structure of the L1 ligase heterodimer (PDB code 2oiu). The final refined structure as described in detail in Robertson & Scott (2007 ▶). Each molecule varies from blue to red as one progresses in the 5′ to 3′ direction. The red/blue interface denotes the ligation-site junction.
3. Results
3.1. A small subset of fragments works best
Although two ribozymes occupy the asymmetric unit of the crystal, simultaneous molecular replacement with one set of four rigid-body fragments, rather than two sets (eight rigid bodies), yielded a better initial solution (and, in combination with the apparent absence of noncrystallographic symmetry, briefly led us to a false conclusion that only one molecule was present in the asymmetric unit rather than two). The solution in which two sets of structural fragments were employed resulted in most of the helices superimposed upon one another, whereas the solution in which only one set of four structural fragments was employed yielded a result in which the four fragments were dispersed throughout the asymmetric unit. The initial fragment model, comprising ∼1/3 of the total mass of RNA actually present in the asymmetric unit, possessed rotational and translational Z scores in Phaser of only 3.3 and 3.9, respectively. One round of positional refinement in PHENIX’s refine module, using all data from 31.3 to 2.6 Å resolution, lowered the R free from 0.526 to 0.523 and the R work from 0.512 to 0.495. The statistics themselves gave little hint of success.
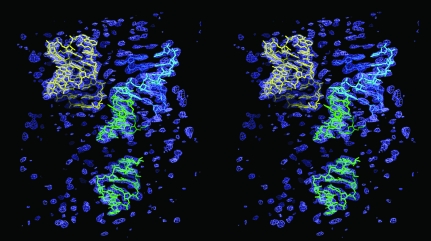
However, examination of the σA-weighted 2F o − F c map that was produced from the initial four-fragment molecular-replacement solution (Fig. 5 ▶) indicated reasonable electron density covering the four RNA fragments at 2σ. More significantly, helical density appeared in unmodeled regions of the map (Fig. 5 ▶) and at 1σ several unmodeled nucleotide bases were resolvable, indicating that the initial phases from the RNA fragments possessed a degree of veracity and predictive phasing power that could not be explained away as model bias. This result inspired us to continue with molecular replacement of individual RNA fragments, typically either A-form helices having five or six base pairs or GNRA tetraloops, in an iterative molecular-replacement procedure until about 75% of the RNA had been modeled.
Figure 5.
The initial map. The σA-weighted 2F o − F c map, contoured at 2σ, produced from the initial four-fragment molecular-replacement solution. Additional helical density and some nucleotide base density is apparent in regions not modeled with the RNA fragments, indicating that the partial model possesses some degree of veracity and predictive phasing power. The color scheme is the same as that used in Fig. 1 ▶.
3.2. Calculation of a ‘pseudo-MIR’ map
After refinement of the iteratively assembled fragments, the lack of sensible sequence connectivity in an otherwise iteratively improving solution suggested that minimizing the molecular-replacement model bias might help to further improve the quality of the electron-density map. This was performed by discarding the original model and treating the molecular-replacement fragment (or partial model) phases as if they were experimentally derived MIR phases that could be improved by solvent flattening. Our previous experiences (Scott et al., 1995 ▶; Martick & Scott, 2006 ▶; Robertson et al., 2005 ▶) suggested that the solvent-flipping procedure, originally introduced in the CCP4 SOLOMON package (Abrahams & Leslie, 1996 ▶) and subsequently incorporated in CNS, produced the best results with RNA experimental phases. Fig. 3 ▶ illustrates the quality of the solvent-flattened ‘pseudo-MIR map’ produced by the solvent-flipping subroutine within CNS, i.e. a readily traceable electron-density map in which purines were easily distinguished from pyrimidines and, in many cases, guanines could be distinguished from adenines.
4. Discussion
To test whether the method is generally applicable to other RNAs and RNA–protein complexes, we used X-ray data for various ribozymes and RNA–protein complexes available from the PDB. We were able to solve two different hammerhead ribozyme structures, a minimal hammerhead (299d) and full-length hammerhead (2oeu), and two hairpin ribozyme structures, a minimal (2oue; MacElrevey et al., 2007 ▶) and a full-length (1m5k) structure, the latter of which is an artificially constructed complex between the hairpin ribozyme and the U1A protein bound to an engineered binding site (Rupert & Ferré-D’Amaré, 2001 ▶), using the same procedure. In the case of the full-length hairpin ribozyme bound to the U1A protein, molecular replacement using only two copies of an unaltered U1A RNA–protein complex (Oubridge et al., 1994 ▶) obtained directly from the PDB (1urn, chains A and P) resulted in successful positioning of both proteins and their associated RNAs within the hairpin ribozyme asymmetric unit. One round of positional refinement within PHENIX produced a refined partial model with an R work of 0.443 and an R free of 0.450 from starting values of 0.468 and 0.470, respectively. This map again revealed significant helical density in unmodeled regions, indicating that the partial model phases from fragments comprising about ∼1/3 of the mass of the complex possessed significant predictive power. In contrast, molecular replacement using four smaller helical fragments corresponding to the four helices of the minimal hairpin ribozyme yielded no such clear solution, even though the fragments comprised ∼3/4 of the mass of the asymmetric unit. However, molecular replacement using only helices 1 and 3 of the minimal hairpin ribozyme yielded a better quality phase set with predictive power.
A consistent result in each test case is that a comparatively sparse subset of fragments yields a better initial molecular-replacement solution. This result is in fact completely counter-intuitive, given the usual assumption that a complete intact and highly homologous three-dimensional structural model, typically better than 1.5 Å r.m.s.d., must be employed to obtain a useful molecular-replacement solution (Chen et al., 2000 ▶; Qian et al., 2007 ▶). In each test case, we found a highly incomplete and fragmented model, consisting of about ∼1/3 of the total mass of the whole crystallized macromolecule, with no prior knowledge of how the fragments are arranged in three-dimensional space, produced useful phases.
Although our tests have not been exhaustive, it appears that many RNA crystal structures of a complexity originally believed to be solvable only via MIR or MAD experimental phasing methods can in fact be solved by molecular replacement using a comparatively sparse sampling of RNA secondary-structural fragments. Initial solutions incorporating about ∼1/3 of the macromolecular contents of the unit cell consistently gave rise to initial phase sets that upon improvement with additional iteratively placed helical fragments and solvent-flattening yielded structural solutions, whereas those with over ∼1/2 the unit-cell contents typically did not.
The fragment-based sparse molecular-replacement approach we describe here has proven successful for moderately sized ribozymes and RNA–protein complexes and notably led to the only viable solution of the L1 ligase structure. Because heavy-atom isomorphous replacement is not only laborious, but is often a serious bottleneck in solving RNA and RNA–protein complex crystal structures that often requires engineering heavy-atom sites (Keel et al., 2007 ▶), we suggest that this approach will likely be of considerable benefit to practitioners of high-throughput RNA crystallography and RNA structural genomics.
Acknowledgments
We thank A. Szoke, B. Luisi, H. Noller, R. Read, the members of the Scott research group and the RNA Center at UCSC for helpful advice and critiques and the NIH (R01 043393) for funding. This procedure was inspired in part by Professor Young-In Chi, who has used a similar helical fragment approach to solve the structure of a hammerhead ribozyme derived from the satellite tobacco ringspot virus RNA.
References
- Abrahams, J. P. & Leslie, A. G. W. (1996). Acta Cryst. D52, 30–42. [DOI] [PubMed]
- Adams, P. D., Gopal, K., Grosse-Kunstleve, R. W., Hung, L.-W., Ioerger, T. R., McCoy, A. J., Moriarty, N. W., Pai, R. K., Read, R. J., Romo, T. D., Sacchettini, J. C., Sauter, N. K., Storoni, L. C. & Terwilliger, T. C. (2004). J. Synchrotron Rad.11, 53–55. [DOI] [PubMed]
- Adams, P. D., Grosse-Kunstleve, R. W., Hung, L.-W., Ioerger, T. R., McCoy, A. J., Moriarty, N. W., Read, R. J., Sacchettini, J. C., Sauter, N. K. & Terwilliger, T. C. (2002). Acta Cryst. D58, 1948–1954. [DOI] [PubMed]
- Antao, V. P. & Tinoco, I. Jr (1992). Nucleic Acids Res.20, 819–824. [DOI] [PMC free article] [PubMed]
- Brünger, A. T., Adams, P. D., Clore, G. M., DeLano, W. L., Gros, P., Grosse-Kunstleve, R. W., Jiang, J.-S., Kuszewski, J., Nilges, M., Pannu, N. S., Read, R. J., Rice, L. M., Simonson, T. & Warren, G. L. (1998). Acta Cryst. D54, 905–921. [DOI] [PubMed]
- Chen, Y. W., Dodson, E. J. & Kleywegt, G. J. (2000). Structure, 8, R213–R220. [DOI] [PubMed]
- Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760–763.
- Eddy, S. R. (2004). Nature Biotechnol.22, 1457–1458. [DOI] [PubMed]
- Emsley, P. & Cowtan, K. (2004). Acta Cryst. D60, 2126–2132. [DOI] [PubMed]
- Keel, A. Y., Rambo, R. P., Batey, R. T. & Kieft, J. S. (2007). Structure, 15, 761–772. [DOI] [PMC free article] [PubMed]
- McCoy, A. J., Grosse-Kunstleve, R. W., Storoni, L. C. & Read, R. J. (2005). Acta Cryst. D61, 458–464. [DOI] [PubMed]
- MacElrevey, C., Spitale, R. C., Krucinska, J. & Wedekind, J. E. (2007). Acta Cryst. D63, 812–825. [DOI] [PMC free article] [PubMed]
- Martick, M. & Scott, W. G. (2006). Cell, 126, 309–320. [DOI] [PMC free article] [PubMed]
- Muirhead, H. & Perutz, M. F. (1963). Nature (London), 199, 633–638. [DOI] [PubMed]
- Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240–255. [DOI] [PubMed]
- Noller, H. F., Kop, J., Wheaton, V., Brosius, J., Gutell, R. R., Kopylov, A. M., Dohme, F., Herr, W., Stahl, D. A., Gupta, R. & Waese, C. R. (1981). Nucleic Acids Res.9, 6167–6189. [DOI] [PMC free article] [PubMed]
- Noller, H. F. & Woese, C. R. (1981). Science, 212, 403–411. [DOI] [PubMed]
- Oubridge, C., Ito, N., Evans, P. R., Teo, C. H. & Nagai, K. (1994). Nature (London), 372, 432–438. [DOI] [PubMed]
- Qian, B., Raman, S., Das, R., Bradley, P., McCoy, A. J., Read, R. J. & Baker, D. (2007). Nature (London)450, 259–264. [DOI] [PMC free article] [PubMed]
- Robertson, M. P. & Ellington, A. D. (1999). Nature Biotechnol.17, 62–66. [DOI] [PubMed]
- Robertson, M. P., Igel, H., Baertsch, R., Haussler, D., Ares, M. Jr & Scott, W. G. (2005). PLoS Biol.3, e5. [DOI] [PMC free article] [PubMed]
- Robertson, M. P. & Scott, W. G. (2007). Science, 315, 1549–1553. [DOI] [PubMed]
- Rupert, P. B. & Ferré-D’Amaré, A. R. (2001). Nature (London), 410, 780–786. [DOI] [PubMed]
- Scott, W. G., Finch, J. T. & Klug, A. (1995). Cell, 81, 991–1002. [DOI] [PubMed]
- Scott, W. G., Murray, J. B., Arnold, J. R., Stoddard, B. L. & Klug, A. (1996). Science, 274, 2065–2069. [DOI] [PubMed]
- Taylor, G. (2003). Acta Cryst. D59, 1881–1890. [DOI] [PubMed]
- Varani, G. (1995). Annu. Rev. Biophys. Biomol. Struct.24, 379–404. [DOI] [PubMed]
- Winn, M. D. (2003). J. Synchrotron Rad.10, 23–25. [DOI] [PubMed]
- Woese, C. R., Magrum, L. J., Gupta, R., Siegel, R. B., Stahl, D. A., Kop, J., Crawford, N., Brosius, J., Gutell, R., Hogan, J. J. & Noller, H. F. (1980). Nucleic Acids Res.8, 2275–2293. [DOI] [PMC free article] [PubMed]