A Virtual Look at Epstein-Barr Virus Infection: Simulation Mechanism

M Shapiro; KA Duca; K Lee; E Delgado-Eckert; J Hawkins; AS Jarrah; R Laubenbacher; NF Polys; V Hadinoto; DA Thorley-Lawson

doi:10.1016/j.jtbi.2008.01.032

. Author manuscript; available in PMC: 2009 Jun 21.

Published in final edited form as: J Theor Biol. 2008 Feb 16;252(4):633–648. doi: 10.1016/j.jtbi.2008.01.032

A Virtual Look at Epstein-Barr Virus Infection: Simulation Mechanism

M Shapiro ^1,^2,^#, KA Duca ^2,^4,^#, K Lee ², E Delgado-Eckert ^1,^2,⁵, J Hawkins ¹, AS Jarrah ², R Laubenbacher ², NF Polys ^2,³, V Hadinoto ¹, DA Thorley-Lawson ^1,^*

PMCID: PMC2515170 NIHMSID: NIHMS55445 PMID: 18371986

Abstract

Epstein-Barr virus (EBV) is an important human pathogen that establishes a lifelong persistent infection and for which no precise animal model exists. In this paper we describe in detail an agent-based model and computer simulation of EBV infection. Agents representing EBV and sets of B and T lymphocytes move and interact on a three-dimensional grid approximating Waldeyer’s ring, together with abstract compartments for lymph and blood. The simulation allows us to explore the development and resolution of virtual infections in a manner not possible in actual human experiments. Specifically, we identify parameters capable of inducing clearance, persistent infection, or death.

INTRODUCTION

Epstein-Barr virus is a common human pathogen which infects greater than 90% of all people by the time they are adults [1, 2]. The most common course of infection is asymptomatic with the virus establishing life-long persistence in the host. Little is known about the early stages of asymptomatic infection. In some patients who first become infected in adolescence, it causes acute infectious mononucleosis, and here its behavior is biphasic. An acute phase involving extensive infection of the memory B-cell compartment resolves into life-long persistent infection at much lower levels. EBV can also become oncogenic, particularly in immune suppressed patients. These realities make it an important object of investigation and several factors recommend it for study via mathematical modeling and computer simulation. Firstly, there is a good working, biological model of EBV infection [2, 3], for which there are still many open questions. Secondly, there is no good animal model for human infection and disease. Thirdly, the sites of infection and persistence – B lymphocytes of Waldeyer’s ring (tonsils and adenoids) and the peripheral blood – are accessible and allow measurements which can be used to derive parameter values and validate the model [4].

EBV is most commonly transmitted by saliva [5]. Throughout its life-cycle, EBV appears to co-opt normal B-cell biology. It infects naïve B-cells in the lymphoid tissue of Waldeyer’s ring transforming these cells into activated B-blasts. These latter enter the germinal centers of Waldeyer’s ring where they undergo differentiation and emerge into the peripheral circulation as latently infected memory B-cells with the virus in a quiescent state [6]. At some later time, infected cells may return to Waldeyer’s ring where they may enter a lytic state in which the virus reproduces and bursts out [7]. This burst of free virus can infect additional naive B-cells or be transmitted to a new host. The immune system mounts a cytotoxic T cell (CTL) response to the infected B-blasts and the lytic B-cells, i.e., those actively producing virus [8, 9]. It also produces antibody against free virions. A summary of the biological model is presented in Figure 1 and a detailed description can be found in [2, 3].

EBV co-opts normal B-cell biology to drive infected B-cells into the resting memory state in the peripheral circulation where they are not subject to immunosurveillance. Upon return to Waldeyer’s ring, they may become lytic cells actively producing infectious virus that can either infect new B cells or be shed into saliva to infect new hosts. The activated blast state (subsumed under B_Lat) and the lytic state (B_Lyt) are removed by CTLs (T_Lat and T_Lyt) and free virus (Vir) cleared by neutralizing antibody [2, 3, 74]. Reproduced from [55] with permission.

It is very much an open question as to what sort of mathematical or computer model¹ is most appropriate to describe this disease process. We are so far dissatisfied with our attempts to model EBV infection using differential equations (Duca, unpublished) and difference equations (Shapiro, Delgado-Eckert, unpublished). Moreover, there are reasons to mistrust the spatial homogeneity and well-mixed assumptions that underlie continuous models based on ordinary differential equations (ODEs) [10–12], despite the success of such models in immunology and virology [13–21]. Disease processes are spatially distributed and it is likely that this spatial distribution is critical in determining the course of infection, as has been argued by many, including [22, 23].

Agent-based modeling is increasingly being recognized as a viable way to simulate biological processes [24–27]. It has the following advantages:

The agent paradigm invites us to view biological processes as the interplay of discrete entities such as cells, pathogens, and molecules interacting in the anatomical arena.
Agent-based models can be made concrete. Most simulated objects and processes or interactions have a straightforward biological interpretation e.g., as cells or pathogens.
Stochasticity, inherent to chemical and biological processes can be incorporated in a natural way.
Agent-based models are typically local in nature, allowing the global picture to emerge from local interactions.
The design of the simulation allows one to choose the level of detail at which one will represent the spatial facts of anatomy and physiology.

One big drawback of using agent-based models is that there is no satisfying mathematical theory that allows for their analysis. Indeed, in the general case, such a theory is out of reach. If we are willing to allow our agents to interact on an infinite strip, it is not hard to see that the actions of an arbitrary Turing machine can be carried out as an agent-based simulation whose agents are 0, 1 and the read head. This implies that all the undecidable problems concerning Turing machines are also undecidable for agent-based simulations [28].

Since [29], there have been many agent-based simulations of the immune system and its responses to disease. Many of these have focused on reproducing and understanding important general properties of the immune response, e.g., [30–45]. It is part of the working faith of any investigator who attempts to simulate the immune system that important features of that system’s overall behavior emerge from the interactions generated by a small set of simple features among its working parts. Even so small an ”immune system” as a 15 × 15 two-dimensional grid is capable of simulating important features of the immune system [32]. Indeed, a C-ImmSim model captures important elements of EBV infection [46]. Other studies using agent-based simulation to address the course of specific diseases include [47–54].

We have built an agent-based simulation of EBV infection, which we refer to as PathSim (Pathogen Simulation). PathSim is based on the generally accepted features of EBV infection regarding the sites of infection and the immune response to it [2, 3]. A schematic diagram of the simulation model is shown in Figure 1 alongside the biological model. PathSim provides a virtual Waldeyer’s ring of tonsils, adenoids and connecting tissue, as well as virtual cells and virus which interact there. To distinguish the virtual entities from the biological entities they represent, we refer to the former as (for example) latently infected B-cells, and their virtual representatives as B_Lats. Similarly we refer to actual virus as virions and their virtual counterparts as Vir.

While PathSim is an extreme simplification of reality, it reproduces many clinically observed features of EBV infection (documented in [55],) e.g., the development of acute and persistent phases, the suggested peak of acute infection based on literature values [56, 57], the exponential decay of the infected B-cell population, and the relative sizes of the latently infected vs. lytically-replicating infected cell pools. PathSim also reproduces many behaviors of the viral population observed in vivo [55].

Here we give a detailed description of this simulation and address further questions of how the course of the simulated disease might be altered by varying the parameters that govern the underlying processes. In a separate report [55] we described in more detail additional biological implications of these and other results obtained using PathSim, as well as end-user issues of special relevance to a biological audience [1]. Of particular significance are “switches” where small changes in parameter values produce large changes in overall outcome, e.g., clearance vs. persistence vs. host death In the case of a “silicon patient” that was never alive, it is difficult to define the meaning of “death”. We make the ad hoc assumption that permanent infection of all the B cells constitutes virtual death.

METHODS

PathSim consists of a simulation engine together with visualization software that allows for two- and three-dimensional data display and analysis. This model omits many features of the immune system and simplifies those it does contain. We will address some of these choices in the discussion. Detailed descriptions of features and parameters, as well as the scientific rationale for our choices are found in a Supplement (Supplement 1) that accompanies this article. The simulation itself is also available as a Supplement (Supplement 2) for download as a tar file at the journal’s web site. For additional details on the visualization and interface aspects, see also [55, 58].

The simulation is performed on a graph that represents the anatomy of Waldeyer’s ring together with abstract compartments for blood and lymph flow. Each vertex of this graph represents a small volume of tissue and is connected by edges to neighboring vertices. The vertices can be grouped according to the type of tissue space they represent. Motion of virtual agents between vertices is controlled according to the type of agent and the type of tissue each vertex represents. Agents can only interact when they are located at the same vertex.

Simulation engine

PathSim provides a discrete geometric approximation of the Waldeyer’s ring together with abstract compartments representing the lymph and the peripheral circulation. These locations are supplied with populations of virtual virus, B-cells, and T-cells which age, change state, move from one location to the next, and interact according to defined rules. All agents are examined and updated at each time step.

Geometry

We model the geometry of Waldeyer’s ring by a three-dimensional graph in which each vertex represents a small amount of tissue (volume = 1.2 × 10⁻⁴ cm³). The edges of this graph connect neighboring volumes of tissue. For a more detailed anatomical description of Waldeyer’s ring, see [59, 60]. The graph provides a geometric representation of Waldeyer’s tonsillar ring which consists of the lingual tonsil, the two palatine tonsils, two tubal tonsils and the adenoid, together with regions of epithelial tissue connecting them (Figure 2A). Each tonsil is built on a roughly elliptical floor plan (Figure 2B) and is composed of hexagonal base units which represent follicles containing germinal centers with adjacent interfollicular tissue (Figure 2C). For ease of construction and manipulation we decided to work with a repeated basic unit. Figure 2C provides a three dimensional depiction of this unit compared to a cross-section of the tissue it represents. The vertices of this repeating unit represent small volumes of tissue. The vertices are classified as surface, epithelium, mantle, or follicle. The tissue locations affect the motion of the agents by restricting where they can go. Additionally, in each hexagonal unit, there is one vertex representing the high endothelial venule and one vertex representing the efferent lymph. These are connected to the circulatory and the lymphatic systems, respectively. Further details are given in Supplement 1.

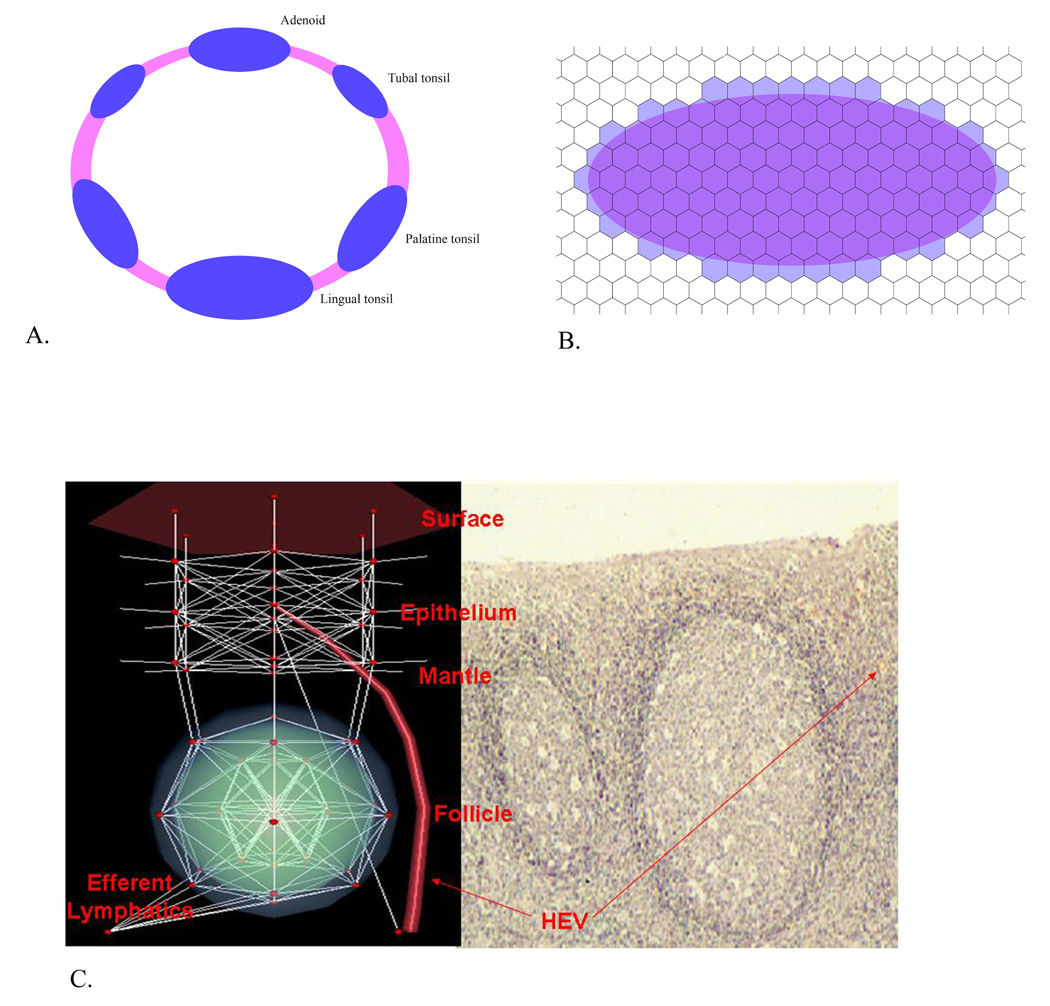
(A) The site of EBV infection (the Waldeyer’s ring, a series of linked lymphoepithelial structures comprising the lingual tonsil, 2 palatine tonsils, 2 tubal tonsils, and adenoids) is approximated by a connected grid where each tonsil is an ellipse. (B) Each tonsil is composed of repeated, basic units that represent individual germinal centers laid out on a hexagonal floor plan. (C) A 3-dimensional view of an individual hexagonal unit (left) is compared with a tissue cross section of germinal centers from tonsil (right). For more detail see [55].

Agent life cycles, interactions and motion

PathSim’s agent types are Vir, B_Naive, B_Lat, B_Lyt, T_Naive, T_Lat and T_Lyt, corresponding to virus, naive B-cells, latently infected B-cells, lytically infected B-cells, naive T-cells, and two types of activated cytotoxic T lymphocytes (CTLs), one directed against each kind of infected B-cell (CTL latent and CTL lytic). The vertices act as containers for these agents. In the course of a simulation, these agents undergo creation, aging, interaction, motion, and death.

We chose to model the virions as individual agents rather than local concentrations partly because we wanted to create an agent-based simulation and partly because this better approximated the actual physiology. In particular, it allows us to give our Virs individual lifespans. While our choice is more computationally demanding, the Vir population remains small enough (its peak is one order of magnitude smaller than T_Lat or B_Lat populations) that it contributes only a small fraction to overall computational cost.

At startup, we create a population of B_Naives and T_Naives and use these to populate the underlying graph. These cells are distributed randomly throughout this entire ring. Whenever an agent is created, we stochastically assign it an individual lifespan. (The numbers of agents created and their lifespans are governed by parameters which are set at initialization. These and other controlling parameters are discussed below and in detail in Supplement 1.) We start an infection by creating a population of Vir and distributing these only on the surface of the Waldeyer’s ring. The simulation then advances in discrete time steps. At each step, agents age, interact, move to neighboring vertices, and undergo certain life cycle events that may be triggered by aging, interaction, or motion. The population of B_Naives in the blood is also replenished whenever it drops. We chose a time step of six minutes to accurately reflect interaction and motion rates (discussed below).

One of the life cycle events induced by aging is death, which happens to Vir and B_Naives at the end of their life-spans. The life cycles of virtual T-cells are handled using a simplifying heuristic. T_Naives are granted immortality by giving them life spans greater than the length of the simulation. These may become virtual CTLs if they are appropriately triggered (discussed below). We recycle virtual CTLs as T_Naives at the end of their life-spans. We use this heuristic as opposed to implementing a mechanistic model of creation and destruction of T-cells, as it is beyond the scope of this initial simulation.

The life cycle of the B_Lat is slightly more complicated. Its possible fates are the following:

to die due to the passage of time. When a B_Lat is created due to infection of a B_Naive, it is stochastically assigned a lifespan. Note that its clock does not tick while it is in the circulation. After is has spent that much time in Waldeyer’s ring, it either dies or becomes a B_Lyt. The default setting is for 40% of B_LatS to become lytic at the end of their lifespan.
to be killed by a T_Lat. Note that B_Lat are not subject to CTL regulation while in the blood compartment.
to become a B_Lyt. In our default parameter set, this occurs due to the passage of time as discussed above. However, we have also experimented with two additional methods to generate B_LytS, both of which are intended to mimic unknown signaling events that trigger lytic replication. In the first instance, when a B_Lat returns to Waldeyer’s ring from the blood, it is stochastically chosen to change state to a B_Lyt, regardless of its age. In the second, a returning B_Lat divides, replacing itself with one B_Lat and one B_Lyt. This second version is inspired by Thorley-Lawson’s application of Lanzavecchia’s ideas about homeostasis of the memory compartment to EBV [7, 61].

The biological signal that initiates turning latently infected B-cells lytic is not well understood [7]. As described above we have provided three methods by which our B_Lats may become B_Lyts. The default method is simply based on the passage of time. The other two are based on return from the blood to Waldeyer’s ring and are set at zero in the default parameter list. In any given run, B_Lats may be subject to one or any combination of these processes depending on the assigned parameter values. Thus, a B_Lat which might have become lytic due to the passage of time, could find this fate pre-empted by one of the other two processes. However, since EBV infection is not associated with viremia, all three of these methods are only allowed to transpire in Waldeyer’s ring and do not operate while the B_Lat is in the blood. Lastly it should be emphasized that all three methods are pre-empted if the B_Lat is killed by a T_Lat.

When B_Lyts reach the end of their cycle, they die and burst virus. The number of Vir in this burst is determined stochastically within a pre-set range based on laboratory estimates of burst size. In vivo, virus can also enter the cells of the epithelium and reproduce within them [62]. While this has not been a major focus of our simulation, we have allowed for continuing production of Vir in the epithelium for some runs. This turns out to have very little (if any) effect on the course of the simulation [55].

Our blood compartment contains both B_Naives and B_Lats. B_Naives are continually supplied to the blood to maintain homeostasis. The infected B-cells in the blood compartment in vivo are resting memory B-cells [63, 64] that do not express antigenic proteins [6] and thus escape immune surveillance. Accordingly, we have excluded virtual T-cells from the blood compartment. In sum, therefore, aging, CTL predation, and initiation of lytic replication for B_Lat occur in the Waldeyer’s ring; they are not allowed to proceed in the blood compartment.

Interactions take place between agents located at the same vertex. Only certain pairs of agents interact. Vir and B_Naives can interact, resulting in replacement of both with one or more B_Lats. (More than one new infected B_Lat would arise as a consequence of proliferation of the freshly infected B-cell post-infection. This proliferation feature is optional and not part of our default run.) Any infected virtual B-cell (B_Lat or B_Lyt) and a virtual naive T-cell can interact, thereby converting the T-cell into a virtual CTL (a T_Lat or T_Lyt, respectively). Virtual CTLs can interact with their cognate infected B-cells by killing them. We have not simulated T-cell memory, antigen presentation, or explicit virus neutralization by antibody, although the relatively short lifespan assigned to Vir implicitly reflects the action of neutralizing antibody. See Tables S3A and S3B in Supplement 1 for more detail concerning lifespans.

Each interaction is stochastically governed by two probabilities: the probability that these two agents encounter each other and the probability that they then interact. Some interaction probabilities are quite high. The probability that a Vir infects a B_Lat is near certainty. On the other hand, there is a rather low probability that a B_Lat will activate a T_Naive. The encounter probabilities depend on the motion of the agents within the small volume represented by the vertex at which they reside. If we ignore chemotaxis we can treat this motion as random, i.e., Brownian motion. This makes the probability a function of the volume in which they are contained, their velocities, and their diameters. We performed a separate in silico experiment to determine the probability of encounter between two individual agents. We then extrapolated to the probability that, for example, a B_Naive will encounter a Vir when there are N Vir at that vertex. If the probability that a single B_Naive meets a single Vir is p, then the probability that it will evade all N of them is (1− p)^N. The probability that it will meet at least one of them is 1− (1− p)^N. If we have M B_Naives and N Vir, we use this probability for each of the B_Naives. This is not strictly correct, since after the first B_Naive is infected, only N−1 viruses remain to infect other B_Naives. See Table S4 in Supplement 1 for detailed encounter and interaction probabilities.

Motion takes place between adjacent vertices in the graph and is carried out stochastically. The probabilities depend on tissue locations, agent types, and populations. Some of them are zero, thus preventing certain movements entirely. These probabilities are also used to mimic short-range effects of chemotaxis. In the absence of chemotaxis, a baseline probability governs the likelihood of motion to an adjacent vertex. We computed these probabilities by a similar Monte Carlo simulation to the one giving us encounter probabilities.

There is a one-way flow of B_Naives and B_Lats from tonsil tissue to the efferent lymph to the lymphatic system to the circulation to high endothelial venule (HEV) and back to the tonsil tissue. (In particular, the blood and the lymph are adjacent to, and therefore, accessible from every section.) We use motion probabilities to restrict Vir to the surface and epithelial layer. T-cells may move through Waldeyer’s ring freely, but are given an incentive to move towards higher concentrations of virtual B-cells in a neighboring vertex (see Supplement 1 for more detail). Infected virtual B-cells may enter the follicle, but B_Naives may not. A more detailed description of allowed motions and their corresponding probabilities is given in Tables S5 and S6 in Supplement 1.

Excluded features

We have made no attempt to model the innate immune system. Antibody activity is only implicitly modeled in Vir life-span. Cytokine signaling is almost entirely absent, save for short-range chemotaxis represented by bias in motion probabilities of T-cells. We have omitted antigen presentation, simplifying this into direct activation of T_Naives by infected B-cells, and we have made no attempt to simulate T-cell memory. Detailed simulation of T-cell activation and homeostasis is beyond the scope of this simulation. As pointed out in the Discussion section (here and in [55]) specific results of our simulation may be artifacts of this choice.

Parameters

PathSim parameters influence aging, motion, interaction, and other life cycle events. In total there are 69 parameters which the user may modify via a parameter input file. Of these 33 control biological factors. The remainder are operational parameters that control things like run length or testing modes, or they control experimental simulation modes which were not used in this work. We give all default values and a detailed description in Supplement 1. Our choice of parameters is driven by two factors: reported values in the literature and values that generate observed experimental outcomes. Not all of these values are biologically accurate (some represent several aggregated processes and, as such, are not directly measurable) and we discuss this further in Supplement 1.

Life cycle parameters include those for the lifespans of the various types of agents and the probability and size of viral bursts. We are also able to set the rate at which Vir is produced in the epithelium. A third sort of life cycle parameter governs what happens when a B_Lat returns from the peripheral circulation to the tonsils. In addition to B_Lats that become lytic due to the passage of time, we can also induce some B_Lats to become B_Lyts directly as a consequence of returning to the Waldeyer’s ring. This simulates possible signals received by the latently infected B-cells that trigger viral replication, although the nature of these signals are not currently well understood [7].

While most lymphocytes in the tonsils are resident in particular areas and not highly mobile, we do permit access to immediately adjacent vertices in order to mimic random Brownian motion and foster interactions. Motion parameters allow us to set the probability that a Vir or a virtual lymphocyte moves from its current location to a neighboring location. PathSim’s key interaction parameters govern the following probabilities: 1) that a Vir infects a B_Naive on contact, 2) that an infected virtual B-cell activates a T_Naive, turning it into a virtual CTL, and 3) that a virtual CTL kills its cognate infected virtual B-cell.

Code verification

PathSim is too complex to admit hand verification of the calculations made in the course of a simulation. We performed code verification by decoupling geometry, aging, interaction, and motion. We put PathSim into known states which are simple enough to verify outcomes, but varied enough to test the underlying functionality.

We used two approaches to verifying PathSim’s geometry: graph theoretic analysis and visual inspection. PathSim is able to record the geometry of its graph to an xml file. We then wrote Perl scripts to test various graph theoretic properties, viz., counts of vertices and edges in selected sub-graphs, connectivity between regions, uniqueness and bidirectionality of edges, and uniformity of the hexagonal units.

We then extracted key sub-graphs from the xml file and visualized them using VRML. This method allowed us to visually inspect the boundary between the tonsils and connecting epithelium, the interconnections of neighboring hexagonal base units, and the internal geometry of these hexagonal sections. With 71 vertices and 586 directed edges, the internal geometry of the hexagonal units is too complex for visual inspection as a single entity. To overcome this limitation, we built special-purpose software to display a hexagonal section in manageable pieces.

To test aging, we turned off motion and interaction and placed known quantities of agents at predetermined locations. We then ran the simulation recording its state at each step. The resulting output is easily evaluated by hand and this process allowed us to run hundreds of test cases.

Tests for motion and interaction proceeded in a similar manner. We placed known populations at predetermined locations and ran the process in question for one step. Since these processes proceed stochastically, evaluating the output is slightly more complicated. We wrote perl scripts to predict the expected values and standard deviations for the outcomes and compared these with the observed results of the tests. Since a single programmer coding the same process twice can easily make the same mistake twice, code for this portion of the simulation and test code were generated by different programmers.

User interface and visualization engine

PathSim is configured to run either from the command line or as a web service (the software is available in Supplement 2). It provides output suitable for graphing in Excel, TimeSearcher (http://www.cs.umd.edu/hci/timesearcher/) [65], Maple, etc. In addition, it is coupled with a three-dimensional visualization engine designed explicitly for ease-of-use and biological insight-generation. Its design and implementation were informed by accepted principles of human-computer interaction and information visualization. Within this virtual environment, agent numbers may be linked with particular parts of the Waldeyer’s ring and viewed in various animated or numerical formats. For details see [55, 58].

RESULTS

The results presented below were obtained with a default set of parameters which we describe in detail in Supplement 1. We discuss additional biological implications of these outcomes in [55]. Here we exhibit the results of varying either the random seed controlling our stochastic choices or values of the parameters themselves. Figure 3–Figure 8 display graphs of times series resulting from running the simulation. Figure 3 and Figure 5, which examine stability with respect to stochasticity, are the only graphs displaying multiple runs for a single parameter set. In all other figures a single line represents a single simulation run.

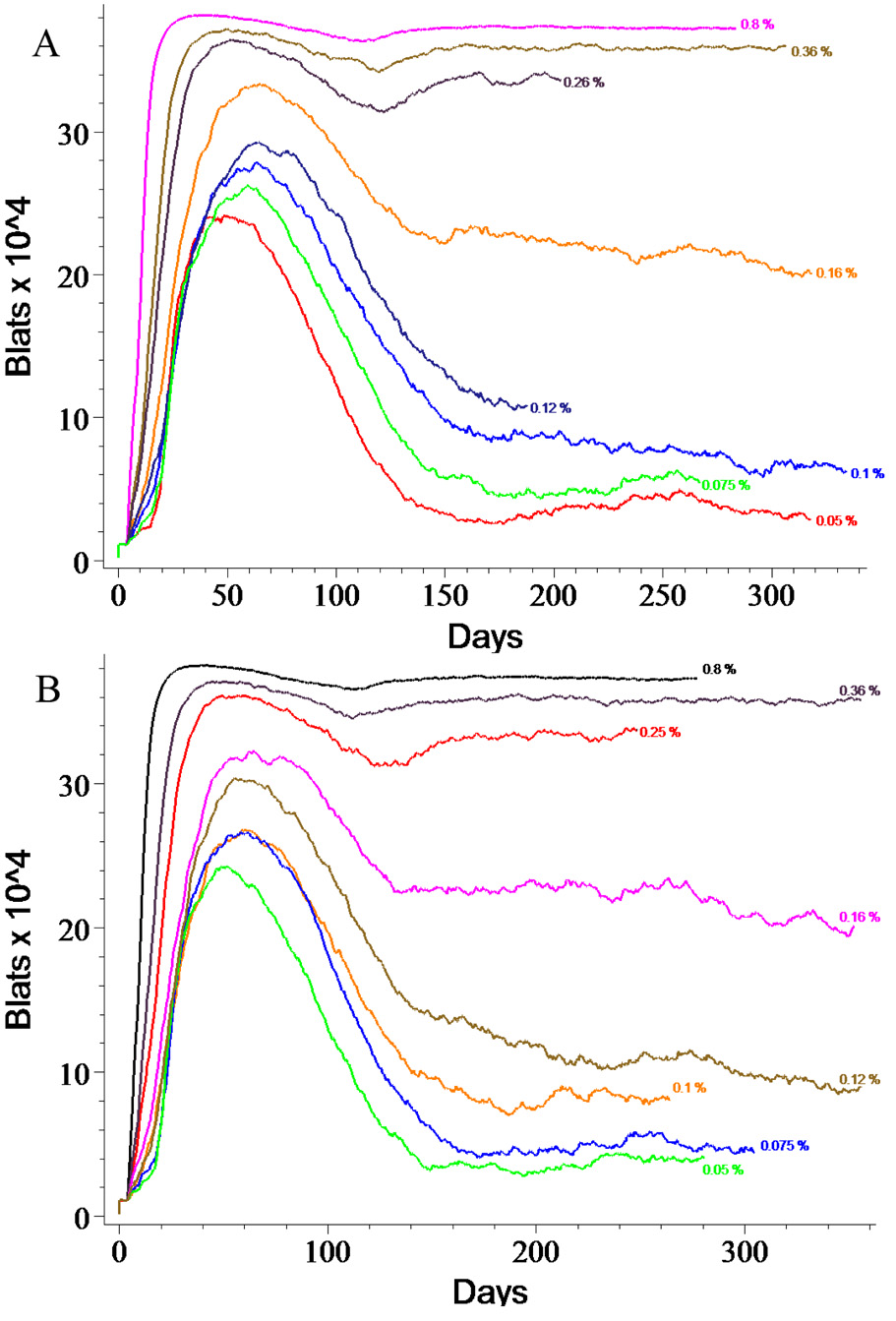
Very small changes in the reactivation rate lead to profoundly different outcomes. Panel A shows the effect of varying the alpha parameter which controls the fraction of B_Lats that commence lytic replication immediately upon return to the tonsils. Panel B depicts the results of changing the Lanzavecchia parameter which determines what fraction of B_Lats divide upon return to the tonsils, thereby producing one B_Lyt and one B_Lat. These two parameters produce nearly identical results and are the most sensitive in our simulation. Each curve is labeled with the value of the parameter that produced it and represents a single run.

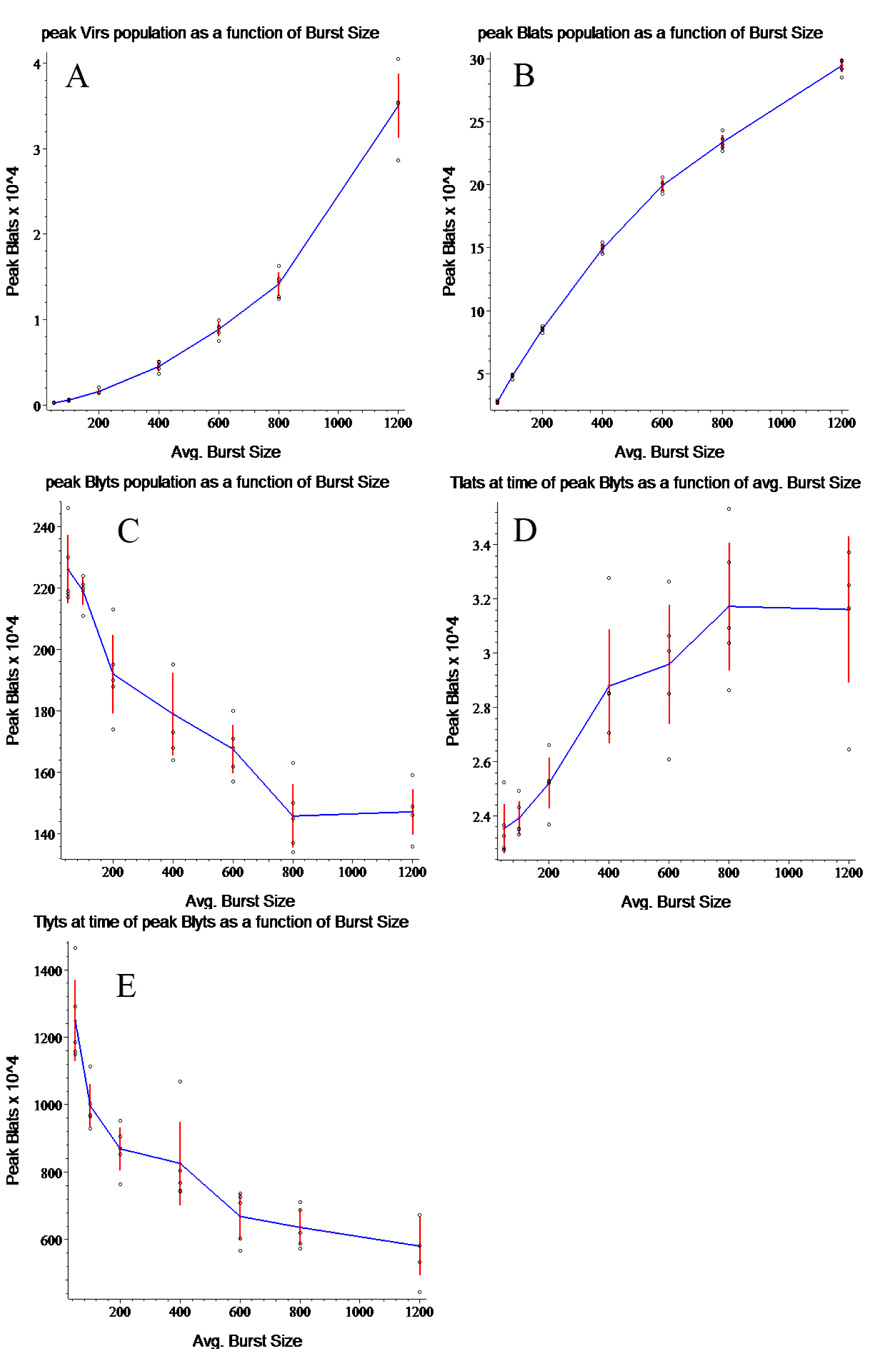
Each graph presents the results of five runs at each of 7 average burst sizes., plotted together with the mean and standard errorof the mean. Peak values from individual runs are plotted as black circles, standard error of the mean is indicated by the vertical red line at each value, and means are connected by the blue curve. The peak response of virus (A) and B_Lats (B) to variation in burst size is as expected, with both rising as burst size increases. Peak B_Lyt numbers (C), however, actually drop as the burst size increases. (D) and (E) show the T_Lat and T_Lyt populations when the B_LytS peak. (The populations of virtual CTLs peak significantly later than those of their cognate virtual B cells.) The default value for average viral burst size is 800.

Stability and overall behavior

In our simulation, stochastic choices are made by referring to the successive values produced by a pseudo-random number generator. Such generators are deterministic in their operation and when started with the same seed will produce the same sequence of numbers, i.e., for our simulation they would produce identical runs. Therefore, in Figure 3, we show the results of running PathSim with our default parameter set and twenty different random seeds (chosen dynamically based on the time at which the run is started). In general we do not want the overall course of our simulation to depend on the exact sequence of random numbers, i.e., different random seeds producing extremely variant outcomes. This kind of dependence should only show up in the case where the system is finely balanced between two differing outcomes. Thus, when we are simulating the generic situation, we expect the overall course of the simulated infection to be independent of initial random seed.

Figure 3 illustrates agent totals for six of the seven agent types in multiple runs. (While T_Naive totals are not shown, the pattern is identical to the other agents.) The runs are virtually superimposable for all seeds and show the characteristic biphasic behavior expected of a primary EBV infection with a peak of acute infection followed by long term low level persistence. Clearly, in the regime which we think best represents the course of infection, there are no critical dependencies on stochastic variation. In subsequent runs analyzing sensitivity to parameter variation we assumed that this stability would hold through the range of parameters tested.

Parameter variation and parameter sensitivity

Our sensitivity analysis focused around variations in our input parameters. We varied these parameters individually or in related pairs, e.g., minimum and maximum viral burst size. We have not explored the parameter space in any systematic way. Our main goal was to bracket physiologically reasonable parameter values and to extend them in either direction to test their effects on the virtual host-virus system. Our choices were dictated by curiosity about how the viral burst size, the strength and speed of the adaptive immune response, the roles (if any) of initial viral dose or ongoing epithelial re-infection and the rate and manner of lytic activation affect outcomes in EBV infection. We were particularly interested in those factors that contribute to long-term persistence. Here we focus specifically on burst size, viral response, and lytic activation.

Burst size

Burst size is controlled by a pair of parameters giving the minimum and maximum number of Vir produced, with the average burst size found at the mid-point in the range. When a B_Lyt bursts, the number of Vir it produces is determined stochastically according to a uniform distribution on the interval between minimum and maximum burst size. As minimum and maximum burst size increase, peak levels of Vir (Figure 4A) and B_Lats (Figure 4B) both increase. Above a certain burst size, the chronic phase is virtually unchanged except for an amplification of stochastic effects. Only at very low burst sizes (8 to 10 Vir per bursting cell) do we see clearance. A burst size of 40 to 60 Vir seems very near the level at which stochastic effects could make the difference between viral clearance and persistence. In contrast to B_Lats, the peak numbers of B_Lyts decrease with increasing viral burst size (See Figure 4C). The default parameter set uses a minimum value of 600 and a maximum value of 1,000.

The simulation enabled an interesting observation relating to the effect of burst size on infected cell populations. Unlike the peak Vir and peak B_Lat populations that grow monotonically as burst size increases (Figure 5A and 5B), the response curve of peak B_Lyt populations to variation in burst size conflicts, at least superficially, with some of our accepted views on the kinetics of EBV infection. As burst size increases, peak B_Lyt (Figure 5C) populations drop, perhaps leveling off at the highest burst size shown.

B_Lyt populations are determined by several factors – the rate at which B_Lats are produced, the number surviving long enough to become B_Lyts, and the average length of time that B_Lyts survive. These average survival times are governed by the virtual CTL response. We have graphed this virtual CTL response in Figure 5D and 5E, where we show the T_Lat and T_Lyt populations at the time of the peak B_Lyt population. (We show this, rather than peak virtual CTL response, since peak virtual CTL response occurs much later and thus has no effect on peak B_Lyt population.) Not surprisingly, the increased B_Lat population produces a higher T_Lat response, while the decrease in B_Lyt population results in lower T_Lyt response. We conclude that it is the decreased survival time of the B_Lats which results in the decrease in B_Lyt population. Our interpretation is that the rise in T_Lat response reduces the number of B_Lats which survive to become lytic. This explanation is supported by the faster rate of decay of B_Lats at higher peak values (Figure 4B).

Proliferation of newly infected B-cells

Our biological model posits that newly infected naïve B-cells enter the germinal centers of Waldeyer’s ring where they differentiate into resting memory B-cells and exit into the peripheral circulation (See Figure 1 and [2–3]). It is not known to what extent they undergo cell division while in the germinal center, but we believe any proliferation must be quite limited. Extensive proliferation would likely be detrimental to the survival of the host. This sort of uncontrolled proliferation is seen in X-linked proliferative disease (XLP), an X chromosome linked predisposition to fatal acute EBV infection [66] and in patients who are immunosuppressed who are susceptible to tumors arising from the unregulated proliferation of EBV infected B cells. That these tumors are rare and oligo- rather than polyclonal suggests that uncontrolled proliferation is a rare event even in the immunosuppressed. (For a more detailed discussion of this issue see [2, 3].) To examine the implications of allowing newly infected B_Lat cells to proliferate, we tested three different amplification factors for newly infected cells in the simulation (1, 2 or 3 rounds of cell division, resulting in 2, 4 or 8 daughters) before allowing them to exit Waldeyer’s ring and enter the bloodstream. There were some changes in the pattern of resolution of the acute phase (small oscillations, especially at the highest amplification), but qualitatively the overall dynamics were not different from those of the default case where there is no amplification of newly infected cells. As the degree of proliferation increased, not surprisingly, we observed higher numbers of B_Lats throughout the simulation and a shift in the peak of acute infection to later times, likely resulting from a delay in the ability of CTLs to catch up with the more rapidly expanding B_Lats (Figure 6A and 6B). Not surprisingly perhaps, the overall trend suggested that more extensive proliferation would overwhelm the virtual host consistent with our idea, expressed above, that extensive proliferation could not be tolerated. This is a particularly interesting area to investigate in the context of EBV associated cancers. It will be important to explore this area in a simulation where B_Lat are divided into blast (proliferating and immune targeted) and memory (resting and immune invisible) compartments as planned in the next iteration of PathSim.

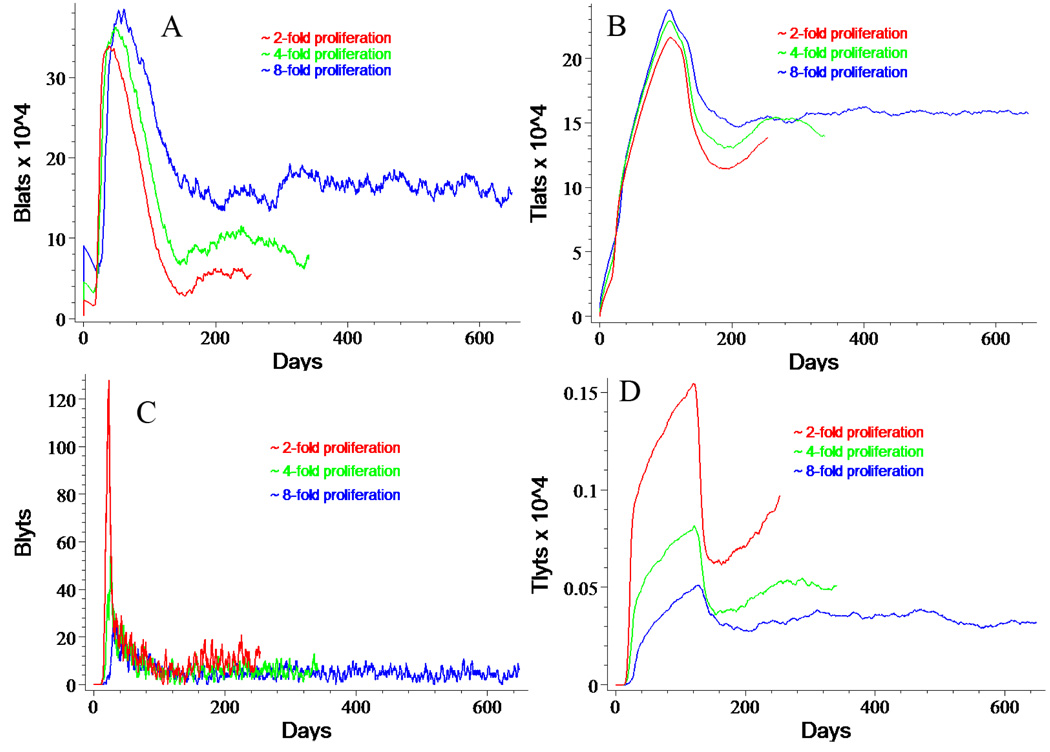
Panels A and C illustrate the effects of allowing 1 (red), 2 (green), or 3 (blue) rounds of cell division immediately following initial infection on the numbers of B_Lat and B_Lyt, respectively. While B_Lat populations grow, B_Lyt populations actually shrink. Cognate virtual CTLs show parallel behavior.

Once again, the B_Lyt dynamics initially appeared somewhat counterintuitive. As the degree of proliferation of newly infected B_LatS rises, the number of B_LytS drops (Figure 6C). T_LytS follow an identical pattern of dropping as proliferation increases (Figure 6D). This result is consistent with the notion that increasing numbers of virtual B_Lat cells engender a more aggressive immune response, thereby shortening their lifespan. Fewer B_LatS live long enough to become B_LytS and the lower numbers of B_Lyt lead to the creation of few T_LytS.

Immune response to infected B-cells

We use a very simplified model of T-cell activation. When a T_Naive encounters either a B_Lat or a B_Lyt there is a chance that it is activated to become a T_Lat or a T_Lyt respectively. The probability governing this outcome is the activation rate. Clearly, this process subsumes a large number of actual biological events, all of which have their own kinetics. The default activation rates are 0.015 for T_Lat and 0.035 for T_Lyt. When a T_Lat or a T_Lyt encounters its cognate infected B-cell, there is a probability that this encounter results in killing that infected cell. We refer to this probability as its kill rate. The activation and kill rates are set separately for latents and lytics. Default values for the kill rate are 0.3 and 0.6, respectively. Varying either the activation rate for T_Lats (Figure 7A) or the kill rate for T_Lats (Figure 7B) results in a monotonic change in peak infection, with maximal peak infection corresponding to minimal activation or kill rate. At very high levels of either activation or kill, we can achieve clearance. At the lowest level of each, we do not appear to achieve the normal recovery from acute illness characterized by low level persistence. Figure 7 illustrates trends when these rates are varied independently.

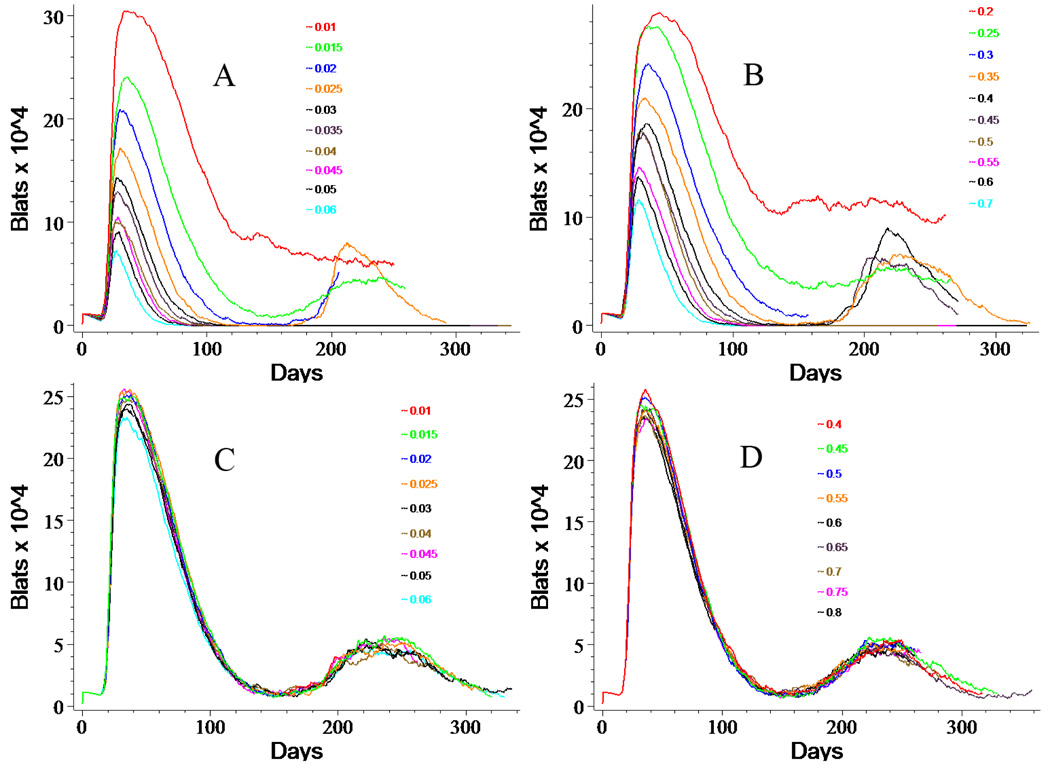
Varying T_Lat activation rate (A) or kill rate (B) or T_Lyt activation rate (C) or kill rate (D) results in the changes illustrated above in B_Lat populations. Increasing either the activation or kill rate of T_LatS decreases the B_LatS ultimately resulting in clearance at the highest values of either of the two parameters, while for T_LytS increasing these two parameters has no significant effect on the B_Lat population. The legend indicates the probability of the event (activation or kill, respectively), where 1.0 corresponds to 100%. The default values for activation are T_Lat=0.015 and T_Lyt=0.035, while those for killing are T_Lat=0.30 and T_Lyt=0.60.

In contrast to T_Lats, varying the activation and kill rates for T_Lyts has no appreciable effect on either B_Lats (Figure 7C and 7D) or B_Lyts (not shown). Perhaps this is because the numbers of B_Lyts are generally so small that few of them are actually killed by T_Lyts before they die at burst. We discuss this further below.

Lytic reactivation of B_Lats

Little is known about the signal which causes latently infected B-cells to exit the memory state and become lytic [7, 61]. In our default parameter set, this state change occurs due to the passage of time in the latent state, i.e., at the end of its life, there is a 60% probability that a B_Lat simply dies but a 40% probability that it will initiate lytic replication of Vir. However, we have experimented with two additional methods of triggering lytic replication of Vir designed to mimic this unknown biological signal and applied them to a small fraction of the returning B_Lats. In the simplest version, returning from the blood to Waldeyer’s ring causes a small, user-determined fraction of B_Lat cells to automatically turn into B_Lyts. This fraction is termed the alpha parameter. The second version is inspired by Thorley-Lawson’s application of Lanzavecchia’s ideas about homeostasis of the memory compartment to EBV [7, 61]. In this case, a small, user-defined fraction of returning B_Lat spontaneously divides, producing one B_Lat and one B_Lyt. We term this fraction the Lanzavecchia parameter. (In the default run, both the alpha parameter and the Lanzavecchia parameter are set to zero.) When either simulated signal is “received” by as few as 0.15% of returning B_Lats, a significant change emerges in simulated disease progression. Both panels in Figure 8 illustrate that at values above 0.050% (red), the number of infected B cells in the chronic phase begins to increase steadily. By 0.16% (orange), the acute phase does not resolve normally. Increasing this value to as little as 0.26% causes the infected cells to overwhelm the healthy B-cell population.

We also observe that these two simulated signals produce indistinguishable results (Figure 8). The equivalence of these two parameters is not unexpected, given that the critical factor is the sharp rise in B_Lat numbers, while the small increase in B_Lyts is negligible. This behavior could provide insight into rare fatal EBV infections.

DISCUSSION

In this paper we have presented a first simulation of EBV infection that is accurate enough to describe many aspects of the infection. Implemented at the level of cells and lymphoepithelial tissue, it contains sufficient detail to generate new biological insights and allow further investigation of the mechanism of infection [55]. Moreover, it sharpens our understanding of specific issues and suggests new experimental investigations.

Living things exhibit homeostasis. That is, in most regimes, they act to maintain their state in the face of random perturbation. PathSim is a stochastic simulation and thus also experiences random fluctuation. The exact course of each simulation depends on the values produced by a random number generator. For this to be a usable simulation of living processes, it should also be stable in most regimes. Figure 3 demonstrates that this sort of stability is indeed observed in our simulation. However, it is not hard to imagine unstable situations, both in vivo and in silico. For example, when there are very few infected cells, small random fluctuations may mean the difference between persistence and clearance. Such a state lives on or near a stochastic border between differing outcomes. In a deterministic system one can find a well-defined border between the basins of attraction for different outcomes. In the presence of random fluctuations, this border may become a region in which different outcomes are likely and unpredictable. We consider these boundaries interesting from a therapeutic viewpoint since they represent the states in which a small intervention could produce a large change in outcome. In reality, this requires the ability to determine that the patient is actually in the right state, to access the patient in that state, and to perform the desired intervention.

We have presented results highlighting those points within the state space of the simulation where small changes in state lead to large changes in outcome. Now consider the case where starting the simulation in the same state leads to different outcomes as a result of small changes in the parameters governing the evolution of the system. (If one considers the parameters part of the state of the system, then this distinction collapses, but the distinction is still useful.) Consider a hypothetical intervention that eliminated one half of the viral load in the tonsils. Such an intervention affects the current state of the system. Contrast this scenario with the administration of an anti-viral drug which reduces viral burst size. In this latter case, we are affecting the dynamics by which the system evolves in time. A systematic search for tipping points either in state or evolution should prove insightful for both biological understanding and developing intervention strategies. This search will require the ability to perform very large numbers of runs, which we hope to do by developing a smaller, simplified, faster-running simulation (see below).

We have identified one parameter whose value has a very dramatic impact on outcome, namely the fraction of B_Lats which are turned lytic immediately upon return from the blood to Waldeyer’s ring (alpha parameter, Figure 8). We believe that there must be strong evolutionary pressure fixing the corresponding rate in vivo. Consider what happens if a mutation in the EBV virus arises in which this rate drops. A virion with this mutation produces fewer copies of itself within the infected individual and thereby decreases its opportunities for transmission. This will act to take the mutant gene out of the gene pool. On the other hand, a mutation which raises this rate might result in host death, removing both that EBV genome and the host from further procreation. While it has been suggested that this strategy may be quite effective for an acutely replicating virus that jumps quickly from host-to-host [67], it would be counter productive for a virus like EBV that uses persistence as a way to maximize infectious spread. Thus, overall, there is evolutionary pressure on the virus to prevent this rate from either rising or falling, and there is pressure on the host to keep it from rising. In this way, selection acts to keep the rate constant, within the constraints of overlapping, and sometimes even contradictory, goals of both virus and host [45]. Now consider a hypothetical case in which a mechanism develops for stabilizing this rate. That mechanism could provide a survival advantage to both virus and host. This raises the question, what has been the impact of this co-evolution on the virus and/or the human immune system and what features have arisen because of it?

We would like our simulation to give us insight into therapeutic targets for drug development. Consider a drug which suppresses viral replication. How effective would such a drug need to be to induce clearance? Our investigation of the effects of viral burst size may provide some guidance about the drug efficacy required for complete clearance. Interpretation of these results, however, depends on information about EBV which we do not yet possess. Figure 4B shows persistence at a burst size around 40 and clearance at a burst size around 10. At some value between 40 and 10, we should see runs on the stochastic boundary described above. Let us assume this occurs at a burst size of 25. We have estimated that a lytically infected B-cell produces approximately 1,000 viral particles [68]. (We know neither what portion is viable, nor precisely what portion is likely to be neutralized by circulating antibodies.) The drug's job is to reduce the number of viable virions produced to a maximum of 25 per burst. This results in a required efficacy of 75% – 97% depending on the precise burst size. If 10% of virions are viable, the drug must be 75% effective. If the viable percentage rises to 50%, the drug must be 95% effective. With 100% viable, the drug must be 97% effective. Clearly, even when only 100 viable virus particles are released, the drug must be highly efficacious to result in simulated clearance.

These numbers are not conclusive. We have set the burst size at the beginning of each run. In reality, the drug would be administered after onset of symptoms, say, around day 50. It is hard to know whether this fact makes it easier to achieve clearance because the immune system has already mounted a response, or harder because the virus has established itself in the peripheral circulation. Moreover, we have neglected the contribution of viral replication in the epithelium, which may alter the dynamics considerably.

PathSim is not sufficiently developed yet to always make trustworthy predictions. The biological validation described in [55] demonstrates that the simulation can reliably describe and make some predictions about the basic dynamics of infection. However, deeper analysis illustrates both the limitations and potential value of this kind of simulation.

In reality, latently infected B-cells are only initially susceptible to CTL regulation. After becoming infected, naïve B-cells become activated blasts and enter the germinal center. While in the activated blast state, they are subject to CTL regulation. They then differentiate into resting memory B-cells and enter the peripheral circulation. In the resting memory state, they do not express viral proteins and are therefore immunologically invisible [2, 3, 6]. In particular, the level of CTL latent activity should not affect the rate at which they subsequently reactivate. Because we have combined both of these B latent states (activated blast and resting memory) in the B_Lat state (which effectively represents all states not actively replicating virus), our simulation cannot tell us which of the two states effectively contributes most strongly to the expansion of the latently infected B-cell population. Therefore, we can not determine if the simulation is making a prediction of interest (increased burst size leads to the decrease in B_Lyts due to increased numbers of newly infected, T_Lat-sensitive B_Lats that get killed before they enter the memory compartment) or an artifact resulting from our simplification.

Our CTL response is highly simplified. When a T cell encounters a target it becomes activated with some probability and when it encounters its target it kills it with some probability. After a fixed period of time the virtual CTL are recycled as naïve T cells. We have also not implemented T cell memory or expansion/proliferation. Although by their nature simulations involve simplifications that could lead to artifacts, qualitatively PathSim dynamics replicate real infection reasonably well, as we demonstrated in [55]. One added insight that this paper contributes is the realization that persistence is relatively easy to achieve and even easier to maintain, given the nature of latently infected B cells. Therefore we would speculate that implementing more detailed T cell biology will not affect the overall dynamics but may well sharpen the quantitative accuracy of our output and thereby give us increased confidence in the accuracy of its predictions.

Our experience with PathSim suggests two opposite directions for further development. On the one hand, PathSim is fairly large. It holds on the order of 10⁶ agents and monitors approximately 10⁵ locations, updating each 10 times per simulated hour. This extracts a high price in computation. Just over one year of simulated time takes about eight days in run time under Linux on a 3 GHz Pentium 4 processor. Consequently, we would like to find ways to simplify the simulation while continuing to model observed behaviors.

On the other hand, PathSim is already an extreme simplification of reality. There is no attempt to simulate the detailed molecular states of the agents, as exemplified by their receptors, signaling pathways, etc. Moreover, there are many immunological facts which we have simplified, approximated, or omitted. There is no simulation of the innate immune response, antigen presentation, cytokine signaling, or memory T-cells. As discussed above, we have also conflated the blast and memory states of infected B-cells. In addition, the geometry of Waldeyer's ring omits the fractal invagination of its surface, and we do not model saliva transport across the surface. Our model of epithelial amplification is also highly simplified.

Our choices were dictated partially by lack of relevant clinical and laboratory data, but also by our belief that an agent-based model best represents the reality of biological interactions. Simple, localized interactions may give rise to complex, global phenomena. The main driving force behind the chosen level of detail, however, is the fact that this is a first attempt whose primary goal was to capture the most basic requirements for acute and persistent infection. In this we have succeeded. In the light of our current results and understanding, the simplifications which we are most eager to rectify are the simplifications of the latently infected states, the lack of T-cell memory, and issues relating to lymphocyte density. (For a discussion of the density, see Supplement 1.)

We doubt that PathSim represents an optimal balance of the opposing quests for simplicity and accuracy. Nevertheless, as we have argued above and in [55], PathSim models many clinically observed features. Given PathSim's simplifications, this resemblance is striking and invites the question of what factors are responsible. We believe it is generic features of our rule set that produce the overall dynamics.

Let us speculate on what those features might be. At the simplest level, PathSim exhibits a mix of positive and negative feedback between the different agent populations. We have a two-step process (latents and lytics) in which the infected virtual B-cells act to increase the populations of virtual CTLs and the virtual CTLs then act to decrease the populations of virtual infected B-cells. Linked to this process are the mechanisms by which the Vir acts to increase its own population by going through the Vir- B_Lat - B_Lyt –Vir cycle with amplification at the last step. This dynamic resembles a spatially distributed predator-prey system such as those studied in [69].

In summary, we do not believe that PathSim has yet evolved to the point where it reliably produces answers, but it is already quite effective at framing questions. Its major contribution is its ability to generate global insights and motivate further experimentation, while suggesting new avenues for its own future development.

Supplementary Material

Supplement 1 – Parameter values. Tables containing the parameters used, their origin, number, type and rationale behind their choice. It also describes the structure of the simulation in detail including the rationale for decisions about simplifications and assumptions made.

NIHMS55445-supplement-01.doc^{(153.5KB, doc)}

Supplement 2. PathSim Software. This supplement includes the PathSim software in two forms:

1. A (mostly) standalone GUI. This gives the user access to most of Pathsim's functionality including the ability to modify parameters, run the simulation and post-process the results for view in excel, timesearcher and as a browseable 3D world which we refer to as an IRVE. This GUI requires basic unix functionality including gcc, make, Perl, x-windows and the Perl module Tk.pm.

2. A full distribution of our web interface. This requires a web server.

Both of these include the Pathsim source code, along with doxygen documentation of this code. We have successfully run the GUI under linux and cygwin, and have run the web interface in a windows environment. We offer this software for our readers to examine and use, however it requires basic knowledge of unix programming. This is not supported software, but users with a modicum of computer expertise should be able to run it.

NIHMS55445-supplement-02.zip^{(34.4MB, zip)}

NIHMS55445-supplement-03.zip^{(14.8MB, zip)}

ACKNOWLEDGEMENTS

Most of the simulation results presented in this paper were produced on the machines of the Math Emporium at Virginia Tech. We wish to thank its director, Michael Williams for giving us access to these machines and Bryan Shake for his technical assistance in using them. Dr. Paul Plassmann contributed additional computing resources. We also gratefully acknowledge Dr. Jerald Mullersman for helpful discussions on EBV pathology and tonsil anatomy.

FUNDING

This work was supported by Public Health Service grants R01 CA65883, R01 AI18757 and RO1 AI062989 to DT-L.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

There is an important philosophical distinction to be made between a model, which is an abstraction, and a simulation, which is the computer program that realizes this model. These may diverge in important ways, e.g., due to round-off errors. Given the discrete nature of our model, we believe there is no substantive divergence i.e., the model and its implementation can be treated as isomorphic. Accordingly, we will not keep up this distinction.

REFERENCES

1.Rickinson AB, Kieff E. Epstein-Barr Virus. In: Knipe D, Howley P, editors. Virology. New York, New York: Lipincott, Williams, and Wilkins; 2001. pp. 2575–2628. [Google Scholar]
2.Thorley-Lawson DA. Epstein-Barr Virus: Exploiting the Immune System. Nature Reviews: Immunology. 2001;1(1):75–82. doi: 10.1038/35095584. [DOI] [PubMed] [Google Scholar]
3.Thorley-Lawson DA, Gross A. Persistence of the Epstein-Barr Virus and the Origins of Associated Lymphomas. New England Journal of Medicine. 2004;350(13):1328–1337. doi: 10.1056/NEJMra032015. [DOI] [PubMed] [Google Scholar]
4.Laichalk LL, et al. The Dispersal of Mucosal Memory B Cells: Evidence from Persistent EBV Infection. Immunity. 2002;16(5):745–754. doi: 10.1016/s1074-7613(02)00318-7. [DOI] [PubMed] [Google Scholar]
5.Hoagland RJ. The Transmission of Infectious Mononucleosis. American Journal of Medical Science. 1955;229:262–272. doi: 10.1097/00000441-195503000-00003. [DOI] [PubMed] [Google Scholar]
6.Hochberg D, et al. Demonstration of the Burkitt's Lymphoma Epstein-Barr Virus Phenotype in Dividing Latently Infected Memory Cells in vivo. Proceedings of the National Academy of Science USA. 2004;101(1):239–244. doi: 10.1073/pnas.2237267100. [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Laichalk LL, Thorley-Lawson DA. Terminal Differentiation into Plasma Cells Initiates the Replicative Cycle of Epstein-Barr Virus in vivo. Journal of Virology. 2005;79(2):1296–1307. doi: 10.1128/JVI.79.2.1296-1307.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Henle W, Henle G. Seroedpidemiology of the Virus. In: Epstein MA, Achong BG, editors. The Epstein-Barr Virus. Berlin: Springer-Verlag; 1979. pp. 61–78. [Google Scholar]
9.Khanna R, Moss DJ, Burrows SR. Vaccine Strategies Against Epstein-Barr Virus-Associated Diseases: Lessons from Studies on Cytotoxic T-Cell-Mediated Immune Regulation. Immunology Reviews. 1999;170:49–64. doi: 10.1111/j.1600-065x.1999.tb01328.x. [DOI] [PubMed] [Google Scholar]
10.Perelson A. Modeling Viral and Immune System Dynamics. Nature Reviews: Immunology. 2002;2(1):28–36. doi: 10.1038/nri700. [DOI] [PubMed] [Google Scholar]
11.Perelson A, Weissbuch G. Immunology for Physicists. Review of Modern Physics. 1995;69(4) [Google Scholar]
12.Segel LA. Spatio-temporal Models in Immunology. Bifurcation and Chaos. 2002;12:2343–2347. [Google Scholar]
13.Ribiero RM, Bonhoeffer S. Production of Resistant HIV Mutants During Antiretroviral Therapy. Proceedings of the National Academy of Science. 2000;97(14):7681–7686. doi: 10.1073/pnas.97.14.7681. [DOI] [PMC free article] [PubMed] [Google Scholar]
14.Chao DL, et al. A Stochastic Model of Cytotoxic T Cell Responses. Journal of Theoretical Biology. 2004;228(2):227–240. doi: 10.1016/j.jtbi.2003.12.011. [DOI] [PubMed] [Google Scholar]
15.Perelson AS, et al. HIV-1 Dynamics in vivo: Virion Clearance Rate, Infected Cell Life-Span, and Viral Generation Time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
16.Neumann AU, et al. Hepatitis C Viral Dynamics in vivo and the Antiviral Efficacy of Interferon α Therapy. Science. 1998;282:103–107. doi: 10.1126/science.282.5386.103. [DOI] [PubMed] [Google Scholar]
17.Nowak MA, Bangham CR. Population Dynamics of Immune Responses to Persistent Viruses. Science. 1996;272:74–79. doi: 10.1126/science.272.5258.74. [DOI] [PubMed] [Google Scholar]
18.Endy D, Kong D, Yin J. Intracellular Kinetics of a Growing Virus: A Genetically Structured Simulation for Bacteriophage T7. Biotechnology and Bioengineering. 1997;55(2):376–389. doi: 10.1002/(SICI)1097-0290(19970720)55:2<375::AID-BIT15>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
19.Bonhoeffer S, et al. Virus Dynamics and Drug Therapy. Proceedings of the National Academy of Science. 1997;94:6971–6976. doi: 10.1073/pnas.94.13.6971. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Davenport MP, et al. Clonal Selection, Clonal Senescence, and Clonal Succession: The Evolution of the T Cell Response to Infection with a Persistent Virus. Journal of Immunology. 2002;168:3309–3317. doi: 10.4049/jimmunol.168.7.3309. [DOI] [PubMed] [Google Scholar]
21.Nowak MA, et al. Viral Dynamics in Hepatitis B Virus Infection. Proceedings of the National Academy of Science. 1996;93:4398–4402. doi: 10.1073/pnas.93.9.4398. [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Beauchemin C. Probing the Effects of the Well-Mixed Assumption on Viral Infection Dynamics. Journal of Theoretical Biology. 2006;242(2):464–477. doi: 10.1016/j.jtbi.2006.03.014. [DOI] [PubMed] [Google Scholar]
23.Durrett R, Levin S. The Importance of Being Discrete (and Spatial) Theoretical Population Biology. 1994;46:363–394. [Google Scholar]
24.Kleinstein S, Seiden P. Simulating the Immune System. Computer Simulations. 2000 Jul/Aug;:69–77. [Google Scholar]
25.Kleinstein SH, Singh JP. Toward Quantitative Simulation of Germinal Center Dynamics: Biological and Modeling Insights from Experimental Validation. Journal of Theoretical Biology. 2001;211(3):253–275. doi: 10.1006/jtbi.2001.2344. [DOI] [PubMed] [Google Scholar]
26.Kreft JU, Booth G, Wimpenny JW. Bacsim, a Simulator for Individual-Based Modelling of Bacterial Colony Growth. Microbiology. 1998;144(12):3275–3287. doi: 10.1099/00221287-144-12-3275. [DOI] [PubMed] [Google Scholar]
27.Neugebauer EA, Tjardes T. New Approaches to Shock and Trauma Reearch: Learning from Multidisciplinary Exchange. Journal of Trauma. 2004;56(5):1156–1165. doi: 10.1097/01.ta.0000119207.14267.63. [DOI] [PubMed] [Google Scholar]
28.Turing AM. In: The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life, Plus the Secrets of Enigma. Copeland BJ, editor. New York, NY: Clarendon Press; 2004. [Google Scholar]
29.Celada F, Seiden PE. A Computer Model of Cellular Interactions in the Immune System. Immunology Today. 1992;13(2):56–62. doi: 10.1016/0167-5699(92)90135-T. [DOI] [PubMed] [Google Scholar]
30.Bernaschi M, Castiglione F. Design and Implementation of an Immune System Simulator. Computers in Biology and Medicine. 2001;31(5):303–331. doi: 10.1016/s0010-4825(01)00011-7. [DOI] [PubMed] [Google Scholar]
31.Bernaschi M, Succi S, Castiglione F. Large-scale Cellular Automata Simulations of the Immune System Response. Physical Review E. 2000;61(2):1851–1854. doi: 10.1103/physreve.61.1851. [DOI] [PubMed] [Google Scholar]
32.Bezzi M, et al. The Transition Between Immune and Disease States in a Cellular Automaton Model of Clonal Immune Response. Physica. 1997;245:145–163. [Google Scholar]
33.Celada F, Seiden PE. Modeling Immune Cognition; IEEE International Conference on Systems, Man, and Cybernetics; 1998. [Google Scholar]
34.Cohn M, Langman R, Mata J. A Computerized Model for Self -Non-Self Discrimination at the Level of the Th (Th Genesis) I. The Origin of 'Primer' Effector Th Cells. International Immunology. 2002;14:1105–1112. doi: 10.1093/intimm/dxf078. [DOI] [PMC free article] [PubMed] [Google Scholar]
35.Cohn M, Langman R, Mata J. A Computerized Model for the Self-Non-Self Discrimination at the Level of the Th (Th Genesis) II. The Behavior of the System upon Encounter with Non-Self Antigens. International Immunology. 2003;15(5):593–609. doi: 10.1093/intimm/dxg059. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Iber D, Maini PK. A Mathematical Model for Germinal Centre Kinetics and Affinity Maturation. Journal of Theoretical Biology. 2002;219(2):153–175. doi: 10.1006/jtbi.2002.3079. [DOI] [PubMed] [Google Scholar]
37.Kohler B, et al. A Systematic Approach to Vaccine Complexity Using an Automaton Model of the Cellular and Humoral Iimmune System I. Viral Characteristics and Polarized Responses. Vaccine. 2000;19(7–8):862–876. doi: 10.1016/s0264-410x(00)00225-5. [DOI] [PubMed] [Google Scholar]
38.Meir-Schellersheim M. Simmune, a Tool for Simulating and Analyzing Immune System Behavior. Hamburg: University of Hamburg; 1999. [Google Scholar]
39.Meyer-Hermann ME, Maini PK, Iber D. An Analysis of B Cell Selection Mechanisms in Germinal Centers. Mathematical Medical Biology. 2006;23(3):255–277. doi: 10.1093/imammb/dql012. [DOI] [PubMed] [Google Scholar]
40.Morpurgo D, et al. Modelling Thymic Functions in a Cellular Automaton. International Immunology. 1995;7(4):505–516. doi: 10.1093/intimm/7.4.505. [DOI] [PubMed] [Google Scholar]
41.Puzone R, et al. ImmSim, A Flexible Model for in machina Experiments on Immune System Responses. Future Generation Computer Systems. 2002;18(7):961–972. [Google Scholar]
42.Seiden PE, Celada F. A Model for Simulating Cognate Recognition and Response in the Immune System. Journal of Theoretical Biology. 1992;158(3):329–357. doi: 10.1016/s0022-5193(05)80737-4. [DOI] [PubMed] [Google Scholar]
43.Stewart JJ, et al. A Solution to the Rheumatoid Factor Paradox: Pathologic Rheumatoid Factors can be Tolerized by Competition with Natural Rheumatoid Factors. Journal of Immunology. 1997;159(4):1728–1738. [PubMed] [Google Scholar]
44.Tay J, Jhavar A. CAFISS: A Complex Adaptive Framework for Immune System Simulations; ACM Symposium for Applied Computing-Bioinformatics; 2005. [Google Scholar]
45.Segel LA, Bar-Or RL. On the Role of Feedback in Promoting Conflicting Goals of the Adaptive Immune System. Journal of Immunology. 1999;163:1342–1349. [PubMed] [Google Scholar]
46.Castiglione F, et al. Simulating Epstein-Barr Virus Infection with C-ImmSim. Bioinformatics. doi: 10.1093/bioinformatics/btm044. submitted. [DOI] [PubMed] [Google Scholar]
47.An G. Agent-Based Computer Simulation and SIRs: Building a Bridge Between Basic Science and Clinical Trials. Shock. 2001;16(4):266–273. doi: 10.1097/00024382-200116040-00006. [DOI] [PubMed] [Google Scholar]
48.An G. In silico Experiments of Existing and Hypothetical Cytokine-Directed Clinical Trials Using Agent-Based Modeling. Critical Care Medicine. 2004;32(10):2050–2060. doi: 10.1097/01.ccm.0000139707.13729.7d. [DOI] [PubMed] [Google Scholar]
49.Forst CV. Host-Pathogen Systems Biology. Drug Discovery Today. 2006;11(5–6):220–227. doi: 10.1016/S1359-6446(05)03735-9. [DOI] [PubMed] [Google Scholar]
50.Garrett-Dancik DJ, Dorman K. An Agent-Based Model for Leishmania Infection. International Journal of Complex Systems. In Press. [Google Scholar]
51.Mansury Y, Diggory M, Deisboeck TS. Evolutionary Game Theory in an Agent-Based Brain Tumor Model: Exploring the 'Genotype-Phenotype' Link. Journal of Theoretical Biology. 2006;238(1):146–156. doi: 10.1016/j.jtbi.2005.05.027. [DOI] [PubMed] [Google Scholar]
52.Walker DC, et al. Agent-Based Computational Modeling of Wounded Epithelial Cell Monolayers. IEEE transactions on nanobioscience. 2004;3(3):153–163. doi: 10.1109/tnb.2004.833680. [DOI] [PubMed] [Google Scholar]
53.Segovia-Juarez JL, Ganguli S, Kirschner D. Identifying Control Mechanisms of Granuloma Formation During M. tuberculosis Infection Using an Agent-Based Model. Journal of Theoretical Biology. 2004;231:357–376. doi: 10.1016/j.jtbi.2004.06.031. [DOI] [PubMed] [Google Scholar]
54.Srivastava R, et al. Stochastic vs. Deterministic Modeling of Intracellular Viral Kinetics. Journal of Theoretical Biology. 2002;(218):309–321. doi: 10.1006/jtbi.2002.3078. [DOI] [PubMed] [Google Scholar]
55.Duca KA, et al. A virtual look at Epstein-Barr virus infection: biological interpretations. PLoS Pathog. 2007;3(10):1388–1400. doi: 10.1371/journal.ppat.0030137. [DOI] [PMC free article] [PubMed] [Google Scholar]
56.Various. C. NIH, FDA, editor. PM Medical Health News; 21st Century Complete Medical Guide to Infectious Mononucleosis and the Epstein-Barr Virus (EBV), Authoritative Government Documents, Clinical References, and Practical Information for Patients and Physicians. 2004
57.Chang RS. Infectious Mononucleosis. Boston, MA: Hall Press; 1980. p. 224. [Google Scholar]
58.Polys N, et al. Web3D Symposium. Monterey, CA: ACM Press; 2004. PathSim Visualizer: An Information Rich Virtual Environment for Systems Biology. [Google Scholar]
59.Abbey K, Kawabata I. Computerized Three-dimensional Reconstruction of the Crypt System of the Palatine Tonsil. Acta Otolaryngol. 1988;454 Suppl:39–42. doi: 10.3109/00016488809125002. [DOI] [PubMed] [Google Scholar]
60.Perry M, Whyte A. Immunology of the Tonsils. Immunology Today. 1998;19(9):414–421. doi: 10.1016/s0167-5699(98)01307-3. [DOI] [PubMed] [Google Scholar]
61.Bernasconi NL, Traggiai E, Lanzavecchia A. Maintenance of Serological Memory by Polyclonal Activation of Human Memory B Bells. Science. 2002;298:2199–2202. doi: 10.1126/science.1076071. [DOI] [PubMed] [Google Scholar]
62.Pegtel DM, Middeldorp J, Thorley-Lawson DA. Epstein-Barr Virus Infection in ex vivo Tonsil Epithelial Cell Cultures of Asymptomatic Carriers. Journal of Virology. 2004;78(22):12613–12624. doi: 10.1128/JVI.78.22.12613-12624.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
63.Babcock GJ, et al. EBV Persistence in Memory B cells in vivo. Immunity. 1998;9(3):395–404. doi: 10.1016/s1074-7613(00)80622-6. [DOI] [PubMed] [Google Scholar]
64.Miyashita EM, et al. Identification of the Site of Epstein-Barr Virus Persistence in vivo as a Resting B-Cell. Journal of Virology. 1997;71(7):4882–4891. doi: 10.1128/jvi.71.7.4882-4891.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
65.Hochheiser H, Schneiderman B. Dynamic Query Tools for Time Series Data Sets, Timebox Widgts fro Interactive Exploration. Information Visualization. 2004;3(1):1–18. [Google Scholar]
66.Seemayer TA, et al. X-linked lymphoproliferative disease: twenty-five years after the discovery. Pediatr Res. 1995;38(4):471–478. doi: 10.1203/00006450-199510000-00001. [DOI] [PubMed] [Google Scholar]
67.Ewald PW. Evolution of Infectious Disease. New York, NY: Oxford University Press; 1994. [Google Scholar]
68.Fourth International Symposium on Epstein-Barr Virus and Associated Malignant Diseases. Hualien, Taiwan: Humana Press; 1990. Epstein-Barr Virus. [Google Scholar]
69.Mobilia M, Georgiev IT, Taeuber UC. Fluctuations and Correlations in Lattice Models for Predator-Prey Interaction. Physical Review E. 2006;73(4) doi: 10.1103/PhysRevE.73.040903. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

NIHMS55445-supplement-01.doc^{(153.5KB, doc)}

Supplement 2. PathSim Software. This supplement includes the PathSim software in two forms:

2. A full distribution of our web interface. This requires a web server.

NIHMS55445-supplement-02.zip^{(34.4MB, zip)}

NIHMS55445-supplement-03.zip^{(14.8MB, zip)}

[R1] 1.Rickinson AB, Kieff E. Epstein-Barr Virus. In: Knipe D, Howley P, editors. Virology. New York, New York: Lipincott, Williams, and Wilkins; 2001. pp. 2575–2628. [Google Scholar]

[R2] 2.Thorley-Lawson DA. Epstein-Barr Virus: Exploiting the Immune System. Nature Reviews: Immunology. 2001;1(1):75–82. doi: 10.1038/35095584. [DOI] [PubMed] [Google Scholar]

[R3] 3.Thorley-Lawson DA, Gross A. Persistence of the Epstein-Barr Virus and the Origins of Associated Lymphomas. New England Journal of Medicine. 2004;350(13):1328–1337. doi: 10.1056/NEJMra032015. [DOI] [PubMed] [Google Scholar]

[R4] 4.Laichalk LL, et al. The Dispersal of Mucosal Memory B Cells: Evidence from Persistent EBV Infection. Immunity. 2002;16(5):745–754. doi: 10.1016/s1074-7613(02)00318-7. [DOI] [PubMed] [Google Scholar]

[R5] 5.Hoagland RJ. The Transmission of Infectious Mononucleosis. American Journal of Medical Science. 1955;229:262–272. doi: 10.1097/00000441-195503000-00003. [DOI] [PubMed] [Google Scholar]

[R6] 6.Hochberg D, et al. Demonstration of the Burkitt's Lymphoma Epstein-Barr Virus Phenotype in Dividing Latently Infected Memory Cells in vivo. Proceedings of the National Academy of Science USA. 2004;101(1):239–244. doi: 10.1073/pnas.2237267100. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R7] 7.Laichalk LL, Thorley-Lawson DA. Terminal Differentiation into Plasma Cells Initiates the Replicative Cycle of Epstein-Barr Virus in vivo. Journal of Virology. 2005;79(2):1296–1307. doi: 10.1128/JVI.79.2.1296-1307.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R8] 8.Henle W, Henle G. Seroedpidemiology of the Virus. In: Epstein MA, Achong BG, editors. The Epstein-Barr Virus. Berlin: Springer-Verlag; 1979. pp. 61–78. [Google Scholar]

[R9] 9.Khanna R, Moss DJ, Burrows SR. Vaccine Strategies Against Epstein-Barr Virus-Associated Diseases: Lessons from Studies on Cytotoxic T-Cell-Mediated Immune Regulation. Immunology Reviews. 1999;170:49–64. doi: 10.1111/j.1600-065x.1999.tb01328.x. [DOI] [PubMed] [Google Scholar]

[R10] 10.Perelson A. Modeling Viral and Immune System Dynamics. Nature Reviews: Immunology. 2002;2(1):28–36. doi: 10.1038/nri700. [DOI] [PubMed] [Google Scholar]

[R11] 11.Perelson A, Weissbuch G. Immunology for Physicists. Review of Modern Physics. 1995;69(4) [Google Scholar]

[R12] 12.Segel LA. Spatio-temporal Models in Immunology. Bifurcation and Chaos. 2002;12:2343–2347. [Google Scholar]

[R13] 13.Ribiero RM, Bonhoeffer S. Production of Resistant HIV Mutants During Antiretroviral Therapy. Proceedings of the National Academy of Science. 2000;97(14):7681–7686. doi: 10.1073/pnas.97.14.7681. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R14] 14.Chao DL, et al. A Stochastic Model of Cytotoxic T Cell Responses. Journal of Theoretical Biology. 2004;228(2):227–240. doi: 10.1016/j.jtbi.2003.12.011. [DOI] [PubMed] [Google Scholar]

[R15] 15.Perelson AS, et al. HIV-1 Dynamics in vivo: Virion Clearance Rate, Infected Cell Life-Span, and Viral Generation Time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]

[R16] 16.Neumann AU, et al. Hepatitis C Viral Dynamics in vivo and the Antiviral Efficacy of Interferon α Therapy. Science. 1998;282:103–107. doi: 10.1126/science.282.5386.103. [DOI] [PubMed] [Google Scholar]

[R17] 17.Nowak MA, Bangham CR. Population Dynamics of Immune Responses to Persistent Viruses. Science. 1996;272:74–79. doi: 10.1126/science.272.5258.74. [DOI] [PubMed] [Google Scholar]

[R18] 18.Endy D, Kong D, Yin J. Intracellular Kinetics of a Growing Virus: A Genetically Structured Simulation for Bacteriophage T7. Biotechnology and Bioengineering. 1997;55(2):376–389. doi: 10.1002/(SICI)1097-0290(19970720)55:2<375::AID-BIT15>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]

[R19] 19.Bonhoeffer S, et al. Virus Dynamics and Drug Therapy. Proceedings of the National Academy of Science. 1997;94:6971–6976. doi: 10.1073/pnas.94.13.6971. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R20] 20.Davenport MP, et al. Clonal Selection, Clonal Senescence, and Clonal Succession: The Evolution of the T Cell Response to Infection with a Persistent Virus. Journal of Immunology. 2002;168:3309–3317. doi: 10.4049/jimmunol.168.7.3309. [DOI] [PubMed] [Google Scholar]

[R21] 21.Nowak MA, et al. Viral Dynamics in Hepatitis B Virus Infection. Proceedings of the National Academy of Science. 1996;93:4398–4402. doi: 10.1073/pnas.93.9.4398. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R22] 22.Beauchemin C. Probing the Effects of the Well-Mixed Assumption on Viral Infection Dynamics. Journal of Theoretical Biology. 2006;242(2):464–477. doi: 10.1016/j.jtbi.2006.03.014. [DOI] [PubMed] [Google Scholar]

[R23] 23.Durrett R, Levin S. The Importance of Being Discrete (and Spatial) Theoretical Population Biology. 1994;46:363–394. [Google Scholar]

[R24] 24.Kleinstein S, Seiden P. Simulating the Immune System. Computer Simulations. 2000 Jul/Aug;:69–77. [Google Scholar]

[R25] 25.Kleinstein SH, Singh JP. Toward Quantitative Simulation of Germinal Center Dynamics: Biological and Modeling Insights from Experimental Validation. Journal of Theoretical Biology. 2001;211(3):253–275. doi: 10.1006/jtbi.2001.2344. [DOI] [PubMed] [Google Scholar]

[R26] 26.Kreft JU, Booth G, Wimpenny JW. Bacsim, a Simulator for Individual-Based Modelling of Bacterial Colony Growth. Microbiology. 1998;144(12):3275–3287. doi: 10.1099/00221287-144-12-3275. [DOI] [PubMed] [Google Scholar]

[R27] 27.Neugebauer EA, Tjardes T. New Approaches to Shock and Trauma Reearch: Learning from Multidisciplinary Exchange. Journal of Trauma. 2004;56(5):1156–1165. doi: 10.1097/01.ta.0000119207.14267.63. [DOI] [PubMed] [Google Scholar]

[R28] 28.Turing AM. In: The Essential Turing: Seminal Writings in Computing, Logic, Philosophy, Artificial Intelligence, and Artificial Life, Plus the Secrets of Enigma. Copeland BJ, editor. New York, NY: Clarendon Press; 2004. [Google Scholar]

[R29] 29.Celada F, Seiden PE. A Computer Model of Cellular Interactions in the Immune System. Immunology Today. 1992;13(2):56–62. doi: 10.1016/0167-5699(92)90135-T. [DOI] [PubMed] [Google Scholar]

[R30] 30.Bernaschi M, Castiglione F. Design and Implementation of an Immune System Simulator. Computers in Biology and Medicine. 2001;31(5):303–331. doi: 10.1016/s0010-4825(01)00011-7. [DOI] [PubMed] [Google Scholar]

[R31] 31.Bernaschi M, Succi S, Castiglione F. Large-scale Cellular Automata Simulations of the Immune System Response. Physical Review E. 2000;61(2):1851–1854. doi: 10.1103/physreve.61.1851. [DOI] [PubMed] [Google Scholar]

[R32] 32.Bezzi M, et al. The Transition Between Immune and Disease States in a Cellular Automaton Model of Clonal Immune Response. Physica. 1997;245:145–163. [Google Scholar]

[R33] 33.Celada F, Seiden PE. Modeling Immune Cognition; IEEE International Conference on Systems, Man, and Cybernetics; 1998. [Google Scholar]

[R34] 34.Cohn M, Langman R, Mata J. A Computerized Model for Self -Non-Self Discrimination at the Level of the Th (Th Genesis) I. The Origin of 'Primer' Effector Th Cells. International Immunology. 2002;14:1105–1112. doi: 10.1093/intimm/dxf078. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R35] 35.Cohn M, Langman R, Mata J. A Computerized Model for the Self-Non-Self Discrimination at the Level of the Th (Th Genesis) II. The Behavior of the System upon Encounter with Non-Self Antigens. International Immunology. 2003;15(5):593–609. doi: 10.1093/intimm/dxg059. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R36] 36.Iber D, Maini PK. A Mathematical Model for Germinal Centre Kinetics and Affinity Maturation. Journal of Theoretical Biology. 2002;219(2):153–175. doi: 10.1006/jtbi.2002.3079. [DOI] [PubMed] [Google Scholar]

[R37] 37.Kohler B, et al. A Systematic Approach to Vaccine Complexity Using an Automaton Model of the Cellular and Humoral Iimmune System I. Viral Characteristics and Polarized Responses. Vaccine. 2000;19(7–8):862–876. doi: 10.1016/s0264-410x(00)00225-5. [DOI] [PubMed] [Google Scholar]

[R38] 38.Meir-Schellersheim M. Simmune, a Tool for Simulating and Analyzing Immune System Behavior. Hamburg: University of Hamburg; 1999. [Google Scholar]

[R39] 39.Meyer-Hermann ME, Maini PK, Iber D. An Analysis of B Cell Selection Mechanisms in Germinal Centers. Mathematical Medical Biology. 2006;23(3):255–277. doi: 10.1093/imammb/dql012. [DOI] [PubMed] [Google Scholar]

[R40] 40.Morpurgo D, et al. Modelling Thymic Functions in a Cellular Automaton. International Immunology. 1995;7(4):505–516. doi: 10.1093/intimm/7.4.505. [DOI] [PubMed] [Google Scholar]

[R41] 41.Puzone R, et al. ImmSim, A Flexible Model for in machina Experiments on Immune System Responses. Future Generation Computer Systems. 2002;18(7):961–972. [Google Scholar]

[R42] 42.Seiden PE, Celada F. A Model for Simulating Cognate Recognition and Response in the Immune System. Journal of Theoretical Biology. 1992;158(3):329–357. doi: 10.1016/s0022-5193(05)80737-4. [DOI] [PubMed] [Google Scholar]

[R43] 43.Stewart JJ, et al. A Solution to the Rheumatoid Factor Paradox: Pathologic Rheumatoid Factors can be Tolerized by Competition with Natural Rheumatoid Factors. Journal of Immunology. 1997;159(4):1728–1738. [PubMed] [Google Scholar]

[R44] 44.Tay J, Jhavar A. CAFISS: A Complex Adaptive Framework for Immune System Simulations; ACM Symposium for Applied Computing-Bioinformatics; 2005. [Google Scholar]

[R45] 45.Segel LA, Bar-Or RL. On the Role of Feedback in Promoting Conflicting Goals of the Adaptive Immune System. Journal of Immunology. 1999;163:1342–1349. [PubMed] [Google Scholar]

[R46] 46.Castiglione F, et al. Simulating Epstein-Barr Virus Infection with C-ImmSim. Bioinformatics. doi: 10.1093/bioinformatics/btm044. submitted. [DOI] [PubMed] [Google Scholar]

[R47] 47.An G. Agent-Based Computer Simulation and SIRs: Building a Bridge Between Basic Science and Clinical Trials. Shock. 2001;16(4):266–273. doi: 10.1097/00024382-200116040-00006. [DOI] [PubMed] [Google Scholar]

[R48] 48.An G. In silico Experiments of Existing and Hypothetical Cytokine-Directed Clinical Trials Using Agent-Based Modeling. Critical Care Medicine. 2004;32(10):2050–2060. doi: 10.1097/01.ccm.0000139707.13729.7d. [DOI] [PubMed] [Google Scholar]

[R49] 49.Forst CV. Host-Pathogen Systems Biology. Drug Discovery Today. 2006;11(5–6):220–227. doi: 10.1016/S1359-6446(05)03735-9. [DOI] [PubMed] [Google Scholar]

[R50] 50.Garrett-Dancik DJ, Dorman K. An Agent-Based Model for Leishmania Infection. International Journal of Complex Systems. In Press. [Google Scholar]

[R51] 51.Mansury Y, Diggory M, Deisboeck TS. Evolutionary Game Theory in an Agent-Based Brain Tumor Model: Exploring the 'Genotype-Phenotype' Link. Journal of Theoretical Biology. 2006;238(1):146–156. doi: 10.1016/j.jtbi.2005.05.027. [DOI] [PubMed] [Google Scholar]

[R52] 52.Walker DC, et al. Agent-Based Computational Modeling of Wounded Epithelial Cell Monolayers. IEEE transactions on nanobioscience. 2004;3(3):153–163. doi: 10.1109/tnb.2004.833680. [DOI] [PubMed] [Google Scholar]

[R53] 53.Segovia-Juarez JL, Ganguli S, Kirschner D. Identifying Control Mechanisms of Granuloma Formation During M. tuberculosis Infection Using an Agent-Based Model. Journal of Theoretical Biology. 2004;231:357–376. doi: 10.1016/j.jtbi.2004.06.031. [DOI] [PubMed] [Google Scholar]

[R54] 54.Srivastava R, et al. Stochastic vs. Deterministic Modeling of Intracellular Viral Kinetics. Journal of Theoretical Biology. 2002;(218):309–321. doi: 10.1006/jtbi.2002.3078. [DOI] [PubMed] [Google Scholar]

[R55] 55.Duca KA, et al. A virtual look at Epstein-Barr virus infection: biological interpretations. PLoS Pathog. 2007;3(10):1388–1400. doi: 10.1371/journal.ppat.0030137. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R56] 56.Various. C. NIH, FDA, editor. PM Medical Health News; 21st Century Complete Medical Guide to Infectious Mononucleosis and the Epstein-Barr Virus (EBV), Authoritative Government Documents, Clinical References, and Practical Information for Patients and Physicians. 2004

[R57] 57.Chang RS. Infectious Mononucleosis. Boston, MA: Hall Press; 1980. p. 224. [Google Scholar]

[R58] 58.Polys N, et al. Web3D Symposium. Monterey, CA: ACM Press; 2004. PathSim Visualizer: An Information Rich Virtual Environment for Systems Biology. [Google Scholar]

[R59] 59.Abbey K, Kawabata I. Computerized Three-dimensional Reconstruction of the Crypt System of the Palatine Tonsil. Acta Otolaryngol. 1988;454 Suppl:39–42. doi: 10.3109/00016488809125002. [DOI] [PubMed] [Google Scholar]

[R60] 60.Perry M, Whyte A. Immunology of the Tonsils. Immunology Today. 1998;19(9):414–421. doi: 10.1016/s0167-5699(98)01307-3. [DOI] [PubMed] [Google Scholar]

[R61] 61.Bernasconi NL, Traggiai E, Lanzavecchia A. Maintenance of Serological Memory by Polyclonal Activation of Human Memory B Bells. Science. 2002;298:2199–2202. doi: 10.1126/science.1076071. [DOI] [PubMed] [Google Scholar]

[R62] 62.Pegtel DM, Middeldorp J, Thorley-Lawson DA. Epstein-Barr Virus Infection in ex vivo Tonsil Epithelial Cell Cultures of Asymptomatic Carriers. Journal of Virology. 2004;78(22):12613–12624. doi: 10.1128/JVI.78.22.12613-12624.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R63] 63.Babcock GJ, et al. EBV Persistence in Memory B cells in vivo. Immunity. 1998;9(3):395–404. doi: 10.1016/s1074-7613(00)80622-6. [DOI] [PubMed] [Google Scholar]

[R64] 64.Miyashita EM, et al. Identification of the Site of Epstein-Barr Virus Persistence in vivo as a Resting B-Cell. Journal of Virology. 1997;71(7):4882–4891. doi: 10.1128/jvi.71.7.4882-4891.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R65] 65.Hochheiser H, Schneiderman B. Dynamic Query Tools for Time Series Data Sets, Timebox Widgts fro Interactive Exploration. Information Visualization. 2004;3(1):1–18. [Google Scholar]

[R66] 66.Seemayer TA, et al. X-linked lymphoproliferative disease: twenty-five years after the discovery. Pediatr Res. 1995;38(4):471–478. doi: 10.1203/00006450-199510000-00001. [DOI] [PubMed] [Google Scholar]

[R67] 67.Ewald PW. Evolution of Infectious Disease. New York, NY: Oxford University Press; 1994. [Google Scholar]

[R68] 68.Fourth International Symposium on Epstein-Barr Virus and Associated Malignant Diseases. Hualien, Taiwan: Humana Press; 1990. Epstein-Barr Virus. [Google Scholar]

[R69] 69.Mobilia M, Georgiev IT, Taeuber UC. Fluctuations and Correlations in Lattice Models for Predator-Prey Interaction. Physical Review E. 2006;73(4) doi: 10.1103/PhysRevE.73.040903. [DOI] [PubMed] [Google Scholar]

PERMALINK

A Virtual Look at Epstein-Barr Virus Infection: Simulation Mechanism

M Shapiro

KA Duca

K Lee

E Delgado-Eckert

J Hawkins

AS Jarrah

R Laubenbacher

NF Polys

V Hadinoto

DA Thorley-Lawson

Abstract

INTRODUCTION

Figure 1. Comparison of the EBV Biological Model and the Computational Model.

METHODS

Simulation engine

Geometry

Figure 2. Geometry of PathSim and Initial Location of Agents.

Agent life cycles, interactions and motion

Excluded features

Parameters

Code verification

User interface and visualization engine

RESULTS

Figure 3. PathSim Stability with Respect to Stochastic Variation.

Figure 8. Lytic Reactivation Rate Strongly Determines Infection Outcomes.

Figure 5. Peak Population Sizes in Relation to Average Viral Burst Size.

Stability and overall behavior

Parameter variation and parameter sensitivity

Burst size

Figure 4. Effects of Variation of Viral Burst Size.

Proliferation of newly infected B-cells

Figure 6. Effects of Cell Division after Initial Infection.

Immune response to infected B-cells

Figure 7. Responses of BLatS to Changes in CTL Parameters.

Lytic reactivation of BLats

DISCUSSION

Supplementary Material

ACKNOWLEDGEMENTS

Footnotes

REFERENCES

Associated Data

Supplementary Materials

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Figure 7. Responses of B_LatS to Changes in CTL Parameters.

Lytic reactivation of B_Lats