Youden Index and Optimal Cut-Point Estimated from Observations Affected by a Lower Limit of Detection

Summary

The receiver operating characteristic (ROC) curve is used to evaluate a biomarker’s ability for classifying disease status. The Youden Index (J), the maximum potential effectiveness of a biomarker, is a common summary measure of the ROC curve. In biomarker development, levels may be unquantifiable below a limit of detection (LOD) and missing from the overall dataset. Disregarding these observations may negatively bias the ROC curve and thus J. Several correction methods have been suggested for mean estimation and testing; however, little has been written about the ROC curve or its summary measures. We adapt non-parametric (empirical) and semi-parametric (ROC-GLM [generalized linear model]) methods and propose parametric methods (maximum likelihood (ML)) to estimate J and the optimal cut-point (c*) for a biomarker affected by a LOD. We develop unbiased estimators of J and c* via ML for normally and gamma distributed biomarkers. Alpha level confidence intervals are proposed using delta and bootstrap methods for the ML, semi-parametric, and non-parametric approaches respectively. Simulation studies are conducted over a range of distributional scenarios and sample sizes evaluating estimators’ bias, root-mean square error, and coverage probability; the average bias was less than one percent for ML and GLM methods across scenarios and decreases with increased sample size. An example using polychlorinated biphenyl levels to classify women with and without endometriosis illustrates the potential benefits of these methods. We address the limitations and usefulness of each method in order to give researchers guidance in constructing appropriate estimates of biomarkers’ true discriminating capabilities.

1 Introduction

Evaluating biomarker levels has become an important method in the investigation and diagnosis of disease. Disease diagnosis by biomarkers is dependent upon a correlation between biomarker levels and disease state, whereby biomarker levels for a certain diseased population are different–usually higher–than in the corresponding non-diseased population. In order to utilize a biomarker for such classification, a cut-point c is established and individuals with biomarker values on one side of the cut-point are labeled as diseased and those with values on the other side are labeled non-diseased or healthy. The accuracy of such a classification can be determined by examining sensitivity (Se) and specificity (Sp), where Se and Sp are the probability of truly identifying diseased and non-diseased individuals respectively at a certain c.

The receiver operating characteristic (ROC) curve can be used to evaluate the effectiveness of a certain biomarker in the determination of a diseased and non-diseased population. The ROC curve is a plot of (Se) versus (1-Sp) at all possible c. When estimating the ROC curve, non-parametric, semi-parametric or parametric methods can be utilized. In previous literature (Pepe, 2003), non-parametric approaches have been developed to construct the ROC curve using calculations of the cumulative density function based on ordered observations of diseased and non-diseased biomarker levels. Semi-parametric, distribution-free methods have also been developed that parameterize the form of the ROC curve without making assumptions about the distributions of test results. In addition, a parametric model was developed by Ogilvie and Creelman (1968) utilizing a finite number of parameters. One of the main obstacles in the applications of the non-parametric, semi-parametric, and parametric approaches is accounting for observations below some limit of detection (LOD), denoted here as d, resulting either from a non-criterion standard or experimental error (Lambert, Peterson and Terpenning, 1991). The result is an intrinsically biased sample, with unregistered observations potentially affecting the estimation of the ROC curve and subsequent summary statistics. To account for the effect of a LOD on the ROC curve, Perkins et al. (2007) adapted a parametric approach for estimating ROC curves affected by an LOD and used this approach to estimate the area under the curve (AUC).

As an extension, this paper focuses on the Youden Index (J), another main summary statistic of the ROC curve used in the interpretation and evaluation of a biomarker, which defines the maximum potential effectiveness of a biomarker. J can be formally defined as J = max_c {Se (c) + Sp (c) − 1}. The cut-point that achieves this maximum is referred to as the optimal cut-point (c*) because it is the cut-point that optimizes the biomarker’s differentiating ability when equal weight is given to sensitivity and specificity (Youden, 1950; Faraggi, 2000; Reiser, 2000; Miller, 1981; Searle, 1971). This paper develops parametric methods as well as adapts non-parametric (empirical) and semi-parametric (generalized linear model) methods to estimate the ROC curve, J and c* when a biomarker of interest is affected by a LOD. Section 2.1 explores the non-parametric and semi-parametric methods for determining the ROC curve and J. Section 2.2 introduces the maximum likelihood (ML) method and demonstrates estimation of J and c* in the general case, the Normal case and the gamma case. Section 3 presents estimated confidence intervals to accompany the parametric, semi-parametric and non-parametric point estimators of J and c*. Section 4 displays the results of simulations that compare the effectiveness of the different methods. Section 5 presents an example using polychlorinated biphenyl (PCB) levels to classify women with and without endometriosis to illustrate the potential benefits of these methods. Section 6 offers conclusions, general remarks and recommendations.

2 Methods

Let y₁ ,…, y_n represent a random sample of biomarker levels from the non-diseased (control) population which come from a random variable (Y) that are sorted in increasing order, and x₁ , … , x_m represent a random sample of biomarker levels from the diseased (case) population which come from a random variable (X) that are sorted in increasing order, with cumulative distributions F and G respectively. If k and j are the number of observations above the LOD for non-diseased and diseased respectively, then there are y_n−k+1 ,…, y_n and x_m−j+1 ,…, x_m, k ≤ n and j ≤ m observations above d. Using these observations above the LOD, the different approaches in estimating the ROC curve can be examined.

2.1 Non-parametric and Semi-parametric methods

2.1.1 Empirical (EMP)

The first approach is the classical non-parametric empirical (EMP) method as applied to censored observations, where ranks are used. By replacing missing values below the LOD with a constant (common values are d/2 and $d/\sqrt{2}$), J and c* can be estimated by the classical ordering of the observations for non-diseased and diseased populations. This alteration of the data in order to utilize the EMP method creates a mass of observations at a specific place that are not intrinsic to the continuous nature of the biomarker but allow missing observations to be included in the estimation. The ROC curve resulting from this replacement technique would be consistent with an EMP ROC curve based on all the data from the points (0, 0) to (1 − Sp (d), Se (d)) and then change to a straight line to (1, 1) (refer to Figure 1). As a result, this estimate of the ROC curve is asymptotically unbiased for all c > d.

Figure 1.

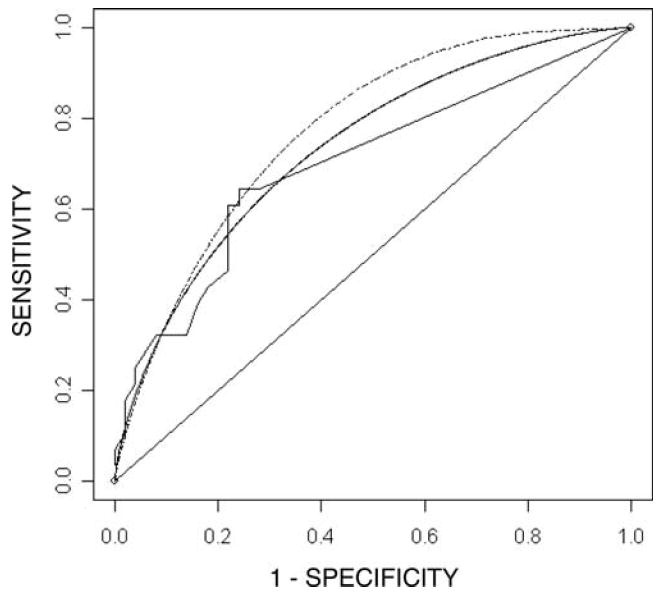
Empirical (solid and jumpy), ROC-GLM (solid and smooth) and Parametric (dashed and smooth) ROC curves based on PCB114 levels for classification of women with and without endometriosis. The data are affected by a limit of detection where measurements are unquantifiable below a level of 0.005. The parametric curve is based on gamma distributions with parameters estimated using maximum likelihood.

Empirical cumulative distributions can be calculated as:

$$\widehat{G}\left(c\right)=\frac{1}{m}\sum _{i=1}^{m}I\left(x_i\le c\right)\widehat{F}\left(c\right)=\frac{1}{n}\sum _{i=1}^{n}I\left(y_i\le c\right),$$

where I(x_i ≤ c)and I(y_i ≤ c) are the indicator functions classifying whether an observation is censored or below c (I(a)= 1 if a is true and 0 otherwise). Having calculated the empirical cumulative distribution functions, J is estimated by:

$${\tilde{J}}_E={\max }_c\left\{\widehat{F}\left(c\right)-\widehat{G}\left(c\right)\right\}c\in \left[x_{m-j+1},\dots ,x_m,y_{n-k+1},\dots ,y_n\right].$$ (1)

The corresponding c* is obtained at the c where J̃_E is determined and always occurs at c ≥ d. As with all non-parametric methods, the EMP method has the benefit of being free of distribution assumptions and thus completely robust to distribution misspecification.

2.1.2 ROC-GLM

The second approach is the semi-parametric ROC-GLM method developed by Pepe for non-censored data sets (Pepe, 2003). In this approach, the ROC curve is parameterized but no assumptions regarding the underlying distributions of diseased and non-diseased populations are made. This approach is essentially a parametric smoothing of the empirical ROC curve to establish estimates for J and c*. Since the empirical ROC curve is biased due to a LOD, smoothing over the entire range of false posititves would create bias here. Thus estimation of parameters is based only on the portion of empirical ROC curve corresponding to actual observations, not replacement values, and these parameter estimates are then applied across the entire range of specificity.

To perform the ROC-GLM method, a parametric form for the ROC curve can be constructed using a link function g and specified functions h = {h₁,…, h_n }:

$$g\left(\mathrm{ROC}\left(t\right)\right)=\sum a_s{h}_n\left(t\right)$$

where ROC (t)= Se (c) and t = 1 − Sp (c). Through the link function, the ROC curve can be parameterized based on specific functions. For example, the ROC curve can be modeled where the link function is g = Φ⁻¹ and the specified functions are h₁(t) = 1 and h₂(t) = Φ⁻¹(t) where Φ represents the standard normal distribution function.

Now, to estimate ROC (t), a placement value, which is the location of an observation in a given population, must first be defined. Utilizing F as the reference distribution for the non-diseased population, the placement value of a test result y in the non-diseased population is:

$$\mathit{Non­diseased\; placement\; value}=P\left[Y\ge y\right]=1-F\left(y\right)=S_F\left(y\right)$$

where S_F(y) is the non-diseased survivor function at y. The placement value is used to define the location of y in the distribution of interest. With this definition, the ROC curve can be defined as the distribution of diseased (X) placement values in the non-diseased distribution (F):

$$\mathrm{ROC}\left(t\right)=P\left[S_F\left(X\right)\le t\right].$$

Having adopted this formation for the ROC curve, a set T where t is an element of T can be chosen to fit the model over. Pepe suggests that T be chosen such that T = {1/m, …, (m − 1)/m } (Alonzo and Pepe, 2002). With this form, a binary variable can be defined denoting whether or not the placement value exceeds t and binary regression methods can be subsequently utilized to estimate the α_s to generate a full ROC curve based on values above the LOD.

Having established the ROC-GLM curve with estimates of α_s, the estimate of J can be found utilizing the basic formal definition presented in the introduction and is J̃_G = max_t (ROC (t) − t). With J, a weighted cut-point can be established by mapping the corresponding ROC (t) (where c* occurs) at which the maximum takes place back to the empirical curve. One is able to situate ROC (t*) within the given diseased distribution and find Se (x_i) ≤ ROC (t*) ≤ Se (x_(i+1). The c* based on a mapping back to the diseased (Se) population is found by weighting the placement of ROC (t) within this interval:

$${\stackrel{\sim }{c}}_G^{\ast }=x_i+(x_{(i+1)}-x_i)(\mathrm{ROC}(t^{\ast })-\mathrm{Se}(x_i))/(\mathrm{Se}(x_{(i+1)})-\mathrm{Se}(x_i)).$$

A mapping back to the non-diseased (1 − Sp) population can be performed in a similar manner. In practice, if sample sizes are equal (m = n) then the choice of Se or Sp is arbitrary but if unequal, then ${\stackrel{\sim }{c}}_G^{\ast }$ should be found by mapping back through the one corresponding to the larger sample size as it will provide a finer mapping.

2.2 Maximum likelihood (ML)

The third parametric approach considered is the maximum likelihood (ML) as it applies to censored observations. This approach attempts to parameterize an observed distribution in order to estimate J. Considering the non-diseased population, y₁ ,…, y_n which comes from a random variable (Y) with distribution F(y; θ_Y)with unknown parameter θ_Y, let Z be defined by:

$$Z=\{\begin{array}{cc}Y;& Y\ge d\\ N/A;& Y<d\end{array}.$$

The likelihood of each observation z_j can be thought of as starting out Bernoulli, reflecting whether the observation is missing (denoted as not available, N/A), or not of the indicator function (I). If the observation is not missing, the likelihood of θ_Y given z_j can be determined. Consequently, ordering the observations starting with the k missing values, the likelihood function is:

$$L({\mathrm{\theta }}_Y;z)\mathrm{\alpha }\prod _{j=1}^n\left[(1-F(d;{\mathrm{\theta }}_Y))\frac{f(z_j;{\mathrm{\theta }}_Y)}{(1-F(d;{\mathrm{\theta }}_Y))}I(z_j\ne N/A)+F(d;{\mathrm{\theta }}_Y)I(z_j\ne N/A)\right]={\left[F(d;{\text{θ}}_Y)\right]}^{n-k}\prod _{j=n-k+1}^n\left[f(z_j;{\text{θ}}_Y)\right],$$

where f(y; θ_Y) is the probability density function of Y. To calculate the maximum likelihood estimate (MLE) θ̂_Y of θ̂_Y, maximize L(θ̂_Y; z) with respect to the parameter. In the case where θ_Y is a vector parameter, maximize L(θ̂_Y; z) with respect to each of it’s elements, separately. (Perkins et al., 2007).

Logically extending the procedure described above for the diseased population, the MLE’s θ̂_x (distribution parameter(s) for diseased) and θ̂_Y (distribution parameter(s) for non-diseased) are obtained. Now, because the MLE is equivariant, substituting θ̂_x and θ̂_Y for their respective parameters yields the estimate ^J= J (θ̂_X, θ̂_Y) and ĉ* = c(θ̂_X, θ̂_Y) which are the MLE’s for J and c* (Refer to Perkins and Schisterman, 2005 for explicit formulas for Ĵ and ĉ*).

Having adopted a general method for determining MLE’s for J and c*, we now apply this method to the specific cases of normal and gamma distributed biomarker levels to obtain ĉ* and Ĵ. The details of these developments for normal and gamma assumptions are left to the Appendix.

3 Estimation of Variance and Confidence Intervals

3.1 Maximum likelihood

Since ĉ* and Ĵ are functions of the MLE’s θ̂_X and θ̂_Y, they are consistent and asymptotically normally distributed. Explicitly, ĉ* and Ĵ are asymptotically normally distributed such that $\sqrt{N}\left({\widehat{c}}^{\ast }-c^{\ast }\right)$ ~ Normal $\left(0,{\sigma }_{c^{\ast }}^2\right)$ and $\sqrt{N}\left(\widehat{J}-J\right)$ ~ Normal $(0,{\sigma }_J^2),$ respectively, where N equals the sum of the diseased and non-diseased observations. Utilizing these distributional properties, α level two-tailed confidence intervals (CI) for c* and J are constructed from ${\widehat{c}}^{\ast }\pm z_{\text{α}/2}\sqrt{\left({\sigma }_{c^{\ast }}^2/N\right)}$ and $\widehat{J}\pm z_{\text{α}/2}\sqrt{\left({\sigma }_J^2/N\right)}$ respectively. When ${\sigma }_{c^{\ast }}^2$ and ${\sigma }_J^2$ are unknown, the estimators ${\widehat{\sigma }}_{c^{\ast }}^2$ and ${\widehat{\sigma }}_J^2$ can be used to compute the approximate α level CI for c* and J (refer to Perkins and Schisterman, 2005 and Perkins et al., 2007 for development of these estimators for the normal and gamma cases).

3.2 EMP and ROC-GLM

The estimated standard errors and confidence intervals of the empirical estimators ${\stackrel{\sim }{c}}_E^{\ast }$ and J̃_E and ROC-GLM estimators J̃_G and ${\stackrel{\sim }{c}}_G^{\ast }$ can be found using the basic percentile (BP) bootstrap method. The bootstrap method is utilized to construct confidence intervals when the distribution of the given estimator is unknown. The BP bootstrap method performed here is a non-parametric re-sampling of the data where all observations of diseased individuals are re-sampled with replacement and all observations of non-diseased are re-sampled with replacement. The empirical estimates of J and c* were then found using the non-parametric empirical or semi-parametric ROC-GLM method, and this process was repeated S times, calculating ${\widehat{J}}_j^{\ast }$ and ${\widehat{c}}_j^{\ast }$ per sample (j = 1 , …, S). With these estimates, (1 − α) 100% CI are constructed by taking the α/2 and 1 − α/2 percentiles of the ${\widehat{J}}_j^{\ast }$ and ${\widehat{c}}_j^{\ast }$ (Wasserman, 2004).

4 Simulations

A simulation study was performed consisting of B = 2000 independent samples of diseased and non-diseased populations (sample sizes of diseased and non-diseased populations equal m = n = 50, 100, 200) to assess the non-parametric and parametric techniques illustrated above over varying sample sizes and populations.

The Normal simulations were executed first, with non-diseased values drawn randomly from a Normal distribution with μ_Y = 2 and ${\sigma }_Y^2=1$. The variance of the diseased population was set at ${\sigma }_X^2=1$ and then repeated at ${\sigma }_X^2=3$ with the mean μ_X generated numerically to achieve an ROC curve with J equal to 0.2, 0.4, 0.6 and 0.8.

In the second set of simulations, non-diseased biomarker levels were generated from a gamma distribution with α_Y = 1:5 and β_Y = 1. Samples of diseased levels were found from a gamma distribution with α_X = 1.5 and repeated with α_X = 2 and β_X found numerically to achieve an ROC curve with a J of 0.2, 0.4, 0.6 and 0.8.

Having generated these samples, J and c* were estimated using the non-parametric EMP (J̃_E and ${\stackrel{\sim }{c}}_E^{\ast }$) and semi-parametric ROC-GLM (J̃_G and ${\stackrel{\sim }{c}}_G^{\ast }$) methods, as well as the parametric ML (Ĵ and ĉ*) method. These estimates were found with varying amounts of data subject to a LOD; scenarios were considered with 0, 20, 40, 60, and 80 percent of the non-diseased observations missing or below the fixed d. In addition, 95% confidence intervals were constructed according to techniques described in Section 3.

Percent bias (bias as a percent of the value of the parameter of interest) and root mean square error (RMSE) were calculated for all point estimates of J and c*. Confidence intervals were assessed using the average width of the interval and coverage, the proportion of confidence intervals that include the true parameter. Tables 1–4 display excerpts of these simulation results for the Normal and gamma cases, respectively, and are representative of the overall relations seen in all simulations (full simulation results can be provided with request).

From these results, the effectiveness of the non-parametric, semi-parametric, and parametric methods in estimating J and c* as well as the effect of sample size on the different methods can be evaluated. The average percent bias of J estimators across all distributional scenarios and levels of missing observations was found to be less than one percent of the true J. The ML and ROC-GLM method show smaller bias and RMSE – except with J = 0.2, 0.4 and a LOD with 80 percent missing – than that of the EMP method (average percent bias Ĵ, J̃_G,J̃_E: 1.85%, 2.58%, 9.46% and average RMSEĴ, J̃_G, J=_E: 0.0083, 0.0075, 0.0090 respectively over all simulations). For the average percent bias of estimates of c* (refer to Tables 2 and 4), the ML method shows smaller bias and RMSE than the EMP method except at large LOD and small J (average percent bias c̃*, ${\stackrel{\sim }{c}}_E^{\ast }$: −0.53%, 3.86% and average RMSE c̃*, ${\stackrel{\sim }{c}}_E^{\ast }$: 0.1271, 0.4605 over all simulations). Comparing the average percent bias for estimates of c* from the ML and ROC-GLM methods where ${\stackrel{\sim }{c}}_G^{\ast }$ occurs above d, the ML has comparable bias and smaller RMSE – except at large J and 80 percent of controls missing – than the ROC-GLM method (average percent bias ĉ*, ${\stackrel{\sim }{c}}_G^{\ast }$ [sensitivity], ${\stackrel{\sim }{c}}_G^{\ast }$ [specificity]: 0.22, 5.76, 4.90 and average RMSE ĉ*, ${\stackrel{\sim }{c}}_G^{\ast }$ [sensitivity], ${\stackrel{\sim }{c}}_G^{\ast }$ [specificity]: 0.1278, 0.3764, 0.3462). Again, we can not compare estimates of c* from the ML and ROC-GLM methods when J̃G corresponds to a cut-point below the LOD because mapping back from the estimated ROC curve to the biomarker scale is not possible. Figures 2 summarize trends in the percent bias and RMSE of J and c* for the different methods utilizing a Normal sample with equal variances for the diseased and non-diseased populations corresponding to a true J = 0.4. The results for this scenario are representative of the complete simulation results.

Figure 2.

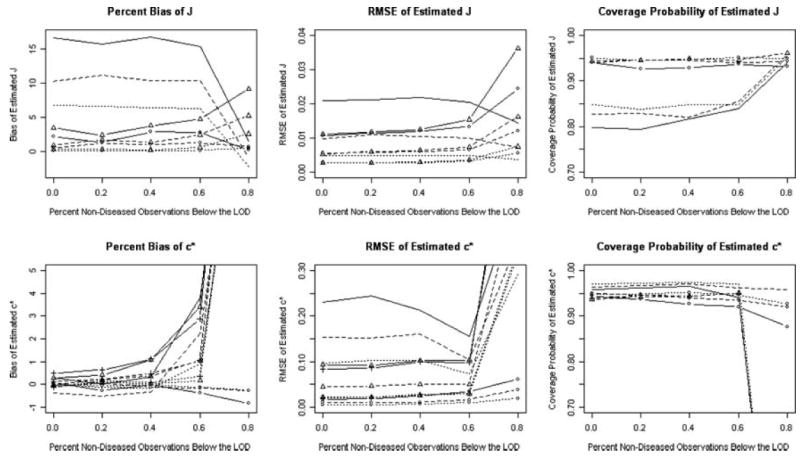
Percent Bias, RMSE and coverage probability of 95% confidence intervals for estimator of J = 0.4 and c* = 2.25 from MLE (circle), GLM (J : triangle; c*: triangle and cross), EMP (smooth) methods as a function of percent below the limit of detection. Graphs display sample sizes of 50 (solid lines), 100 (dashed lines), and 200 (dotted lines).

The coverage probabilities using ML techniques are nominal, showing a slight decrease in the coverage probability with small J (J = 0.2, 0.4) and a large LOD corresponding to 60 and 80 percent missing. In terms of the coverage probability of J for the ML method with respect to the EMP method, while the two methods have comparable confidence interval widths, the coverage probabilities for the ML method are much closer to nominal than those of the EMP method except at small J and a LOD yielding 80 percent missing (average coverage Ĵ, J̃_E,: 0.9368, 0.8280 over all simulations). In addition, the coverage probabilities of J for the EMP method increase slightly to the nominal as the LOD becomes larger. The coverage probabilities for c* using the EMP and ML methods are comparable and nominal, except for small J (J = 0.2, 0.4) and large LOD where the EMP is unable to cover the true J at all. In addition, the ML generally produces confidence interval widths for c* that are substantially smaller than the EMP method.

The coverage probabilities and confidence intervals for the ROC-GLM method were computed only for J = 0.4 for the gamma (α_X = 1:5) and Normal $({\sigma }_X^2=1)$ and for LODs of 0, 20, 40, 60 and 80 percent of the controls missing due to the computationally intensive nature of the ROC-GLM method and its nested loops. The coverage probabilities for J of the ROC-GLM method are nominal across Normal and gamma simulations and similar to those of the corresponding ML method and cover better than the corresponding EMP method (average coverage probability Ĵ, J̃_G, J̃_E: 0.9406, 0.9424, 0.8530). For c*, the ROC-GLM method produces confidence interval widths that are slightly larger than the ML method but smaller than the EMP method except for large LOD. The coverage probabilities for the ROC-GLM method are comparable to the EMP and ML methods and nominal, except for 80 percent missing where the ROC-GLM method is unable to cover c* at all because no mapping back to the distributions is possible. Figure 2 also summarizes trends in the coverage probability of J and c* for the different methods utilizing a Normal sample with equal variances for the diseased and non-diseased populations corresponding to a true J = 0.4. The results for this scenario are representative of the complete simulation results.

In addition, as the sample size increases, the confidence interval widths for the ML and EMP methods decrease and the coverage probabilities increase to the nominal. The bias and RMSE of all methods (ML, ROC-GLM, EMP) decrease as the sample size increases.

In order to assess the robustness of the ML method, we generated Student’s t distributed data (5, 10, and 25df) and lognormally distributed data and performed estimation based on normal and gamma assumptions, respectively. The means and variances of the alternative distributions were matched to those of the normals and gammas in the original simulations. The average percent bias for Ĵ over all simulations (bias Ĵ/true J) of the Student’s t and lognormally distributed data was 0.56 percent and 1.76 percent respectively. The average RMSE of Ĵ for the Student’s t and lognormally distributed data was found to be comparable to that based on data from the actual normal and gamma distributions. The coverage probability of Ĵ was nominal at small d for both types of data and decreased slightly with larger d. The average percent bias for ĉ* over all simulations (bias ĉ*/true c*) of the Student’s t and lognormally distributed data was 1.07 percent and 11.7 percent respectively. The 11.7 percent relative bias demonstrates how sensitive ĉ*, location of optimal differentiation, is to the assumed shape of distributions in contrast to the relatively robust Ĵ, level of optimal differentiation. The average RMSE of ĉ* for the Student’s t distributed data was again found to be comparable to that based on data from actual normal distributions and the coverage probability was found to be nominal at small d and decrease slightly with fewer degrees of freedom, smaller J, and larger d. The average RMSE of ĉ* for the lognormally distributed data was substantially larger then that based on the actual gamma distributions and the coverage probabilities ranged from 0.90 to as low as almost no coverage. Higher coverages corresponded to scenarios of high missingness and low sample sizes but coverages decreased as sample sizes increased and missingness decreased, scenarios where correct distributional assumptions should be easier to formulate. As a result, while misspecifying the true distribution of the data does introduce bias, the ML method was robust to this departure for estimating Ĵ and differentially affected in the estimation of ĉ*.

5 Example

Endometriosis is a gynecological disorder that occurs primarily in women of reproductive age. Symptoms of endometriosis may include pain, discomfort and infertility. The causes of this condition remain unclear, and diagnosis is difficult, usually requiring invasive confirmation by laparoscopy. It is a disease exclusive to species that menstruate such as humans and primates. Much of the experimental evidence regards a potential association between dioxin and polychlorinated biphenyls (PCBs) and endometriosis and includes data from experimental animal, primate and human studies (Louis et al., 2005).

An incident case-control study of 28 cases and 50 controls, as determined by laparoscopy, was evaluated to determine how various PCBs classified endometriosis status. Investigators were interested specifically in polychlorinated biphenyl 114. The LOD was experimentally set at d = 0.005 resulting in a censoring of 76 percent of the controls and 36 percent of the cases. The observed cases had a mean of 0.0194 and standard deviation of 0.0110 while the observed controls had a mean of 0.0144 and a standard deviation of 0.0072. Empirical analysis led to the non-smooth ROC curve in Figure 1 with J̃_E = 0.4029 (95% confidence interval: 0.2043, 0.6214) and ${\stackrel{\sim }{c}}_E^{\ast }=0.0075$ (95% confidence interval: 0.0070, 0.0160). The ROC-GLM and ML techniques developed here were also applied. The ROC-GLM method produced the solid line in Figure 1 with J̃_G = 0.3441 (95% confidence interval 0.1184 0.6125). However, because the ROC-GLM method estimated a J with a corresponding cut-point below the LOD, the method was unable to extrapolate back to the empirical curve and estimate c*. Prior to employing the ML technique, histograms (see Histogram 1) of the diseased and non-diseased distributions and quantile plots were examined. These showed the Normal distribution to be a poor choice, and suggested that gamma distributions with parameters equal to ML estimates fit well. In addition, PCB levels are naturally restricted to non-negative numbers, which is intrinsic to the gamma and not the Normal distribution. The dashed ROC curve in Figure 1 is based on cases and controls following gamma distributions with ML estimates substituted for parameters. The ML method found Ĵ = 0.4059 (95% confidence interval: 0.1744, 0.6400) and the subsequent ĉ*= 0.00329 (95% confidence interval: 0.0011, 0.0055).

Histogram 1.

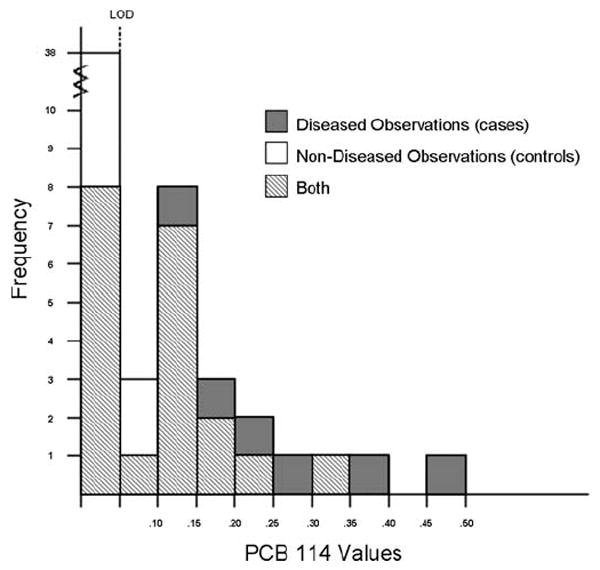
Histogram of diseased and non-diseased observations for example.

The simulation closest to this scenario, m = n = 50 with J = 0:4 and 80% missing, shows that percent bias (Ĵ, J̃_G, J̃_E: 6.18, 8.00, 7.68) and RMSE (Ĵ, J̃_G, J̃_E: 0.033, 0.028, 0.015) for estimates of J are similar with ML confidence intervals providing slightly better coverage than EMP. Notable results of estimates of c* for this level of censoring are that while the confidence interval based on ML has coverage probability of 0.85, due to bias from relatively small sample size, it overwhelmingly out performed that based on EMP, coverage probability of 0.0 due to the true cut-point being below the LOD. This is likely to be the case with a J = 0:4 and 80% of our controls below the LOD.

The results of the above example show that the EMP, ROC-GLM, and ML methods give estimates for J with similar width confidence intervals. In addition, the ROC-GLM and ML methods establish that the c* giving rise to J is below the LOD while the EMP approach reports J occurs above the LOD. Also, this example shows a significant limitation in the ROC-GLM method, that while it is able to estimate a J below d, it is unable to establish a corresponding cut-point. The overall result of this example is that the ROC-GLM and ML methods, unlike the EMP method, suggest the need for improved laboratory measurements for the marker PCB114 to reach its maximum discriminatory power, as it occurs below the experimentally determined LOD.

6 Discussion

In a review of current practices, it has become standard to utilize the non-parametric empirical method to obtain J and c*. However, as shown in the simulations and example, the ML and ROC-GLM methods perform much better in terms of coverage probability, bias, and RMSE than the positively-biased EMP method in estimating J in the presence of LOD, especially for a relatively small LOD.

Another common practice is to replace measurements below the LOD with some value and then estimate J and c* as if the data were real observations. Using a replacement value with the empirical method is acceptable because censored measurements are treated as ties already. The standard ROC-GLM approach based on replacement values assumed to be true biomarker levels would lead to negatively biased estimates of the ROC curve and J. Replacement values in conjunction with ML techniques result in bias, the direction of which would be unpredictable due to the complexity of the parameters of interest and the degree would worsen with increases in sample size.

However, even when using these three methods correctly there are limitations. In order to utilize ML techniques, assumptions must be made about the underlying distributions of the diseased and non-diseased populations. This leads to a not insignificant assumption that the biomarker is modeled by a known distribution. Although this presents as a theoretical limitation, in practice most continuous biomarkers can be modeled quite well by known distributions, and considering the Normal and Gamma families provides some flexibility in this assumption. While not evaluated here, other continuous distributions (i.e., Weibull, Student’s t) could be handled similarly if thought to be more appropriate and it is also possible to log-transform skewed data to attempt to use normal ML techniques. However, as censoring below the LOD increases, this necessary distributional assumption becomes increasingly difficult to accurately assess. This difficulty was exemplified here by the substantial censoring, 76 percent of the levels of controls, of PCB 114 in the example. As we showed in Section 4, the ML estimators are robust to small departures from normal and gamma distributions with the caveat that ĉ* is more susceptible to bias because of its intrinsic dependence on the shape of the distributions. Other authors have shown that parametric ROC estimates do not perform well under gross violations of distributional assumptions (Molodianovitch et al., 2006).

For the non-parametric EMP and semi-parametric ROC-GLM method it is not necessary to model the underlying distribution and thus frees investigators from possible misspecification. However, neither method can estimate a c* below a LOD. The EMP method can only estimate the location of J, c*, as low as the boundary and while the ROC-GLM can estimate J below the LOD, a corresponding c* estimate is unattainable because we can not map back through the empirical distribution. Interestingly, because of this limitation in the empirical method, as the LOD increases, the bias and RMSE of J̃_E decrease and the coverage probability for J increases because the method is positively biased when there is no LOD. As a result, the simulation study (represented in Figure 2) shows that when the true J occurs below the LOD, the EMP method can perform well estimating J̃_E at a biased ĉ*.

Whether or not these limitations are acceptable depends on many factors. When estimating only J, our tables and simulation section give sound advice regarding the levels of bias and RMSE to expect, with the caveat the EMP method limits our capability to assess potential discriminatory ability because J̃_E can never occur below the LOD. If, as in the example, a researcher uses the EMP method and J̃_E occurs at the LOD, additional resources to develop improved measurement techniques, thus lowering the LOD and realizing the potential discriminatory ability of the biomarker, would not be warranted unless the potential was adequately estimated using the ROC-GLM and/or the ML methods. Now say the ROC-GLM is utilized and J̃_G occurs below the LOD. Allocation of resources to improve measurements of biomarker levels may now be warranted but because one is unable to map back to a ${\stackrel{\sim }{c}}_G^{\ast }$, there is no estimate of the magnitude of measurement improvement necessary to realize the J̃_G. If the unknown ${\stackrel{\sim }{c}}_G^{\ast }$ is unattainable by any level of additional resources then attempting to achieve J̃_G would be blindly futile. The ML method is the only method of the three that consistently estimates J and c* below the LOD. While the ML method requires distributional assumptions, we have shown this method to be robust to minor distributional misspecification in estimating J for both normal and gamma distributed biomarker levels. In addition, the methods developed here can logically be extended to upper limits of detection as well as cases involving both lower and upper detection limits.

It should be noted that it is impossible to determine whether or not c* actual occurs below the LOD. However, one could test this hypothesis in a fairly straight forward manner using the standard error of c* and the fixed LOD.

Accounting for a biomarker’s potential discriminating ability is important when comparing biomarkers. In comparison of biomarkers affected and unaffected by an LOD, underestimation of the discriminatory ability of the affected marker may lead to choosing the less discriminatory biomarker without an LOD. However, the ML or the ROC-GLM methods have the ability to account for a biomarker’s potential with an LOD and suggest the need for improved measurement techniques. The ML and ROC-GLM method developed here properly account for the missingness of observations below the LOD and provide investigators with consistent estimates of biomarkers’ true discriminating capabilities.

Appendix

Normal Case

Gupta (1952) and Cohen (1950) independently examined the situation of a normally sampled population censored above some value. From this censored sample, Gupta developed a likelihood function and subsequently, MLE’s for the mean, μ, and standard deviation, σ. Utilizing this method for a biomarker censored below a fixed d, the log likelihood function for the normally distributed non-diseased population is found to be (Gupta, 1952):

$$\log L({\mathrm{\mu }}_Y,{\mathrm{\sigma }}_Y\mid z)=C-k\log {\mathrm{\sigma }}_Y-\frac{1}{2{\mathrm{\sigma }}_Y^2}\sum _{j=1}^k{(z_j-{\mathrm{\mu }}_Y)}^2-\left(n-k\right)\log \mathrm{\Phi }({\mathrm{\eta }}_Y)$$

with η_Y = (d − μ_Y)/σ_Y and C a constant. The maximization of the log likelihood function can be performed by differentiating with respect to μ_Y and σ_Y. Setting the maximized equations equal to zero, they can be combined such that ${\widehat{\mathrm{\mu }}}_Y=\overline{z}+({\widehat{\mathrm{\sigma }}}_Y^2-s_Z^2)/\left(d-\overline{z}\right)$ where $\overline{z}=\frac{1}{k}\sum _{j=1}^k{z}_j,s_Z^2=\frac{1}{k_Y}{\sum _{j=1}^k(z_j-\overline{z})}^2$. This can be written as ${\widehat{\mathrm{\sigma }}}_Y^2+(d-{\widehat{\mathrm{\mu }}}_Y)\left(d-\overline{z}\right)-(s_Z^2+{\left(d-\overline{z}\right)}^2)=0$ and solved for σ̂_Y numerically and μ̂_Y by substitution. Performing these steps similarly for cases and controls yield MLE’s for all four parameters necessary to calculate Ĵ and ĉ*.

Subsequently, if the diseased and non-diseased populations are normally distributed (a ROC curve formed by normally distributed diseased and non-diseased biomarker levels is called a binormal curve), the MLE’s for μ and σ can be obtained for both populations. Thus Ĵ is found to be:

$$\widehat{J}=\mathrm{\Phi }(({\widehat{c}}^{\ast }-{\widehat{\mathrm{\mu }}}_Y)/{\widehat{\mathrm{\sigma }}}_Y)-\mathrm{\Phi }(({\widehat{c}}^{\ast }-{\widehat{\mathrm{\mu }}}_X)/{\widehat{\mathrm{\sigma }}}_X)$$ (2)

and ĉ* with unequal variances (refer to Perkins and Schisterman, 2005 for derivation of c*):

$${\widehat{c}}^{\ast }=\frac{({\widehat{\mathrm{\mu }}}_X{\widehat{\mathrm{\sigma }}}_Y^2-{\widehat{\mathrm{\mu }}}_Y{\widehat{\mathrm{\sigma }}}_X^2)-{\widehat{\mathrm{\sigma }}}_Y{\widehat{\mathrm{\sigma }}}_X\sqrt{{({\widehat{\mathrm{\mu }}}_Y-{\widehat{\mathrm{\mu }}}_X)}^2+({\widehat{\mathrm{\sigma }}}_Y^2-{\widehat{\mathrm{\sigma }}}_X^2)\log ({\widehat{\mathrm{\sigma }}}_Y^2/{\widehat{\mathrm{\sigma }}}_X^2)}}{({\widehat{\mathrm{\sigma }}}_Y^2-{\widehat{\mathrm{\sigma }}}_X^2)}.$$ (3)

With equal variances, ĉ* is found to be:

$${\widehat{c}}^{\ast }=\frac{{\widehat{\mathrm{\mu }}}_X+{\widehat{\mathrm{\mu }}}_Y}{2}.$$

Gamma Case

Given that biomarker values sometimes follow a skewed distribution, it is prudent to consider the case of diseased and non-diseased populations having gamma distributions. The log likelihood equation for the censored gamma non-diseased population, z_y, is (Harter and Moore, 1967):

$$\log L\left({\mathrm{\alpha }}_Y,{\mathrm{\beta }}_Y\mid z\right)=C-k\left[\log \mathrm{\Gamma }\left({\mathrm{\alpha }}_Y\right)+\log {\mathrm{\beta }}_Y\right]-\left({\mathrm{\alpha }}_Y-1\right)\sum _{j=n-k+1}^n\log z_j^{\ast }-\sum _{j=n-k+1}^n{z}_j^{\ast }+\left(n-k\right)\log F\left({\mathrm{\eta }}_Y\right),$$

where C is a constant, $z_j^{\ast }=\frac{z_j}{{\mathrm{\beta }}_Y},F\left({\mathrm{\eta }}_Y\right)=\underset{0}{\overset{{\mathrm{\eta }}_Y}{\int }}\frac{1}{\mathrm{\Gamma }\left({\mathrm{\alpha }}_y\right)}{y}^{\mathrm{\alpha }-1}{e}^{-1}dy$ and ${\mathrm{\eta }}_Y=\frac{d}{{\mathrm{\beta }}_Y}$.

Since the two equations formed by differentiating with respect to alpha and beta cannot be combined to solve for one parameter, the likelihood function needs to be maximized with respect to both parameters simultaneously. This maximizing can be easy solved numerically by standard software and the MLE’s for α_y and β_Y obtained. By extending the above process, the MLE’s for the diseased population parameters α_x and β_x can be found.

As a result, ĉ* must be found numerically (f(c; θ̂_Y)= g(c; θ̂_X)) in most instances because no closed form solution exists, except when α_X = α_Y or β_X = β_Y (Schisterman and Perkins, 2007). ĉ* is obtained at this intersection because it is the cut-point that optimizes the biomarker’s differentiating ability when equal weight is given to sensitivity and specificity. Letting F and G be the cumulative distribution functions for their respective status, the MLE for J is:

$$\widehat{J}=\widehat{F}\left({\widehat{c}}^{\ast }\right)-\widehat{G}\left({\widehat{c}}^{\ast }\right).$$ (4)

By substituting the MLE’s α̂_X; β̂_X, α̂_Y and β̂_Y into F and G, respectively, ĉ* is estimated numerically and Ĵ can be estimated utilizing Eq. (4).