Abstract
We assessed the spatial-tuning properties of units in the cat’s anterior auditory field (AAF) and compared them with those observed previously in the primary (A1) and posterior auditory fields (PAF). Multi-channel, silicon-substrate probes were used to record single- and multi-unit activity from the right hemispheres of α-chloralose-anesthetized cats. Spatial tuning was assessed using broadband noise bursts that varied in azimuth or elevation. Response latencies were slightly, though significantly shorter in AAF than A1, and considerably shorter in both of those fields than in PAF. Compared to PAF, spike counts and latencies were more poorly modulated by changes in stimulus location in AAF and A1, particularly at higher sound pressure levels. Moreover, units in AAF and A1 demonstrated poorer level tolerance than units in PAF with spike rates modulated as much by changes in stimulus intensity as changes in stimulus location. Finally, spike-pattern-recognition analyses indicated that units in AAF transmitted less spatial information, on average, than did units in PAF—an observation consistent with recent evidence that PAF is necessary for sound-localization behavior, whereas AAF is not.
INTRODUCTION
In the present study, we have continued our assessment of spatial tuning in the auditory cortex by recording from the anterior auditory field (AAF) of the cat. With the addition of these data, our survey of the major fields of the cat’s auditory cortex is now largely complete. Although intact auditory cortex is necessary for the localization of sounds in space (Jenkins and Masterton 1982; Jenkins and Merzenich 1984; Malhotra et al. 2004; Neff et al. 1956), its actual role in this behavior has yet to be clearly established. Consistent with some role in spatial hearing, the responses of neurons throughout the cat’s auditory cortex have been shown to be modulated by, and thus transmit information about, the locations of sound sources (Imig et al. 1990; Middlebrooks and Pettigrew 1981; Middlebrooks et al. 1998; Stecker et al. 2003, 2005a). Unlike the somatosensory and visual cortices, however, there is no evidence for a topographic representation of space within the auditory cortex (Masterton and Imig 1984; Middlebrooks et al. 1998; Middlebrooks and Pettigrew 1981). Cortical neurons tend to have broad spatial tuning and, despite some similarities of spatial receptive fields within local neural populations (Middlebrooks and Pettigrew, 1981; Imig et al. 1990; Stecker et al. 2005a), no auditory space map has been demonstrated in any field yet studied. Instead, neurons in the auditory cortex are said to represent space “panoramically” (Middlebrooks et al. 1994, 1998) in the sense that the responses of single neurons vary systematically with sound-source locations throughout up to 360° of space, with higher-resolution representations of auditory space likely emerging only through population-level interactions (Furukawa et al., 2000; Stecker et al. 2005b).
The auditory cortex of the cat comprises a number of fields that differ in their anatomical connections (Huang and Winer 2000; Lee and Winer, 2007; Morel and Imig 1987; Rouiller et al. 1991) and physiological response properties (Imaizumi et al. 2004; Lee et al. 2004a, b; Phillips and Irvine 1981, 1982; Reale and Imig 1980). Three of these fields—the primary (A1), anterior (AAF), and posterior (PAF) auditory fields—receive robust input from the ventral division of the medial geniculate body (MGB) (Morel and Imig 1987; Huang and Winer 2000). The three fields differ in the laminar distributions of their thalamic inputs (Huang & Winer 2000), however, and have also been shown to receive input from other divisions of the MGB. For example, in addition to the robust input AAF receives from the ventral division of the MGB, AAF also receives a substantial projection from the lateral part of the posterior group of thalamic nuclei (Huang and Winer 2000; Lee et al. 2004a; Morel and Imig 1987), whereas field PAF receives input from the medial and dorsal divisions of the MGB (Huang and Winer 2000; Morel and Imig 1987). The observation that a vast majority of thalamic projections to matched frequency regions in A1 and AAF arise from distinct sources suggests that these fields, although similar in many respects, might process different forms of auditory information in parallel (Lee et al. 2004a).
Physiologically, fields A1, AAF and PAF exhibit tonotopic maps of characteristic frequency. Field A1, situated dorsally on the middle ectosylvian gyrus (MEG), shares a high-frequency border with AAF rostrally, and a low-frequency border with PAF caudally (Merzenich et al. 1975; Knight 1977; Reale and Imig 1980). As was the case anatomically, however, physiological differences have been noted amongst these fields. For example, the representation of the audible spectrum appears to be less complete and uniform in AAF than in A1, with the range between 1 and 5 kHz being underrepresented in AAF, and the range between 20 and 30 kHz being over-represented in AAF (Imaizumi et al. 2004). There is also evidence that multi-peaked frequency response areas (FRAs) may be more common in PAF and AAF than in ventral A1 (Knight 1977; Loftus and Sutter 2001). Although Sutter and Schreiner (1991) described a number of neurons with multi-peaked FRAs in A1, > 90% of these were located in the field’s dorsal region near the suprasylvian sulcus. That region probably corresponded to the “dorsal zone” (DZ; Middlebrooks and Zook 1983), an area that we now regard as a distinct auditory field (Stecker et al. 2005a). Compared to A1, units in AAF also tend to have shorter first-spike latencies (by up to 4 ms), higher thresholds (particularly above 16 kHz), broader frequency tuning (particularly between 2 and 32 kHz), and higher best modulation frequencies (Eggermont 1998; Knight 1977; Merzenich et al. 1975; Schreiner and Urbas 1988; Imaizumi et al. 2004). Field PAF differs markedly from both of these fields in that its first-spike latencies are considerably longer and more robustly modulated by changes in sound features including frequency and spatial location, and its rate-versus-level functions are more likely to be non-monotonic (Phillips and Orman 1984; Stecker et al. 2003).
Despite notable differences amongst auditory cortical fields in terms of their non-spatial response properties, the mode and quality of their spatial coding have proven remarkably similar (for a review see Middlebrooks et al. 2007). For example, units in A1 (Imig et al. 1990; Middlebrooks and Pettigrew 1981; Stecker et al. 2003), the anterior ectosylvian area (Middlebrooks et al. 1998), and A2 (Furukawa and Middlebrooks 2002; Middlebrooks et al. 1998) show broad spatial tuning, with robust responses to stimuli presented from locations throughout a hemifield or more of auditory space. Perhaps most importantly, the spike-count-based tuning widths of units in these fields tend to broaden significantly with increasing SPL, even as these levels are increased from near threshold to just moderate levels (Imig et al. 1990; Middlebrooks et al. 1998). More recently, studies of units in PAF (Stecker et al. 2003) and DZ (Stecker et al. 2005a) have revealed enhanced spatial sensitivity that can be attributed, at least in part, to location-dependent variation of response latency and greater tolerance of changes in stimulus level. The fact that the rate- and latency-versus-azimuth functions of neurons in these fields show weaker mutual correlation than was observed in A1 suggests that the two coding dimensions may convey unique, rather than redundant, information in PAF and DZ (Stecker et al. 2003, 2005a). The possibility that PAF, in particular, may play a more central role in spatial behavior than AAF, for example, is supported by behavioral studies demonstrating profound localization deficits following reversible deactivation of PAF but not AAF (Malhotra and Lomber 2007; Malhotra et al. 2004).
To complete our survey of spatial tuning in the major fields of the cat’s auditory cortex, here we have recorded from field AAF. To place these data into an appropriate context, observations made of AAF will be compared with those made previously in two other areas, the primary (A1) and posterior (PAF) auditory fields (Stecker et al. 2003, 2005a). In each animal, two 16-channel recording probes typically were inserted into some combination of fields AAF, A1, and PAF, allowing for the simultaneous assessment of neural activity at up to 32 sites. Multiple pairs of probe placements were made in each animal. Multi-channel neural activity was recorded in response to noise bursts that varied in azimuth, elevation, and SPL, and pure tones that varied in frequency and SPL.
Consistent with earlier reports, first-spike latencies were considerably shorter in AAF and A1 than PAF, frequency-response areas (FRAs) were often more complex in AAF and PAF than (ventral) A1, and rate-versus-level functions (RLFs) were more monotonic in AAF and A1 than PAF. Although the responses of neurons in each field were modulated by changes in sound-source location, units in AAF and A1 exhibited considerably less latency modulation than those in PAF. More importantly, however, the spatial tuning of units in AAF and A1 was far less tolerant of changes in sound pressure level (SPL) than in PAF units. In fact, spike rates in AAF and A1 were often modulated as much by changes in SPL as they were by changes in sound-source location. The relative quality of spatial coding in these three fields is largely consistent with evidence that PAF, but not AAF, is necessary for normal sound-localization behavior in the cat (Malhotra et al. 2004; Malhotra and Lomber 2007).
MATERIALS AND METHODS
Animal Preparation
The data presented here were obtained from a total of 19 purpose-bred cats (13 male, 6 female) weighing between 2.8 and 7.0 kg (median 3.6 kg). The female cats had participated previously in combined behavioral and physiological experiments in which they were trained to perform a non-spatial auditory discrimination for food reward; male cats were only used in these acute experiments. All surgical procedures were in compliance with the guidelines of the University of Michigan Committee on Use and Care of Animals and were virtually identical to those described in earlier reports from this lab (Middlebrooks et al. 1998; Stecker et al. 2003, 2005a). Initial anesthesia was induced and maintained throughout surgery using isoflurane, changing to an intravenous α-chloralose drip (~3mg·kg−1·h−1) during the physiological recording. During the recording, the animal was suspended in a fabric sling in the center of a sound-attenuating chamber with its head supported from behind by a bar attached to the skull. Its external ears were held in a natural forward position with thin wire supports, if necessary. Experiments lasted between 24 and 110 hours (median 73 hours) after which time the already-anesthetized animals were euthanized by intravenous injection of potassium chloride. The brain was removed and stored in buffered formalin for later visual confirmation of recorded areas.
Experimental Apparatus and Stimulus Generation
The apparatus and procedures used here were similar to those described in earlier reports from this lab (Middlebrooks et al. 1998; Stecker et al. 2003, 2005a). The animal was positioned in the middle of a sound-attenuating room (inside dimensions 2.6 × 2.6 × 2.5 m) whose surfaces were lined with acoustic foam. Two circular hoops were centered on the cat’s head, each with a radius of 1.2 m, in the horizontal and midsagittal (i.e., vertical) planes. Loudspeakers were attached to the hoops in 20° increments. The horizontal hoop consisted of 18 loudspeakers spanning 360° with the speaker located straight ahead designated 0° and those to the right and left assigned positive and negative values, respectively. The vertical hoop consisted of 14 loudspeakers spanning 260° from 60° below the frontal horizon (−60°) up and over the head to 20° below the rear horizon (+200°). Experiments were controlled using a personal computer running custom MATLAB scripts (The Mathworks, Natick, MA). Acoustic stimuli were digitally generated using equipment from Tucker-Davis Technologies (TDT, Alachua, FL) with 24-bit precision at a 100-kHz sampling rate. Stimuli were either 80-ms Gaussian noise bursts with abrupt onsets and offsets or 80-ms tones with 5-ms raised-cosine ramps. Speaker outputs were equalized by multiplying the desired stimulus spectrum with the inverse transfer function of the speaker from which the stimulus was to be presented (Zhou et al. 1992).
Experimental Procedure
Probe placements were guided visually by gross anatomical landmarks, including the anterior and posterior ectosylvian sulci and the suprasylvian sulcus, and physiologically by the tonotopic gradients observed within each cortical field. Field A1 occupies the dorsal portion of the middle ectosylvian gyrus and is bordered dorsally by field DZ, which is distinguished from A1-proper by longer latencies and more complex frequency tuning (He and Hashikawa 1998; Stecker et al. 2005a). Field AAF occupies the dorsal portion of the anterior ectosylvian gyrus, is bordered dorsally by the suprasylvian sulcus, and is more or less ventral and rostral to the tip of the anterior ectosylvian sulcus (Huang and Winer 2000). Its border with A1 is marked by a high-frequency reversal of the tonotopic gradient (Imaizumi et al. 2004; Knight 1977; Merzenich et al. 1975; Reale and Imig 1980). Field PAF occupies the caudal bank of the dorsal posterior ectosylvian sulcus and shares a low-frequency tonotopic border with caudal A1 (Phillips and Orman 1984; Reale and Imig 1980). Although Reale and Imig (1980) have identified a fourth tonotopic area, the ventral posterior auditory field, we typically did not sample far enough ventrally on the posterior ectosylvian gyrus to access that area. Penetrations into each field were generally made oblique to the cortical surface and thus sampled all cortical laminae. We have made no attempt to identify the lamina from which individual recordings were made. Broadband noise search stimuli were presented from contralateral (−40°) or overhead locations (+80°) during probe placements and the position, orientation, and depth of each probe was adjusted to maximize the number of active channels across the recording array. Once we were satisfied with the observed responses, the recording well was filled with a warmed agar solution and allowed to set. The agar served to increase the stability of recording sessions by reducing movements of the brain relative to the fixed recording probes. The collection of neural data usually began after a stabilization period of ~30 min.
Study of the units in each penetration began by estimating their sensitivity to broadband noise bursts presented from several locations in 5- or 10-dB increments of SPL. During the threshold estimation series, noise bursts were typically presented from three locations in the horizontal plane (0°, +40° and −40°) and one in the vertical midline plane (+80°). Thresholds typically varied among recording sites and between 16-site recording probes by no more than ~10 dB. The modal threshold was taken as the representative threshold for each penetration. In cases where larger differences were observed between the two probes, the threshold estimate was adjusted toward the lower of the two. Frequency tuning was assessed using 80-ms pure tones in 1/6-octave steps from 0.5 to 30 kHz whose levels were varied in 10-dB steps from −10 to ~50 dB SPL. Tones were presented from an overhead location (+80°) where the cat’s head-related transfer function typically is flattest and therefore has the smallest effect on neuronal frequency tuning (Xu and Middlebrooks 2000).
Azimuthal sensitivity was assessed by presenting 80-ms noise bursts from the horizontal speaker array in 20° steps from −180° to 160°. Elevation sensitivity was assessed in a separate series by presenting noise bursts from the vertical speaker array in the midsagittal plane in 20° steps from −60° (i.e., 60° below the frontal horizon) up and over the head to 200° (20° below the rear horizon). Stimuli were presented at 20 and 40 dB above threshold. The specific combination of stimulus parameters (e.g., stimulus location and level) to be presented on each trial was selected following a quasi-random schedule, and each possible combination of stimulus parameters was presented once before any combination was repeated. Recording epochs generally extended from 50 ms before to 200 ms after stimulus onset. The estimation of level, spectral, and spatial tuning properties was often followed by the presentation of additional stimulus sets to address other experimental questions.
Data Acquisition and Spike Sorting
Extracellular neural activity was recorded using multi-site, silicon-substrate probes provided by the University of Michigan Center from Neural Communication Technology (Anderson et al. 1989). The probes used here had a linear array of 16 sites, spaced 150 µm apart, with surface areas of 177 µm2 and impedances between 1 and 4 MΩ. Two such probes generally were placed in some combination of fields A1, AAF, and PAF, allowing activity to be recorded simultaneously from up to 32 sites. Pairs of probes were placed successively at multiple locations in each cat. Activity at each site was amplified and digitized with a multi-channel bioamplifier and digital signal processing system (TDT, model RA16), bandpass filtered between 0.2 and 2.0 kHz, resampled at 12.5 kHz, and stored to disk for offline analysis. Activity was monitored online using custom software that allowed for the estimation of neural thresholds, frequency tuning, and spatial tuning. Offline spike sorting used custom software that utilized principal component analysis of wave shapes (Furukawa et al. 2000; Stecker et al. 2003). In the majority of cases, a single cluster of principal component weights and, therefore, a single neural “unit,” was identified at each recording site. In this context, the term neural unit refers to the presumed generator(s) of the sorted responses but need not be assumed to be a single neuron. Indeed, in the absence of strong evidence to the contrary (e.g., discrete clustering in principal component space, consistent spike amplitudes, and an absence of interspike intervals < 1 ms), we have assumed that the clustered responses are the unresolved responses of two or more neurons (i.e., multi-unit clusters). Spike times were stored relative to stimulus onset with 20-µs resolution. To avoid the analysis of units that were unresponsive or unstable during the recording period, the population was screened by requiring that each unit produce a mean response of ≥1 spike per trial for its most effective stimulus and that the average response rate during the first and second halves of a stimulus series differ by a factor <2. Units were screened separately for their responses in the azimuth and elevation series and those failing to satisfy these criteria were excluded from further analysis.
Data Analysis
Spatial sensitivity assessed by analysis of spike count and latency
Following spike sorting, spike times were stored as latencies relative to stimulus onset at the loudspeaker, including 3.5 ms of travel time between their transduction at the speaker and their arrival at the cat's head (i.e., 1.2 m at 344 m·s−1). Modulations of spike rates and response latencies were then used to assess spatial sensitivity. We defined for each unit the normalized mean spike count, C, and the mean latency, L, as the normalized arithmetic mean spike count and geometric mean first spike latency at each combination of stimulus parameters (i.e., location and SPL). In an effort to prevent spontaneous activity from influencing count and latency measures, spikes occurring prior to stimulus onset were excluded from all calculations. Spike counts were normalized by dividing by the maximum mean spike count across azimuth separately at each SPL to give the proportion of the unit's maximum, SPL-specific response and thus ranged from 0, for locations giving no response, to 1, for locations giving the maximum response. Two measures of overall response latency were used: the median and the minimum value of L across location and SPL. Trials that failed to elicit at least one spike were excluded from the calculation of L.
Spatial tuning depth
The depth of response modulation, or spatial tuning depth, indicates the extent to which response latencies or spike counts varied across azimuth or elevation at a particular SPL. The modulation of spike count, ΔC, was based on the maximum and minimum normalized spike count (Cmax and Cmin, respectively; by definition, Cmax = 1) at each tested SPL, and indicated the proportional reduction of spike count; ΔC = Cmax − Cmin.
Spatial tuning width
The spatial tuning width characterizes the range of spatial locations that elicit maximal spike counts. Values of C (normalized spike count) were interpolated in 0.2° steps between tested locations. The spatial tuning width was defined as the range of locations that elicited C > 0.5 (i.e., within 50% of the maximum normalized spike count) at each SPL, and has units of degrees. These locations were not necessarily contiguous.
Spatial centroid
Consistent with our previous reports (e.g., Middlebrooks et al. 2003; Stecker et al. 2003, 2005b), the spatial centroid, an estimate of a unit's preferred location, was defined as the location of the spike-count weighted peak response, and can be considered as the center of mass of the peak response. In cases where the value of C (normalized spike count) failed to fall below 0.50 at any location, i.e., when units were poorly modulated, the unit was classified as having no centroid (NC). Values of C were interpolated in 0.2° steps between locations, and the range of contiguous locations eliciting values of C > 0.75 (including Cmax), i.e., the peak response, was determined at each SPL. The centroid was calculated by generating vectors at each of the interpolated locations within the peak response. For each vector, the angle was the interpolated location in degrees and the length was the interpolated value of C at that location. The centroid was then defined as the angle of the resultant of the vectors included in the peak response. As in our previous studies (e.g., Stecker et al., 2003; 2005a) we computed the centroid over only the peak response. In pilot studies, we found that computation of centroids over the entire range of tested locations often resulted in centroids that deviated from the apparent peak response areas due to the influence of the broad tails of spatial response areas. Centroids were computed separately for azimuth and elevation and at 20 and 40 dB above threshold.
Spatial sensitivity assessed by network analysis of spike patterns
A pattern recognition algorithm based on artificial neural networks was used to estimate the spatial information transmitted by neural responses. As in previous reports (Furukawa and Middlebrooks 2001, 2002; Stecker et al. 2003, 2005a), the obtained neural responses (trial-by-trial vectors of spike times) were divided into two sets referred to as the “training” and “test” sets, from odd- and even-numbered trials. Average response patterns were obtained from the training and test sets by randomly drawing 8 responses (with replacement) from the pool of available responses at each stimulus location in each set. The pool of responses in each set included 20 trials at each of two tested levels (20 and 40 dB above threshold) at each location. A total of forty of these average response patterns were obtained from the training and test sets at each stimulus location, convolved with a Gaussian impulse (σ = 1 ms), and re-sampled with 2-ms resolution to create spike-density functions (SDFs). SDFs are smoothed response patterns and served as the input to the pattern-recognition algorithm. In a separate analysis, algorithm inputs were scalars representing the spike count or response latency of each SDF. The response latency was the geometric mean first-spike latency across 8 trials of responses (excluding trials without spikes), whereas the spike count input was the arithmetic mean number of spikes across 8 trials. Spike counts and response latencies for these “reduced” inputs were normalized prior to this analysis and ranged from 0 to 1 (the minimum to the maximum across the stimulus ensemble) (Furukawa & Middlebrooks 2002).
The pattern recognition algorithm used for classification was based on radial basis functions (Ghosh and Nag 2001; Wasserman 1993) and was implemented using a customized version of the MATLAB Neural Network Toolbox (The Mathworks, Natick, MA). A classifier unit was assigned to each stimulus location, and SDFs from the test set were compared to the average SDF of the training set at each classifier location. In response to a test SDF, each classifier unit output a scalar value that was inversely related to the Euclidean distance between the average training set SDF and the test SDF. Following earlier reports from this lab (Stecker et al. 2003, 2005a), the classifier unit with the largest scalar value—indicating the smallest difference between the classifier’s SDF and the test SDF—was selected as the algorithm’s “response.” Ultimately, this response amounts to the algorithm’s decision about the stimulus location most likely to have elicited the observed SDF.
Network estimates of stimulus locations were then expressed as joint stimulus-response probabilities in a confusion matrix. The probabilities within a column of a confusion matrix indicate the distribution of the network’s classifications given the distribution of neural responses for one target location (example confusion matrices for several AAF units can be seen in Figure 1). Each column represents trials associated with a particular target location, while each row represents trials yielding a particular classifier response location. The confusion matrix was then used to estimate the total stimulus-related (TSR) spatial information, in bits, for each unit (Furukawa and Middlebrooks 2001). With 18 azimuthal locations, perfect classification of neural response patterns would yield a confusion matrix with a joint stimulus-response probability of 1 on the diagonal and 4.17 bits of information (the entropy of the system which is given by log2(n), where n is the number of classifiers or possible stimulus locations). We calculated the transmitted information (TSR) from network classifications of full spike patterns, or scalar (reduced) inputs based on spike counts or response latencies alone. Although these information estimates are susceptible to a number of sources of bias, all units should be equally susceptible and, since we are interested in making comparisons between fields rather than absolute estimates of transmitted information within them, this issue will not be treated further here. For more detailed estimates and a discussion of bias in this information measure, see the reports by Stecker and colleagues (2003, 2005a). Because the features of spike patterns generally vary as a function of both stimulus level and location, networks trained to classify SDFs obtained at one stimulus level often perform poorly when tested at a different level (Stecker et al. 2005b). In these analyses, SDFs were drawn both from trials presented both at 20 and at 40 dB above threshold, and networks were forced to make use of level-independent response features.
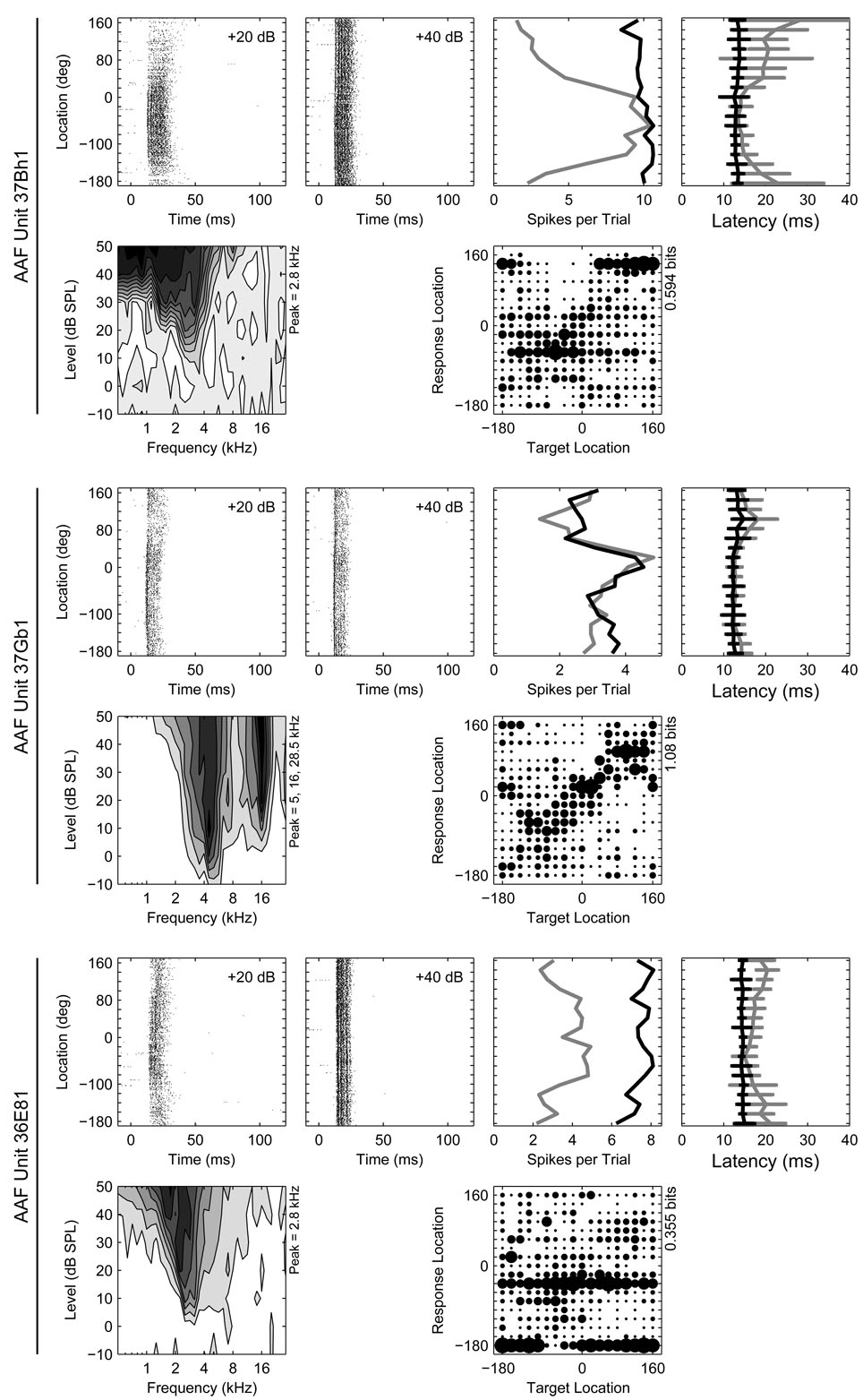
Figure 1.
Response properties of three representative units recorded from AAF. Six panels of data are provided for each unit. From left to right in the top row for each unit are the azimuth raster at 20 and 40 dB above threshold, the rate-azimuth function (RAF), and the latency-azimuth function (LAF). In the azimuth raster, the times of occurrence of spikes (x-axis) elicited by stimuli at particular locations (y-axis) are represented by dots. In the RAF and LAF, the mean spike count or first-spike latency (x-axis) is plotted as a function of stimulus location (y-axis) separately at 20 (gray) and 40 dB (black) above threshold. The error bars on the LAF indicate ±1 standard deviation of the mean. The FRA is plotted in the first column in the second row with the confusion matrix from the azimuth series plotted in the third column. In the FRA, the average spike count is plotted as a function of stimulus frequency (x-axis) and intensity (y-axis) with darker shading representing higher spike counts. The position(s) of each unit’s frequency peak(s) is indicated on the y-axis. The confusion matrix represents network classifications (y-axis) of neural responses (x-axis) as joint stimulus-response probabilities. The size of the symbol in each cell of the matrix represents the relative likelihood of classifying a neural response from a particular location on the x-axis to a particular location on the y-axis, with larger symbols indicating higher likelihoods. Each column therefore represents the distribution of classifications of responses elicited by stimuli at a particular location. An estimate of the total stimulus-related information (TSR, in bits) derived from each confusion matrix is indicated on the y-axis.
Statistical procedures
Distributions of statistics between fields were typically compared using non-parametric permutation tests. Under the null hypothesis, the distributions do not differ and group labels can be randomly reassigned without affecting the statistics of those distributions. Regardless of the response feature of interest (e.g., response latency, tuning width, etc.), we compared the observed difference between two cortical fields (e.g., the difference between the median response latencies in AAF and A1) to a sampling distribution of differences obtained from 5000 permutations of the same distributions with randomly assigned field labels. We then determined the proportion of permuted median differences that were greater than or equal to the difference observed when the original labels were used. This proportion represents the probability of type I error and can be expressed as a p value whose sensitivity is limited by the number of permutations (with 5000 permutations this limit is p ≥ 0.0002). We have adopted a criterion of p < 0.05 for statistical significance, but report obtained p values to one significant digit to indicate the magnitudes of test statistics. Analysis of variance (ANOVA) was performed using the Statistical Package for the Social Sciences (SPSS) and Pearson correlation was performed using the MATLAB Statistics Toolbox (The Mathworks, Natick, MA).
RESULTS
The data reported here were obtained from a total of 127 probe placements made in the right hemispheres of 19 cats (Table 1). Forty-three probes were placed in AAF yielding 620 units that satisfied our stability criteria in the azimuth and/or the elevation series (see Methods). Twenty-four of these probes were placed as simultaneous pairs in AAF, with the remaining probes placed in combination with another field. Thirty-three probes were placed in A1 yielding 397 units. The remaining 51 probes were placed in PAF yielding 503 units. Although all of the AAF units are new to this report, the A1 and PAF data from cats 0101–0202 were first reported by Stecker and colleagues (2003), and the A1 and PAF data from cat 0203–0405 were first reported by Stecker and colleagues (2005a). These A1 and PAF data are presented here for comparison purposes with AAF data, along with new data from 78 additional A1 units and 31 additional PAF units.
Table 1.
Summary of the number of units recorded and number of probe placements in each field for each animal. The units included in this table satisfied the response criteria for either the azimuth or the elevation series (see Methods). Of the 19 cats used, 6 were female and 13 were male. Female cats had been trained to perform a non-spatial auditory discrimination for food reward and, in some cases, had been involved in studies of chronic physiological recording. A1 and PAF units from cats 0101–0405 have been described previously (Stecker et al. 2003, 2005a). All of the AAF units and all units from cats 0408–0412 are new to this report.
| Cat | Sex | Wt. | AAF | A1 | PAF | Total |
|---|---|---|---|---|---|---|
| 0101 | F | 3.00 | — | 15 / 1 | 50 / 8 | 65 / 9 |
| 0102 | M | 6.96 | — | 24 / 3 | 19 / 3 | 43 / 6 |
| 0103 | M | 5.20 | — | — | 10 / 2 | 10 / 2 |
| 0105 | F | 3.40 | — | 15 / 1 | 50 / 4 | 65 / 5 |
| 0201 | M | 5.50 | — | — | 59 / 4 | 59 / 4 |
| 0202 | M | 4.00 | — | 63 / 8 | 79 / 10 | 142 / 18 |
| 0203 | M | 3.55 | — | 89 / 6 | 10 / 2 | 99 / 8 |
| 0204 | M | 4.30 | — | 16 / 1 | 99 / 8 | 115 / 9 |
| 0302 | M | 3.90 | — | — | 60 / 5 | 60 / 5 |
| 0303 | M | 3.04 | — | 3 / 1 | 36 / 3 | 39 / 4 |
| 0305 | F | 2.83 | — | 29 / 2 | — | 29 / 2 |
| 0306 | F | 3.64 | 72 / 5 | 15 / 1 | — | 87 / 6 |
| 0307 | F | 3.64 | 162 / 11 | — | — | 162 / 11 |
| 0401 | M | 4.56 | 155 / 10 | — | — | 155 / 16 |
| 0404 | F | 5.04 | 35 / 3 | 14 / 1 | — | 49 / 4 |
| 0405 | M | 4.00 | 78 / 5 | 36 / 3 | — | 114 / 8 |
| 0408 | M | 3.64 | 1 / 1 | 16 / 1 | — | 17 / 2 |
| 0411 | M | 3.60 | 39 / 3 | 47 / 3 | — | 86 / 6 |
| 0412 | M | 3.04 | 78 / 5 | 15 / 1 | 31 / 2 | 124 / 8 |
| Totals | 620 / 43 | 397 / 33 | 503 / 51 | 1520 / 127 | ||
First-spike latencies were shorter and less strongly modulated in AAF and A1 than PAF
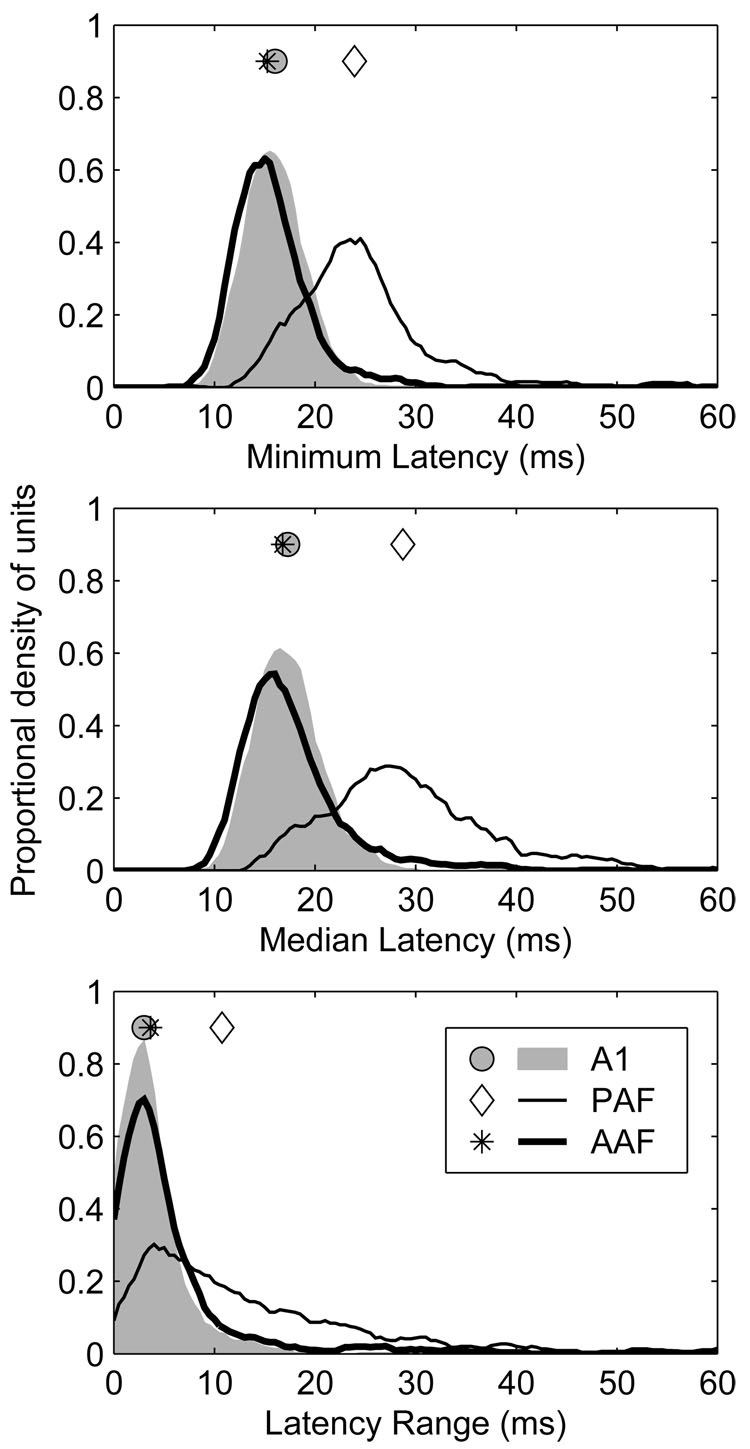
General response properties of representative units recorded in field AAF are plotted in Figure 1. In many respects, the responses of units in AAF were similar to those observed in A1 and, together, they were quite distinct from those observed in PAF (see Stecker et al. 2005a, Figure 1, for examples of representative A1 and PAF units). Response latencies have previously been shown to be shorter in A1 and AAF than in surrounding fields (Imaizumi et al. 2004; Knight 1977; Phillips and Irvine 1981, 1982; Phillips and Orman 1984) and, consistent with those reports, overall response latencies (i.e., the median, geometric mean first spike latency across all azimuths) were shorter in AAF than A1 (16.8 and 17.6 ms, respectively, p = 0.02), and shorter in both of those fields than in PAF (28.7 ms, p < 0.0002) (Figure 2, middle).
Figure 2.
Response latencies in AAF and A1 were shorter and less strongly modulated by stimulus location than in PAF. Response latency characteristics were derived from the azimuth series. Top: distributions of minimum geometric mean first-spike latency for each unit. Middle: distributions of median geometric mean first-spike latency for each unit. Bottom: distributions of location-dependant latency modulation (ΔL) for each unit. ΔL represents the difference between the maximum and minimum geometric mean first-spike latency across all azimuths. Each value represents the difference between the maximum and the minimum geometric mean first-spike latency. Symbols represent the median of each distribution.
Response latencies were also modulated less by changes in sound-source azimuth in AAF and A1 than in PAF (Figure 2, bottom). At 40 dB above threshold, for example, the median latency range across all azimuths (ΔL) in AAF and A1 was 3.65 and 3.01 ms, respectively (p < 0.0002), whereas in PAF it was 10.77 ms (PAF vs. A1 and AAF, p < 0.0002). Because of the slightly greater spatial variation of response latency observed in AAF than A1, and the considerably greater variation seen in PAF than in either of those fields, we derived a second estimate of response latency that was less sensitive to this variation: the minimum, geometric mean first spike latency across azimuth (Figure 2, top). Using this measure, which better reflects the earliest stimulus-dependent activity in each field, latencies were shorter in AAF than A1 (15.3 and 16.0 ms, respectively, p < 0.0002), and shorter in both of those fields than in PAF (23.9 ms, p < 0.0002).
Trial-to-trial variability of first-spike latencies was highest in PAF, lowest in A1, and intermediate in AAF
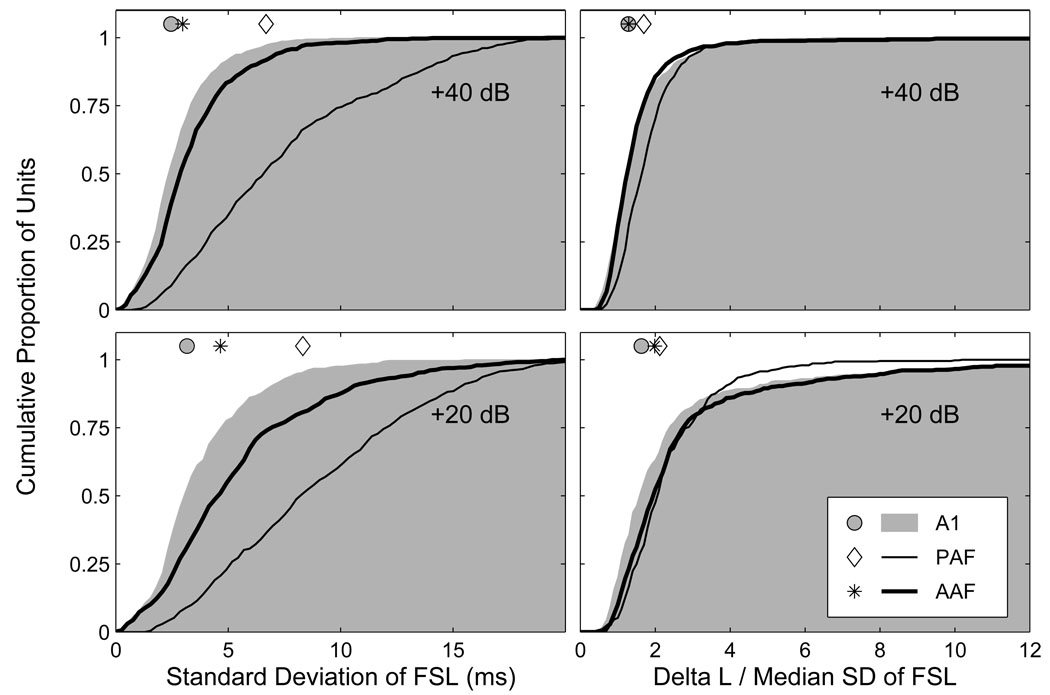
Spike-timing-based representations of auditory space are most robust when the temporal variation between source locations is high, and that within source locations is low. To quantify the trial-to-trial temporal variation of first-spike latencies (FSLs), we determined the standard deviation (SD) of FSLs at each combination of source azimuth and SPL, and then obtained the median value across all azimuths separately at each SPL. Cumulative distributions of these temporal-variability estimates are plotted on the left side of Figure 3 at 20 (bottom) and 40 dB (top) above threshold. At the lower SPL, the median temporal variation in AAF, A1 and PAF was 4.6, 3.2 and 8.3 ms, respectively. At the higher SPL, the median temporal variation in AAF, A1 and PAF was 3.0, 2.5 and 6.7 ms, respectively. At both levels, the greatest trial-to-trial variability was observed in PAF, the least variability was observed in A1, and an intermediate amount of variability was observed in AAF (p < 0.0002). In each field, there was a significant reduction in trial-to-trial temporal variation with increasing SPL (p < 0.0002). To quantify this level-dependent change in temporal variability, we analyzed the difference between each unit’s median SD at 20 and 40 dB above threshold. The median reduction in temporal variability for AAF, A1 and PAF was 1.4, 0.6 and 1.1 ms, respectively. The differences between A1 and AAF, and A1 and PAF were both highly significant (p < 0.0002), with the difference between AAF and PAF also achieving significance (p = 0.04). These results indicate that there was not only less trial-to-trial variability in FSLs in A1 than in the other fields, but that this variability was much less level-dependent in A1, particularly when it was compared to AAF.
Figure 3.
Response latencies in AAF and A1 show less trial-to-trial variability than in PAF. Plotted on the left are cumulative distributions of the median standard deviation (SD) of first-spike latencies across all azimuths separately at 20 (bottom) and 40 dB (top) above threshold. There was a significant reduction in variability at the higher level in each field, with the smallest reduction in variability in A1, and the largest reduction in AAF. A1 had the least variable first-spike latencies, PAF the most. Symbols represent the median of each distribution. Plotted on the right are cumulative distributions of the ratio of ΔL to the median SD of FSLs across azimuth, a ratio that expresses the spatial modulation of response latencies as a proportion of the trial-to-trial variability of response latencies. The highest median ratio was observed in PAF, whereas the lowest median ratio was observed in AAF (AAF did not differ from PAF at the lower level or from A1 at the higher level).
This estimate of trial-to-trial variability can be used to normalize the spatial-modulation of FSLs. By dividing ΔL by the median SD of FSLs across all azimuths, we can express the location-dependent latency modulation as a proportion of the trial-to-trial latency variation. Plotted on the right side of Figure 3 are cumulative distributions of these normalized latency modulation values at 20 (bottom) and 40 dB (top) above threshold. At the lower level, the median values for AAF, A1 and PAF were 1.99, 1.63 and 2.12, respectively. The value in A1 was significantly lower than those in AAF and PAF (p < 0.0002), whereas the difference between AAF and PAF was not significant (p = 0.06). At the higher level, the median values for AAF, A1 and PAF were 1.29, 1.28 and 1.70, respectively. The difference between AAF and A1 was not significant (p = 0.4), but the values in both fields were lower than in PAF (p < 0.0002). The fact that the median values in each field were lower at the higher SPL (p < 0.0002) indicates that although there was less trial-to-trial variability of FSLs at the higher level (Figure 3, left), there was also less location-dependent latency modulation. Because of the greater trial-to-trial variability of response latencies in PAF, differences between the fields with respect to the spatial sensitivity of their FSLs are more modest than the nominal values of ΔL might suggest.
Rate-level functions were more monotonic in AAF and A1 than PAF
Previous studies have shown that units in A1 tend to exhibit monotonic rate-level functions with response rates increasing with SPL such that the maximum response rate is observed at the highest tested level (Phillips and Irvine 1982). In contrast, studies have shown that a majority of units in PAF respond non-monotonically to changes in stimulus level and can therefore be said to be “level-tuned” (Phillips and Orman 1984; Phillips et al. 1995). To characterize the degree of monotonicity of the units in our sample, we computed a monotonicity ratio (Kitzes and Hollrigel 1996; Loftus and Sutter 2001): the ratio of the response rate at the highest tested level to the maximum response rate across all tested levels (generally from −10 to 50 dB SPL) (Stecker et al. 2003, 2005a). Stimuli were 80-ms broadband noise bursts presented from an overhead location. Monotonic rate-level functions would result in ratios near 1 (maximum response at the highest tested level), whereas non-monotonic functions result in ratios closer to 0 (minimum response at the highest tested level). Adopting a ratio of 0.50 to distinguish monotonic from non-monotonic responses (Kitzes and Hollrigel 1996), 85% of AAF units and 86% of A1 units were monotonic, compared to 68% of PAF units (Figure 4). Although, a majority of units in each area had monotonic rate-level functions, median monotonicity ratios were significantly higher in AAF (0.84) and A1 (0.81) than in PAF (0.69) (PAF vs. AAF and A1, p < 0.0002; AAF vs. A1, p = 0.2). Thus, a greater proportion of AAF and A1 units exhibited monotonic rate-level functions.
Figure 4.
Rate-level functions in AAF and A1 are more monotonic than in PAF. Plotted are cumulative distributions of monotonicity ratios, i.e., the ratio of the spike count at the highest tested level to the maximum spike count, for each population. The ratio ranges from 0 (highly non-monotonic) to 1 (highly monotonic). Symbols represent the median of each distribution.
Frequency-response areas were more complex in AAF and PAF than A1
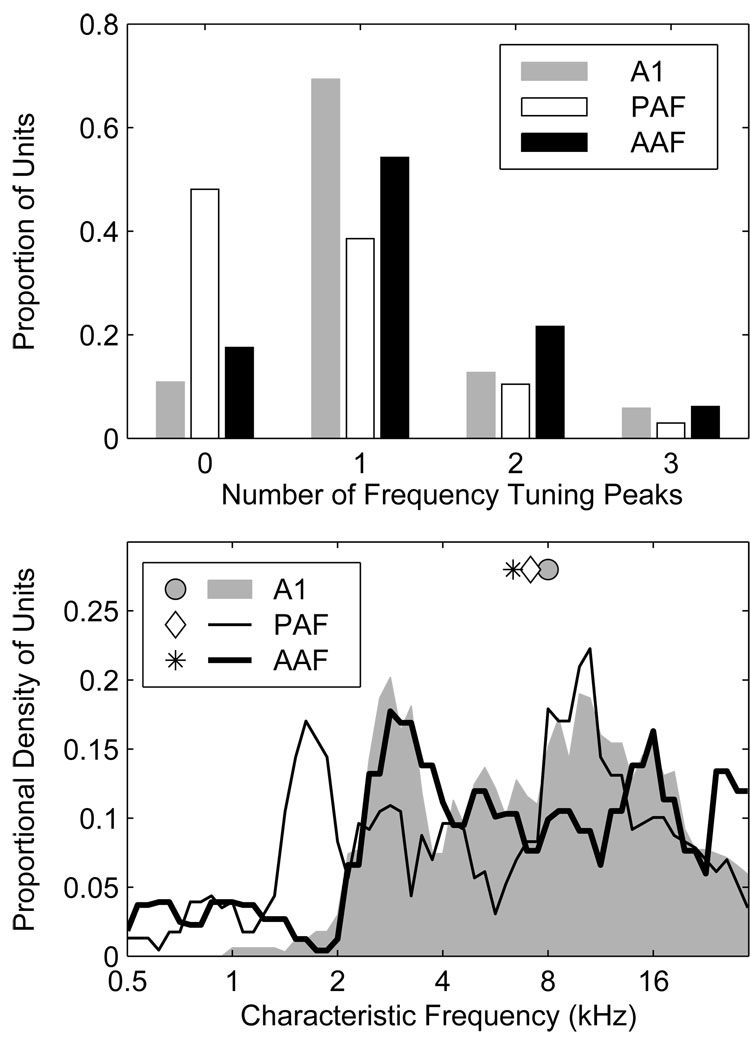
Previous studies have noted differences in frequency tuning among units in A1, AAF, and PAF. For example, whereas most A1 units exhibit relatively narrow, v-shaped FRAs with a single characteristic frequency (CF) (Merzenich et al. 1975; Phillips and Irvine 1982, 1981), the frequency tuning of units in PAF and AAF is often more complex with units being more broadly tuned or possessing multiple frequency tuning peaks (Imaizumi et al. 2004; Knight 1977; Loftus and Sutter 2001; Tian and Rauschecker 1994). Here, frequency tuning was assessed using 80-ms pure tones having frequencies ranging from 0.5 to 30 kHz in 1/6-octave steps, and levels ranging from −10 to 50 or 60 dB SPL in 10-dB steps. The CF was defined as the frequency of the tuning peak exhibiting the lowest threshold, where threshold was defined as a spike count equal to 40% of the unit’s maximum (Stecker et al. 2005a; Sutter and Schreiner 1991). In this report, the CF is said to be undefined if the FRA lacked coherent structure; a few units were excluded from the CF sample because they were not tested at a sufficiently low SPL. Additional frequency tuning peaks were defined in cases where they were evident provided that the response rate at frequencies between the CF and candidate tuning peak decreased by 50% or more.
Characteristic frequencies were defined for a majority of units in AAF (82%) and A1 (89%) in contrast to only slightly more than half (52%) of units in PAF (Figure 5, upper panel); in the figure, “0” peaks indicates that the CF was undefined. If we consider only those units with defined CFs, a majority in each field had FRAs characterized by a single peak (AAF 66%, A1 78%, and PAF 74%). Considering all units, multi-peaked units were most common in AAF (28%) and least common in PAF (13%), compared to 20% in A1. Distributions of CF, smoothed with a 0.5-octave wide rectangular window, are plotted in Figure 5 (bottom). In our sample, the median CF observed in AAF was 6.4 kHz, as compared to 8.0, and 7.1 kHz in A1 and PAF, respectively. The slightly higher median CF in our A1 sample reflects an almost complete absence of A1 units with CFs ≤ 2 kHz, likely due to our failure to sample adequately down the bank of the posterior ectosylvian sulcus where such units would be most likely. Despite the almost complete absence of low-frequency A1 units, an over-abundance of PAF units with CFs between 1 and 2 kHz, and a small over-representation of the frequency range between 26 and 28 kHz in AAF, our recordings appear to have sampled the frequency range between 2 and 30 kHz with some uniformity in all three fields. It is important to note that because our probe placements were not distributed evenly across each field, these CF distributions reflect the characteristics of our sample, and not necessarily the characteristics of fields themselves.
Figure 5.
A greater proportion of units in AAF and A1 have defined characteristic frequencies (CFs) than in PAF. A single CF defined the FRAs of most units, although multi-peaked FRAs were not uncommon, particularly in AAF. An example of a multi-peaked AAF unit can be seen in the middle panels of Figure 1. Top: the proportion of units with undefined CFs is indicated by the bars at Number of Peaks = 0. The other bars indicate the proportions of units having from 1 to 4 CFs. Bottom: distributions of primary CF (i.e., the CF with the lowest threshold), smoothed with a 0.5-octave-wide rectangular window. The slightly higher median CF in A1 is caused by an almost complete absence of A1 units with CFs below 2 kHz.
Spatial sensitivity assessed by spike count variation
We characterized each unit’s spatial tuning by constructing rate-azimuth (RAF) and rate-elevation functions. These functions represent a unit’s average response rate as a function of stimulus location and can be used to derive an estimate of the unit’s preferred location or centroid—i.e., the location to which it responds with the greatest response rate. Distributions of centroids, the spike-count-weighted center of mass of the function’s peak response, are plotted in Figure 6 and Figure 7 for azimuth and elevation, respectively, for stimuli presented at 20 (bottom) and 40 dB (top) above threshold.
Figure 6.
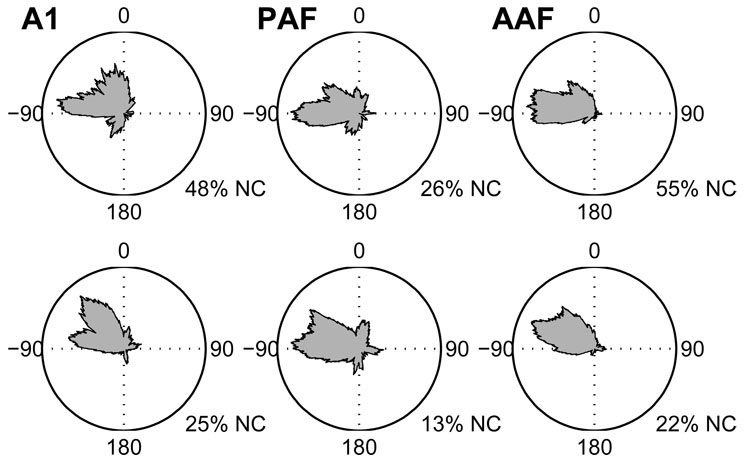
Distributions of azimuth centroids for stimuli presented 20 (bottom) and 40 dB (top) above unit threshold. Distributions are plotted from an overhead perspective with 0° being directly in front of the animal, 180° being directly behind, and −90° and +90° indicating locations to the animal’s left and right, respectively. In each field, fewer units had defined centroids at 40 than 20 dB above threshold. The percentage of units with no centroid (NC) is given under each plot. Note, however, that whereas only 45 and 52% of AAF and A1 units had defined centroids at the higher SPL, respectively, 74% of PAF units did.
Figure 7.
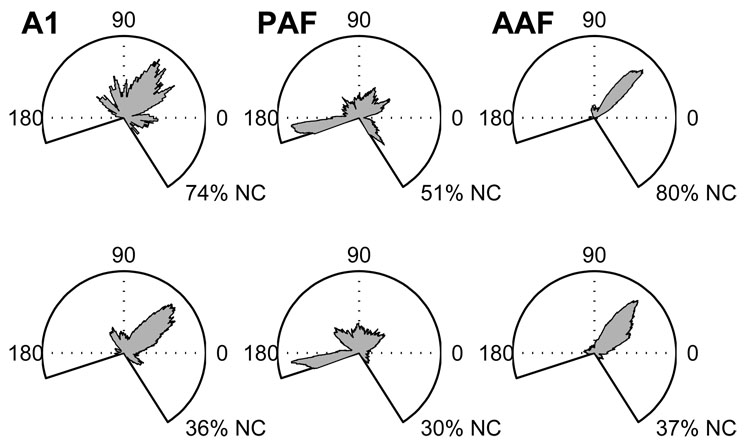
Distributions of elevation centroids for stimuli presented 20 (bottom) and 40 dB (top) above unit threshold. In the elevation plots, the perspective is from the side with 0° being directly in front of the animal, 180° being directly behind, and +90° being directly above. Similar to the situation observed for azimuth centroids, only 20 and 26% of AAF and A1 units had defined centroids at the higher SPL, respectively, compared to 49% of PAF units. The percentage of units with no centroid (NC) is given under each plot.
Distributions of azimuth centroids were biased toward the contralateral hemifield in all three fields, with a more extreme bias in AAF and PAF than in A1. At the lower SPL, azimuth centroids clustered near the acoustic axis of the contralateral ear, where the acoustic gain of the external ear is maximal (Middlebrooks and Pettigrew 1981). At the higher SPL, centroids were closer to the lateral pole. At 20 dB above threshold, the median centroid locations in AAF, A1, and PAF were −54.3°, −38.3°, and −55.9° azimuth, respectively. At 40 dB above threshold, the median centroid locations were −70.4°, −49.9°, and −63.3°, respectively. Centroids were undefined when the spike count failed to fall below 50% of its maximum value at any location. Overall, 57% of AAF units had an undefined centroid at one or the other level, compared to 50% of A1 units and 28% of PAF units. Moreover, 20% of AAF units had undefined centroids at both levels, compared to 22% of A1 units and only 12% of PAF units. At 20 dB above threshold, azimuth centroids were undefined for a similar proportion of units in all three fields (AAF 22%, A1 25%, PAF 13%). At 40 dB above threshold, however, azimuth centroids were undefined for a majority (55%) of AAF units, a near majority (48%) of A1 units, but only 26% of units in PAF.
The observation that the median of each field’s centroid distribution shifted between 7.4° (PAF) and 16.1° (AAF) deeper into the contralateral hemifield with increasing SPL need not indicate that the centroids of individual units were consistently shifted toward more lateral locations. Plotted in the main panel of Figure 8 are the locations of each unit’s centroid at 20 and 40 dB above threshold, for those units having defined centroids at both levels. Only 43% of AAF units (255/588) met this criterion, compared to 50% of A1 (188/378) and 72% of PAF units (318/441). Data points on or near the marked diagonal indicate a close correspondence between centroids at the two levels. Although many points fell away from the diagonal, they were as likely to fall above the diagonal as below it, indicating no consistent unit-by-unit shift of azimuth centroids with increasing level. However, it should be noted that centroids rarely shifted across the midline from one lateral hemifield to the other. With the dense clustering of centroids in the anterior half of the contralateral hemifield, the limitation imposed by the midsagittal plane would permit a greater range of lateral than medial shifts in centroid locations, accounting for the 7.5−16° lateral shifts in the medians of the centroid distributions with increasing level. Centroids were far less likely to be defined at the higher than the lower level. This is evident in the right and top panels of Figure 8, which plot the locations of centroids for units lacking centroids at either 20 or 40 dB, respectively. In AAF, 35% of units had a defined centroid at 20 but not at 40 dB above threshold, compared to 26% of A1 and 15% of PAF units. Very few units (<2%) in any field had centroids that were defined at 40 dB but not 20 dB (Figure 8, right panel).
Figure 8.
Plotted in the main panel are the locations of azimuth centroids at 20 and 40 dB above threshold for units where these were defined at both levels. Data points on or near the diagonal indicate a close correspondence between centroids at the two levels. The paucity of data points within the top-left and bottom-right quadrants indicates that centroids rarely shifted from one lateral hemifield to the other with changing level, suggesting that most units maintained at least their basic tuning properties. In the top panel are the centroid locations of those units having centroids at 20 but not 40 dB above threshold. In the right panel are the centroid locations of those units having centroids at 40 but not 20 dB above threshold. There are no data points obscured by the figure legend.
Rate-elevation functions were measured for sound sources in the vertical midline plane (Figure 7). Most elevation centroids in A1 and AAF were located above the horizontal plane, with a majority of units responding most robustly to sounds ~50° above the frontal horizon. That upward bias generally corresponds to the location of the acoustic axis of the pinna. The distribution of elevation centroids in PAF was more uniform. As was the case in azimuth, a higher percentage of units in AAF (80%) and A1 (75%) had undefined centroids at higher SPLs than was observed in PAF (51%).
Spike counts at higher SPLs were poorly modulated in AAF and A1
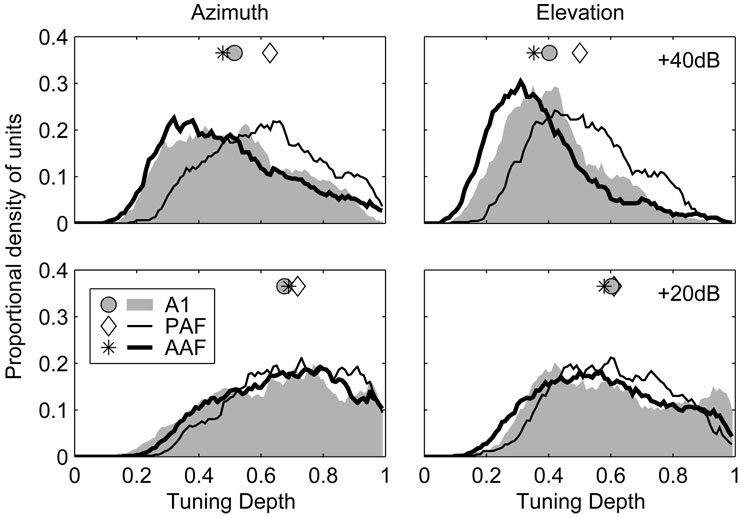
The observation that fewer AAF and A1 units had defined centroids at higher SPLs can be attributed to a reduction of spike-count modulation at those levels—a reduction evident when spatial tuning depths are compared at 20 and 40 dB above threshold. The spatial tuning depth reflects the proportional reduction of the normalized spike count across azimuth or elevation and is calculated for each unit as Cmax−Cmin separately at each level. Distributions of azimuth- and elevation-based spatial tuning depths are plotted at 20 and 40 dB above threshold in Figure 9. In azimuth at 20 dB above threshold, the median spatial tuning depth in AAF (0.69) did not differ from that in A1 (0.68, p = 0.2) or PAF (0.72, p = 0.06), although the difference between A1 and PAF did achieve significance (p = 0.03). Overall, this indicates that the spike count dropped to at least ~30% of its maximum value at some location for over half of the units in each field. At 40 dB above threshold, however, tuning depths were significantly reduced in all three fields (p < 0.0002). The median spatial tuning depth in AAF (0.48) was significantly lower than in A1 (0.52, p = 0.03) and PAF (0.63, p < 0.0002), and lower in A1 than PAF (p < 0.0002). The median change in spatial tuning depth with increasing SPL, calculated separately for each unit, was −0.16, −0.11, and −0.07 in AAF, A1 and PAF, respectively (AAF > AI > PAF, p < 0.0004). This indicates that the unit-by-unit reduction in tuning depth with increasing SPL was largest in AAF and smallest in PAF. A similar pattern was observed in elevation, where the median tuning depths at 20 and 40 dB above threshold were 0.58 and 0.35 in AAF, 0.60 and 0.40 in A1, and 0.61 and 0.50 in PAF.
Figure 9.
Unit responses in AAF and A1 are less strongly modulated by changes in stimulus location than in PAF, particularly at higher stimulus levels. Plotted are distributions of spatial tuning depth in azimuth (left) and elevation (right) for stimuli presented 20 (bottom) and 40 dB (top) above threshold. Symbols represent the median of each distribution.
Given their inverse relationship, it is not surprising that as spatial-tuning depths decreased with increasing SPL, spatial-tuning widths increased. The spatial tuning width reflects the range of locations that elicit a robust response, specifically, a response within 50% of the maximum response. Distributions of azimuth- and elevation-based tuning widths are plotted at 20 and 40 dB above threshold in Figure 10. Tuning widths in each field generally were broad, particularly at higher SPLs. The median azimuth-based tuning widths at 20 and 40 dB above threshold were 256° and 360° in AAF, compared to 278° and 356° in A1, and 242° and 308° in PAF. At the lower level, tuning widths were broader in A1 than in AAF or PAF (p < 0.02). The difference between AAF and PAF was not significant (p = 0.1). At the higher level, the median spatial tuning width was broadest in AAF and narrowest in PAF (AAF vs. A1, p = 0.03, A1 and AAF vs. PAF, p < 0.0002). At least half of the units in AAF had tuning widths that equaled the maximum possible width of 360°; that follows from the median spatial tuning depth in AAF being <0.5. The median unit-by-unit increase in tuning width with increasing SPL was largest in AAF (53.2°), intermediate in A1 (27.2°), and smallest in PAF (21.4°) (AAF > A1 and PAF, p < 0.0002, A1 = PAF, p < 0.2). A similar pattern of results was also seen in elevation. The median spatial tuning widths in elevation at 20 and 40 dB above threshold were 245° and 260° in AAF, 235° and 260° in A1, and 233° and 260° in PAF. The fact that the median tuning width was at or close to its maximum possible value (260°) in each field demonstrates how broadly units are tuned in this dimension at both tested SPLs.
Figure 10.
Units in AAF and A1 have broader spatial tuning than units in PAF, particularly at higher SPLs. Plotted are distributions of spatial tuning width in azimuth (left) and elevation (right) for stimuli presented 20 (bottom) and 40 dB (top) above threshold. Symbols represent the median of each distribution.
Spatial tuning was less level tolerant in AAF and A1 than PAF
The results just described indicate that the responses of many units, particularly in AAF and A1, exhibit poor tolerance of increasing SPL. When RAFs are compared at 20 and 40 dB above threshold, for example, the responses of many AAF and A1 units appear to be modulated as much, if not more, by changes in stimulus level than stimulus location. This poor level tolerance would present a challenge to a spatial code based on spike counts because counts are as strongly affected by variation in the nuisance dimension (level) as the dimension of interest (location). Indeed, the effectiveness of a conventional rate code would be extremely limited when levels are free to vary and unknown to the animal (Stecker et al. 2005b).
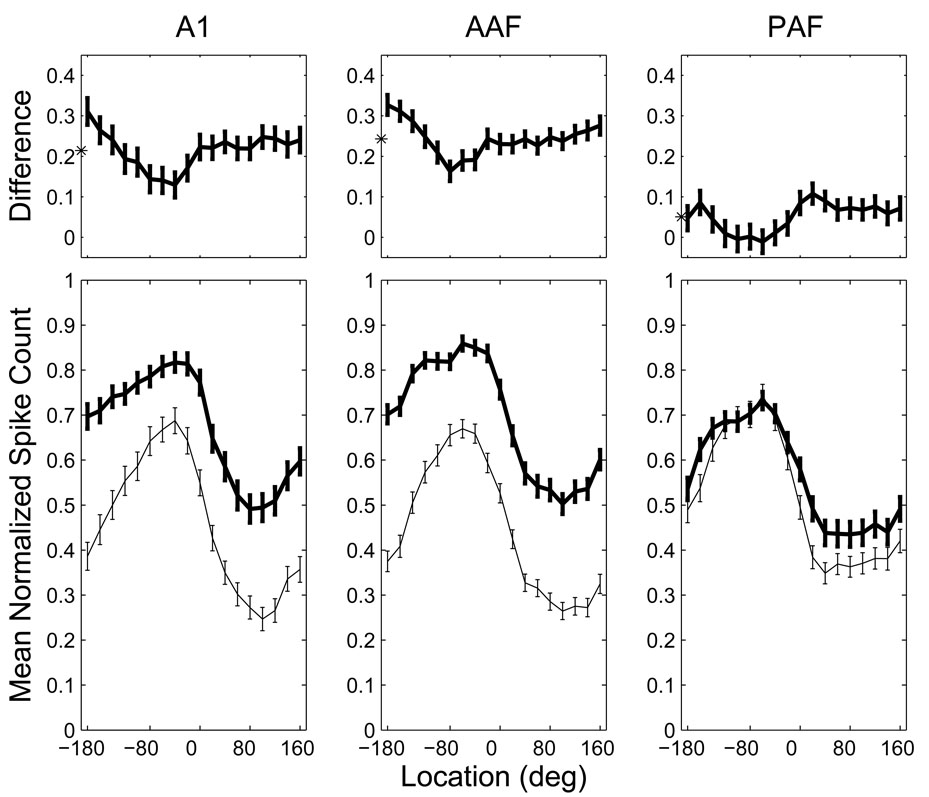
To better characterize this problem, we derived normalized, grand-mean RAFs for contralaterally tuned units in each neural population. For each unit having a defined azimuth centroid at 20 dB above threshold located between −10° and −170° (i.e., at least 10° into the contralateral hemifield), we determined the mean spike count at each combination of stimulus location and level. From our original populations, 360 AAF units, 198 A1 units, and 240 PAF units satisfied these criteria for inclusion. For each unit, these spike counts were then normalized by the maximum mean spike count across all locations and both levels to give the proportion of the unit’s overall, maximum response. Each population’s RAFs were then formed from the grand mean of these unit-normalized RAFs at each level (Figure 11, bottom).
Figure 11.
Population rate-azimuth functions in AAF and A1 are more adversely affected by increases in SPL than those in PAF. Bottom: normalized, grand-mean RAFs for each population at 20 (thin line) and 40 dB (thick line) above threshold. In AAF and A1, these RAFs were almost completely non-overlapping. Top: the difference between the population RAFs at the two levels illustrates the tendency for significant increases in responsiveness and decreases in response modulation at higher SPLs in AAF and A1, but not PAF. The asterisks indicate the mean difference between the RAFs at the two SPLs. Error bars represent 95% confidence intervals of the mean.
Population RAFs were then subjected to analysis of variance (ANOVA) with area (AAF, A1 and PAF), location (−180 to 160 in 20° steps) and SPL (20 and 40 dB above threshold) as factors. There were significant effects of SPL and location (p < 0.001) indicating that population response rates were affected by variation in each factor. The effect of SPL was not uniform across locations or areas (p < 0.001), and the significant interaction between the three factors (p < 0.001) indicates that the effects of SPL and location were not equivalent across the three cortical fields. As can be seen in Figure 11, when the stimulus level was increased from 20 to 40 dB above threshold, the population RAFs of AAF and A1 shifted upwards and were somewhat flattened (i.e., the spatial tuning depth was reduced). In PAF, on the other hand, the effect of increasing level was negligible throughout most of contralateral space and minimal, though apparent, throughout ipsilateral space.
To specifically characterize the interaction between location and level in each area, we then analyzed the difference between the RAFs at each level (Figure 11, top). The magnitude of the level effect was location dependant with smaller effects observed near the peak of each population RAF. Most importantly, there was a significant effect of area on the magnitude of this level effect (p < 0.001), with the largest effect in AAF (0.24) and the smallest effect in PAF (0.05). The difference in the level effect between AAF and A1 (0.24 vs. 0.21), though modest, was statistically significant (p = 0.03); the differences between PAF and the other fields were highly significant (p < 0.001). These results indicate a much higher degree of level-tolerance in PAF than in the other two fields, with the poorest level-tolerance in AAF.
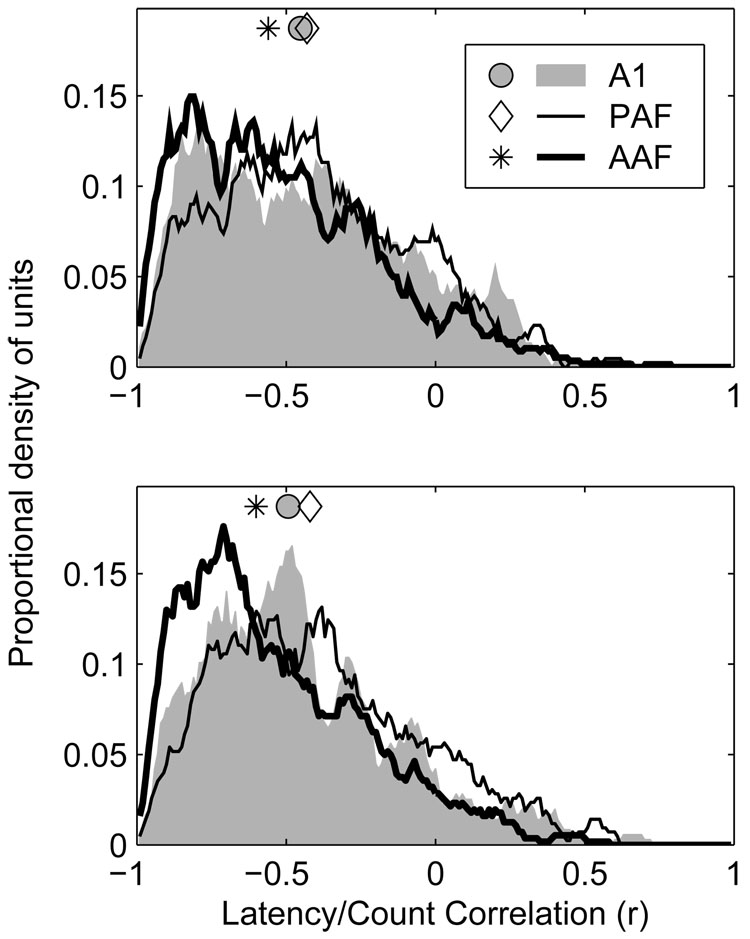
Spike counts and latencies are most strongly correlated in AAF
Changes in stimulus azimuth produced changes in the first-spike latencies of units as well as changes in their spike counts. Generally, stimuli that produced greater spike counts produced shorter latencies. For that reason, one might expect a close correspondence between a unit’s rate azimuth function (RAF) and latency azimuth function (LAF) (see Figure 1 for examples of RAFs and LAFs). To quantify this relationship, we determined the correlation coefficient for the relationship between C (the normalized mean spike count) and L (the geometric mean first spike latency) across all azimuths, separately at each level. This coefficient could range from −1 (when C and L had a perfect inverse relationship) to +1 (when C and L had a perfect positive relationship). The expected correspondence between C and L described above would predict a relationship close to −1. Distributions of latency/count correlation at 20 and 40 dB above threshold are plotted in the lower and upper panels of Figure 12, respectively.
Figure 12.
Rate- and latency-based spatial representations are more highly correlated in AAF and A1, than in PAF. Plotted are distributions of correlation coefficients between rate- (RAF) and latency-azimuth functions (LAF) of units in each population at 20 (bottom) and 40 dB (top) above threshold. Symbols represent the median of each distribution.
In a majority of cases, a negative correlation was observed between the stimulus dependence of a unit’s spike count and latency, supporting the expectation that locations that produce higher spike counts also produce shorter latencies, while those that produce lower spike counts produce longer latencies. At 20 and 40 dB above threshold, however, the median correlation coefficients observed in AAF (−0.60 at +20 dB, −0.56 at +40 dB) were more extreme than those observed in either A1 (−0.49 at +20 dB, −0.45 at +40 dB) or PAF (−0.42 at +20 dB, −0.43 at +40 dB) (p < 0.0002). The difference between A1 and PAF was significant at 20 dB (p = 0.004), but not 40 dB (p = 0.2) above threshold. This suggests that although the response latencies of units in AAF may be more strongly modulated by stimulus location than those of units in A1, any information conveyed by this modulation of response latency is likely to be redundant with, though perhaps supportive of, that conveyed by modulation of spike count. This can be contrasted with the situation in PAF where, in some cases, spike count and latency may represent independent dimensions for the coding of spatial and other forms of information (Stecker et al. 2003). Although the correlation coefficients observed in A1 and PAF were similar, particularly at the higher SPL, the underlying explanations are likely quite different. This is because correlation coefficients fail to distinguish situations where both response features are strongly modulated but do not co-vary, as is the case in PAF, from those in which one feature (i.e., spike count) is modulated but the other (i.e., spike latency) is not, as is the case in A1 (see Stecker et al. 2003, Figure 3).
Units in AAF and A1 are less spatially informative than units in PAF
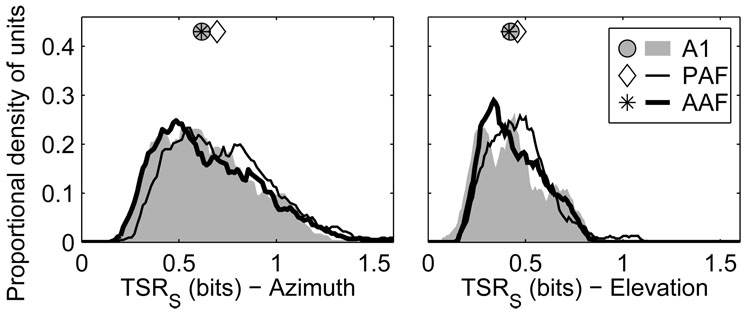
We used a pattern-recognition algorithm to quantify the information about sound-source location transmitted by stimulus-dependent characteristics of spike patterns, including spike count, first-spike latency, and any other stimulus-related features (Furukawa and Middlebrooks 2002; Furukawa et al. 2000; Middlebrooks et al. 1994, 1998; Stecker et al. 2003, 2005a). The pattern recognition algorithm was first used to estimate the spatial information transmitted by complete neural responses. Spike density functions (SDFs) were formed from training- and test-set halves of the data by averaging a subset of responses at each location (see Methods). The algorithm then compared each SDF in the test set to each SDF in the training set to determine which pair had the greatest similarity. On each permutation of the test, the location corresponding to the training-set SDF that was most similar to the particular test-set SDF became the algorithm’s “response”. The more consistent and unique the SDFs were for each location, the greater the likelihood that the algorithm would select the appropriate location as the one most likely to have elicited the particular response. The classifications of the algorithm were expressed as probabilities in joint stimulus-response matrices from which estimates of partial and total stimulus related information (TSR) were derived (Furukawa and Middlebrooks 2002).
When full spike patterns were used (Figure 13), units in AAF and A1 transmitted less azimuth information than did units in PAF (p < 0.0004). The median TSR in AAF was 0.61 bits, compared to 0.58 and 0.68 bits in A1 and PAF, respectively. Field PAF had a slightly higher percentage of units that transmitted >1 bit of information: 14.5% of PAF units compared to 10% of AAF units and 8.5% of A1 units (PAF vs. A1 or AAF, p < 0.0002; AAF vs. A1, p = 0.3). The situation was similar in elevation, with units in AAF (0.41 bits) and A1 (0.42 bits) transmitting less information than units in PAF (0.45 bits) (AAF vs. A1, p = 0.3; PAF vs. A1 and AAF, p = 0.006). Few units transmitted more than 1 bit of elevation-related information in any field.
Figure 13.
Units in AAF and A1 transmit less information about the locations of sound sources than in PAF. Plotted are distributions of total stimulus-related information (TSR) transmitted by neural responses for azimuth (left) and elevation (right) when full spike patterns were used. Symbols represent the median of each distribution.
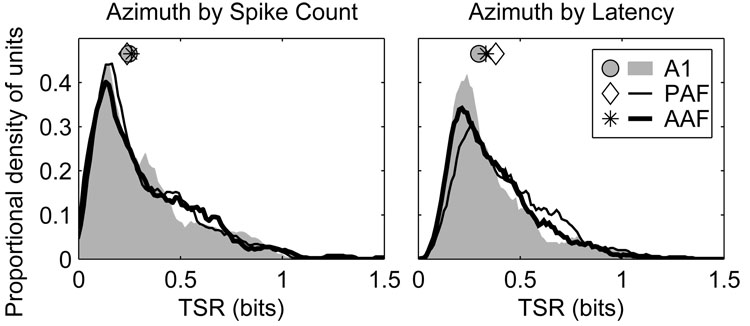
Transmission of stimulus-related information by uni-dimensional spike counts or latencies were quantified by classifying those values using a pattern-recognition algorithm similar to that used for full spike patterns (Figure 14). When spike counts alone were evaluated there were no significant differences between any of the fields (AAF 0.26 bits, A1 0.25 bits, PAF 0.24 bits, p > 0.2). When response latencies were evaluated, however, units in PAF (0.38 bits) transmitted more information than units in either AAF (0.33 bits) or A1 (0.30 bits) (p < 0.002). Units in AAF were slightly more informative than those in A1 (p = 0.02)—an observation consistent with the slightly greater spatial modulation of response latency observed in AAF than A1.
Figure 14.
The responses of units in AAF and A1 transmit less azimuth information using first-spike latency than in PAF. Plotted are distributions of total stimulus-related information (TSR) transmitted by neural responses reduced to spike counts (left) and first-spike latencies (right). Symbols represent the median of each distribution.
DISCUSSION
In summary, the responses of units in the anterior auditory field (AAF) were often similar to those of units in the primary field (A1) and, together with that field, were quite distinct from those observed in the posterior auditory field (PAF). Specifically, in AAF and A1, first-spike latencies were shorter and more poorly modulated by stimulus location, rate-level functions were more highly monotonic, FRAs were generally marked by one or two well-defined frequency-tuning peaks, rate- and latency-azimuth functions were highly correlated, and spatial-tuning widths and depths were adversely affected by increasing stimulus levels. In fact, spike counts in AAF and A1 were modulated as much, if not more, by changes in stimulus level as stimulus location. These similarities notwithstanding, there were several differences between AAF and A1. In AAF, response latencies were shorter but exhibited more trial-to-trial variability, FRAs were more likely to be multi-peaked, spatial tuning was more adversely affected by increasing SPL, and location-specific spike counts and latencies showed higher mutual correlation. In PAF, on the other hand, first-spike latencies were longer and more strongly modulated by stimulus location, rate-level functions were less strongly monotonic, CFs were less easily identified from FRAs, and rate- and latency-azimuth functions were less strongly correlated and far more tolerant of increasing SPL. The responses of units in AAF and A1 also transmitted somewhat less spatial information, on average, than units in PAF, particularly when inputs to the pattern-recognition algorithm were restricted to first-spike latencies alone. Nevertheless, units in AAF and A1 did transmit some information about the spatial locations of sound sources. In the discussion that follows, we begin by relating the current observations to previous reports, and then consider the possible roles of these fields in the auditory behavior of the cat.
First-spike latencies are slightly shorter in AAF than A1, and considerably shorter in both fields than in PAF
In response to broadband noise, units in our AAF population begin to respond just 15.3 ms after stimulus onset or, after correcting for the 3.5 ms of travel time from the speaker to the ear, 11.8 ms after the sounds began to be transduced by the cochlea. The median first-spike latencies observed in A1 and PAF were 12.5 and 20.4 ms after stimulus transduction, respectively. For AAF and A1, these latencies are similar to those described in earlier reports (Eggermont 1998; Imaizumi et al. 2004; Knight 1977; Phillips and Irvine 1982). Differences between the response latencies of units in AAF and A1, although not apparent in the reports of Knight (1977) or Phillips and Irvine (1982), were evident in later reports particularly when broadband and/or impulsive stimuli were used (Eggermont 1998) or when comparisons were restricted to units with lower CFs (Imaizumi et al. 2004). The observed first-spike latencies in PAF were likewise comparable to those reported previously (Phillips and Orman 1984). The present study provides additional evidence that first-spike latencies in AAF are slightly, though significantly, shorter than those in A1, and considerably shorter in AAF and A1 than PAF.
Units in AAF and A1 are less sensitive to changes in stimulus location, particularly at higher SPLs
The highly monotonic rate-level functions of units in AAF and A1 might have compromised their ability to represent the locations of sound sources in a level-tolerant manner. By most measures, including spatial-tuning widths and depths, units in AAF and, to a lesser extent, A1, were less well tuned for auditory space than units in PAF, particularly at higher stimulus levels. The responses of our AAF units were similar to those described by Korte and Rauschecker (1993) in their study comparing spatial tuning in normal and blind-reared cats. The spatial-tuning depths they reported were similar to those observed in the present study and their units appeared to have the same problems with level tolerance as were observed in our study. In our sample of units, as the stimulus level was increased from 20 to 40 dB above threshold, the average increase in spatial-tuning width and the average decrease in spatial-tuning depth were largest in AAF and smallest in PAF. In fact, at 40 dB above threshold the median tuning width in AAF equaled the maximum possible tuning width of 360°, indicating that >50% of units responded with at least half-maximal spike counts to all source azimuths. The adverse effects of increasing SPL on spatial tuning in AAF and A1 can also be seen in those fields’ population rate-azimuth functions (Figure 11). Not only were these RAFs flattened at higher SPLs, an observation consistent with the reductions in tuning depths just noted, but the spatial-modulation of spike count evident within a sound level was often equaled or exceeded by the level-modulation of spike count seen within a source location. This stands in marked contrast to the situation in PAF where not only was the spatial modulation of spike count similar at both tested levels, but the overall effect of stimulus level on response rates was negligible, particularly in the contralateral hemifield.
AAF and A1 units are only slightly less spatially informative than PAF units
Despite the adverse effects of increasing SPL on the spatial-tuning properties of units in AAF and A1, units in both fields transmitted only slightly less information on average than units in PAF when network classifications were based on full-spike patterns. Units in all three fields transmitted a similar amount of information when the algorithm operated on spike counts alone, and transmitted more information when the algorithm operated on first-spike latencies alone than spike counts alone. The fact that units in AAF and A1 transmitted only slightly less information than units in PAF when classifications were based on first-spike latencies was particularly interesting given the poorer modulation of this response feature in the two former fields. Across units, the average spatial modulation of response latency (ΔL) was 3.01 and 3.65 ms in A1 and AAF, respectively, and 10.77 ms in PAF. Despite having almost 3 times the modulation of response latency in PAF than AAF, the average PAF unit transmitted only 0.05 bits (i.e., 1.15 times) more azimuth information than the average AAF unit (0.38 vs. 0.33 bits, respectively) based on latency alone.
There are several factors that have likely contributed to the relatively small differences in information transmission observed between these fields. One factor involves our use of general anesthesia. Responses tend to be more diverse in the awake cortex than under α-chloralose anesthesia, with various combinations of onset, sustained, suppressive, and offset responses appearing against a background of spontaneous and task-dependant activity (see Mickey & Middlebrooks 2003, Figure 4). Indeed, given recent observations that the tuning properties of cortical neurons are sensitive to the demands of the behavioral task in which the animal is engaged (e.g., Fritz et al. 2003; 2005; Lee et al., 2006), further study of awake and behaving animals might reveal even greater differences between cortical fields.
A second factor is that although there is less between-location latency variation in AAF and A1 than in PAF, there is also less trial-to-trial within-location latency variance. In order to be an effective information-bearing feature, the amount of neural response variation between two (or more) stimuli need only be greater than the amount of variation within each of the two (or more) stimuli. Although the mean FSLs of PAF units show considerably more spatial modulation, when this temporal modulation is normalized by the trial-to-trial variability or “jitter” of response latencies, the differences between PAF and the other fields become more modest. In their study of temporal variability, Heil and Irvine (1998) observed that whereas the least variable 75% of A1 units had <1 ms of jitter (i.e., the standard deviation of first-spike latencies), the least variable 75% of PAF units had only <10 ms of jitter (Heil and Irvine 1998). Our findings are in agreement with those of Heil and Irvine (1998). In our sample, the best 75% of A1 units have <3.5 ms of jitter, compared to <10.3 ms for PAF and <4.3 ms for AAF. Compared to the responses observed in AAF and A1, therefore, those in PAF are more temporally delayed, modulated, and variable.
These observations raise an important question: If the location of a sound source can be represented with reasonable accuracy when first-spike latencies are modulated by as little as 3 ms, why should units in PAF increase their latency modulation to 10 ms or more? Furthermore, what is gained when this increased latency modulation is accompanied by a corresponding increase in the variability of first-spike latencies? One possibility is that the elongated latencies in PAF reflect putative intra-cortical mechanisms that enhance the temporal overlap of cortical responses to simultaneous auditory, visual, and somatosensory stimuli. Post-stimulus latencies in primary cortical areas tend to be longer in the visual and somatosensory cortices than in the auditory cortex. Indeed, the responses of units in A1 and AAF are complete long before they even begin in the primary visual cortex (Ouellette & Casanova 2006). In addition to the multimodal interactions known to occur within the superior colliculus (e.g., Meredith and Stein 1983, 1986; King and Palmer 1985), the delayed and more temporally modulated responses of fields like PAF might facilitate multi-sensory interactions at the cortical level by promoting temporal binding.
Do AAF and A1 operate independently?
Given the similarities of AAF and A1—e.g., similar thalamic inputs, response latencies, and tonotopic organization—it was suggested early on that the two fields “…are virtually mirror images of one another…” and that they might be involved in “…processing acoustic information in a parallel manner rather than in a hierarchical manner” (Knight 1977). Although Phillips and Irvine (1982) agreed that the two fields were simultaneously activated by sound and could therefore be said to operate in parallel, it was then unknown whether the two fields operated independently by virtue of receiving segregated inputs from their shared thalamic sources, or concurrently on common thalamic inputs (e.g., branched collaterals). The answer to this question has been provided by more recent anatomical studies that not only demonstrate that the thalamic sources of the two fields differ to some degree, but that the vast majority of projections from common thalamic regions arise from distinct neural populations (Lee et al. 2004a). Moreover, recent physiological evidence (e.g., this study; Imaizumi et al. 2004) demonstrates that beneath their superficial similarities, the response properties of units in AAF and A1 differ in some important respects. For example, stimulus-related activity begins sooner in AAF than A1, the representation of the cochlear partition is more complete and uniform in A1 than AAF, and FRAs are more likely to be multi-peaked in AAF than A1 proper (Imaizumi et al. 2004; present study). But despite anatomical evidence of their largely independent thalamocortical inputs and physiological evidence of differences in their responses properties, an important question remains: For what, if anything, are these fields specialized?
Functional specializations within the auditory cortex of the cat
Although each of the fields described in this report receives robust input from the ventral division of the MGB, and moderate input from the medial division of the MGB, each also receives input from some combination of its dorsal divisions (Huang & Winer 2000). These differences in thalamocortical projections, combined with the physiological differences described here and in earlier reports (e.g., Imaizumi et al. 2004; Knight 1977; Phillips and Irvine 1981; Phillips and Orman 1984; Stecker et al. 2003), suggest that these fields might play different roles in cortical processing and auditory behavior.
One approach to the identification of functional specializations within the cortex is to look for behavioral deficits following the surgical ablation or reversible deactivation of particular cortical areas (see Lomber 1999). Given the somewhat enhanced spatial sensitivity of units in PAF and DZ (Stecker et al. 2003, 2005a), for example, one might expect these fields to be necessary for sound-localization behavior. On the other hand, given the comparatively poor representation of auditory space in AAF and evidence that units in AAF show some selectivity for the rate and direction of frequency modulation (Tian and Rauschecker 1994) and are able to follow amplitude modulation to considerably higher frequencies than units in other fields including A1 and PAF (Schreiner and Urbas 1988), one might expect this field to be necessary for the identification and/or discrimination of complex sounds. In a recent study, cats were tested for the ability to perform a sound-localization or temporal-pattern-discrimination task before, during, and after the cryogenic deactivation of either AAF or PAF (Lomber and Malhotra 2003). Consistent with the expectations outlined above, the ability to perform the localization task was adversely affected by the deactivation of PAF but not AAF, whereas performance of the temporal pattern discrimination task was affected by the deactivation of AAF but not PAF. In addition, deactivation of A1 and DZ, either separately or in combination, has also been shown to result in localization deficits (Malhotra et al. 2004, in press).
As was already noted, although units in PAF and DZ tend to be more spatially informative than units in fields not necessary for sound-localization behavior (e.g., AAF), the differences between these fields are modest at best (Stecker and Middlebrooks 2003; Stecker et al. 2003, 2005a). It is somewhat surprising that deactivation of A1, whose spatial sensitivity is more comparable to that of AAF than either PAF or DZ, produces such complete localization deficits (Lomber and Malhotra 2003). One possibility is that the deficits observed following the deactivation of certain cortical fields (e.g., A1) might reveal less about that field’s inherent response properties, than the specializations of its downstream targets (Middlebrooks et al., 2002; Stecker et al., 2005b). In other words, some auditory cortical fields may only be specialized insofar as the fields to which they distribute their outputs are specialized.
Field A1 projects strongly to PAF (Rouiller et al. 1991), so one might imagine that localization deficits following A1 inactivation reflect elimination of critical input to PAF. This interpretation is complicated, however, by demonstrations that PAF receives independent thalamic input from sources similar to those that target A1 (Huang and Winer 2000), and, likely by virtue of these inputs, that many basic responses properties of units in PAF are unchanged following the ablation of ipsilateral A1 (Kitzes and Hollrigel 1996). We have proposed elsewhere (Stecker and Middlebrooks 2003) that the responses of A1 units might provide an effective temporal reference against which the first-spike latencies of PAF units might be read out. Inactivation of A1 might eliminate a time stamp that is needed for readout of the information carried by PAF latencies, thereby resulting in deficits in localization behavior. In fact, if A1 was providing such a time stamp, its poorly modulated and low-variability first-spike latencies could be seen as an asset rather than a liability (Stecker and Middlebrooks 2003).
Why is spatial information so ubiquitous in the auditory cortex?
One final question to be addressed is why some level of spatial tuning has been observed in every auditory cortical field studied so far. We have argued previously (Middlebrooks et al. 2002) that spatial cues can enhance every auditory task, regardless of whether that task requires the overt localization of a sound source or not. For instance, spatial cues contribute strongly to spatial release from informational masking and to spatial stream segregation (e.g., Shinn-Cunningham 2005). One indication that AAF units might use spatial cues for a non-localization function comes from ongoing studies in our laboratory of spatial stream segregation (J. C. Middlebrooks, E. A. Macpherson, & C-.C. Lee, unpublished observations). We find AAF units that show striking evidence of spatial stream segregation even in cases in which there is essentially no modulation of responses by the location of a single sound source. In this instance, the spatial sensitivity of units in AAF is a means to an end—the segregation of (spatially disparate) acoustic streams—rather than the end itself as it might be in PAF. We are confident that future studies will demonstrate the contribution of spatial sensitivity to various cortical fields in their specialized roles in sound localization and in the interpretation of communication and other environmental sounds.
ACKNOWLEDGMENTS
The authors would like to thank Zekiye Onsan for technical and administrative support, Chen-Chung Lee for assistance in data collection, and Chen-Chung Lee and Kevin Otto for helpful discussions of these results and for comments on an earlier version of this manuscript.
SUPPORT Funding was provided by the National Institute on Deafness and Other Communication Disorders (NIDCD: R01 DC-00420, P30 DC-05188, F32-DC-006113, T32 DC-00011, and R03 DC-006809), and by the National Science Foundation (NSF: DBI-0107567). Probes were provided by the University of Michigan Center for Neural Communication Technology (CNCT: NIBIB P41 EB002030).
Abbreviations and symbols used
- ΔC
spatial modulation of normalized mean spike count
- ΔL
median latency range across all azimuths
- A1
primary auditory cortex
- A2
second auditory field
- AAF
anterior auditory field
- AEG
anterior ectosylvian gyrus
- ANOVA
analysis of variance
- C
normalized mean spike count
- CF
characteristic frequency
- DZ
dorsal zone
- FRA
frequency response area
- FSL
first spike latency
- L
geometric mean first spike latency
- MΩ
mega-ohms
- MEG
middle ectosylvian gyrus
- MGB
medial geniculate body
- NC
no centroid
- PAF
posterior auditory field
- RAF
rate-versus-azimuth function
- RLF
rate-versus-level function
- SDF
spike density function
- SPL
sound pressure level
- TSR
total stimulus-related spatial information
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- Anderson DJ, Najafi K, Tanghe SJ, Evans DA, Levy KL, Hetke JF, Xue XL, Zappia JJ, Wise KD. Batch-fabricated thin-film electrodes for stimulation of the central auditory system. IEEE Trans Biomed Eng. 1989;36:693–704. doi: 10.1109/10.32101. [DOI] [PubMed] [Google Scholar]
- Eggermont JJ. Representation of spectral and temporal sound features in three cortical fields of the cat: Similarities outweigh differences. J Neurophysiol. 1998;80:2743–2764. doi: 10.1152/jn.1998.80.5.2743. [DOI] [PubMed] [Google Scholar]
- Fritz J, Shamma S, Elhilali M, Klein D. Rapid task-related plasticity of spectrotemporal receptive fields in primary auditory cortex. Nat Neurosci. 2003;6:1216–1223. doi: 10.1038/nn1141. [DOI] [PubMed] [Google Scholar]
- Fritz JB, Elhilali M, Shamma SA. Differential dynamic plasticity of A1 receptive fields during multiple spectral tasks. J Neurosci. 2005;25:7623–7635. doi: 10.1523/JNEUROSCI.1318-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furukawa S, Middlebrooks JC. Cortical representation of auditory space: information-bearing features of spike patterns. J Neurophysiol. 2002;87:1749–1762. doi: 10.1152/jn.00491.2001. [DOI] [PubMed] [Google Scholar]
- Furukawa S, Middlebrooks JC. Sensitivity of auditory cortical neurons to locations of signals and competing noise sources. J Neurophysiol. 2001;86:226–240. doi: 10.1152/jn.2001.86.1.226. [DOI] [PubMed] [Google Scholar]
- Furukawa S, Xu L, Middlebrooks JC. Coding of sound-source location by ensembles of cortical neurons. J Neurosci. 2000;20:1216–1228. doi: 10.1523/JNEUROSCI.20-03-01216.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh J, Nag A. An overview of radial basis function networks. In: Howlett RJ, Jain LC, editors. Radial Basis Function Networks 2: New Advances in Design. Amsterdam: Physica-Verlag; 2001. pp. 1–36. [Google Scholar]
- He J, Hashikawa T. Connections of the dorsal zone of cat auditory cortex. J Comp Neurol. 1998;300:334–348. doi: 10.1002/(sici)1096-9861(19981026)400:3<334::aid-cne4>3.0.co;2-9. [DOI] [PubMed] [Google Scholar]
- Heil P, Irvine DR. Functional specialization in auditory cortex: responses to frequency-modulated stimuli in the cat's posterior auditory field. J Neurophysiol. 1998;79:3041–3059. doi: 10.1152/jn.1998.79.6.3041. [DOI] [PubMed] [Google Scholar]
- Huang CL, Winer JA. Auditory thalamocortical projections in the cat: laminar and areal patterns of input. J Comp Neurol. 2000;427:302–331. doi: 10.1002/1096-9861(20001113)427:2<302::aid-cne10>3.0.co;2-j. [DOI] [PubMed] [Google Scholar]
- Imaizumi K, Priebe NJ, Crum PAC, Bedenbaugh PH, Cheung SW, Schreiner CE. Modular functional organization of cat anterior auditory field. J Neurophysiol. 2004;92:444–457. doi: 10.1152/jn.01173.2003. [DOI] [PubMed] [Google Scholar]
- Imig TJ, Irons WA, Samson FR. Single-unit selectivity to azimuthal direction and sound pressure level of noise bursts in cat high-frequency primary auditory cortex. J Neurophysiol. 1990;63:1448–1466. doi: 10.1152/jn.1990.63.6.1448. [DOI] [PubMed] [Google Scholar]
- Jenkins WM, Masterton RB. Sound localization: effects of unilateral lesions in central auditory system. J Neurophysiol. 1982;47:987–1016. doi: 10.1152/jn.1982.47.6.987. [DOI] [PubMed] [Google Scholar]
- Jenkins WM, Merzenich MM. Role of cat primary auditory cortex for sound-localization behavior. J Neurophysiol. 1984;52:819–847. doi: 10.1152/jn.1984.52.5.819. [DOI] [PubMed] [Google Scholar]
- King AJ, Palmer AR. Integration of visual and auditory information in bimodal neurones in the guinea-pig superior colliculus. Exp Brain Res. 1985;60:492–500. doi: 10.1007/BF00236934. [DOI] [PubMed] [Google Scholar]
- Kitzes LM, Hollrigel GS. Response properties of units in the posterior auditory field deprived of input from the ipsilateral primary auditory cortex. Hear Res. 1996;100:120–130. doi: 10.1016/0378-5955(96)00103-7. [DOI] [PubMed] [Google Scholar]
- Knight PL. Representation of the cochlea within the anterior auditory field (AAF) of the cat. Brain Res. 1977;130:447–467. doi: 10.1016/0006-8993(77)90108-1. [DOI] [PubMed] [Google Scholar]
- Korte M, Rauschecker JP. Auditory spatial tuning of cortical neurons is sharpened in cats with early blindness. J Neurophysiol. 1993;70:1717–1721. doi: 10.1152/jn.1993.70.4.1717. [DOI] [PubMed] [Google Scholar]
- Lee C-C, Macpherson EA, Harrington IA, Middlebrooks JC. Task-dependence of spatial sensitivity in the dorsal zone (area DZ) of cat auditory cortex. Assoc Res Otolaryngol Abs. 2007;425 doi: 10.1152/jn.00104.2005. [DOI] [PubMed] [Google Scholar]
- Lee CC, Imaizumi K, Schreiner CE, Winer JA. Concurrent tonotopic processing streams in auditory cortex. Cereb Cortex. 2004a;14:441–451. doi: 10.1093/cercor/bhh006. [DOI] [PubMed] [Google Scholar]
- Lee CC, Schreiner CE, Imaizumi K, Winer JA. Tonotopic and heterotopic projection systems in physiologically defined auditory cortex. Neuroscience. 2004b;128:871–887. doi: 10.1016/j.neuroscience.2004.06.062. [DOI] [PubMed] [Google Scholar]
- Lee CC, Winer JA. The distributed auditory cortex. Hear Res. 2007;229:3–13. doi: 10.1016/j.heares.2007.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loftus WC, Sutter ML. Spectrotemporal organization of excitatory and inhibitory receptive fields of cat posterior auditory field neurons. J Neurophysiol. 2001;86:475–491. doi: 10.1152/jn.2001.86.1.475. [DOI] [PubMed] [Google Scholar]
- Lomber SG. The advantages and limitations of permanent or reversible deactivation techniques in the assessment of neural function. J Neurosci Methods. 1999;86:109–117. doi: 10.1016/s0165-0270(98)00160-5. [DOI] [PubMed] [Google Scholar]
- Lomber SG, Malhotra S. Society for Neuroscience. New Orleans, LA: 2003. Double dissociation of “what” and “where” processing in auditory cortex. [DOI] [PubMed] [Google Scholar]
- Malhotra S, Lomber SG. Sound localization during homotopic and heterotopic bilateral cooling deactivation of primary and non-primary auditory cortical areas in the cat. J Neurophysiol. 2007;97:26–43. doi: 10.1152/jn.00720.2006. [DOI] [PubMed] [Google Scholar]
- Malhotra S, Hall AJ, Lomber SG. Cortical control of sound localization in the cat: unilateral cooling deactivation of 19 cerebral areas. J Neurophysiol. 2004;92:1625–1643. doi: 10.1152/jn.01205.2003. [DOI] [PubMed] [Google Scholar]
- Malhotra S, Stecker GC, Middlebrooks JC, Lomber SG. Sound localization deficits during reversible deactivation of primary auditory cortex and/or the dorsal zone. J Neurophysiol. doi: 10.1152/jn.01228.2007. in press. [DOI] [PubMed] [Google Scholar]
- Masterton RB, Imig TJ. Neural mechanisms for sound localization. Annu Rev Physiol. 1984;46:275–287. doi: 10.1146/annurev.ph.46.030184.001423. [DOI] [PubMed] [Google Scholar]
- Meredith MA, Stein BE. Interactions among converging sensory inputs in the superior colliculus. Science. 1983;221:389–391. doi: 10.1126/science.6867718. [DOI] [PubMed] [Google Scholar]
- Meredith MA, Stein BE. Visual, auditory, and somatosensory convergence on cells in superior colliculus results in multisensory integration. J Neurophysiol. 1986;56:640–662. doi: 10.1152/jn.1986.56.3.640. [DOI] [PubMed] [Google Scholar]
- Merzenich MM, Knight PL, Roth GL. Representation of cochlea within primary auditory cortex in the cat. J Neurophysiol. 1975;38:231–249. doi: 10.1152/jn.1975.38.2.231. [DOI] [PubMed] [Google Scholar]
- Mickey BJ, Middlebrooks JC. Representation of auditory space by cortical neurons in awake cats. J Neurosci. 2003;23:8649–8663. doi: 10.1523/JNEUROSCI.23-25-08649.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks JC, Zook JM. Intrinsic organization of the cat’s medial geniculate body identified by projections to binaural response-specific bands in the primary auditory cortex. J Neurosci. 1983;3:203–224. doi: 10.1523/JNEUROSCI.03-01-00203.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks JC, Clock AE, Xu L, Green DM. A panoramic code for sound location by cortical neurons. Science. 1994;264:842–844. doi: 10.1126/science.8171339. [DOI] [PubMed] [Google Scholar]
- Middlebrooks JC, Harrington IA, Macpherson EA, Stecker GC. Sound localization and the auditory cortex. In: Dallos P, Oertel D, editors. The Senses: A Comprehensive Review (Audition) London: Academic Press; 2007. [Google Scholar]
- Middlebrooks JC, Pettigrew JD. Functional classes of neurons in primary auditory cortex of the cat distinguished by sensitivity to sound location. J Neurosci. 1981;1:107–120. doi: 10.1523/JNEUROSCI.01-01-00107.1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Middlebrooks JC, Xu L, Eddins AC, Green DM. Codes for sound-source location in nontonotopic auditory cortex. J Neurophysiol. 1998;80:863–881. doi: 10.1152/jn.1998.80.2.863. [DOI] [PubMed] [Google Scholar]
- Middlebrooks JC, Xu L, Furukawa S, Macpherson EA. Cortical neurons that localize sounds. Neuroscientist. 2002;8:73–83. doi: 10.1177/107385840200800112. [DOI] [PubMed] [Google Scholar]
- Morel A, Imig TJ. Thalamic projections to fields A, AI, P, and VP in the cat auditory cortex. J Comp Neurol. 1987;265:119–144. doi: 10.1002/cne.902650109. [DOI] [PubMed] [Google Scholar]
- Neff WD, Fisher JF, Diamond IT, Yela M. Role of auditory cortex in discrimination requiring localization of sound in space. J Neurophysiol. 1956;19:500–512. doi: 10.1152/jn.1956.19.6.500. [DOI] [PubMed] [Google Scholar]
- Ouellette BG, Casanova C. Overlapping visual response latency distributions in visual cortices and LP-pulvinar complex of the cat. Exp Brain Res. 2006;175:332–341. doi: 10.1007/s00221-006-0555-y. [DOI] [PubMed] [Google Scholar]
- Phillips DP, Irvine DR. Responses of single neurons in physiologically defined primary auditory cortex (AI) of the cat: frequency tuning and responses to intensity. J Neurophysiol. 1981;45:48–58. doi: 10.1152/jn.1981.45.1.48. [DOI] [PubMed] [Google Scholar]
- Phillips DP, Irvine DR. Properties of single neurons in the anterior auditory field (AAF) of cat cerebral cortex. Brain Res. 1982;248:237–244. doi: 10.1016/0006-8993(82)90581-9. [DOI] [PubMed] [Google Scholar]
- Phillips DP, Orman SS. Responses of single neurons in posterior field of cat auditory cortex to tonal stimulation. J Neurophysiol. 1984;51:147–163. doi: 10.1152/jn.1984.51.1.147. [DOI] [PubMed] [Google Scholar]
- Phillips DP, Semple MN, Kitzes LM. Factors shaping the tone level sensitivity of single neurons in posterior field of cat auditory cortex. J Neurophysiol. 1995;73:674–686. doi: 10.1152/jn.1995.73.2.674. [DOI] [PubMed] [Google Scholar]
- Reale RA, Imig TJ. Tonotopic organization in auditory cortex of the cat. J Comp Neurol. 1980;192:265–291. doi: 10.1002/cne.901920207. [DOI] [PubMed] [Google Scholar]
- Rouiller EM, Simm GM, Villa AE, de Ribaupierre Y, de Ribaupierre F. Auditory corticocortical interconnections in the cat: evidence for parallel and hierarchical arrangement of the auditory cortical areas. Exp Brain Res. 1991;86:483–505. doi: 10.1007/BF00230523. [DOI] [PubMed] [Google Scholar]
- Schreiner CE, Urbas JV. Representation of amplitude modulation in the auditory cortex of the cat. II. Comparison between cortical fields. Hear Res. 1988;32:49–63. doi: 10.1016/0378-5955(88)90146-3. [DOI] [PubMed] [Google Scholar]
- Shinn-Cunningham BG. Influences of spatial cues on grouping and understanding sound; Proceedings of the Forum Acusticum; 2005. [Google Scholar]
- Stecker GC, Harrington IA, Macpherson EA, Middlebrooks JC. Spatial sensitivity in the dorsal zone (area DZ) of cat auditory cortex. J Neurophysiol. 2005a;94:1267–1280. doi: 10.1152/jn.00104.2005. [DOI] [PubMed] [Google Scholar]
- Stecker GC, Harrington IA, Middlebrooks JC. Location coding by opponent neural populations in the auditory cortex. PLoS Biol. 2005b;3:e78. doi: 10.1371/journal.pbio.0030078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stecker GC, Mickey BJ, Macpherson EA, Middlebrooks JC. Spatial sensitivity in field PAF of cat auditory cortex. J Neurophysiol. 2003;89:2889–2903. doi: 10.1152/jn.00980.2002. [DOI] [PubMed] [Google Scholar]
- Stecker GC, Middlebrooks JC. Distributed coding of sound locations in the auditory cortex. Biol Cybern. 2003;89:341–349. doi: 10.1007/s00422-003-0439-1. [DOI] [PubMed] [Google Scholar]
- Sutter ML, Schreiner CE. Physiology and topography of neurons with multipeaked tuning curves in cat primary auditory cortex. J Neurophysiol. 1991;65:1207–1226. doi: 10.1152/jn.1991.65.5.1207. [DOI] [PubMed] [Google Scholar]
- Tian B, Rauschecker JP. Processing of frequency-modulated sounds in the cat’s anterior auditory field. J Neurophysiol. 1994;71:1959–1975. doi: 10.1152/jn.1994.71.5.1959. [DOI] [PubMed] [Google Scholar]
- Wasserman PD. Advanced methods in neural computing. New York: Van Nostrand Reinhold; 1993. [Google Scholar]
- Xu L, Middlebrooks JC. Individual differences in external-ear transfer functions of cats. J Acoust Soc Am. 2000;107:1451–1459. doi: 10.1121/1.428432. [DOI] [PubMed] [Google Scholar]
- Zhou B, Green DM, Middlebrooks JC. Characterization of external ear impulse responses using Golay codes. J Acoust Soc Am. 1992;92:1169–1171. doi: 10.1121/1.404045. [DOI] [PubMed] [Google Scholar]