Abstract
A long-standing goal in evolutionary biology is to identify the conditions that promote the evolution of reproductive isolation and speciation. The factors promoting sympatric speciation have been of particular interest, both because it is notoriously difficult to prove empirically and because theoretical models have generated conflicting results, depending on the assumptions made. Here, we analyze the conditions under which selection favors the evolution of assortative mating, thereby reducing gene flow between sympatric groups, using a general model of selection, which allows fitness to be frequency dependent. Our analytical results are based on a two-locus diploid model, with one locus altering the trait under selection and the other locus controlling the strength of assortment (a “one-allele” model). Examining both equilibrium and nonequilibrium scenarios, we demonstrate that whenever heterozygotes are less fit, on average, than homozygotes at the trait locus, indirect selection for assortative mating is generated. While costs of assortative mating hinder the evolution of reproductive isolation, they do not prevent it unless they are sufficiently great. Assortative mating that arises because individuals mate within groups (formed in time or space) is most conducive to the evolution of complete assortative mating from random mating. Assortative mating based on female preferences is more restrictive, because the resulting sexual selection can lead to loss of the trait polymorphism and cause the relative fitness of heterozygotes to rise above homozygotes, eliminating the force favoring assortment. When assortative mating is already prevalent, however, sexual selection can itself cause low heterozygous fitness, promoting the evolution of complete reproductive isolation (akin to “reinforcement”) regardless of the form of natural selection.
UNDERSTANDING the conditions that give rise to new species is one of the oldest and most intriguing questions in evolutionary biology (Darwin 1859). There is a general consensus that spatially separated populations can diverge through time to the point where previously separated individuals become unable to mate and/or to produce fit progeny should they come into contact. This divergence can be driven by natural or sexual selection or can arise stochastically via random genetic drift. While genetic divergence is inevitable among isolated populations (allopatric speciation; e.g., Orr and Orr 1996), it can also arise when individuals are arrayed across a spatial landscape without strict barriers to migration, as long as the selective forces leading to local adaptation and divergence are stronger than the opposing forces of migration and recombination (parapatric speciation; e.g., Gavrilets et al. 1998, 2000; Doebeli and Dieckmann 2003). By contrast, there is a great deal of debate about the importance of sympatric speciation, whereby divergence occurs in situ, without any substantial degree of spatial isolation. Several models demonstrate that sympatric speciation is possible given the right combination of disruptive selection, mating preferences, and genetic variation (e.g., Dieckmann and Doebeli 1999; Kondrashov and Kondrashov 1999; Doebeli and Dieckmann 2000; see reviews by Kirkpatrick and Ravigné 2002; Gavrilets 2003, 2004). The core of the debate centers on exactly where the boundary delineating the “right” combination of parameters lies. This boundary has been difficult to determine both because of the large number of possible parameters and alternative scenarios and because the majority of studies of speciation in sexual populations are numerical. Here, we develop and analyze a two-locus diploid model of speciation, where one locus affects a trait subject to frequency-dependent or -independent selection and the second modifies the degree of assortative mating with respect to the trait locus. Using a combination of analytical techniques, we determine exactly when speciation is possible and when it is not.
We refer the reader to recent reviews of speciation (Turelli et al. 2001; Kirkpatrick and Ravigné 2002; Gavrilets 2003, 2004; Coyne and Orr 2004) and provide only a brief background to place this work in context.
As described by Felsenstein (1981), there are two classes of speciation models: “one-allele” and “two-allele” (see also Endler 1977). This classification refers to the genetic change required to turn a randomly mating population into two species. In one-allele models, the spread of a single allele throughout the population is sufficient to cause reproductive isolation. For example, the allele might increase the tendency to remain within particular habitats (e.g., Maynard Smith 1966; Balkau and Feldman 1973) or the tendency to mate assortatively with respect to a phenotype under selection [e.g., Maynard Smith 1966; Felsenstein's (1981) “D” locus; Dieckmann and Doebeli's (1999) “mating character”]. An example of such a one-allele mechanism acting to increase the degree of assortative mating was recently found in sympatric populations of Drosophila pseusoobscura and D. persimilis (Ortíz-Barrientos and Noor 2005). In two-allele models, different alleles (say M1 and M2) must establish in each of the nascent species for reproductive isolation to arise. For example, if individuals mate assortatively with respect to the M1 and M2 alleles, then reproductive isolation will result if each allele becomes established in a different subgroup of the population [e.g., Udovic 1980; Felsenstein's (1981) “A” locus; Dieckmann and Doebeli's (1999) “marker character”; Doebeli 2005]. Alternatively, if the M1 and M2 alleles alter female preferences, then reproductive isolation will result if each allele becomes established in the subgroup containing the preferred male (e.g., Higashi et al. 1999; Kondrashov and Kondrashov 1999; Doebeli 2005).
Speciation is more difficult in two-allele models because the two alleles must remain associated with their subgroups, which is hampered when recombination breaks down linkage disequilibrium between the locus bearing the two alleles and loci responsible for the trait differences between the subgroups. Only if selection and assortative mating are sufficiently strong and/or linkage between the loci sufficiently tight will speciation ensue (Felsenstein 1981). By contrast, one-allele models are more conducive to speciation, because they are not as sensitive to the development of disequilibria and, hence, to the rate of recombination (Felsenstein 1981).
In this article, we limit our attention to a one-allele diploid model and ask under what conditions can a modifier allele, M, spread if it increases the strength of assortative mating. Alleles at the modifier locus “M” tune the degree of assortment, which can range from zero in a random-mating population to one with complete reproductive isolation. Exactly who mates with whom is based on the strength of assortment (controlled by the M locus) and by who appears similar to whom (based on a locus A). Locus A is assumed to be polymorphic and to affect a trait subject to natural selection; for simplicity, we call this the trait locus. This scenario, where the trait locus A forms the basis of assortative mating and is subject to selection, is particularly conducive to sympatric speciation (a so-called “magic” trait, e.g., Gavrilets 2004; Schneider and Bürger 2006). If separate traits controlled these functions, recombination would tend to disassociate them, rendering speciation more difficult (Felsenstein 1981; Gavrilets 2004). It should thus be kept in mind that we are considering a class of models that is most likely to lead to sympatric speciation.
Three analytical studies have recently investigated the evolution of assortative mating, using modifier models similar to the one investigated here (Matessi et al. 2001; de Cara et al. 2008; Pennings et al. 2008). For brevity, we have summarized the key differences between the models in Table 1, providing references in the text to related results from these studies, as appropriate. Although our study focuses only on one trait locus (unlike de Cara et al. 2008), focusing on a single-trait locus allows us to explore a broad array of forms of assortative mating and to consider both strong and weak selection, modifiers of strong and weak effect, and arbitrary costs.
TABLE 1.
Comparison between current and related models
| This study | Matessi et al. (2001) | Pennings et al. (2008) | de Cara et al. (2008) | |
|---|---|---|---|---|
| No. of selected loci | One | One | One | Arbitrary |
| Method of analysis | Stability and QLEa | Stability | Stability | QLE |
| Form of selection on trait | General | Quadratic frequency dependence | Gaussian competition | General |
| Dynamics of trait allele | Equilibrium or changing | Equilibrium | Equilibrium | Equilibrium |
| Frequency at trait locus | General | 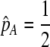 |
General (focus on 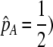
|
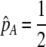 |
| Form of assortment | Preference based or group based | Preference based | Preference based or neutralizedb | Preference based or neutralizedb |
| Preference function | General | General (focus on Gaussianc) | General (focus on Gaussianc) | General (focus on Gaussian or quadraticc) |
| Sexual selection | Present or absent | Present | Present or absent | Present or absent |
| Costs of assortment | General | General | Absent | Strong (plant model) or absent (neutralizedb) |
These studies focus on a trait that is subject to natural selection and that forms the basis of assortative mating, the strength of which is determined by a modifier locus.
QLE denotes a “quasi-linkage equilibrium” analysis, which assumes that genetic associations equilibrate faster than allele frequencies change. We use the term QLE even when considering genetic associations, such as the departure from Hardy–Weinberg, that do not involve “linkage.”
To eliminate sexual selection, these articles consider a “neutralized” model of preference-based assortative mating, where females mate preferentially but then the mating success of all genotypes is equalized (not necessarily for each sex separately, but across both sexes).
With one locus, a Gaussian preference function is a particular form of matrix (3), where 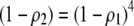 , while a quadratic preference function sets
, while a quadratic preference function sets 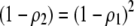 .
.
The main strength of this article is that we allow the nature of selection acting on the trait locus A to be completely general: fitnesses may be constant or frequency dependent, and selection may be directional (favoring the spread of one allele) or balancing (maintaining a polymorphism). Frequency-dependent selection is commonly considered in speciation models because it can, under the right circumstances, generate disruptive selection while maintaining a polymorphism. Frequency-dependent selection arises under a wide variety of different circumstances: for example, when individuals compete for resources, when predators more readily detect common genotypes, when pathogens more readily infect previously common genotypes, when pollinators prefer common genotypes (or unusual ones), or when females mate preferentially with common males (or unusual ones). Density-dependent selection can also be approximated using a model of frequency-dependent selection if one assumes that population size dynamics equilibrate rapidly relative to the timescale of selection, in which case the fitness of each genotype rapidly approaches a constant value given the current genotypic frequencies. Many speciation models have focused on specific causal mechanisms that give rise to frequency- or density-dependent natural selection; such specific models are helpful in clarifying the ecological conditions that facilitate speciation, but they are less general in scope and can obscure the fundamental processes driving the evolution of assortment.
As we shall see, the evolution of some amount of assortative mating within an initially random-mating population occurs when (a) selection is directional and the average fitness of homozygotes is greater than heterozygotes or (b) there is a polymorphic equilibrium at which selection is disruptive, with heterozygotes less fit than either homozygote. Furthermore, any costs of assortative mating must be sufficiently weak that they do not overpower the benefit of assortative mating that lies in the reduced frequency of heterozygotes among descendants. Potential costs of assortative mating include the energetic costs of searching for appropriate mates, the risk of rejecting all potential mates and remaining unmated, the costs of mechanisms permitting perception of mate similarity, and the fitness costs of mating at a suboptimal time or place to mate with similar individuals. The magnitude of these costs may or may not depend on the composition of the population; for example, search costs should decline as the relative frequency of compatible mates increases (a “relative” cost), but mechanistic costs should remain the same (a “fixed” cost).
Even when costs of assortment are sufficiently weak, sexual selection complicates the picture and can prevent the evolution of strong assortment. As described more fully below, models of assortative mating may or may not induce sexual selection on the A locus (Gavrilets 2003, 2004). Sexual selection raises two distinct obstacles in models of speciation (Kirkpatrick and Nuismer 2004). First, sexual selection can induce directional selection at the selected loci, leading to the loss of the trait polymorphism that is required for assortment to evolve. And, second, sexual selection can cause disruptive selection to become stabilizing (in our model, altering whether homozygotes or heterozygotes are more fit), eliminating the selective benefit of assortative mating. The reverse is also possible, however, and sexual selection itself can induce disruptive selection and facilitate the speciation process (Verzijden et al. 2005). We describe the conditions under which sexual selection blocks or facilitates the evolution of higher levels of assortative mating.
We turn now to a description of the model, followed by the key results of two different types of analysis: a quasi-linkage equilibrium (QLE) analysis and a local stability analysis. Because these approaches require different assumptions, the joint results provide a more complete picture of how and when assortative mating evolves in response to selection at a single gene.
MODEL
We develop a two-locus diploid model where one locus, A, is subject to selection and determines the similarity of potential mates and a second modifier locus, M, alters the strength of assortative mating, ρ. Recombination occurs between the two loci at rate r. The key question that we address is whether modifier alleles altering the level of ρ can invade a population. If so, we wish to know the conditions under which high levels of assortative mating might evolve (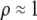 ), thereby generating substantial reproductive isolation among genotypes.
), thereby generating substantial reproductive isolation among genotypes.
Our model is similar to that of Udovic (1980) in assuming that the A locus is subject to frequency-dependent selection of an arbitrary nature, with fitnesses of the three diploid genotypes (AA, Aa, and aa) given by the functions
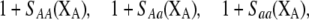 |
(1) |
where 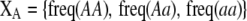 is the vector of genotypic frequencies at the A locus and the Si are selection coefficients that depend on these frequencies. The fitness functions are assumed constant over time, so that the fitness of an individual remains the same as long as the genotypic frequencies remain constant but may change as the genotypic frequencies evolve. We use Equation 1 to derive a number of results without specifying the exact nature of the fitness functions.
is the vector of genotypic frequencies at the A locus and the Si are selection coefficients that depend on these frequencies. The fitness functions are assumed constant over time, so that the fitness of an individual remains the same as long as the genotypic frequencies remain constant but may change as the genotypic frequencies evolve. We use Equation 1 to derive a number of results without specifying the exact nature of the fitness functions.
We investigate the conditions under which alleles increasing the degree of assortment spread at the modifier locus. We define assortative mating broadly as any mechanism that makes it more likely for individuals to mate with genotypically similar individuals. There is a plethora of ways that such assortment can be accomplished, and we investigate two classes of models: “group-based” and “preference-based.”
Group-based model:
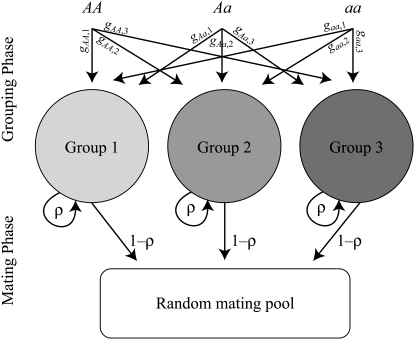
The first class of assortment models is based on group membership (O'Donald 1960; Felsenstein 1981). We assume that each individual is a member of a group; females mate within their group with probability ρ, choosing randomly among the males within the group, and otherwise mate with a male chosen randomly from the entire population. Groupings might be spatial (e.g., genotypes prefer different host plants) or temporal (e.g., individuals release pollen or are most active at different times of day). Grouping might also occur by self-referent phenotype matching (Hauber and Sherman 2001) if phenotypically similar individuals tend to aggregate together. Specifically, we consider three groups, whose composition is based on the genotype at the A locus, such that individuals of genotype i join group j with probability 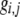 (Figure 1), where
(Figure 1), where  . The model can also be applied to the case where only two groups form by setting
. The model can also be applied to the case where only two groups form by setting  for one of the three groups. Assortative mating is most efficient when each genotype forms its own group (
for one of the three groups. Assortative mating is most efficient when each genotype forms its own group (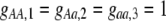 ), which we refer to as “genotypic grouping.” We assume that any unmated females and all males join a random-mating pool, which for brevity we call a “lek.” For example, the probability that a female of genotype AA mates with a male of genotype Aa is
), which we refer to as “genotypic grouping.” We assume that any unmated females and all males join a random-mating pool, which for brevity we call a “lek.” For example, the probability that a female of genotype AA mates with a male of genotype Aa is
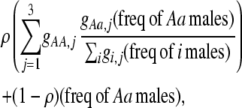 |
(2) |
where i sums over the three genotypes 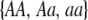 . The first term accounts for the probability that an AA female is in a particular group, j, and mates with an Aa male within her group, while the last term accounts for mating within the random-mating pool.
. The first term accounts for the probability that an AA female is in a particular group, j, and mates with an Aa male within her group, while the last term accounts for mating within the random-mating pool.
Figure 1.—
Grouping model of assortative mating. A population is structured into groups, wherein mating occurs randomly with probability ρ. Assortative mating results because different genotypes at locus A have different probabilities of joining the different groups. Following the period of assortative mating, we assume that all unmated females mate at random by choosing mates at times or places where each genotype is proportionately represented (e.g., in flight rather than on a host plant, during a swarming period, or in a lek). We assume that all individuals are a part of some group, although they may or may not mate within their group.
Alleles at the modifier locus alter the probability that a female mates within her group according to
 |
Modifier alleles that increase ρ strengthen the degree of assortative mating because individuals that mate within their group are more likely to mate with a genetically similar individual at the A locus. In appendix a, we consider two variants to this core model: (1) males that mate within the group do not join the lek, and (2) the groups and the lek form simultaneously, with individuals joining one or the other.
In the grouping model, females pay no inherent costs for mating assortatively because each female is guaranteed an equal chance of mating, either within her group or within the lek. To this basic model, we add two potential costs of assortative mating. One is a fixed cost, 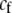 , paid by females that mate within their group, which is paid regardless of the size of the group. A fixed cost might arise if mating within the group is risky or suboptimal (e.g., before the optimal time in the season for mating). A second relative cost,
, paid by females that mate within their group, which is paid regardless of the size of the group. A fixed cost might arise if mating within the group is risky or suboptimal (e.g., before the optimal time in the season for mating). A second relative cost, 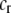 , is added that depends on the frequency of the group. We assume that the density of mates within a group scales with the frequency of that group, so that females have an easier time encountering mates in groups that are well populated. Specifically, the fitness of a female is multiplied by a factor,
, is added that depends on the frequency of the group. We assume that the density of mates within a group scales with the frequency of that group, so that females have an easier time encountering mates in groups that are well populated. Specifically, the fitness of a female is multiplied by a factor, 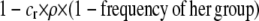 , which falls from 1 to 1 −
, which falls from 1 to 1 − 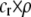 as mates become scarcer (i.e., as the frequency of her group falls from 1 toward 0). This relative cost represents the additional time and energy needed to find a mate within a group containing few individuals. We assume that the relative cost of assortment declines linearly as the frequency of the group rises. The cost of restricting mating to within a group might, however, be negligible unless group size is very small. Cost functions that decline more rapidly toward zero as the frequency of the group rises would be more conducive to the evolution of assortative mating than the linear cost function explored here.
as mates become scarcer (i.e., as the frequency of her group falls from 1 toward 0). This relative cost represents the additional time and energy needed to find a mate within a group containing few individuals. We assume that the relative cost of assortment declines linearly as the frequency of the group rises. The cost of restricting mating to within a group might, however, be negligible unless group size is very small. Cost functions that decline more rapidly toward zero as the frequency of the group rises would be more conducive to the evolution of assortative mating than the linear cost function explored here.
Preference-based model:
In the second type of model considered, females prefer to mate with certain males over others, according to a preference matrix
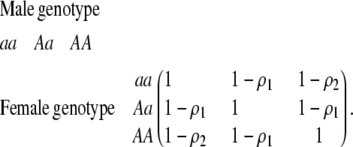 |
(3) |
The terms 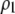 and
and 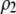 measure the degree to which a female dislikes males that differ by one allele and two alleles, respectively. We measure the relative ability of a female to distinguish males that differ by one vs. two alleles, using
measure the degree to which a female dislikes males that differ by one allele and two alleles, respectively. We measure the relative ability of a female to distinguish males that differ by one vs. two alleles, using 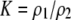 . The ρ terms are assumed to be positive (or zero) and to depend on the female's genotype at the modifier locus (e.g., MM females dislike males that differ by two alleles by an amount
. The ρ terms are assumed to be positive (or zero) and to depend on the female's genotype at the modifier locus (e.g., MM females dislike males that differ by two alleles by an amount 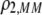 ). In the text, we focus on assortative mating using the symmetrical preference matrix (3), but the results for a general preference matrix are analogous and are presented in appendix b.
). In the text, we focus on assortative mating using the symmetrical preference matrix (3), but the results for a general preference matrix are analogous and are presented in appendix b.
Each female encounters a male and chooses to mate with him with a probability equal to the appropriate entry in matrix (3). For example, consider an encounter involving a female of genotype AA at the trait locus and genotype k at the modifier locus (k = MM, Mm, or mm). The probability that the encounter is with a male of genotype Aa and results in mating is 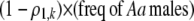 . Summed over all possible types of males, the overall probability that an AA female of modifier genotype k accepts a male during a mating encounter is
. Summed over all possible types of males, the overall probability that an AA female of modifier genotype k accepts a male during a mating encounter is
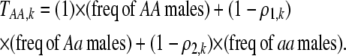 |
(4) |
If a female rejects a male, she may or may not be able to recuperate the lost mating opportunity. To account for this potential cost, we assume that a fraction of the time, 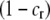 , a female is able to recover the fitness lost by rejecting a dissimilar mate, and otherwise she suffers a loss in fitness. The overall chance that a female of trait genotype AA and modifier genotype k mates (which we refer to as her “fertility”) is then
, a female is able to recover the fitness lost by rejecting a dissimilar mate, and otherwise she suffers a loss in fitness. The overall chance that a female of trait genotype AA and modifier genotype k mates (which we refer to as her “fertility”) is then 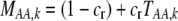 , which is reduced below one to the extent that the female is choosy. This cost of assortative mating is relative; even a very picky female suffers no loss in fertility if every male encountered is similar.
, which is reduced below one to the extent that the female is choosy. This cost of assortative mating is relative; even a very picky female suffers no loss in fertility if every male encountered is similar.
To be concrete, the overall fraction of matings between a female of genotype i at the trait locus and k at the modifier locus and a male of genotype j at the trait locus is
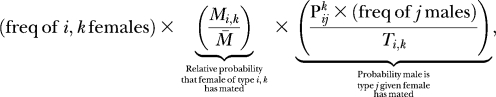 |
(5) |
where 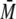 is the average fertility of females,
is the average fertility of females,
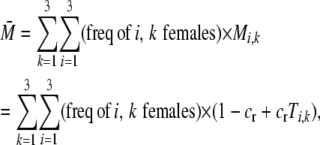 |
and 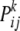 refers to the entry in the ith row and the jth column of matrix (3) for females of genotype k at the modifier locus.
refers to the entry in the ith row and the jth column of matrix (3) for females of genotype k at the modifier locus.
When relative costs are absent (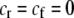 ), all females have equal fertility. This special case has been called the “animal” model of assortment (Kirkpatrick and Nuismer 2004), a reference to animals with lek-based mating systems where the cost of searching for a different mate is presumed negligible. In contrast, when lost mating opportunities are never recovered (
), all females have equal fertility. This special case has been called the “animal” model of assortment (Kirkpatrick and Nuismer 2004), a reference to animals with lek-based mating systems where the cost of searching for a different mate is presumed negligible. In contrast, when lost mating opportunities are never recovered (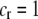 ), the fertility of females of genotype i relative to the average fertility,
), the fertility of females of genotype i relative to the average fertility, 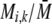 , becomes
, becomes 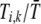 , which is less than one if type i, k females reject more males than other females. This special case was described by Moore (1979) and has been called the “plant” model of assortment (Kirkpatrick and Nuismer 2004); it is appropriate for plants that are pollen limited (or animals that are limited by mating opportunities), such that any tendency to reject pollen (males) directly reduces fertility.
, which is less than one if type i, k females reject more males than other females. This special case was described by Moore (1979) and has been called the “plant” model of assortment (Kirkpatrick and Nuismer 2004); it is appropriate for plants that are pollen limited (or animals that are limited by mating opportunities), such that any tendency to reject pollen (males) directly reduces fertility.
We also allowed for a fixed cost of assortment, 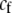 , which is paid by choosy females regardless of the types of males encountered. Specifically, the fitness of a female of genotype k at the modifier locus was multiplied by a fixed factor,
, which is paid by choosy females regardless of the types of males encountered. Specifically, the fitness of a female of genotype k at the modifier locus was multiplied by a fixed factor, 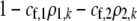 .
.
A critical feature of the preference-based model is that it induces strong sexual selection on the A locus. The mating scheme embodied in matrix (3) selects against rare genotypes (positive frequency-dependent selection) because the most common females prefer males with their own genotype. In contrast, the grouping model ensures that everybody gets an equal “kick-at-the-bucket” (each individual belongs to one and only one group, and the number of receptive females per male is the same in each group) and so induces little sexual selection on the A locus. (Technically, some sexual selection is induced by the grouping model if males that mate within the group are also allowed to join the lek, but the induced selection is very weak unless the modifier has a strong effect on the level of assortative mating; in variant model 1 of appendix a, where males that mate within the group do not join the lek, even this slight sexual selection is eliminated.)
Recursions were developed in Mathematica (supplemental online material), on the basis of the life cycle: natural selection, mating, recombination and gamete production, and gamete union within mated pairs. Allele frequencies and genetic associations were then assessed among the offspring (the census point). These recursions were analyzed using two approaches. We first assumed that selection was weak and allowed genetic associations to reach their steady-state values given the current allele frequencies; essentially, we performed a separation of timescales, assuming that departures from Hardy–Weinberg and linkage disequilibria equilibrate on a faster timescale than allele frequencies change. This is known as a QLE analysis (Barton and Turelli 1991; Nagylaki 1993; Kirkpatrick et al. 2002). Second, we assumed that the population had reached a polymorphic equilibrium at the A locus, at which point a new modifier allele M was introduced. A local stability analysis was then performed to determine the conditions under which M would spread. By combining the two approaches—a QLE that assumes weak selection and a stability analysis that allows strong selection but is valid only near equilibria—we gain a more complete picture of the forces favoring and impeding the evolution of assortative mating. All derivations are presented in the accompanying Mathematica files, and a list of variables and parameters is provided in Table 2.
TABLE 2.
Model variables and parameters
| Terms | Model | Definitions |
|---|---|---|
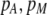 |
Frequency of allele A at trait locus A or allele M at modifier locus M; 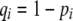 . . |
|
| r | Rate of recombination between loci A and M. | |
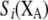 |
Strength of natural selection acting on genotype i. | |
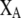 |
Array of genotype frequencies; 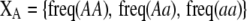 . . |
|
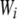 |
Total fitness of genotype i, accounting for both natural and sexual selection. Wi also depends on the composition of the population. | |
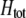 |
Total fitness advantage of homozygotes over heterozygotes 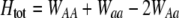 , accounting for natural , accounting for natural 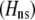 and sexual and sexual 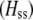 selection. selection. |
|
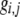 |
(G) | The probability that genotype i joins group j (Figure 1). |
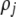 |
(G) | Strength of assortative mating for a female of genotype j (MM, Mm, or mm); specifically, the probability that a female chooses a mate from within her group. 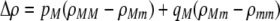 measures the difference in strength of assortment if a female carries allele M instead of m. measures the difference in strength of assortment if a female carries allele M instead of m. |
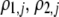 |
(P) | Strength of assortative mating for a female of genotype j (MM, Mm, or mm) as described by matrix (3). |
| K = ρ1,j/ρ2,j | (P) | Strength of assortative mating against males that differ by one trait allele relative to those that differby two in the preference-based model. |
| Ti | (P) | The probability that a female of genotype i accepts a male during a mating encounter, given the current population composition and her preferences. |
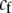 |
A fixed cost that directly selects against assortative mating in proportion to the strength of assortative mating. | |
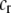 |
A relative cost that directly selects against assortative mating in proportion to the difficulty of finding a preferred mate. | |
| R | (G) | The rarity of males experienced by females averaged over all groups; ΔR measures the difference in rarity if a female carries allele M instead of m. |
| θ | (G) | The effect of mating within a group on homozygosity at locus A; Δθ measures the difference in production of homozygotes if a female carries allele M instead of m. |
| mate1, mate2 | (P) | The probability that a potential mate differs by one or two alleles at the A locus. |
| DAM, DA,M | Linkage disequilibrium within (cis) or between (trans) homologous chromosomes. | |
| DA,A | Excess homozygosity at locus A; 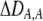 measures the effect of the modifier on DA,A following a single round of mating. measures the effect of the modifier on DA,A following a single round of mating. |
|
| DAM,A | Trigenic disequilibrium measuring the association between allele M and excess homozygosity at locus A. |
Terms specific to the group-based or preference-based model are denoted in the second column by (G) or (P). The value of a parameter x averaged over the population is denoted by 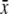 . The QLE value of a variable D is denoted by
. The QLE value of a variable D is denoted by 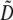 .
.
The results for the group-based and preference-based models were confirmed by computer simulations, which numerically iterated the exact recursion equations. These simulations consisted of two steps. In the first, the allele frequencies at locus A were allowed to equilibrate under a combination of frequency-dependent natural selection, using 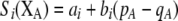 for the fitnesses in Equation 1 and assortative mating as determined by the ancestral genotype at the modifier locus (mm). In the second step, the modifier allele M was introduced in linkage equilibrium with the alleles at locus A, and evolution proceeded until a final equilibrium was reached in the system or until the modifier was lost or spread to fixation.
for the fitnesses in Equation 1 and assortative mating as determined by the ancestral genotype at the modifier locus (mm). In the second step, the modifier allele M was introduced in linkage equilibrium with the alleles at locus A, and evolution proceeded until a final equilibrium was reached in the system or until the modifier was lost or spread to fixation.
QLE RESULTS ASSUMING LOW LEVELS OF ASSORTMENT
QLE in the group-based model of assortative mating:
We begin by assuming that selection coefficients are small [ , where ɛ is small], as are the initial levels of assortment [
, where ɛ is small], as are the initial levels of assortment [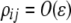 ] and the costs of assortment [
] and the costs of assortment [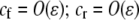 ]. In this case, all genetic associations, including linkage disequilibria and departures from Hardy–Weinberg, rapidly reach a steady-state value that is small, of order ɛ. At this point, the frequency
]. In this case, all genetic associations, including linkage disequilibria and departures from Hardy–Weinberg, rapidly reach a steady-state value that is small, of order ɛ. At this point, the frequency  of allele A changes across a generation by an amount
of allele A changes across a generation by an amount
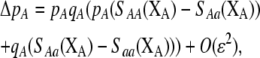 |
(6) |
where 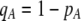 . Only frequency-dependent natural selection (1) enters into Equation 6 and not the mating parameters (
. Only frequency-dependent natural selection (1) enters into Equation 6 and not the mating parameters (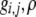 ), confirming that the grouping model does not induce sexual selection on the A locus to leading order (see appendix a). In later sections, we report results from a QLE analysis when assortment is already prevalent and from a stability analysis that allows for strong selection.
), confirming that the grouping model does not induce sexual selection on the A locus to leading order (see appendix a). In later sections, we report results from a QLE analysis when assortment is already prevalent and from a stability analysis that allows for strong selection.
Of greater relevance, the frequency of allele M (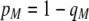 ) changes across a generation by an amount
) changes across a generation by an amount
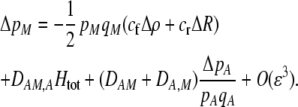 |
(7) |
In the following paragraphs, we describe the terms in Equation 7.
The first line of (7) reflects the costs of assortative mating, which directly select against modifier alleles that increase the level of assortative mating. The cost is multiplied by a factor of  because the modifier is expressed only in females and thus only females pay the cost of assortment. Here,
because the modifier is expressed only in females and thus only females pay the cost of assortment. Here, 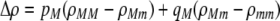 measures the effect of allele M on the level of assortative mating, given the current modifier frequency.
measures the effect of allele M on the level of assortative mating, given the current modifier frequency. 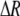 is the difference in the rarity of mates experienced by a female that carries an M allele in place of an m allele. Under our assumption that the relative cost to a female of mating within her group declines linearly with the frequency of her group, the rarity of mates experienced by females is, on average,
is the difference in the rarity of mates experienced by a female that carries an M allele in place of an m allele. Under our assumption that the relative cost to a female of mating within her group declines linearly with the frequency of her group, the rarity of mates experienced by females is, on average,
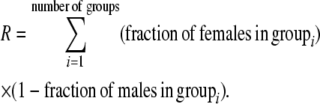 |
(8) |
For example, if there are three groups comprising 20, 70, and 10% of the population, respectively, then 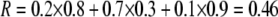 . The minimum value of R is zero and occurs when there is only one group (all females occur in the same group as all of the males); the maximum value of R is
. The minimum value of R is zero and occurs when there is only one group (all females occur in the same group as all of the males); the maximum value of R is 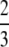 and occurs when all three groups are equal in size (every female is in a group containing one-third of the males). To evaluate the change in modifier frequency (Equation 7), we need only keep leading-order terms within
and occurs when all three groups are equal in size (every female is in a group containing one-third of the males). To evaluate the change in modifier frequency (Equation 7), we need only keep leading-order terms within 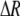 , and so we can calculate the frequencies of each group without accounting for genetic associations (for example, “freq of group1” =
, and so we can calculate the frequencies of each group without accounting for genetic associations (for example, “freq of group1” = 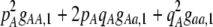 , see Figure 1). Doing so, we determined that
, see Figure 1). Doing so, we determined that 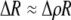 when assortative mating is rare, but when assortative mating is prevalent (or with different group structures, as in variant 2 of appendix a),
when assortative mating is rare, but when assortative mating is prevalent (or with different group structures, as in variant 2 of appendix a), 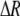 must be calculated from the effect of a change in assortative mating on (8). Depending on the group structure (i.e., on
must be calculated from the effect of a change in assortative mating on (8). Depending on the group structure (i.e., on 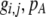 ), mates may become harder or easier to find as assortative mating becomes more prevalent, causing the costs of assortment to rise or fall.
), mates may become harder or easier to find as assortative mating becomes more prevalent, causing the costs of assortment to rise or fall.
The second line in (7) reflects indirect selection on the modifier arising from genetic associations. In this article, we use the central-moment association measures defined in Barton and Turelli (1991). The term 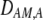 is the genetic association between the modifier allele M and excess homozygosity at the A locus. This term is multiplied by
is the genetic association between the modifier allele M and excess homozygosity at the A locus. This term is multiplied by 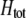 , which measures the degree to which homozygotes are, on average, more fit than heterozygotes at the A locus with respect to total fitness, W,
, which measures the degree to which homozygotes are, on average, more fit than heterozygotes at the A locus with respect to total fitness, W,
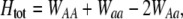 |
(9a) |
which in turn depends on the current genotypic frequencies. Because sexual selection is absent in the grouping model (to leading order), 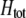 equals the average fitness advantage of homozygotes over heterozygotes due to natural selection alone:
equals the average fitness advantage of homozygotes over heterozygotes due to natural selection alone:
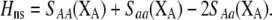 |
(9b) |
In the preference-based models of assortment, sexual selection will also contribute to 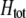 by an amount
by an amount 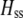 . The degree to which homozygotes are more fit than heterozygotes,
. The degree to which homozygotes are more fit than heterozygotes, 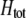 , plays a critical role in selecting for assortative mating (Endler 1977).
, plays a critical role in selecting for assortative mating (Endler 1977). 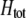 is zero whenever selection at the A locus is additive; it is positive whenever the average fitness of homozygotes is higher than the fitness of heterozygotes; and it is negative whenever the average fitness of homozygotes is lower than the fitness of heterozygotes. Finally, the terms,
is zero whenever selection at the A locus is additive; it is positive whenever the average fitness of homozygotes is higher than the fitness of heterozygotes; and it is negative whenever the average fitness of homozygotes is lower than the fitness of heterozygotes. Finally, the terms, 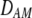 and
and 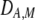 in Equation 7 measure linkage disequilibrium between loci A and M on the same chromosome (in cis) and on homologous chromosomes (in trans), respectively. More generally (i.e., even if the loci are unlinked),
in Equation 7 measure linkage disequilibrium between loci A and M on the same chromosome (in cis) and on homologous chromosomes (in trans), respectively. More generally (i.e., even if the loci are unlinked), 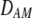 and
and 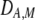 measure the association between alleles at loci A and M inherited from the same parent vs. different parents.
measure the association between alleles at loci A and M inherited from the same parent vs. different parents.
To interpret Equation 7, we need to determine the genetic associations in terms of the parameters of the model. We do this by setting the change in the association measures across a generation to zero and solving for the D terms to order ɛ given the current allele frequencies. That is, we assume that the association measures have reached their steady-state values expected at QLE, denoting these steady-state values as 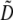 . Doing so reveals that the cis and trans linkage disequilibria
. Doing so reveals that the cis and trans linkage disequilibria 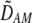 and
and 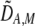 are zero to this order, while
are zero to this order, while
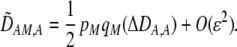 |
(10) |
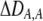 measures the effect of the modifier on the QLE departure from Hardy–Weinberg. We can relate
measures the effect of the modifier on the QLE departure from Hardy–Weinberg. We can relate 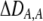 to the mating parameters by considering how mating within a group affects the production of homozygous offspring, relative to the parental generation:
to the mating parameters by considering how mating within a group affects the production of homozygous offspring, relative to the parental generation:
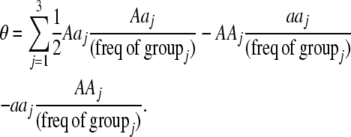 |
(11) |
Mating among heterozygotes increases homozygosity by a factor of  , whereas mating among opposite homozygotes decreases homozygosity. In Equation 11,
, whereas mating among opposite homozygotes decreases homozygosity. In Equation 11, 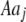 is shorthand for the frequency of genotype Aa in group j. Putting Equation 11 in words, the more that heterozygotes mate with one another, the more efficient assortative mating is in converting heterozygotes into homozygotes, and the larger θ becomes. If groups form randomly in a population at Hardy–Weinberg equilibrium,
is shorthand for the frequency of genotype Aa in group j. Putting Equation 11 in words, the more that heterozygotes mate with one another, the more efficient assortative mating is in converting heterozygotes into homozygotes, and the larger θ becomes. If groups form randomly in a population at Hardy–Weinberg equilibrium, 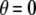 . If each genotype forms its own group (
. If each genotype forms its own group (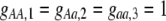 in Figure 1), half of the heterozygotes are converted into homozygotes by each generation of assortative mating [
in Figure 1), half of the heterozygotes are converted into homozygotes by each generation of assortative mating [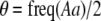 ], which is the most efficient form of assortative mating. If individuals make errors in which group they join, this effectively reduces θ (toward the case of random mating) and makes assortative mating less efficient. By altering the tendency to mate within a group, a modifier allele M affects the production of homozygotes by an amount,
], which is the most efficient form of assortative mating. If individuals make errors in which group they join, this effectively reduces θ (toward the case of random mating) and makes assortative mating less efficient. By altering the tendency to mate within a group, a modifier allele M affects the production of homozygotes by an amount, 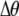 , following a single round of mating at QLE. In terms of
, following a single round of mating at QLE. In terms of 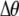 , Equation 10 is equivalent to
, Equation 10 is equivalent to
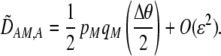 |
(12) |
(The  enters from the definition of
enters from the definition of 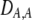 , where
, where 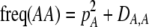 , so that
, so that 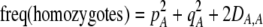 . Consequently,
. Consequently, 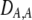 measures only half the excess homozygosity caused by assortative mating.)
measures only half the excess homozygosity caused by assortative mating.)
When assortment is rare, a modifier allele that increases the degree of assortative mating (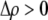 ) increases the rate of production of homozygous offspring by
) increases the rate of production of homozygous offspring by 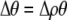 . Consequently, the modifier allele tends to be found in individuals with higher levels of homozygosity at the A locus (
. Consequently, the modifier allele tends to be found in individuals with higher levels of homozygosity at the A locus (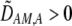 from Equation 10b). This association indirectly selects for the modifier allele if homozygotes are more fit, on average, than heterozygotes (Equation 7). Following up on suggestions made earlier by Dobzhansky (1940, 1941), Endler (1977) argued that assortative mating would evolve whenever
from Equation 10b). This association indirectly selects for the modifier allele if homozygotes are more fit, on average, than heterozygotes (Equation 7). Following up on suggestions made earlier by Dobzhansky (1940, 1941), Endler (1977) argued that assortative mating would evolve whenever 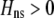 . To do so, he ignored all genetic associations except the departure from Hardy–Weinberg at the A locus; this method does not exactly predict the change in the modifier (the magnitude of
. To do so, he ignored all genetic associations except the departure from Hardy–Weinberg at the A locus; this method does not exactly predict the change in the modifier (the magnitude of 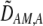 is not right), but the qualitative result is correct.
is not right), but the qualitative result is correct.
Whenever heterozygotes are less fit, on average, assortative mating is favored, whether or not the population is at equilibrium. For example, if frequency-independent selection favors the spread of a beneficial allele A, modifiers that increase assortative mating will rise in frequency as long as A is partially recessive (so that 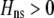 ). Conversely, disassortative mating would be favored if A were partially dominant. Such a process is transient, however; as soon as the A allele fixes, all individuals belong to the same group, and mating within a group becomes equivalent to mating at random within the population at large. Nevertheless, the potential for assortment would persist if fixed costs are negligible, and assortment would be revealed once genetic variation reappears. Furthermore, the recurrent spread of partially recessive beneficial alleles could select for increasingly high levels of assortative mating. Although beneficial alleles are not typically recessive, dominance varies among traits and among alleles, and it is plausible that beneficial alleles will tend to be partially recessive in the face of certain environmental challenges (e.g., Anderson et al. 2003). Selection in such environments would then promote assortment.
). Conversely, disassortative mating would be favored if A were partially dominant. Such a process is transient, however; as soon as the A allele fixes, all individuals belong to the same group, and mating within a group becomes equivalent to mating at random within the population at large. Nevertheless, the potential for assortment would persist if fixed costs are negligible, and assortment would be revealed once genetic variation reappears. Furthermore, the recurrent spread of partially recessive beneficial alleles could select for increasingly high levels of assortative mating. Although beneficial alleles are not typically recessive, dominance varies among traits and among alleles, and it is plausible that beneficial alleles will tend to be partially recessive in the face of certain environmental challenges (e.g., Anderson et al. 2003). Selection in such environments would then promote assortment.
If we assume that the population is at a polymorphic equilibrium such that 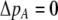 in (6), then
in (6), then 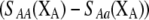 and
and 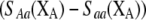 must have opposite signs, implying either overdominance (
must have opposite signs, implying either overdominance (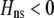 ) or underdominance (
) or underdominance (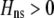 ). In the absence of frequency-dependent selection, the polymorphic equilibrium is stable only with overdominance, in which case assortative mating would be selected against (Equation 7). With frequency-dependent selection, a local stability analysis shows that a polymorphism is possible with underdominance as long as
). In the absence of frequency-dependent selection, the polymorphic equilibrium is stable only with overdominance, in which case assortative mating would be selected against (Equation 7). With frequency-dependent selection, a local stability analysis shows that a polymorphism is possible with underdominance as long as
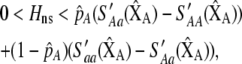 |
(13) |
where 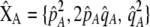 , a caret indicates a value at equilibrium, and S′ refers to the derivative of the selection coefficient with respect to
, a caret indicates a value at equilibrium, and S′ refers to the derivative of the selection coefficient with respect to 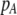 evaluated at the equilibrium (assuming mating is nearly random). Condition (13) requires that the fitness of individuals bearing the A allele declines fast enough as the frequency of A rises, relative to the fitness of individuals bearing the a allele. In models where competition for resources induces frequency-dependent selection (such as that considered by Dieckmann and Doebeli 1999 and Pennings et al. 2008), condition (13) requires that the resources are better utilized by a polymorphic population than by a fixed population and would be even more fully utilized if there were an excess of homozygotes over Hardy–Weinberg expectations. With multiple loci, de Cara et al. (2008) identify epistasis as playing a similar role to
evaluated at the equilibrium (assuming mating is nearly random). Condition (13) requires that the fitness of individuals bearing the A allele declines fast enough as the frequency of A rises, relative to the fitness of individuals bearing the a allele. In models where competition for resources induces frequency-dependent selection (such as that considered by Dieckmann and Doebeli 1999 and Pennings et al. 2008), condition (13) requires that the resources are better utilized by a polymorphic population than by a fixed population and would be even more fully utilized if there were an excess of homozygotes over Hardy–Weinberg expectations. With multiple loci, de Cara et al. (2008) identify epistasis as playing a similar role to  , so that indirect selection favors assortative mating if epistasis or
, so that indirect selection favors assortative mating if epistasis or 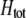 is positive; in either case, extreme phenotypes are fitter than intermediate ones.
is positive; in either case, extreme phenotypes are fitter than intermediate ones.
Costs of assortative mating always hinder the evolution of assortative mating. If these costs are substantially larger than the strength of natural selection acting at the A locus, assortative mating cannot evolve. For example, consider the case where each genotype forms its own group [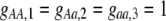 , so that
, so that 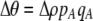 and
and 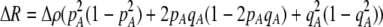 ]. Plugging Equation 12 into Equation 7, we find that assortment cannot evolve despite the fact that homozygotes are fitter, on average, than heterozygotes (
]. Plugging Equation 12 into Equation 7, we find that assortment cannot evolve despite the fact that homozygotes are fitter, on average, than heterozygotes (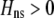 ) if the fixed cost of assortment is greater than
) if the fixed cost of assortment is greater than
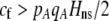 |
(14a) |
or if the relative cost of assortment is greater than
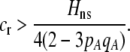 |
(14b) |
These conditions are illustrated in Figure 2. Clearly, costs cannot be too substantial for assortment to evolve. All else equal, relative costs are less prohibitive to the evolution of assortative mating than fixed costs, especially as the allele frequency approaches zero or one. This is because the relative costs become negligible if most individuals find themselves in well-populated groups.
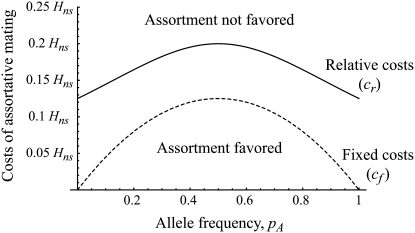
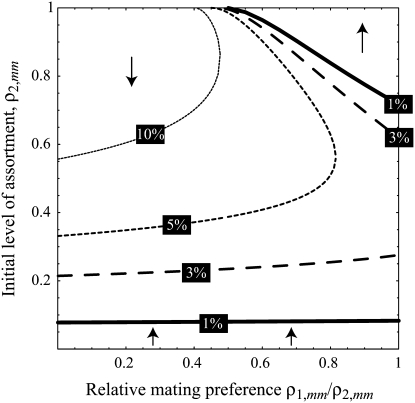
Figure 2.—
Strong costs prohibit the evolution of assortative mating. In the grouping model, assortative mating will evolve if homozygotes are, on average, more fit (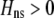 , Equation 9) and if the costs of assortative mating are sufficiently weak (below curves, from Equation 14). Here we assume that Aa individuals form their own group (
, Equation 9) and if the costs of assortative mating are sufficiently weak (below curves, from Equation 14). Here we assume that Aa individuals form their own group (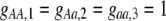 ) and consider costs to be either fixed (dashed curve) or relative to the difficulty of finding a mate (solid curve). Given that
) and consider costs to be either fixed (dashed curve) or relative to the difficulty of finding a mate (solid curve). Given that 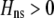 , assortative mating can evolve only if costs lie below the appropriate curve and only as long as the A locus remains polymorphic. Note that the y-axis is measured relative to
, assortative mating can evolve only if costs lie below the appropriate curve and only as long as the A locus remains polymorphic. Note that the y-axis is measured relative to 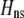 (Equation 9b), the degree to which homozygotes are more fit, on average, than heterozygotes given the current genotype frequencies.
(Equation 9b), the degree to which homozygotes are more fit, on average, than heterozygotes given the current genotype frequencies.
QLE in the preference-based model of assortative mating:
In this model, females exhibit mating preferences, which induce sexual selection. For the mating preference scheme given by matrix (3), a QLE analysis assuming weak selection in a population with initially weak assortative mating shows that the frequency of allele A changes by an amount given by Equation 6 due to natural selection plus
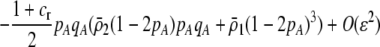 |
(15) |
due to sexual selection, where costs of assortment are allowed to be weak or strong. Here, an overbar is used to denote an average across the population. For example, 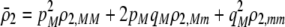 . According to (15), assortative mating (
. According to (15), assortative mating (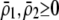 ) selects against A when rare (
) selects against A when rare (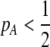 ) and favors A when common (
) and favors A when common (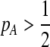 ), thereby generating positive frequency-dependent selection. This potentially places a break on the evolution of assortative mating under frequency-dependent selection because a polymorphism at locus A can be sustained only while sexual selection remains weak relative to natural selection (Kirkpatrick and Nuismer 2004). The force of sexual selection acting on the A locus is twice as strong in the plant model (
), thereby generating positive frequency-dependent selection. This potentially places a break on the evolution of assortative mating under frequency-dependent selection because a polymorphism at locus A can be sustained only while sexual selection remains weak relative to natural selection (Kirkpatrick and Nuismer 2004). The force of sexual selection acting on the A locus is twice as strong in the plant model (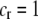 ) as in the animal model (
) as in the animal model (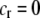 ); in the plant model, the rare allele is selected against in both females and males, while in the animal model, only males experience sexual selection.
); in the plant model, the rare allele is selected against in both females and males, while in the animal model, only males experience sexual selection.
Although the QLE results derived below do not require that the A locus is at equilibrium, it is worth considering the conditions under which there would be a protected polymorphism at locus A when both sexual and natural selection act. Specifically, we wish to know the conditions under which 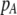 rises when A is rare (
rises when A is rare (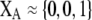 ) and falls when A is common (
) and falls when A is common (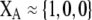 ). Adding Equation 15 to Equation 6 reveals that a protected polymorphism is guaranteed if
). Adding Equation 15 to Equation 6 reveals that a protected polymorphism is guaranteed if
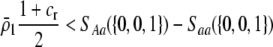 |
and
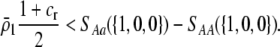 |
(16) |
When homozygous females at the A locus strongly prefer similar homozygotes over heterozygotes (so that 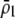 is large), the alternative allele at the A locus cannot spread when rare because it finds itself in heterozygotes that are less likely to obtain a mate. Thus, mating preferences against individuals that differ by one allele (
is large), the alternative allele at the A locus cannot spread when rare because it finds itself in heterozygotes that are less likely to obtain a mate. Thus, mating preferences against individuals that differ by one allele (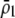 ) cannot evolve to very high frequency before the fixation states become stable. Interestingly, a mating preference against individuals that differ by two alleles (
) cannot evolve to very high frequency before the fixation states become stable. Interestingly, a mating preference against individuals that differ by two alleles (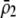 ) does not affect the conditions for a protected polymorphism; this is because the dynamics of a rare allele at the A locus are insensitive to preferences against the opposite homozygote because such homozygotes are so rare. In summary, the evolution of sexual preferences will stabilize the fixation of alleles at the A locus if females avoid mating with genotypes that differ by one allele. Even when both fixation states are stable, however, frequency-dependent natural selection could still maintain a stable polymorphism at an intermediate allele frequency, as long as negative frequency-dependent natural selection is strong enough to dominate sexual selection near the polymorphic equilibrium (see also Verzijden et al. 2005).
) does not affect the conditions for a protected polymorphism; this is because the dynamics of a rare allele at the A locus are insensitive to preferences against the opposite homozygote because such homozygotes are so rare. In summary, the evolution of sexual preferences will stabilize the fixation of alleles at the A locus if females avoid mating with genotypes that differ by one allele. Even when both fixation states are stable, however, frequency-dependent natural selection could still maintain a stable polymorphism at an intermediate allele frequency, as long as negative frequency-dependent natural selection is strong enough to dominate sexual selection near the polymorphic equilibrium (see also Verzijden et al. 2005).
With preference-based assortative mating, the change in frequency of the M modifier allele is
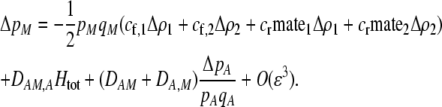 |
(17) |
Again, the first line in (17) reflects direct selection against modifier alleles arising from the costs of assortative mating. Here, the effect of the modifier on female preferences against males differing by i alleles is given by 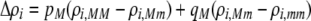 . As mentioned previously,
. As mentioned previously, 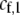 and
and 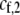 are the fixed costs of being able to detect males that differ by one and two alleles, respectively. The term
are the fixed costs of being able to detect males that differ by one and two alleles, respectively. The term 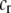 is the relative cost to a female of rejecting a potential mate when she is unable to replace this lost mating opportunity. The relative cost enters twice, first, when multiplied by the probability that a female encounters a male differing by one allele [
is the relative cost to a female of rejecting a potential mate when she is unable to replace this lost mating opportunity. The relative cost enters twice, first, when multiplied by the probability that a female encounters a male differing by one allele [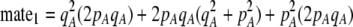 ] times the increased probability that such males are rejected by a female carrying the M allele (
] times the increased probability that such males are rejected by a female carrying the M allele (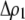 ) and, second, when multiplied by the probability that a female encounters a male differing by two alleles [
) and, second, when multiplied by the probability that a female encounters a male differing by two alleles [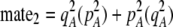 ] times the increased probability that such males are rejected by a female carrying the M allele (
] times the increased probability that such males are rejected by a female carrying the M allele (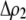 ). As expected, both fixed and relative costs hinder the evolution of assortative mating. Indeed, with strong costs (of order one, as in the plant model where
). As expected, both fixed and relative costs hinder the evolution of assortative mating. Indeed, with strong costs (of order one, as in the plant model where 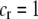 ), the first line in (17) becomes large (of order ɛ), the second line becomes negligible (of order
), the first line in (17) becomes large (of order ɛ), the second line becomes negligible (of order 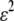 ), and modifier alleles that increase the strength of preferences (
), and modifier alleles that increase the strength of preferences (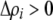 ) always decline in frequency. In particular, we find that assortative mating can never evolve in the plant model because potential mates are rejected and never replaced (as found by de Cara et al. 2008).
) always decline in frequency. In particular, we find that assortative mating can never evolve in the plant model because potential mates are rejected and never replaced (as found by de Cara et al. 2008).
We next focus on the second line in Equation 17, which measures the indirect selective forces acting on assortative mating, assuming that the costs of assortment are small (of order ɛ). There is one key difference between the change in modifier frequency in the preference-based model (Equation 17) and that observed in the grouping model (Equation 7): sexual selection alters the relative fitness of homozygotes vs. heterozygotes at the A locus. With both natural and sexual selection acting, 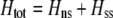 , where the contribution due to natural selection is given by (9b) and the contribution due to sexual selection is
, where the contribution due to natural selection is given by (9b) and the contribution due to sexual selection is
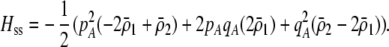 |
(18) |
Preferences against genotypes differing by one allele (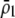 ) increase the fitness of homozygotes relative to heterozygotes, causing
) increase the fitness of homozygotes relative to heterozygotes, causing 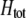 to become more positive and facilitating the evolution of assortment. In contrast, preferences against genotypes differing by two alleles (
to become more positive and facilitating the evolution of assortment. In contrast, preferences against genotypes differing by two alleles (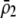 ) decrease the fitness of homozygotes relative to heterozygotes, causing
) decrease the fitness of homozygotes relative to heterozygotes, causing 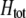 to become less positive and hindering the evolution of assortment. More generally, when females dislike males of all other genotypes (
to become less positive and hindering the evolution of assortment. More generally, when females dislike males of all other genotypes (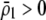 and
and 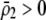 ), sexual selection will hinder the evolution of assortative mating (by decreasing
), sexual selection will hinder the evolution of assortative mating (by decreasing  ) unless homozygotes are common and
) unless homozygotes are common and 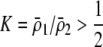 .
.
Assuming that selection is weak relative to recombination, we again calculated the steady-state (QLE) values of the genetic associations. Unlike the grouping model, cis and trans linkage disequilibria are generated in the preference-based model,
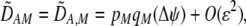 |
(19a) |
where 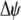 measures the effect of the modifier allele M on
measures the effect of the modifier allele M on 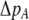 due to a single round of nonrandom mating (i.e., the effect of the modifier on sexual selection):
due to a single round of nonrandom mating (i.e., the effect of the modifier on sexual selection):
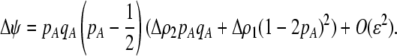 |
(19b) |
Unless the allele frequency is  , a modifier increasing the level of assortative mating (
, a modifier increasing the level of assortative mating (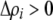 ) induces sexual selection favoring the more common of the two alleles at the A locus (
) induces sexual selection favoring the more common of the two alleles at the A locus (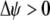 if
if 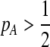 and vice versa). This in turn generates genetic associations between the modifier and the more common allele (
and vice versa). This in turn generates genetic associations between the modifier and the more common allele (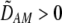 and
and 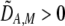 if
if 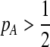 and vice versa). These associations develop because males carrying the common allele are more often preferred by females (because females that also carry the common allele are more abundant). This coupling of preference alleles with the trait alleles that are preferred is typical of Fisherian models of sexual selection (e.g., Kirkpatrick 1982). According to Equation 17, cis and trans linkage disequilibria will then favor the spread of a modifier increasing the level of assortment as long as the common allele is increasing in frequency. Note that if the A locus is at equilibrium (
and vice versa). These associations develop because males carrying the common allele are more often preferred by females (because females that also carry the common allele are more abundant). This coupling of preference alleles with the trait alleles that are preferred is typical of Fisherian models of sexual selection (e.g., Kirkpatrick 1982). According to Equation 17, cis and trans linkage disequilibria will then favor the spread of a modifier increasing the level of assortment as long as the common allele is increasing in frequency. Note that if the A locus is at equilibrium (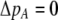 ), the cis and trans linkage disequilibria have no influence on the modifier (Equation 17).
), the cis and trans linkage disequilibria have no influence on the modifier (Equation 17).
In addition to the cis and trans linkage disequilibria, the change in the modifier (17) depends on the genetic association,  , between the modifier allele, M, and excess homozygosity, which at QLE is
, between the modifier allele, M, and excess homozygosity, which at QLE is
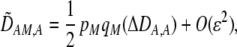 |
(20a) |
where
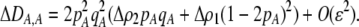 |
(20b) |
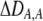 again measures the effect of the modifier on the departure from Hardy–Weinberg following a single round of mating at QLE. A modifier allele that increases the level of assortment (
again measures the effect of the modifier on the departure from Hardy–Weinberg following a single round of mating at QLE. A modifier allele that increases the level of assortment (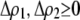 causing
causing 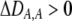 ) tends to be found in individuals with higher levels of homozygosity at the A locus (
) tends to be found in individuals with higher levels of homozygosity at the A locus (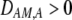 ). According to Equation 17, this association indirectly selects for the modifier allele if homozygotes are more fit, on average, than heterozygotes (
). According to Equation 17, this association indirectly selects for the modifier allele if homozygotes are more fit, on average, than heterozygotes (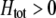 ).
).
In summary, the results from the preference-based model of assortative mating differ from the grouping model in three ways. The first is that sexual selection induces positive frequency-dependent selection on the A locus, which makes it less likely that a polymorphism will persist (if 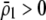 ). The second is that linkage disequilibria develop that couple modifier alleles increasing the level of assortative mating with the common allele at the A locus, which can cause the evolution of increased assortative mating if the common allele is rising in frequency. The third is that sexual selection alters the fitness of homozygotes relative to heterozygotes. Assortative mating is favored only while homozygotes are more fit than heterozygotes, on average (
). The second is that linkage disequilibria develop that couple modifier alleles increasing the level of assortative mating with the common allele at the A locus, which can cause the evolution of increased assortative mating if the common allele is rising in frequency. The third is that sexual selection alters the fitness of homozygotes relative to heterozygotes. Assortative mating is favored only while homozygotes are more fit than heterozygotes, on average ( ); sexual selection can make this condition harder or easier to satisfy as assortative mating evolves, depending on the relative mating success of homozygotes and heterozygotes, which in turn depends on the values of
); sexual selection can make this condition harder or easier to satisfy as assortative mating evolves, depending on the relative mating success of homozygotes and heterozygotes, which in turn depends on the values of 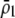 and
and 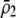 , as well as the allele frequency,
, as well as the allele frequency, 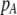 .
.
Evolutionarily stable strategy:
We can use result (17) of this QLE analysis to determine the level of assortative mating that can evolve before selection on subsequent modifier alleles equals zero (to leading order), as would occur at an evolutionarily stable strategy (ESS). For clarity of presentation, we assume that there are no direct costs of assortment (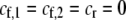 ), that mating is initially random, and that the A locus is initially at a stable equilibrium with
), that mating is initially random, and that the A locus is initially at a stable equilibrium with 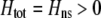 . When
. When 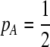 and the population is at Hardy–Weinberg proportions, increased levels of assortative mating cause heterozygotes to become fitter because heterozygous males appeal to the large class of heterozygous females (see Equation 18), decreasing
and the population is at Hardy–Weinberg proportions, increased levels of assortative mating cause heterozygotes to become fitter because heterozygous males appeal to the large class of heterozygous females (see Equation 18), decreasing 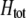 , and decreasing selection for assortative mating. Indeed, assortative mating is expected to evolve only to the point at which heterozygotes have the same average fitness as homozygotes (
, and decreasing selection for assortative mating. Indeed, assortative mating is expected to evolve only to the point at which heterozygotes have the same average fitness as homozygotes (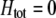 ). Combining (9b) and (18) and setting
). Combining (9b) and (18) and setting 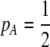 , this point occurs at
, this point occurs at
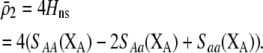 |
(21) |
Equation 21 represents the evolutionarily stable level of assortative mating when 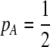 and costs are absent. This result is consistent with the results of Matessi et al. (2001), who identified the ESS as
and costs are absent. This result is consistent with the results of Matessi et al. (2001), who identified the ESS as 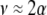 [our
[our 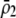 is their
is their 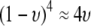 , and
, and 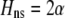 with their quadratic fitness function]. More generally, Figure 3 plots the ESS level of assortative mating as a function of the equilibrium allele frequency. When
with their quadratic fitness function]. More generally, Figure 3 plots the ESS level of assortative mating as a function of the equilibrium allele frequency. When 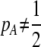 , however, sexual selection may favor the common allele at the A locus so strongly that the internal polymorphism is destabilized, preventing assortment from evolving to the
, however, sexual selection may favor the common allele at the A locus so strongly that the internal polymorphism is destabilized, preventing assortment from evolving to the 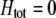 curve and precluding an ESS along this curve. To determine whether there is a stable polymorphism on the
curve and precluding an ESS along this curve. To determine whether there is a stable polymorphism on the 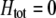 curve requires that the form of frequency dependence be specified and that a stability analysis be performed. This was done in Figure 3, using the linear form of frequency-dependent selection:
curve requires that the form of frequency dependence be specified and that a stability analysis be performed. This was done in Figure 3, using the linear form of frequency-dependent selection: 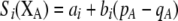 . Only when frequency-dependent selection (
. Only when frequency-dependent selection (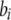 ) was sufficiently strong was there a stable polymorphism along the
) was sufficiently strong was there a stable polymorphism along the 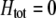 curve; in these cases, simulations introducing modifier alleles with small effects confirmed that assortment levels evolved to a point along this curve and then ceased to evolve further.
curve; in these cases, simulations introducing modifier alleles with small effects confirmed that assortment levels evolved to a point along this curve and then ceased to evolve further.
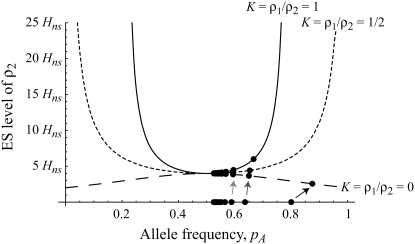
Figure 3.—
Evolutionarily stable level of assortative mating in the preference-based model without costs. Assortative mating initially evolves when 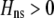 , but this process is self-limiting if heterozygotes more readily find mates. Once the strength of sexual selection generated by assortment causes heterozygotes and homozygotes to become equally fit (
, but this process is self-limiting if heterozygotes more readily find mates. Once the strength of sexual selection generated by assortment causes heterozygotes and homozygotes to become equally fit (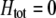 ; curves), further increases in the level of assortative mating are no longer favored (Equation 17). Whether or not a stable internal polymorphism exists along these curves depends on the form of frequency-dependent natural selection. The solid circles show stable equilibrium points,
; curves), further increases in the level of assortative mating are no longer favored (Equation 17). Whether or not a stable internal polymorphism exists along these curves depends on the form of frequency-dependent natural selection. The solid circles show stable equilibrium points, 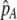 , using a specific model of frequency dependence:
, using a specific model of frequency dependence: 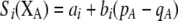 with
with 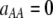 ,
, 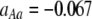 ,
, 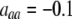 ,
, 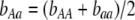 , and
, and 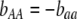 . Frequency-dependent natural selection becomes weaker as
. Frequency-dependent natural selection becomes weaker as 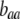 is reduced from 1 to 0.1 in increments of −0.1 (solid circles from left to right, without assortment along the x-axis or with assortment along the
is reduced from 1 to 0.1 in increments of −0.1 (solid circles from left to right, without assortment along the x-axis or with assortment along the 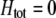 curves). Assortative mating drives the frequency of allele A away from
curves). Assortative mating drives the frequency of allele A away from 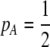 (arrow with light shading,
(arrow with light shading, 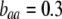 ; arrow with dark shading,
; arrow with dark shading, 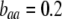 ; solid arrow,
; solid arrow, 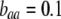 ). A stable internal equilibrium exists along the
). A stable internal equilibrium exists along the 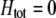 curve only if frequency-dependent natural selection is sufficiently strong (
curve only if frequency-dependent natural selection is sufficiently strong (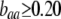 when
when 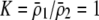 ;
; 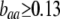 when
when 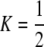 ;
; 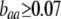 when
when 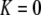 ). Otherwise, the frequency of allele A rises as assortment evolves, until the polymorphism is lost. Note that the y-axis is measured relative to
). Otherwise, the frequency of allele A rises as assortment evolves, until the polymorphism is lost. Note that the y-axis is measured relative to 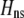 in the current population.
in the current population.
Thus, starting at a low level of assortative mating with weak natural selection, the level of assortment will rise until the relative fitnesses of homozygotes and heterozygotes become equal. This requires that sexual selection favors heterozygotes, which occurs when 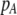 is initially near
is initially near  and/or when females discriminate more strongly against males that differ by two alleles than males that differ by one allele (
and/or when females discriminate more strongly against males that differ by two alleles than males that differ by one allele (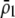 small relative to
small relative to 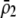 ). Under such conditions, heterozygous males more readily find mates than homozygous males. Because we have assumed in this section that natural selection is weak, the degree of assortative mating evolves only to a small multiple of
). Under such conditions, heterozygous males more readily find mates than homozygous males. Because we have assumed in this section that natural selection is weak, the degree of assortative mating evolves only to a small multiple of  (the degree to which natural selection favors homozygotes over heterozygotes) before being counterbalanced by sexual selection (Figure 3). In other cases (
(the degree to which natural selection favors homozygotes over heterozygotes) before being counterbalanced by sexual selection (Figure 3). In other cases ( far from
far from  and
and 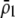 large relative to
large relative to 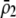 ), however, a balance between sexual and natural selection is not reached, and we must expand our analysis to consider what happens in populations once the level of assortment becomes high.
), however, a balance between sexual and natural selection is not reached, and we must expand our analysis to consider what happens in populations once the level of assortment becomes high.
QLE ALLOWING HIGH LEVELS OF ASSORTMENT
The above results suggest that higher and higher levels of assortment should evolve in the grouping model, that assortment will often halt at an ESS with only a low level of assortment in the preference-based model when costs are weak (as in the animal model), and that random mating should prevail if costs are sufficiently strong (as in the plant model). These results assume that natural selection is weak and that modifier alleles increase assortment by a small amount. They further assume that the degree of assortment is currently low. Here we extend the QLE analysis to populations that already exhibit a substantial degree of assortment (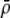 is of constant order).
is of constant order).
QLE in the group-based model with high levels of assortment:
When the rate of assortative mating is high in the grouping model, the departure from Hardy–Weinberg equilibrium at the A locus, 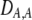 , is no longer small. Unfortunately, the QLE calculations become unwieldy for the generic grouping model, so we focus only on the case where each genotype forms its own group (
, is no longer small. Unfortunately, the QLE calculations become unwieldy for the generic grouping model, so we focus only on the case where each genotype forms its own group (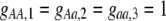 ). The steady-state value of
). The steady-state value of 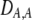 then equals
then equals
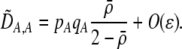 |
(22) |
Whenever the steady-state value of an association measure is of constant order, there is no guarantee that it will be approached quickly, calling into question the validity of a QLE analysis. Fortunately, the departure from Hardy–Weinberg rapidly approaches (22), as long as a substantial degree of random mating remains. Specifically, the departure of 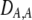 from its QLE value changes from generation to generation by a factor
from its QLE value changes from generation to generation by a factor 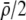 ,
,
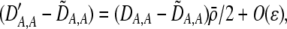 |
(23) |
implying that the system will be close to (22) after only a few generations. This rapid approach occurs because the force causing  to decay (random mating) immediately returns the offspring produced by random mating to Hardy–Weinberg proportions. Below, we assume that the population has reached the steady-state departure from Hardy–Weinberg given by (22). All remaining associations rapidly approach a steady-state value that is small (of order ɛ) as long as the effective rate of recombination rate is sufficiently high. (This requires that the rate of assortative mating not be too near one, because with
to decay (random mating) immediately returns the offspring produced by random mating to Hardy–Weinberg proportions. Below, we assume that the population has reached the steady-state departure from Hardy–Weinberg given by (22). All remaining associations rapidly approach a steady-state value that is small (of order ɛ) as long as the effective rate of recombination rate is sufficiently high. (This requires that the rate of assortative mating not be too near one, because with  , most loci are homozygous and recombination becomes ineffective at breaking down linkage disequilibria.)
, most loci are homozygous and recombination becomes ineffective at breaking down linkage disequilibria.)
Recalculating the association measures to order ɛ, we find that Equation 7 continues to describe the frequency change at the modifier locus, 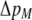 , with the term
, with the term 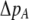 replaced by Equation 6. Furthermore, the cis and trans linkage disequilibria
replaced by Equation 6. Furthermore, the cis and trans linkage disequilibria 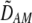 and
and 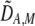 remain zero to order ɛ, and Equation 10 continues to apply, while (12) becomes
remain zero to order ɛ, and Equation 10 continues to apply, while (12) becomes
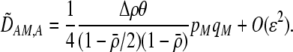 |
(24) |
Thus, in the grouping model with 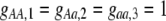 [implying
[implying 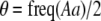 ], there are only two changes that must be made to the QLE prediction for
], there are only two changes that must be made to the QLE prediction for 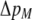 once assortative mating becomes common. First, the effect of the modifier on the efficiency of assortment,
once assortative mating becomes common. First, the effect of the modifier on the efficiency of assortment, 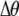 , in Equation 12 becomes
, in Equation 12 becomes 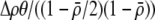 . Second, the effect of the modifier on the rarity of mates,
. Second, the effect of the modifier on the rarity of mates, 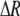 , in Equation 7 must be updated; this value of
, in Equation 7 must be updated; this value of  is somewhat complicated (see supplemental Mathematica file) because it accounts for two effects of the modifier: the direct effect caused by changing a female's tendency to mate within a group and an indirect effect caused by changing the groups to which males and females belong.
is somewhat complicated (see supplemental Mathematica file) because it accounts for two effects of the modifier: the direct effect caused by changing a female's tendency to mate within a group and an indirect effect caused by changing the groups to which males and females belong.
As the current level of assortative mating rises, genetic associations reach higher QLE values. In particular, 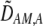 increases in magnitude, accelerating the rate at which further assortative mating evolves. On the other hand, the relative costs of assortative mating can become more or less severe as the level of assortment rises; the costs increase in severity when heterozygotes are relatively common (i.e., when
increases in magnitude, accelerating the rate at which further assortative mating evolves. On the other hand, the relative costs of assortative mating can become more or less severe as the level of assortment rises; the costs increase in severity when heterozygotes are relatively common (i.e., when 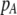 is near
is near  and
and 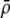 is small) but decrease in severity when homozygotes are already the most common class, because further increases in homozygosity then make it easier to encounter a mate. Regardless, it can be shown that, if
is small) but decrease in severity when homozygotes are already the most common class, because further increases in homozygosity then make it easier to encounter a mate. Regardless, it can be shown that, if 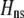 remains constant and if the relative costs,
remains constant and if the relative costs, 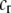 , are small enough that modifier alleles introducing assortative mating are able to spread within a randomly mating population, then modifier alleles increasing assortment will always be favored, no matter how high
, are small enough that modifier alleles introducing assortative mating are able to spread within a randomly mating population, then modifier alleles increasing assortment will always be favored, no matter how high 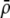 gets. That is, the costs do not rise fast enough to overwhelm the benefits experienced by a modifier as the level of assortment rises. Consequently, higher levels of assortment are expected to evolve unless costs are substantial, in which case random mating is stable.
gets. That is, the costs do not rise fast enough to overwhelm the benefits experienced by a modifier as the level of assortment rises. Consequently, higher levels of assortment are expected to evolve unless costs are substantial, in which case random mating is stable.
This assumes, however, that  is relatively constant, but frequency-dependent natural selection can alter the relative fitness of homozygotes vs. heterozygotes as homozygotes become increasingly common, altering the magnitude and even the sign of
is relatively constant, but frequency-dependent natural selection can alter the relative fitness of homozygotes vs. heterozygotes as homozygotes become increasingly common, altering the magnitude and even the sign of  . If the average fitness of heterozygotes ever becomes equal to the average fitness of homozygotes (
. If the average fitness of heterozygotes ever becomes equal to the average fitness of homozygotes (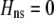 ), then in the absence of costs, the level of assortative mating will cease to evolve (to the order of magnitude of our approximations). This phenomenon was observed in the model of density-dependent competition studied by Pennings et al. (2008). In their model, if homozygotes are unable to completely utilize the resources available to heterozygotes, the fitness of heterozygotes relative to homozygotes rises with increasing levels of assortment (i.e., as heterozygotes become rarer). In this case, assortment levels evolve only to the point where
), then in the absence of costs, the level of assortative mating will cease to evolve (to the order of magnitude of our approximations). This phenomenon was observed in the model of density-dependent competition studied by Pennings et al. (2008). In their model, if homozygotes are unable to completely utilize the resources available to heterozygotes, the fitness of heterozygotes relative to homozygotes rises with increasing levels of assortment (i.e., as heterozygotes become rarer). In this case, assortment levels evolve only to the point where 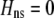 (their Equation 12), and the three genotypes are all stably maintained within the population, with Aa heterozygotes occupying their own ecological niche (see their Figure 1, partial-isolation regime).
(their Equation 12), and the three genotypes are all stably maintained within the population, with Aa heterozygotes occupying their own ecological niche (see their Figure 1, partial-isolation regime).
QLE in the preference-based model with high levels of assortment:
A general QLE analysis is not possible for the preference-based models because the sexual selection induced in these models is typically strong (of constant order) once assortative mating becomes common, invalidating the QLE assumption that allele frequencies change slowly. There are, however, three cases where sexual selection on the A locus is weak: when assortative mating is rare (analyzed above), when assortative mating is nearly complete (where a QLE analysis is not valid), and when 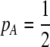 .
.
Here, we briefly consider the preference-based model in the absence of costs when 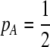 , so that sexual selection on the two alleles is exactly balanced. A QLE analysis, assuming weak selection and a modifier causing only small changes to the degree of assortment, was performed. As summarized in Figure 4, when assortative mating is present but not very common, the level of assortative mating decreases toward the ESS given by Equation 21, with selection on the modifier being strong (now of order ɛ, rather than
, so that sexual selection on the two alleles is exactly balanced. A QLE analysis, assuming weak selection and a modifier causing only small changes to the degree of assortment, was performed. As summarized in Figure 4, when assortative mating is present but not very common, the level of assortative mating decreases toward the ESS given by Equation 21, with selection on the modifier being strong (now of order ɛ, rather than 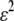 as before). Interestingly, if assortative mating is very common [above the thick curve in Figure 4, such that
as before). Interestingly, if assortative mating is very common [above the thick curve in Figure 4, such that 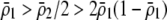 ], then even higher levels of assortment can evolve. This result was obtained by examining when the sign of
], then even higher levels of assortment can evolve. This result was obtained by examining when the sign of  switches according to the QLE approximation, but this switch coincides exactly with the point at which heterozygotes become less fit than homozygotes (
switches according to the QLE approximation, but this switch coincides exactly with the point at which heterozygotes become less fit than homozygotes ( switches from negative to positive). This switch occurs not because of natural selection but because of sexual selection. Indeed, natural selection can be absent (
switches from negative to positive). This switch occurs not because of natural selection but because of sexual selection. Indeed, natural selection can be absent (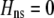 ) and yet the mating preferences would lead to complete assortative mating above the thick curve (Figure 4), solely because of the sexual selection induced (as noted by Arnegard and Kondrashov 2004).
) and yet the mating preferences would lead to complete assortative mating above the thick curve (Figure 4), solely because of the sexual selection induced (as noted by Arnegard and Kondrashov 2004).
Figure 4.—
Evolution when assortative mating is already common. The QLE results are shown for the preference-based model when 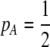 , as a function of the current level of assortment (vertical axis) and the relative preference against individuals that differ by one allele,
, as a function of the current level of assortment (vertical axis) and the relative preference against individuals that differ by one allele, 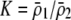 (horizontal axis). Modifiers that increase the rate of assortative mating decrease in frequency (
(horizontal axis). Modifiers that increase the rate of assortative mating decrease in frequency (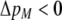 ) for the majority of the parameter space; assortment is expected to decrease until it reaches the ESS at
) for the majority of the parameter space; assortment is expected to decrease until it reaches the ESS at 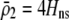 (horizontal line, illustrated for
(horizontal line, illustrated for 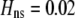 ). If
). If 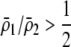 and if assortative mating is sufficiently common (above the thick curve), then higher rates of assortative mating are expected to evolve. If
and if assortative mating is sufficiently common (above the thick curve), then higher rates of assortative mating are expected to evolve. If 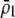 is a constant multiple of
is a constant multiple of 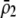 , then preferences will evolve either up or down (no horizontal movement). The preference function used by Matessi et al. (2001) constrains preferences to evolve along the dashed curve; the two points at which the QLE predicts that
, then preferences will evolve either up or down (no horizontal movement). The preference function used by Matessi et al. (2001) constrains preferences to evolve along the dashed curve; the two points at which the QLE predicts that 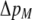 switches sign (the ESS at the solid star and the repelling point at the open star) are consistent with their numerical results for weak selection (their Table 3). The graph assumes no direct cost of assortative mating, weak selection, and modifiers of small effect. The shading at the top serves to remind the reader that the QLE assumptions fail to hold if reproductive isolation is nearly complete.
switches sign (the ESS at the solid star and the repelling point at the open star) are consistent with their numerical results for weak selection (their Table 3). The graph assumes no direct cost of assortative mating, weak selection, and modifiers of small effect. The shading at the top serves to remind the reader that the QLE assumptions fail to hold if reproductive isolation is nearly complete.
When assortative mating is rare and 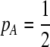 , the most common females are Aa heterozygotes, who prefer to mate with similar heterozygous males, inducing heterozygote advantage via sexual selection. If assortative mating is sufficiently common, as might be expected for previously allopatric populations that are already partially reproductively isolated, most females are homozygous and favor similar homozygous males, inducing heterozygote disadvantage via sexual selection (above the thick curve in Figure 4). While
, the most common females are Aa heterozygotes, who prefer to mate with similar heterozygous males, inducing heterozygote advantage via sexual selection. If assortative mating is sufficiently common, as might be expected for previously allopatric populations that are already partially reproductively isolated, most females are homozygous and favor similar homozygous males, inducing heterozygote disadvantage via sexual selection (above the thick curve in Figure 4). While 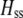 due to sexual selection is more complicated in the case of high levels of assortative mating (not presented), one can already see from Equation 18 that
due to sexual selection is more complicated in the case of high levels of assortative mating (not presented), one can already see from Equation 18 that 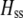 would increase as homozygotes become more common as long as females dislike males that differ by a single allele at least half as much as they dislike males that differ by two alleles (
would increase as homozygotes become more common as long as females dislike males that differ by a single allele at least half as much as they dislike males that differ by two alleles (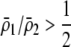 ). Once above the thick curve (Figure 4), sexual selection itself induces disruptive selection, facilitating the evolution of complete reproductive isolation. The bistability of low and high levels of assortative mating was also found by Doebeli (1996), Matessi et al. (2001), and Pennings et al. (2008) in similar modifier models and by Kirkpatrick and Ravigné (2002) in a model examining the dynamics of linkage disequilibrium between selected loci given a certain amount of assortative mating. The generality of this result suggests that, if preference-based assortative mating is commonplace, the evolution of higher rates of assortative mating would be more efficient at completing the process of speciation (“reinforcement,” in this case due to heterozygous “hybrids” having a hard time finding a mate) than initiating it.
). Once above the thick curve (Figure 4), sexual selection itself induces disruptive selection, facilitating the evolution of complete reproductive isolation. The bistability of low and high levels of assortative mating was also found by Doebeli (1996), Matessi et al. (2001), and Pennings et al. (2008) in similar modifier models and by Kirkpatrick and Ravigné (2002) in a model examining the dynamics of linkage disequilibrium between selected loci given a certain amount of assortative mating. The generality of this result suggests that, if preference-based assortative mating is commonplace, the evolution of higher rates of assortative mating would be more efficient at completing the process of speciation (“reinforcement,” in this case due to heterozygous “hybrids” having a hard time finding a mate) than initiating it.
Exact numerical simulations of the recursion equations confirm the existence of the two curves shown in Figure 4, using the fitness function 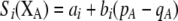 with the parameter values given in Figure 3 and with
with the parameter values given in Figure 3 and with 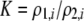 set to 0, 0.25, 0.5, 0.75, and 1. Particularly, even when
set to 0, 0.25, 0.5, 0.75, and 1. Particularly, even when 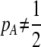 , a modifier allele that strengthens the degree of assortative mating increases when
, a modifier allele that strengthens the degree of assortative mating increases when  is small, decreases when
is small, decreases when  is between
is between  and the thick curve shown in Figure 4, and increases to fixation when
and the thick curve shown in Figure 4, and increases to fixation when 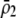 is above the thick curve.
is above the thick curve.
The above results ignored costs of assortment, but they remain valid if such costs are sufficiently weak. With strong costs, however, assortative mating is selected against at QLE, regardless of the current level of assortative mating. In particular, in the plant model with 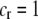 , the costs of rejecting dissimilar males and thereby losing the offspring that would have been produced are too severe to permit the evolution of nonrandom mating.
, the costs of rejecting dissimilar males and thereby losing the offspring that would have been produced are too severe to permit the evolution of nonrandom mating.
STABILITY ANALYSES
QLE analyses allow complex models to be analyzed more readily, because the steady-state values of the genetic associations are calculated in a separate step from assessing the allele-frequency dynamics. But QLE analyses require that selection be weak and that modifier alleles do not cause a large change in the level of assortment; otherwise the genetic associations can depart significantly from their steady-state values. In this section, we supplement the above results with local stability analyses, assuming that a new modifier allele, M, is introduced into a population at a stable equilibrium that is polymorphic for alleles A/a and fixed for allele m. Because these local stability analyses require the analysis of rather complicated stability matrices, we focus on two cases: the grouping model where Aa individuals form their own group (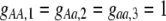 in Figure 1) and the preference-based model, ignoring costs in both cases. The technical details are presented in appendix c and in the Mathematica package available as supplemental material. As we shall see, the above conclusions remain valid qualitatively, even with strong selection and strong modifiers.
in Figure 1) and the preference-based model, ignoring costs in both cases. The technical details are presented in appendix c and in the Mathematica package available as supplemental material. As we shall see, the above conclusions remain valid qualitatively, even with strong selection and strong modifiers.
Stability analysis in the grouping model of assortative mating:
Several special cases of the genotypic grouping model with 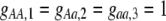 were considered (see appendix c). In each case, a modifier that increases the degree of assortative mating is able to spread when introduced into a population at an equilibrium where homozygotes are more fit, on average, than heterozygotes, regardless of the strength of selection or the effect of the modifier on levels of assortment. These results are entirely consistent with the QLE analysis.
were considered (see appendix c). In each case, a modifier that increases the degree of assortative mating is able to spread when introduced into a population at an equilibrium where homozygotes are more fit, on average, than heterozygotes, regardless of the strength of selection or the effect of the modifier on levels of assortment. These results are entirely consistent with the QLE analysis.
Stability analysis in the preference-based model of assortative mating:
In appendix c, we also describe results from stability analyses assuming 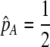 in the preference-based model. We first summarize the results when natural selection is weak. As in the QLE analysis, lower levels of assortative mating are generally favored except when the population mates nearly at random (and
in the preference-based model. We first summarize the results when natural selection is weak. As in the QLE analysis, lower levels of assortative mating are generally favored except when the population mates nearly at random (and 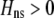 ) or when assortative mating is prevalent and females dislike males that differ by one allele almost as much as males that differ by two alleles. Indeed, the parameter space in which modifiers that increase assortment are favored is exactly as in Figure 4, based on the QLE analysis. The stability analysis provides the additional insight that modifiers causing a very large change in the level of assortative mating are favored if and only if modifiers causing a very small change are also favored. Ironically, this means that it is possible for a modifier causing complete assortment to invade a random-mating population but not a population in which there is already some level of assortment (between the line at
) or when assortative mating is prevalent and females dislike males that differ by one allele almost as much as males that differ by two alleles. Indeed, the parameter space in which modifiers that increase assortment are favored is exactly as in Figure 4, based on the QLE analysis. The stability analysis provides the additional insight that modifiers causing a very large change in the level of assortative mating are favored if and only if modifiers causing a very small change are also favored. Ironically, this means that it is possible for a modifier causing complete assortment to invade a random-mating population but not a population in which there is already some level of assortment (between the line at  and the thick curve in Figure 4). Numerical simulations using the fitness function
and the thick curve in Figure 4). Numerical simulations using the fitness function 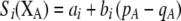 indicate that modifiers slightly increasing assortment within a randomly mating population spread only to a point at which
indicate that modifiers slightly increasing assortment within a randomly mating population spread only to a point at which 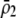 approximates
approximates 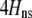 , while modifiers causing high levels of assortment (above the thick curve in Figure 4) are able to invade and spread to fixation.
, while modifiers causing high levels of assortment (above the thick curve in Figure 4) are able to invade and spread to fixation.
The stability analysis also allows us to investigate cases where natural selection is strong. Assuming that natural selection favors homozygotes (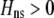 ), Figure 5 demonstrates that stronger natural selection facilitates the evolution of assortative mating by increasing the parameter space in which homozygotes have an overall higher fitness than heterozygotes under the combined forces of natural and sexual selection (
), Figure 5 demonstrates that stronger natural selection facilitates the evolution of assortative mating by increasing the parameter space in which homozygotes have an overall higher fitness than heterozygotes under the combined forces of natural and sexual selection (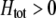 ). This result was also observed by Matessi et al. (2001), for the specific case where frequency-dependent selection (1) is a quadratic and symmetric function of the allele frequencies. Interestingly, the strength of natural selection does not have to be inordinately high to relax considerably the conditions under which assortative mating can evolve. Indeed, if natural selection favors homozygotes over heterozygotes by ≥10%, higher levels of assortative mating are able to invade an equilibrium with
). This result was also observed by Matessi et al. (2001), for the specific case where frequency-dependent selection (1) is a quadratic and symmetric function of the allele frequencies. Interestingly, the strength of natural selection does not have to be inordinately high to relax considerably the conditions under which assortative mating can evolve. Indeed, if natural selection favors homozygotes over heterozygotes by ≥10%, higher levels of assortative mating are able to invade an equilibrium with 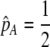 , regardless of the current level of assortative mating, as long as females dislike males that differ by one allele at least half as much as they dislike males that differ by two alleles (
, regardless of the current level of assortative mating, as long as females dislike males that differ by one allele at least half as much as they dislike males that differ by two alleles (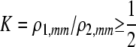 ). Thus, if natural selection in favor of homozygotes is sufficiently strong, bistability disappears, and assortative mating can evolve from initially low to high levels. Qualitatively similar results were obtained from a numerical stability analysis using a specific model of frequency-dependent selection with
). Thus, if natural selection in favor of homozygotes is sufficiently strong, bistability disappears, and assortative mating can evolve from initially low to high levels. Qualitatively similar results were obtained from a numerical stability analysis using a specific model of frequency-dependent selection with  (supplemental material).
(supplemental material).
Figure 5.—
Parameter space in which modifiers increasing the level of assortative mating are able to invade. The results of a local stability analysis for the preference-based model without costs are shown. Arrows indicate whether a modifier allele M that increases the level of assortative mating (by any amount) is able to invade an equilibrium with m fixed and  . The curves specify the parameter combinations at which
. The curves specify the parameter combinations at which 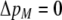 , which coincide with when
, which coincide with when 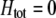 . Each curve is associated with a particular percentage by which natural selection favors homozygotes over heterozygotes, at the equilibrium before the M allele is introduced (solid boxes). Only when natural selection is weak (natural selection favors homozygotes by ∼ ≤1%) are the results similar to the QLE results summarized in Figure 4. The vertical axis gives the initial level of assortment
. Each curve is associated with a particular percentage by which natural selection favors homozygotes over heterozygotes, at the equilibrium before the M allele is introduced (solid boxes). Only when natural selection is weak (natural selection favors homozygotes by ∼ ≤1%) are the results similar to the QLE results summarized in Figure 4. The vertical axis gives the initial level of assortment 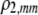 , while the horizontal axis measures how much females dislike males that differ by one allele relative to those that differ by two alleles,
, while the horizontal axis measures how much females dislike males that differ by one allele relative to those that differ by two alleles, 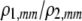 .
.
CONCLUSIONS
In this article, we have developed a framework for describing the evolutionary forces acting on the strength of assortative mating in response to selection at a single locus. Our goal was to keep the assumptions as general as possible: allowing for any form of frequency-dependent selection and for a range of mechanisms by which assortative mating can be accomplished, with or without costs. We assume that the level of assortative mating depends on the alleles carried at a modifier locus, M, and that assortative mating is based on the trait influenced by the selected locus itself, A. This framework describes a one-allele mechanism (Felsenstein 1981) because assortative mating can arise from the spread of a single allele at the M locus throughout the population. Our main results are as follows:
Higher levels of assortative mating are favored when homozygotes are, on average, fitter than heterozygotes.
This evolutionary force is countered by any costs of assortment, but assortative mating can still evolve as long as the costs are weak.
Assortative mating based on group formation is particularly favorable to the evolution of assortative mating; complete assortative mating can evolve in small or large steps from random mating as long as I continues to hold.
Assortative mating based on female mating preferences complicates matters by inducing sexual selection on the selected locus, which typically hinders but can sometimes facilitate the evolution of assortative mating, as discussed below.
These results are based on two techniques: a separation of timescales assuming weak selection (a “QLE” analysis) and a local stability analysis, the combination of which provides a fairly complete picture of the evolution of assortative mating in response to selection at a single-trait locus. These results are consistent with other studies (e.g., Matessi et al. 2001; Pennings et al. 2008), but by describing the general conditions under which higher levels of assortative mating can evolve—without recourse to specific assumptions about the nature of frequency-dependent selection or mating scheme—this article contributes to the large body of theoretical work on speciation by clarifying the key requirements for assortative mating to evolve in response to selection on a focal gene (see also de Cara et al. 2008 for an analysis of the multilocus case).
Several comments are in order. In an equilibrium population, homozygotes are, on average, fitter than heterozygotes (as required by result I) only if there is underdominance. Frequency-dependent selection favoring rare alleles is, however, necessary to maintain a polymorphism that exhibits underdominance. Models of competition can create such conditions (e.g., Dieckmann and Doebeli 1999; Matessi et al. 2001; Pennings et al. 2008), as can a number of other biologically relevant scenarios, for example, mating preferences for unusual mates, antagonistic species interactions with predators, herbivores, or parasites that are less able to recognize rare types, and mutualistic interactions that reward rare types (see, e.g., Doebeli and Dieckmann 2000).
Our model clarifies, however, that underdominance is not necessary for the evolution of assortative mating; in nonequilibrium populations, all that is required is that the heterozygote be closer in fitness to the less fit of the two homozygotes, not that the heterozygote be the least fit. For example, whenever a partially recessive beneficial allele arises and spreads within a population, assortative mating would be favored along the way. This process is self-limiting, however, because once the beneficial allele is fixed there is only one genotype at the trait locus and assortative mating is no different from random mating. Nevertheless, substantial levels of assortative mating could accumulate should variation be regenerated at any locus affecting the trait (through migration or mutation). Similarly, cases of coevolutionary cycles or arms races can generate persistent directional selection, which could drive the evolution of nonrandom mating. Indeed, we have recently shown that assortative mating is often favored in parasites, leading to host specialization (Nuismer et al. 2008).
If assortative mating is based on female preferences for similar males, the resulting sexual selection alters the relative fitnesses of heterozygotes and homozygotes. In certain cases, sexual selection can cause the fitness of heterozygotes to rise above the average fitness of homozygotes, preventing the further evolution of assortment. In particular, if heterozygotes are common (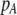 near
near  ) and/or if heterozygous males are relatively well liked by homozygous females (
) and/or if heterozygous males are relatively well liked by homozygous females (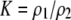 small), then heterozygous males have an easier time finding a mate than homozygous males, counteracting any fitness advantage of homozygotes generated by natural selection. In this case, as the level of assortative mating rises, mating preferences eliminate the fitness advantage of homozygotes necessary for the evolution of further increases in assortment. As a consequence, assortment tends to evolve from random mating only up to a point (
small), then heterozygous males have an easier time finding a mate than homozygous males, counteracting any fitness advantage of homozygotes generated by natural selection. In this case, as the level of assortative mating rises, mating preferences eliminate the fitness advantage of homozygotes necessary for the evolution of further increases in assortment. As a consequence, assortment tends to evolve from random mating only up to a point ( when
when  is near
is near  ; see Figure 3), as found by Matessi et al. (2001) using a particular form of frequency-dependent selection.
; see Figure 3), as found by Matessi et al. (2001) using a particular form of frequency-dependent selection.
On the other hand, if heterozygotes are rare (because assortative mating is already common or 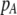 is far from
is far from  ) and if heterozygous males are not well liked by homozygous females (large
) and if heterozygous males are not well liked by homozygous females (large 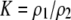 ), then sexual selection will itself contribute to the low fitness of heterozygotes experienced at the A locus. Essentially, this occurs whenever heterozygotes have a harder time finding a willing mate than homozygotes. Under these conditions, natural selection need not act at all (or indeed could induce some overdominance), and yet assortative mating by sexual selection can create the conditions (result I) needed for the evolution of more extreme levels of assortment, as found by Arnegard and Kondrashov (2004). This phenomenon is observed in the upper right-hand corner of Figure 4 for
), then sexual selection will itself contribute to the low fitness of heterozygotes experienced at the A locus. Essentially, this occurs whenever heterozygotes have a harder time finding a willing mate than homozygotes. Under these conditions, natural selection need not act at all (or indeed could induce some overdominance), and yet assortative mating by sexual selection can create the conditions (result I) needed for the evolution of more extreme levels of assortment, as found by Arnegard and Kondrashov (2004). This phenomenon is observed in the upper right-hand corner of Figure 4 for 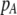 near
near  and on the right-hand side of supplemental Figure S2 for
and on the right-hand side of supplemental Figure S2 for 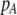 near
near 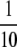 . An important implication is that if assortative mating is already commonplace, sexual selection can drive the evolution of complete reproductive isolation because heterozygotes have such difficulties finding mates. Thus, we predict that mechanisms of assortative mating that induce sexual selection (i.e., based on female preferences rather than group membership) should be particularly prevalent in cases where assortment evolves after previously isolated populations come back into contact and have some degree of reproductive isolation (reinforcement).
. An important implication is that if assortative mating is already commonplace, sexual selection can drive the evolution of complete reproductive isolation because heterozygotes have such difficulties finding mates. Thus, we predict that mechanisms of assortative mating that induce sexual selection (i.e., based on female preferences rather than group membership) should be particularly prevalent in cases where assortment evolves after previously isolated populations come back into contact and have some degree of reproductive isolation (reinforcement).
Even if total fitness (accounting for both natural and sexual selection) continues to exhibit underdominance, a further problem arises when assortative mating is based on mating preferences: carriers of the more common allele have less trouble finding a receptive mate than carriers of the rarer allele. Sexual selection thus favors the fixation of the common allele. When assortative mating is rare, this force is weak, but if assortative mating becomes common, sexual selection on the A locus becomes strong, unless the two alleles are nearly equal in frequency (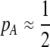 ). Thus, to maintain a polymorphism in the face of sexual selection, frequency-dependent natural selection must strongly favor the rarer allele (as in supplemental Figure S2).
). Thus, to maintain a polymorphism in the face of sexual selection, frequency-dependent natural selection must strongly favor the rarer allele (as in supplemental Figure S2).
In short, two obstacles to the evolution of assortative mating arise when females prefer similar mates: such preferences can (a) generate heterozygote advantage and (b) lead to the fixation of the common allele. In contrast, assortative mating that arises because individuals tend to cluster into groups within which they mate randomly raises no such obstacles, so that the degree of assortative mating will continue to rise as long as homozygotes remain fitter than heterozygotes.
It is worth emphasizing that when fitness is frequency dependent, the relative fitness of heterozygotes and homozygotes may very well change as assortative mating evolves. Depending on the nature of frequency dependence, it may be that underdominance is exhibited when the population is near Hardy–Weinberg, but that overdominance is exhibited when heterozygotes are rare. In this case, natural selection will favor the evolution of only partial assortative mating rather than complete assortative mating. This phenomenon was very nicely described by Pennings et al. (2008), using a model of competition. As they point out, if each genotype has a relatively narrow niche, then as homozygotes become increasingly common, a third niche opens up in the middle that can be filled by heterozygotes. Thus, as can be seen from their Figure 1, the evolution of complete assortative mating requires that the spectrum of resources that can be used by a genotype is narrow enough that the extremes of the resource distribution remain underutilized in a population at Hardy–Weinberg but not too narrow, or else the homozygotes will not exhaust the resource supply available to heterozygotes. Other forms of frequency-dependent selection may or may not lead to a switch from underdominance to overdominance as assortative mating evolves (for example, the model of rare-allele advantage used to generate supplemental Figure S2 does not). Clearly, the exact form of frequency-dependent natural selection is important to be able to predict whether partial or complete assortative mating is expected to evolve.
Overall, our results suggest that assortative mating that induces sexual selection (e.g., based on female mating preferences for similar mates) is not very conducive to the evolution of complete assortative mating starting from a random-mating population. Only when natural selection favors homozygotes over heterozygotes, natural selection is strong, the costs of assortment are low, and females prefer their own genotype over other genotypes (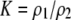 sufficiently large; see Figure 5 and supplemental Figure S2) do we expect complete assortment to evolve from no assortment. In contrast, assortative mating based on group formation is less restrictive, and we expect to see the evolution of complete assortative mating as long as homozygotes are more fit, on average, than heterozygotes and there is a low cost of assortment.
sufficiently large; see Figure 5 and supplemental Figure S2) do we expect complete assortment to evolve from no assortment. In contrast, assortative mating based on group formation is less restrictive, and we expect to see the evolution of complete assortative mating as long as homozygotes are more fit, on average, than heterozygotes and there is a low cost of assortment.
Interestingly, many purported cases of sympatric speciation can arguably be described as following a group-based form of assortative mating. Host races of phytophagous insects are thought to have evolved because individuals group together and mate on their preferred plant host (Berlocher and Feder 2002), as exemplified by the poster child of sympatric speciation: the apple maggot fly, Rhagoletis pomonella, in which a new host race formed on apples in the mid-1800s (Filchak et al. 2000). Cases of sympatric speciation in plants are often associated with shifts in flowering time (Gustafsson and Lonn 2003; Silvertown et al. 2005; Antonovics 2006; Savolainen et al. 2006) or shifts in pollen placement (Maad and Nilsson 2004), such that mating tends to occur within groups of similar plants. Similarly, grouping by location or timing during mating has been implicated in the evolution of assortative mating in salmon and birds (Hendry et al. 2007).
It is important to emphasize that focusing on a single-trait gene that is the target of both natural selection and nonrandom mating preferences, as we have done here, is particularly favorable to the evolution of assortative mating (Gavrilets 2003). Most importantly, whether or not assortment is favored does not depend on the rate of recombination between the modifier locus and the selected locus (observe that the recombination rate, r, does not enter into any of the QLE results and does not qualitatively affect the stability analyses). If mating preferences were based on similarity at a different locus (say “B”) than the target of natural selection A, recombination between these loci would weaken the link between assortative mating (at B) and the production of excess homozygotes (at A). Thus, our results can be seen as describing the necessary conditions for assortative mating to evolve in response to selection at a single selected gene; for models where assortment is based on a marker gene, not only must these necessary conditions be met, but also selection favoring excess homozygosity at the A locus must be sufficiently strong relative to the effective amount of recombination between the A and B loci. Because the effective rate of recombination goes down as the level of assortative mating goes up (recombination is only relevant in double heterozygotes), we conjecture that the higher the current level of assortative mating is, the less of a difference should be seen between our results and those from a model of assortative mating based on a separate marker locus.
Acknowledgments
We are grateful for the helpful and insightful comments provided by Alistair Blachford, Michael Doebeli, Fred Guillaume, Joachim Hermisson, Jason Hoeksema, Yannis Michalakis, Patrick Nosil, Michael Whitlock, and two anonymous reviewers. We also thank Nick Barton, Mark Kirkpatrick, and Joachim Hermisson for graciously sharing their unpublished manuscripts. Support was provided by the Natural Sciences and Engineering Research Council of Canada (S.P.O.), the National Science Foundation (NSF) [grant nos. DEB-0614166 (M.R.S.) and DEB-0343023 and DMS-0540392 (S.L.N.)], and the National Evolutionary Synthesis Center [NSF no. EF-0423641 (S.P.O., M.R.S.)].
APPENDIX A
Two variants of the grouping model discussed in the text (the “standard” grouping model) were explored to determine the sensitivity of the results to model assumptions.
Variant 1—mated males do not join the random-mating pool:
In the text, all males were allowed to join the lek, regardless of whether or not they had previously mated. Consequently, the standard grouping model does not ensure that all males have the same reproductive success, even though all females do, so the possibility of sexual selection remains. As an alternative, we considered a model where only unmated males join the lek, so that all females and all males have equal reproductive success. Specifically, the probability that a male genotype joins the random-mating pool is one minus the probability that it mated within a group. The QLE results for this alternative model are identical to Equations 6–12. Sexual selection is absent to order ɛ (see Equation 6) both in the grouping model considered above and in this variant model. The standard grouping model does, however, induce sexual selection to lower order than ɛ. When natural selection is absent, that is, when the fitnesses (1) are equal to one and the costs of assortment are zero, it can be shown that disequilibria develop and allele frequencies do change, but very slowly, at the modifier and selected loci in the standard grouping model but not in this variant. Nevertheless, we focus on the standard grouping model because the recursions are simpler.
Variant 2—the random-mating pool is a separate group:
Finally, we considered a model whereby individuals join a mixed-group lek with probability 1 − ρ during the grouping phase, rather than after the grouping phase. The remainder of the population, ρ, form into three groups according to their A-locus genotype, as described in Figure 1. Mating then occurs randomly within the lek and within the three groups. For example, during the mating season, individuals could either choose to swarm (joining the lek) or return to the host plant that they prefer (influenced by the A locus). In this variant model, the probability that a female of genotype AA at the trait locus and k at the modifier locus (k = MM, Mm, or mm) mates with a male of genotype Aa becomes
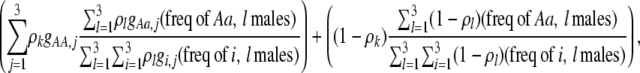 |
(A1) |
where j sums over the three groups, i sums over the three male genotypes at the trait locus 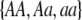 , and l sums over the three male genotypes at the modifier locus
, and l sums over the three male genotypes at the modifier locus 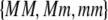 . A QLE analysis was performed on this variant model, assuming an initially low level of assortative mating. To leading order, the efficiency of assortative mating, θ, is the same as in the text, except that assortment has twice the effect on
. A QLE analysis was performed on this variant model, assuming an initially low level of assortative mating. To leading order, the efficiency of assortative mating, θ, is the same as in the text, except that assortment has twice the effect on 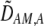 (doubling Equations 10 and 12) because males that are in a group are also likely to carry the modifier, doubling the chance that the modifier becomes associated with excess homozygosity. An additional difference is that assortative mating now occurs in groups that are smaller in number, because groups are restricted to those individuals who choose to mate assortatively, not all individuals. Thus, the relative costs of assortative mating are much larger, with
(doubling Equations 10 and 12) because males that are in a group are also likely to carry the modifier, doubling the chance that the modifier becomes associated with excess homozygosity. An additional difference is that assortative mating now occurs in groups that are smaller in number, because groups are restricted to those individuals who choose to mate assortatively, not all individuals. Thus, the relative costs of assortative mating are much larger, with 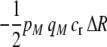 in (7) becoming
in (7) becoming 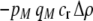 , whether or not individuals in the lek pay the relative cost of finding mates. Accounting for these changes, the QLE results (6)–(12) continue to hold.
, whether or not individuals in the lek pay the relative cost of finding mates. Accounting for these changes, the QLE results (6)–(12) continue to hold.
APPENDIX B
Here we consider the preference-based model of sexual selection with the generalized preference matrix:
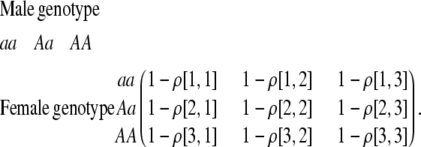 |
(B1) |
The modifier locus alters these preferences to  in MM females,
in MM females,  in Mm females, and
in Mm females, and 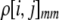 in mm females. While the preference matrix in the text (Equation 3) focused on assortative mating, matrix (B1) is much more general and can be used to describe disassortative mating (smaller diagonal elements) or mating preferences that are independent of the female's trait (rows are equivalent). A QLE analysis assuming weak selection in a population with initially weak assortative mating was performed, producing results analogous to those in the main text (Equations 15–21). Here, we present the specific changes caused by using preference matrix (B1) in place of (3). The frequency of allele A now changes by an amount given by Equation 6 due to natural selection plus
in mm females. While the preference matrix in the text (Equation 3) focused on assortative mating, matrix (B1) is much more general and can be used to describe disassortative mating (smaller diagonal elements) or mating preferences that are independent of the female's trait (rows are equivalent). A QLE analysis assuming weak selection in a population with initially weak assortative mating was performed, producing results analogous to those in the main text (Equations 15–21). Here, we present the specific changes caused by using preference matrix (B1) in place of (3). The frequency of allele A now changes by an amount given by Equation 6 due to natural selection plus
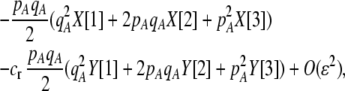 |
(B2a) |
where
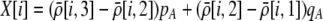 |
(B2b) |
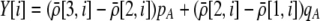 |
(B2c) |
and where 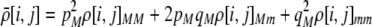 is the average mating preference that females of genotype i at the A locus exhibit toward males of genotype j at the A locus. The first row in (B2a) measures the effect of sexual selection on males that carry the A allele instead of the a allele, while the second row measures selection due to mating costs acting on females that carry the A allele instead of the a allele. The change in frequency of the modifier allele remains the same (compare to Equation 17), except that the costs of sex must be adjusted for the new mating scheme:
is the average mating preference that females of genotype i at the A locus exhibit toward males of genotype j at the A locus. The first row in (B2a) measures the effect of sexual selection on males that carry the A allele instead of the a allele, while the second row measures selection due to mating costs acting on females that carry the A allele instead of the a allele. The change in frequency of the modifier allele remains the same (compare to Equation 17), except that the costs of sex must be adjusted for the new mating scheme:
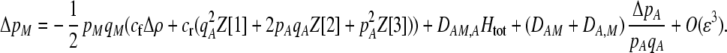 |
(B3a) |
Here,  measures the fixed costs of the new modifier allele, and
measures the fixed costs of the new modifier allele, and  measures the effect of the modifier on the degree of choosiness of females of genotype i at the A locus, given the current composition of the male population,
measures the effect of the modifier on the degree of choosiness of females of genotype i at the A locus, given the current composition of the male population,
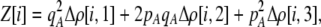 |
(B3b) |
where 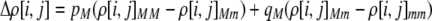 measures the effect of the modifier allele M on
measures the effect of the modifier allele M on  . If the costs of assortment are substantial (much larger than ɛ), the first line of (B3a) dominates the second, and modifiers that reduce female preference,
. If the costs of assortment are substantial (much larger than ɛ), the first line of (B3a) dominates the second, and modifiers that reduce female preference,  , will be favored.
, will be favored.
Henceforth, we assume that the costs of assortment are small (of order ɛ) and describe the contribution of the genetic associations in (B3a). The relative fitness of homozygotes vs. heterozygotes at the A locus is 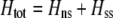 , where
, where 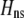 is given by (9b) and
is given by (9b) and
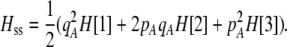 |
(B4a) |
Here, 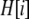 measures the impact of mate choice by females of genotype i at the A locus on
measures the impact of mate choice by females of genotype i at the A locus on  :
:
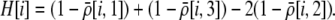 |
(B4b) |
Equations 19a and 20a continue to describe the QLE values of the disequilibria. The effect of the modifier allele M on 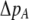 due to a single round of nonrandom mating becomes
due to a single round of nonrandom mating becomes
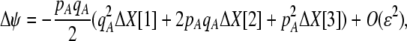 |
(B5a) |
where
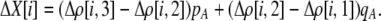 |
(B5b) |
 is positive if the modifier allele M increases the strength of sexual selection favoring the A allele and the A allele is currently preferred by females (i.e., the first line of B2a is positive). Plugging (B5) into Equation 19a and then into (B3) indicates that cis and trans linkage disequilibria favor the spread of modifiers that increase the strength of assortment as long as the sexually preferred allele is increasing in frequency. The final term that is needed to predict the change in modifier frequency is the effect of the modifier on the departure from Hardy–Weinberg (generalizing Equation 20b):
is positive if the modifier allele M increases the strength of sexual selection favoring the A allele and the A allele is currently preferred by females (i.e., the first line of B2a is positive). Plugging (B5) into Equation 19a and then into (B3) indicates that cis and trans linkage disequilibria favor the spread of modifiers that increase the strength of assortment as long as the sexually preferred allele is increasing in frequency. The final term that is needed to predict the change in modifier frequency is the effect of the modifier on the departure from Hardy–Weinberg (generalizing Equation 20b):
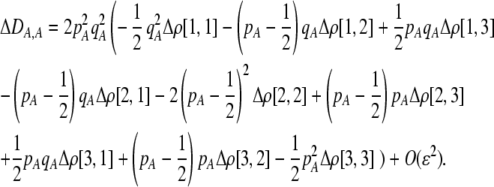 |
(B6) |
Modifier alleles that increase the production of homozygotes cause  to be positive. Equations B2–B6 reduce to Equations 17–20 given the symmetric preference matrix (3).
to be positive. Equations B2–B6 reduce to Equations 17–20 given the symmetric preference matrix (3).
APPENDIX C
Stability analysis in the grouping model of assortative mating:
We performed a local stability analysis of the genotypic grouping model with  (Figure 1) in the absence of costs. With m fixed, a potential equilibrium must satisfy
(Figure 1) in the absence of costs. With m fixed, a potential equilibrium must satisfy
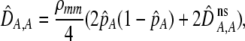 |
(C1) |
where we use a caret to denote an equilibrium value and “ns” to denote the value of a term after natural selection (all other terms are measured after offspring production). With m fixed, it can be shown that the equilibrium allele frequency is the same before and after natural selection in the grouping model (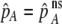 ). Because
). Because 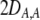 can never be <
can never be < 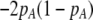 if measured at the same point in the life cycle, it follows that
if measured at the same point in the life cycle, it follows that 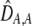 is positive (or zero) in the grouping model. We assume that the form of frequency-dependent selection is such that there is a stable internal polymorphism satisfying (C1) with allele frequency given by
is positive (or zero) in the grouping model. We assume that the form of frequency-dependent selection is such that there is a stable internal polymorphism satisfying (C1) with allele frequency given by 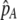 (depending on the form of frequency dependence, there may be multiple equilibria, each of which can be analyzed as follows). Introducing a small frequency of the M allele and linearizing the recursions around the equilibrium, we obtain a 7 × 7 local stability matrix, three of whose eigenvalues equal zero, and the remainder are the four roots of a quartic equation.
(depending on the form of frequency dependence, there may be multiple equilibria, each of which can be analyzed as follows). Introducing a small frequency of the M allele and linearizing the recursions around the equilibrium, we obtain a 7 × 7 local stability matrix, three of whose eigenvalues equal zero, and the remainder are the four roots of a quartic equation.
In the symmetric case with 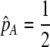 , the quartic factors into two quadratic equations, which are more readily analyzed, so we consider this special case first. If we were to consider a new modifier that has no effect (
, the quartic factors into two quadratic equations, which are more readily analyzed, so we consider this special case first. If we were to consider a new modifier that has no effect (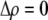 ), we would expect one of the eigenvalues to equal one (as expected for a neutral allele); this is true for one of the quadratic equations, so we concentrate on this equation, which has the form
), we would expect one of the eigenvalues to equal one (as expected for a neutral allele); this is true for one of the quadratic equations, so we concentrate on this equation, which has the form 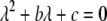 . It can be shown that the minimum of this quadratic lies between −1 and +1. Furthermore, we are guaranteed that the leading eigenvalue will be real and nonnegative by the Perron–Frobenius theorem (because the matrix is nonnegative; Gantmacher 1989). Thus, the condition required for a new modifier to invade (i.e., for a solution of
. It can be shown that the minimum of this quadratic lies between −1 and +1. Furthermore, we are guaranteed that the leading eigenvalue will be real and nonnegative by the Perron–Frobenius theorem (because the matrix is nonnegative; Gantmacher 1989). Thus, the condition required for a new modifier to invade (i.e., for a solution of 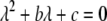 to be greater than one) is satisfied if and only if the value of the quadratic is negative when λ is set to one (because the quadratic equation must rise and become positive as λ goes to positive infinity). The value of the characteristic polynomial when λ is set to one can be calculated and equals
to be greater than one) is satisfied if and only if the value of the quadratic is negative when λ is set to one (because the quadratic equation must rise and become positive as λ goes to positive infinity). The value of the characteristic polynomial when λ is set to one can be calculated and equals
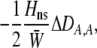 |
(C2) |
where 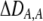 measures the effect of the modifier on the departure from Hardy–Weinberg following a single round of mating, given by
measures the effect of the modifier on the departure from Hardy–Weinberg following a single round of mating, given by 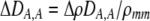 . According to (C2), a modifier allele that increases assortative mating will invade if and only if homozygotes are favored by frequency-dependent selection at the polymorphic equilibrium (
. According to (C2), a modifier allele that increases assortative mating will invade if and only if homozygotes are favored by frequency-dependent selection at the polymorphic equilibrium (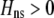 ).
).
Unfortunately, it is difficult to interpret the characteristic polynomial when 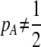 because we are left with a quartic equation, which does not factor and can have multiple roots greater than one. Nevertheless, we examined three other special cases, which could be analyzed using perturbation techniques (summarized in Otto and Day 2007): (i) weak natural selection (i.e., fitnesses in Equation 1 near one), (ii) a weak modifier allele (
because we are left with a quartic equation, which does not factor and can have multiple roots greater than one. Nevertheless, we examined three other special cases, which could be analyzed using perturbation techniques (summarized in Otto and Day 2007): (i) weak natural selection (i.e., fitnesses in Equation 1 near one), (ii) a weak modifier allele (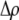 near zero), and (iii) a low or a high frequency of allele A (
near zero), and (iii) a low or a high frequency of allele A (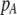 near zero or one). In each case, the results obtained were consistent with the conclusion that a modifier can spread if and only if
near zero or one). In each case, the results obtained were consistent with the conclusion that a modifier can spread if and only if 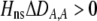 . Furthermore, it can be shown that when
. Furthermore, it can be shown that when 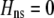 , the leading eigenvalue is always one and rises above one as
, the leading eigenvalue is always one and rises above one as 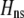 increases from zero for a modifier that increases assortative mating (
increases from zero for a modifier that increases assortative mating (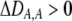 ). (Detailed results and proofs are provided in the accompanying online Mathematica package.) Thus, in all cases of the grouping model considered, modifiers that increase assortment invade if homozygotes are more fit, on average, than heterozygotes at an equilibrium with frequency-dependent selection.
). (Detailed results and proofs are provided in the accompanying online Mathematica package.) Thus, in all cases of the grouping model considered, modifiers that increase assortment invade if homozygotes are more fit, on average, than heterozygotes at an equilibrium with frequency-dependent selection.
Stability analysis in the preference-based model of assortative mating:
With allele m fixed and 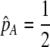 in a model of female preferences, the system reaches an equilibrium at which the departure from Hardy–Weinberg depends on the current degree of assortative mating:
in a model of female preferences, the system reaches an equilibrium at which the departure from Hardy–Weinberg depends on the current degree of assortative mating:
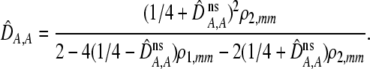 |
(C3) |
Introducing a small frequency of the M allele and linearizing the recursions around the equilibrium, we obtain a 7 × 7 local stability matrix, three of whose eigenvalues again equal zero, and the remainder are the four roots of a quartic equation, which factors into two quadratics when 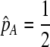 . Again only one of the quadratic equations gives an eigenvalue of one when the modifier is neutral (
. Again only one of the quadratic equations gives an eigenvalue of one when the modifier is neutral (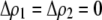 ), so we concentrate on this equation. It can be shown that the minimum of this quadratic lies between −1 and +1. Furthermore, the leading eigenvalue will again be real and nonnegative by the Perron–Frobenius theorem. Thus, a new modifier will invade if and only if the value of the quadratic is negative when λ is set to one. The value of the characteristic polynomial when λ is set to one can be calculated and equals
), so we concentrate on this equation. It can be shown that the minimum of this quadratic lies between −1 and +1. Furthermore, the leading eigenvalue will again be real and nonnegative by the Perron–Frobenius theorem. Thus, a new modifier will invade if and only if the value of the quadratic is negative when λ is set to one. The value of the characteristic polynomial when λ is set to one can be calculated and equals
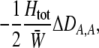 |
(C4) |
where again 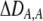 measures the effect of the modifier on the departure from Hardy–Weinberg following a single round of mating, given by
measures the effect of the modifier on the departure from Hardy–Weinberg following a single round of mating, given by
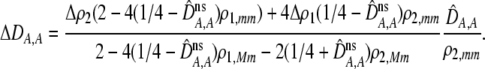 |
(C5) |
Thus, a modifier allele that increases assortative mating (causing 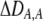 to be positive) will invade if and only if homozygotes have a higher fitness, on average, at the polymorphic equilibrium, accounting for both natural and sexual selection (
to be positive) will invade if and only if homozygotes have a higher fitness, on average, at the polymorphic equilibrium, accounting for both natural and sexual selection (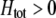 ). We determined when
). We determined when 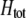 would remain at zero by solving for equilibria that also satisfy (C3); the result is illustrated in Figure 5. According to (C4), no further change in assortative mating is expected along these curves.
would remain at zero by solving for equilibria that also satisfy (C3); the result is illustrated in Figure 5. According to (C4), no further change in assortative mating is expected along these curves.
References
- Anderson, J. B., C. Sirjusingh, A. B. Parsons, C. Boone, C. Wickens et al., 2003. Mode of selection and experimental evolution of antifungal drug resistance in Saccharomyces cerevisiae. Genetics 163 1287–1298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antonovics, J., 2006. Evolution in closely adjacent plant populations X: long-term persistence of prereproductive isolation at a mine boundary. Heredity 97 33–37. [DOI] [PubMed] [Google Scholar]
- Arnegard, M. E., and A. S. Kondrashov, 2004. Sympatric speciation by sexual selection alone is unlikely. Evolution 58 222–237. [PubMed] [Google Scholar]
- Balkau, B. J., and M. W. Feldman, 1973. Selection for migration modification. Genetics 74 171–174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton, N. H., and M. Turelli, 1991. Natural and sexual selection on many loci. Genetics 127 229–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berlocher, S. H., and J. L. Feder, 2002. Sympatric speciation in phytophagous insects: Moving beyond controversy? Annu. Rev. Entomol. 47 773–815. [DOI] [PubMed] [Google Scholar]
- Coyne, J. A., and H. A. Orr, 2004. Speciation. Sinauer Associates, Sunderland, MA.
- Darwin, C., 1859. The Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. Modern Library, New York. [PMC free article] [PubMed]
- de Cara, M. A. R., N. H. Barton and M. Kirkpatrick, 2008. A model for the evolution of assortative mating. Am. Nat. 171 580–596. [DOI] [PubMed] [Google Scholar]
- Dieckmann, U., and M. Doebeli, 1999. On the origin of species by sympatric speciation. Nature 400 354–357. [DOI] [PubMed] [Google Scholar]
- Dobzhansky, T., 1940. Speciation as a stage in evolutionary divergence. Am. Nat. 74 312–321. [Google Scholar]
- Dobzhansky, T., 1941. Genetics and the Origin of Species. Columbia University Press, New York.
- Doebeli, M., 1996. A quantitative genetic competition model for sympatric speciation. J. Evol. Biol. 9 893–909. [Google Scholar]
- Doebeli, M., 2005. Adaptive speciation when assortative mating is based on female preference for male marker traits. J. Evol. Biol. 18 1587–1600. [DOI] [PubMed] [Google Scholar]
- Doebeli, M., and U. Dieckmann, 2000. Evolutionary branching and sympatric speciation caused by different types of ecological interactions. Am. Nat. 156 S77–S101. [DOI] [PubMed] [Google Scholar]
- Doebeli, M., and U. Dieckmann, 2003. Speciation along environmental gradients. Nature 421 259–264. [DOI] [PubMed] [Google Scholar]
- Endler, J. A., 1977. Geographic Variation, Speciation, and Clines. Princeton University Press, Princeton, NJ. [PubMed]
- Felsenstein, J., 1981. Skepticism towards Santa Rosalia, or why are there so few kinds of animals? Evolution 35 124–138. [DOI] [PubMed] [Google Scholar]
- Filchak, K., J. Roethele and J. Feder, 2000. Natural selection and sympatric divergence in the apple maggot Rhagoletis pomonella. Nature 407 739–742. [DOI] [PubMed] [Google Scholar]
- Gantmacher, F. R., 1989. The Theory of Matrices, Vol. 2. Chelsea, New York.
- Gavrilets, S., 2003. Perspective: models of speciation: What have we learned in 40 years? Evol. Int. J. Org. Evol. 57 2197–2215. [DOI] [PubMed] [Google Scholar]
- Gavrilets, S., 2004. Fitness Landscapes and the Origin of Species. Princeton University Press, Princeton, NJ/Oxford.
- Gavrilets, S., H. Li and M. D. Vose, 1998. Rapid parapatric speciation on holey adaptive landscapes. Proc. Biol. Sci. 265 1483–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gavrilets, S., H. Li and M. D. Vose, 2000. Patterns of parapatric speciation. Evol. Int. J. Org. Evol. 54 1126–1134. [DOI] [PubMed] [Google Scholar]
- Gustafsson, S., and M. Lonn, 2003. Genetic differentiation and habitat preference of flowering-time variants within Gymnadenia conopsea. Heredity 91 284–292. [DOI] [PubMed] [Google Scholar]
- Hauber, M. E., and P. W. Sherman, 2001. Self-referent phenotype matching: theoretical considerations and empirical evidence. Trends Neurosci. 24 609–616. [DOI] [PubMed] [Google Scholar]
- Hendry, A. P., P. Nosil and L. H. Rieseberg, 2007. The speed of ecological speciation. Funct. Ecol. 21 455–464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higashi, M., G. Takimoto and N. Yamamura, 1999. Sympatric speciation by sexual selection. Nature 402 523–526. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick, M., 1982. Sexual selection and the evolution of female choice. Evolution 36 1–12. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick, M., and S. L. Nuismer, 2004. Sexual selection can constrain sympatric speciation. Proc. R. Soc. Lond. B Biol. Sci. 271 687–693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick, M., and V. Ravigné, 2002. Speciation by natural and sexual selection: models and experiments. Am. Nat. 159 S22–S35. [DOI] [PubMed] [Google Scholar]
- Kirkpatrick, M., T. Johnson and N. Barton, 2002. General models of multilocus evolution. Genetics 161 1727–1750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov, A. S., and F. A. Kondrashov, 1999. Interactions among quantitative traits in the course of sympatric speciation. Nature 400 351–354. [DOI] [PubMed] [Google Scholar]
- Maad, J., and L. A. Nilsson, 2004. On the mechanism of floral shifts in speciation: gained pollination efficiency from tongue- to eye-attachment of pollinia in Platanthera (Orchidaceae). Biol. J. Linn. Soc. 83 481–495. [Google Scholar]
- Matessi, C., A. Gimelfarb and S. Gavrilets, 2001. Long-term buildup of reproductive isolation promoted by disruptive selection: How far does it go? Selection 2 41–64. [Google Scholar]
- Maynard Smith, J., 1966. Sympatric speciation. Am. Nat. 100 637–650. [Google Scholar]
- Moore, W. S., 1979. A single locus mass-action model of assortative mating, with comments on the process of speciation. Heredity 42 173–186. [Google Scholar]
- Nagylaki, T., 1993. The evolution of multilocus systems under weak selection. Genetics 134 627–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuismer, S. L., S. P. Otto and F. Blanquart, 2008. Host-parasite interactions and the evolution of non-random mating and parasite speciation. Ecol. Lett. (in press). [DOI] [PubMed]
- O'Donald, P., 1960. Assortative mating in a population in which two alleles are segregating. Heredity 15 389–396. [Google Scholar]
- Orr, H. A., and L. H. Orr, 1996. Waiting for speciation: the effect of population subdivision on the time to speciation. Evolution 50 1742–1749. [DOI] [PubMed] [Google Scholar]
- Ortíz-Barrientos, D., and M. Noor, 2005. Evidence for a one-allele assortative mating locus. Science 310 1467. [DOI] [PubMed] [Google Scholar]
- Otto, S., and T. Day, 2007. A Biologist's Guide to Mathematical Modeling in Ecology and Evolution. Princeton University Press, Princeton, NJ.
- Pennings, P. S., M. Kopp, G. Meszena, U. Dieckmann and J. Hermisson, 2008. An analytically tractable model for competitive speciation. Am. Nat. 171 E44–E71. [DOI] [PubMed] [Google Scholar]
- Savolainen, V., M. C. Anstett, C. Lexer, I. Hutton, J. J. Clarkson et al., 2006. Sympatric speciation in palms on an oceanic island. Nature 441 210–213. [DOI] [PubMed] [Google Scholar]
- Schneider, K. A., and R. Bürger, 2006. Does competitive divergence occur if assortative mating is costly. J. Evol. Biol. 19 570–588. [DOI] [PubMed] [Google Scholar]
- Silvertown, J., C. Servaes, P. Biss and D. Macleod, 2005. Reinforcement of reproductive isolation between adjacent populations in the Park Grass Experiment. Heredity 95 198–205. [DOI] [PubMed] [Google Scholar]
- Turelli, M., N. H. Barton and J. A. Coyne, 2001. Theory and speciation. Trends Ecol. Evol. 16 330–343. [DOI] [PubMed] [Google Scholar]
- Udovic, D., 1980. Frequency-dependent selection, disruptive selection, and the evolution of reproductive isolation. Am. Nat. 116 621–641. [Google Scholar]
- Verzijden, M. N., R. F. Lachlan and M. R. Servedio, 2005. Female mate-choice behavior and sympatric speciation. Evolution 59 2097–2108. [PubMed] [Google Scholar]