Loss of Least-Loaded Class in Asexual Populations Due to Drift and Epistasis

Abstract

We consider the dynamics of a nonrecombining haploid population of finite size that accumulates deleterious mutations irreversibly. This ratchet-like process occurs at a finite speed in the absence of epistasis, but it has been suggested that synergistic epistasis can halt the ratchet. Using a diffusion theory, we find explicit analytical expressions for the typical time between successive clicks of the ratchet for both nonepistatic and epistatic fitness functions. Our calculations show that the interclick time is of a scaling form that in the absence of epistasis gives a speed that is determined by size of the least-loaded class and the selection coefficient. With synergistic interactions, the ratchet speed is found to approach zero rapidly for arbitrary epistasis. Our analytical results are in good agreement with the numerical simulations.

IN an asexual population of size N, even the fittest individuals can be lost by stochastic fluctuations arising due to the finiteness of the population size. If the individual's genome is long enough that the back mutations can be ignored and recombination is absent, the minimum number of deleterious mutations (least-loaded class) in a finite population increases irreversibly (Muller 1964; Felsenstein 1974). For this reason, this process has been invoked as a potential cause for the evolution of sex and recombination (Hurst and Peck 1996; Judson and Normark 1996; Barton and Charlesworth 1998), degeneration of nonrecombining parts like Y chromosome (Charlesworth 1978) and mitochondrial DNA (Loewe 2006) of sexually reproducing organisms, and extinction of obligately asexual populations by mutational meltdown (Gabriel et al. 1993).

Due to the irreversible accumulation of deleterious mutations, the process described above acts like a ratchet, each click of which corresponds to the loss of the least-loaded class. In the simplest model known as Muller's ratchet, the ratchet clicks at a constant rate that depends on the population size N, mutation rate U, and selection coefficient s. The ratchet speed is also known to depend on other biologically relevant factors such as recombination rate (Bell 1988; Charlesworth et al. 1993), epistatic interactions (Kondrashov 1994; Butcher 1995; Schultz and Lynch 1997), fraction and selection coefficient of favorable mutations (Woodcock and Higgs 1996; Bachtrog and Gordo 2004), and spatial structure of the population (Combadão et al. 2007). Although extensive numerical data for the ratchet speed are available, very few analytical results are known.

As it is desirable to stop or at least slow down the ratchet, several mechanisms with this objective have been proposed (Bell 1988; Wagner and Gabriel 1990; Charlesworth et al. 1993). One such proposal is to include epistatic interactions in the genome fitness (Charlesworth et al. 1993; Kondrashov 1994). It has been observed experimentally that the gene loci do not always contribute independently to the genome fitness (Wolf et al. 2000; De Visser and Elena 2007) and the effect of two deleterious mutations can be better (antagonistic) or worse (synergistic) than were they to act independently. For Muller's ratchet operating under epistatic selection, it was noted using numerical simulations that “sufficiently strong synergistic epistasis can effectively halt the action of Muller's ratchet” (Kondrashov 1994, p. 1469). However it was not shown how the ratchet speed approaches zero asymptotically and how much epistatic interaction is required to halt the ratchet.

In this article, besides the classic Muller's ratchet that assumes haploid asexual population evolving on a fitness landscape in which each gene locus contributes independently to the fitness of the genome, we also study Kondrashov's model that considers fitness functions with epistatic interactions. We assume that an individual with k mutations has a fitness

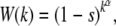(1)

where s is the selection coefficient. For α = 1, the epistatic interactions are absent while α > 1 corresponds to synergistically epistatic fitness. Our main purpose is to obtain explicit analytical expressions for the typical time 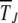elapsed between the (J − 1)th and Jth click of the ratchet in these models. If the time spent between any two successive clicks is found to be constant, then the ratchet turns with a finite speed 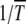, while it is said to be halted at large times if the interclick time increases with the number of accumulated mutations.

In the past, Muller's ratchet has been investigated using a diffusion approximation that assumes that the population n₀ of the least-loaded class is large and applies to a slowly clicking ratchet (Stephan et al. 1993; Gordo and Charlesworth 2000a; Stephan and Kim 2002). The opposite situation of small n₀ and high ratchet rate has been described by a moments method (Gabriel et al. 1993; Gessler 1995; Higgs and Woodcock 1995; Prügel-Bennett 1997; Rouzine et al. 2003). In this article, we adopt the first method that works in the parameter range for which 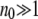and the ratchet clicks are slow enough that the population can equilibrate between successive clicks. This requires the knowledge of the steady-state properties of an infinitely large population that are known exactly for Muller's ratchet (Kimura and Maruyama 1966; Higgs 1994) but have been studied numerically for the epistatic case (Kondrashov 1994). After defining the models in the following section, we solve the deterministic quasi-species equation in steady state for α > 1 and show that the population frequency of the class with a minimum number J of mutations increases with J. These deterministic results are then used to find an expression for the typical time 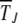in terms of a double integral over the frequency of the least-loaded class that has been evaluated numerically for α = 1 (Stephan et al. 1993; Gordo and Charlesworth 2000a). Here we estimate these integrals analytically and find that for a broad range of parameters, the average interclick time is of a scaling form (29) for any α ≥ 1. For α = 1, it is shown that the ratchet speed is a function of the number n₀ = Ne^−U/s in the least-loaded class and the selection coefficient s and not n₀ alone as assumed in previous studies (Haigh 1978). With epistatic interactions, the time 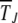is found to increase faster than any power law with J for any α > 1. Thus, an arbitrarily small amount of epistasis is sufficient to halt the ratchet with the ratchet speed approaching zero as ∼1/t for large time t.

MODELS

We consider a haploid asexual population evolving via mutation–selection dynamics starting with an initial condition in which all the individuals in the population have zero mutations. The genome length is assumed to be infinite so that back mutations can be ignored. If the population has a finite size N, it evolves stochastically following the discrete-time Wright–Fisher dynamics. An offspring in generation t + 1 chooses a parent in the previous generation with a probability proportional to the fitness of the parent. Then the probability P(n) that a parent p carrying k mutations and with fitness W(k; p) has n descendants in one generation is given by

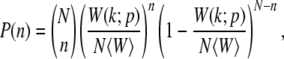(2)

where 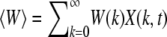is the average fitness of the finite population in generation t. Here we have defined X(k, t) as the fraction of the population with k mutations in a single sampling of the Wright–Fisher process. From the above equation, it follows that the average number of offspring produced in one generation is proportional to the parent's fitness and the relative variance in offspring number decays as 1/N. This fact is useful in defining the diffusion coefficient (24) within the diffusion approximation discussed in a later section. Following replication, mutations are introduced, where the number of new mutations is a random variable chosen from a Poisson distribution with mean U. In the simulations, the above process was implemented but the order of mutation and selection was reversed. An individual picked randomly from the population at time t was first mutated and the resulting mutant was allowed to survive at t + 1 with a probability equal to its fitness. This process was repeated until the generation t + 1 has N members and the population fraction X(k, t + 1) was recorded. It is useful to define X_J(k, t) = X(J + k, t), where J is the minimum number of mutations in the population at time t so that X_J(k, t) = 0 for k < 0. If X_J(0, τ_J) becomes zero, the least-loaded class J is lost and the ratchet has clicked at time τ_J.

The ratchet effect due to which the least-loaded class is lost is essentially a stochastic problem arising due to the finite number N of individuals in the population. However, as we describe later, the population fluctuates close to the deterministic frequency between two clicks of the ratchet. For this reason, we also study the problem of an infinite population for which the density fluctuations vanish and the average population fraction with k mutations at time t obeys a deterministic quasi-species equation (Eigen 1971; Jain and Krug 2007). Similar to the finite population problem, we define 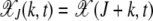, where 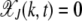for k < 0. Then neglecting the back mutations for a genome of infinite length (Higgs 1994), the fraction 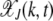evolves according to the difference equation

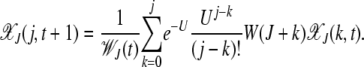(3)

In this equation, the population fraction with k mutations replicates with fitness W(k) and accumulates further mutations that are Poisson distributed with a mean U. The average fitness 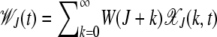in the denominator ensures that the number density is conserved.

STEADY STATE OF THE QUASI-SPECIES MODEL

Here we calculate the steady-state population frequency 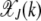in the error class J + k. Unlike for the multiplicative fitness case, the frequency 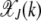depends on J for the epistatic fitness function (Haigh 1978). In particular, the fraction 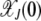(later abbreviated as 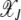) in the least-loaded class is expected to increase with J for α > 1 and decrease for α < 1. This can be explained by a simple argument that has also been used to understand the error threshold phenomenon (Eigen 1971; Jain and Krug 2007) in which the fittest genomic sequence can get lost beyond a critical mutation rate in populations evolving on epistatic fitness landscapes (Wiehe 1997). Consider the ratio 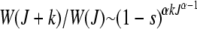for 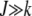. For synergistic interactions, the error class J + k in the neighborhood of the least-loaded class has a fitness much worse than the fitness of class J, rendering selection effective in localizing the population in the class with J mutations. With increasing J, the selection pressure increases further. Thus we may expect the population frequency 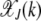to peak around J and 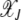to increase with J. On the other hand, in the case of antagonistic epistasis (α < 1), the fitness landscape is nearly neutral at large J so that the least-loaded sequence can be lost even in the deterministic limit (finite error threshold) (Wiehe 1997).

In the steady state, the quasi-species Equation 3 reduces to

(4)

where 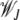is the average fitness in the steady state when the least-loaded class is J. The equation for j = 0 immediately shows that

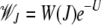(5)

(Kimura and Maruyama 1966; Haigh 1978). For j = 1 in (4), we have

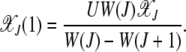Plugging this expression in the equation for j = 2, after some algebra we obtain

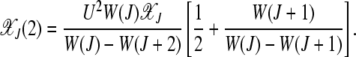Similarly, the fraction in the error class J + 3 is

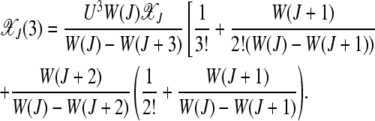From the expressions for 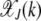for k = 2, 3 shown above, it is clear that in the weak selection limit s → 0, the leading-order contribution to 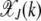comes from the last term. In general, we can write

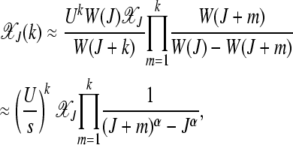(6)

where the population 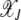in the least-loaded class is determined using the normalization condition .

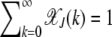Using the preceding equation for the multiplicative fitness function, we obtain the well-known result

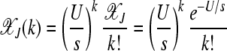(7)

(Kimura and Maruyama 1966). The fraction 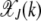for all k is seen to be independent of J (Haigh 1978). For a synergistically epistatic fitness landscape with α = 2 in fitness function (1), we have

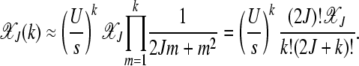(8)

On summing both sides over k, we find

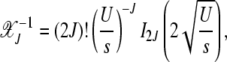(9)

where I_n(z) is the modified Bessel function of the first kind (Abramowitz and Stegun 1964). The fraction 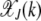with J + k mutations is then given by

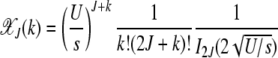(10)

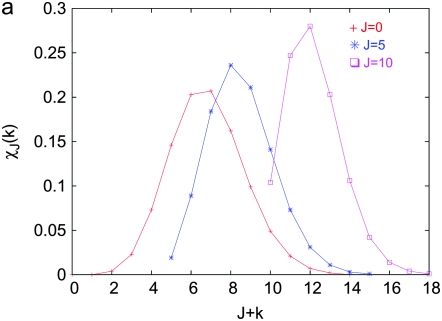
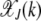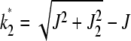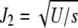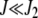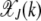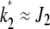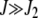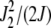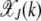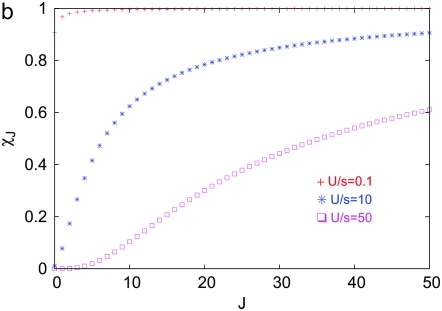
and is plotted in Figure 1a as function of J + k at a fixed U/s. From the above equation, we find that for a given J, the fraction is centered at , where . For , the distribution peaks at , while for , it is maximized at (see Figure 1a). Thus for large J, as argued at the beginning of this section, the distribution localizes close to k = 0. The behavior of the least-loaded fraction 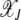shown in Figure 1b also depends on J₂. For large J₂ (i.e., weak selection), the fraction 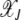increases toward unity slower than for small J₂. Using the asymptotic expansion of the Bessel function I_n(z) for large orders (Abramowitz and Stegun 1964) in (9), we have

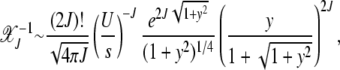(11)

where we have defined y = J₂/J. For 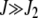, the above expression can be simplified to give 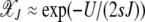, which asymptotically approaches unity. Thus with increasing J, most of the population tends to stay in the least-loaded class.

Figure 1.—

Steady state of the quasi-species model on the synergistic fitness landscape with α = 2. (a) Fraction 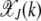as a function of J + k for U/s = 50 given by (10). (b) Fraction 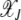of the least-loaded class J calculated using (9).

For arbitrary α > 1, it does not seem possible to obtain an explicit expression for 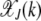. However, using the insights obtained from the α = 2 case, we can find 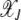for large J. We expect that for any α > 1, a least-loaded class J_α exists such that the population frequency 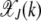with 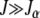is nonzero for 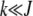. In such a case, the denominator under the product sign in (6) can be expanded for 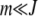to leading orders and yield

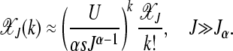(12)

As 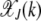decays fast with k, we can sum over both sides of the above solution to obtain

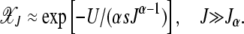(13)

This expression matches the exact results for α = 1 and 2 discussed above. The product in (6) seems hard to calculate for 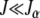. But for J = 0, we immediately have

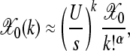(14)

which peaks at 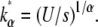By analogy with the α = 2 case, this suggests that J_α = (U/s)^1/α.

TIME BETWEEN SUCCESSIVE CLICKS OF THE RATCHET

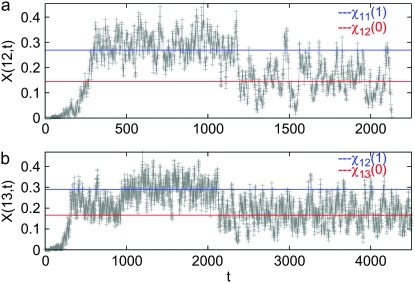
In this section, we first describe the process by which the ratchet clicks and then calculate an expression for the typical time between successive clicks using a diffusion theory (Ewens 1979). Let X(k, t) denote the fraction of population with k mutations at time t in a single realization of the Wright–Fisher process. Figure 2 shows the time evolution of X(k, t) for k = 12 and 13 starting from an initial condition in which all the N individuals carry zero mutations. As Figure 2a illustrates, the fraction X(12, t) increases from zero to a steady-state fraction about which it fluctuates until a time τ₁₁ = 1194 after which it relaxes to another steady state before finally dropping to zero at τ₁₂ = 2130 due to stochastic fluctuations. At t = τ₁₂, the ratchet is said to have clicked as the least-loaded class with 12 mutations gets irreversibly lost and the class with 13 mutations shown in Figure 2b becomes the new least-loaded class that itself gets lost at τ₁₃ = 5235. Since the ratchet is clicking at a slow rate, X(k, t) has an opportunity to equilibrate. As Figure 2b shows, soon after time τ₁₂, the fraction X(13, t) fluctuates about a steady-state fraction that is close to the deterministic frequency 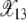given by (9). Similarly, X(12, t) in Figure 2a oscillates about 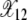after the 11th error class is lost until time τ₁₂. As a click of the ratchet is signaled by the change in the average value of X(k, t), it follows that the 11th class is lost at τ₁₁. For τ₁₁ < t < τ₁₂ as there are at least 12 mutations in the population, the fraction X(13, t) equilibrates about the frequency 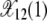. Thus the population fraction X(k, t) for fixed k passes through a series of steady states with frequency 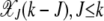before reaching the final absorbing state X(k, τ_k) = 0. Note that this description of the mechanism by which the ratchet clicks assumes that the population 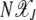in the currently least-loaded class J far exceeds one and thus has a chance to attain equilibrium before the next click.

Figure 2.—

Time evolution of the fraction X(k, t) for k = 12 (a) and 13 (b) to illustrate the advance of the ratchet on epistatic fitness landscapes. Here α = 2, N = 256, U = 0.25, and s = 0.005.

We use the diffusion approximation proposed in Stephan et al. (1993) to find the average interclick time 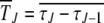between the (J − 1)th and Jth click of the ratchet where 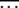stands for averaging over stochastic histories. Let the random variable X_J ∈ [0, 1] denote the population fraction in the least-loaded class J. If X_J = 0 at time t, the current least-loaded class J is lost forever and the ratchet is said to have clicked at t. We are interested in calculating the average time 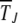required to reach the absorbing state X_J = 0 starting from 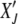at t′. The probability distribution P(X_J, t | 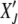, t′) obeys the backward Fokker–Planck equation

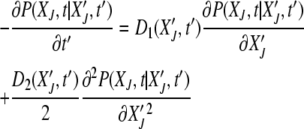(15)

(Risken 1996), where

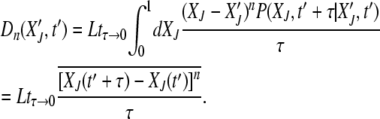(16)

As the coefficients D_n in (15) are independent of t′ (see below), the average interclick time 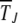defined as

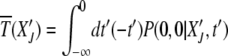(17)

obeys the ordinary differential equation

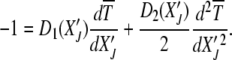(18)

Since 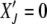is an absorbing state, the solution to the above equation is subjected to the boundary condition 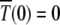. Furthermore as the population in the Jth class equilibrates about the mean 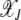after the (J − 1)th click, we can choose the initial distribution of random variabl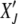e to be 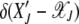. Then the time 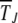during which J is the least-loaded class obtained by solving (18) is given by

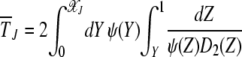(19)

(Ewens 1979), where ψ(Y) = exp .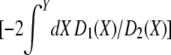

We now determine the coefficients D₁ and D₂. The drift coefficient D₁ defined in (16) measures the change in the average fraction of the least-loaded class over a generation. As the population is in local equilibrium, this can be determined using the quasi-species Equation 3 for j = 0. Thus the drift coefficient is given by

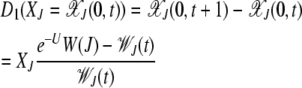(20)

(Stephan et al. 1993; Gordo and Charlesworth 2000a). As expected, D₁ vanishes when the population is either in the steady state [see (5)] or in the absorbing state (X_J = 0). Equation 20 for D₁ does not close in X_J but one can obtain an approximate expression for D₁ using the linear response theory (Risken 1996). As D₁ is proportional to the deviation from a steady-state quantity, we can write

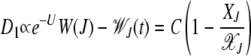(21)

(Stephan et al. 1993), where C is a constant. Thus the drift coefficient can be written in terms of X_J as

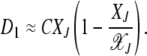(22)

As Figure 2 shows, when the ratchet clicks (X_J = 0) and the Jth class is lost, the population quickly relaxes to the equilibrium frequency of the (J + 1)th class so that the deviation in the fitness 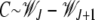= 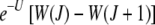, where we have used (5). For s → 0, expanding the fitness W(J) to leading orders in s, we get

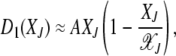(23)

where for large J.

The diffusion coefficient D₂ in (16) gives the fluctuations in the frequency of the least-loaded class about the mean value. These fluctuations arising due to the finiteness of the population can be determined using (2), which gives the variance in the number of offspring produced in one generation as

(24)

(Ewens 1979). The last expression on the right-hand side of the above equation captures the fact that the fluctuations vanish when either the population size N is infinite or the population is in the absorbing state X_J = 0.

Using the coefficients (23) and (24) in (19), the average interclick time can be written as

(25)

where

(26)

and

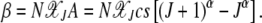(27)

In the absence of epistasis, both A and 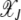are independent of J so that typical time spent between any two successive clicks is constant and the ratchet turns with a finite speed equal to 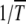. For epistatic fitness α ≠ 1, 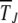depends explicitly on J and is expected to increase with J for α > 1 and decrease for α < 1 (Kondrashov 1994). In the following discussion, we restrict ourselves to α ≥ 1.

After some simple manipulations, we can rewrite (25) as

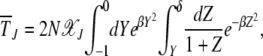(28)

which implies that the scaled time 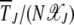is a function of two variables, namely 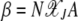and 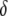= 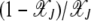. The nature of 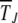depends on the parameter βδ², which can be seen as follows. Consider the Gaussian 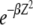in the rightmost integral in (28) that is centered at ∼Z = 0 and has a width 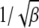. If the upper limit δ of this integral exceeds the width, i.e., 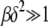, the integral can be cut off at 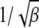, thus eliminating the dependence on δ. In such a case, 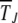is of the scaling form

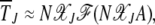(29)

where 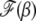is the scaling function determined below. If 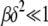, then the interclick time depends on δ as well. Since 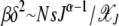and 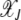is bounded above by one, 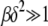for large J when epistatic interactions are synergistic. For α = 1, the parameter βδ² exceeds unity if 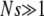. Here we restrict ourselves to the 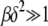case that has nice scaling properties although the double integral in (28) can be estimated for 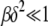also.

We now proceed to find the scaling function 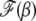. If the width of the Gaussian is large, i.e., 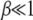, we can approximate 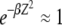for 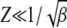in the rightmost integral in (28). Since 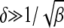, as argued above, this integral needs to be carried out from Y to 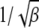. This yields

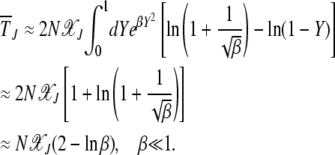(30)

To find the scaling function in the opposite limit 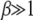, we first consider the inner integral in (28),

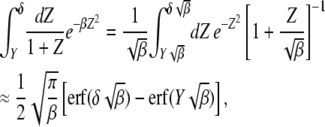(31)

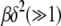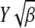where erf(z) is the error function (Abramowitz and Stegun 1964) and we have kept terms to leading orders in and for 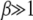. On using the above integral in (28), we obtain

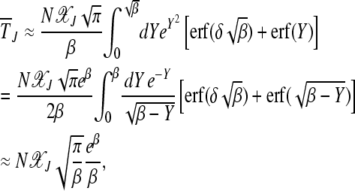(32)

where we have used that both βδ² and β are large. From the above discussion, we find that the scaling function

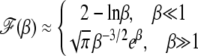(33)

is a U-shaped function of β reaching a minimum when β ∼ 1. We now discuss the above results in more detail for α = 1 and α > 1.

Nonepistatic fitness landscapes:

As we have already argued, when α = 1 the ratchet clicks with a finite speed equal to 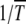. When the rate at which the ratchet clicks is large, analytical results can be obtained using the traveling wave approach (Rouzine et al. 2003). For the slowly clicking ratchet that is the subject of this article, the problem was formulated analytically within a diffusion approximation first by Stephan et al. (1993). However, a better agreement between the diffusion theory and the simulation results was obtained in Gordo and Charlesworth (2000a,b). A possible reason for this difference is that Stephan et al. (1993) included terms besides those in (22) in the expansion of the drift coefficient that is not consistent with the assumption of linear response, while the expression for D₁ in Gordo and Charlesworth (2000a) is the same as (22). In fact, the expression for the interclick time given by (28) with c = 0.6 is identical to that reported in Gordo and Charlesworth (2000a). However, the integrals were computed numerically by these authors while here we estimate them analytically and find that the average interclick time is given by

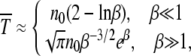(34)

where 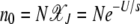is the number of individuals in the least-loaded class and β = n₀cs is the scaling parameter. The interclick time calculated numerically using the integral (28) and the above expression (34) is shown in Table 1 and the two are seen to be in good agreement.

TABLE 1.

Comparison of simulation data plotted in Figure 3 with analytical results

β	N	U	s	n0	(2 SE)
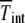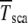0.121	7,500	0.02	0.004	50.5	453 (34)	230	207
	15,000	0.01	0.002	101.1	906 (69)	460	416
	30,000	0.005	0.001	202.1	1,805 (111)	920	831
0.242	3,000	0.1	0.02	20.2	141 (7)	86	69
	6,000	0.05	0.01	40.4	271 (23)	172	138
	12,000	0.025	0.005	80.8	559 (39)	344	276
1.212	15,000	0.1	0.02	101.1	506 (41)	479	451
	30,000	0.05	0.01	202.2	1,008 (101)	959	902
	60,000	0.025	0.005	404.2	1,950 (133)	1,918	1,804
2.424	30,000	0.1	0.02	202.1	1,490 (149)	1,487	1,071
	45,000	0.067	0.013	303.2	2,104 (218)	2,230	1,608
	60,000	0.05	0.01	404.2	2,579 (257)	2,974	2,143

The interclick time 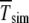is obtained in simulations, 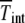by numerically evaluating the integrals in (28) for α = 1, and 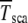by using the scaling form (34).

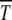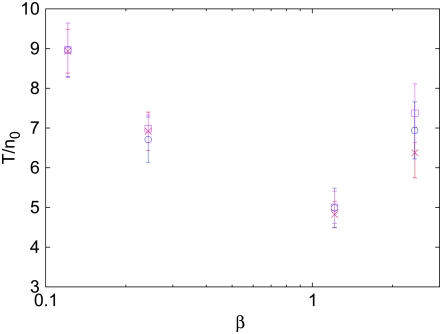
Our first result concerning Muller's ratchet is the scaling form for time when parameters N, U, and s are chosen such that 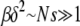is satisfied. The results of our numerical simulations testing this scaling form are shown in Figure 3, where we have differentiated data points at fixed β for clarity. The scaled time 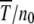indeed shows a very good data collapse and a nonmonotonic dependence on β. Higgs and Woodcock (1995) unsuccessfully attempted to obtain a scaling form for the ratchet rate by using Ns as the scaling parameter for 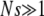. The scaling function in (34), however, shows that the scaling parameter is a function of the population number n₀ in the least-loaded class and not the total population N.

Figure 3.—

Data collapse of the scaled time 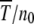when plotted against the scaling parameter β = n₀cs for the multiplicative fitness landscape where c = 0.6. The simulation data were averaged over 100 stochastic runs.

In many studies (Haigh 1978; Bell 1988; Gessler 1995), the size n₀ of the least-loaded class has been regarded as an important parameter in determining the ratchet speed. If 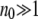, the population is close to the deterministic limit and the ratchet clicks slowly whereas for 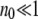, the ratchet speed is high. However, the simulations show that the size n₀ of the least-loaded class is not sufficient to predict the ratchet rate (Stephan et al. 1993; Gordo and Charlesworth 2000a). This is indeed captured by diffusion approximation as (34) is not a function of n₀ alone. However, if s is kept fixed, 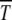increases monotonically with n₀ in accordance with the above expectation and simulations (Gabriel et al. 1993; Gordo and Charlesworth 2000a). The dependence of 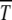on s for given n₀ is, however, nonmonotonic, similar to that seen in numerical studies (Gordo and Charlesworth 2000a). To understand this behavior qualitatively, consider the situation where the population number n₀ is kept constant by keeping N and U/s fixed. As increasing s tends to localize population and hence increase 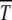, increasing U has the opposite delocalizing effect that decreases 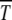. At a given U and s, one of these two competing forces wins. According to (34), as the scaling function overturns when n₀s ∼ 1, the mutation takes over for U > U* = s ln(Ns) whereas below U*, selection dominates and 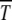is large.

The solution (34) gives an initial logarithmically slow drop in s and an exponential increase for larger s with the minimum of the U-shaped curve occurring at a selection coefficient that scales as 1/n₀. The simulation results of Gordo and Charlesworth (2000a) (also see Table 1), however, show a much faster drop at small s. A good agreement with simulation data was obtained in Gordo and Charlesworth (2000b) by adding 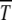and time T_a ∼ 1/s required by the population to relax to new steady state just after a click. However, the full expression for T_a is not of scaling form (29) although the simulation data in Figure 3 show an excellent data collapse even for small s. In view of this, a better understanding of the time T_a is desirable. Of course, for both n₀ and s fixed, the time 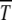is predicted to be independent of N and U, which is confirmed by simulations (Gordo and Charlesworth 2000a).

Epistatic fitness landscapes:

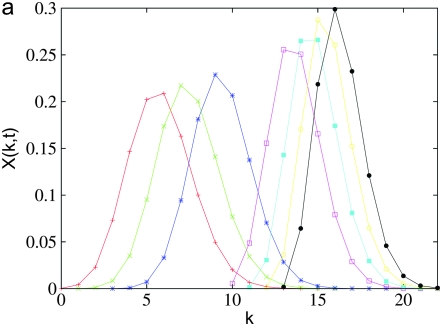
For synergistic interactions, the ratchet is expected to halt at large times (Charlesworth et al. 1993; Kondrashov 1994). Figure 4a shows the population fraction 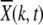with k deleterious mutations at several time slices. Two points are noteworthy: the ratchet does not turn with a constant speed as is evident by the rate at which the population accumulates the average number of mutations at late times. Second, unlike for the multiplicative fitness case (Rouzine et al. 2003), the population fraction does not maintain its shape as the width of the distribution 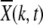decreases with increasing time. Thus the number frequency of an asexual population under epistatic selection does not behave like a traveling wave moving with a constant speed.

Figure 4.—

Loss of least-loaded class on epistatic fitness landscapes with α = 2, N = 256, U = 0.25, s = 0.005. (a) Average fraction 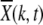in the kth class at t = 50, 100, 200, 1250, 2500, 5000, 10,000 (from left to right). The data have been averaged over 1000 stochastic histories. (b) Average interclick time 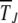as a function of J, where each data point has been averaged over 500 histories. Comparison with 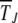obtained by evaluating integral (28) numerically and using the scaling form (29) at large J is also shown. A reasonably good agreement is obtained with c = 0.9.

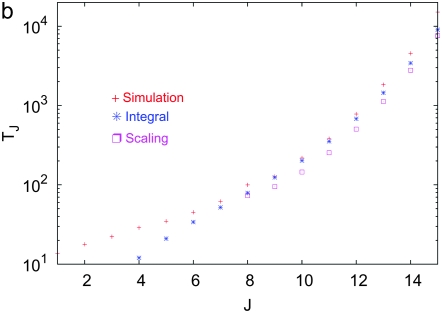
The simulation data for average interclick time shown in Figure 4b increase with the minimum number J of deleterious mutations in the population, thus indicating the arrest of the ratchet at large times. The time 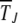obtained by integrating (28) for α = 2 is also shown for comparison and we find that it agrees well with the simulation results. As the scaling parameter β defined in (27) increases as a power law with J for 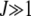, we have 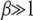for large J. In such a case, 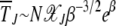, which increases exponentially fast with β. As 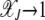for large J, the interclick time 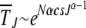increases faster than any power law with J and for any α > 1. Thus an arbitrarily small α − 1 is capable of slowing down the ratchet under synergistic selection.

To estimate how the ratchet speed approaches zero, we use the following argument. The average speed 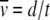, where d is the number of minimum mutations accumulated in time interval t. Since T_J is the time between the (J − 1)th and Jth click of the ratchet, we have

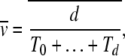(35)

where d is fixed. Assuming the distribution for click times has nice scaling properties, we may write

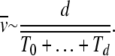(36)

If T_J does not depend on the least-loaded class J, we have 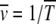as expected for the α = 1 case. For α > 1 as the average interclick time increases faster than the power law with J, the sum 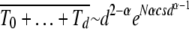, which is reasonable as the sum is dominated by 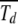for large d. This gives 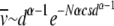or, in terms of t,

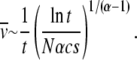(37)

Thus in the presence of epistasis, the average speed of the ratchet approaches zero as 1/t with α-dependent logarithmic corrections.

DISCUSSION

In this article, we considered the effect of drift and epistasis on the loss of the least-loaded (or the fittest) class in an asexual population. When the population size is infinite, the drift is absent and the population evolves due to the elementary processes of selection and mutation. As selection tends to localize the population at the fittest sequence while mutation has the opposite tendency to delocalize it, an error threshold may exist beyond which the fittest class cannot be sustained in the population (Eigen 1971). Such a phase transition is known to occur for asexual populations evolving deterministically on fitness landscapes defined by (1) when α < 1 (Wiehe 1997). However, for α ≥ 1, the population frequency 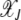in the least-loaded class J remains nonzero for any finite U, s. In fact, for synergistic interactions, the frequency 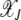given by (13) increases with J toward unity.

If, however, the population size is finite, as illustrated in Figure 2, the population frequency X_J(t) fluctuates with time and can become zero even for α ≥ 1. Numerical simulations have shown that this loss occurs at a constant speed when α = 1 (Haigh 1978) but at a decelerating rate when α > 1 (Charlesworth et al. 1993; Kondrashov 1994). In this article, we focused on the stochastic dynamics of the loss of the fittest class for α ≥ 1 and calculated explicit analytical expressions for the typical time 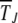during which the least-loaded class J survives using a diffusion theory (Ewens 1979). Although this approach has been considered previously to attack the Muller's ratchet problem (Stephan et al. 1993), the resulting solution in the form of a double integral was evaluated numerically, which does not allow one to infer the functional dependence of 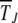on parameters N, U, s, and J.

When the interactions between gene loci are assumed to be absent and 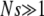, the interclick time 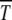is found to be of the scaling form (34). Although this result is derived using diffusion theory that is based on several approximations, the numerical simulations show an excellent data collapse, suggesting that (29) may be an exact statement. For fixed n₀, the time 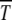is seen to be a U-shaped function of s arising due to competition between mutation and selection. Such a behavior is reminiscent of the error threshold phenomenon in infinite populations discussed above. Although the least-loaded class is never lost in the deterministic limit on multiplicative fitness landscapes (Wagner and Krall 1993), the selection–mutation competition manifests itself in the time duration during which the least-loaded (fittest) class can support a finite population. For given s, the survival time 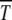initially increases linearly with n₀, approaching the deterministic limit of N → ∞ with an exponential rise with n₀ as increasing N decreases the effect of drift.

Muller's ratchet has been proposed as a possible mechanism for the degeneration and eventual extinction of asexual organisms and nonrecombining parts of sexually reproducing populations. For bacterial populations with N ∼ 10⁶, U ≈ 0.003 (Drake et al. 1998), and s ≈ 10⁻³, using (34) we find it takes 10¹⁵ generations for one click to occur, which does not seem plausible. However, reducing s by a factor of half gives 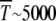and further reduction to s ≈ 0.25 × 10⁻³ gives just 50 generations for a single click. Muller's ratchet has also been invoked to understand the degeneration of the nonrecombining neo-Y chromosome that originated ∼1 million years ago in Drosophila miranda (Charlesworth 1978; Gordo and Charlesworth 2000a). Assuming that a few thousand deleterious mutations have occurred over this time span, the time between successive turns of the ratchet is of the order of 10³ generations. From (34), the time 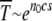for large 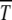, which gives n₀s ≈ 14. If s ≈ 10⁻², the population size N required for Muller's ratchet to be a viable mechanism works out to be ∼700e^100U, which depends sensitively on U due to the exponential dependence. For instance, for U = 0.07, the required population is of the order 5 × 10⁵ while it reduces by a factor of 20 for U = 0.04. A similar sensitive dependence of extinction time on s for given N and U has been noted in the problem of the degeneration of human mitochondrial DNA also (Loewe 2006). This suggests that very precise estimates of U and s may be required to determine whether Muller's ratchet might be in operation.

The scaling form (29) holds for α > 1 also but the speed of the ratchet under epistatic selection is found to decay rapidly with time for any α > 1. Although Muller's ratchet under synergistically epistatic selection has the interesting feature of arresting the loss of the least-loaded class, the generality of this mechanism seems unclear as general support for synergistic epistasis has not been found in the experiments (De Visser and Elena 2007) and the slowing-down effect is sensitive to the inclusion of biologically relevant details such as distribution of mutational effects (Butcher 1995). Recent experimental evidence suggests that fitness decline down to a plateau can be attributed to the presence of epistasis (Silander et al. 2007). This can be due to negative epistasis (Kondrashov 1994) or compensatory epistasis (Silander et al. 2007). It would be interesting to compare the results discussed in this work with models that include compensatory mutations (Wagner and Gabriel 1990; Wilke et al. 2003).