Population Bottlenecks Increase Additive Genetic Variance But Do Not Break a Selection Limit in Rain Forest Drosophila

Abstract

According to neutral quantitative genetic theory, population bottlenecks are expected to decrease standing levels of additive genetic variance of quantitative traits. However, some empirical and theoretical results suggest that, if nonadditive genetic effects influence the trait, bottlenecks may actually increase additive genetic variance. This has been an important issue in conservation genetics where it has been suggested that small population size might actually experience an increase rather than a decrease in the rate of adaptation. Here we test if bottlenecks can break a selection limit for desiccation resistance in the rain forest-restricted fly Drosophila bunnanda. After one generation of single-pair mating, additive genetic variance for desiccation resistance increased to a significant level, on average higher than for the control lines. Line crosses revealed that both dominance and epistatic effects were responsible for the divergence in desiccation resistance between the original control and a bottlenecked line exhibiting increased additive genetic variance for desiccation resistance. However, when bottlenecked lines were selected for increased desiccation resistance, there was only a small shift in resistance, much less than predicted by the released additive genetic variance. The small selection response in the bottlenecked lines was no greater than that observed in the control lines. Thus bottlenecks might produce a statistically detectable change in additive genetic variance but this change has no impact on the response to selection.

NATURAL populations may periodically experience fluctuations in population size. Understanding the effects of dramatic decreases in population size, or bottlenecks, has been an important issue in the conservation of endangered species and in the domestication and intense selective breeding of many agricultural species. Assuming neutral and additive gene action, bottlenecks are expected to decrease additive genetic variance (V_A) (Chakraborty and Nei 1982; Lynch and Hill 1986) and reduce the evolutionary potential of populations (Frankham et al. 2002; Willi et al. 2006). However, bottlenecks have also been invoked as a driving mechanism in several speciation and adaptive evolutionary paradigms, including founder flush speciation models (Mayr 1963; Carson 1968, 1982; Templeton 1980) and Wright's shifting balance theory (Wright 1931). These models propose that genetic drift in small populations will dramatically change the genetic background and allow populations to reach new adaptive peaks. Whether bottlenecks reduce or enhance evolution is not clear and has attracted considerable controversy in recent years.

If the genetic architecture underlying a trait is controlled by genes that are acting additively, a population bottleneck is predicted to reduce V_A proportional to the inbreeding coefficient (Falconer and Mackay 1996). Thus, for additive traits, population bottlenecks are expected to decrease the adaptability of populations. However, models assuming dominance and/or epistasis predict that there is some chance for an increase in V_A for quantitative traits within populations that go through a bottleneck. When there are dominance interactions between alleles within loci, a population bottleneck may increase the frequency of recessive alleles, increasing their overall effect and V_A (Robertson 1952; Willis and Orr 1993; Wang et al. 1998). Under a dominance model, changes in trait means are also expected. If there is complementary directional dominance, that is, the signs of the dominance effects across loci are generally in the same direction, there is likely to be a change in the trait mean in the general direction of the dominance effects (Mather 1973). However, rare recessive alleles are likely to be at low frequencies if they are deleterious. Thus any increase in V_A due to an increase in the effect of deleterious alleles will lead to inbreeding depression and is unlikely to be beneficial or stable, as natural selection will favor reversion to the previous state unless there is a strong genotype-by-environment interaction that reverses the sign of the effect of the alleles (Lopez-Fanjul et al. 2000).

Theoretical studies have also suggested that V_A following a population bottleneck can increase due to epistatic interactions between alleles at different loci (Goodnight 1988; Cheverud and Routman 1996; Lopez-Fanjul et al. 1999, 2000; Barton and Turelli 2004; Hill et al. 2006; Turelli and Barton 2006). Although dependent on weighted variances and covariance among the different effects, an increase in V_A is predicted when the proportion of epistatic (V_AA) to V_A is high (V_AA > 4V_A) (Cockerham and Tachida 1988; Barton and Turelli 2004). Cheverud and Routman (1996) have shown that additive × dominance (V_AD) and dominance × dominance epistasis (V_DD) can also inflate V_A after a bottleneck, at least at intermediate allele frequencies. Increases in V_A due to the conversion of epistatic to additive genetic variance after a bottleneck has received considerable attention as inbreeding depression is not necessarily expected. However, epistatic variance is notoriously hard to measure and is generally expected to be too small to inflate V_A after bottlenecks (Turelli and Barton 2006).

Empirical studies on laboratory populations have reported an increase in V_A following a population bottleneck in several species, for morphological traits (Bryant et al. 1986; Whitlock and Fowler 1999) as well as life history traits (Lopez-Fanjul and Villaverde 1989; Garcia et al. 1994; Fernandez et al. 1995; Briggs and Goldman 2006). Life history traits closely associated with fitness are, on average, more likely to show an increase in V_A after a bottleneck than morphological traits (Van Buskirk and Willi 2006; Willi et al. 2006), probably because life history traits are more likely to have a nonadditive genetic architecture than morphological traits (Roff and Emerson 2006). While V_A was higher in the bottleneck lines than in control lines, these empirical studies were unable to show whether adaptability had increased; where an increase in V_A for a fitness trait was found (Lopez-Fanjul and Villaverde 1989; Garcia et al. 1994; Fernandez et al. 1995; Wade et al. 1996; Briggs and Goldman 2006), this increase was accompanied by inbreeding depression, as predicted by an increased expression of recessive deleterious alleles (Wang et al. 1998). However, more empirical data on the role of dominance and epistasis for adaptive evolution in small populations and on traits of ecological relevance are needed.

While studies suggest that increases in V_A after a bottleneck are likely to be the result of increased expression of deleterious recessive alleles (Wang et al. 1998) or chance fluctuations in predominately additive systems (Whitlock and Fowler 1999; Turelli and Barton 2006), no empirical investigations have directly distinguished between dominance and epistasis as the causative agents. Furthermore, no studies have considered the impact of bottlenecks on traits that constitute an evolutionary limit, particularly in species with restricted distributions. As V_A levels for many traits are high, changes in genetic variance due to bottlenecks may have little impact on adaptation. However, novel V_A arising after a bottleneck could accelerate adaptive evolution in species with restricted ecological distributions, when V_A for traits that limit selection responses is low (Futuyma et al. 1995; Blows and Hoffmann 2005). Bottlenecks might then have the potential to have a dramatic effect, as the ratio of nonadditive to additive effects is predicted to be high (Lopez-Fanjul et al. 2000) and could break selection limits.

Recent work has found that two rain forest-restricted Drosophila species, Drosophila birchii and D. bunnanda (Schiffer et al. 2004), have very low levels of V_A for the ecologically important trait, desiccation resistance, and appear to be at an evolutionary limit for this trait (Hoffmann et al. 2003; Kellermann et al. 2006). Both species also have a low level of desiccation resistance compared to more widespread relatives, suggesting that the low resistance levels might act as an evolutionary limit for spreading to the drier environments outside the humid tropical habitat where these species are found. Both species offer an opportunity to investigate whether a bottleneck can increase V_A for a trait with no detectable V_A and whether such an increase is of adaptive significance.

The aims of this study were to investigate the effect of a single-generation bottleneck of two individuals of the rain forest-restricted D. bunnanda on V_A and to test whether changes in V_A influence selection response for desiccation resistance. Additionally, we used a powerful line-cross design to examine whether epistasis and/or dominance contributed to any divergence in resistance after bottlenecking. We also investigated the effect of a bottleneck on V_A in sternopleural bristle number, a trait expected to be of lower adaptive importance and governed mainly by additive effects, in contrast to desiccation resistance.

METHODS

Stocks:

D. bunnanda flies were collected in May 2005 from Kirrama in northeastern Queensland, Australia (latitude 18°11′45″E, longitude 145°52′07″E). Isofemale lines were initiated with the progeny of 20 single field-collected females. Two generations after collection, a mass-bred population was founded with 10 males and 10 females from each of 20 lines. The mass-bred population was kept at 25° under continuous light in three 250-ml bottles containing 20 ml of potato, yeast, and sucrose media. Densities were ∼300–350 flies per bottle to ensure a census population size of 1000 individuals.

Bottlenecking:

After five generations of mass breeding, 100 single-pair matings were established. Pairs were tipped onto new media every 3 days for 2 weeks. In the next generation, 20 randomly chosen full sibs were allowed to reproduce within each line, and this was increased to 500 in the third generation and ∼1000 in total, thereafter spread over three bottles per line. Three replicate control lines were maintained throughout the experiment, each in three bottles containing ∼1000 individuals.

Heritability analysis:

We assessed heritability of desiccation resistance and sternopleural bristle number in the lines by parent–offspring regression, three generations after the bottleneck event. Variance components (V_P, V_A, V_E) and narrow-sense heritability (h²) were estimated for one control line and nine bottlenecked lines. To initiate the parental generation and to control for density effects, 7-day-old females were allowed to oviposit for 12 hr on watch glasses containing treacle media dyed green. Eggs were collected and transferred to individual 50-ml vials (40 per vial) containing 15 ml of potato medium. Fifty replicate vials per line were set up. The emerging flies from these vials constituted the parental generation.

Emerging flies were collected, pooled over vials, sexed under CO₂, and separated within 12 hr of eclosion to ensure that females were virgins, and 250 pair matings (constituting 250 families) were established per line. Because of the number of flies involved in the offspring generation, it was not possible to control density by counting eggs/larvae into vials in this generation. However, to provide some control of density, pairs were initially aged in 50-ml vials containing 15 ml of potato medium and tipped onto fresh medium every 3 days. On day 7, pairs produced their offspring generation by being held in vials for 24 hr. This was repeated for a further two 24-hr laying periods to provide three sets of vials where the density was low (flies emerging from each vial: 2–50; mean = 12.24). Offspring in vials developed at 25° under constant light until emergence. Differences between the three vials were used to estimate common environment effects.

Parental flies were assessed for resistance between days 10 and 13 after emergence. Pairs of flies of each bottleneck line were split into four different “blocks” (∼40 families per line per block) to handle the large number of individuals in the experiment. Blocks were stressed on successive days by transferring individual flies into separate empty vials covered with gauze. These vials were then placed in a desiccator (as described in Kellermann et al. 2006) at 8–15% relative humidity (RH) at 25°. Mortality was scored at hourly intervals until all flies were dead. Sternopleural bristle number (on the right side only) and sex were scored after death, within 2 weeks of the desiccation assay.

Offspring were stressed the same way and at the same age as the parents. Emerging offspring were collected and sexed under CO₂, and two males and two females were sampled from each of two vials (in total four males and four females per family, from two of the three vials set up for that family).

An animal model approach was utilized to estimate environmental and genetic variance components (DFREML v. 3) (Meyer 1989). Estimates of h², V_A, environmental variance (V_E), phenotypic variance (V_P), and maternal and common environment effects were calculated using the simplex linear algorithm option on the basis of all available kin relationships (restricted maximum-likelihood analysis produced qualitatively similar results). Sex and generation were included as fixed effects in the model. Common environment and maternal genetic effects were included only if they significantly improved the model, which was assessed using a likelihood-ratio test (Wilson et al. 2006). Maternal effects did not significantly improve any of the models and were not considered further. For desiccation resistance, inclusion of common environment effects significantly improved models and these were therefore included. For sternopleural bristle number the common environment effects were not significant and therefore not included. Equation 1 represents the final univariate model for sternopleural bristle number, while Equation 2, including a common environment effect, was used for desiccation resistance: The equations were

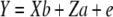(1)

and

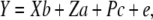(2)

where Y is a vector of phenotypic values, b and a are the vectors of fixed and additive genetic effects, respectively, c is the vector of common environment random effects, e is the vector of residual effects, and X, Z, and P are the corresponding design matrices that relate the effects to Y. The coefficient of additive genetic variance (CV_A) standardizes V_A estimates so that they are comparable across traits and species and was calculated following Houle (1992).

Analysis of variance (ANOVA) with line nested within treatment (bottleneck or nonbottleneck) was undertaken to examine whether a single-generation bottleneck influenced desiccation resistance and/or sternopleural bristle number. To determine whether estimates of h² or V_A were significantly different from zero overall in the bottlenecked lines, we computed probabilities from Z scores and combined these across bottleneck lines as outlined in Sokal and Rohlf (1995). Variance estimates and heritabilities in the bottleneck and control lines were compared with t-tests, using separate variance corrections where variances differed between the two sets of lines.

Line-cross experiment:

Line crosses between a control line (c2) and each of two bottleneck lines were performed to examine whether additive effects, dominance effects, digenic epistatic interactions, maternal effects, interactions between additive/dominance effects and maternal effects, cytoplasmic effects, and Y-linked effects were contributing to the differences in observed means and V_A for desiccation resistance. One of the chosen bottleneck lines (no. 43, see below) had higher desiccation resistance and V_A than the control lines, while the other bottleneck line (no. 27, see below) had a similar level of desiccation resistance and V_A as the control lines (as estimated from animal model analysis of the offspring data). Sternopleural bristle number was also examined.

For each pair of lines, we set up 14 crosses similar to the procedure outlined in Gilchrist and Partridge (1999) and Schiffer et al. (2006). Briefly, crosses were made between the two parental lines and the subsequent F₁ and F₂ generations. The F₁ generation was then backcrossed to the parents. Each cross included a reciprocal cross. Reestablishing the parental and F₁ crosses each generation allowed all 14 crosses and parentals to be tested simultaneously. Three replicate vials were established for every cross, each initiated with at least 30 virgins of each sex. Flies were tipped daily to control larval density.

The traits were scored in a similar fashion to the parent–offspring assessment. Briefly, flies were sexed under CO₂ anesthesia 48–72 hr prior to stressing. Desiccation resistance was measured on 11-day-old flies as described above. Approximately 15 females and 15 males per replicate vial were scored (totaling 45 females and 45 males per cross/generation). The number of sternopleural bristles on the right side of these desiccated flies was counted under a dissecting microscope after stressing.

Observed and expected generation means were calculated for each sex separately and analyzed with the methods outlined in Mather and Jinks (1997) and as described in Gilchrist and Partridge (1999) and Schiffer et al. (2006). In brief, the observed generation means were used to estimate the overall trait mean (m) and the composite additive ([a]) and dominance ([d]) effects. Observed and expected generation means were then tested for goodness of fit using the chi-square statistic. If a simple additive dominance model was insufficient to explain the data (determined by a significant chi-square value), additional parameters including digenic epistatic ([aa], [ad], and [dd]), additive maternal ([a]m), dominance maternal ([d]m), cytoplasmic ([c]), and Y-linked ([Y]) effects were added in this order. The aim is to identify the simplest model to satisfactorily explain the observed means and only parameters that significantly improved the model (determined by a likelihood-ratio test) were included. Model parameters, their errors, and chi-square values were estimated using weighted least-squares methods, expanded to incorporate vial variances. Standard errors of generation means were calculated to take into account within- and between-vial variation on generation means.

Selection experiment:

To examine whether increases in V_A following a bottleneck could be selected to increase mean desiccation resistance, three control lines and the nine bottleneck lines were artificially selected for increased desiccation resistance for 11 generations. Artificial selection was initiated after four generations of flushing (the bottlenecked lines were at a census size of 1000 individuals), in the same generation (from eggs laid earlier) as the parents from the heritability experiment. Selection was undertaken by exposing ∼500 flies (5–7 days after eclosion) from each selection line (10 flies per vial) to <15% RH, as described above. When ∼30–40% of the flies were still alive, the flies were removed and immediately transferred to laboratory medium. Further mortality often occurred after flies were removed from the desiccation tank, so the number of flies alive the following day was scored, and 20 flies per vial (at least five vials per selection line) were transferred onto new media every 2 days to initiate the next generation. Each line was maintained at a census size of ∼500 flies each generation, with no less than 100 flies contributing to the next generation after selection. Due to difficulties in obtaining 500 offspring following the generation of selection, selection was performed every second generation. Thus the selection procedure encompassed 22 generations of fly culture, including 11 generations of artificial selection for desiccation resistance.

To investigate the selection response, desiccation resistance was assessed in the selected and nonselected bottlenecked and control lines, one generation after the final 11th generation of selection had been completed. Larval density for this assessment was partly controlled by allowing ∼100 adult flies per vial (unsexed) to oviposit for 12 hr. Six replicate vials were set up for each treatment for each line, with <40 flies emerging from one vial. Sixty females and 60 males were assessed for desiccation resistance in each selected and unselected bottlenecked and control line. Assessment of the desiccation resistance was undertaken on 11-day-old flies.

To compare selected and unselected control and bottleneck lines for desiccation resistance after 11 generations of artificial selection, a mixed-model nested ANOVA was used. Line, as a random variable, was nested within treatment, which included nonbottlenecked (control) lines and bottleneck lines with high estimates of h² (>2 SE from 0) as well as lines with estimates of h² close to 0. A sex term was also included in the ANOVA. A Wilcoxon signed-ranks test was used to examine whether a trend for a selection response was evident in males or females from the bottlenecked lines. This comparison was not attempted for the controls because there were only three lines. To determine whether any particular lines had responded to selection, an ANOVA was performed comparing selected and unselected line data for each sex (corrected for multiple comparisons using the Bonferroni procedure). Expected responses to selection were calculated for each generation as R = ih²σ_P, where i was the intensity of selection, h² values were obtained from the animal model, and σ_P was the phenotypic standard deviation (Falconer and Mackay 1996), and expected cumulative responses were then compared to the observed responses using t-tests.

RESULTS

Bottleneck effects on variance components:

Overall, a single-generation bottleneck in D. bunnanda increased V_A for desiccation resistance (Table 1). The average V_A of the nine bottleneck lines (0.320) was more than twice that of the control lines (0.139). While the estimates of V_A for the control lines were not significantly different from zero (combined P = 0.19), the V_A for the bottlenecked lines was significantly above zero (combined P = 0.001). Furthermore, a t-test indicated the bottlenecked lines had significantly higher values of V_A than the control lines when adjusted by 0.75 (t = 2.64, d.f. = 6.5, P = 0.018). These patterns suggest that the underlying genetic architecture of desiccation resistance in D. bunnanda is not strictly additive.

TABLE 1.

Narrow-sense heritability (h²), and additive (V_A), environmental (V_E), and phenotypic (V_P) variances (all plus or minus standard errors), and coefficient of additive genetic variation (CV_A) for desiccation resistance in D. bunnanda control and bottleneck lines estimated with animal models

Line	h2 ± SE	VA ± SE	VE ± SE	VP ± SE	CVA	N
c1	0.070 ± 0.048	0.160 ± 0.111	2.128 ± 0.134	2.288 ± 0.091	6.098	1279
c2	0.000 ± 0.057	0.000 ± 0.111	3.591 ± 0.249	3.591 ± 0.158	0	1040
c3	0.092 ± 0.054	0.258 ± 0.152	2.545 ± 0.136	2.803 ± 0.120	7.591	1199
c average	0.054	0.139	2.755	2.894	4.563	3518
b23	0.129 ± 0.057	0.394 ± 0.178	2.662 ± 0.164	3.056 ± 0.140	9.345	1050
b27	0.066 ± 0.056	0.163 ± 0.138	2.285 ± 0.126	2.447 ± 0.106	6.217	1153
b35	0.140 ± 0.069	0.409 ± 0.206	2.514 ± 0.165	2.925 ± 0.145	9.243	937
b42	0.070 ± 0.055	0.228 ± 0.180	3.017 ± 0.176	3.245 ± 0.143	6.891	1087
b43	0.160 ± 0.064	0.509 ± 0.211	2.680 ± 0.193	3.188 ± 0.149	10.414	990
b74	0.030 ± 0.055	0.073 ± 0.135	2.367 ± 0.126	2.442 ± 0.113	4.430	1015
b90	0.049 ± 0.066	0.116 ± 0.160	2.277 ± 0.135	2.394 ± 0.125	5.446	893
b100	0.166 ± 0.069	0.485 ± 0.208	2.443 ± 0.184	2.927 ± 0.143	10.636	895
b101	0.192 ± 0.068*	0.474 ± 0.175*	1.989 ± 0.141	2.462 ± 0.121	10.333	955
b average	0.100	0.320	2.47	2.420	8.106	8975

^*Line with heritability and additive genetic variance that are significantly different from zero after Bonferroni correction.

This increase in V_A for the bottleneck lines also led to an increase in h² (Table 1) and significant estimates of h² (combined P = 0.001), suggesting the bottleneck lines should show a significant response to selection. Environmental variances were similar between the bottleneck lines compared to the controls (Table 1) and did not differ significantly between groups (t = 0.994, d.f. = 10, P = 0.344). Estimates of h² were significantly higher in the bottleneck lines when compared to the controls adjusted by the 0.75 value (t = 2.48, d.f. = 5.9, P = 0.024) and the increases in h² were therefore due to increases in V_A rather than decreases in environmental variance.

The effects of bottlenecking on variance components and h² for desiccation resistance contrast with those for sternopleural bristle number. V_A for sternopleural bristle number was lower in the bottleneck lines than in the control lines (Table 2; 0.140 vs. 0.197). In fact, the decrease in V_A was almost exactly as predicted under additive genetic theory (0.148). Values did not differ significantly from this expectation by a t-test (t = 2.036, d.f. = 8, P = 0.076) and values in the bottlenecked lines did not differ significantly from those of the control lines (adjusted by 0.75) (t = 0.263, d.f. = 9, P = 0.800). Narrow-sense heritability was also lower in the bottleneck lines (0.18) compared to the control lines (0.22) as expected and did not differ by t-tests after adjustment (t = 0.464, d.f. = 9, P = 0.654). Environmental variances were similar in the bottleneck lines compared to the controls (Table 2) and did not differ significantly (t = 1.259, d.f. = 9, P = 0.240).

TABLE 2.

Narrow-sense heritability (h²), components of additive (V_A), environmental (V_E), and phenotypic (V_P) (plus or minus standard error) variance, and coefficient of additive genetic variation (CV_A), as above, for sternopleural bristle number in D. bunnanda control and bottleneck lines estimated by the animal model

Line	h2± SE	VA ± SE	VE ± SE	VP ± SE	CVA	N
c1	0.182* ± 0.063	0.151* ± 0.054	0.680 ± 0.056	0.831 ± 0.032	4.971	1359
c3	0.253* ± 0.050	0.243* ± 0.052	0.718 ± 0.048	0.863 ± 0.041	6.297	1199
c average	0.218	0.197	0.699	0.847	5.634	2558
b23	0.204* ± 0.054	0.176* ± 0.050	0.687 ± 0.047	0.863 ± 0.040	5.318	1050
b27	0.191* ± 0.049	0.162* ± 0.044	0.685 ± 0.045	0.847 ± 0.036	5.136	1153
b35	0.185* ± 0.053	0.133* ± 0.040	0.586 ± 0.042	0.719 ± 0.034	4.702	937
b42	0.206* ± 0.053	0.167* ± 0.046	0.642 ± 0.045	0.810 ± 0.036	5.181	1087
b43	0.087 ± 0.046	0.067 ± 0.036	0.704 ± 0.045	0.771 ± 0.035	3.358	990
b74	0.227* ± 0.057	0.150* ± 0.041	0.509 ± 0.371	0.659 ± 0.031	5.366	1015
b90	0.218* ± 0.058	0.160* ± 0.046	0.577 ± 0.042	0.737 ± 0.037	5.255	893
b100	0.182* ± 0.059	0.156* ± 0.052	0.698 ± 0.054	0.853 ± 0.041	5.108	895
b101	0.118 ± 0.048	0.086 ± 0.036	0.643 ± 0.042	0.728 ± 0.034	4.106	955
b average	0.180	0.140	0.637	0.776	4.836	8975

^*Line with heritability and additive genetic variance that are significantly different from zero after Bonferroni correction.

Bottleneck effects on trait means:

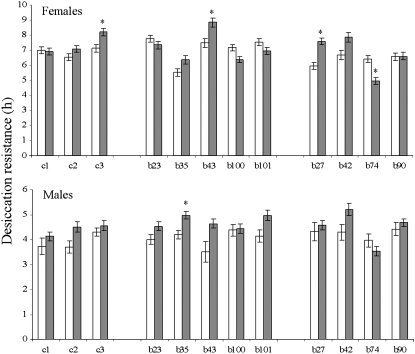
A nested ANOVA indicated that the single-generation bottleneck in D. bunnanda did not have a significant effect on desiccation resistance (F_1,10 = 0.133, P = 0.723); however, there was a significant line effect within the bottlenecked lines (F_8,8 = 6.343, P < 0.01), as well as a sex effect (F_1,8 = 1175.966, P < 0.001) and a significant line (within bottlenecked treatment) × sex interaction (F_8,9012 = 4.407, P < 0.001). Bottlenecking did not influence mean desiccation resistance in a consistent direction (Figure 1); a post hoc analysis (Bonferroni) revealed some bottleneck lines had significantly higher mean desiccation resistance than the control lines (b35) and (b43), while others had a significantly lower mean desiccation resistance (b74) and (b90). These results indicate that bottlenecking did not lead to consistent inbreeding depression in desiccation resistance.

Figure 1.—

Mean desiccation resistance of control (solid diamonds) and bottleneck (open diamonds) lines (both sexes) four generations after the bottleneck event, before starting the selection experiment. Error bars are plus or minus standard errors. The asterisk indicates bottleneck lines significantly different from control lines (Bonferroni post hoc test).

There was also no effect of bottlenecking on mean sternopleural bristle number (F_1,9 = 0.899, P = 0.368). However, there was a significant line effect within the bottlenecked lines (F_8,8 = 16.070, P < 0.001), as well as a sex effect (F_1,8 = 443.702, P = 0.001) and a significant line (within bottlenecked treatment) × sex interaction (F_8,9001 = 5.896, P < 0.001). A post hoc analysis (Bonferroni) found three bottleneck lines (b74, b90, and b101) had significantly lower mean sternopleural bristle number than the control lines (Figure 2).

Figure 2.—

Mean sternopleural bristle number in D. bunnanda control (solid diamonds) and bottleneck lines, four generations after the bottleneck event (open diamonds). Error bars are ±1 standard error. The asterisk indicates bottleneck lines significantly different from control lines (Bonferroni post hoc test).

Line-cross experiment:

Desiccation resistance:

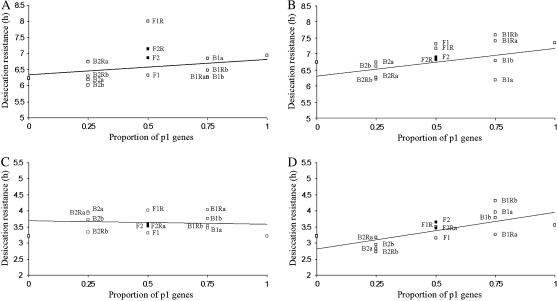
Line crosses were performed between the original base population and b27, a line that had shown no net change in V_A after the bottleneck, and b43, which had experienced an increase in V_A relative to the outbred control (Table 1). A t-test examining parental means found significant differences between females from b43 and the control line (t = −3.126, d.f. = 43, P < 0.01), but not for males of this cross (t = 0.318, d.f. = 32, P = 0.753) or for males (t = −0.823, d.f. = 32, P = 0.416) and females (t = −1.743, d.f. = 43, P = 0.088) from the cross between b27 and the control line. Line-cross analysis for the pair including the control line and b27 revealed that genetic divergence was mainly based on additive gene effects, although a significant negative additive maternal effect was detected for females (Table 3), evident in the lower level of desiccation resistance in the backcrosses where the dam was from b27 (Figure 3B). Significant additive × dominance effects were detected for males (evident in the high desiccation resistance of the backcrosses to the bottleneck parent, Figure 3D); however, including this parameter did not significantly improve the model.

TABLE 3.

Estimates of genetic effects underlying divergence in desiccation resistance between bottleneck lines and the original nonbottleneck line

		Line pair
Sex	Parameter	b27 × c2	b43 × c2
Females	m	1.258 ± 0.081***	4.093 ± 0.929***
	[a]	0.888 ± 0.214***	1.351 ± 0.290***
	[d]		−6.352 ± 2.116**
	[aa]		−2.629 ± 0.897**
	[ad]		*
	[dd]		4.380 ± 1.254***
	[a]m	−0.472 ± 0.147**	−0.682 ± 0.155***
	a.dm		−1.523 ± 0.387***
	χ2	12.332, NS	9.584, NS
Males	m	−1.607 ± 0.064***	−1.354 ± 0.067***
	[a]	0.569 ± 0.134***
	[ad]	*
	d.am		**
	χ2	19.684, NS	15.349, NS

The χ²-values were calculated using models that include only the parameters whose values are shown. Asterisks without numbers include parameters that were not necessary to produce a satisfactory model, but that significantly improved the fit between the model and the data. *P < 0.05; **P < 0.01; ***P < 0.001; NS, not significant.

Figure 3.—

Mean desiccation resistance, measured as hours to mortality, as a function of the proportion of genes derived from p1, the most resistant (bottleneck) parent, in each cross (A, b43 × c2 females; B, b27 × c2 females; C, b43 × c2 males; and D, b27 × c2 males). The solid line is the expectation of a maximum-likelihood additive model. For clarity, standard errors are not shown, but the height of the symbols used is approximately half a standard error in all cases. Labels indicate parents in each cross (see supplemental Table 1 for details).

On the other hand, analysis of data for the pair including the “higher V_A” line of b43 revealed that a simple additive model was not able to adequately explain genetic divergence. Many parameters, including [d], [aa], [ad], [dd], [a]_m, and a.dm had to be included to explain the generation means between females (Table 3). Furthermore, the magnitudes of [d], [aa], and [ad] were quite high in comparison to [a] (Table 3). In this line combination, females from the reciprocal F₁ generation (with the control line as the dam) were more desiccation resistant than either parent, suggesting negative dominance and/or maternal effects, while the F₁ with the dam coming from line b43 tended to be much less desiccation resistant than the reciprocal F₁ and either parent (Figure 3A), which could be due to a breakdown of additive × additive interactions. Interestingly, this pattern of higher resistance in the reciprocal cross was also evident in the F₂ generation, however, with levels of desiccation resistance intermediate to the F₁ and reciprocal F₁, again indicative of a negative maternal dominance effect and simple dominance effects. Levels of desiccation resistance in the backcross generations tended to be lower than expected, which could be due to dominance × dominance effects (Figure 3A). Similar to the trend noted by Kearsey and Pooni (1996), [d] and [dd] were opposite in sign, indicating duplicate rather than complementary epistasis. Because [aa] and [ad] are influenced by dispersion (the distribution of alleles in the parental populations), the direction of these effects is less clear. In contrast to the females, the genetic effects underlying desiccation resistance between males in crosses between the control and b43 were predominately additive; although a significant positive dominance × additive maternal effect was detected, adding this effect did not significantly improve the model (Table 3).

Sternopleural bristle number:

With the exception of the cross between the control and b43, where females were found to have significant additive effects ([a] = 0.2051, P < 0.001), models without genetic effects were sufficient to describe the observed means for sternopleural bristle number in crosses (c2 × b27 females, χ² = 16.066, P = 0.246; c2 × b27 males, χ² = 13.169, P = 0.435; c2 × b43 males, χ² = 15.094, P = 0.302). These results indicate that bottlenecking did not generate any nonadditive genetic variance for sternopleural bristle number.

Response to selection for increased desiccation resistance:

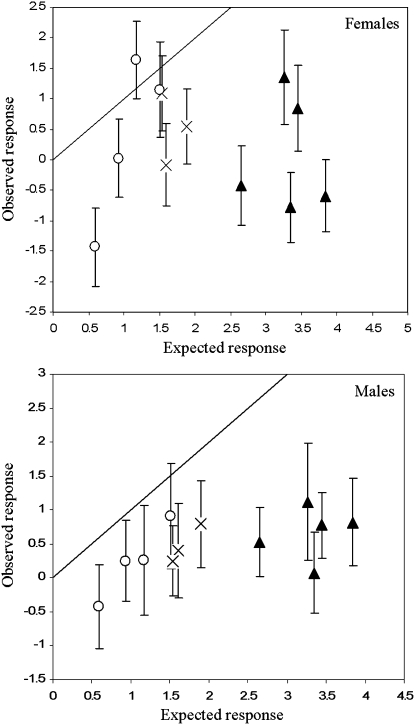
After 11 generations of strong selection, a nested ANOVA (Table 4) detected no overall significant difference in desiccation resistance between the selected and unselected lines (F_1,9 = 4.218, P = 0.070). Additionally, there was no significant interaction between selection and line type (F_2,9 = 0.087, P = 0.918), indicating that any change in desiccation resistance due to selection was the same between the control lines, the bottleneck lines that showed relatively high heritability values, and the bottleneck lines that showed heritabilities close to zero. However, a significant interaction between sex, selection, and line (nested within treatment) was observed (F_18,2221 = 5.535, P < 0.001), reflecting significant increases in desiccation resistance for certain sexes in some lines (Figure 4). In a Wilcoxon signed ranks test there was a significant trend for a response in the male bottlenecked lines (one-tailed, P = 0.014), but not in female bottleneck lines (one-tailed, P = 0.285). Despite a trend for a response in males and a significant response in some lines, responses were not strong (1.275-fold increase in resistance in the line with the strongest response). Furthermore, there was no correlation between the expected and the observed response (Figure 5); the response to selection was significantly less than expected in the five bottleneck lines that showed an increase in V_A (t = 11.072, d.f. = 9, P < 0.001), in the bottleneck lines that did not show an increase in heritability (t = 3.072, d.f. = 7, P < 0.05), and in the controls (t = 7.013, d.f. = 5, P < 0.001).

TABLE 4.

Mean square values from a nested ANOVA examining the effects of selection on the control and bottleneck lines

	d.f.	Mean square
Treatment	2	13.416
Selection	1	70.711
Sex	1	3270.802***
Line within treatment	9	26.497
Treatment × selection	2	1.454
Selection × line within treatment	9	16.859
Treatment × sex	2	23.160
Selection × sex	1	2.972
Treatment × selection × sex	2	6.142
Selection × sex × line within treatment	18	14.967***
Error	2221	2.704

Probabilities for F ratio, ***P < 0.001. Treatments are control, bottleneck lines with h² > 2 SE from zero, and bottleneck lines with estimates of h² close to zero.

Figure 4.—

Mean desiccation resistance of unselected (open bars) and selected (11 generations) (shaded bars) control and bottleneck lines for females (top) and males (bottom). Lines are grouped on the basis of whether they are control lines (left), lines with h² estimates two standard errors above zero (middle), and lines with h² estimates close to zero (right). The asterisk indicates a significant (P < 0.05) difference between unselected and selected lines after Bonferroni correction.

Figure 5.—

Observed response to selection for increased desiccation resistance against the expected response (based on heritability and standard deviation of V_P estimated from parent–offspring analysis and selection intensity) in females (top) and males (bottom) in the three control lines (crosses), the five bottleneck lines with narrow sense heritabilities >2 SE from zero (solid triangles), and the four bottleneck lines with heritability estimates close to zero (open circles). Error bars are 95% confidence intervals of observed response.

DISCUSSION

While it has been shown theoretically and empirically that a bottleneck can increase V_A for traits with a nonadditive genetic basis, it is unclear whether this increase has any impact on selection responses and thereby evolutionary potential. Experimental studies to date have focused on laboratory populations of model organisms and traits that already exhibit high levels of V_A. Where an increase in V_A has been found following bottlenecks, severe inbreeding depression has hindered a response above outbred controls. In this study, we examined whether a bottleneck could release V_A and break the evolutionary limit for desiccation resistance in the rain forest-restricted D. bunnanda. As previously described in Kellermann et al. (2006), we found extremely low levels of V_A, which were not significantly different from zero, for desiccation resistance in the outbred control lines of D. bunnanda. In this study we found that V_A and narrow-sense heritability for desiccation resistance were on average higher in the bottleneck lines than in the control lines and significantly different from zero. Despite this result, a strong increase in desiccation resistance through artificial selection was not realized.

Previous bottleneck studies have not been able to directly disentangle factors contributing to an increase in V_A following bottlenecks. Consequently, there is little consensus whether dominance or epistatic gene effects underlie increases in V_A following bottlenecks. However, inbreeding depression in fitness traits showing increases in V_A following a bottleneck suggests that increases in these cases are due to the conversion of dominance to V_A (Willi et al. 2006). Wang et al. (1998) compared the empirical observation of increases in V_A for viability in D. melanogaster to their own predictions based on a dominance model, using parameters derived from various mutation-accumulation experiments on D. melanogaster. They found the dominance model could explain the observed increase in V_A for viability with bottlenecking in this species (Lopez-Fanjul and Villaverde 1989; Garcia et al. 1994) and concluded that dominance alone is likely to be generally responsible for changes in V_A after bottlenecking. In contrast, others have agued that epistasis has contributed to increases in V_A following a bottleneck. Bryant et al. (1986) inferred that epistasis contributed to the inflation of V_A for morphometric traits in the housefly, Musca domestica, because increases in V_A were highest in bottlenecks of intermediate size. However, for epistasis there is not always a strict relationship between the magnitude of V_A increasing and the level of inbreeding (Goodnight 1988). Furthermore, Bryant and Meffert (1993) did not find the same pattern, and they concluded that models of both dominance and epistasis fit their data. However, they had few replicate lines and insufficient power to discriminate whether increases in V_A were due to dominance, epistasis, or chance fluctuations in an additive system. Cheverud et al. (1999) suggested epistasis was responsible for V_A not decreasing as predicted under an additive model for body weight in inbred lines of mice. However, this was based on previous findings of extensive epistatic interactions between body weight quantitative trait loci in mice and the assumption that single-locus dominance effects should not lead to an increase in V_A at their intermediate levels of inbreeding because recessive alleles will be at intermediate frequencies.

Models have predicted that V_A will increase after a bottleneck with a small inbreeding coefficient only if V_AA is more than four times V_A (Cockerham and Tachida 1988; Barton and Turelli 2004). However, an increase in adaptive evolution has been considered unlikely as the allele frequencies and magnitude of epistasis conducive to an increase in V_A are unrealistic for natural populations experiencing natural selection (Lopez-Fanjul et al. 2002; Turelli and Barton 2006). Furthermore, due to the stochastic nature of genetic drift, it is possible that following a bottleneck V_A may be larger than expected under an additive model even with a purely additive architecture (Lynch 1988). In this study, a line-cross design was able to directly show that a range of dominance, maternal, and epistatic effects were involved in the divergence in desiccation resistance between females (but not males) of the original control line and a bottlenecked line exhibiting increased V_A for desiccation resistance. In the former cross, the levels of nonadditive effects were high in comparison to additive effects, suggesting that epistasis and dominance effects may be substantial for desiccation resistance in D. bunnanda females. However, the level of additive × additive epitasis was not strong in comparison to dominance and dominance × dominance interactions. No studies have directly modeled how V_DD or V_AD will influence V_A after a bottleneck. Cheverud and Routman (1996) predicted V_A will also increase with V_DD and V_AD, but to a much lesser extent than predicted for V_AA. Their model was based on intermediate initial allele frequencies, and it is unclear what size of variance components will lead to an enhancement of V_A. Although this study suggests both epistasis and dominance effects were involved in the observed changes in V_A after a bottleneck in females from one bottleneck line showing an increase in V_A, such effects were not found in males of the same cross. They were also not found in either males or females from the cross between the original control population and a bottleneck line where no change in mean resistance or V_A was observed. Additional line crosses in multiple-bottleneck lines are required to test if these patterns generally occur and whether the genetic architecture underlying resistance in D. bunnanda varies between the sexes.

Maternal effects were evident in three of four crosses and these may arise from X chromosome effects or from other factors like maternal environmental effects. Our crossing design allowed Y and cytoplasmic effects to be estimated (none were found), but not X chromosome effects. If only X linkage had been involved, males from parental mothers with a relatively high level of resistance might be expected to have a higher level of resistance than those from the reciprocal cross, and female offspring that obtain X chromosomes from both parents might not be expected to show maternal effects. However, maternal effects were detected for both sexes in this experiment, suggesting the effects cannot be explained purely on the basis of X linkage. Maternal effects for desiccation resistance were common in crosses between tropical and temperate populations of D. melanogaster from Australia and South America (Kennington et al. 2001) but were not detected in crosses between D. serrata populations (Blows 1993).

These results for desiccation resistance contrast to what we found for sternopleural bristle number, a trait we predicted should predominately be under additive gene action. In accordance with Kristensen et al. (2005), who found a decrease in V_A with inbreeding in D. melanogaster, changes in V_A after a bottleneck for sternopleural bristle number in D. bunnanda were almost exactly as predicted assuming a purely additive genetic architecture. Furthermore, line-cross analysis found no evidence for any dominance or epistatic effects underlying divergence between the control and two bottleneck lines. One other study has compared the changes in variance for a fitness trait and a morphological trait. Similar to the results obtained in this study, the authors found a much stronger decrease in V_A for the morphological trait after a bottleneck (Wade et al. 1996).

Other studies that have used artificial selection on bottleneck lines with increased V_A have been unable to increase the trait mean above values for control lines. Lopez-Fanjul and Villaverde (1989) found the response to selection was 6.5 times higher in bottlenecked (F = 0.25) relative to control lines for increased viability in D. melanogaster, but this response was only enough to recover from half of the inbreeding depression incurred. Similarly, Garcia et al. (1994) found no difference in the mean viability of inbred selection lines compared to controls after 27 generations of selection. In these cases, it appears that the variation released with inbreeding was deleterious and did not provide a source of variation for increasing traits beyond the original mean. In our study we found an increase in V_A and statistically significant heritabilities but no inbreeding depression, indicating that the variation released was not necessarily deleterious. However, there was only a weak response to selection in the bottlenecked males and in some female lines, which was uncorrelated to levels of V_A in the bottleneck lines.

Several reasons might help to explain why the observed selection response was much less than the expected response based on the narrow-sense heritability estimates. First, our estimates of h² may have been inaccurate. However, the standard errors computed from the animal model analyses were low, and the responses were much less than expected as can be seen from the lack of overlap between the 95% confidence interval of the observed response in Figure 5. Second, it is possible that any increase in V_A may have been only transient and not high enough to sustain a selection response. Third, as a response occurs, further changes in allele frequencies are expected along with changes in V_A influenced by allele frequencies and genetic background. As novel V_A released through dominance and epistatic effects is dependent on genetic background, it is vulnerable to rapid elimination by natural selection, although we might then expect at least some selection response. Finally, there could be another underlying reason besides low levels of V_A for a weak response to selection for increased desiccation resistance in this species. Negative maternal effects for desiccation resistance, evident in two of the four line crosses, suggest there could be an antagonistic maternal effect of desiccation resistance, which could reduce a selection response (Kirkpatrick and Lande 1989; Wolf et al. 1998; Wilson and Reale 2006). Additionally, artificial selection may have been opposed by natural selection on this trait in the laboratory, particularly as the bottlenecking procedure would have exposed recessives with deleterious effects on fitness-related traits; if antagonistic natural selection is important, selecting every second generation may have exaggerated this effect. Hidden pleiotropic effects inducing stabilizing selection on one character may hinder directional selection on another (Baatz and Wagner 1997). Furthermore, genetic interactions with other traits can also limit selection responses even when V_A is present (Blows and Hoffmann 2005). It would be worthwhile to select for desiccation sensitivity in these lines, perhaps through family-level selection, to investigate whether selection in this direction is possible. Also, selecting under different environmental conditions and using a less intense desiccation stress may have more success. Furthermore, as we did see a sex-specific trend for a response in some lines, we could attempt to select for a longer time and at a higher intensity. However, high-intensity artificial selection for 30 generations also failed to increase desiccation resistance in an outbred laboratory population of the rain forest-restricted D. birchii despite a trend for a response early on (Hoffmann et al. 2003). Nonetheless, whether shifts in desiccation resistance can occur in natural populations in response to selection is unknown.

The results from our study have implications for the evolutionary importance of bottlenecks. Despite the absence of inbreeding depression, additive genetic variation released by bottlenecking in D. bunnanda did not result in a stronger selection response. Unfortunately, it appears that D. bunnanda and other rain forest Drosophila may not easily respond to selection for increased desiccation resistance (Hoffmann et al. 2003; Kellermann et al. 2006). The results from these rain forest species are in sharp contrast to the rapid and strong responses to selection obtained for this trait in other Drosophila species (Blows and Hoffmann 1993; Hoffmann and Parsons 1993). There may be other ways of generating novel variation for selection, such as by decreasing canalization or through the creation of novel mutations via X-ray mutagenesis. However, inhibition of Hsp90 via the chemicals geldanamycin and radicicol failed to increase variation for desiccation resistance in D. birchii (Kellermann et al. 2007), suggesting that this approach is also not useful for increasing the response to selection for increased desiccation resistance in these species. In light of the predicted changes in climate and increasing levels of other anthropogenic stresses, more research needs to be conducted on ways to break selection limits in species with low V_A.