Skip to main content
NCBI home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2008 Aug 4;105(32):11182–11187. doi: 10.1073/pnas.0802524105

Dynamic energy landscape view of coupled binding and protein conformational change: Induced-fit versus population-shift mechanisms

Kei-ichi Okazaki 1, Shoji Takada 1,*
PMCID: PMC2516237  PMID: 18678900

Abstract

Allostery, the coupling between ligand binding and protein conformational change, is the heart of biological network and it has often been explained by two representative models, the induced-fit and the population-shift models. Here, we clarified for what systems one model fits better than the other by performing molecular simulations of coupled binding and conformational change. Based on the dynamic energy landscape view, we developed an implicit ligand-binding model combined with the double-basin Hamiltonian that describes conformational change. From model simulations performed for a broad range of parameters, we uncovered that each of the two models has its own range of applicability, stronger and longer-ranged interaction between ligand and protein favors the induced-fit model, and weaker and shorter-ranged interaction leads to the population-shift model. We further postulate that the protein binding to small ligand tends to proceed via the population-shift model, whereas the protein docking to macromolecules such as DNA tends to fit the induced-fit model.

Keywords: allostery, multiple-basin model, coarse-grain model

Biological network is constructed by series of molecular recognitions and responses, which are ultimately attributed to conformational change of biomolecules on binding to their partners. Traditionally, the coupling between the binding and the conformational transition was explained by the 50-year-old induced-fit model of Koshland (1), in which proteins are in their apo conformations in the unbound state, and binding to the apo forms induces conformational transition to the holo conformations. This model is apparently supported by accumulated examples of x-ray structures of the same protein in apo (open) form without the ligand and in holo (closed) form with the ligand (2, 3). Recently, however, growing evidence, primarily by NMR and computer simulations, suggests that protein is dynamic, and that intrinsic dynamics of a protein in the unbound state involves transient motion toward closed and functional conformation (4–7). An emerging view thus is that proteins in the unbound state exist in many conformers that include open and closed ones and that, on binding, the dominant population shifts from the open form to the closed one. This “population-shift,” or conformational selection model, originated from the Monod–Wyman–Changeux model of allostery (8) is more popular in recent years (9, 10).

Interestingly, the induced-fit model, or induced folding model when the unbound state is disordered, was suggested many times for protein–protein and protein–DNA binding (11–13), whereas the population-shift model was proved primarily for antigen-antibody binding and substrate-binding to enzymes (14–16). A single-molecule observation showed that, depending on ligand, the binding mechanism can change between the two (17). These may suggest that each of two alternative models may have its own range of applicability and motivated us to investigate for what system and under what condition one mechanism fits better than the other.

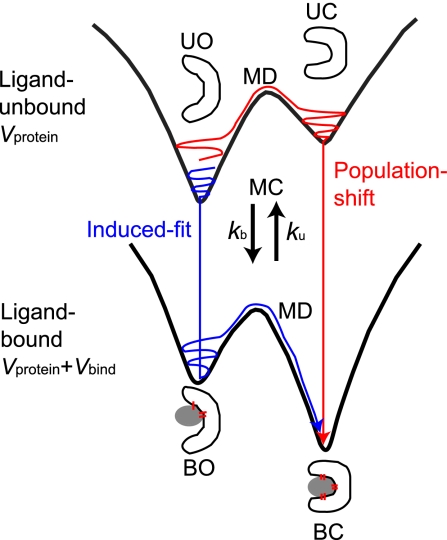
To address these issues, we need to deal with ensemble aspects of protein dynamics, which may be best realized by the global energy landscape perspective of proteins (18, 19): The protein has a globally funnel-like energy landscape, and when the bottom of the funnel is magnified, multiple minima exist among which protein dynamically transits in functional motion. On top of this standard landscape view, the energy landscape shape needs to be altered on binding or releasing its interacting partner (20, 21). This led us to a view of dynamic energy landscape (20–22). A protein in the unbound state resides primarily in an open form with the lowest energy, and a less-stable minimum may exist near a closed form (Fig. 1). Binding to the ligand changes the energy landscape so that the closed form becomes the lowest energy (Fig. 1). By modeling binding and release as jumps between two energy landscapes, we can naturally represent the induced-fit and the population-shift scenarios as specific routes on the two landscapes. We note that it tends to be thought that the dynamic energy landscape theory is directly linked to the population-shift model, but this is not true. In the induced-fit scenario, a protein sitting at the open conformer on the unbound surface (UO in Fig. 1) binds the ligand to jump onto the bound surface (BO), which is followed by the conformational change to the closed conformation (BC). Conversely, in the population-shift scenario, the protein preexists in the closed form without ligand (UC in Fig. 1) at some small probability and this fraction can bind the ligand directly to reach the BC. The majority of the molecules resides in the UO state before binding. Part of this fraction promptly makes the conformational transition to UC state so that the system achieves the equilibrium on the unbound surface. Thus, for the majority, the protein transits from UO to UC, and to BC. The question is, thus, which is the on-pathway intermediate from UO to BC, BO (which suggests the induced-fit) or UC (suggesting the population-shift)?

Fig. 1.

Fig. 1.

Open in a new tab

A schematic view of the dynamic energy landscape. Protein can reside on one of two energy landscapes, one landscape for ligand-unbound (U) and the other for bound (B) states. Each landscape has (at least) two minima, one for open (O) and the other for closed (C) conformations. Thus, there are four states, UO, UC, BO, and BC. Protein can jump between two landscapes by the ligand binding/unbinding.

We investigated what kinds of ligand-binding processes employ the induced-fit route and vice versa, by performing a series of molecular simulations of coupled binding and conformational transition with a minimalist model of proteins. Technically, the multiple-basin energy landscape is realized by the structure-based multiple-basin model Hamiltonian recently proposed (23–26), and the ligand-binding model is proposed here as the stochastic jump between two surfaces. We used glutamine-binding protein as a model protein for illustration of the idea (Fig. 2A). The relative simplicity of the model made it possible to simulate binding and unbinding processes coupled with conformational change so many times for a variety of parameter sets. Instead of concentrating on one set of parameters that could be closest to the protein, here, we emphasize the advantage of exploring a broad range of parameters. In this way, we can get better insights on the allostery. We found that stronger and longer-ranged interaction tends to favor the induced-fit pathway, and vice versa. In the end, we postulate that the protein binding to small ligand favors the population-shift pathway, whereas the protein docking to macromolecules may primarily be via the induced-fit pathway.

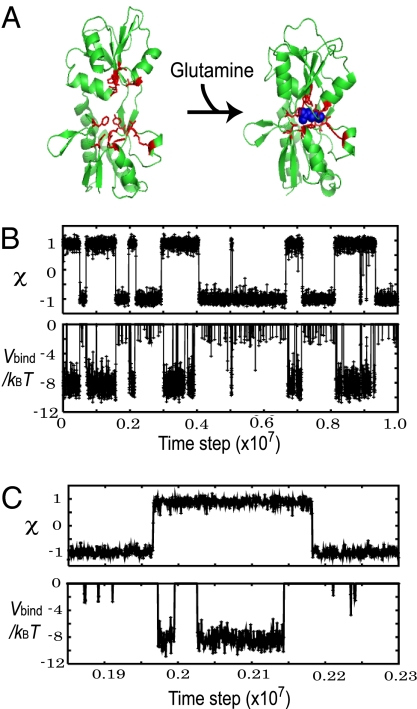
Fig. 2.

Fig. 2.

Open in a new tab

A representative trajectory of the model protein. (A) The open and closed structures of glutamine-binding protein and its ligand, glutamine (blue). The ligand-binding residues are represented in red sticks. (B Upper) A representative time course of the conformational change coordinate χ. Its negative (positive) value corresponds to the open (closed) conformation. (B Lower) A time course of the ligand-binding energy, Vbind, for the same trajectory as Upper. (C) A small time window in the trajectory of B is magnified.

Results

Modeling Ligand Binding and Protein Conformational Transition.

We described that a protein has two distinct ligand-binding states; bound (B) and unbound (U) states. In the unbound state, the protein has just its intraenergy, Vprotein, whereas the protein in the bound state has the intraenergy plus the ligand-binding energy, Vprotein + Vbind. The protein intraenergy Vprotein is expressed by all of the Cα-atoms, and is set up so that it has the global minimum at the open (O) conformation and a less-stable minimum at the closed (C) conformation (see Materials and Methods for explicit expressions). The ligand-binding energy Vbind does not contain the explicit coordinates of the ligand atoms, but is a function of the Cartesian coordinates of ligand-binding sites of the protein (see Materials and Methods for details). Vbind takes negative and large absolute value when the local environment around the binding pocket is close to that of the closed (C) conformation, and Vprotein + Vbind has its global minimum at the closed conformation. We note that in the reference x-ray structures the open (O) conformation corresponds to the ligand-unbound (U) state and the closed (C) corresponds to the bound (B) state, but this is not explicitly imposed in the simulation so that the protein experiences BO and UC states at some, albeit small, probabilities.

In time propagation, the protein conformation is moved by the standard molecular dynamics (MD) simulation, whereas the ligand-binding state (B or U) is stochastically changed by the rates kb (binding) and ku (unbinding) implemented as the Metropolis Monte Carlo (MC) scheme (Fig. 1). While in the unbound state, a ligand molecule reaches the binding pocket at every Δtb time with probability p = kbΔtb = kD[L]Δtb. With this probability, the state changes to the bound (B) one. Here, kb is the apparent first-order rate for binding, kD is the diffusion-controlled second-order rate constant for binding, and [L] is the ligand concentration. While in the bound state, at every Δtu time, the bound ligand has a chance to dissociate at a probability that depends on Vbind. The mixed MD-MC scheme proposed here is a convenient way of simulating protein conformational dynamics coupled with ligand binding. (See Materials and Methods for details.)

The strength of interaction Vbind is controlled by a coefficient denoted as clig and the range of Vbind interaction is defined by the length-scale parameter σ (see Materials and Methods for expressions), both of which will play crucial roles below.

Binding and Conformational Transitions Are Stochastically Coupled.

By using the glutamine-binding protein as a model system (Fig. 2A), we simulated binding-coupled conformational dynamics at various parameters. Fig. 2B is a representative time course when about half of the time the protein was in the bound state. In Fig. 2B Upper, the reaction coordinate χ that monitors the conformation is negative (positive) at the open (closed) conformations. The conformation changed reversibly and quite abruptly (Each transition completed in ≈1,000 MD steps) many times in the trajectory. The ligand-binding energy Vbind of the same trajectory in Fig. 2B Lower also showed sudden transitions, but their timings were not identical to those of conformational transitions (More clearly, see Fig. 2C, which is a close-up of a particular time window). Vbind took roughly three energy levels; 0 (unbound), ≈−3kBT (weak-binding energy) and ≈−8kBT (strong-binding energy). Comparing to the time course of χ, we see that the closed conformation tended to have strong-binding energy, whereas the open-form protein took weak-binding energy or the unbound state.

Notably, conformational transitions and bindings/releases did not occur simultaneously. In the trajectory of Fig. 2C, we see that the protein tended to change its conformation from the open to the closed conformation slightly before ligand-binding, suggesting the population-shift mechanism. Conversely, when the protein transited from closed to open conformations, the ligand-unbinding was followed by the conformational transition. It is interesting to note that the conformational change to the closed form initiated the binding, that is, the population-shift scenario, whereas the unbinding initiated the conformational change to the open form: Thus, the sequences of events are reversed. Below, we investigated these coupling mechanisms in more detail depending on the nature of binding interactions.

Free-Energy Surface of Conformational Change and Ligand Binding.

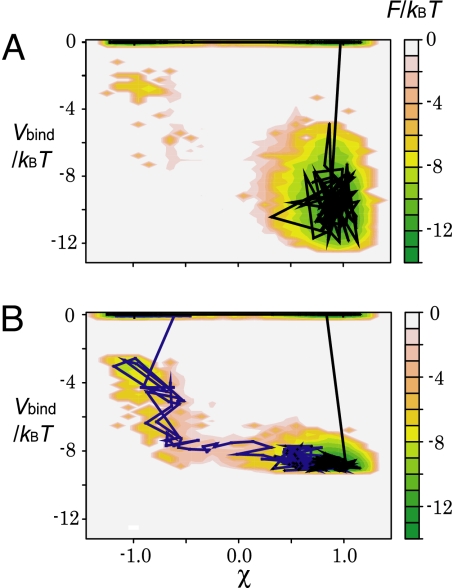
To see the coupling between protein conformational change (monitored by χ) and ligand binding (monitored by Vbind) more directly, we computed the free-energy surface on the χ − Vbind plane (Fig. 3 where typical trajectories are superimposed). Four states, unbound open (UO), unbound closed (UC), bound open (BO), and bound closed (BC) states, are seen on the free-energy surfaces. We note that the ligand-binding state here is discrete, that is, either bound or unbound, and thus the free-energy surfaces and trajectories are discontinuous between Vbind = 0 and Vbind < 0. Results for two different ranges of interactions are shown in Fig. 3 A and B; the former (latter) corresponds to shorter (longer) range interactions. We note that the strength coefficient clig of interaction was tuned for each case so that about half of the time the protein was in the bound state.

Fig. 3.

Fig. 3.

Open in a new tab

Two-dimensional free-energy surfaces as a function of protein conformational change (χ) and the ligand-binding energy (Vbind). (A) The case of the short-ranged interaction σ/r0ij = 0.05. The black line is a representative trajectory. (B) The case of the long-ranged interaction σ/r0ij = 0.15. The black and blue lines are two representative trajectories.

With a shorter-range interaction (σ = 0.05r0ij), the dominant pathway from UO to BC passed through UC, suggesting that it corresponded to the population-shift pathway: Conformational change was followed by the ligand binding (Fig. 3A). On the contrary, with a longer-range interaction (σ = 0.15r0ij) (Fig. 3B), in addition to the population-shift pathway, we saw the alternative induced-fit pathway, where the binding was followed by the conformational change (Fig. 3B). The range of ligand-binding interaction directly altered the coupling between the binding and the conformational change.

Induced-Fit Versus Population-Shift: Four States Analysis.

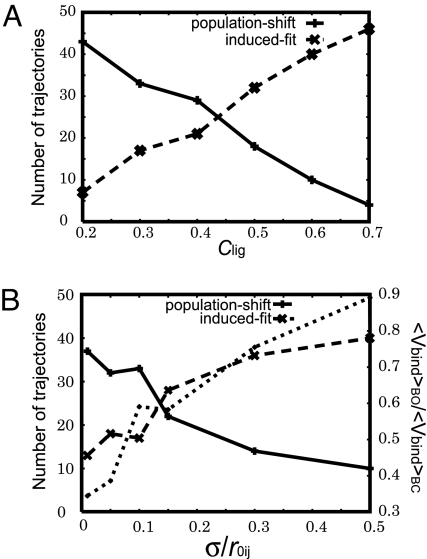
For more quantitative argument, we conducted the first-passage analysis. Starting from the UO state, we performed simulations until the protein reached the BC state for the first time. Once the protein reached the BC state, we observed from which it reached, either BO or UC. We simulated 50 runs for each parameter set.

First, we looked into the effect of the interaction strength clig (Fig. 4A) onto the pathway. We found that, as the ligand interaction became stronger, the ratio of the induced-fit pathway increased. This suggests that stronger interaction between the ligand and the protein tends to favor the induced-fit mechanism.

Fig. 4.

Fig. 4.

Open in a new tab

The first-passage analysis from UO to BC. Of 50 trajectories, the number of trajectories that went through BO (dashed line, denoted as induced-fit) and UC (solid line, denoted as population-shift) is plotted. (A) The ligand-binding strength (clig) is altered. (B) The interaction range σ is altered, whereas the strength of ligand interaction (clig) is tuned, in each point, so that the ligand is bound for half of the simulation time in equilibrium condition. In B, the ratio of the average ligand-binding energy in the BO state relative to that in the BC state, 〈Vbind〉BO/〈Vbind〉BC, is also plotted with the dotted line, for which the scale on the right applies.

Next, we investigated the effect of the range of interactions σ. Because, as in the previous paragraph, we know that the shift in equilibrium between unbound and bound drastically changes the pathway, for each value of σ, we tuned the parameter clig so that the time spent in the bound state is 50%. The result showed clear dependence of the ratio of the population-shift pathway on the range of ligand interaction (Fig. 4B): The shorter-range ligand interaction favors the population-shift pathway and vice versa.

In summary, as ligand-binding interaction becomes stronger, the dominant pathway shifts from population-shift to induced-fit. When the ligand affinity is the same, shorter-range ligand interaction favors the population-shift pathway, and vice versa.

Transition Rates and Equilibrium Constants in Four States Representation.

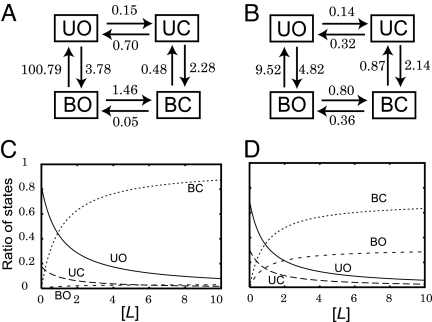
For further dissecting the transitions among four states, we calculated every transition rate between two-adjacent states in the four states representation, which also gave us the equilibrium constants (See supporting information (SI) Text for details). We note that the binding rate constant given here is an apparent first-order rate for a given concentration of the ligand. The resulting rates are shown in Fig. 5A (in unit of 10−5 per MD step) for a short-ranged interaction σ = 0.05r0ij and in Fig. 5B for a long-ranged one σ = 0.03r0ij. In either case, the strength coefficient clig was tuned up so that ligand was bound for half of the time.

Fig. 5.

Fig. 5.

Open in a new tab

The rate constants between the four states (in units of 10−5 per MD step). The binding rate constants here are apparent first-order rates at a given ligand concentration. (A) The case of the short-ranged ligand interaction (σ = 0.05rij). (B) The case of the long-ranged ligand interaction (σ = 0.3r0ij). (C and D) The equilibrium titration curves of four states against the ligand concentration. c was derived from the equilibrium constants in a, and d was derived from the equilibrium constants in b.

In the case of short-ranged interaction (Fig. 5A), the rate constant from BO to UO is markedly large. The short-ranged interaction is sensitive to the conformation of the binding site. Because the binding is assumed to be optimized at the closed conformation, the binding energy at the open form (BO) is small in absolute value, which led to the low-equilibrium population in BO. A simple steady-state analysis from UO to BC resulted in that the population-shift pathway is twice as probable as the induced-fit pathway (see SI Text for details).

On the contrary, for the long-ranged interaction case (Fig. 5B), the same steady-state analysis gave that the induced-fit pathway is three times as probable as the population-shift. The longer-range interaction is less sensitive to the conformation of the binding site, so that the BO state has more stability. The transition from UO to BO is fast. Thus, the population of BO is relatively large and it is possible for it to be promptly refilled, which makes the induced-fit pathway favored.

Because the apparent first-order rate constants of the ligand-binding are proportional to the ligand concentration, we can put the ligand-concentration dependence back in the diagrams in Fig. 5 A and B. From these, we calculated the equilibrium titration curves of four states, as depicted in Fig. 5 C and D. [L] is scaled as the unit of the ligand concentration used in simulations. For both short- and long-ranged interaction cases, as expected, the concentration of BC increased, and that of UO decreased with the ligand concentration. When we focus on the regime where the concentrations of UO and BC are comparable ([L] ∼ 1), the short-ranged case (Fig. 5C) results in UC being more favored than BO, whereas the long-ranged interaction (Fig. 5D) gives comparable concentrations of BO and UC.

Discussion

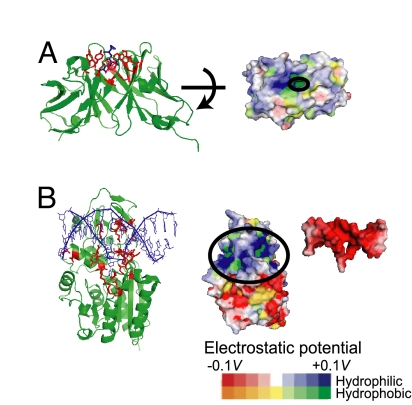
We elucidated that strong and long-ranged ligand interaction favors the induced-fit mechanism, whereas weak and short-ranged ligand interaction leads to the population-shift mechanism in the simulation study. Now, we look into some examples for which the coupling mechanisms were relatively well established experimentally. Binding of an antigen, hapten DNP-Ser, to an antibody, SPE7, was characterized to take the population-shift pathway (14). SPE7 in its unbound state is in equilibrium between two preexisting conformers (Ab1 and Ab2), one of which (Ab2) corresponds to the ligand-bound conformation. Looking into the binding site characteristics, we noticed that the binding site of SPE7 is hydrophobic surrounded by many bulky aromatic rings. Its partner, hapten, is also hydrophobic having an aromatic ring (Fig. 6A). Thus, their interaction is primarily a hydrophobic interaction and specific hydrogen bonding, both of which are short-ranged. This is consistent with our finding.

Fig. 6.

Fig. 6.

Open in a new tab

Molecular examples that were suggested to show the population-shift (A) and the induced-fit (B) mechanisms. (A) An antibody, SPE7, and its ligand hapten DNP-ser. (Left) SPE7 dimer in cartoon with its binding sites in red sticks. Hapten DNP-Ser in blue stick. (Right) Hydrophobicity/hydrophilicity and the electrostatic potential of SPE7 are shown by color. The ligand-binding site is highly hydrophobic. (B) M.HhaI (DNA cytosine C5 methyltransferase) binding to DNA via the induced-fit mechanism. (Left) M.HhaI in cartoon with its binding sites in red-stick representation, and DNA is in blue. (Right) Hydrophobicity/hydrophilicity and the electrostatic potential of both molecules. The binding sites of M.HhaI (DNA) have high (low) electrostatic potential, indicating that their binding is via the electrostatic potentials. The electrostatic potentials were drawn by eF-site and PDBjViewer (38).

The induced-fit mechanism has been suggested for various DNA-protein binding. Here, we picked up M.HhaI, DNA cytosine C5 methyltransferase, which binds to DNA substrates (27). A flexible loop within M.HhaI (residues 80–100) recognizes the cognate DNA. It has been shown that the loop is reorganized to the closed conformer when the enzyme binds to cognate DNA, but not closed when it binds to nonspecific DNA, suggesting that the recognition process of the loop is induced-fit. Not surprisingly for the DNA-binding protein, the binding loop of the protein is positively charged, and DNA is negatively charged. (Fig. 6B). Thus their interaction is mainly electrostatic and, thus, is long-ranged. On top, because DNA is a relatively large ligand, the interaction energy between M.HhaI and DNA is likely to be very large. All these are consistent with our finding.

Although the allostery is inherently the dynamic problem, its kinetics is constrained by the underlying energetics. Energetically, putting aside kinetics, the induced-fit pathways would be favored when both of the following conditions hold: (i) With a high concentration of ligand in solution, the BO state is significantly more stable than the UO, and (ii) the BC is more stable than the BO. We assume that the ligand binding is strongest at the closed conformation and that the fraction of the ligand–protein interaction in the BC state is formed in the BO state. We directly see that the stronger ligand-binding energy tends to satisfy the above two conditions, thus guiding to the induced-fit pathways. Long-ranged interaction between protein and ligand tends to satisfy the first condition above because long-ranged interaction makes the interaction energy less sensitive to the conformation of protein and, thus, the ligand–protein interaction at the open conformer is increased, that is, the first condition above, which thus supports the induced-fit mechanism. We tested this interpretation by computing 〈Vbind〉BO/〈Vbind〉BC, and found that this ratio correlates very well with the fraction of the induced-fit pathway (the dotted line in Fig. 4B). If the interaction range is too large, however, the interaction energy becomes nearly the same between the open and closed conformers, which is opposed to the second condition above. In the limit, the conformation would not change to the closed form. In this context, probably, having a large interface between protein and ligand would be beneficial to have the induced-fit pathway, in part, because the large interface implies strong interaction and, in part, because the large interface makes it easy to have a partial, yet significant, interaction in the BO state and the rest of interaction achieved in the BC state. Therefore, we postulate that protein interaction with small ligand tends to favor the population-shift pathway as in the cases of antibody-antigen and enzyme-substrate, whereas protein docking to DNA, RNA, or protein with large interface favors the induced-fit.

Although we shed light on relatively simple cases, real molecular systems must contain more complexity. First, conformational change does not proceed uniformly, but may be hierarchic. For example, a substructure near the binding site may move differently from the rest of the protein. In this two-mode case, one mode may correspond to the population-shift model, whereas the other mode may fit the induced-fit (28). A specific role of a loop near an active site was characterized for horse liver alcohol dehydrogenase (29). Another very plausible scenario is the “population-shift followed by induced-fit” pathway. Unbound protein has a transient local minimum, which is not identical but is directed toward the closed conformation. Ligand binding shifts the population to this partially closed conformation, which further induces conformational change up to the closed conformation. Substrate binding and product release in enzymes turns on another type of complexity because the substrate and the product are not the same, opening a possibility that binding and release have different pathways.

Conclusions

By using the multiple-basin model of protein conformational change and a newly developed implicit ligand-binding model, we investigated the interplay between the induced-fit and the population-shift mechanisms of coupled binding and conformational transition process. We found that strong and long-ranged interaction favors the induced-fit pathway, whereas weak and short-ranged interaction leads to the population-shift pathway. These are consistent with many available experimental data.

The coarse-grained model of coupled binding and conformational change developed here is quite general and can be applied to simulate a broad range of large-amplitude motion in the biomolecular complex, such as ATPase and other macromolecular machines (30, 31).

Materials and Methods

Model Protein.

We chose glutamine-binding protein as a model protein throughout the article. On binding to a glutamine its conformation changes from open to closed form, which is an archetypical hinge-bending motion (Fig. 2A). We used two x-ray structures, ligand-free open form (PDB ID code 1GGG) and ligand-bound closed form (PDB ID code 1WDN). In simulations, we used 5–224 residues, discarding those missing in the PDB structures. We note that we used this protein for illustrative purpose: Parameters in the model do not necessarily faithfully correspond to those in the real glutamine-binding protein.

The Protein Intraenergy.

The protein intraenergy Vprotein is defined as the multiple-basin model, which was recently proposed (25). In brief, in this study, we used two fiducial structures of the protein, open Ropen and closed Rclosed structures. First we prepared single-basin Go potentials for each of two fiducial structures, V(R|Ropen) and V(R|Rclosed), where we used Clementi et al.'s version of the off-lattice Gō potential (32). For purely technical reasons, we modified the repulsive part of the Go model, as presented in ref. 25. Parameter values for the single Go potentials are identical to those in ref. 25 (see SI Text for details). By connecting these single-basin potentials smoothly, we constructed the two-basin potential,

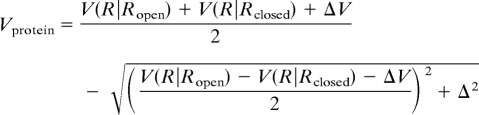graphic file with name zpq03208-4128-m01.jpg

where Δ is a coupling constant that regulates the energy barrier height between two states, ΔV is a parameter that sets the relative stability of two basins. Here, we used Δ = 74 kBT and ΔV = −2.7 kBT, except for the first passage analysis (there, ΔV = −4.8 kBT was used). With these parameters, the open conformation had lower free energy than the closed conformation. The reaction coordinate χ defined by exp2χ = (V(R|Ropen) − Vprotein)/(V(R|Rclosed) − Vprotein) is useful for monitoring the conformational transition, which takes negative (positive) in open (closed) conformation.

Ligand-Binding Model.

The ligand-binding energy Vbind does not contain the explicit coordinates of the ligand atoms, but is a function of the Cartesian coordinates of protein amino acids that are directly involved in ligand binding, which is somewhat similar to ref. 35. We first identified the residues involved to ligand binding by using LIGPLOT (36). Among these residues, we then defined “ligand-mediated contact pairs” as pairs of which Cα–Cα distance is <10Å and that is not included in the native contact pair. For each of these ligand-mediated pairs, we adopted a Gaussian function so that we can separately control the minimum and the width of the potential,

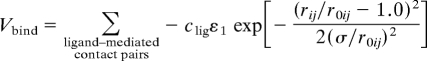graphic file with name zpq03208-4128-m02.jpg

where ε1 is the depth for the native contact, clig is a parameter that changes strength of ligand-mediated contact. r0ij is the distance between i- and jth residues at the closed form and, thus, Vbind takes the minimum value when the local environment around the binding pocket coincides with that of the closed form. σ/r0ij defines the interaction range.

The MD-MC Simulations.

The protein structure was propagated by the standard MD method, whereas the ligand-binding state was updated via a MC method. MD simulation was carried out by using the constant temperature Newtonian dynamics, where the mass of all residues was set to identical. The velocity Verlet algorithm was used for time propagation with a simple Berendsen thermostat (33). We estimated the folding temperatures of single-basin Go models for the open and the closed forms by using the Weighted Histogram Analysis Method (34), and used 0.8 times the lower of two folding temperatures as the simulation temperature.

The MC transition between ligand-bound and unbound states was characterized by binding and unbinding rate constants kb and ku. At a given [L], the apparent ligand-binding rate is given by kb = kD[L]. The binding is assumed to be diffusion-controlled, and so the second-order rate constant kD is given as kD = 4DS(R) (37). D is the diffusion constant for a glutamine. Based on comparison with all-atom simulation, we estimated a MD step of the current model as 100 fs. This, together with an experimental estimate of the diffusion constant, we set D = 1.0 × 10−2 [Å2 per MD step]. S(R) is the length scale of the binding site, for which we adopted the distance between Phe-50 and Lys-115 that are located on the edge of the binding site. This depends on protein conformation; S(R) ≈ 22.7 Å in the open form, and S(R) ≈ 8.6 Å in the closed form. So, the ligand access is easier in the open form. The ligand concentration [L] is set as 0.1 M unless otherwise stated. The ligand unbinding rate is given by ku = Δtu−1 exp(−|Vbind|/kBT), where Δtu corresponds to a period of fluctuations of a residue in the binding site, and is now set to 100 MD time steps.

Supplementary Material

Supporting Information
supp_105_32_11182__index.html (662B, html)

Acknowledgments.

This work was supported in part by a Ministry of Education, Science, Sports, and Culture of Japan Grant-in-Aid for scientific research in priority areas “Chemistry of Biological Processes Created by Water and Biomolecules.” K.O. is supported by Research Fellowships of the Japan Society for the Promotion of Science for Young Scientists.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/cgi/content/full/0802524105/DCSupplemental.

References

  • 1.Koshland D. Application of a theory of enzyme specificity to protein synthesis. Proc Natl Acad Sci USA. 1958;44:98–104. doi: 10.1073/pnas.44.2.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Flores S, et al. The Database of Macromolecular Motions: New features added at the decade mark. Nucleic Acids Res. 2006;34:D296–D301. doi: 10.1093/nar/gkj046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Qi G, Lee R, Hayward S. A comprehensive and non-redundant database of protein domain movements. Bioinformatics. 2005;21:2832–2838. doi: 10.1093/bioinformatics/bti420. [DOI] [PubMed] [Google Scholar]
  • 4.Volkman BF, Lipson D, Wemmer DE, Kern D. Two-state allosteric behavior in a single-domain signaling protein. Science. 2001;291:2429–2433. doi: 10.1126/science.291.5512.2429. [DOI] [PubMed] [Google Scholar]
  • 5.Henzler-Wildman KA, et al. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
  • 6.Bahar I, Chennubhotla C, Tobi D. Intrinsic dynamics of enzymes in the unbound state and relation to allosteric regulation. Curr Opin Struct Biol. 2007;17:633–640. doi: 10.1016/j.sbi.2007.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Ikeguchi M, Ueno J, Sato M, Kidera A protein structural change upon ligand binding: Linear response theory. Phys Rev Lett. 2005;94 doi: 10.1103/PhysRevLett.94.078102. 078102. [DOI] [PubMed] [Google Scholar]
  • 8.Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions: A plausible model. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
  • 9.Bosshard HR. Molecular recognition by induced fit: How fit is the concept? News Physiol Sci. 2001;16:171–173. doi: 10.1152/physiologyonline.2001.16.4.171. [DOI] [PubMed] [Google Scholar]
  • 10.James LC, Tawfik DS. Conformational diversity and protein evolution—A 60-year-old hypothesis revisited. Trends Biochem Sci. 2003;28:361–368. doi: 10.1016/S0968-0004(03)00135-X. [DOI] [PubMed] [Google Scholar]
  • 11.Bui JM, McCammon JA. Protein complex formation by acetylcholinesterase and the neurotoxin fasciculin-2 appears to involve an induced-fit mechanism. Proc Natl Acad Sci USA. 2006;103:15451–15456. doi: 10.1073/pnas.0605355103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Levy Y, Onuchic JN, Wolynes PG. Fly-casting in protein-DNA binding: Frustration between protein folding and electrostatics facilitates target recognition. J Am Chem Soc. 2007;129:738–739. doi: 10.1021/ja065531n. [DOI] [PubMed] [Google Scholar]
  • 13.Sugase K, Dyson HJ, Wright PE. Mechanism of coupled folding and binding of an intrinsically disordered protein. Nature. 2007;447:1021–1025. doi: 10.1038/nature05858. [DOI] [PubMed] [Google Scholar]
  • 14.James LC, Roversi P, Tawfik DS. Antibody multispecificity mediated by conformational diversity. Science. 2003;299:1362–1367. doi: 10.1126/science.1079731. [DOI] [PubMed] [Google Scholar]
  • 15.Arora K, Brooks CL., III Large-scale allosteric conformational transitions of adenylate kinase appear to involve a population-shift mechanism. Proc Natl Acad Sci USA. 2007;104:18496–18501. doi: 10.1073/pnas.0706443104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Hanson JA, et al. Illuminating the mechanistic roles of enzyme conformational dynamics. Proc Natl Acad Sci USA. 2007;104:18055–18060. doi: 10.1073/pnas.0708600104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Nevo R, Brumfeld V, Elbaum M, Hinterdorfer P, Reich Z. Direct discrimination between models of protein activation by single-molecule force measurements. Biophys J. 2004;87:2630–2634. doi: 10.1529/biophysj.104.041889. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of protein folding: The energy landscape perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
  • 19.Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
  • 20.Tsai CJ, Ma B, Nussinov R. Folding and binding cascades: Shifts in energy landscapes. Proc Natl Acad Sci USA. 1999;96:9970–9972. doi: 10.1073/pnas.96.18.9970. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Kumar S, Ma B, Tsai CJ, Sinha N, Nussinov R. Folding and binding cascades: dynamic landscapes and population shifts. Protein Sci. 2000;9:10–19. doi: 10.1110/ps.9.1.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Gulukota K, Wolynes PG. Statistical mechanics of kinetic proofreading in protein folding in vivo. Proc Natl Acad Sci USA. 1994;91:9292–9296. doi: 10.1073/pnas.91.20.9292. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Maragakis P, Karplus M. Large amplitude conformational change in proteins explored with a plastic network model: Adenylate kinase. J Mol Biol. 2005;352:807–822. doi: 10.1016/j.jmb.2005.07.031. [DOI] [PubMed] [Google Scholar]
  • 24.Best RB, Chen YG, Hummer G. Slow protein conformational dynamics from multiple experimental structures: the helix/sheet transition of arc repressor. Structure. 2005;13:1755–1763. doi: 10.1016/j.str.2005.08.009. [DOI] [PubMed] [Google Scholar]
  • 25.Okazaki K, Koga N, Takada S, Onuchic JN, Wolynes PG. Multiple-basin energy landscapes for large-amplitude conformational motions of proteins: Structure-based molecular dynamics simulations. Proc Natl Acad Sci USA. 2006;103:11844–11849. doi: 10.1073/pnas.0604375103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Miyashita O, Onuchic JN, Wolynes PG. Nonlinear elasticity, proteinquakes, and the energy landscapes of functional transitions in proteins. Proc Natl Acad Sci USA. 2003;100:12570–12575. doi: 10.1073/pnas.2135471100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Estabrook RA, Reich N. Observing an induced-fit mechanism during sequence-specific DNA methylation. J Biol Chem. 2006;281:37205–37214. doi: 10.1074/jbc.M607538200. [DOI] [PubMed] [Google Scholar]
  • 28.Formaneck MS, Ma L, Cui Q. Reconciling the “old” and “new” views of protein allostery: a molecular simulation study of chemotaxis Y protein (CheY) Proteins. 2006;63:846–867. doi: 10.1002/prot.20893. [DOI] [PubMed] [Google Scholar]
  • 29.Hayward S, Kitao A. Molecular dynamics simulations of NAD+-induced domain closure in horse liver alcohol dehydrogenase. Biophys J. 2006;91:1823–1831. doi: 10.1529/biophysj.106.085910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Koga N, Takada S. Folding-based molecular simulations reveal mechanisms of the rotary motor F1-ATPase. Proc Natl Acad Sci USA. 2006;103:5367–5372. doi: 10.1073/pnas.0509642103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Hyeon C, Onuchic JN. Mechanical control of the directional stepping dynamics of the kinesin motor. Proc Natl Acad Sci USA. 2007;104:17382–17387. doi: 10.1073/pnas.0708828104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Clementi C, Nymeyer H, Onuchic JN. Topological and energetic factors: What determines the structural details of the transition state ensemble and “en-route” intermediates for protein folding? An investigation for small globular proteins. J Mol Biol. 2000;298:937–953. doi: 10.1006/jmbi.2000.3693. [DOI] [PubMed] [Google Scholar]
  • 33.Berendsen HJC, Postma JPM, van Gunsteren WF, DiNola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. [Google Scholar]
  • 34.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J Comput Chem. 1992;13:1011. [Google Scholar]
  • 35.Whitford PC, Miyashita O, Levy Y, Onuchic JN. Conformational transitions of adenylate kinase: Switching by cracking. J Mol Biol. 2007;366:1661–1671. doi: 10.1016/j.jmb.2006.11.085. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Wallace AC, Laskowski RA, Thornton JM. LIGPLOT: A program to generate schematic diagrams of protein-ligand interactions. Protein Eng. 1995;8:127–134. doi: 10.1093/protein/8.2.127. [DOI] [PubMed] [Google Scholar]
  • 37.Shoup D, Lipari G, Szabo A. Diffusion-controlled bimolecular reaction rates. The effect of rotational diffusion and orientation constraints. Biophys J. 1981;36:697–714. doi: 10.1016/S0006-3495(81)84759-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Kinoshita K, Nakamura H. eF-site and PDBjViewer: Database and viewer for protein functional sites. Bioinformatics. 2004;20:1329–1330. doi: 10.1093/bioinformatics/bth073. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_105_32_11182__index.html (662B, html)
0802524105_0802524105SI.pdf (132.6KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES