Abstract
Are humans able to perceive the circularity of a cylinder that is grasped by the hand? This study presents the findings of an experiment in which cylinders with a circular cross-section had to be distinguished from cylinders with an elliptical cross-section. For comparison, the ability to distinguish a square cuboid from a rectangular cuboid was also investigated. Both elliptical and rectangular shapes can be characterized by the aspect ratio, but elliptical shapes also contain curvature information. We found that an elliptical shape with an aspect ratio of only 1.03 could be distinguished from a circular shape both in static and dynamic touch. However, for a rectangular shape, the aspect ratio needed to be about 1.11 for dynamic touch and 1.15 for static touch in order to be discernible from a square shape. We conclude that curvature information can be employed in a reliable and efficient manner in the perception of 3D shapes by touch.
Keywords: Aspect ratio, Circle, Ellipse, Square, Rectangle, Dynamic touch, Static touch
Introduction
The shape of a standard drinking glass is a cylinder with a round contour, but is the contour really a circle? One way to check is by measuring the diameter at several places with a ruler, or a vernier caliper. Alternatively, you may grasp the glass and judge whether the shape feels circular or not. However, does your haptic sense provide you with accurate and reliable information about the shape of the drinking glass? If you grasp another object, like a square glass vase, are you able to distinguish whether the contour of the vase is a square or a rectangle? Are you better in judging the regularity of circles or squares?
Klatzky et al. (1985) showed that humans are accurate and fast in recognizing daily life objects by touch. However, daily life objects are characterized by a multitude of properties, like shape, weight, temperature, and compressibility. To study the role of shape information in object perception and recognition, objects that are made from the same material but differ in shape should be used as stimuli. Studies that focused on shape recognition performance used stimuli like polyhedrons (Lakatos and Marks 1999), unfamiliar objects created from LEGO bricks (Newell et al. 2001), or solid copies of bell peppers (Norman et al. 2004). Using stimuli like these provide insight into the global and local aspects that are characteristic for objects that are explored by touch; however, an inconvenience is that many aspects of the stimuli that are compared change concurrently.
A more systematic approach to shape perception uses a stimulus set in which the elements are from the same, geometrically well-defined class; successive stimuli vary only slightly in the magnitude of a single stimulus parameter. Roland and Mortensen (1987) investigated discrimination performance of 3D objects like ellipsoids and parallelepipeds. The task was to discriminate the more oblong object from the less oblong object, for objects of equal volume. They found a high performance for the ellipsoids, shapes that are characterized by differences in local curvature. Ellipsoids are geometrically well-defined shapes but rather complex, since, in terms of size, they are described by three independent parameters; the curvature is defined locally by two independent parameters. The complexity of the stimulus makes it difficult to relate the performance of the subject to the shape of the stimulus.
In order to obtain a more direct relationship between shape and perception, several discrimination studies have been conducted that used stimuli with a constant curvature. Using this kind of stimuli allowed systematic variations in the stimulus size and the exploration mode. One group of studies concentrated on shape perception by static touch, either with a single fingertip (Goodwin et al. 1991, 1997; Jenmalm et al. 2003), with a part of the hand (Pont et al. 1997, 1999), or with the whole hand (Vogels et al. 1999). Other studies focussed on curvature perception by dynamic touch, which was performed with a single finger (Gordon and Morison 1982; Pont et al. 1998, 1999; Van der Horst and Kappers 2007), with various amount of fingers (Davidson 1972) or with the whole hand (Kappers et al. 1994; Kappers and Koenderink 1996). Analogous experiments have been conducted on shapes that were created in a virtual environment (Henriques and Soechting 2003; Provancher et al. 2005; Drewing and Ernst 2006). This overview is far from complete but illustrates the variety of studies that have been performed on constant curvature shape perception. These studies have shown that human subjects are able to perceive small differences in curvature but can be biased by differences in the orientation of the stimulus (Pont et al. 1998; Henriques and Soechting 2003), the length of exploration (Pont et al. 1999), or the finger that is employed (Van der Horst and Kappers 2007).
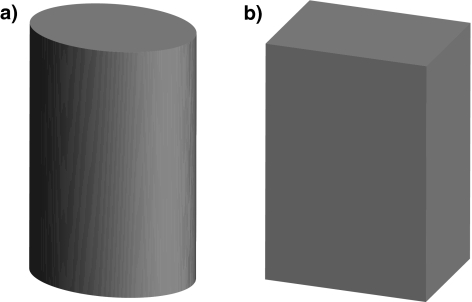
The stimuli that were used in these studies were not whole objects, only surface parts. In general, the task for a subject was to compare the curvature of one surface to the curvature of another surface. The question arises whether this ability to discriminate curvature differences can be used when judgments are made about the shape of complete 3D objects, like drinking glasses. Therefore, we designed stimuli that contained curvature differences in one direction within a stimulus and, for comparison, stimuli without curvature information. The first category of stimuli is cylinders with an elliptical cross-section; the other category is cuboids, which have a rectangular cross-section (see Fig. 1). Since the cross-sections are the determining aspects, we refer to these stimuli as ellipses and rectangles, respectively.
Fig. 1.
Illustrations of the stimuli, a right elliptical cylinder (a) and a cuboid (b). The horizontal cross-sections of these stimuli are an ellipse and a rectangle, respectively. The height of a stimulus was 150 mm. Details about the dimensions of the cross-sections are provided in Fig. 2
In the experiment that we conducted, subjects had to distinguish either an ellipse from a circle or a rectangle from a square. For the rectangles, only the ratio between the lengths of the perpendicular main axes is informative about the shape. For the ellipses, differences in local curvature may provide additional information to this aspect ratio information. However, this theoretical advantage for ellipses does not necessarily result in a higher performance since the performance depends on the ability and accuracy to extract information from the stimulus. When the orientation of the stimulus is unknown in advance, it is evident in which directions the two main axes of a rectangle are oriented; thus, it is obvious which lengths should be compared, but this is not true for an ellipse. This suggests that, if the judgement is only based on aspect ratio information, performance should be better for rectangles than for ellipses.
This disadvantage in obtaining aspect ratio information from ellipses might be compensated or overcome when curvature information can be used. The local curvature varies over the surface of an ellipse, whereas it is constant for a circle. Hence, an ellipse can be distinguished from a circle when differences or changes in curvature can be perceived. However, the ability to extract shape information from an object may be biased by spatial factors and exploratory procedures. When elliptical contours were traced in the horizontal plane with a finger in a thimble, an ellipse that was elongated in the tangential direction (aspect ratio of 1.06) was perceived as a circle (Hammerschmidt 1934; Von Skramlik 1937). Henriques and Soechting (2003) found similar biases for ellipses that were traced in a virtual environment. Experiments on length perception have also shown that radially explored lengths were overestimated compared to tangentially explored lengths; the magnitude of the effect depended on the exploration mode (e.g., Armstrong and Marks 1999; McFarland and Soechting 2007). Depending on the spatial orientation of the stimulus or the manner of exploration, a square may be perceived as a rectangle and a circle may be perceived as an ellipse, or vice versa.
The manner of exploration might determine how accurate and efficient shape information can be obtained from the stimulus. As mentioned, several factors may bias the result. In the current experiment we made a distinction between static touch and dynamic touch. In static touch, the stimulus is touched by a single grasp with the hand; in dynamic touch, free explorations around the stimulus surface are allowed. Manipulation of the stimulus is not allowed in order to exclude inertia differences that could influence shape perception (see e.g., Turvey 1996). Judging the shape of an ellipse by static touch might be difficult, since the local curvature impression at one place of the hand should be compared to the local curvature impression at another place of the hand. Dynamic touch seems advantageous, since touching a circle gives a constant impression over time, whereas an ellipse provides a changing profile. For the rectangles, dynamic touch may also be more informative than static touch. In static touch, the side lengths of the stimulus should be compared with different parts of the hand. In dynamic touch, a combination of different grasping postures and movements along the stimulus surface may provide more information. For both ellipses and rectangles, dynamic touch may provide more but possibly conflicting information, due to exploratory dependent biases. This may impair the performance in dynamic touch.
Methods
Stimuli
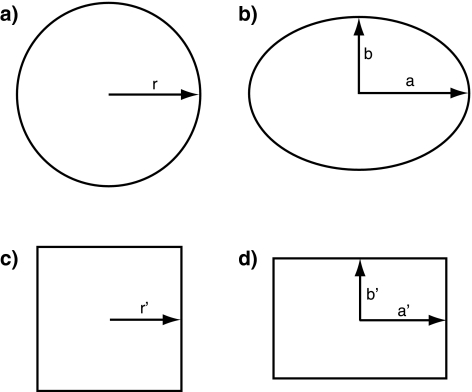
The stimuli were made of a compound of polyurethane foam and artificial resin (Cibatool BM 5460) and manufactured on a computer controlled milling machine. The stimuli are right cylinders, which means that all horizontal cross-sections lie directly on top of each other. The height was 150 mm. The stimuli are defined in terms of the aspect ratio of the horizontal cross-section (α), which is defined as the quotient of the semi major axis (a) and the semi minor axis (b). The product of a and b is equal for all ellipses, which means that the areas of the cross-sections are equal and thus the volumes of the elliptical stimuli are equal. A circle is a special case of an ellipse, in which the length of a and b are equal and coincide with the radius (r) of the circle. The length of r is 35 mm. The areas of the cross-sections of the rectangles are also equal but differ from the areas of the cross-sections of the ellipses. The dimensions of the rectangles are chosen in such a way that the perimeter of the square equals the perimeter of the circle. Fig. 2 illustrates the cross-sections of the stimuli.
Fig. 2.
Schematic illustrations of the cross-sections of the stimuli. a Cross-section of a circular cylinder with radius r of 35 mm. b Cross-section of a noncircular, elliptical cylinder, with semi major axis a and semi minor axis b. The aspect ratio is the quotient of a and b. The product of a and b is equal to r squared. c Cross-section of a square cuboid. The perimeter of this square equals the perimeter of the circle in (a). d Cross-section of a rectangular cuboid. The product of a′ and b′ is equal to r′ squared
In each condition, a reference stimulus was combined with seven test stimuli. For the conditions with the ellipses, test stimuli with aspect ratios of 1.006, 1.010, 1.016, 1.020, 1.04, 1.06, and 1.08 were used; the reference stimulus was a circle. For the conditions with the rectangles, aspect ratios of 1.06, 1.08, 1.10, 1.12, 1.17, 1.22, and 1.27 were used; the reference stimulus was a square. The ranges of the test stimuli were based on pilot experiments.
Procedure
Subjects were seated behind a table. A blindfold prevented them from seeing the stimuli. A stimulus was placed in front of the subject at 40 cm from the edge of the table. The experimenter held the stimulus at the upper part to prevent translation or rotation of the stimulus. The orientation of the stimuli, i.e., the direction of the semi major axis in the plane of the table, was random, but for the rectangle conditions, similar for both stimuli within a trial. During a trial, a subject touched a test stimulus and subsequently a reference stimulus, or vice versa. The task was to indicate which of the two stimuli was the circle (square).
In the dynamic conditions, subjects explored the stimuli with their right hand. They were free to explore the surface of the stimuli in the way that they liked but were not allowed to explore the surfaces and edges at the upper and lower parts of the stimuli. In practice, they performed a combination of grasping and sliding movements. In the static conditions, subjects were instructed to grasp the stimuli with the whole hand without making further sliding contact with the surface of the stimuli.
Each condition consisted of 98 trials, which were presented in a pseudorandom order: groups of all possible combinations of test and reference stimuli were randomized and presented successively. Four conditions (two shapes × two exploration modes) were included. The order in which the conditions were measured was different for each subject; either two condition with the same exploration mode or two conditions with the same shape were presented in a single session. A single session lasted about 60–90 min. For one subject, we had to repeat the experiment in the rectangle × static condition with an adjusted stimulus range.
Subjects
The results for eight paid subjects (four male and four female, mean age 20 years) are reported. The result of another subject was not included, since no psychometric curve could be fitted to the data of two conditions. All subjects were right-handed, as established by a standard questionnaire (Coren 1993).
Analysis
For each subject and condition, the fraction of correct responses was calculated for each test stimulus value. The data were plotted against the relative aspect ratio (α − 1), which is a Weber fraction, on a logarithmic scale. The logarithmic scale enables an analysis that assumes that performance is at a chance level when the relative aspect ratio reaches zero.
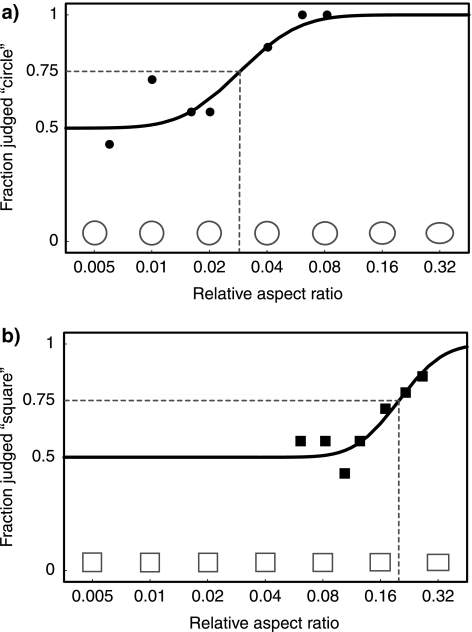
The detection threshold was determined by fitting a psychometric function (cumulative Gaussian) to the data. Fig. 3 shows an example of two psychometric curves for one subject in an ellipse condition and in a rectangle condition.
Fig. 3.
Examples of psychometric curves for an ellipse condition (a) and for a rectangle condition (b). The response is plotted against the relative aspect ratio, which is defined as the aspect ratio minus 1. Note that a logarithmic scale is used. The ellipses (rectangles) that are drawn above the horizontal axis illustrate the shape of the ellipse (rectangle) for the values that are indicated on the horizontal axis. A psychometric function was fitted to the data. The detection threshold is defined as the relative aspect ratio value for which the psychometric function equals 0.75
Results
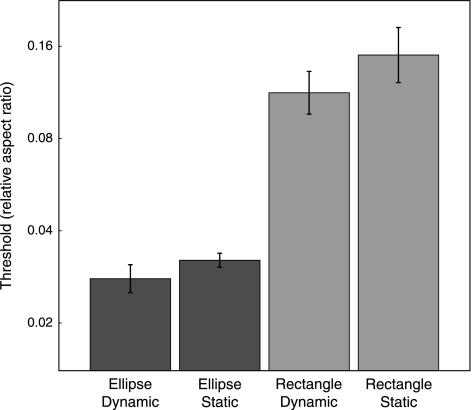
Figure 4 shows the mean detection thresholds for eight subjects in all conditions. The error bars represent the standard errors. Note that the results are plotted on a logarithmic scale. The significance of the results was tested by performing a two (shape) by two (exploration) ANOVA. Both main factors were significant (F 1,7 = 55, P < 0.001 for shape; F 1,7 = 6.4, P = 0.04 for exploration), but there was no significant interaction between shape and exploration (F 1,7 = 0.6, P = 0.5).
Fig. 4.
Mean detection threshold results of eight subjects in all conditions. The error bars represent standard errors. Note that the scale is logarithmic
Discussion
The experiment reveals a considerable difference in performance to distinguish an ellipse from a circle and a rectangle from a square. The mean threshold for the ellipses is about four times lower than for the rectangles. In addition, the experiment shows that allowing dynamic touch improves the performance in comparison to static touch, although this effect is rather modest. The large difference in performance between ellipses and rectangles indicates that curvature information can be used in a reliable manner.
Roland and Mortensen (1987) showed previously that curvature differences could be used in the detection of 3D shapes that varied in three dimensions. The stimuli that we used were also 3D objects, but the informative shape varied only in two dimensions, which allows a comparison with several studies that have been conducted previously.
Comparison with 2D tasks
A visual analogue of our experiment was conducted by Zanker and Quenzer (1999), who used 2D ellipses and rectangles that were presented on a computer screen. They found similar thresholds for distinguishing an ellipse from a circle and a rectangle from a square (on average 0.04 and 0.05, respectively). Obviously, task and performance in the visual experiment were different from those in our experiment; we found a slightly better performance for the ellipse conditions and a much worse performance for the rectangle conditions (on average 0.03 and 0.13, respectively).
Helbig and Ernst (2007) compared visual and haptic performance for ellipse discrimination of small, elliptical ridges (circle radius of 5 mm). In the haptic condition, the top of a ridge was explored with a single index finger; subjects had to judge whether the stimulus was elongated in the horizontal or vertical direction. The thresholds75 were 0.03 in the visual condition and 0.07 in the haptic condition.1 We should be careful in comparing the findings of Helbig and Ernst to our results, since the dimensions of the stimuli differed between the studies and the designs of the experiments were different (discrimination experiment versus detection, respectively). However, the thresholds differ by more than a factor of two, which indicates that extracting the 2D shape from the surface of a 3D object is more efficient than when only the top surface and edges are used.
In the introduction, we referred to studies in which orientation dependent biases were found when elliptical contours were traced (Hammerschmidt 1934; von Skramlik 1937; Henriques and Soechting 2003). In addition, the thresholds that Henriques and Soechting (2003) reported were on average 0.17, which is much higher than the threshold of 0.03 that we found. We cannot exclude the possibility that the thresholds found in our experiment were influenced by orientation dependent biases, since we did not measure this. However, a large effect would have resulted in higher detection thresholds. Our findings confirm a previous observation (Van der Horst and Kappers 2007) that shape perception with bare fingers is much more reliable than perceiving shapes in a virtual environment, as in the study by Henriques and Soechting (2003).
Comparison with curvature discrimination
It would be interesting to make a quantitative comparison between the results of the ellipses and the results of previous studies on curvature discrimination. The curvature range of the stimuli that Van der Horst and Kappers (2007, 2008) used coincides with the range of local curvature of the ellipses. In their curvature discrimination experiment, two curved surfaces were presented subsequently in the same orientation and were explored by dynamic touch. The task was to indicate which of the two stimuli felt more curved. The mean threshold75 expressed in terms of a Weber fraction is 0.06.
An ellipse might be distinguished from a circle by perceiving the difference between the maximum and minimum curvature within the ellipse. A difficulty might be that these points of curvature extrema are at perpendicular orientations with respect to each other and, in addition, that the ellipses were positioned randomly with respect to the external space. However, to perform the detection task, it is not necessary to know the positions of the curvature extrema and to discriminate the maximum from the minimum curvature, but it is sufficient to detect that there are curvature differences within the stimulus, which seems to be an easier task to perform.
The detection thresholds that we measured are expressed in terms of relative aspect ratio. How can we convert these values into relative curvature differences? An obvious way is to take the difference between the maximum and minimum curvature and to divide this value by the curvature of the circle, which results in 0.09. However, it has been shown that curvature discrimination is not based on the comparison of local curvatures but on a comparison of the differences in slope over the contact length (Gordon and Morison 1982; Pont et al. (1997, 1999). Applied to the ellipses, it is probably more realistic to assume that curvature differences are perceived by comparing the mean curvature at one place of the ellipse to the mean curvature at another place on the ellipse.
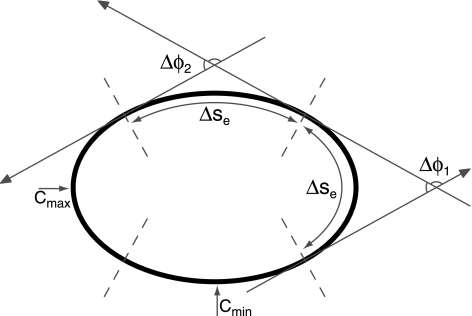
The mean curvature of a part of an ellipse with arc length Δs is defined as the change in turning angle Δφ divided by the arc length Δs. In the limit that Δs approaches zero, the mean curvature is equal to the local curvature (dφ/ds). Fig. 5 illustrates the magnitude of Δφ for equal lengths of Δs, positioned symmetrically around the points of maximum and minimum curvature, C max and C min, respectively. For this situation, a new value for the relative curvature difference at the mean threshold75 level can be calculated by dividing the difference between Δφ 1/Δs e and Δφ 2/Δs e by the curvature of the circle. This results in a value of 0.06, which is clearly lower than the value previously calculated but similar to the value obtained by Van der Horst and Kappers (2007, 2008).
Fig. 5.
Illustration of the ellipse parameters curvature (C), arc length (Δs) and turning angle (Δφ). C max and C min represent points of local maximum and minimum curvature. The arc length between two of these local extrema is Δs e. The dashed lines mark the points halfway the local extrema, hence the arc length between these points is also Δs e. Tangent lines are drawn at these places. The turning angles between two subsequent tangent lines are represented by Δφ 1 and Δφ 2, respectively
This analysis indicates that the performance to distinguish an ellipse from a circle is similar to the discrimination of curved surfaces. However, the finding of a quantitative similarity does not necessarily mean that the detection task is performed as in a discrimination task, by comparing the mean curvature at one part of the ellipse to the mean curvature at another part of the ellipse. Alternatively, humans might be sensitive to the change in curvature within the ellipse, information that is not available in the curvature discrimination tasks that we discussed.
Comparison with length discrimination
Curvature information is not available when a rectangle has to be distinguished from a square. Only the ratio between the perpendicular lengths provides information about the shape. Gepshtein and Banks (2003) investigated the ability to discriminate the distance that is perceived when two parallel surfaces are grasped between the thumb and index finger. They found a threshold75 of 0.07; this value is lower than the values that we found for the rectangles (on average 0.11 in dynamic touch and 0.15 in static touch). However, in the experiment of Gepshtein and Banks, the lengths that had to be compared were at the same place and in the same direction. Orientation and exploration dependent anisotropies might have caused an increase of the detection thresholds, as we previously suggested.
Dynamic versus static touch
The experiment showed that the detection performance was higher in dynamic touch than in static touch. This difference was especially clear for the detection of rectangles from squares. In dynamic touch, subjects grasped the stimulus from different directions, which provided more information than they could obtain from the single grasp in static touch. For the detection of circles from ellipses, the difference in performance in surprisingly small. We expected to find a better performance for dynamic touch than for static touch. In static touch, only the instantaneous curvature profile on the hand is available. In dynamic touch, additional temporal information might be obtained when the stimulus is explored; the temporal profile of a circle is constant, whereas the profile of an ellipse changes in time. Performance was slightly better for dynamic touch, but the low performance for static touch shows that humans are able to judge whether the curvature profile on the hand is constant or not by only applying static contact.
Conclusions
This study demonstrates that humans are proficient in extracting available curvature information from the surface of objects that are perceived by touch. In contrast, performance was much poorer when curvature information was lacking. It suggests that the haptic sense is suitable to perceive shape aspects from an object, like curvature information, but is less appropriate to obtain veridical information about spatial aspects, like lengths and orientations.
Finally, we return to our original questions about the ability to judge the circularity of a drinking glass and the squareness of a square vase. By only using the haptic sense, we can confidently judge that our drinking glass is circular, otherwise we should be able to feel this. However, for the judgments about a square vase, it might be better to rely on our eyes.
Acknowledgments
This research was supported by a grant from the Netherlands Organisation for Scientific Research (NWO).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Footnotes
Threshold75 means that the magnitude of the threshold was determined originally in a discrimination experiment at a 84% level, but converted by us to a 75% level. The conversion factor is 0.67.
References
- Armstrong L, Marks LE. Haptic perception of linear extent. Percept Psychophys. 1999;61:1211–1226. doi: 10.3758/bf03207624. [DOI] [PubMed] [Google Scholar]
- Coren S. The left-hander syndrome. New York: Vintage Books; 1993. [Google Scholar]
- Davidson PW. Haptic judgments of curvature by blind and sighted humans. J Exp Psychol. 1972;93:43–55. doi: 10.1037/h0032632. [DOI] [PubMed] [Google Scholar]
- Drewing K, Ernst MO. Integration of force and position cues for shape perception through active touch. Brain Res. 2006;1078:92–100. doi: 10.1016/j.brainres.2005.12.026. [DOI] [PubMed] [Google Scholar]
- Gepshtein S, Banks MS. Viewing geometry determines how vision and haptics combine in size perception. Curr Biol. 2003;13:483–488. doi: 10.1016/S0960-9822(03)00133-7. [DOI] [PubMed] [Google Scholar]
- Goodwin AW, John KT, Marceglia AH. Tactile discrimination of curvature by humans using only cutaneous information from the fingerpads. Exp Brain Res. 1991;86:663–672. doi: 10.1007/BF00230540. [DOI] [PubMed] [Google Scholar]
- Goodwin AW, Macefield VG, Bisley JW. Encoding of object curvature by tactile afferents from human fingers. J Neurophysiol. 1997;78:2881–2888. doi: 10.1152/jn.1997.78.6.2881. [DOI] [PubMed] [Google Scholar]
- Gordon IE, Morison V. The haptic perception of curvature. Percept Psychophys. 1982;31:446–450. doi: 10.3758/bf03204854. [DOI] [PubMed] [Google Scholar]
- Hammerschmidt O. Über die Genauigkeit der haptischen Verwirklichung geometrischer Grundbegriffe. Zeulenroda: B Sporn; 1934. [Google Scholar]
- Helbig HB, Ernst MO. Optimal integration of shape information from vision and touch. Exp Brain Res. 2007;179:595–606. doi: 10.1007/s00221-006-0814-y. [DOI] [PubMed] [Google Scholar]
- Henriques DYP, Soechting JF. Bias and sensitivity in the haptic perception of geometry. Exp Brain Res. 2003;150:95–108. doi: 10.1007/s00221-003-1402-z. [DOI] [PubMed] [Google Scholar]
- Jenmalm P, Birznieks I, Goodwin AW, Johansson RS. Influence of object shape on responses of human tactile afferents under conditions characteristic of manipulation. Eur J Neurosci. 2003;18:164–176. doi: 10.1046/j.1460-9568.2003.02721.x. [DOI] [PubMed] [Google Scholar]
- Kappers AML, Koenderink JJ. Haptic unilateral and bilateral discrimination of curved surfaces. Perception. 1996;25:739–749. doi: 10.1068/p250739. [DOI] [PubMed] [Google Scholar]
- Kappers AML, Koenderink JJ, Te Pas SF. Haptic discrimination of doubly curved surfaces. Perception. 1994;23:1483–1490. doi: 10.1068/p231483. [DOI] [PubMed] [Google Scholar]
- Klatzky RL, Lederman SJ, Metzger SJ. Identifying objects by touch: an “expert” system. Percept Psychophys. 1985;37:299–302. doi: 10.3758/bf03211351. [DOI] [PubMed] [Google Scholar]
- Lakatos S, Marks LE. Haptic form perception: relative salience of local and global features. Percept Psychophys. 1999;61:895–908. doi: 10.3758/bf03206904. [DOI] [PubMed] [Google Scholar]
- McFarland J, Soechting JF. Factors influencing the radial-tangential illusion in haptic perception. Exp Brain Res. 2007;178:216–227. doi: 10.1007/s00221-006-0727-9. [DOI] [PubMed] [Google Scholar]
- Newell FN, Ernst MO, Tjan BS, Bülthoff (2001) Viewpoint dependence in visual and haptic object recognition. Psychol Sci 12:37–42 [DOI] [PubMed]
- Norman JF, Norman HF, Clayton AM, Lianekhammy J, Zielke G. The visual and haptic perception of natural object shape. Percept Psychophys. 2004;66:342–351. doi: 10.3758/bf03194883. [DOI] [PubMed] [Google Scholar]
- Pont SC, Kappers AML, Koenderink JJ. Haptic curvature discrimination at several regions of the hand. Percept Psychophys. 1997;59:1225–1240. doi: 10.3758/bf03214210. [DOI] [PubMed] [Google Scholar]
- Pont SC, Kappers AML, Koenderink JJ. The influence of stimulus tilt on haptic curvature matching and discrimination by dynamic touch. Perception. 1998;27:869–880. doi: 10.1068/p270869. [DOI] [PubMed] [Google Scholar]
- Pont SC, Kappers AML, Koenderink JJ. Similar mechanisms underlie curvature comparison by static and dynamic touch. Percept Psychophys. 1999;61:874–894. doi: 10.3758/bf03206903. [DOI] [PubMed] [Google Scholar]
- Provancher WR, Cutkosky MR, Kuchenbecker KJ, Niemeyer G. Contact location display for haptic perception of curvature and object motion. Int J Robot Res. 2005;24:691–702. doi: 10.1177/0278364905057121. [DOI] [Google Scholar]
- Roland PE, Mortensen E. Somatosensory detection of microgeometry, macrogeometry and kinesthesia in man. Brain Res Rev. 1987;12:1–42. doi: 10.1016/0165-0173(87)90017-8. [DOI] [PubMed] [Google Scholar]
- Turvey MT. Dynamic touch. Am Psychol. 1996;51:1134–1152. doi: 10.1037/0003-066X.51.11.1134. [DOI] [PubMed] [Google Scholar]
- Van der Horst BJ, Kappers AML. Curvature discrimination in various finger conditions. Exp Brain Res. 2007;177:304–311. doi: 10.1007/s00221-006-0670-9. [DOI] [PubMed] [Google Scholar]
- Van der Horst and Kappers (2008) Haptic curvature comparison of convex and concave shapes. Perception (in press) [DOI] [PubMed]
- Vogels IMLC, Kappers AML, Koenderink JJ. Influence of shape on haptic curvature perception. Acta Psychol. 1999;100:267–289. doi: 10.1016/S0001-6918(98)00041-9. [DOI] [PubMed] [Google Scholar]
- Von Skramlik E. Psychophysiologie der Tastsinne. Leipzig: Akademische Verlagsgesellschaft; 1937. [Google Scholar]
- Zanker JM, Quenzer T. How to tell circles from ellipses: perceiving the regularity of simple shapes. Naturwissenschaften. 1999;86:492–495. doi: 10.1007/s001140050661. [DOI] [PubMed] [Google Scholar]