Abstract
In this perspective, we first review some of the published literature on structural modeling of the mechanical properties of the lung parenchyma. Based on a recent study, we demonstrate why mechanical dysfunction accompanying parenchymal diseases such as pulmonary fibrosis and emphysema can follow a very different course from the progression of the underlying microscopic pathophysiology itself, particularly in the early stages. The key idea is related to the concept of percolation on elastic networks where the bulk modulus of the network suddenly changes when the fibrotic stiff regions or the emphysematous holes become suddenly connected across the network. We also introduce the concept of depercolation as a basis for the rational optimization of tissue repair. Specifically, we use these network models to predict the functional improvements that a hypothetical biological or tissue engineering repair could achieve. We find that rational targeted repair can have significant benefits over generic random repair. This concept may find application in the treatment of lung fibrosis, surgical, bronchoscopic, or biological lung volume reduction, or any future alveolar regeneration or tissue engineering solution to the repair of connective tissue damage of the lung.
Keywords: fibrosis, emphysema, percolation, network modeling
INTRODUCTION
The lung provides gas exchange for the body with an efficiency and tolerance that is sufficient to maintain life under extreme conditions, such as during heavy exercise or at high altitude. In disease, the functional reserves of the lung become reduced, and in advanced cases may severely limit the normal activities of life or even lead to death.
The main diseases of the lung tissue include emphysema [1] and fibrosis [2]. Following remodeling in emphysema, alveolar walls become weak [3,4] and are eventually ruptured by the cyclic mechanical stresses imposed during breathing [5]. The successive mechanical failures result in a lung that becomes progressively more compliant with time [6]. In contrast, the fibrotic lung becomes progressively stiffer due to the deposition of collagen in the tissues [7]. This reduces lung volume and increases the work of breathing [8]. Nevertheless, the derangements in lung mechanics at the organ level accompanying emphysema [9] and fibrosis [10] are not simply determined by the amount of tissue loss or remodeling. Lung parenchymal stiffness is, to a significant extent, determined by the complex interconnections of the protein, fibrils and fibers of the tissue. In other words, alterations in elasticity are emergent phenomena that arise from the way in which the lesions of disease are arranged spatially. Computer models have proven essential for investigating how such phenomena develop, both in emphysema [6,11] and fibrosis [12]. However, as far as we are aware, there has not yet been any attempt to use computer models to explore how these diseases might be treated most effectively.
Currently, there is no way to reverse either emphysema [13] or pulmonary fibrosis [14], so lung transplantation remains the only intervention that could be considered curative. Partial relief from the symptoms of emphysema can be achieved in some patients by Lung Volume Reduction Surgery (LVRS) [15], where selected regions of the lung are surgically removed. This allows the remaining portions of the lung to inflate within the thoracic cavity, restoring lung elastic recoil to some degree and reducing dyspnea [16]. Unfortunately, the benefits of LVRS are temporary and seem to disappear at a rate inversely related to the degree of initial improvement [17]. No such stop-gap measure currently exists for fibrosis.
Progress in tissue engineering and stem cell biology gives hope that cures may eventually be developed for emphysema and fibrosis, perhaps similar to the technique now being used to replace blood vessels with tissue engineered vascular grafts [18]. However, the selection of location in the treatment of blood vessels is not objective, but rather is based on the judgment of the physician. In the case of the lung, the efficacy of treatments would clearly be maximized by targeted delivery of drugs, cells, or engineered tissues to those sites that result in the greatest reversal of symptoms. The question thus arises as to where treatment should be directed, and in what quantity, to achieve reasonable improvements in lung function. Unfortunately, methods do not currently exist that can identify regions in the lung where treatment should be directed even if such treatment technology was available. Computer modeling, on the other hand, has the potential to allow us to identify and evaluate the efficacy of various treatment schemes. Appropriate modeling can perhaps even contribute to the development of novel treatments.
We have previously developed a network model of the lung to mimic the progression of the parenchymal destruction caused by emphysema and the remodeling due to fibrosis [12]. In this perspective, we will first briefly review this model and then show how it can be used in reverse to provide an in silico approach for the rational design of strategies for the targeted delivery of therapies for treating lung parenchymal disease.
MODELS OF LUNG ELASTICTY AND DISEASES
Overview of network models of the lung parenchyma
Several network-type models have been developed in the past to account for the elasticity of lung parenchyma. The first significant effort was that of Mead et al. [19] who developed a model of hexagonal elastic cells to study mechanical interdependence between airways and parenchyma. Wilson extended this approach analytically to examine the deformation of elastic tubes embedded in parenchyma [20]. Subsequently, a geometrically more realistic finite element model of the alveolar duct was developed that included surface tension [21]. A nonlinear elastic network model has also been introduced to account for heterogeneity and force transmission among alveolar walls [22]. By incorporating torsional springs to resist the folding of line element in the network model, it is possible to estimate the Young’s moduli of alveolar walls and collagen fibers [23]. Using this approach, for example, it has been shown that increasing the surface tension of the air-liquid interface in the lung may have a beneficial effect in emphysema by increasing recoil [24].
The progression of emphysema has also been modeled using network models by allowing individual network elements to fail under mechanical stress [6,11,25]. Extending this approach to large networks, we have recently shown that a sudden change in macroscopic tissue stiffness occurs when the isolated lesions become numerous enough to connect in a contiguous pathway across a large expanse of tissue [12]. This is an emergent phenomenon known to occur at the so called percolation threshold [26], and may explain why the time-course of degradation in lung function does not always mirror the progression of underlying pathology in diseases of the lung parenchyma. Below, we first review percolation thresholds in elastic networks [27] as models of parenchymal disease progression [12], and then explore how the reverse process might be exploited to study the efficacy of targeted parenchymal repair
Network models of the fibrotic and emphysematous lung
Our model of the lung parenchyma is a two-dimensional hexagonal network of ideal linearly-elastic springs with spring constants of 1 (arbitrary units) and a rectangular boundary. The individual springs represent alveolar walls. The outer borders of the network are held fixed such that each spring is prestressed to correspond to a given lung volume. At any stage, the equilibrium configuration of the network is calculated by minimizing the elastic energy (E) of the network using simulated annealing [28]. Starting from some initial configuration, the total energy of the network is calculated as the sum of all individual spring energies. Each spring junction point is then moved a small distance in the direction of the net force acting on it and E recalculated. If the change in energy (ΔE) is negative, the new configuration is accepted. However, to reduce the likelihood of the energy solution becoming trapped in a local minimum, configurations for which ΔE>0 are occasionally also accepted with a probability p = exp(−ΔE/T) where T is a control parameter. These steps are repeated until a convergence criterion is reached. As a measure of the functional properties of the model, we calculate the two-dimensional bulk modulus (B) of the network by increasing its linear dimensions biaxially by 0.001%, and then recalculating the new equilibrium configurations of all the springs. The resulting increase in stress (ΔS = increase in force per unit length and unit thickness) is then divided by the increase in linear strain to yield B. Thus, B is a measure of the overall stiffness of the network, and is the model equivalent of the inverse of lung compliance. Further details can be found in [23,29].
To simulate the collagen deposition that occurs in fibrosis, we used a network of 1171 springs and randomly stiffened a certain percentage of them by a factor of 100. To simulate emphysema we used a much larger network of 67276 springs in which, rather than cutting the springs randomly, we invoked the notion that alveolar walls experiencing high stress are more likely to break than walls under less stress [5]. We therefore began the simulation by randomly breaking 1% of the springs in the network in order to seed a random destructive process in the beginning. We then determined the new equilibrium configuration of the network and cut the next 7% springs that were under the greatest stress. This was repeated until B fell to zero.
Linking microscopic alterations to lung function via percolation
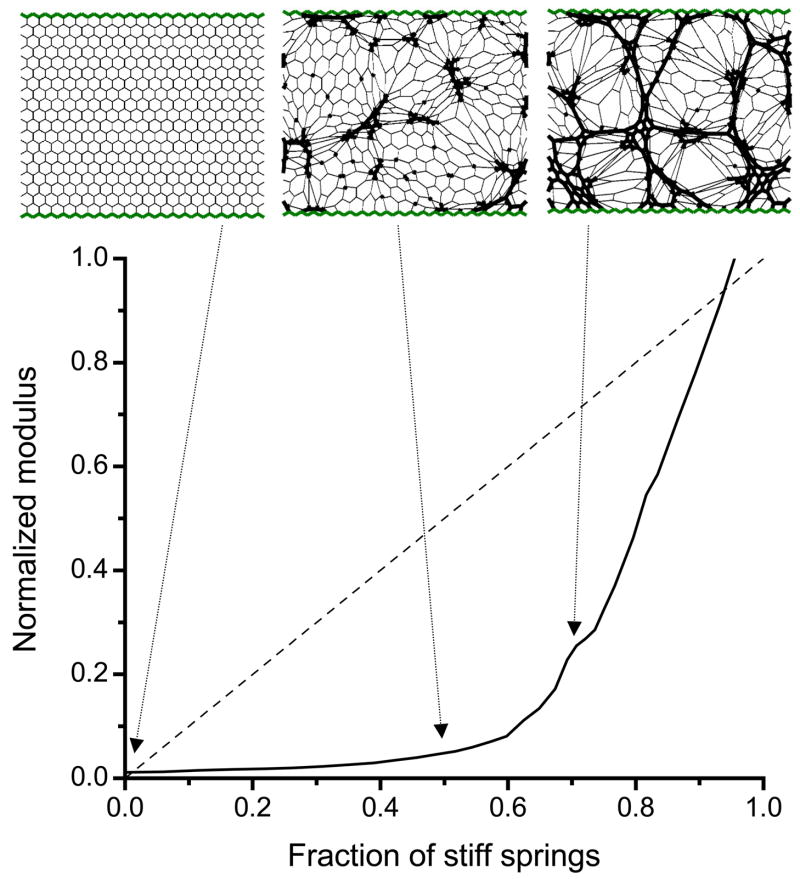
The modulus B for our network model of fibrosis versus the fraction c of randomly stiffened springs changes relatively slowly when c is below about 0.6 and much more quickly when c is above 0.6 (Fig. 1). The knee in the relationship at about the c=0.6 indicates a threshold, called the percolation threshold, at which at least one contiguous pathway of stiff springs spans the entire network. The percolation threshold separates widely differing rates of change of mechanical function. We also include in Fig. 1 a diagonal straight line corresponding to the constant rate of change in B occurring when the stiffness of each spring in the network increases progressively and simultaneously. Also shown in Fig. 1 are example network configurations at baseline (uniform spring stiffness) and when the model has two different fractions of stiff springs. When c is about 0.5, the stiff springs clump together in groups that are still separated by soft springs. At c=0.65 the stiff springs percolate, i.e. they span the network both vertically and horizontally in unbroken chains. Note how the network begins in a homogeneous configuration at c=0, and becomes increasingly heterogeneous reaching maximum heterogeneity at about c=0.65.
Figure 1.
Simulation of the progression of pulmonary fibrosis. The solid line shows the bulk modulus B of the elastic network versus the fraction of springs c randomly stiffened by a factor of 100. If all of the spring constants were uniformly stiffened in a gradual manner from the baseline value of 1 to 100, the modulus would follow the dashed diagonal line. Shown at the top are the network configurations obtained when c=0, c=0.5 and c=0.67 with thick line showing stiff springs.
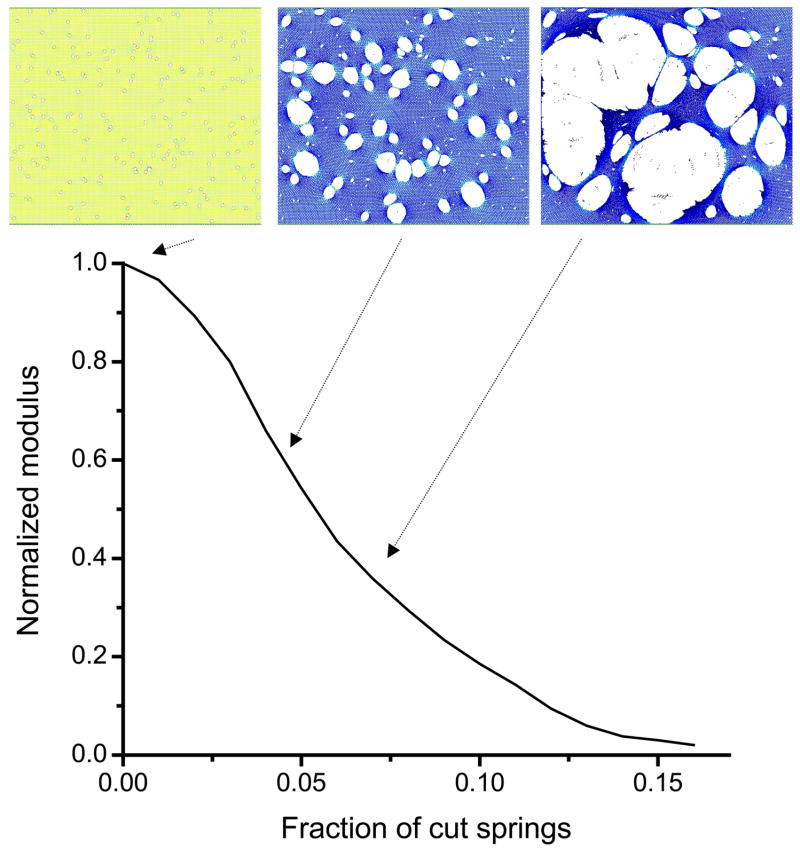
For the simulation of the progression of emphysema, the cutting of the springs was not random, but rather was targeted to those springs with the highest stress. This caused the holes in the network to be spatially correlated and made B fall toward zero much more rapidly than if all the cutting had been completely random. Figure 2 shows the progression of B with the fraction c of cut springs and demonstrates an initially accelerating rate of decline that eventually decelerates as B approaches zero when about 15% of the spring have been cut, i.e. c=0.15. The point at which B=0 represents another percolation threshold, this time corresponding to the complete loss of network elasticity. The three examples of the network shown in Fig. 2 demonstrate how an initial set of randomly located small holes progresses to a series of large holes that span the network in an almost contiguous pathway. The heterogeneity of the structure also increases as the network undergoes progressive breakdown.
Figure 2.
Simulation of the progression of emphysema. The curve shows the bulk modulus B of the elastic network (normalized to the modulus of the network when fully intact) versus the fraction of springs c cut on the basis of the amount of force they carry (see text for details). Shown at the top of the figure are the network configurations obtained at three points along this process. The forces in the individual springs are indicated by color coding, with yellow indicating high stress and decreasing stress corresponding to progressively darker shades of blue.
The network structures in Figs. 1 and 2 imply that the geographical nature of lung pathology should exert an important influence on its physiological manifestations. Nevertheless, merely ascribing mechanical dysfunction of the parenchyma to the vagaries of lesional organization is unhelpful without an understanding of how the two are linked. Our above results show that such a link can be forged through the concept of percolation [12], which has been invoked previously to account for numerous natural processes involving transmission of events across networks [26,27,30,31]. These simulations suggest that tissue undergoes a sharp change in its macroscopic mechanical properties at the percolation threshold, which may correspond to the point in the disease course when patients experience a sudden downturn in clinical symptoms. Percolation may thus explain why there is often a disconnect between the microscopic progression of parenchymal pathology and the development of symptomatic decrements in lung function [12].
MODELING LUNG PARENCHYMAL REPAIR
Percolation can thus link microscopic alterations in lung parenchymal structure to measurable clinical parameters, which in turn can have a close link to symptoms. Since percolation deals with geometric connectivity within a structure, the macroscopic properties of the lung that contribute to physiologic function, and hence quality of life, are to a large extent determined by how efficiently the fibrotic or emphysematous lesions propagate across the parenchyma. We have illustrated this for two specific patterns of disease progression – spatially random lesions in the case of fibrosis (Fig. 1), and lesions that are spatially correlated through linkage to regions of high stress in the case of emphysema (Fig. 2). But now suppose that reversing the percolation process we have just described corresponds to the repair or regeneration of damaged tissue. In the fibrotic case, this would be equivalent to replacing stiff springs with normal ones, while for emphysema it would mean the addition of missing springs. There are, of course, a large number of different sequences in which the individual springs could be repaired or replaced, not all of which will lead to the same time-course of symptomatic relief. Indeed, some sequences will lead to more rapid relief than others. For example, we might expect a much larger reversal of abnormal lung function in fibrosis if a treatment breaks up a percolating pathway of contiguous lesions into two or more isolated clusters, than if the treatment merely ablates an isolated lesion. This opens up the possibility of identifying optimal strategies for targeted delivery of therapies.
We will now use our network model to investigate approaches to targeted tissue repair. We will assume that the repair is ideal in the sense that it returns a local region of tissue to normality without adverse biological side effects. In the case of fibrosis, this means that local parenchymal stiffness can be returned from pathologically high to normal, while in the case of emphysema it means that we can either regenerate alveolar walls in situ or insert engineered parenchymal tissue into the lung at desired locations. We will assess the functional consequences of these in silico therapies in terms of their effects on B during both random and targeted repair or replacement of springs.
Repairing fibrotic lesions
Figure 3 compares random and targeted repair of a fibrotic network. We start with a concentration of stiff springs of c=0.649 and modulus B = 26.6. The initial network configuration is shown in Fig. 3A, along the bottom of which appears a percolating cluster of stiff springs. By randomly replacing 45 of the 760 stiff springs with soft springs we reduce c to 0.611. However, B is only reduced by 15% to 22.6, and there is still a percolating cluster of stiff springs across the network (Fig. 3B). Next, we target the percolating cluster and manually select stiff springs to be replaced by soft ones such that the cluster is broken down to several smaller isolated clusters. By softening only 22 of these springs to make c=0.630 (Fig. 3C), we find that B is reduced to 16. This is a 32% reduction in stiffness, which is more than twice that achieved when more than double the number of springs were softened randomly. Clearly, there is substantial therapeutic gain to be had in the elimination of percolating clusters, a process we call “depercolation”. On the other hand, the likelihood of selecting a depercolating spring at random is very small, so repair has to be targeted. Although the technology is not yet available to achieve this in practice, our modeling indicates that substantial recovery of function can be achieved even with therapies that produce minimal repair if the tissue therapies are optimally targeted.
Figure 3.
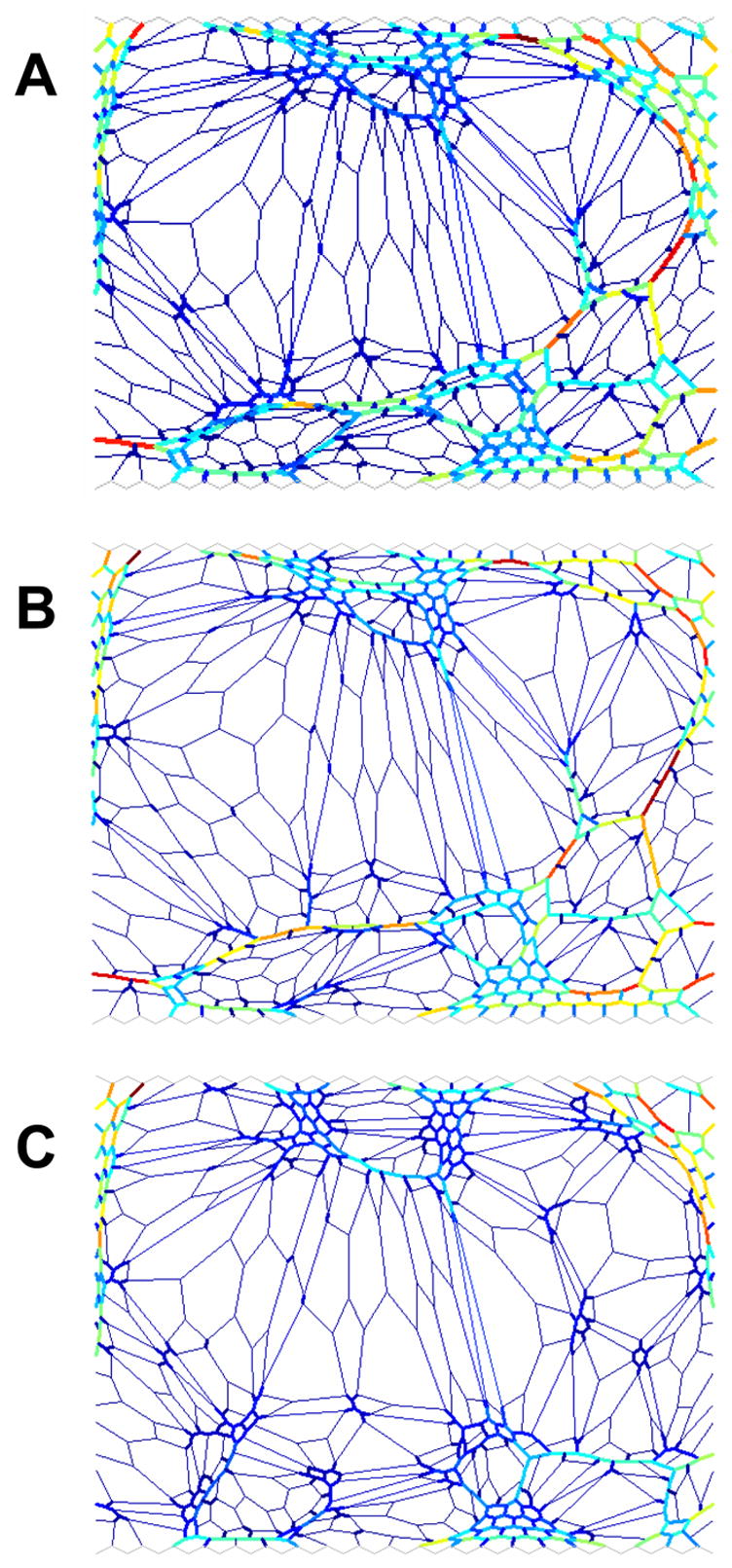
Modeling the repair of the fibrotic lung. The colors are related to the force the elements carry as in Fig. 2. The thick and thin lines denote stiff and soft springs, respectively. A) shows the initial configuration with the concentration of stiff springs c=0.649 and the bulk modulus B=26.6. B) shows the configuration of the network following random repair with c=0.611 and B=22.6. C) shows the configuration of the network following targeted repair with c=0.63 and B=16.
Repairing emphysematous lesions
The comparison of random and targeted repair of an emphysematous network is shown in Fig. 4. We begin with a network containing 312 holes of area (A)=1810±12650, c=0.034, and B=0.622. By inserting 8 springs at random locations (Fig. 4B), we increase recoil and reduce heterogeneity to obtain c=0.027, B=0.824 and A=1751±6254. Adding 3 or 4 springs at targeted cites designed to divide large holes into smaller ones gives only modest improvements of B=0.778 and B=0.802, respectively, which is still not as good as the 8 random springs. We do somewhat better with 5 targeted replacements to obtain c=0.03, B=0.851 and A=1766±4909 (Fig. 4C), but the improvement over the 8 random springs is not spectacular. The benefits of targeted compared to random repair in emphysema thus do not appear to be as great as in fibrosis. This is because a relatively large number of missing springs are associated with large holes in emphysema, so randomly replacing a spring has a reasonable chance of bridging a large hole. This reduces the advantages of targeted compared to random replacement. Of course, there are multiple ways one can bridge a large hole with a single spring, and our initial experiments suggest that the best approach may be to try and maximize both the distance that an added spring bridges and the increase it causes in local strain energy within the network. Thus, improved functionality (increased B and reduced heterogeneity) can be expected with targeted and optimized rather than random repair even when the progression of disease is spatially correlated as during the stress-induced sequential rupture of alveolar walls.
Figure 4.
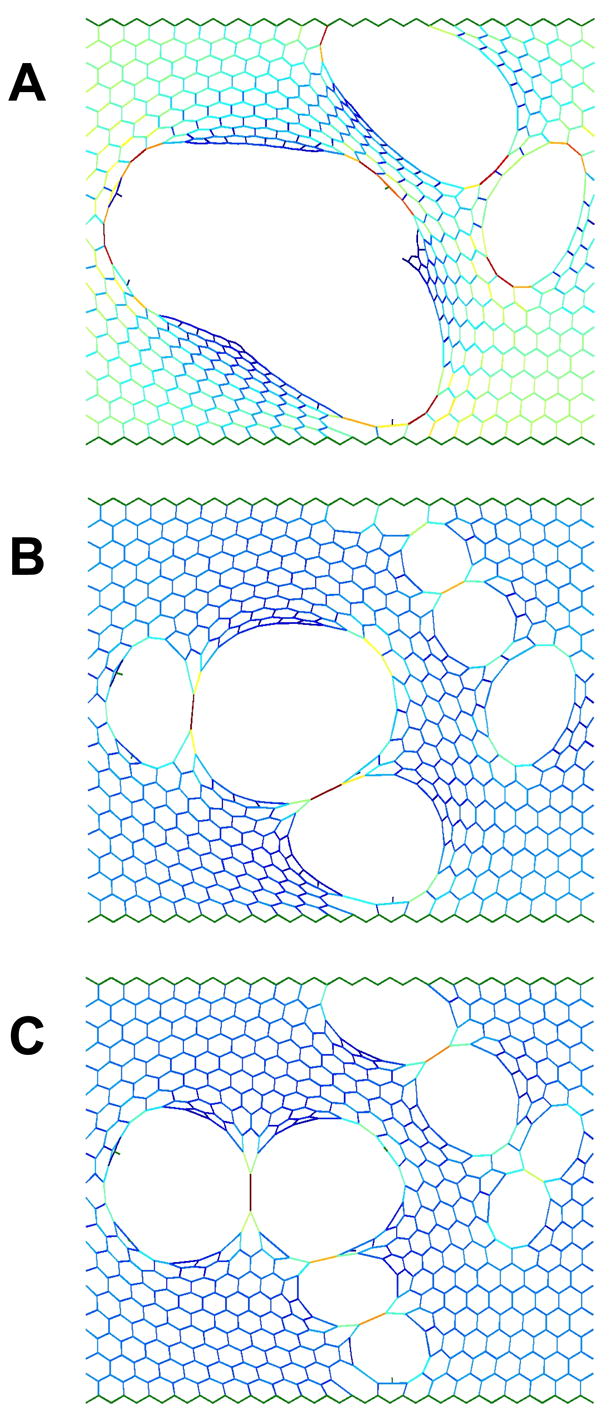
Modeling the repair of the emphysematous lung. The colors are related to the force the elements carry as in Fig. 2. A) shows the initial configuration with the concentration of missing springs c=0.034 and the bulk modulus B=0.635. B) shows the configuration of the network following random repair with c=0.027 and B=0.824. C) shows the configuration of the network following targeted repair with c=0.03 and B=0.851.
Before concluding, some general remarks should be made. First, if we assume that we can find the optimal site for repair in the sense of achieving maximum functional improvement, then failure of repair at such cites will also lead to the largest reversal of improvement in both the fibrotic and emphysematous networks. This introduces a potential fragility into the process because the consequences of repair failure will be significant. Optimal repair may thus require that robustness be considered along with location. Second, the issue of selecting a site for repair may, in the future, be guided by macro or micro imaging. For example, specific features of low attenuation areas on lung CT images may help in the optimization process [25]. In principle, it should be possible to map a CT image into an elastic network which could subsequently be used to test the effectiveness of various repair procedures without having to carry them out in a patient. Finally, we note that the characteristic of targeted repair is reminiscent of the error and attack tolerance seen in large complex networks such as the internet where the network is tolerant against random perturbations but vulnerable against targeted intervention [32].
CONCLUSION
We have reviewed an in silico network modeling approach that provides insight into the progressive nature of connective tissue diseases of the lung. In particular, we have shown that the concept of percolation provides a link between pathology at the microscopic scale and macroscopic function. Additionally, we have introduced the concept of depercolation as a basis for the rational optimization of tissue repair. This concept may find application in the treatment of lung fibrosis, surgical [16], bronchoscopic [33], or biological [34] lung volume reduction, or any future alveolar regeneration or tissue engineering solution to the repair of connective tissue damage. The concept of network model based targeted repair may also find applications in other tissues and organs where function is based on the mechanical properties of the connective tissues.
Acknowledgments
This study was supported by NIH grants HL59215, HL67273, HL75593.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Snider GL. Chronic obstructive pulmonary disease: a definition and implications of structural determinants of airflow obstruction for epidemiology. Am Rev Respir Dis. 1989;140(3 Pt 2):S3–8. doi: 10.1164/ajrccm/140.3_Pt_2.S3. [DOI] [PubMed] [Google Scholar]
- 2.Swigris JJ, et al. Idiopathic pulmonary fibrosis: challenges and opportunities for the clinician and investigator. Chest. 2005;127(1):275–283. doi: 10.1378/chest.127.1.275. [DOI] [PubMed] [Google Scholar]
- 3.Lucey EC, et al. Remodeling of alveolar walls after elastase treatment of hamsters. Results of elastin and collagen mRNA in situ hybridization. Am J Respir Crit Care Med. 1998;158(2):555–564. doi: 10.1164/ajrccm.158.2.9705021. [DOI] [PubMed] [Google Scholar]
- 4.Vlahovic G, et al. Cellular and connective tissue changes in alveolar septal walls in emphysema. Am J Respir Crit Care Med. 1999;160(6):2086–2092. doi: 10.1164/ajrccm.160.6.9706031. [DOI] [PubMed] [Google Scholar]
- 5.Kononov S, et al. Roles of mechanical forces and collagen failure in the development of elastase-induced emphysema. Am J Respir Crit Care Med. 2001;164(10 Pt 1):1920–1926. doi: 10.1164/ajrccm.164.10.2101083. [DOI] [PubMed] [Google Scholar]
- 6.Suki B, et al. On the progressive nature of emphysema: roles of proteases, inflammation, and mechanical forces. Am J Respir Crit Care Med. 2003;168(5):516–521. doi: 10.1164/rccm.200208-908PP. [DOI] [PubMed] [Google Scholar]
- 7.Ebihara T, et al. Changes in extracellular matrix and tissue viscoelasticity in bleomycin-induced lung fibrosis. Temporal aspects. Am J Respir Crit Care Med. 2000;162(4 Pt 1):1569–1576. doi: 10.1164/ajrccm.162.4.9912011. [DOI] [PubMed] [Google Scholar]
- 8.Hart N, et al. Changes in pulmonary mechanics with increasing disease severity in children and young adults with cystic fibrosis. Am J Respir Crit Care Med. 2002;166(1):61–66. doi: 10.1164/rccm.2112059. [DOI] [PubMed] [Google Scholar]
- 9.Foronjy RF, et al. Structural emphysema does not correlate with lung compliance: lessons from the mouse smoking model. Exp Lung Res. 2005;31(6):547–562. doi: 10.1080/019021490951522. [DOI] [PubMed] [Google Scholar]
- 10.Goldstein RH, et al. Failure of mechanical properties to parallel changes in lung connective tissue composition in bleomycin-induced pulmonary fibrosis in hamsters. Am Rev Respir Dis. 1979;120(1):67–73. doi: 10.1164/arrd.1979.120.1.67. [DOI] [PubMed] [Google Scholar]
- 11.Ito S, et al. Early emphysema in the tight skin and pallid mice: roles of microfibril-associated glycoproteins, collagen, and mechanical forces. Am J Respir Cell Mol Biol. 2006;34(6):688–694. doi: 10.1165/rcmb.2006-0002OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bates JHT, et al. Linking parenchymal disease progression to changes in lung mechanical function by percolation. Am J Respir Crit Care Med. 2007;176(6):617–623. doi: 10.1164/rccm.200611-1739OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Barnes PJ, Stockley RA. COPD: current therapeutic interventions and future approaches. Eur Respir J. 2005;25(6):1084–1106. doi: 10.1183/09031936.05.00139104. [DOI] [PubMed] [Google Scholar]
- 14.Raghu G, Chang J. Idiopathic pulmonary fibrosis: current trends in management. Clin Chest Med. 2004;25(4):621–636. doi: 10.1016/j.ccm.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 15.Fessler HE, Permutt S. Lung volume reduction surgery and airflow limitation. Am J Respir Crit Care Med. 1998;157(3 Pt 1):715–722. doi: 10.1164/ajrccm.157.3.9608004. [DOI] [PubMed] [Google Scholar]
- 16.Gelb AF, et al. Lung function 4 years after lung volume reduction surgery for emphysema. Chest. 1999;116(6):1608–1615. doi: 10.1378/chest.116.6.1608. [DOI] [PubMed] [Google Scholar]
- 17.Brenner M, et al. Rate of FEV1 change following lung volume reduction surgery. Chest. 1998;113(3):652–659. doi: 10.1378/chest.113.3.652. [DOI] [PubMed] [Google Scholar]
- 18.Shin’oka T, et al. Midterm clinical result of tissue-engineered vascular autografts seeded with autologous bone marrow cells. J Thorac Cardiovasc Surg. 2005;129(6):1330–1338. doi: 10.1016/j.jtcvs.2004.12.047. [DOI] [PubMed] [Google Scholar]
- 19.Mead J, et al. Stress distribution in lungs: a model of pulmonary elasticity. J Appl Physiol. 1970;28(5):596–608. doi: 10.1152/jappl.1970.28.5.596. [DOI] [PubMed] [Google Scholar]
- 20.Wilson TA. A continuum analysis of a two-dimensional mechanical model of the lung parenchyma. J Appl Physiol. 1972;33(4):472–478. doi: 10.1152/jappl.1972.33.4.472. [DOI] [PubMed] [Google Scholar]
- 21.Denny E, Schroter RC. The mechanical behavior of a mammalian lung alveolar duct model. J Biomech Eng. 1995;117(3):254–261. doi: 10.1115/1.2794178. [DOI] [PubMed] [Google Scholar]
- 22.Maksym GN, et al. Force heterogeneity in a two-dimensional network model of lung tissue elasticity. J Appl Physiol. 1998;85(4):1223–1229. doi: 10.1152/jappl.1998.85.4.1223. [DOI] [PubMed] [Google Scholar]
- 23.Cavalcante FS, et al. Mechanical Interactions between Collagen and Proteoglycans: Implications for the Stability of Lung Tissue. J Appl Physiol. 2005;98:672–679. doi: 10.1152/japplphysiol.00619.2004. [DOI] [PubMed] [Google Scholar]
- 24.Ingenito EPTL, Majumdar M, Suki B. On the Role of Surface Tension in the Pathophysiology of Emphysema. Am J Respir Crit Care Med. 2005 doi: 10.1164/rccm.200406-770PP. in press. [DOI] [PubMed] [Google Scholar]
- 25.Mishima M, et al. Complexity of terminal airspace geometry assessed by lung computed tomography in normal subjects and patients with chronic obstructive pulmonary disease. Proc Natl Acad Sci U S A. 1999;96(16):8829–8834. doi: 10.1073/pnas.96.16.8829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Stauffer D, Aharony A. Introduction to percolation theory. Taylor & Francis; 1992. [Google Scholar]
- 27.Tang W, Thorpe MF. Percolation of elastic networks under tension. Physical Review B Condensed Matter. 1988;37(10):5539–5551. doi: 10.1103/physrevb.37.5539. [DOI] [PubMed] [Google Scholar]
- 28.Kirkpatrick S, et al. Optimization by simulated annealing. Science. 1983;220:671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
- 29.Bates JH, Lauzon AM. Parenchymal Tethering, Airway Wall Stiffness, and the Dynamics of Bronchoconstriction. J Appl Physiol. 2007 doi: 10.1152/japplphysiol.00980.2006. [DOI] [PubMed] [Google Scholar]
- 30.Janssen HK, et al. Generalized epidemic process and tricritical dynamic percolation. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;70(2 Pt 2):026114. doi: 10.1103/PhysRevE.70.026114. [DOI] [PubMed] [Google Scholar]
- 31.Coniglio A, et al. Percolation and Burgers’ dynamics in a model of capillary formation. Phys Rev E Stat Nonlin Soft Matter Phys. 2004;69(5 Pt 1):051910. doi: 10.1103/PhysRevE.69.051910. [DOI] [PubMed] [Google Scholar]
- 32.Albert R, et al. Error and attack tolerance of complex networks. Nature. 2000;406(6794):378–382. doi: 10.1038/35019019. [DOI] [PubMed] [Google Scholar]
- 33.Ingenito EP, et al. Bronchoscopic volume reduction: a safe and effective alternative to surgical therapy for emphysema. Am J Respir Crit Care Med. 2001;164(2):295–301. doi: 10.1164/ajrccm.164.2.2011085. [DOI] [PubMed] [Google Scholar]
- 34.Reilly J, et al. Biological Lung Volume Reduction*A New Bronchoscopic Therapy for Advanced Emphysema. Chest. 2007;131(4):1108–1113. doi: 10.1378/chest.06-1754. [DOI] [PubMed] [Google Scholar]